Strategies for Extracting Structural Information from 2D IR Spectroscopy of Amyloid: Application to Islet Amyloid Polypeptide

Abstract

The 37-residue human islet amyloid polypeptide (hIAPP or amylin) self-assembles into fibers, the assembly of which has been associated with the disease mechanism of type II diabetes. Infrared spectroscopy in conjunction with isotope labeling is proving to be a powerful tool for studying the aggregation process of hIAPP and other amyloid forming proteins with residue specific structure and kinetic information, but the relationship between the spectroscopic observables and the structure is not fully established. We report a detailed analysis of the linear and 2D IR spectra of hIAPP fibers isotope labeled at seven different residue positions. The features of the 2D IR spectra, including the frequencies, linewidths, intensities, and polarization dependence of the diagonal and cross-peaks, rely heavily on the position of the isotope labeled residue. In order to understand how these measured parameters depend on fiber secondary and tertiary structure, we have simulated 1D and 2D IR spectra utilizing idealized structural models in addition to a recently published solid-state NMR based model of the amyloid fibril. The analysis provides a more rigorous foundation for interpreting the infrared spectra of amyloids. In addition, we demonstrate that 2D IR spectra can be employed to distinguish between residues in β-sheets versus those in turn regions, and that transitional residues between secondary structures can be identified by the suppression of their cross-peaks in 2D IR spectra. This latter approach is not limited to amyloid fibrils and will be generally useful in identifying regions of secondary structure in proteins using 2D IR spectroscopy and isotope labeling.

1. Introduction

The mechanism by which proteins aggregate into amyloid fibers is one of the most actively investigated problems in biophysics. Amyloid aggregation is probed using a variety of experimental approaches including solid-state NMR spectroscopy,^1,2 X-ray diffraction,^3,4 electron spin resonance spectroscopy,^5,6 electron microscopy,^4,7 circular dichroism,⁸ and fluorescence spectroscopies.^9,10 One approach that holds much promise in elucidating the structural details of the aggregation process is infrared spectroscopy. Infrared spectroscopy has the advantages that it can be straightforwardly applied to aggregated^11–14 or membrane bound systems,^15,16 has distinct spectral features for β-sheets, α-helices, and other secondary structures,^17,18 and has a time resolution of only a few picoseconds when used in conjunction with a femtosecond laser. Thus, it is well-suited to obtaining both structural and kinetic information on amyloid aggregation.

However, infrared spectroscopy is often underutilized, because the structural information being obtained from most infrared studies on amyloids is not residue-specific. The resolution of IR spectroscopy is generally only adequate for assessing the overall secondary structural content of amyloid fibers, which is useful for monitoring global structural kinetics, for example, but does not provide residue specific structural information. Indeed, this is a general problem in the field, and the lack of a nonperturbing method which can provide residue specific information in kinetic and static studies is a major problem. The information content of such infrared experiments is very similar to circular dichroism spectroscopy. However, infrared spectroscopy has the potential to resolve the secondary structure and environments of individual residues when used in conjunction with isotope labeling. By isotope labeling the backbone carbonyl groups with ¹³C, the amide I band is shifted by 40 cm^–1 and thus resolved from the rest of the peptide or protein. ¹³C=¹⁸O isotope labeling resolves individual residues in even larger systems, since the 54 cm^–1 shift places the mode of interest in a transparent region of the infrared spectrum between the amide I and II bands. Isotope labeling in conjunction with vibrational spectroscopy has been extensively employed in looking at α-helices^19,20 and β-hairpins.^21,22 So far, only a few studies have used isotope edited IR spectroscopy to study amyloids.¹³ These include studies on fragments of amyloidogenic peptides^14,23–26 and the Aβ amyloid peptide involved in Alzheimer's disease.^24,27 Several studies have also been conducted in which the infrared spectra of amyloid fibers were simulated.^25,28,29 While few in number, together, these studies have established that the vibrational coupling in amyloid fibers is quite strong and can be utilized to study their structures and kinetics. In this study, we use ¹³C=¹⁸O isotope labeling to study the human islet amyloid polypeptide (hIAPP), which is involved in type 2 diabetes.

The accuracy with which structural information can be extracted from isotope edited IR spectroscopy depends on a detailed understanding of how protein vibrational modes are dictated by the fiber structure. The primary aim of this paper is to better understand this relationship between structure and spectroscopy. hIAPP is a good amyloidogenic peptide with which to test this relationship because it can be synthesized, and thus straightforwardly isotope labeled, and a structural model for hIAPP was recently generated from solid-state NMR data (ssNMR).¹ Thus, experimental infrared spectra can be interpreted on the basis of known structural features and empirical relations drawn, or spectra can be quantatively simulated using vibrational couplings calculated from the structure itself. In this paper, we use both approaches. We have measured the 1D and 2D IR spectra of hIAPP labeled with ¹³C=¹⁸O at seven different residues. We find empirically that the frequency, lineshapes, and cross-peak intensities of the labeled residues as well as the unlabeled residues depend upon which residue is labeled. We then probe the origin of these empirical trends by simulations using canonical β-sheet structures as well as the solid-state NMR structure. Comparison of the experiments and simulations points to several strategies for probing amyloid and protein structures with isotope labeling and 2D IR spectroscopy.

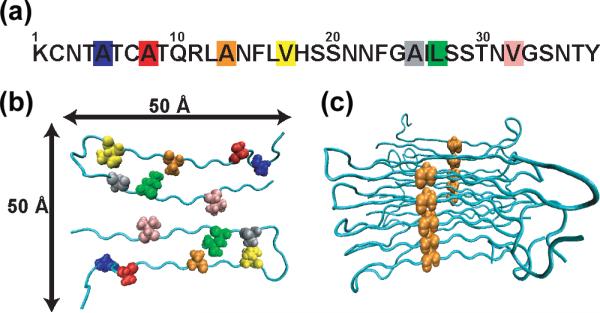
The NMR structural model is shown in Figure 1.¹ In the fully formed fibrils, the model predicts that each of the 37-residue polypeptides is involved in two parallel β-sheets running along the length of the fibers, which is the common motif in amyloid systems.^2,30 Residues 8–17 form one β-sheet and residues 28–37 form the other. The first seven residues are not involved in β-sheet formation, primarily because they are constrained by a disulfide bond between residues 2 and 7. Two columns of peptides twist around each other to form a total of four parallel β-sheets. The fiber structure is considered a “model” rather than a rigorous “structure”, because the number of NMR constraints is insufficient to unambiguously characterize the fold. In the experiments reported here, we synthesize peptides with one residue isotope labeled at a time. Since the fibers are composed of two columns of stacked peptides, each labeled residue forms a column, which is illustrated in Figure 1 for Ala-13. We seek to understand how the vibrational modes of hIAPP depend on the position of the isotope label and whether that information can be used to extract the labeled residue's secondary structure and position within the fiber structure. For example, we want to be able to determine whether a labeled residue lies in a β-sheet or the turn region based on the diagonal and cross-peaks in the 2D IR spectra. If in a β-sheet, we want to know whether it is in the middle or on the edge. In principle, it should be possible to extract information of this kind by analyzing the amide I bands arising from the labeled as well as the unlabeled residues. The amide I bands of the labeled residues provide the coupling strengths between the labeled residues, and thus information on their secondary structure and relative arrangements. Labeling also alters the unlabeled amide I band by disrupting its vibrational modes, and thus provides information on the position of the labels in the global fold. Cross-peaks between the labeled and unlabeled residues identify the regions in which the labeled residues lie. Taken together, we find that the diagonal and cross-peaks in 2D IR spectroscopy of isotope labeled peptides provide residue-specific insight into the secondary structure of amyloid fibers.

Figure 1.

hIAPP fiber model dervied from the ssNMR data. (a) The sequence of hIAPP with seven isotope labeled residues highlighted: Ala-5 (blue), Ala-8 (red), Ala-13 (orange), Val-17 (yellow), Ala-25 (silver), Leu-27 (green), and Val-32 (pink). (b) Cross section of a fiber demonstrating that the fibers are composed of two columns of random coil/β-sheet/turn/β-sheet structure. (c) Protofiber as viewed from the side with single labeled residue (Ala-13) exhibiting the formation of two isotopically labeled columns.

In what follows, we report the linear and 2D IR spectra of mature hIAPP fibers isotope labeled at seven different residues. We find that the 2D IR spectrum depends strongly on which residue is isotope labeled. We have measured the frequencies, linewidths, and intensities of the diagonal and cross-peaks in our spectra, as well as their intensity dependence on the polarization of the pulse sequence. To understand how these measured parameters depend on the secondary and tertiary structure of the fibers, we have simulated 1D and 2D IR spectra using idealized structural models as well as the NMR structural model. From a comparison of simulations to experiment, we correlate the vibrational modes to β-sheet stacking, turn stacking, β-sheet twist character, and cross-β coupling. Besides providing a more rigorous foundation for interpreting the infrared spectra of amyloids, we reach five specific conclusions regarding the information content that can be obtained with isotope editing of amyloid fibers, which are tabulated in the Conclusions section. One key result is that 2D IR spectra can be employed to distinguish between residues in β-sheets versus those in the turn region by monitoring the frequency shifts of the isotope labels as well as the remaining unlabeled amide I band. Another important conclusion is that the transitional residues between secondary structures can be identified by their suppression of cross-peaks in the 2D IR spectra. We believe that these effects will be generally useful in identifying the secondary folds of amyloids as well as other proteins using IR spectroscopy and isotope labeling.

2. Materials and Methods

Sample Preparation

Samples were prepared on the basis of previously reported protocols.^11,12,31,32 hIAPP labeled with ¹³C=¹⁸O isotopes was synthesized in the Raleigh lab as previously reported. These samples were dissolved in deuterated hexafluoro-isopropanol (d-hfip) to generate an ~0.8 mM stock solution. An aliquot of the stock solution was removed, and the d-hfip solvent was evaporated under a steady flow of N₂ to create a peptide film. This film was then dissolved in 6 μL of 20 mM deuterated potassium phosphate buffer, yielding a peptide solution with a pH of 7 and a concentration of ~1 mM. The peptide solution was placed between two CaF₂ windows separated by a 75 μm thick Teflon spacer. The sample was then monitored with FTIR spectroscopy until the amide I spectral features remained static. Samples were generally allowed to incubate for a day, which was sufficient for complete aggregation. Transmission electron microscopy was used to verify a shared morphology among the fiber samples, as has been reported previously by our group.^11,13

Linear and Two-Dimensional IR Spectroscopy

FTIR spectra were taken using a Thermo-Electron Nicolet iS10 spectrometer. Spectra were collected at room temperature (22 °C) and yielded optical densities (OD) between 0.3 and 0.5. Large ODs have been shown to yield artificially broad linewidths in 2D-IR, especially along the ω_pump axis. However, studies conducted on n-methylacetamide³³ found that, in going from an OD of 0.2 to an OD of 0.45, the linewidths along the ω_probe and ω_pump axes are within error of one another. This indicates that the discrepancies in OD for our samples should have little bearing on our linewidths.

Two-dimensional infrared spectra were collected using a pump–probe beam geometry whereby the pulse train is generated electronically rather than mechanically using a mid-IR pulse shaper,³⁴ as has been described previously.^35,36 Briefly, a difference frequency generation based optical parametric amplifier was used to generate ultrafast mid-IR pulses with wavelengths centered at 6.1 μm (1640 cm^–1). A portion of each pulse was dispersed into the frequency domain using a 150 g/mm ruled grating. The frequency dispersed pulse was amplitude and phase modulated using a sinusoidal amplitude mask before being recombined at a second grating. By varying the period of the sine wave, we create two pump pulses, k₁ and k₂, with a variable time delay. We scanned over 2560 fs of the first waiting time in 24 fs steps to generate our spectra. Roughly 10% of the pulse was split off before the Ge AOM and used as a probe pulse, k₃. The collinear k₁ and k₂ pulses interact with the k₃ pulse at the sample, at which point a third-order electric field is emitted in the same direction as the k₃ beam, which also serves as a local oscillator. The third-order field and k₃ beam are combined using spectral interferometry after being dispersed through a monochromator. Four π-phase shifted pump pulses were used to improve the signal-to-noise by removing the transient absorption background. Additionally, phase cycling was employed to reduce noise from scatter. Spectra were taken using polarization geometries in which the two pump pulses (k₁ and k₂) had polarizations oriented parallel and perpendicular to the probe (k₃) pulse. The polarization dependence of cross-peak intensities allows for the calculation of projection angles among those features giving rise to a given cross-peak.^37–39 Details about the method for collecting 2D IR spectra using pulse shaping have recently been compiled in a review paper. ³⁶ 2D IR spectra are normalized to the β-sheet fundamental intensity because the peptide concentrations are difficult to determine precisely. Thus, intensities of the diagonal and cross-peaks are reported as ratios.

Simulations

Simulations of 1D and 2D IR spectra were performed for several β-sheet and fiber structures. Idealized secondary structures were studied to approximate the dominant features of hIAPP fibers. Idealized β-sheets were generated by creating polypeptide strands with Ramachandran angles of ϕ = –118° and ψ = 113°. Idealized turns were generated using the dihedral angles from the ssNMR structure, as discussed below. To convert these structures into infrared spectra, an excitonic Hamiltonian was used

$$H=\sum _i{E}_i{A}_i^{+}{A}_i+\sum _{i,j}{B}_{ij}{A}_i^{+}{A}_j-\frac{\Delta }{2}\sum _i{\left(A_i^{+}\right)}^2{\left(A_i\right)}^2$$ (1)

where A_i⁺ and A_i are raising and lowering operators, E_i is the energy of mode i, and Δ (=14 cm^–1) is the diagonal anharmonicity. Coupling constants, B_ij, between residues not covalently bound to one another were calculated using transition dipole coupling. We used a transition dipole strength of 3.144 D with its origin lying 0.868 Å from the carbonyl carbon and oriented at an angle of 20° relative to the C=O bond.⁴⁰ For B_ij of adjacent, covalently bound residues, a coupling map, which provides the coupling B_ij (in cm^–1) as a function of ϕ (deg) and ψ (deg), derived from ab initio calculations, was employed.⁴¹ Unlabeled residues exhibiting β-sheet structure are assigned E_i = 1644 cm^–1. In order to account for decreased hydrogen bonding among backbone carbonyls in the turn region, unlabeled turn residues are assigned E_i = 1654 cm^–1. Given that ¹³C=¹⁸O isotope labeling creates a 54 cm^–1 shift in the amide I local mode frequency, we use E_i = 1590 cm^–1 for isotope labeled residues. Coupling among amide I modes gives rise to the excitonic states that can extend over large regions of the structure. Frequencies in the FTIR and 2D IR spectra are arrived at by calculating the eigenvalues of eq 1. The eigenvectors of eq 1 are used to generate linear combinations of ${\overrightarrow{\mu }}_i$. The eigenvalue frequencies and their corresponding intensities were used to generate stick spectra, which were then convoluted with either a 1D or 2D line shape generated using response functions in the Bloch limit with homogeneous and inhomogeneous linewidths of 11 cm^–1. Details of the protocol have been reported previously for other systems.^37,42

3. Results

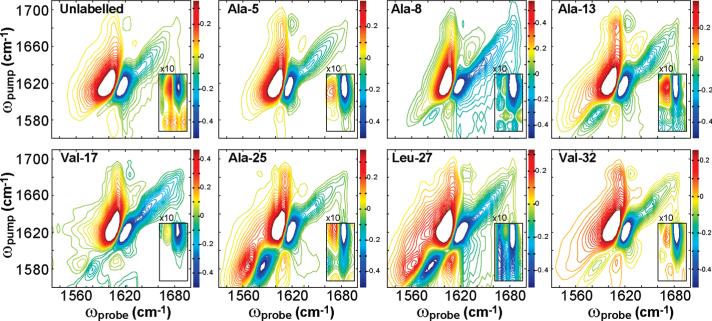
We collected FTIR and 2D IR spectra in the amide I region for mature hIAPP fibers isotope labeled with ¹³C=¹⁸O at seven different residues–Ala-5, Ala-8, Ala-13, Val-17, Ala-25, Leu-27, and Val-32–as well as an unlabeled sample. These eight residues span nearly the entire length of the peptide, and their positions in the final fiber structure are shown in Figure 1. 2D IR spectra were generated using both parallel and perpendicular beam geometries. In what follows, we begin by describing the global features common to all of the samples using peptides labeled at Ala-13 as a representative example. We then present simulations of 1D and 2D IR spectra using several structural models in order to predict the infrared signatures for specific structural features. Finally, the predictions are tested against the experimental spectra to establish meaningful correlations.

3.1. Experimental 2D IR Spectra of Isotope Labeled hIAPP

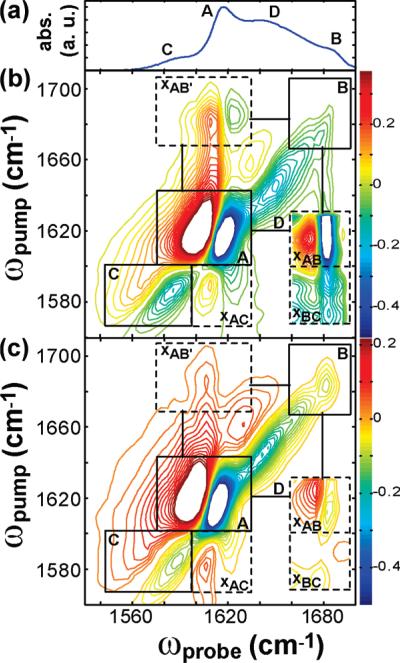
The 2D IR spectra of the seven isotopically labeled peptides are plotted in Figures 2 and 3 as well as in Figure S1 of the Supporting Information. The global features of these spectra are similar, although the frequencies, linewidths, and intensities of the diagonal and off-diagonal peaks differ. The major features we analyze below are labeled in Figure 2 for Ala-13, which we use as a representative example. Each spectrum is dominated by a pair of peaks (box A) appearing on the diagonal between 1615 and 1620 cm^–1. These features have been studied extensively and are ascribed to the antisymmetric stretching mode along the parallel β-sheet axis. The symmetric stretch mode also contributes to this frequency range, and the two modes are not resolved in parallel β-sheets like those found in many amyloid fibers.⁴³ In box A, a doublet arises because the fundamental as well as the sequence band of the low frequency β-sheet mode are probed. Vibrational modes usually give rise to doublets in 2D IR spectra, which is why pairs of out-of-phase peaks appear along the diagonal (and in the off-diagonal cross-peaks). Another, weaker doublet appears near 1685 cm^-1 (box B) which we attribute to the residues in the turn region based on long-standing empirical assignments⁴⁴ and the fact that the fibers are composed of parallel β-sheets. Also present is a doublet along the diagonal near 1585 cm^–1 (box C). This feature is the amide I band of the isotope labeled residue. Between the high and low frequency features is a third doublet with a broad width along the diagonal (box D). This doublet is created by residues adopting a random coil structural distribution.

Figure 2.

FTIR (a) and parallel (b) and perpendicular (c) 2D IR spectra of hIAPP isotopically labeled at Ala-13. Solid boxes designate features due to β-sheet (box A), turn (box B), isotope label (box C), and random coil (box D). Dashed boxes indicate cross-peaks due to coupling between the turn and β-sheet (box x_AB and x_AB′), the label and β-sheet (box x_AC), and the label and turn (box x_BC). Contours are evenly spaced from 50% of the minimum to 50% of the maximum, with zero contours removed to reduce noise.

Figure 3.

Perpendicular 2D IR spectra for the seven isotopically labeled residues. Spectra are normalized to the β-sheet fundamental intensity. The x_AB cross-peak is magnified 10 times. Contours are evenly spaced from 50% of the minimum to 50% of the maximum, with zero contours removed to reduce noise.

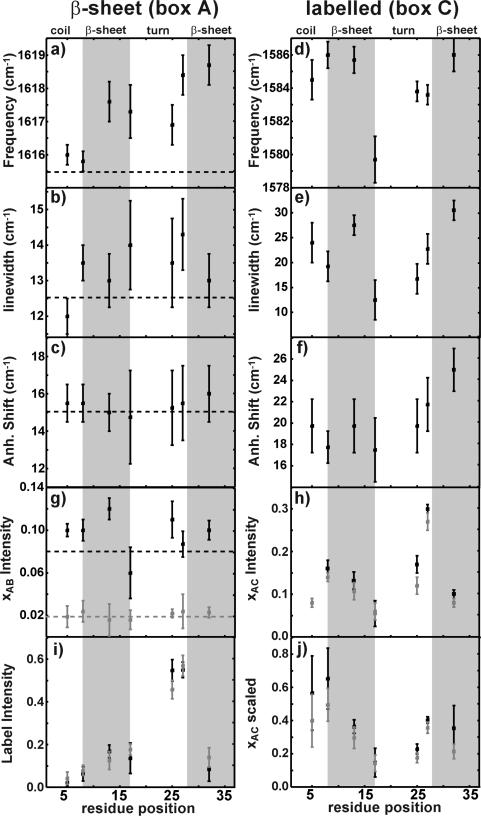
Frequencies, on-diagonal linewidths, and anharmonic shifts were extracted for the β-sheet (box A) and for the isotope labeled (box C) features, which are plotted in Figure 4a–c. Error bars were empirically derived to account for systematic errors in the fits used to generate the data in Figure 4. For the unlabeled amide I band, the frequency of the low frequency β-sheet fundamental mode (box A) increases from 1615.5 to 1618.0 cm^-1 between Ala-5 and Val-32 but not monotonically (Figure 4a). The diagonal widths of the low frequency β-sheet mode fundamental are around 13 cm^–1 for all of the samples (Figure 4b). Finally, the anharmonic shift of the low frequency β-sheet mode doublet, which is the frequency separation between the fundamental and sequence band peaks, is about 15 cm^–1 (Figure 4c). Since these eight samples do not differ in their fibril structure but only in the presence or location of the isotope labels, differences in these quantities are due to the isotope labels that disrupt the normal mode vibrations of the unlabeled residues. One of the goals of this study is to understand how this information can be interpreted with regard to the fibril structure.

Figure 4.

Parameters extracted from the 2D IR spectra. The frequencies, inhomogeneous linewidths, and anharmonicities are plotted for the unlabeled β-sheet feature (a–c) and the isotope labeled feature (d–f). The normalized x_AB and x_AC cross-peak intensities are plotted in parts g and h for both perpendicular (black) and parallel (gray) spectra. Label intensities and the x_AC cross-peak scaled to the geometric mean of its parent features are plotted in parts h and i. Gray boxes designate regions of β-sheet structure as determined by ssNMR.

For the labeled features (box C), the three quantities discussed above are graphed in Figure 4d–f. The frequencies of the labeled features fall within 1584.0 and 1586.0 cm^–1, except in the case of Val-17, which appears below (1579.7 cm^–1) this range (Figure 4d). The diagonal linewidths of the labeled features are narrowest for Val-17 and largest for Ala-5, Ala-13, and Val-32 (Figure 4e). The anharmonic shifts observed for labeled features fall within error of one another (Figure 4f), and are generally larger than those of the unlabeled low frequency β-sheet mode. Similarly, the linewidths of the isotope labeled peaks are all larger than the unlabeled amide I band. Excitonic coupling typically decreases linewidths and anharmonic shifts, indicating that excitonic coupling among the unlabeled residues is more extensive than for the labeled residues.⁴⁵ Heterogeneous structural environments can alter the frequencies and linewidths of the isotopically labeled bands. These environmental factors can be accounted for experimentally by conducting isotope dilution experiments, as we have done here and in previous work.¹³

By examining the frequency differences between the labeled feature in an isotopically pure sample and one in which two-thirds of the monomers are unlabeled, we can extract values for the coupling constants. This was done for monomers labeled at Ala-8, Ala-13, Ala-25, Leu-27, and Val-32, yielding frequency shifts of 4, 9.3, 6.2, 3.4, and 3 cm^–1, respectively (data in Table S1 of the Supporting Information). We also plot, in Figure 4i, the labeled amide I band intensity. We find that Ala-25 and Leu-27 labeled sites have the most intense peaks relative to the unlabeled low frequency β-sheet feature and that this ratio generally decreases toward the ends of the peptide.

We also analyzed the intensities of the cross-peaks in the 2D IR spectra for all seven labeled peptides. The most intense cross-peaks in the unlabeled region of the spectra appear due to coupling between the turn at 1685 cm^–1 and the low frequency β-sheet mode at 1615.7 cm^–1 (boxes A and B). These are highlighted by solid rectangles in Figure 2 (box x_AB) for Ala-13. A second set of cross-peaks, which we also assign to coupling between the high frequency turn and low frequency β-sheet modes, appears in the upper left-hand portion of the spectrum (box x_AB′). There are also cross-peaks between the labeled mode and the low frequency β-sheet mode (box x_AC) as well as between the label and the turn region (box x_BC). For each sample, 2D IR spectra were collected with the polarizations of the pump and probe beams equal as well as perpendicular, which we refer to as parallel and perpendicular polarizations, respectively. The changes in peak intensities between parallel and perpendicularly polarized spectra highlight the anisotropy of the cross-peaks. Diagonal peaks decrease in intensity by ⅓ from parallel to perpendicular polarizations, as do cross-peaks arising from transition dipoles oriented parallel to one another.³⁹ The intensities from nonparallel transition dipoles decrease less (and in some pulse sequences change phase as well).⁴⁶ For example, it is readily apparent in Figure 2 that for Ala-13 the x_AB cross-peaks are more intense in the perpendicular beam geometry; there is a 5-fold increase in the cross-peak intensity relative to the diagonal features in going from the parallel to the perpendicular beam geometry. Thus, the transition dipoles of the low frequency β-sheet and turn modes are not parallel. The polarization dependence of the x_AB′ cross-peaks is not as pronounced as x_AB because of overlap with the broad β-sheet and random coil sequence band features (peaks in boxes A and D). Cross-peaks that overlap with diagonal features always exhibit weaker polarization dependence because the diagonal peaks are created from each laser pulse interacting with the same transition dipole and thus are perfectly parallel (omitting energy transfer and other processes). Diagonal features A and C completely obscure the x_AC′ cross-peaks expected to be observed on the upper half of the 2D IR spectra, and thus are not labeled in the figures.

For each of the samples, the intensities of the x_AB, x_AC, and x_BC cross-peaks were measured. In Figure 4g, the x_AB cross-peak intensities are plotted for the parallel (solid) and perpendicular (dashed) spectra taken from all seven samples (slices through the 2D IR spectra used to obtained the x_AB intensities are shown in Figure S2 of the Supporting Information). Ala-25 exhibits slightly more intense β-sheet/turn cross-peaks than its neighbors to the left and right, respectively. Ratios of the perpendicular to parallel cross-peak intensity lie in between 1.3 and 1.5 for the x_AB peaks of the Ala-5, Ala-8, Ala-13, Val-17, and Val-32 samples, yielding projection angles of 63–70°. The cross-peak intensity ratios for Ala-25 and Leu-27 lie slightly outside of this range and yield projection angles of 78 and 55°. The intensity of the x_AC cross-peak is plotted in Figure 4h (2D IR slices are plotted in Figure S3 of the Supporting Information). Leu-27 exhibits the largest x_AC intensity followed by Ala-8, Ala-13, and Ala-25, which exhibit normalized intensities of ~0.15. The projection angles of the labeled exciton relative to the β-sheet exciton are 0° for all of the labeled samples excluding Ala-25, Leu-27, and Val-32, which exhibit projection angles of 30, 27, and 10°, respectively. The x_BC cross-peaks are not plotted in Figure 4, as some of them are too weak to be meaningful, despite the fact that many are prominent in the slices shown in Figure S3 of the Supporting Information. Due to differences among the intensities of the labeled features, in Figure 4j, the x_AC cross-peaks scaled by the geometric means of their parent feature intensities are plotted. These scaled cross-peak intensities are weakest for Val-17 and Ala-25 and increase in moving outward toward the ends of the peptide.

3.2. Simulations of hIAPP Infrared Spectra

Having presented the experimental data, we now turn to simulations that were performed to predict how isotope labeling alters the IR spectra and better understand how to extract structural information from these spectra. In what follows, we present simulated 1D and 2D IR spectra calculated using (1) the solid-state NMR structure and (2) idealized structural models of β-sheets and turns. Spectra were simulated from these structures using a coupling map for covalently bonded residues and transition dipole coupling (TDC) for the rest, as described in Materials and Methods. Coupling constants computed in this manner are quite reliable, although more sophisticated coupling models and methods for simulating infrared spectra exist, including methods that account for spectral diffusion and structural dynamics.^47–49 However, the purpose of this paper is not to exactly reproduce or fit the infrared spectra but rather to provide a guide for the interpretation of amyloid infrared spectra, and for the design of strategies for using isotope labeling to probe secondary structures of proteins.

3.2.1. Simulations and Assignment of Unlabeled Features

We begin by presenting simulations of parallel β-sheet and amyloid structures that lack isotope labels. These simulations were carried out to assign and characterize the vibrational modes of the unlabeled portions of the experimental spectra. We investigate (1) the origin of peaks in the linear spectrum of the ssNMR structure, (2) how the frequencies of the β-sheet vibrational modes depend upon its size, (3) what features in the infrared spectra come from the turn region, (4) the origin of the cross-peaks between the turn and the low frequency β-sheet mode, and (5) the effects of rotation and (6) stacking of β-sheets on the IR spectra. These simulations provide a basis for which to interpret how the unlabeled features change upon isotope substitution.

Spectral Features of the ssNMR Structure

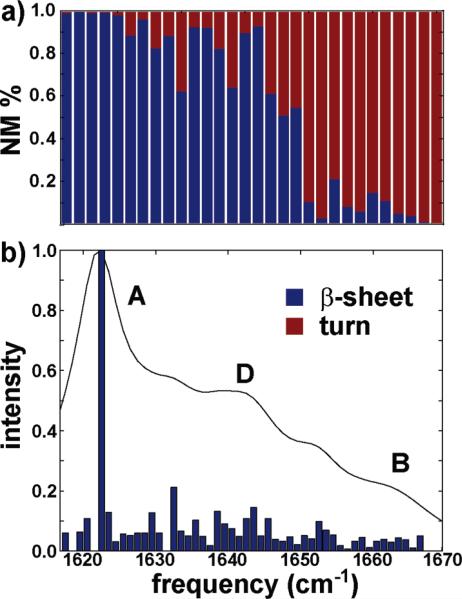
The ssNMR model proposed by Tycko and co-workers¹ assigns a random coil structure to the first seven residues of the amylin peptide, followed by a 10-residue β-sheet connected to a second 10-residue β-sheet by a 10-residue turn region. The model (Figure 1) consists of two sets of five peptides arranged so as to generate an extended fiber structure. In this section, we assign the features in a simulated linear infrared spectrum of the most rigid portion of the fiber (residues 8–37) for one five-peptide stack to either turn or β-sheet secondary structure based on residue participation in a given normal mode. The normal mode decomposition is plotted in the upper panel of Figure 5 and attributes the low frequency peak at 1622 cm^–1 to residues in the β-sheet (8–17 and 28–37) and the high frequency peak at 1665 cm^–1 to residues in the turn region (18–27). These assignments are similar to those previously reported for simulations of Aβ₄₂.²⁸ The frequencies of the β-sheet and turn modes can be attributed to negative and positive coupling among vertically stacked residues, respectively, and will be further addressed in subsequent sections. Residues lying within the β-sheet regions exhibit canonical dihedral angles of –150° ≤ ϕ ≤ –110° and 110° ≤ ψ ≤ 150°, which yield adjacent coupling constants of 3 cm^–1 ≤ B ≤ 6 cm^–1. These through bond coupling constants will be important in assessing the effects of isotope labeling on the infrared spectra.

Figure 5.

FTIR simulation of the truncated (8–37) ssNMR model. The percent contributions of β-sheet (8–17 and 28–37) and turn (18–27) residues to the underlying spectral features are presented in part a. The simulated FTIR plotted with the normal mode stick spectrum is featured in part b.

Spectral Features of the β-sheet Region

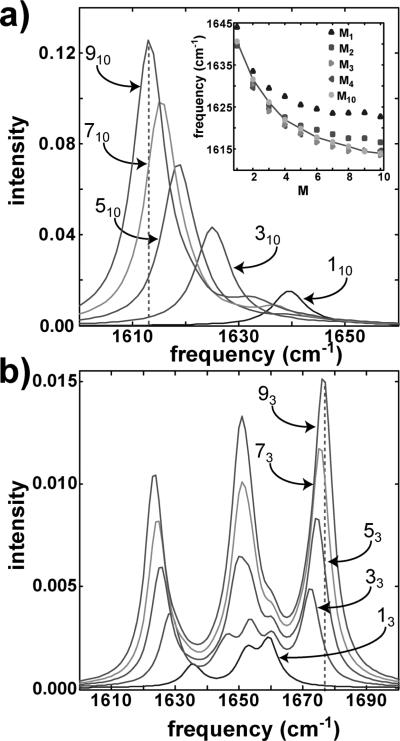
The basic structural motif of hIAPP fibers are parallel β-sheets running along the length of the fibers and separated by a turn region. In this section, we focus on the vibrational modes of the parallel β-sheets. The amide I infrared signatures of parallel β-sheets have been well-studied using both theoretical and experimental approaches,^{14,42,43,50,51} and our results are similar. We simulated 1D spectra for an idealized parallel β-sheet structure with the canonical dihedral angles, ϕ = –118° and ψ = 113°, that ranged in size from 1 to 10 strands (M) and from 1 to 10 residues (r), which we denote M_r. The centers of mass for each strand are separated by 4.5 Å in the direction of the β-sheet axis. Shown in Figure 6a are the linear spectra for those idealized β-sheet structures for M₁₀ with M = 1, 3, 5, 7, and 9. β-sheets with M > 1 are dominated by a feature that is created by the coupling (B = –8.8 cm^–1) between vertically stacked residues. As the number of strands within the β-sheet increases, this β-sheet feature shifts monotonically to the red, converging at E = 1614 cm^–1, which is plotted in the inset of Figure 6a. In addition to the M₁₀ frequencies, the values of the low-frequency β-sheet mode for r = 1, 2, 3, and 4 are plotted in the inset of Figure 6a. It is evident that an increase in r, especially at low r values, leads to a red-shift of the low frequency β-sheet mode. The degree of this shift varies depending on the through bond coupling magnitude, and increases in going from B = 3 to B = 6 cm^–1 (the values predicted by the ab initio coupling map). As both the M and r values dictate the value of the low frequency β-sheet mode, the β-sheet frequency alone cannot uniquely identify the size of the β-sheet. Moreover, the frequency becomes insensitive to size for β-sheets of about 50 residues without regard to the number or length of the strands. However, the integrated peak intensity scales linearly with the number of oscillators in the β-sheet, regardless of the β-sheet length and width. Thus, growth of the fibers, which can reach hundreds of nanometers in length and contain thousands of strands, is better monitored using the amide I intensity, which depends linearly on the number of strands in the approximation of excitonic coupling.

Figure 6.

(a) Simulated FTIR spectra for M_r = 1₁₀, 3₁₀, 5₁₀, 7₁₀, and 9₁₀. The inset demonstrates how the β-sheet frequency varies for small r values. (b) Simulated FTIR spectra for an idealized turn region in which the number of stacked strands was varied.

Spectral Features of the Turn Region

To simulate the turn region, an idealized turn segment consisting of three amino acids was generated using the dihedral angles between residues 20 and 23 from the ssNMR structure and then replicated by 4.5 Å separations to form the bend in the fiber (in the same manner as used to generate the idealized β-sheet above). The final structure is shown in Figure 7a, and computed FTIR spectra are shown in Figure 6b. For a single peptide, the eigenstates from the turn spanned about 25 cm^–1. As additional strands were added to form the turn of a fiber, the eigenstates spread to cover more than 50 cm^–1. The reason that the eigenstates spread is because the turn contains both negative and positive vertical coupling constants between the strands; the coupling constants for the vertical stacking of residue 1 is B = –6.5 cm^–1, 2 is B = 4.9 cm^–1,and 3 is B = 3.1 cm^–1. The negative couplings lead to low frequency features and the positive couplings to high frequency features as linear chains of excitons are formed between the strands, as is discussed below in section 3.2.2. The degree to which the spectra spread depends sensitively upon the coupling parameters, but it should also be diminished by the amount of disorder in the structures. Since these model simulations do not include structural disorder, which is presumably large in the turn region, they probably predict too wide a frequency range of the turn. Indeed, the ssNMR structural model consists of five peptides stacked into a fiber, and the turn region of each peptide is different. We only present the simulations of one peptide. Simulations of the other peptides also predict a broadening of the spectrum, although the degree of broadening differs, since each structure has different coupling signs and strengths.

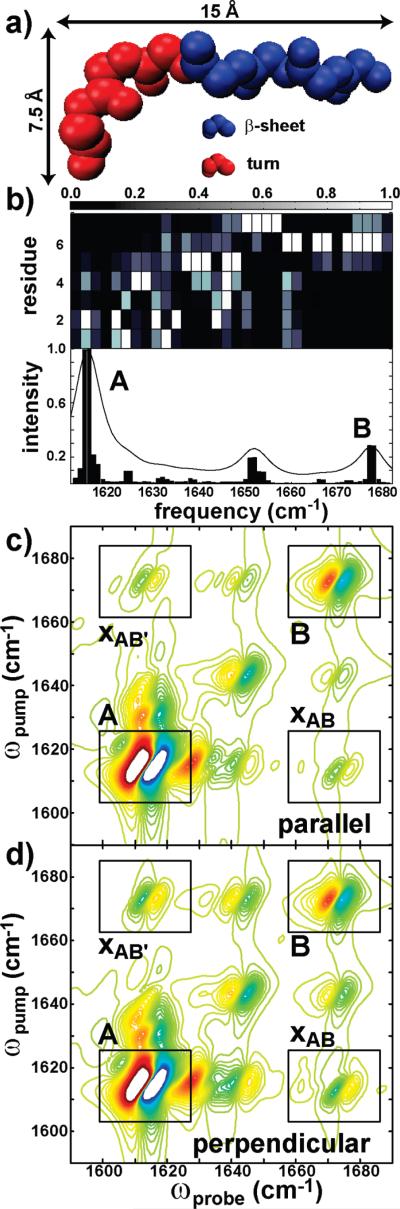
Figure 7.

(a) Structure of the idealized turn/β-sheet structure. Residues in the turn are labeled in red, and those in the β-sheet are labeled in blue. (b) Simulated FTIR spectrum for the idealized turn/β-sheet structure. The top panel shows the contribution of each residue to the corresponding spectral features in a 2.7 cm^–1 window. The bottom panel includes normalized FTIR and stick spectra for the turn/β-sheet structure. Simulated parallel (a) and perpendicular (b) 2D IR spectra for the structure in part a are plotted with boxes designating features due to the β-sheet (box A), turn (box B), and turn/β-sheet cross-peak (boxes x_AB and x_AB′).

Cross-Peaks between the β-sheet and Turn

In order to understand the coupling between the normal modes of the β-sheet and turn, we combined the β-sheet and turn motifs described above into a single structure, shown in Figure 7a for one of the eight stacked strands used in the simulations. This structural model was subsequently used to generate linear and 2D IR spectra. A linear spectrum for this structure is illustrated in Figure 7b. An underlying stick spectrum designates the frequencies and intensities of each of the normal modes that give rise to the simulated spectrum. The top panel of Figure 7b indicates to what degree the normal modes that give rise to the features in a 2.7 cm^–1 window are localized on any given residue in the turn/β-sheet structure. The eigenstates that lead to the dominant feature at 1615 cm^–1 (box A) in the simulated linear spectrum are predominantly localized on the β-sheet residues. Those eigenstates corresponding to the higher frequency features at 1641 and 1650 cm^–1 (box B) are predominantly localized on residues in the turn region of the structure. These features also appear in the simulated parallel (Figure 7c) and perpendicular (Figure 7d) 2D IR spectra (boxes A and B), as well as cross-peaks between them (boxes x_AB). The cross-peak intensity is 2.1 times larger in the perpendicular spectrum than in the parallel spectrum, because the most intense β-sheet and turn vibrational modes are separated by a 52° angle in the seven-residue, eight-strand turn/β-sheet structure. This angle increases to 61° as additional strands are added because the transition dipoles of the turn rotate relative to the fiber axis. The rotation makes the cross-peak ratio even larger. Thus, the polarization dependence of the x_AB and x_AB′ cross-peaks is caused by transition dipoles in the turn structure that orient nearly perpendicular to the fiber axis.

In the experimental spectra, we have assigned the feature at 1685 cm^–1 (peak B in Figure 2) to amide I vibrational modes at the turn, even though the simulations predict that the turn appears at 1677.5 cm^–1. Our assignment is based on longstanding empirical evidence for the frequency range of turn confirmations, as well as agreement with the polarization dependence of the cross-peaks described above and the effects of isotope labeling described below. We do not expect the simulations to accurately predict the absolute frequencies of modes associated with the turn, because our model Hamiltonian neglects differences in diagonal frequencies caused by hydrogen bonding and environmental electrostatics. As a result, the diagonal frequencies of amide I groups involved in β-sheets are the same as the amide I groups in the turn, even though the turn residues are not as strongly hydrogen bonded and thus should have higher diagonal frequencies. This effect can be accounted for quantitatively with new electrostatic mapping methods and molecular dynamics simulations,^47,52 but for the purpose of this study, our simulations are sufficient to gain an intuitive understanding of the amide I vibrational modes of amyloids.

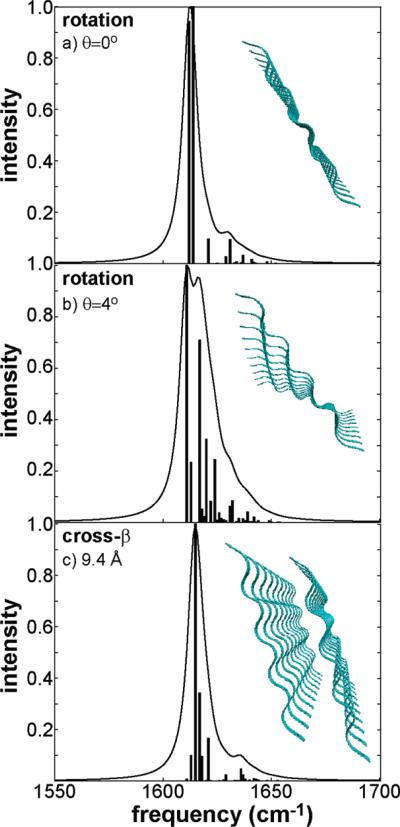
The Effects of β-sheet Rotation

Amyloid fibers are typically twisted in a super helical fashion along their axes. To study the effects of this twist on the IR spectra, we used the ideal 10-residue, 10-strand (10₁₀) β-sheet structures and rotated each strand according to twist in the ssNMR structure. We note that we use twist to refer to the relative twist of the fibril, not to the twist of an individual β-strand. Twist is commonly used in the protein structure literature to refer to the twist along a single β-strand within a sheet, but we are referring to the over all twist of the fibril. The ϕ/ψ angles were held constant and the strands rotated around a point ~6 Å removed from the center of mass of each strand and lying on a vector perpendicular to the β-sheet plane. Simulated spectra are shown in Figure 8a,b for an untwisted β-sheet and one twisted by θ = 4° between strands. We find that rotation broadens the β-sheet feature by 8 cm^–1 and shifts it 2 cm^–1 to higher frequencies. This effect is observed because the rotation increases the distance between strands and thus decreases their coupling constants. Furthermore, a three-dimensional structure is generated. Three-dimensional structures typically have more IR allowed transitions than 2D structures due to their decreased symmetry.

Figure 8.

Simulated FTIR spectra for a 10₁₀ β-sheet demonstrating no rotation about the β-sheet axis (a), 4° rotation about the β-sheet axis (b), and broadening due to cross-β coupling (c).

The Effects of β-sheet Stacking

The infrared signatures of stacked β-sheets, a structural motif common to amyloid fibers, were also investigated. We calculated linear spectra for two 10₁₀ parallel β-sheets over a range of distances separating the β-sheet pairs. A computed IR spectrum is shown in Figure 8c for a β-sheet pair separated by 9 Å. At separations of 9–12 Å, distances that span the range expected in nature, the largest couplings between residues in opposite β-sheets are between 0.5 and 0.6 cm^–1. These intersheet couplings perturb the eigenstate distributions of the individual β-sheets (compare parts a and c of Figure 8), but the differences are not large compared to the natural linewidth of the amide I band, and thus will be difficult to observe. These simulations do not include solvent contributions to the local mode frequencies, which should reflect the dehydration that must accompany fiber formation. The consequences of such dehydration will be a blue-shift of the diagonal frequencies. Thus, due to weak coupling, we expect the effects of stacking to have little bearing on the infrared spectra, unless stacking of β-sheets is accompanied by dehydration.

3.2.2. Simulations of Isotope Labeled Features and Their Cross-Peaks

Having simulated the general features of the unlabeled regions of the spectra, we now turn to simulations of the isotope labeled features and the cross-peaks between the unlabeled and isotope labeled features.

Linear Chain Excitons

As described in the Introduction, isotope labeling a single carbonyl creates a column of chromophores running along the length of the fibril. To a good approximation, the vibrational modes of this linear chain of isotope labels are independent of the unlabeled residues, as isotope substitution with ¹³C=¹⁸O shifts the fundamental frequency by about 54 cm^–1 from the random coil. A 54 cm^–1 shift places the natural frequency of the local carbonyl oscillators (e.g., the diagonal frequency) at about 1590 cm^–1, with some variation caused by differences in hydrogen bonding and environmental electrostatics, to create an ~30 cm^–1 gap between the isotope labeled modes and the low frequency β-sheet mode. Since the low frequency β-sheet mode comprises the lowest frequency eigenstates in the manifold of the unlabeled residues, the frequency separation to all of the other unlabeled modes is even larger. Thus, since a 30 cm^–1 frequency gap will not create more than a 2 cm^–1 shift in the isotope label frequency (assuming a coupling of 10 cm^–1), to a first approximation, it should be possible to model the isotope labeled features without considering coupling to the unlabeled modes. Therefore, we apply a linear chain excitonic Hamiltonian to describe the vibrational modes of the columns. A linear chain of coupled oscillators only has one infrared allowed mode,⁵³ which appears at

$$E=E_i+2B$$ (2)

where E_i is the fundamental frequency of the degenerate isotope labels and B is the coupling constant between stacked residues vibrating in phase. Thus, the observed isotope label frequency can be used to ascertain the coupling constant. Most of the residues labeled in this article should reside in β-sheet regions of the fiber, which will have negative coupling constants and hence features at <1590 cm^–1. For residues in the turn region, we may expect some residues to have positive coupling constants (see section 3.2.1) and thus their eigenstates will appear at >1590 cm^–1. E_i may also differ between residues. The equation above applies to an infinitely long linear chain. Shorter chains have ends which break the symmetry and cause eigenstates other than the lowest one to have observable infrared transitions. However, simulations using β-sheets derived from the amyloid fiber structure confirm that eq 2 applies for chain lengths longer than six residues, in which case the additional modes lie within 4 cm^–1 of the symmetry allowed mode, and thus will be mostly obscured by the homogeneous linewidth of the low frequency mode. The comparison between the simulations and experiments that follows indicates that the linear chain approximation is qualitatively correct for hIAPP, as discussed below. This approximation will not be as accurate for peptides labeled solely with ¹³C, for which there is only a 10 cm^–1 gap between the unlabeled and isotope labeled manifolds.

Effects of Isotope Labeling on the Cross-Peaks

The analysis in the section above neglects the coupling between the labeled and unlabeled amide I groups. However, the experimental 2D IR spectra exhibit cross-peaks between these two regions. Thus, while the effects of the couplings are small on the frequencies of the diagonal features, they are still measurable through the off-diagonal cross-peaks. This section is devoted to interpreting the frequencies, intensities, and polarization dependence of the cross-peaks between the labeled and unlabeled features. Toward this end, 2D IR spectra were simulated for the ideal β-sheet and turn/β-sheet structures described earlier in section 3.2.1.

Figure 9 illustrates how isotope labeling affects the x_AC cross-peaks in an ideal β-sheet with nine residues and seven strands. 2D IR spectra are shown for a perpendicular beam polarization with the first amino acid labeled (Figure 9a) and the fifth (Figure 9b), which lies in the middle of the β-sheet. The cross-peak intensity is 7 times larger when the β-sheet is isotope labeled at the middle than on the edge (see slices through the 2D IR spectra in Figure 9a,c). The cross-peak intensity is plotted in Figure 9c for labels at positions 1–5. A cross-peak is present at all positions but has the largest intensity in the middle third of the β-sheet.

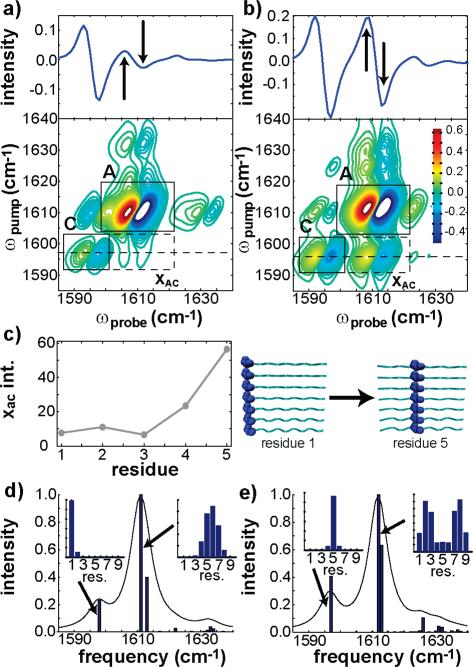
Figure 9.

(a) Simulated perpendicular 2D IR spectrum for a 7₉ β-sheet labeled at residue 1. The top panel is a slice through the labeled feature along the ω_probe axis. (b) Simulated perpendicular 2D IR spectrum for a7₉ β-sheet labeled at residue 5. The top panel is a slice through the labeled feature along the ω_probe axis. The x_ac cross-peak intensity is plotted as a function of residue position in part c along with illustrations depicting the residue positions for parts a and b. In parts d and e, the simulated FTIR spectra are plotted with their corresponding normal mode spectra for 7₉ β-sheets labeled at positions 1 and 5, respectively. Residue contributions to the labeled and most intense normal mode are plotted in the insets.

The reason that the x_AC cross-peaks are largest for isotope labels that appear in the middle of the β-sheet is due to the following. The strongest IR allowed mode for parallel β-sheets is the antisymmetric stretch mode, in which residues in the middle of the strands have a larger contribution. For instance, in a parallel β-sheet with seven strands and nine residues in each strand (M_r = 7₉), residues 4, 5, and 6 contribute the most oscillator strength to the IR-allowed antisymmetric stretch. When residue 1 is isotope labeled, the β-sheet composed of the unlabeled residues reduces to M_r = 7₈ and now residues 5 and 6 contribute the most oscillator strength to the unlabeled β-sheet antisymmetric stretch, as shown in Figure 9d. Thus, the transition dipoles of the labeled and unlabeled β-sheet eigenstates are spatially separated by four to five residues, and thus not strongly coupled. However, if residue 5 is isotope labeled instead, then two M_r = 7₄ β-sheets are created with residues 2 and 3 contributing the most oscillator strength to one of the unlabeled β-sheets and residues 7 and 8 to the other (Figure 9e). Thus, the coupling between the labeled and unlabeled modes should be much larger, because they are now only spatially separated by one or two residues. For larger β-sheets, like M_r = 6₁₂, the cross-peak intensities maximize for isotope labels within four residues of the edge of a strand, not the middle residues, because a small unlabeled β-sheet needs to be created to enhance the coupling. However, since most β-sheets in nature are made up of β-strands which are less than 10 residues, the general rule holds that the largest cross-peaks appear for isotope labeling near the middle of the strand. Therefore, we conclude that the intensity of the x_AC cross-peaks can be used to gauge if β-sheet isotope labels lie near the middle of the strands. Although not studied here, we expect similar predictions in isotope labeled α-helices.

Figure 10 illustrates how isotope labeling affects the x_AB cross-peaks in a structure that includes both a β-sheet and turn. The structure is shown in Figure 6 where the first four residues are β-sheet and residues 5–7 are turn. Representative 2D spectra are shown in Figure 10a,b for structures labeled at residues 2 and 5. The x_AB cross-peak is the cross-peak between the β-sheet and the turn residues, and it is apparent from these three spectra that the cross-peak intensity depends strongly on the position of the isotope label. In Figure 10c, the intensity of these cross-peaks is plotted for isotope labeling at each of the seven residues in the structure. In these simulations, the x_AB cross-peaks are present unless the label resides near the interface between the β-sheet and turn. At these positions, the x_AB cross-peak intensity decreases by a factor of 5–20, as compared to the cross-peak intensity when the labels reside many residues away from the interface.

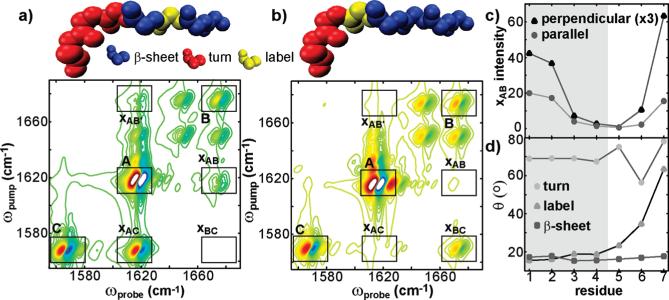
Figure 10.

Structures and simulated perpendicular 2D IR spectra for idealized turn/β-sheet structures labeled at positions 3 (a) and 5 (b). Solid boxes designate features corresponding to the β-sheet region (box A), turn (box B), and label (box C), while dashed boxes designate cross-peaks that arise due to coupling between these features (boxes x_AB, x_AB′, x_AC, and x_BC). The intensity of the turn/β-sheet cross-peak (box x_AB) is plotted as a function of residue position (c). The projection angles of the label, turn, and β-sheet relative to the fiber axis are also plotted as a function of residue position (d).

There are two reasons that isotope labeling suppresses the cross-peak in the interface region. First, the strongest coupling between the β-sheet and turn regions is created from covalently bonded residues (5–10 cm^–1). Thus, when either residues 4 or 5 are isotope labeled, the β-sheet and turn vibrations become largely independent of one another and the cross-peaks weaken. Second, if the normal modes of either the β-sheet or the turn change intensity or frequency, then the x_AB cross-peaks will weaken or shift frequencies. For instance, when residues 2 or 3 are isotope labeled, the x_AB cross-peaks diminish because the β-sheet that is still coupled to the turn is only one or two residues wide, and thus has a higher fundamental frequency that causes the cross-peaks to appear over a much wider frequency range. Likewise, isotope labeling residue six dramatically alters the turn normal modes. Thus, the relative intensities of the x_AB cross-peaks can be used to probe the transition region between the β-sheet and turn by locating the residues for which they are suppressed. This approach, of suppressing the cross-peaks of unlabeled features in 2D IR spectra, should be generally applicable to locating regions of secondary structure in proteins.

Polarization anisotropy serves as a further means for distinguishing between labels that reside within the β-sheet versus those in the turn regions. The angles of the label, β-sheet, and turn normal mode are plotted in Figure 10d relative to the fiber axis. For β-sheet residues, the transition dipoles of neither the turn nor the β-sheet are altered by more than 2.5°. As a result, the x_AB cross-peaks in the simulated 2D IR spectra are always about 2 times larger in the perpendicular than the parallel spectra. However, when the isotope labels reside in the turn region, the transition dipoles of the turn are altered so that they lie between 56 and 78° which gives rise to x_AB cross-peaks that are 4 times more intense in the perpendicular spectra. The structural variation of the turn region does not guarantee that this trend will be true for all turn structures, but we conclude that perpendicular spectra with x_AB cross-peaks 4 times larger than in parallel polarized spectra is strong evidence that the labeled residues reside in a turn or disordered region of the structure.

Isotope Labeling Effects on the Unlabeled Diagonal Peaks

Isotope labeling a column of residues alters the unlabeled amide I features in the 2D IR spectra by disrupting their Hamiltonian. It is clear from the experimental spectra that the extent of disruption depends on the location of the isotope labels in the fiber. Thus, it should be possible to not only use the cross-peaks but also the shift in the unlabeled amide I frequency as a structural marker. In order to study this effect, we simulated linear IR spectra for a series of extended β-sheets. As examples, we plot in Figure 11a the unlabeled β-sheet frequency for M_r with M = 6, 8, and 10 strands and r = 10 residues per strand, in which each residue was subsequently labeled. We find that when the amino acids within two residues of the ends are labeled, the β-sheet frequency is altered <1cm^–1. However, when the isotope label falls near the third or fourth residue from either end, then the frequency shifts 3–4 cm^–1 to around 1615–1616 cm^–1. The magnitude of the shift is smaller for β-sheets comprised of longer strands and β-sheets with more strands. The reason for the frequency changes is because the isotope labels section the β-sheet into two smaller sheets. For instance, isotope labeling the third residue in a β-sheet of M_r = M₆ residues creates a two- and three-residue β-sheet M_r = M₂ and M₃. Thus, to a good approximation, the resulting IR spectrum is a superposition of two smaller β-sheets. Small β-sheets yield higher frequency peaks than larger β-sheets, which was discussed in section 3.2.1 and illustrated in Figure 6. Since the frequency range of the low frequency β-sheet mode is typically smaller than the amide I linewidth, the two β-sheet modes will not usually be resolved. Instead, the final spectrum will appear to broaden and shift to higher frequencies. For β-sheets composed of 10 strands or more, simulations of sheets with r ≥ 4 all have the same antisymmetric stretch frequency to within 1 cm^–1. Thus, a frequency shift is only observed if one of the two superimposed β-sheets is comprised of strands of one to three residues in length. However, there is a second consideration as well, which is the peak intensities of the two β-sheets. If one β-sheet has many more oscillators than the other, its spectrum will dominate. Therefore, the reason that isotope labeling has a smaller effect on larger sheets is because when a large β-sheet is sectioned to create a one- to three-residue β-sheet, the other β-sheet section will still be large and thus will dominate the measured spectrum. (In principle, if the β-sheets had 20 or more strands, then isotope labeling would have no effect, because no matter what the size of the two β-sheet sections, they would each have the asymptotic frequency of 1615 cm^–1. In practice, however, the excitons are probably not localized over more than 5–10 strands, due to the structural disorder of the system.) In summary, we conclude that when isotope labeling causes an appreciable shift in the low frequency β-sheet mode, two structural properties can be deduced. First, that the isotope label appears within three to four residues of the edge and, second, that two β-sheets of roughly equal number of oscillators are being created. Thus, together, the frequency shift of the unlabeled β-sheet mode and the x_AC cross-peaks (above) provide two criteria for gauging the position of isotope labels in β-sheets.

Figure 11.

Frequencies of the β-sheet feature are plotted as a function of residue position for 6₁₀, 8₁₀, and 10₁₀ β-sheets (a). Frequencies of the turn feature are plotted as a function of residue position for idealized turn/β-sheet structures containing 6, 8, and 10 strands (b).The corresponding structures and the extreme residue positions are included above each plot.

The effects of isotope labeling on the spectral signatures of the turn were also studied. In Figure 11b, the frequency of the most intense normal mode (peak B) is plotted as a function of residue position, using the turn/β-sheet structure from this section, which is shown again in Figure 11b. We find that the degree to which a labeled residue alters the frequency of this mode correlates directly with the degree to which the labeled residue participates in its normal mode vibration. For example, the coefficients of each residue for the mode considered here are shown in the inset. For this mode, residue 6 has the largest contribution. Thus, when residue 6 is isotope labeled, the largest shift in frequency is observed. Although the frequency shift cannot be used to judge a priori the location of a single residue within a turn, the relative contributions of each residue to the turn vibrational modes can be estimated, and a series of isotope labels could be used to bracket the residues that compose the turn. Furthermore, frequency shifts should agree with the polarization anistropy of the x_AB cross-peaks discussed earlier in this section.

4. Comparison of Simulations to Experiment

Our principal aim is to better interpret the linear and 2D IR spectra of isotope labeled amyloid fibers with regard to their secondary structure. Having presented the experimental spectra and simulations above, we now turn to a comparison between the two.

4.1. Frequency of the Unlabeled β-sheet Feature

As predicted by simulations, we find that the frequency of the low frequency β-sheet mode (box A in Figure 2) in the experimental 2D IR spectra depends on which residue in hIAPP is isotope labeled. The measured frequencies of the diagonal peak are plotted in Figure 4a. On the basis of our simulations of ideal parallel β-sheets (section 3.2.1 and Figure 11), we conclude that (1) isotopic substitution should only alter the low frequency mode for residues directly involved in a β-sheet and (2) for residues that are involved in the β-sheets, isotopic substitution should cause the largest red-shift of the frequency when the labeled residues reside within a few (three to four) residues from the edge of a β-sheet. Thus, Ala-5 and Ala-8 are not involved in β-sheet formation, since isotope labeling these two residues causes negligible frequency shifts (<0.5 cm^–1), whereas residues Leu-27 and Val-32 lie within a few residues of the edge of a well-formed β-sheet, since isotope labeling these residues creates 2.5 cm^–1 frequency shifts that are comparable to those predicted in the simulations. The other three residues studied here also alter the β-sheet frequency by about 1.5 cm^–1. Frequency shifts in this range most likely indicate that the residues lie within one or two residues from the edge of a β-sheet or that the β-sheet is very disordered. Disordered structures will decrease the delocalization of the vibrational wave functions that this analysis rests on, and decrease the apparent frequency shifts caused by isotope labeling.

4.2. Frequency of the Labeled Feature

Our simulations predict that in-register labeled residues within the fiber exhibit linear chain excitonic behavior and therefore produce an IR mode at E = E_i + 2B. The features of the seven residues that we have labeled appear between 1580 and 1586 cm^–1 (see section 3.1 and Figure 3) and have fundamental frequencies around E_i = 1590 cm^–1. Thus, they all have negative coupling constants between –1.5 and –5.0 cm^–1 and the magnitude of the coupling constant increases as the labeled residue's location moves toward the middle of the peptide. Negative coupling is consistent with residues residing in β-sheets, but since both positive and negative coupling were observed among stacked residues in the turn region for our simulations, it is difficult to make definitive structural assignments based on labeled feature positions alone. However, it is worth noting that Ala-8, Ala-13, and Val-32, all residues expected to exhibit definitive β-sheet character according to the ssNMR structure, yield nearly identical frequencies (1586, 1585.7, and 1586 cm^–1, respectively) and corresponding coupling constants of –2, –4, and –1.5 cm^–1. In addition to the observed shifts in frequency, shifts in the inhomogeneous linewidth values of the labeled features further indicate the presence of a heterogeneous structural environment for these fibers. In order to best assess the solvent effects on labeled residue lineshapes, experiments are currently underway in which the lineshapes extracted from isotope diluted samples will be compared to the results of molecular dynamics simulations.

4.3. Cross-Peaks between the Unlabeled Turn and β-sheet Features

According to the simulations, the x_AB cross-peaks between the turn and β-sheet features should help to reveal which residues separate these two structural features. Simulations presented in section 3.2.2 and Figure 10 found that the intensity of the x_AB cross-peak becomes 40 times weaker for isotopic substitution of residues located in a region of the peptide that constitutes the border of these two secondary structures, as compared to unlabeled peptides or residues directly involved in β-sheet structure. From the experiments (Figure 4g), we find that Ala-5, Ala-8, Ala-13, Ala-25, and Val-32 do little to diminish the intensities of the x_AB cross-peaks. Thus, these five residues are not the cause of the coupling between the β-sheets and the turn and do not link the two secondary structures. Labeling at residue Val-17 partially diminishes the x_AB cross-peak intensity by a factor of 2. Labeling at Leu-27 diminishes the x_AB cross-peak intensity by a factor of 1.2 relative to Ala-25 and Val-32 and yields the second weakest x_AB intensity of those residues included in our investigation. Thus, our interpretation of the 2D IR data is that these two residues contain both β-sheet and “turn” character. In practice, we do not expect to observe a factor of 40, because hIAPP has three transitional regions in the fiber structure and a considerably larger turn region than was simulated. Moreover, residues other than the seven studied here may lie at more precise locations. Nonetheless, our interpretation of the 2D IR data is that these two residues contribute to the normal modes of the β-sheet and turn, and thus lie in regions of transitional secondary structure. Comparing the disruption of the x_AB intensity to an unlabeled standard is difficult, as we are normalizing to an unlabeled β-sheet fundamental that includes contributions from 36 residues in the case of our labeled samples and 37 residues in the case of the unlabeled sample and is not diminished by excitonic disruption due to the presence of labels. Our interpretation of the data is complicated by the sensitivity of the x_AB cross-peak to sample heterogeneity and shifts in the frequency of the probe beam. Our simulations could, therefore, be further verified by employing multiple, sequential isotope labels in regions of transitional secondary structure.

4.4. Cross-Peaks between the Labeled and β-sheet Features

The most intense set of cross-peaks are x_AC, which arise due to coupling between the low-frequency β-sheet feature and the labeled peak (Figure 2). Simulations presented in section 3.2.2 and Figure 9 suggest that a labeled residue's position within the parallel β-sheet can be deduced on the basis of the intensity of this feature. The experimental spectra also exhibit strong variations in the cross-peak intensity (Figure 4i in section 3.1). Leu-27 exhibits a cross-peak intensity that is twice as large as that of Ala-8, Ala-13, and Ala-25, which, in turn, exhibit x_AC intensities that are twice as large as those of the remaining labeled fibers. These values suggest that Leu-27 is most deeply entrenched in a β-sheet region of the fiber and that Ala-8, Ala-13, and Ala-25 lie in regions closer to the edge of a β-sheet region; however, this interpretation is complicated by the dependence of the cross-peak intensities on the off-diagonal anharmonicities and the geometric mean of their parent feature intensities. Hence, given the intensity of the Ala-25 and Leu-27 labeled features relative to their corresponding x_AC cross-peaks, we expect that the β-sheet character of the Ala-25 and Leu-27 residues is considerably less than what is indicated by the normalized cross-peak intensity, although Leu-27 retains more β-sheet character than does Ala-25. Normalizing to the geometric mean of the parent features suggests that β-sheet character increases in going from the center of the peptide to the N- and C-termini. The natural isotope abundances of ¹³C and ¹⁸O are 1.07 and 0.205, respectively. These natural abundances lead to randomly positioned, isotopically labeled backbone carbonyls that comprise ~1% of the total number of carbonyls. This seemingly small portion is relevant in relation to the percentage of deliberately isotope labeled residues present in the sample (2.7%). Randomly positioned isotope labels containing only ¹³C or only ¹⁸O and residing in β-sheet regions will couple more strongly to the β-sheet by a factor of 2–3 according to our simulations (not shown) given their reduced frequency shift and may contribute to the cross-peak intensities of labeled features that are minimally shifted from the low frequency β-sheet feature.

4.5. Comparison with NMR Structure

According to the simulations, the experimental data suggests that Val-32, Leu-27, and Ala-13, which create 3.2, 2.9, and 2.1 cm^–1 shifts to the unlabeled β-sheet features, are most deeply entrenched in the β-sheet structures, whereas Ala-5 and Ala-8, which negligibly alter the unlabeled feature, are less involved in β-sheet formation. Val-17 induces a slightly smaller shift (1.8 cm^–1) than does Ala-13 but is still large enough to be consistent with it residing in a β-sheet structure. Finally, Ala-25, which the ssNMR structure predicts to reside in the turn region, exhibits a shift of 1.4 cm^–1 relative to the unlabeled fiber. While this is a more significant shift than is observed for Ala-5 or Ala-8 labeled hIAPP, this shift is smaller than those induced by the labeled residues closest to Ala-25 and expected to reside in the β-sheet. This analysis suggests that Ala-25 exhibits more β-sheet character than predicted by ssNMR. The difference between the 2D IR and ssNMR results may be because the IR data is sensitive to the coupling between stacked Ala-25 residues and not ϕ/ψ angles. It should be noted that our simulations were conducted using stable and rigid β-sheets that are perfectly ordered. In nature, one would expect that the C- and N-terminal ends of the fibers experience a higher degree of disorder than the middle, which will tend to decrease the effects of the isotope labeling. Thus, the frequency shift should be more pronounced for those labeled amino acids residing in the middle of the fiber. Structural disorder can be accounted for by simulating 2D IR spectra from molecular dynamics simulations. Nonetheless, it appears that the IR results, with the exception of Val-17, are largely in agreement with the ssNMR model.

We found that, for both parallel and perpendicular beam geometries, Val-17 exhibited the weakest turn/β-sheet cross-peak intensities (Figure 4g). Hence, trends observed for the turn/β-sheet cross-peak (x_AB) intensity indicate that Val-17 occupies a region in which the turn and β-sheet secondary structures border one another. This observation falls in line with what would be expected from the ssNMR structure, which predicts that Val-17 lies at the extreme C-terminus edge of the first β-sheet region. Leu-27, which is predicted to lie at the extreme C-terminus edge of the turn region, would be expected to diminish the x_AB cross-peak intensity as well. Leu-27 yields a diminished x_AB intensity as well, yet its x_AC cross-peak intensity and the induced shift in the β-sheet fundamental suggest that it exhibits more β-sheet character than predicted by the ssNMR structure. These observations, however, are complicated by the fact that the low frequency β-sheet and high frequency turn features do not arise due to pure transitions and are most likely corrupted by normal modes localized on the turn and β-sheet structures, respectively, as well as by random coil contributions. Regardless, the weak cross-peak intensity observed for Val-17 and Leu-27 is highly suggestive of the placement of these residues in regions of converging secondary structure.

5. Conclusions

In this investigation, we relate the structure of hIAPP to changes in the infrared spectra that arise due to isotope labeling. Our methods were used to generate a framework by which to interpret the spectral features that arise due to the random coil/β-sheet/turn/β-sheet structures associated with various fiber forming peptides, in particular hIAPP. Our simulations indicate that (1) the frequency of the β-sheet feature is sensitive to the β-sheet length and the position of isotope labels within the β-sheet; (2) β-sheet stacking and the marginal twist associated with amyloid β-sheet has little effect on our spectra; (3) the high frequency feature in our spectra is due to positive coupling in the turn region and is sensitive to label position within the turn; (4) coupling between the turn and β-sheet regions is indicated by a cross-peak, whose intensity is sensitive to isotope label position; and (5) coupling between the labeled feature and the β-sheet is also indicated by a cross-peak, whose intensity increases as the isotope label moves from the edge to the center of the β-sheet. These conclusions provide a basis for interpreting isotope labeled FTIR and 2D IR data, as well as for designing isotope labeling strategies to extract secondary structure information. One of the most promising methods outlined here is using the suppression of 2D IR cross-peaks to identify residues that represent transitions between secondary structure. In principle, absolute structural constraints can be generated from individual or a few labeled peptides, but in practice, the comparison of many isotope labels will provide the most interesting data through relative comparisons. Advances in peptide synthesis mean that it is becoming easier to synthesize large polypeptides and proteins with non-native amino acids and isotope labels, so the range of systems in which 2D IR spectroscopy can be applied is rapidly increasing. Moreover, all of these parameters can be monitored with ultrafast time resolution and thus applied to study the structural evolution of dynamic systems.