Common phenotype of resting mouse extensor digitorum longus and soleus muscles: equal ATPase and glycolytic flux during transient anoxia

Abstract

Rates of ATPase and glycolysis are several times faster in actively contracting mouse extensor digitorum longus muscle (EDL) than soleus (SOL), but we find these rates are not distinguishable at rest. We used a transient anoxic perturbation of steady state energy balance to decrease phosphocreatine (PCr) reversibly and to measure the rates of ATPase and of lactate production without muscle activation or contraction. The rate of glycolytic ATP synthesis is less than the ATPase rate, accounting for the continual PCr decrease during anoxia in both muscles. We fitted a mathematical model validated with properties of enzymes and solutes measured in vitro and appropriate for the transient perturbation of these muscles to experimental data to test whether the model accounts for the results. Simulations showed equal rates of ATPase and lactate production in both muscles. ATPase controls glycolytic flux by feedback from its products. Adenylate kinase function is critical because a rise in [AMP] is necessary to activate glycogen phosphorylase. ATPase is the primary source of H⁺ production. The sum of contributions of the 13 reactions of the glycogenolytic and glycolytic network to total proton load is negligible. The stoichiometry of lactate and H⁺ production is near unity. These results identify a default state of energy metabolism for resting muscle in which there is no difference in the metabolic phenotype of EDL and SOL. Therefore, additional control mechanisms, involving higher ATPase flux and [Ca²⁺], must exist to explain the well-known difference in glycolytic rates in fast-twitch and slow-twitch muscles in actively contracting muscle.

Introduction

Mammalian skeletal muscles display a range of mechanical, energetic and metabolic phenotypes. Mouse extensor digitorum longus (EDL) and soleus (SOL) muscles are commonly used experimental models for the two main classes, fast glycolytic and slow oxidative muscles, respectively. These characteristics are based on distinct mechanical and energetic properties of actively contracting muscle (Close, 1972), and on assays of enzyme activity and protein isoforms (Barany, 1967; Nemeth et al. 1979; Pette & Staron, 1993; Hughes et al. 1999). The rate of heat production during working contractions is 5-fold higher in EDL than in SOL muscle (Barclay et al. 1993). The ATPase rate and glycolytic flux measured during tetanic contractions are approximately 3- to 4-fold higher in EDL than in SOL (Crow & Kushmerick, 1982; Moerland & Kushmerick, 1994).

However, the characteristic differences in phenotype distinguished in actively contracting fast and slow muscle are not clearly demonstrated in the resting state. The oxygen uptake rate at rest is not different at 20°C in mouse EDL and SOL muscles (Crow & Kushmerick, 1982), suggesting equal ATPase rates. The resting heat production rate is just 1.4 times higher in mouse SOL than in EDL (Wendt & Barclay, 1980; Barclay et al. 2009), but in rat muscles the rates differed by only 1.1-fold in the opposite direction (Cox & Gibbs, 1997). Similarities in metabolic rate in resting muscle are also found in feline muscles in which the basal rates of oxygen uptake in fast-twitch and slow-twitch muscles in vivo are the same (Bockman, 1983). The significance of a finding that different muscle types behave similarly at rest but differently during activity would be that a muscle's phenotype depends on its physiological state, and that regulation of metabolic fluxes is different at rest and during activity.

Muscle can achieve a range of steady energetic states in which the rate of ATP usage is balanced by an equal rate of ATP synthesis. The lowest rate of energy utilization occurs at rest. Our experimental design is the simplest possible to alter the metabolic state in resting muscle. We do this by reducing the ATP supply in contrast to the more commonly used method that increases ATP utilization by contractile activity to induce an energy imbalance. Temporary anoxia transiently perturbs the steady state of energy balance between ATP usage and synthesis because there is no ATP synthesis by oxidative phosphorylation. The only possible source of ATP synthesis is glycolysis and the experiments will show that glycolytic ATP synthesis rate in resting muscle is less than the rate of ATP usage. Thus, the experiments cause PCr to decrease without muscle activation. We use this perturbation without active contraction in resting muscle to test the hypothesis that glycolytic flux is regulated by feedback control mechanisms and add numerical simulations (Vinnakota et al. 2006) of the experimental results to reveal the operation of metabolic feedback mechanisms without any of the effects downstream of membrane depolarization and Ca²⁺ signalling in active muscle. This experimental design also tests whether the resting ATPase and glycolytic flux is the same in fast-twitch EDL and slow-twitch SOL.

Methods

Experiments were performed at 25–26°C with soleus muscles (SOL) and extensor digitorum longus muscles (EDL) dissected from the legs of Swiss Webster mice aged 2–5 months; 74 mice were used for the experiments reported here. Procedures followed the policies recommended by The Journal of Physiology (Drummond, 2009). Animals had free access to food and water until the morning of the experiment. Animal care was provided by, and the experimental protocol approved by, the Division of Comparative Medicine, University of Washington School of Medicine in compliance with the animal welfare policy of the US Department of Health and Human Services. Anaesthesia was induced by inhalation of 5% isoflurane in oxygen and a deep surgical plane of anaesthesia was maintained by 2.5% isoflurane in oxygen during muscle dissection. Silk sutures were tied to the proximal and distal tendons of each muscle with the knee fully extended and the ankle fully plantar-flexed. The muscles were dissected with the blood supply intact, and the length between the sutures was defined as the in vivo length. The muscles were removed from the animal and placed at this length in a filtered (0.22 μm filter) physiological saline containing (mm): NaCl, 127; KCl, 4.6; NaHCO₃, 30; MgSO₄, 1.16; CaCl₂, 2.5 with gentamycin (1 mg l⁻¹) and gassed with 5% CO₂ and 95% O₂ to pH 7.2, as previously reported (Crow & Kushmerick, 1982). The anaesthetized animals were killed after both pairs of muscles were removed by increasing isoflurane concentration to 5% for 3 min followed by cervical dislocation.

Experimental design

Four SOL or EDL muscles were mounted on a glass tube (2.5 mm o.d.; 1 mm i.d.) parallel to the long axis, and this assembly was placed into a standard 5 mm NMR glass tube (4.7 mm i.d., Wilmad Lab Glass, Buena, NJ, USA) (Fig. S1 in Supplementary material). The dry weight of muscles in the NMR tube ranged from 15 to 26 mg depending on muscle type and age of the mouse. There is no evidence that muscle size influenced any of the results presented. The physiological saline was pumped past the muscles at a flow rate of approximately 4 ml min⁻¹ (Fig. S1 in Supplementary material). A valve mounted near the tubes outside the magnet enabled a change from saline equilibrated with 5% CO₂ in oxygen to a saline equilibrated with 5% CO₂ in nitrogen which flowed for 2 min (the duration of one NMR spectrum) to achieve anoxia. Then flow of saline was stopped. Control experiments with sodium cyanide showed this procedure is sufficient to block oxidative phosphorylation (see Supplementary material). To re-establish normoxia, flow of saline equilibrated with 5% CO₂ and 95% O₂ was restarted. The rate constant for exchange of CO₂ and permeable solutes into and out of the muscle is approximately 0.5 min⁻¹ so that the change to anoxia was complete during the acquisition of one NMR spectrum (Figs S3, S4 and S5 in Supplementary material).

The experimental design collected NMR spectra every 2 min. The duration for aerobic control and baseline was fixed at 20 min (10 spectra). The duration of anoxia was set to one of the following durations: 16, 30, 46 or 60 min for EDL and 16, 30 or 46 min for soleus. Spectra were collected during aerobic recovery for 40 min. At least 10 additional minutes of aerobic conditions elapsed before the next experiment began. Typically three cycles of anoxic stress and recovery were obtained in the same preparation. The criterion for stopping data collection was greater than a 20% decrease in PCr with a concomitant increase in orthophosphate (Pi) in fully relaxed spectra after aerobic recovery.

NMR spectroscopy

³¹P NMR spectra were obtained at 7 Tesla in an Oxford 89 mm vertical bore magnet with a Varian Inova spectrometer. A high-resolution probe for conventional 5 mm glass tubes was modified such that the inner coil was tuned for the phosphorus nucleus; this arrangement maximizes the volume of muscle in the detection volume of the radio-frequency coil. The outer coil was tuned to 300 mHz for the proton nucleus. The water signal was used to optimize the uniformity of the magnetic field over the muscles. The line width of PCr peak ranges between 4 and 10 Hz (0.03 and 0.08 ppm) without exponential filtering. Reference spectra are fully relaxed FID (free induction decay) signals obtained under baseline conditions of the aerobic, resting muscles using a recycle time of 15 s with a 90 deg pulse width of typically 5 μs. Spectra before, during and following anoxia are obtained with a recycle time of 4 s and a 75 deg pulse width averaging 30 FIDs in 2 min. These spectra are therefore obtained under partly saturating NMR conditions. This method typically gives a signal-to-noise ratio for PCr in each 2 min spectrum of approximately 30:1 for EDL and of approximately 15:1 for SOL when the spectra are processed with a line broadening equal to the observed line width of PCr. The signal-to-noise ratio in SOL is lower than in EDL because of the lower concentrations of PCr and ATP in SOL. Proton decoupling was not used to obtain ³¹P spectra. Quantification of the spectral peaks was performed using a time-domain fitting algorithm (see Supplementary material).

At the end of each experiment, the muscles were frozen and lyophilized for 48 h in a vacuum (approximately 5 μTorr). The sutures and visible tendons were removed and a dry weight was obtained because muscle oedema occurs during the experiment. The intracellular water volume is calculated from this dry weight for each muscle by the formula: intracellular water (μl) = (dry weight in mg) × (3.8)/0.67. Separate experiments measured the wet-to-dry ratio of freshly dissected mouse muscle without tendon to obtain a value of 3.8 (N= 23, coefficient of variation 8%) (see Supplementary material). The factor, 0.67, accounts for the fraction of intracellular water per unit wet weight of muscle (Sjogaard & Saltin, 1982). Thus, chemical concentrations are given in millimoles per liter of intracellular water, abbreviated mm. pH is measured from the difference in chemical shift of Pi peak from PCr peak at the measured temperature of the experiment (Kost, 1990) (see Supplemental material). All peaks were scaled to a standard content of ATP of 8.3 mm in intracellular water in EDL and 5.5 mm in SOL as measured by prior biochemical analysis (e.g. Kushmerick et al. 1992).

Lactate assay

All of the lactate produced during the period of anoxia remains in the NMR tube (in the muscle and in the surrounding saline) because there is no flow of saline then. Re-establishing flow of saline at the onset of aerobic recovery washes the lactate from the NMR tube and muscle with approximately 100 exchanges of volume surrounding the muscles (approximately 0.4 ml). The rate of lactate washout measured in preliminary experiments showed that 10 min is sufficient to collect all of the lactate. The time constant for lactate washout is approximately 0.5 min⁻¹ (Fig. S6 in Supplementary material), which is the same rate as for the other solutes (Figs S3, S4 and S5 in Supplementary material). Saline flowing over the muscle after 10 min contains no detectable lactate above the detection limit of the assay, 0.015 mm min⁻¹.

Statistics and data reduction

All tabulation and calculations with the data are made using Excel software (Microsoft Inc.). For regression analyses GraphPad Prism version 4.0b for Macintosh OSX (GraphPad Software, San Diego, CA, USA; http://www.graphpad.com) was used. Statistical tests are given with each set of data analysed. Comparisons between independent means having different N and s.d. are made as suggested on p. 115 of Snedecor & Chochran (1967). Statistical significance is set at P≤ 0.05.

Computer model construction and simulations

A previously published model of glycogenolysis by (Vinnakota et al. 2006) with pH computations was integrated with an empirical model of oxidative phosphorylation (Jeneson et al. 1996). This model is used to describe the measured PCr, Pi, ATP, pH time courses and the lactate produced in the transition from normoxia to anoxia and back to normoxia in mouse EDL and SOL muscles. The empirical oxidative phosphorylation flux model is used to establish a steady state during normoxia and the recovery at the end of anoxia. We previously developed methods for computing pH time course due to a biochemical reaction network and enzyme kinetics and biochemical reaction thermodynamics as a function of pH (Vinnakota et al. 2006) when the system is closed. These methods are extended in the present study to compute pH time course in an open system by including proton transport mechanisms on the sarcolemma which include the two isoforms of lactate proton symporters i.e. monocarboxylate transporter MCT1 and MCT4 and carbonic anyhdrase. A schematic diagram of the reaction network of the model is given in Fig. S12 in Supplementary material.

The model construction and simulation methodology consisted of the following steps:

1. Augmentation of our published model with fluxes for the present model and parameterization for each muscle type described in detail in the Supplemental material.

2. Setting initial conditions appropriate for EDL or SOL, and initial adjustment of model parameters to obtain a stable baseline corresponding to the experimentally measured baseline.

3. Optimization of eight adjustable parameters for each experiment using a weighted least squares objective function.

Simulations of the resting aerobic steady state

We adapted the computational model of glycogenolysis in Vinnakota et al. (2006) for use with dissected muscles superfused with saline while mounted in the NMR tube. The complete model, described below and in the Supplementary material, is fitted to experimental data by adjusting a subset (eight) of the parameters (Table 2).

Table 2.

Parameter values adjusted and optimized to match model simulations to the data from EDL muscles for all durations of anoxia

Parameter	Definition	Reported value, EDL	Optimized value, EDL	Coefficient of variation (%)	Reported value, SOL	Optimized value, SOL	Coefficient of variation (%)
KATP	Rate constant for ATP consumption	0.065 min−1a	0.0828 min−1	7.81	0.12 min−1a	0.124 min−1	7.39
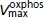	Vmax of oxidative phosphorylation	3.4 × 10−3m min−1 b	3.75 × 10−3m min−1	11.87	3.2 × 10−3m min−1b	3.71 × 10−3m min−1	19.03
	Phenomenological ADP kinetic constant for oxidative phosphorylation	4.4 × 10−5mc	4.83 × 10−5m	–	4.4 × 10−5mc	4.19 × 10−5m	–
	Hill coefficient of ADP for oxidative phosphorylation	>2c	2.27	–	>2c	2.22	–
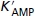	AMP concentration for half-maximal activation of GPb	1.4 × 10−5md	3.54 × 10−6m	16.4	1.4 × 10−5md	5.31 × 10−6m	22.49
nH	Hill coefficient for AMP activation of GPb	1.75d	1.88	–	1.75d	1.62	–
βfixed	Intrinsic buffer capacity (non-phosphate, non-bicarbonate)	–e	0.016 m	72.44	–e	0.0034 m	35.96
VMCT	Vmax of MCT	–e	4.7 × 10−3m min−1	74.42	–e	7.47 × 10−4m min−1	95.05

a, derived from equivalent ATPase fluxes from experimental measurement of ATPase rate in Fig. 4 using ATPase flux =K_ATP×[ATP] and converting to the stated units; b, derived from the rate constant for PCr resynthesis from experimental data (0.12 min⁻¹ for EDL and 0.22⁻¹ for SOL) and the approximation: V_max= (resting PCr) × rate constant; c, Jeneson et al. 1996; d, Crerar et al. 1995; e, no reported data for mouse EDL and SOL.

Simulation of the resting aerobic muscle at the beginning of the experiment required a function simulating oxidative phosphorylation not present in the original model. The kinetics of oxidative phosphorylation ATP synthesis flux (J_oxphos) is modelled by an empirical sigmoid function of [ADP] (Jeneson et al. 1996).

This is the same descriptive model of oxidative phosphorylation used previously for analyses of human data (Vicini & Kushmerick, 2000); we use it rather than a more detailed biophysical model (e.g. Beard, 2005), for two reasons. First, the sole role of this model for cellular respiration is to establish physiologically meaningful steady states at the beginning and end of the experiment, and second, the experiments and the simulation analysis focus on glycogenolysis and glycolysis rather than aerobic metabolism. For this purpose, the parameters V_max, K_ADP and n_H were optimized to match the experimental data for each muscle at rest and during recovery from anoxia.

Simulations of the open system for H⁺, CO₂, O₂ and lactate transport

Muscles in the experimental apparatus are open systems exchanging protons with the extracellular saline through proton transport mechanisms on the sarcolemma. The major H⁺ and lactate symport mechanism, MCT, is included in the model; the kinetic equations are given in Supplemental material. EDL has a higher proportion of MCT4 (the isoform with lower affinity for lactate) and a higher transport activity (Table 2) than does SOL, and SOL has a higher proportion of MCT1 (the isoform with higher affinity) than in EDL (Halestrap & Price, 1999; Bonen, 2001). We simplified the model by making the approximation that each muscle type has only its predominant isoform of MCT (Table 2).

Details of the buffers in muscle cells and the equations used to evaluate buffer capacity and intracellular pH are given in the Supplementary material. CO₂ and O₂ transport occurs by passive diffusion. The oxygen consumption flux is calculated in the model from the oxidative phosphorylation ATP synthesis flux with an assumed P/O₂ ratio of 4.2, the average of recent measurements in mouse muscle under resting conditions (Marcinek et al. 2004, 2005), recognizing that the P/O₂ appears to be higher, in the order of 5.5 to 6 (Crow & Kushmerick, 1982; Harkema & Meyer, 1997) in actively contracting muscle. From this computed oxygen consumption flux, CO₂ flux 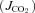is calculated as the product of oxygen consumption flux and the respiratory quotient (RQ; the moles of CO₂ produced per mole of O₂ used in mitochondria). RQ is assumed to be 0.8, reflecting the source of metabolic fuel as a mixture of carbohydrate and fatty acid at rest.

The simulations were not sensitive to the RQ value; adopting a value of RQ = 1 measured in mouse EDL and SOL (Crow & Kushmerick, 1982) changed the results only slightly (data not shown).

Enzyme activities specific for EDL and SOL in the simulations

The enzyme activities and the metabolite concentrations in the equations are those appropriate for mouse fast-twitch (EDL) and slow-twitch (SOL) muscles to obtain a model specific for each muscle type without a change in the kinetic mechanism for the enzymes or in the differential equations. Glycerol-3-phosphate dehydrogenase (G3PDH) is included because it is present in muscle tissue and adds a degree of freedom, thus eliminating an obligatory coupling of NADH/NAD⁺ in GAPDH and lactate dehydrogenase (LDH). Most enzyme activities specific for each reaction in the glycolytic pathway in mouse EDL and SOL are available in the literature; the others were estimated from data for other murine muscles because enzymes in the upper and lower halves of the pathway for glycogenolysis and glycolysis have known ratios to each other (Pette & Hofer, 1979; Hughes et al. 1999; Lambeth & Kushmerick, 2002; see Supplementary material). The values for V_max for the enzymes in the model for each muscle are given in Table 1. All kinetic equations are reversible. Equivalence of forward and reverse V_max is calculated by the Haldane relationship using pH-dependent equilibrium constants. V_max for most enzymes is adjusted for the observed intracellular pH by empirical functions describing their pH dependence; no pH adjustments were made for those enzymes without this information (see Supplementary material).

Table 1.

Enzyme activities in mouse EDL and SOL muscles

Enzyme (EC number)	Enzyme abbreviation	EDL (m min−1)	SOL (m min−1)	Source
Glycogen phosphorylase (2.4.1.1)	GPb	0.0127	0.0037	Reichmann & Pette, 1984
Phosphoglucomutase (2.7.1.41)	PGLM	0.0177	0.0052	*Riol-Cimas & Melendez-Hevia, 1986
Phosphoglucoisomerase (5.3.1.9)	PGI	1.3155	0.3833	Lindena et al. 1986
Phosphofructokinase (2.7.1.11)	PFK	0.0127	0.0037	Reichmann & Pette, 1984
Aldolase (4.1.2.13)	ALD	0.0412	0.0120	Reichmann & Pette, 1984
Triosephosphate isomerase (5.3.1.1)	TPI	0.3430	0.1406	*Riol-Cimas & Melendez-Hevia, 1986
Glyceraldehyde-3-phosphate dehydrogenase (1.2.1.12)	GAPDH	0.1865	0.0765	Reichmann & Pette, 1984
Glycerol-3-phosphate dehydrogenase (1.1.1.8)	G3PDH	0.631	0.0557	MacDonald & Marshall, 2000; Okumura et al. 2005
Phosphoglycerate kinase (2.7.2.3)	PGK	0.0212	0.0087	*Riol-Cimas & Melendez-Hevia, 1986
Phosphoglycerate mutase (5.4.2.1)	PGM	0.2046	0.0839	*Riol-Cimas & Melendez-Hevia, 1986
Enolase (4.2.1.11)	EN	1.9430	0.7966	Petell et al. 1984
Pyruvate kinase (2.7.1.40)	PK	0.0996	0.0408	Reichmann & Pette, 1984
Lactate dehydrogenase (1.1.1.27)	LDH	0.2687	0.0956	Reichmann & Pette, 1984
Adenylate kinase (2.7.4.3)	AK	2.5627	2.0299	Lindena et al. 1986
Creatine kinase (2.7.3.2)	CK	11.1371	8.8215	Reichmann & Pette, 1984

^*Unavailable value for mouse, measured in rat.

Differential equations and optimization of the model to fit the data

The detailed model (Vinnakota et al. 2006) plus the added features described above define the set of differential equations used in the simulations (see Supplementary material). We then optimized the fit of the model to the data with adjustments of the minimal set of parameters specified in Table 2. The system of ordinary differential equations describing this model is solved using ODE15s solver in MATLAB (The MathWorks Inc., Natick, MA, USA). The models for aerobic, resting EDL and SOL were run to simulate 100,000 min with glycogen and cytosolic pH clamped at values from a set of approximate initial conditions to obtain a steady state condition at the start of the experiments. No state variables are clamped during the simulations of the actual experiments.

The experiments had three phases: 20 min of aerobic baseline data acquisition, followed by a variable period of anoxia, further followed by a period of data acquisition during aerobic recovery. The flux of oxidative phosphorylation is stopped to simulate the duration of the anoxic period by setting the V_max of oxidative phosphorylation flux to zero. Adjustable parameters in Table 2 for each muscle were initially fitted to the 60 min anoxia data set for EDL and the 46 min anoxia data set for SOL using a MATLAB implementation of the PIKAIA 1.2 genetic algorithm based optimizer with generational replacement (Charbonneau, 2002a,b;). We computed an approximate variance–co-variance matrix using the method specified in eqns 10–12 in Landaw & DiStefano (1984). Parameters pertaining to allosteric activation of glycogen phosphorylase b (GPb; [AMP] for half-maximal activation (K′_AMP) and n_H) and oxidative phosphorylation flux expression showed high coefficients of variation due to strong correlations between themselves. When only one parameter from each of those model components, i.e. K′_AMP for GPb and V_max of oxidative phosphorylation for the OxPhos flux (V^oxphos_max), was considered to be adjustable, we obtained low coefficients of variation demonstrating that all model fluxes were important and identifiable (see Supplementary material). Estimates of independently identifiable parameters were refined by constrained non-linear optimization of using FMINCON function from the MATLAB optimization toolbox and their coefficients of variation are reported in Table 2. The data sets corresponding to the longest durations of anoxia were used for optimizing the adjustable parameters since they contained the most information on the glycolytic flux. The cost function for optimization is a weighted sum of squares of residuals, where the standard deviations of individual measurements were used as the weights. This optimized simulation also accounts for the individual data sets with only one poor fit for the shortest duration of anoxia in EDL (see Supplementary material).

Model parameters accounting for biochemical thermodynamics include ion-binding affinities to biochemical species and enthalpies of binding and free energies of formation for the reference species, which are taken from the literature and are not adjusted in the model analyses. Parameters for the kinetic characteristics of the enzymes in the model taken from the literature are the maximal enzyme velocities, substrate affinities in the context of rapid equilibrium kinetic models, inhibition and activation constants, and cooperativity coefficients. Parameters describing the experimental conditions specific for the experiments simulated are the muscle volume, volume of fluid in the NMR tube and flow rate of the saline. The major reaction fluxes measured experimentally are basal ATPase rate, rate constant for aerobic PCr recovery, the rate of change of intracellular pH, and the rate and extent of lactate production. To simulate specific mechanisms of regulation of glycolysis, selected parameters were clamped and explained with those tests.

The basis of the model is a solution of differential equations representing biochemical reactions occurring in dilute solutions; thus, enzymes and metabolites are considered to be dissolved in a biochemical reaction mixture. Data from Scopes (1974a,b); validate the basic model (Vinnakota et al. 2006). When the product of an enzyme is a substrate for another, the simultaneous solution of the differential equations in the model ‘couples’ these reactions. Thus, the network of 13 enzymes constituting glycolytic flux forms a set of coupled reactions that in turn interact with the other reactions (ATPase, creatine kinase (CK), adenylate kinase (AK) and oxidative phosphorylation) to form the integrated network of the model simulations. We use the term ‘glycolytic flux’ to mean the flux in the network of reactions from glycogen phosphorylase to lactate dehydrogenase; this is calculated by flux in LDH and is a valid measure because the simulations show equivalent flux through all of the enzymes (Fig. S17 in Supplemental material). Simulations give flux through any specific reaction or set of reactions and this is specified when the data are presented. The operation of solving these differential equations yields concentrations of each reactant and product, and reactions fluxes as a function of time. The effective H⁺ stoichiometry of reactions and transporters is pH dependent, due to buffering. The proton production is calculated by summing the contributions of each reaction using its physical–chemical properties by multiplying the net proton production or uptake by the flux of each reaction; the total proton flux is the sum of proton fluxes from individual reactions and transporters.

Results

The results show EDL and SOL have indistinguishable rates of ATPase and of lactate production during anoxia despite the characteristic differences in enzyme activity discussed in the Introduction. The model simulations show that the ATPase rate sets the glycolytic flux and therefore the rate of lactate production, and that the primary mechanism is feedback kinetic control of glycogen phosphorylase by AMP, a product of ATPase. Together the results define a default phenotype that is the same in the resting state for EDL and SOL.

Concentrations of PCr, Pi and pH during anoxia

Table 3 contains the mean concentrations in SOL and EDL at rest in control conditions from NMR-fully-relaxed spectra and from the first 20 min of experiments before the change to anoxia. The higher concentration of PCr in EDL and of Pi in SOL – as well as spectral areas for γATP, PCr and Pi, as a fraction of the total ³¹P measured in those spectra – are consistent with prior results (Kushmerick et al. 1992; Meyer & Foley, 1996). The agreement in the values between the two different NMR acquisition conditions (partially saturated and fully relaxed) shows that adequate accounting was made for NMR saturation factors in quantifying areas of the spectral peaks.

Table 3.

Concentrations of PCr, Pi and ATP and intracellular pH in EDL and SOL muscles at rest in normoxia

	PCr ±s.e.m. (mm)§	Pi ±s.e.m. (mm)§	ATPC (mm)§	pH ±s.e.m. (mm)§	γATP/Total P ±s.e.m.	PCr/Total P ±s.e.m.§	Pi/Total P ±s.e.m.§
EDLAN= 35	27.9 ± 0.9	1.6 ± 0.5	8.3	7.14 ± 0.02	0.14 ± 0.005	0.48 ± 0.02	0.07 ± 0.01
EDLBN= 51	27.9 ± 0.7	2.1 ± 0.2		7.05 ± 0.02
SOLAN= 29	14.5 ± 0.8	5.4 ± 0.5	5.5	7.22 ± 0.02	0.15 ± 0.004	0.40 ± 0.01	0.14 ± 0.009
SOLBN= 32	14.9 ± 0.4	5.2 ± 0.2		7.22 ± 0.01

^§Difference between EDL and SOL is statistically different, P < 0.01. Notes: A, data from experiments with fully relaxed NMR spectra in normoxia. B, data from control spectra during first 20 min of the experiments, under partly saturating NMR pulse conditions. C, these data are from Kushmerick et al. (1992). D, Total P is the total phosphate in the spectrum and is given by the sum of the α, β and γ peaks of ATP, of Pi and of PCr.

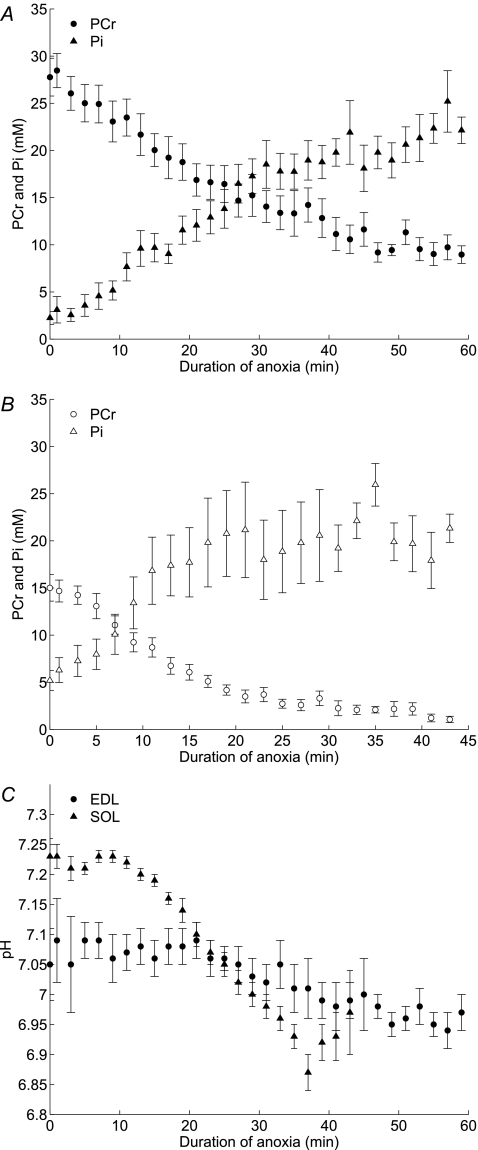
Anoxia decreases [PCr] and increases [Pi] without appreciable change in [ATP] in both muscles. The main features of the changes measured by ³¹P NMR spectra are illustrated by the spectra recorded with EDL in one experiment (Fig. S2 in Supplemental material). The extents of the chemical changes are as large as those found during a tetanic stimulation reported by Crow & Kushmerick (1982). The chemical changes occur at a much slower rate at rest and are quantified and displayed in Fig. 1, which shows the anoxic time course of averaged chemical changes during anoxia in all experiments (for EDL, N= 49; for SOL, N= 32). The point plotted at zero time is the average of the data during 20 min of aerobic control (same data as given in Table 2). [PCr] decreases to 2 mm in SOL and to 10 mm in EDL. Longer durations of anoxia were not studied because 60 min of anoxia in EDL and 46 min in SOL are the longest durations from which aerobic recovery is complete. Data for all groups of experiments are plotted individually in Figs S8, S9 and S10 in Supplementary material.

Figure 1.

Mean changes in [PCr] and [Pi] and pH during anoxia for all experiments Changes in [PCr] (circles) and [Pi] (triangles) are displayed for EDL experiments (filled symbols) in A and for SOL experiments (open symbols) in B. The mean pH changes for both muscles are displayed in C (EDL filled circles and SOL filled triangles). Error bars equal one s.e.m. The data are displayed as a function of time during the anoxic interval only. Data for controls in normoxia are shown as the mean values at zero time. The number of experiments averaged per graphical point is not equal because all durations of anoxia are included and different numbers of experiments were completed for EDL and SOL. For EDL the mean of 14 experiments (with 60 min of anoxia) are plotted from 0 to 60 min, but the plotted data from 46 to 60 min include only those experiments. Five experiments (with 46 min of anoxia) are added to the means so that 19 experiments are plotted from 30 to 46 min. Twenty-one experiments (with 30 min of anoxia) are added to the means so that 40 experiments are plotted from 16 to 30 min. Nine experiments (with 16 min of anoxia) are added to the means so that 49 experiments are plotted from 0 to 16 min for EDL. The corresponding numbers of experiments plotted for SOL are: 10 experiments from 30 to 46 min; from 16 to 30 min, those plus 11 experiments (with 30 min of anoxia); from 0 to 16 min, all preceding plus 11 experiments (with 16 min of anoxia) for a total of 32 SOL experiments.

Resting pH in normoxia during the first 20 min of the experiment is plotted at time zero (Fig. 1; also Table 2). pH is 0.1–0.2 units more alkaline in SOL than in EDL; the difference in pH is statistically significant (unpaired t test, unequal variance and N; P < 0.001). The intracellular pH measured in mouse SOL agrees with the value of 7.23 measured by microelectrodes at 28°C (Aickin & Thomas, 1977). At the end of anoxia (46 min for SOL and 60 min for EDL), the pH is similar in both muscles, approximately 6.9. During the initial 10–15 min of anoxia in both muscles there is a tendency for pH to increase, seen more prominently in the data from SOL and in the simulations. Thereafter, pH decreases until the end of anoxia, and was restored to control during recovery. The novelty of these results lies in the mechanism for perturbing energy balance by transiently reducing ATP synthesis in the resting basal state, and in the magnitude of the PCr and other chemical changes that occurred more slowly but are as large as occurs in tetanic contractions. The pattern of reversible decrease in [PCr] and increase in [Pi] without change in [ATP] is the classical pattern for perturbations of energy metabolism in skeletal muscle (Kushmerick, 1983; Meyer & Foley, 1996).

Lactate synthesis rates in EDL and SOL are equal

In both muscles, lactate production increases during anoxia, showing an increase in glycolytic flux after a delay of approximately 11 min. Net lactate production from glycogen is the only mechanism for ATP synthesis during anoxia because oxidative phosphorylation is blocked and glucose is not present in the saline. In aerobic muscle, the glycolytic flux is not detectable, but could be as high as 0.015 mm of lactate per minute, which is the limit of detection of the assay. Figure 4 displays the result of the total lactate produced during 16, 30, 46 and 60 min of anoxia in EDL and to 46 in SOL, plus the results from simulations described below. From 16 to 60 min in EDL and from 16 to 46 min in SOL, the rate of lactate production is the same. Linear regression analysis of the SOL data yields a slope of 0.18 ± 0.013 mm lactate min⁻¹, a value not different from the slope of 0.21 ± 0.026 mm lactate min⁻¹ found in EDL (ANOVA, P= 0.59). The intercepts on the time axis for zero lactate production are approximately 11 min. These data show the glycolytic fluxes in EDL and SOL are indistinguishable during resting anoxia and begin at a rate more than 10-fold higher (0.2 mm min⁻¹) than in resting aerobic muscle only after a delay of 11 min. The ATP produced is equivalent to 0.3 mm min⁻¹ because the reaction stoichiometry with glycogen as substrate is 1.5 ATP/lactate.

Figure 4.

Total lactate output of EDL and SOL as a function of duration of anoxia The graphical points (filled triangles, EDL; filled squares, SOL) are measured data. Error bars represent one s.d. Integrating total flux through LDH (continuous black line, EDL; the dashed black line, SOL) simulated total lactate synthesis by the muscle. The lower grey lines represent the same simulation and integration of LDH flux when the V_max of AK reaction is set to zero; dash–dotted line, EDL and dotted line, SOL.

Same ATPase at rest in EDL and SOL

The basal ATPase rate in the absence of ATP synthesis can be estimated before the onset of lactate synthesis from the rate of decrease of PCr because the ATPase and creatine kinase are the only reactions with significant flux during the first 10 min of anoxia. Regression analysis of the PCr content against duration of anoxia to 10 min (Fig. 2) indicates the rate of PCr decline is not statistically different between EDL (0.54 ± 0.12 mm min⁻¹; regression slope ±s.e.) and SOL (0.66 ± 0.07 mm min⁻¹; ANOVA, P= 0.46). The slope common to both sets of data is 0.59 ± 0.08 mm min⁻¹. The PCr content of SOL reaches low values sooner than in EDL because SOL has significantly lower concentrations of PCr (Table 1 and Fig. 1). The rate of lactate production (and glycolytic ATP synthesis) during anoxia is not sufficient to balance the resting rate of ATPase, and this imbalance is the mechanism for the continued decline of PCr. This analysis per se does not provide evidence for a constant ATPase throughout the experiment but the results of the model simulations giving the same simulated ATPase as measured experimentally during this interval (see Simulation results below) provides this evidence because it is fitted to the data during all the phases of the experiment (resting aerobic, anoxic and aerobic recovery).

Figure 2.

Mean data for [PCr] are plotted as a function of time during the first 10 min of anoxia to estimate resting ATPase rate EDL, filled symbols; SOL, open symbols. Four sets of data for EDL are plotted: circles, 16 min of anoxia (9 experiments); squares, 30 min of anoxia (21 experiments); triangles, 46 min of anoxia (5 experiments); and diamonds, 60 min of anoxia (14 experiments). Three sets of data for SOL are plotted: circles, 16 min of anoxia (11 experiments); squares, 30 min of anoxia (11 experiments); and triangles, 46 min of anoxia (10 experiments). Abscissa gives time (min) from the onset of anoxia. Linear regressions equations were fitted to all of the individual experimental data starting with the normoxic control at time zero, not the means displayed here, in order to weigh each datum properly. The fitted equations, with standard errors of the slopes and intercepts are: For EDL: PCr(t) = 28.2 ± 0.83 – time × 0.57 ± 0.14; R²= 0.44. For SOL: PCr(t) = 16.0 ± 0.40 – time × 0.63 ± 0.07; R²= 0.85. As there is no statistical difference between the slopes of the two regression lines (ANOVA, P= 0.46), a common slope for both muscles was calculated: 0.59 ± 0.08 (95% confidence level: −0.76 to −0.43).

Aerobic recovery

In contrast to the default phenotype of equal glycolytic fluxes in EDL and SOL, the aerobic recovery is faster in SOL than in EDL. Each anoxic perturbation is followed by an interval of normoxia before a subsequent experiment and this provides information on aerobic ATP synthesis in these muscles. The resynthesis of ATP by oxidative phosphorylation restores the decreased PCr and pH and the elevated Pi to their resting control values during recovery (data given in Fig. S11 and Table S2 in Supplementary material). The PCr increase and Pi decrease follows an exponential time course. The rate constant for PCr recovery for all durations of anoxia in SOL (0.22 min⁻¹) is twice that in the EDL (0.12 min⁻¹). The recovery of pH is 5 times slower than recovery of PCr and Pi. These results are consistent with published results in fast and slow muscles (Meyer & Foley, 1996) and with higher activities of citrate synthase and cytochrome oxidase in mouse SOL than EDL (Moerland & Kushmerick, 1994) These results for aerobic recovery make the distinction that the default phenotype in resting muscle is specific for resting ATPase and for glycogenolytic and glycolytic metabolism.

Numerical simulations of metabolic perturbation by transient anoxia

Fitting a detailed model of glycogenolysis and glycolysis to the data provides a test of the validity of the model for EDL and SOL. Optimizations of the model to the four sets of experiments in EDL and the three sets of data in SOL require adjustments to only the eight parameters listed in Table 2 to fit the model equations to the data for each muscle. All other state and adjustable parameters, derived from measured values reported in the literature, were held constant for each muscle type and are given in Table S5 in Supplementary material.

Inspection of the results in Fig. 3 show that the model simulations match the experimentally observed changes in PCr, Pi and pH obtained for transient anoxia in EDL (60 min) and in SOL (46 min); fits of the same optimized simulation to the data for the other durations of anoxia individually are given in Fig. S13 in the Supplemental material. Simulations of [PCr] and [Pi] lie within the errors of the data. [ATP] does not change during the experiment and the simulations for [ATP] show this result. The PCr content at the end of 46 min of anoxia decreased almost to zero in contrast to the EDL which approached 10 mm at 60 min of anoxia both in the data and simulations. The simulation of pH change for SOL lies outside the error bars for the data for approximately 15 min at the onset of anoxia, but the remainder of the simulations lies within the data errors and the slope is parallel to the decrease in pH during anoxia.

Figure 3.

Numerical simulations superimposed on data for the entire set of data for 60 min of anoxia in EDL (A and B) and 46 min of anoxia in SOL (C and D) These data are included in the means for all of the experiments displayed in Fig. 1. A, the EDL muscles were normoxic for 20 min, then anoxic for the next 60 min and restored to normoxia after 80 min. Lines are the simulation results for the entire time course of the experimental measurements; the continuous line, PCr; the dashed line, Pi; dotted line, ATP. Filled circles are the mean data for PCr with one s.d. The open circles are the mean data for Pi with one s.d. B, pH data from experiment shown in A. Continuous line is the simulation of pH for the entire time course of the experimental measurements. Filled squares are the mean data for pH with one s.d. C, the SOL muscles were normoxic for 20 min, then anoxic for the next 46 min and restored to normoxic after 66 min. Lines are the simulation results for the entire time course of the experimental measurements; the continuous line, PCr; the dashed line, Pi; dotted line, ATP. Filled circles are the mean data for PCr with one standard deviation. The open circles are the averaged data for Pi with one s.d. D, pH data from experiment shown in C. Continuous line is the simulation of pH for the entire time course of the experimental measurements. Filled squares are the averaged data for pH with one s.d.

Table 2 contains the reported values for the eight adjustable parameters and the optimized values for EDL and SOL. For EDL the fitted rate constant for ATPase flux (K_ATP) is 0.085 min⁻¹. Multiplying this value by the [ATP] of 8.3 mm gives a flux of 0.7 mm min⁻¹; the corresponding values for SOL are 0.129 min⁻¹, 5.5 mm and ATPase flux = 0.7 mm min⁻¹. These values agree with the experimentally measured ATPase (Fig. 2) common to both muscles of 0.59 ± 0.08 mm min⁻¹. The fact that the experimental flux is derived from the rate of decrease of [PCr] whereas the model is fitted to all [PCr], [Pi], [ATP] and pH data throughout the entire experiment provides direct evidence for a constant rate of resting ATPase during the experiment. Simulations of oxidative phosphorylation during the initial 20 min of resting muscle and during the final recovery match the data for PCr and Pi, and, as expected, the three kinetic parameters (V^oxphos_max, K^oxphos_ADP and n^oxphos_H) match reported values.

Figure 4 shows the simulations of the lactate production and the measured extent of lactate output for all durations of anoxia. Lactate production was simulated by integrating the flux of LDH as a function of time during anoxia. Inspection of the data and simulations show both the experimental and simulation results have a delay of approximately 11 min before the onset of lactate production. The simulated lactate production is within the error bars of the experimental data for EDL but was higher than the data for SOL.

We use a Hill type allosteric AMP activation model for GPb from Lambeth & Kushmerick (2002). The model fits to the data give values for the kinetic parameters of GPb close to published ones derived from in vitro measurements (Crerar et al. 1995), namely a Hill coefficient (n_H) of 1.75, showing high cooperativity in the intact muscle as in vitro, and a half-maximal activation concentration of AMP (K′_AMP) of 3.5–5.3 μm that is lower than the in vitro value.

Reported values for the permeability–surface area product per unit cell volume (PS/V_cell) are not available for EDL and SOL, and are necessary for the simulations because this parameter is in the equations for transport of CO₂ across the sarcolemma. The parameter PS/V_cell for CO₂ was estimated to be 2.31 by fitting the pH time course data obtained during a 0% to 50% transient acidification experiment conducted on SOL muscles (Supplementary material), which was used in our simulations. As the surface area-to-volume ratio for EDL and SOL do not differ significantly (Chin et al. 2003) we use the same PS/V_cell value estimate (2.31) for both EDL and SOL. Another estimate of this parameter is the inverse of the time constant of wash-in and wash-out of a cell-permeable molecule, which is equal to PS/V_cell (Stein, 1990). In the present study, the inverse of the mean time constant of CO₂ and triethyl-phosphate wash-in and wash-out (0.45 min⁻¹) is 2.22 min, which is close to our estimate from fitting the model solution to the transient experiment.

As a priori values for the intrinsic buffer capacity, β, are not available, β is an adjustable parameter in Table 2. The optimized results for the intrinsic buffer capacity are 14 mm in EDL and 4 mm in SOL. The total buffer capacity sums the intrinsic buffer capacity and buffering due to Pi, bicarbonate/CO₂ and all the other metabolites, and varies between 16 mm in EDL and 3.4 mm in SOL in the aerobic resting state and 24.2 and 12.7 mm at the end of 60 min anoxia for EDL and 46 min anoxia for SOL, respectively (Fig. S14, Supplementary material).

Flux in glycolysis is a function of ATPase

The next question concerns the regulation of glycolytic flux and the identity of the reaction that determines the flux. We test the hypothesis that the ATPase reaction, outside of the main pathway of glycogenolysis and glycolysis, sets the pace of glycolysis using numerical simulations. These simulations used the fitted parameters from the results presented above and forced the ATPase rate to increase as a multiple of the measured rate at rest. Lactate output is calculated as the integrated flux in LDH during a simulated anoxia of 40 min. These simulations show that the glycolytic flux is a sensitive function of ATPase (Fig. 5), increasing approximately 2-fold per unit increase in ATPase. After a 2.4-fold increase in ATPase, the solutions of the model equations for SOL oscillate preventing analysis of higher ATPase rates. The simulations for EDL were extended to a 5-fold increase in ATPase and the lactate output increased linearly 14-fold (result not shown). The main result is that in the neighbourhood of resting ATPase rate, the extent of glycolytic flux is governed by the ATPase rate in EDL and SOL. A mechanism for this control is feedback regulation of glycolysis by products of ATPase.

Figure 5.

Numerical tests simulate the relationship between relative ATPase and lactate flux Calculated lactate flux is plotted as the ratio of a test to the simulated resting lactate flux as in Fig. 4 on the ordinate. The test is conducted with ATPase as a multiple of the observed resting ATPase on the abscissa. Continuous line represents EDL and the dashed line SOL. Simulations are made for reference and test as in Fig. 4 except for calculating the LDH flux to the end of 40 min of the anoxic interval for each muscle.

Role of adenylate kinase in regulation of glycolytic flux

Glycogen phosphorylase b requires both Pi as a substrate and AMP as an allosteric activator. As [PCr] decreases, [ADP] increases by the CK reaction leading to a greater increase in [AMP] due to the quadratic stoichiometry of the AK reaction. We tested the requirement of AK function on lactate production by setting the AK flux to zero in the simulation. Without AK activity, the increase in glycolytic flux is reduced. The lower set of curves in Fig. 4 show only a small increase in lactate synthesis in the absence of AK activity, indicating that AK activity leading to a rise in [AMP] is necessary to increase lactate production as measured in anoxic resting muscle. [AMP] calculated in the simulation increases almost two orders of magnitude from approximately 10⁻⁸m in both EDL and SOL to 18 μm in EDL and 55 μm in SOL. Further analyses (Figs S15 and S16 in Supplementary material) show a greater dependence of glycolytic flux on [AMP] than on [Pi] or [ADP]. The correlation of glycolytic flux with increased [AMP] indicates that the pathway is regulated by feedback mechanisms, with the primary one being the increase in [AMP], a product of the combined action of ATPase, CK and AK. Thus, the role of AK and [AMP] is critical to account for experimentally measured flux. With adenylate kinase zeroed (bottom curves in Fig. 4), there is some increase in glycolytic flux in anoxia because Pi and ADP are required substrates. However, the increases in [Pi] and [ADP] do not account for the measured lactate flux because the effects by mass action are smaller than the allosteric effects of AMP on GPb as the results in the next section amplify.

Kinetic role of glycogen phosphorylase b

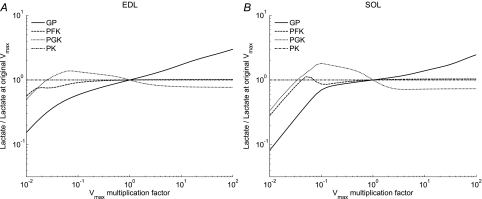
The simulations in Fig. 4 with AK at zero indicate the requirement for increased [AMP] to increase glycolytic flux and show that GPb is an important regulator of flux in resting muscle. We simulate the effects of modifying the activity of the enzymes that are usually thought to have a role in control of glycogenolysis and glycolysis (GPb, PFK, PGK and PK). These reactions have the largest free energy change in the pathway (discussed below). The test is simulation of the lactate output at a fixed duration of anoxia as a function of enzyme activity. For these simulations, the V_max of each of these enzymes is individually varied from 10⁻² to 10² times the reference activity (Table 1), and the ratio of the test lactate output to the reference lactate output at 40 min of anoxia in EDL is calculated. Figure 6 displays the result of simulations at discrete multiples of V_max for each enzyme. Glycolytic flux increases monotonically with the activity of GPb in both muscles. At low V_max, variable flux occurs, whereas at increased enzyme activity (higher multiples of V_max) flux is independent of the activity of PFK, PGK and PK. These simulations demonstrate that GPb is the important kinetic step in the regulation of glycolytic flux in resting muscle and that the other enzymes play a minor role at most.

Figure 6.

Numerical tests of the influence of enzyme activity on the extent of lactate production for selected enzymes A displays results for EDL; B for SOL. The ordinate displays ratios of a simulation of lactate production with the activity for a single enzyme altered in the numerator to the simulation for reference lactate production with unaltered enzyme activities in the denominator. The references are simulated as in Fig. 4 and calculated at 40 min for the specified multiplication factor. The abscissa is the factor by which the V_max for each of the enzymes was multiplied in the simulation where V_max is the reference value used in the model (Table 1). Only the indicated reaction was modified for the simulation. Calculating each ordinate value at many discrete multiples of enzyme activity and connecting the points by continuous lines constructed the graph. GPb, continuous line; PFK, dashed line; PGK, dotted line; PK dash–dot line.

Simulations show the rise in [AMP], while necessary for activation of GPb, is not sufficient to increase glycolytic flux enough to sustain energy balance. It is possible to define conditions for numerical simulations that do achieve energy balance, but these are not attainable physiologically. Figure 7 shows time courses of PCr and Pi in simulations performed by setting [AMP] to maximally activate GPb, with Pi clamped or with Pi freely varying. These simulations also test the requirement for sufficient [Pi] and pH near neutrality for sustained glycolytic flux. The conclusion from these simulations is that the enzyme activities used in the model are sufficient to achieve glycolytic flux that can sustain energy balance during anoxia. However, in the default condition of rest, the metabolic conditions do not attain the required increase in flux to achieve energy balance. The failure to achieve energy balance is due to insufficient [AMP] to activate the glycolytic flux at GPb and this is caused by the low rate of resting ATPase flux coupled to CK and AK. The fraction of ATPase provided by glycolytic flux does increase during anoxia. In simulations for 60 min of anoxia in EDL (Fig. S22, Supplementary material) the fraction rises to approximately 20% between 20 and 40 min of anoxia and reaches 80% during the last 20 min of anoxia. In simulations of SOL for 46 min of anoxia, the fraction of ATPase provided by glycolytic flux rises rapidly to oscillate between 80 and 100% after 20 min or anoxia. Thus, ATP synthesis by the glycolytic network cannot achieve or sustain full energy balance in either muscle during anoxia.

Figure 7.

Simulations of [PCr], [Pi] and [ATP] before and during anoxia, with and without numerically fixing [Pi] and [AMP] The simulation from 0 to 20 min reproduces that in Fig. 1 for each muscle; A, EDL; B, SOL. At 20 min of the simulation [AMP] is clamped at 0.1 mm. At the same time [Pi] was clamped to 2.3 mm or allowed to vary as an adjustable parameter; continuous lines, [PCr]; dashed lines, [Pi]; and dotted lines, [ATP]. Black continuous lines are the PCr results with [Pi] clamped and grey continuous lines are the results with [Pi] freely varying. The simulations displayed in this figure also have pH clamped at 7.0 after 20 min; if not clamped, pH declines and none of the simulated results go into a steady state. When Pi is not clamped (grey dashed lines) its concentration falls to zero and PCr (grey continuous lines) does not reach a steady state.

Inorganic phosphate is a required substrate for glycogenolysis and can contribute to the regulation of glycolytic flux by mass action effects by increased [Pi]. The next simulations test the effects of [Pi] on glycolytic flux by fixing [AMP] at 10⁻⁴m in order to activate GPb maximally; the results are displayed in Fig. 7. These are not physiological conditions but do provide relevant information. The simulation of the resting aerobic state is the same as shown in Fig. 3. When anoxia begins at 20 min, [Pi] is clamped (or not), [AMP] is clamped at 10⁻⁴m, pH is clamped at 7.0 and the adenylate kinase reaction is zeroed so no changes in [AMP] occur. When [Pi] is clamped at initial resting values (approximately 2.5 mm) the simulations show that eventually a steady state energy balance is achieved with modest reduction in [PCr] (Fig. 7, black lines). With [AMP] equal to 10⁻⁴m and without clamping [Pi] (grey continuous and dashed lines), energy balance is not achieved. Glycolytic flux decreases to zero because the required substrate, Pi, decreases; conservation of total phosphate in the cell is maintained because Pi accumulates in the phosphorylated intermediates in the glycolytic pathway (Figs S18 and S19 in Supplemental material). Note that pH is clamped at 7.0 for all of these results. If pH is not held at pH 7 in the simulation, pH decreases and glycolytic flux cannot maintain ATP synthesis or sustain energy balance even with high [AMP] and [Pi]. The conclusion is that in resting muscle, glycolytic flux can only increase enough to balance resting ATP consumption rate with sufficient [AMP] and [Pi], and pH near 7, whereas the physiological state of the glycolytic network coupled to resting ATPase cannot achieve the required conditions.

Energetics of the reactions in the pathway

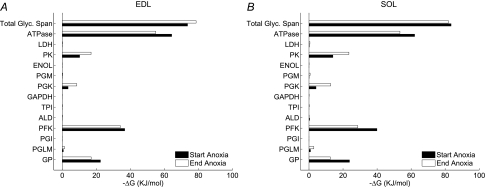
Simulation results so far show that the increase in glycolytic flux is kinetically regulated by feedback from products of ATPase on GPb. Here we ask whether the overall free energy from glycogen to lactate is sufficient to drive the fluxes required for simple feedback kinetic regulation. We calculated the Gibbs free energy (ΔG) of each reaction in the pathway for the aerobic control at rest and for the final 5 min of anoxia for EDL and SOL (i.e. at 55 min of anoxia for EDL and 41 min for SOL). The sum of ΔG for all 13 reactions exceed (more negative) the ΔG of ATPase by 20–30 kJ mol⁻¹, accounting for the net flux of glycolysis to lactate formation coupled to glycolytic ATP synthesis. Figure 8 shows the ΔG at GPb, PFK, PGK and PK are the largest in the pathway, in the range of −10 to −40 kJ mol⁻¹ and the magnitudes are similar in EDL and SOL. The size of the ΔG is in the order PFK > GPb > PK > PGK. Except for ATPase, all the other reactions have low free energy and therefore are close to biochemical equilibrium in the cellular conditions of the model.

Figure 8.

The apparent free energy of the reactions in the pathway for glycogenolysis and glycolysis are calculated for simulations for EDL (A) and for SOL (B) under normoxia and at the end of the anoxia transient The apparent free energy is equal to the standard transformed free energy of the biochemical reactions as defined by Alberty (2003) and applied to muscle in Vinnakota et al. (2006). Filled bars give the value during the initial aerobic period; open bars are derived from the simulations shown in Fig. 3 and give the mean value during the final 5 min of anoxia (74 to 79 min in EDL and 40 to 45 min in SOL). Each reaction in the glycolytic network is given from GPb (GB) on the bottom to LDH. The apparent free energy of ATP hydrolysis reaction is labelled ‘ATPase’. The sum of the apparent free energies of the thirteen reactions in the network is labelled ‘Total Glyc. Span’.

We define the efficiency of glycolytic ATP synthesis as the ratio of free energy expended for ATP synthesis by the pathway to the free energy expended in metabolism of glycogen to lactate. The average efficiency during anoxia was found to be 65.8% EDL and 63.4% for SOL. The average fraction of ATP demand met by glycolysis is 54% for EDL and 59% for SOL; the rest of the demand is satisfied by PCr breakdown. Thus, in a network of reactions such as glycogenolysis and glycolysis, a significant amount of chemical potential is utilized to alter the concentrations of substrates and products that are necessary for altered fluxes (Figs S18 and S19 in Supplementary material).

The overall conclusion from this thermodynamic analysis is that there is sufficient chemical potential in glycogen metabolism to drive all of the reactions in the network. The function of glycogenolysis and glycolysis in anoxia is considered to be the generation of ATP, and it is surprising that only 2/3rd of the available free energy is converted into the apparent Gibbs free energy of ATP hydrolysis reaction.

Generation and uptake of H⁺

Model simulations give sufficient information to answer definitely which reactions generate H⁺ and which take up H⁺, and thus settle long-standing debates about the source of H⁺ in muscle glycolysis. The apparent H⁺ stoichiometry of a biochemical reaction is influenced by differences in the pKa between substrates and products (Alberty, 2003; Vinnakota et al. 2006). As the model includes full accounting of proton and ion binding and the thermodynamics for each reaction, the simulations can calculate H⁺ flux during the experiment for any reaction as well as sums for groups of reactions. Figure 9 shows that the proton fluxes for components of the metabolic network are similar in both muscles during the anoxia transients.

Figure 9.

Simulations of proton flux in selected components and reactions during the entire experimental protocol for 60 min of anoxia in EDL (A and B) and 46 min of anoxia in SOL (C and D) Ordinates give the proton consumption fluxes. Positive quantities represent H⁺ uptake and negative ones H⁺ production. Units on the ordinate are m min⁻¹× 10⁻³ and thus equal to mm min⁻¹. Units on the abscissa are simulated elapsed time during the experiment. A and C show H⁺ flux in the creatine kinase reaction (CK), in the combined ATPase and its reversal by oxidative phosphorylation (ATPase + Oxphos), in carbonic anyhdrase reaction (CO₂ hydration) and by the lactate proton transporter (MCT). B and D compare the total flux of the system (Total, all fluxes) with the proton flux contributed by the sum of all of the reactions in glycogenolysis and glycolysis (glycogenolysis).

Proton fluxes due to ATPase and oxidative phosphorylation balance each other during normoxia when the other reaction and proton fluxes are negligible. At the start of anoxia, oxidative phosphorylation stops and PCr breakdown begins. These reactions cause the alkalinization (proton uptake) seen in the simulation of the pH time course and detectable in the data at the onset of anoxia. The net proton stoichiometry of the combined ATPase and creatine kinase reactions is positive in the pH range of this experiment (approximately 7.1–6.9), and this causes proton consumption by the net reaction of PCr breakdown to creatine and Pi, classically called the Lohmann reaction (the sum of ATPase and CK). As time progresses, glycolytic flux increases and ATP synthesis by glycolysis is accompanied by the decrease in CK proton flux. At a constant ATPase rate the increase in glycolytic ATP synthesis proportionately decreases CK flux. This combination leads to net acidification due to the proton generation from continued ATP hydrolysis flux but lower CK flux (Fig. 9, panels A and C). Panels B and D show that the sum of reactions from glycogen to lactate per se does not contribute significantly to the proton fluxes. The individual reactions do have substantial H⁺ production or uptake (Figs S20 and S21 in Supplemental material). The role of carbonic anyhdrase and CO₂ and bicarbonate exchange is significant but smaller than ATPase and CK. Large H⁺ producers are PFK, PGK and GAPDH reactions with smaller contributions from phosphoglycerate mutase and enolase. Strong H⁺ uptake occurs at LDH and PK with smaller contribution from aldolase. Phosphoglucoisomerase, phosphoglucomutase and G3PDH make no significant contribution to H⁺ balance. The relevant physiological point is that constraints of physical chemistry of the reactions are such that the H⁺ balance of the individual reactions within the glycogenolytic pathway sums to near zero in the achievable pH range.

Stoichiometry of net H⁺ and lactate anion production

The stoichiometry of overall H⁺ production and lactate synthesis is presented in Fig. 10 to estimate their ratio and to test whether the ratio is constant during anaerobic lactate synthesis. H⁺ production is the sum of all of the fluxes as presented in Fig. 9 integrated over time interval. The lactate synthesis is the total flux of LDH integrated over the same time. The graph shows a 1:1 stoichiometry for H⁺ and lactate⁻ production during the experimental phase when glycolytic flux is generating lactate and synthesizing ATP, that is, from approximately 40 min to approximately 80 min in EDL and from approximately 40 min to 70 min in SOL. The significance of this result is that the many processes involved in H⁺ generation and uptake sum to a simple stoichiometric ratio that is constant with respect to the lactate anion and H⁺ produced. The 1:1 stoichiometry is of course not observed when glycolytic flux is negligible. The value of the simulations is that they allow a dissection and quantification of the specific reactions that are involved in the reaction network.

Figure 10.

Numerical solutions of the model showing the stoichiometric relationships between total H⁺ production in the network of reactions (‘proton load’) and total lactate synthesis (‘lactate’) as a function of time during an entire experiment A gives simulations for EDL, 60 min anoxia; B gives simulations for SOL, 46 min anoxia. Proton load is the sum of all the H⁺ production and uptake for every reaction in the network: ATPase, CK, AK and the 13 reactions of glycogenolysis/glycolysis pathway. It is the net total H⁺ generation as a function of time. Total lactate synthesis is the flux in LDH reaction integrated over the same time interval.

Discussion

Metabolic perturbation by transient anoxia

The experimental results reported here for resting EDL and SOL contrast with the classically defined differences in metabolic phenotypes in actively contracting fast and slow muscle where the ATPase and glycolytic rates differ by a factor of 3 or more between muscle types. Thus, the present results define a novel phenotype of energy metabolism in these resting muscles that is a default phenotype for glycolysis.

In this default description, the resting ATPase rates are consistent with the oxygen consumption measured in mouse EDL and SOL (Crow & Kushmerick, 1982) and in fast-twitch and slow-twitch cat muscles in vivo (Bockman, 1983) and with some, but not all, of the data for resting rates of heat production (Wendt & Barclay, 1980; Cox & Gibbs, 1997; Barclay et al. 2009). The muscle phenotype changes from the default to the conventional one with contractile activity that is classically used to distinguish muscle types. Therefore, the phenotype for glycolytic regulation of muscle depends on the physiological state and reverts to this default state at rest where the metabolic activity is minimal. A corollary is that additional mechanisms beyond feedback by [AMP] occur in active muscle. Mechanisms downstream of sarcolemmal depolarization and increased [Ca²⁺] are necessary to manifest the conventional phenotypes of actively contracting fast and slow muscle.

Although there is some discrepancies in the literature for the resting heat rates between EDL and SOL muscles described in the Introduction, the most recent results (Barclay et al. 2009) convincingly show that the resting metabolism in SOL is higher than in EDL by a factor of 1.4 at 20°C, close to the temperature of the present experiments. We conclude that there is no difference in the resting ATPase in the two muscles (Fig. 2), but our chemical measurements have greater relative error. The ratio of the ATPase for SOL to EDL is 1.1 (0.63/0.57); the 95% confidence limits cannot exclude a ratio of their difference as high as 1.3 (0.76/0.59). Thus, there may not be a conflict between our results with the measured ratio of the resting heat rate. The model results are more precise and indicate no difference between SOL and EDL. The experimentally determined ATPase rates were based on linear regression of the first 10 min of PCr decline from the beginning of the anoxic interval. The model estimate of ATPase rate is based on the entire experiment as opposed to the limited amount of data used for direct estimation of ATPase rate. To address the question on the limits of ATPase estimates for each muscle, we computed the probability of acceptance of the model simulations over a range of ATPase rates for EDL and SOL (see Supplementary material). The probability of acceptance is defined as the average cumulative probability of the value of a parameter in the model simulation assuming that each data point is normally distributed with the estimated mean and s.d.s derived from all experiments. This analysis yields the probability distribution of ATPase in SOL peaks at a value of 0.73 mm min⁻¹, a value that is 6% higher than that of EDL (0.69 mm min⁻¹). The probability that the model estimated ATPase rate of SOL is different from that of EDL is 0.0053, and that the probability of the model estimated ATPase rate of EDL is different from that of SOL is 0.0124. We conclude that there may be a difference between the chemical and myothermal measurements of resting metabolism, and testing that possibility requires further experimentation.

Commonly, studies of muscle energetics perturb the steady state from rest by increasing the ATPase rate with twitch or tetanic contractions wherein ATP usage exceeds ATP resynthesis, decreasing [PCr]. In contrast, the experiments described here maintain the resting ATPase and perturb the steady state by decreasing the rate of ATP synthesis. The changes in [PCr] and [Pi] and in pH induced by transient anoxia during anoxia are the same order of magnitude as those achieved by tetanic stimulation, but occur more than 200-fold slower. ATPase at rest averages 0.6 mm min⁻¹ in both muscles whereas in isometric tetanus ATPase is 4.7 mm s⁻¹ in EDL and 2.4 mm s⁻¹ in SOL, measured during the first 12 sec of isometric tetanus (Crow & Kushmerick, 1982); similar differences are documented in other fast and slow twitch muscles (Meyer & Foley, 1996). The similar patterns and extents of chemical change in both resting and actively contracting muscle mean that the regulation of the coupled cellular ATPases with the creatine kinase in the cellular environment are robust over a 200-fold range of the reaction flux whether the energy balance is perturbed by an increase in ATPase rate or a decrease in ATP synthesis rates; in all cases the [ATP] does not change because CK buffers against changes in [ATP] by decreasing [PCr].

Simulations account for the experimental data

Mathematical models are useful adjuncts to analyse experimental results when the model fits the available experimental data. We fitted the model to grouped data that combined all experiments for a single optimization with the same cost function for data from each muscle. Figure 3 shows that the simulated results pass through the data points from experiments for 60 min anoxia in EDL and for 46 min anoxia in SOL, as well as for experiments for other durations of anoxia (Fig. S13 in Supplementary material). Comparisons between initial values for parameters obtained from published values and optimized values from fitting the model to the data (Table 2) show only minor differences. Coefficients of variation for the adjustable parameters in the model are given in Table 2. Additional tests showing the covariance among the adjustable parameters, the necessity of these parameters to describe the data and the ability to identify them uniquely in the model are given in the Supplementary material. We also optimized each experimental group separately, and values for the adjustable parameters varied little from those in Table 2. The quality of the fits allows us to conclude that this model represents well the ATPase rate, the rate of lactate production, the pH changes and the change in flux of glycogenolysis and glycolysis and the aerobic recovery, and that the conclusions discussed above on the mechanism of regulation of glycolytic flux are valid. The significance of these analyses is that enzyme properties and parameters based on in vitro biochemical experiments and solution thermodynamics are sufficient to account for the observed flux and chemical changes in resting muscle by mass action and feedback mechanisms. The corollary is that more complex ideas of compartmentalization of enzymes and substrates, association of glycolytic enzymes with intracellular macromolecules and structures, and alteration of enzyme kinetic properties by molecular crowding are not needed to account for the present results that pertain to the default metabolic state of resting muscle; these may be important to account for the higher fluxes in active muscle.

The model fit to the data is not perfect but the simulations with the model are of sufficiently high quality that they can be used to give an account of the regulation of glycolytic flux in resting muscle and untangle details of the biochemical mechanisms involved in regulating the flux. The simulated fluxes match the time courses of [PCr] decline and [Pi] increase in anoxia and the recovery on return to normoxia, and show the absence of change in [ATP] (Fig. 3). Of course, there is a reduction in [ATP] due to increase [ADP] in the 10⁻⁶m range and [AMP] in the 10⁻⁸m range, too small to be detectable in the figure but apparent in the simulations. Simulations match the experimental alkalinization at the onset of anoxia but the measured pH changes are small and the data are particularly noisy (Figs 1 and 3). The simulated decrease in pH tends to lag the decrease in the data, but the rate of decline is matched well. In both muscles, lactate production increases after a delay (Fig. 4). The simulated lactate flux is a function of the pH buffering and calculations of H⁺ uptake and release by all the reactions in the network including CO₂ flux into the external solution. The rate constant for ATPase is the only adjustable parameter in the ATP flux equations and is determined by fitting the model to the data for [PCr], Pi], [ATP] and pH. The ATPase is measured experimentally by the rate of decrease of PCr during the first 10 min of anoxia whereas the entire data set for the time course of PCr, Pi, ATP and pH is used to fit the model to the data and to obtain the simulated ATPase. For all these reasons we conclude that the simulations adequately describe the data and that conclusions drawn from the simulations are relevant and valid for the intact muscle.

The measured [ATP] and [PCr] and related metabolites in SOL are lower than in EDL, and as shown experimentally, 46 min of anoxia nearly completely depletes PCr in SOL whereas depletion of PCr in EDL is not so great after 60 min of anoxia. As a consequence, the rise in [AMP], calculated in the simulation, is 5 times higher in SOL than in EDL, and this difference may be the reason for the oscillations in flux simulated in SOL but not in EDL. We did not explore these aspects of the regulation of glycolytic flux as they have been in other systems (Termonia & Ross, 1981a,b; Goldbeter, 1996). High [AMP] occurs in oscillations in these systems. An important result of CK and AK activity is to limit the rise in ADP and AMP concentrations in muscle.

We use a Hill-type allosteric AMP activation model for GPb from Lambeth & Kushmerick (2002). Regulation of GPb is complex and may be species specific; it is definitely different in brain and muscle (Crerar et al. 1995). Our parameter estimates show a similar degree of cooperativity in the value for the Hill coefficient and a lower AMP half-maximal activation concentration when compared to the reported values for rabbit muscle GPb (Crerar et al. 1995) based on in vitro assays (Table 2). The difference could be due to a difference between the species and between the in vitro assay conditions and intracellular milieu.

Estimates for the parameter for the intrinsic pH buffer capacity are applicable to the small range of pH changes measured, and any model application to a larger pH range will require a re-estimation of this parameter based on pH data pertaining to that range. In muscle homogenates, the non-phosphate buffer capacity corresponds to the intrinsic buffer capacity. In the study by Adams et al. (1990) the non-phosphate buffer capacity of rat gastrocnemius, cat biceps and cat soleus varied as non-linear functions of pH with maxima at the edges of the pH range (6 to 8), with a region of nearly constant buffer capacity containing the minimum value and spanning about 0.3 pH units located near pH 7. This flat section of the function corresponds to the region of our pH measurements and estimates of the intrinsic buffer capacity. Leem et al. (1999) interpret their intrinsic buffering capacity data (approximately 30 mm at pH 7) as a mixture of two buffers with pKa values of 6.03 and 7.57 in guinea pig ventricular myocytes, which would result in pH dependency of intrinsic buffer capacity similar to the results obtained by Adams et al. (1990), namely non-phosphate buffer capacity is between 20 and 40 mm depending on the specific muscle. We find the intrinsic buffer capacity is 16 and 3.4 mm, respectively, in EDL and SOL (Table 2) with large coefficients of variation. The total buffer capacity adds buffering due to bicarbonate, phosphate and other metabolites to the intrinsic buffers. In our model, all of the metabolite buffering is calculated from the computed metabolite concentrations, and intrinsic buffer capacity is added to it to compute the total buffer capacity time course. The Results show that the total buffer capacity rises to 24 and 13 mm in EDL and SOL, respectively, towards the end of 60 min and 46 min of anoxia (Fig. S14, Supplementary material).

Feedback regulation of glycogenolytic and glycolytic flux by ATPase

Homeostasis in a metabolic network which balances supply and demand for chemical energy can be attained even if the reaction that sets the demand is outside the pathway for supply (Fell, 1998; Thomas & Fell, 1998; Hofmeyr & Cornish-Bowden, 2000). The requirements for regulation in such a system are that one metabolite is common to both the supply and demand components and that there is feedback to the supply pathway by products of the demand reaction. Flux control in the supply network by demand is nearly complete when the sensitivity of the supply to the common metabolite greatly exceeds the sensitivity of the demand (Hofmeyr & Cornish-Bowden, 2000). Experimental results and model simulations show that the demand of cellular ATPase and the supply of ATP by glycolysis form such a network and mechanism for regulation. Simulations show the mechanism of regulation of glycolytic flux (the supply network) is the ATPase (the demand reaction). The ATPase demand is independent of [AMP] but the supply is strongly regulated by [AMP] (Figs 4 and 7). The ATPase is independent of its primary products, ADP and Pi, and secondary product (AMP via AK reaction) because the ATPase rate is linear over the first 10 min of anoxia (Fig. 2) and because the ATPase rates obtained from the simulations using the entire set of data are close to that measured (Table 2). Since the ATPase in resting EDL and SOL are similar, the expectation is that the rate of lactate production is also similar, and this result is shown experimentally and by simulation (Fig. 4).

The metabolic state of resting muscle is the default condition that limits glycogenolytic and glycolytic flux by the low [AMP]. The delay in the onset of increased glycolytic flux and concomitant ATP synthesis is due to the time needed for [AMP] to increase GPb activity. Flux is uniform and equal in the enzymes of the pathway (Fig. S17 in Supplemental material). There is no thermodynamic limitation to flux at any reaction step in the pathway (Fig. 8). Thus, the results in intact muscle are the same as found in experiments with reconstituted glycolytic enzymes in vitro (Scopes, 1974a,b;). ATPase was the independent variable and determined the glycolytic flux; simulation of those experiments (Vinnakota et al. 2006) also shows regulation of flux by ATPase demand. Thus, the kinetic regulation of the glycolytic flux by ATPase in the default phenotype is fundamentally different from conventional views of its regulation (Connett & Sahlin, 1996) and forms the base upon which more complex regulation can be added. The regulation of glycolytic flux in resting muscle occurs by feedback control by products of ATPase, primarily AMP via AK; this regulation is necessary to account for the experimental results reported here.

Why is energy balance not attained during anoxia?

Experimental results also show that glycolytic flux cannot be activated sufficiently in resting muscle to attain energy balance. [PCr] declines during anoxia and therefore the rate of glycolytic ATP synthesis is less than ATPase. There is a delay of approximately 11 min before AMP rises sufficiently above about 3 × 10⁻⁸m to increase flux in GPb. The reason the rise in [AMP] is not sufficient to increase glycolytic flux to match resting ATPase is due to constraints of the CK and AK reactions. At the onset of anoxia, CK flux prevents large changes in [ATP] and [ADP] as [PCr] declines; thus [ADP] rises in the micromolar range whereas increases in [Pi] are in the millimolar range. These same reactions slow the rise in [AMP] necessary to increase glycolytic flux and constrain [AMP] to remain in the micromolar range, well below that which achieves energy balance (Fig. 7). Note that the increase in [Pi] is not itself sufficient even though it is a substrate for GPb. Thus, the kinetic and thermodynamic properties of CK and AK combined with the low rate of ATPase constrain the increase in [AMP] and prevent energy balance in anoxic resting muscle.

The limited glycolytic flux (less than ATPase) is not due to low values of enzyme activity used in the calculations. The activity of the enzymes (Table 1) are representative of intact muscle and are sufficient for high glycolytic flux as observed in tetanically stimulated mouse muscles (Crow & Kushmerick, 1982). Yet the flux in resting anoxia muscle is more than 100-fold smaller than that in tetanic contractions seen by comparing 0.6 mm min⁻¹ at rest (Fig. 2) to 281 mm min⁻¹ in EDL and 146 mm min⁻¹ in SOL during 12 sec tetani reported by Crow & Kushmerick (1982). Model simulation in Fig. 7 shows that energy balance can be attained under conditions that are not physiologically possible in resting anoxic muscle. The constraints just discussed can be relieved by calculations to fix high [AMP], constant [Pi] in the millimolar range and constant, neutral pH. The implication of the present experiments and simulations, and of the results in tetanic stimulations (Crow & Kushmerick, 1982) is that Ca²⁺ and downstream effects of muscle depolarization are needed, in addition to increases in critical metabolites, for full activation of glycolysis. Studies of human muscle in situ came to a similar conclusion on the critical role for muscle activity in regulating glycolytic flux (Conley et al. 1997; Crowther et al. 2002a,b;).

Sources of proton uptake and release

Much discussion in recent years concerned the biochemical mechanisms that generate lactate and H⁺ (e.g. Robergs et al. 2004, 2005; Boning et al. 2005; Kemp, 2005; Lindinger et al. 2005; Prakash et al. 2008). The present experimental data and simulations with the thermodynamically and mechanistically validated model answer definitively the questions relevant to the muscle cell; processes outside the cells in the intact animal were not investigated here. Lactic acid production and transport are properties inherent in the system of chemical reactions in the muscle cell. A major advantage of using the model is its ability to simulate fluxes and proton loads in individual reactions as well as groups (Fig. 9 and Figs S20 and S21 in Supplementary material). In anoxia, continued ATPase generates H⁺ and feedback by its products activates increased flux in glycogenolysis and glycolysis with a 1:1 stoichiometry of H⁺ to lactate anion (Fig. 10). This lactic acid (a weak acid, fully dissociated within the cell) is transported by MCT symport into the extracellular space leading to the well-known lactic acid production by muscle.

Our more detailed simulations show that ATPase dominates H⁺ production and CK dominates H⁺ uptake, as pointed out by Gevers (1977), Hochachka & Mommsen (1983) and Robergs et al. (2004), but none of these authors made the detailed analysis as we do here. Simulations show that the primary generator of H⁺ within the cell is the ATPase flux and the primary uptake of H⁺ is the CK flux or the reversal of ATPase by oxidative phosphorylation in aerobic conditions. Glycolytic flux generates lactate anion specifically at the LDH reaction. Our analysis excludes the sum of the reactions of the glycogenolytic and glycolytic pathway as contributors to net proton production to any significant extent (Fig. 9). Some of those reactions produce significant H⁺ as glycogenolytic and glycolytic flux proceeds (see Figs S20 and S21 in Supplementary material), e.g. PFK, PGK and GAPDH, whereas others absorb significant H⁺, e.g. PK and LDH, but the sum of proton production by all 13 reactions within the glycolytic network is nearly zero with physiological changes of [PCr] and [Pi] and of pH (Fig. 9). Thus, the sum of all of the reactions in this network is the generation of dissociated lactic acid. The simplified stoichiometry worked out by Kushmerick (1997) for ATPase and creatine kinase with glycolytic synthesis of ATP, as used for many experimental analyses (e.g. Conley et al. 1997; Crowther et al. 2002a,b;) is consistent with the more detailed simulations given here. The main conclusion is that the combined system of reactions from ATPase to LDH including CK and AK forms a network in which the emergent property is the synthesis of lactate anion and H⁺ in a 1:1 ratio (Fig. 10).

Interactions of metabolic H⁺ production and cellular H⁺ transport

A novel aspect of our work is the demonstration that proton balance and pH regulation in the cytoplasm is the net result of the integration of mechanisms of metabolic H⁺ production and uptake, including buffers, and mechanisms of transmembrane H⁺ transport. This insight is not surprising because there is a common pool of reactions generating H⁺ and taking up H⁺ that interact with cellular buffers. This means that mechanisms adding or subtracting H⁺ by advancement of metabolic reactions or by extracellluar perturbations such as pulses of high or NH₃ interact in the same way because all the biochemical reactions involve uptake or release of H⁺ as the reactions advance (Vinnakota et al. 2006). The metabolic reactions can themselves be influenced by fluxes of H⁺, CO₂ and other metabolites across the sarcolemma (Adams et al. 1991). This means for muscle cells that all the reactants and products in metabolic pathways that have pKa values in the physiological range participate in H⁺ buffering and need to be added to the interactions considered in the analysis of intracellular H⁺ diffusion (Swietach et al. 2003). There is sufficient thermodynamic driving force in the overall free energy change from glycogen to lactate to drive all of these reactions and transport processes forward (Fig. 8).

The present model for the open muscle system contains mechanisms for flux of H⁺, CO₂ and lactate across the sarcolemma in addition to intracellular mechanisms for H⁺ production and uptake. These details are necessary for the simulations to account for the experimental results of transient anoxia in EDL and SOL. Without equations describing transport and hydration of CO₂ and transport of lactate and H⁺ by MCT, simulations do not reproduce the pH transients, and lead to poorer fits of the model to PCr and Pi data than those shown in Fig. 3.

Glossary

Abbreviations

ΔG

Gibbs free energy of reaction

ATPase

sum of all ATP utilizing reactions in resting cell

EDL

extensor digitorum longus muscle

FID

free induction decay, the basic physical measurement in NMR

MCT

Monocarboxylate Transporter i.e., sarcolemmal lactate⁻/H⁺ symport

P/O₂

the ratio of moles of ATP synthesized in mitochondria per mole of oxygen used

PS/V_cell

the product of permeability of a solute times the cellular surface area, per unit cellular volume

RQ

respiratory quotient

SOL

soleus muscle

Author contributions

The experimental work was conducted at the University of Washington. Development of the model was started at the University of Washington and completed at the Medical College of Wisconsin. M.J.K. and K.V. designed the project. M.J.K., L.P. and J.R. performed experiments. K.V. developed the model and executed the simulations. E.S. contributed NMR methods and quantification of spectra. M.J.K., E.S., L.P. and J.P. analysed data. M.J.K. and K.V. wrote the paper, and all authors approved the final version.

SUPPLEMENTAL MATERIAL AND DATA

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors