Abstract
Previous research has suggested that three-dimensional (3D) structure-from-motion (SFM) perception in humans involves several motion-sensitive occipital and parietal brain areas. By contrast, SFM perception in nonhuman primates seems to involve the temporal lobe including areas MT, MST and FST. The present functional magnetic resonance imaging study compared several motion-sensitive regions of interest including the superior temporal sulcus (STS) while human observers viewed horizontally moving dots that defined either a 3D corrugated surface or a 3D random volume. Low-level stimulus features such as dot density and velocity vectors as well as attention were tightly controlled. Consistent with previous research we found that 3D corrugated surfaces elicited stronger responses than random motion in occipital and parietal brain areas including area V3A, the ventral and dorsal intraparietal sulcus, the lateral occipital sulcus and the fusiform gyrus. Additionally, 3D corrugated surfaces elicited stronger activity in area MT and the STS but not in area MST. Brain activity in the STS but not in area MT correlated with interindividual differences in 3D surface perception. Our findings suggest that area MT is involved in the analysis of optic flow patterns such as speed gradients and that the STS in humans plays a greater role in the analysis of 3D SFM than previously thought.
Keywords: functional MRI, humans, perception, temporal lobe, visual
Introduction
Motion parallax and other components of optic flow are powerful cues for the perception of depth and the three-dimensional (3D) shape and surface structure of objects (Rogers & Graham, 1979; Koenderink, 1986; Andersen, 1996). Previous research in humans suggested that 3D structure-from-motion (SFM) perception involves an occipitoparietal network (Orban et al., 1999, 2003; Paradis et al., 2000; Vanduffel et al., 2002; Klaver et al., 2008). Functional magnetic resonance imaging (fMRI) revealed stronger blood oxygenation level-dependent (BOLD) responses for moving lines defining 3D objects than for lines moving along a two-dimensional (2D) plane in V2/V3, the lateral occipital sulcus (LOS), V3A (a visual area located near dorsal V3), the ventral and dorsal intraparietal sulcus (VIPS and DIPS), and POIPS, the junction of the parietooccipital sulcus (POS) and the IPS (Vanduffel et al., 2002). Other fMRI studies (Orban et al., 1999, 2003) have reported that perception of 3D SFM involved the middle temporal (MT) complex (MT+) and ventral occipital lobe in addition to parietal structures. Moving dots defining a 3D sphere elicited stronger responses than 2D radial motion in the superior occipital gyrus (V3/V3A), the parieto-occipital junction, the ventral part of the occipitotemporal junction, and MT+ (Paradis et al., 2000).
By contrast, SFM perception in nonhuman primates seems to involve an occipitotemporal network. In macaques, 3D objects defined by moving lines elicited stronger BOLD responses than 2D planes in V2/V3, V4, MT and FST, the fundus of the superior temporal sulcus (STS) (Vanduffel et al., 2002). Another fMRI study (Nelissen et al., 2006) reported several distinct regions along the superior temporal lobe of macaques, in particular MT, medial superior temporal (MST) dorsal (-d), MST ventral (-v) and FST, that were more active during 3D SFM than during 2D plane perception. Neurons in the anterior superior temporal polysensory area of monkeys are able to differentiate between structured and unstructured optic flow patterns of a 3D transparent sphere (Anderson & Siegel, 2005).
The discrepancy between human and nonhuman primates regarding 3D SFM perception has been attributed to interspecies differences (Vanduffel et al., 2002; Orban et al., 2003). However, previous fMRI studies on humans focused on the parietal cortex, and the role of the temporal stream in human SFM perception may have been underestimated. Most previous studies examined group-averaged statistical parametric maps. This approach tends to underestimate the role of small brain areas as individual brain images need to be normalized to a template brain. In most previous studies 3D SFM was tested by moving lines (Orban et al., 1999, 2003; Vanduffel et al., 2002). Lines while they are moving in 3D continuously change their relative speed and location differently than lines moving in 2D. Although several control experiments (Vanduffel et al., 2002; Orban et al., 2003) adequately demonstrated that the 3D SFM-related activity observed in the IPS, LOS and MT+ did not depend on low-level stimulus attributes, activity differences between 3D and 2D stimuli in other brain areas (e.g. V2, V3 and V3A) were contingent on the type of 2D control used. The density of moving stimuli may affect neural responses in MT and other STS regions by motion opponency (Heeger et al., 1999). Other researchers have used moving dots forming a 3D sphere (Paradis et al., 2000) or 3D cube (Klaver et al., 2008). However, stimuli for the 2D control condition were non-rigid. Thus, differences in imaging results could be due to whether the stimuli were rigid or non-rigid rather than due to the 3D structure. Most previous studies only loosely controlled for attention while observers watched the 3D and 2D stimuli. Attention affects neural processing of motion (Beer & Röder, 2004, 2005) in motion-sensitive brain areas including V1 and MT (Watanabe et al., 1998). It is possible that some of these factors obscured the role of the temporal cortex in 3D SFM perception.
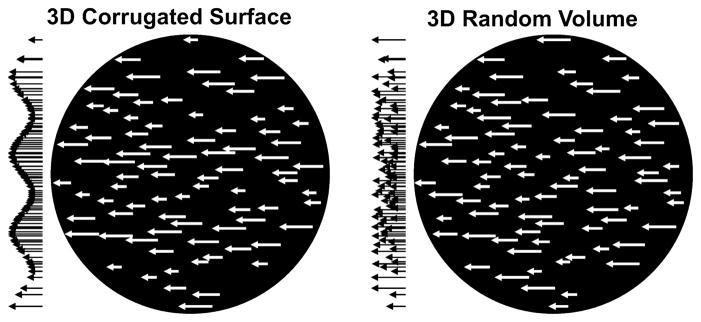
The present fMRI study examined the role of several motion-sensitive human brain areas in 3D SFM perception using a region-of-interest (ROI) approach. Our stimuli defined either a 3D corrugated surface (COR) or a 3D random motion volume (RND). The dot density, dot size and distribution of velocity vectors were identical for the COR and RND stimuli (Fig. 1). Thus, the only difference between our 3D rigid structure and the 3D rigid volume conditions was whether the display simulated a surface. Observers’ ability to perceive the motion-defined surface was assessed prior to the fMRI session. A speed-change detection task while viewing the dot patterns controlled for attention. We found that perception of motion-defined 3D surfaces involved several parietal and temporal brain areas including the STS. Moreover, BOLD responses in the STS correlated with the observers’ ability to perceive 3D surfaces.
Fig. 1.
Schematic illustration of COR and RND stimuli. Both the 3D COR (left) and the 3D RND (right) stimuli were composed of horizontally moving white dots on a black background, here indicated by velocity vectors. The distribution of the velocity vectors is depicted to the left of each circular aperture. For COR stimuli the distribution of velocity vectors varied sinusoidally along the vertical axis giving rise to an impression of a surface that is corrugated in depth. The same velocity vectors were used for RND stimuli though randomly distributed along the vertical axis. Subsequently, observers perceived dots moving randomly on a plane or within a 3D volume.
Materials and methods
Participants
Participants were six normal volunteers (paid $25 per scan h, $18 for the two behavioral experiments) and one co-author. All participants (five female, two male) reported normal or corrected-to-normal vision. All were right-handed. Their mean age was 28.8 years (range 23–49). Informed consent was obtained prior to the experiment. The study conformed with the Code of Ethics of the World Medical Association (Declaration of Helsinki) and was approved by the Institutional Review Board of the Massachusetts General Hospital.
Stimuli
Two types of stimulus were used throughout the experiment: a 3D COR stimulus and a 3D RND stimulus (Fig. 1). Both stimulus types were composed of white dots (2 pxl2, 12 dots/deg2, 150 cd/m2) moving horizontally in one direction (100% coherence) on a black background (10 cd/m2) within a circular aperture (10° diameter). For COR stimuli the speed of individual dots varied sinusoidally along the vertical axis, resulting in a perception of a 3D corrugated surface (Andersen, 1996). Accordingly, the speed vector for each individual dot was calculated from the formula vi = v0 + a × sin(2 × π × f × yi + ph) × v0, where yi [deg] is the vertical location of the dot relative to fixation, f [cycles/deg] is the spatial frequency of the COR, ph reflects a phase shift of the sinusoid (see below), the factor a quantifies the amplitude of the COR, v0 [deg/s] is the baseline speed of all dots and vi [deg/s] is the resulting speed vector at which an individual dot translated. The baseline speed v0 was 4 deg/s. This optic flow pattern induces, depending on the amplitude and spatial frequency, a compelling percept of a 3D corrugated surface (Andersen, 1996). The 3D RND stimuli were generated by randomly reassigning the velocities of the COR stimuli to different dots. Consequently, the dots appeared to move randomly, depending on the amplitude factor a, either on a plane or in a 3D volume without rendering a specific structure. Note that the COR and RND stimuli had identical local velocity vectors. A small static circle (diameter 8 pxl) in the center of the display served as fixation marker.
The duration of each stimulus was 4 s throughout the study. Dots were moving leftwards in half of the trials and rightward in the other half. The phase of the sinusoid for the COR stimuli was shifted 180 deg for half of the trials: ph = {0, π}.
Behavioral procedure
Two behavioral experiments were conducted prior to the fMRI sessions. Their goal was to assess whether observers perceived the moving dots as moving along a 3D surface and to identify optimal stimulus parameters for each individual. Stimuli during behavioral experiments were presented on a CRT monitor (1024 × 768 pxl, 75 Hz, 40 × 30 cm, viewing distance 60 cm) while the participant’s head rested on a chin rest.
In Experiment 1 participants either saw a COR or a RND stimulus. After the stimulus had disappeared, participants were asked to indicate by pressing one of two buttons whether they perceived the dots as moving in a structured manner (e.g., horizontal stripes or waves) or as uniformly distributed. If they responded ‘structure’ they were subsequently asked whether the structure appeared to be a ‘3D corrugated surface’ or a ‘2D stripe pattern’. Alternatively, they were asked whether the dots appeared to move in ‘3D depth’ or on a ‘2D plane’. Both the amplitude factor and the spatial frequency of the sinusoid used to calculate the speed distribution of dot vectors were varied across trials. Four amplitude factor levels (a = {2/15, 4/15, 6/15, 8/15} corresponding to a maximum-to-minimum velocity ratio vmax/vmin = {1.31, 1.73, 2.33, 3.29}) and four levels of spatial frequency (f = {0.2, 0.3, 0.4, 0.5} [cycles/deg]) were tested. The experiment consisted of five blocks of 64 trials each. For each participant an amplitude and spatial frequency level that allowed for best discrimination between structured (COR) and uniform (RND) stimuli as measured by d′ (Swets, 1973) and that gave a compelling 3D impression were chosen for subsequent tasks.
Experiment 2 was aimed at identifying a speed change threshold separately for each stimulus type. At a random time between 1 and 3 s after stimulus onset, dots briefly (i.e. for 80 ms) moved faster than usual. Individual dot speed vectors were multiplied by a factor varying logarithmically from 1 to 2.5 along 15 levels. Participants’ task was to press the space bar whenever they saw the dots briefly moving faster. Only single responses during each trial that occurred between 150 ms and 1000 ms after the speed change onset were considered correct responses. Speed change detection thresholds were estimated by the adaptive method of bestPEST (Lieberman & Pentland, 1982) starting with the highest speed change value. The experiment consisted of one block containing 40 trials of each stimulus type. Trials within the block were arranged in the same way as during fMRI runs. In particular, the block started with a 16-s fixation-only period. Then, 10 sets of COR–RND fixation trials were presented. Each set consisted of four consecutive trials of COR stimuli (16 s epoch) and four consecutive trials of RND stimuli (16 s epoch), followed by a 16-s fixation-only period. The order of COR and RND stimuli alternated each set. In half of the sets the phase of the sine wave was ph = 0 and in the other half the phase was ph = π. For each stimulus type a speed change factor slightly above the 75% correct threshold was used for the subsequent Experiment 3.
fMRI task
During Experiment 3 participants lay supine in an MRI scanner in a dimmed room. Stimuli were projected (1024 × 768 pxl, 75 Hz, 32 × 24 cm) on a transparent screen and were viewed via a back-mirror mounted on top of the coil. Viewing distance was 57 cm.
The fMRI experiment (Experiment 3) consisted of two or three blocks (runs) similar to the second behavioral task. Each block started with a 16-s fixation period, which was followed by 10 sets with a COR epoch (16 s), RND epoch (16 s) and a fixation epoch (16 s). The order of COR and RND epochs was counterbalanced across sets. The direction of moving dots alternated every 4 s. The phase was balanced across sets. Participants were asked to press a button with their right index finger whenever they recognized an increase in the dot speed. However, in contrast to the behavioral task, the same speed increase as indicated above was used throughout the session.
Definition of ROIs
A separate fMRI session served to identify ROIs. Retinotopic areas [V1, V2, V3, ventral V3 (VP) and visual area V4 (V4v)] were defined by their visual field representations (DeYoe et al., 1996). Accordingly, observers viewed (in blocks of 16 s) colored flickering checkerboards that covered either the horizontal meridian, the vertical meridian or the upper or lower half of the visual field. First, the visual cortex was classified into dorsal (d) and ventral (v) regions by contrasting activity maps for lower vs. upper visual field stimulation. In particular, stimulating the lower visual field was expected to activate regions dorsal to the center of the calcarine sulcus whereas stimulating the upper visual field was expected to activate ventral visual areas. Then, horizontal and vertical meridian representations were identified by contrasting activity maps for horizontal vs. vertical meridian stimulation. These meridian representations demarcated the borders segregating V1d/v from V2d/v (vertical meridian), V2d/v from V3/VP (horizontal meridian), and V3/VP from its neighbors V4v and V3A (vertical meridian).
Motion-sensitive regions of interests were identified by separate motion localizer runs. In particular, 16-s blocks of high-contrast whole-field radially moving dots were alternated with 16-s blocks of static dots. Brain areas [V3A, MT+, LOS, fusiform gyrus (FG), STS, parietoinsular cortex (PIC), POIPS, VIPS and DIPS] were labeled as described in previous studies (Orban et al., 1999, 2003; Sunaert et al., 1999). The contrast of radially moving dots vs. static dots for identifying motion-sensitive ROIs was chosen as radial motion is relatively rich in motion cues. For instance, it contains local and global motion as well as optic flow patterns. Note, however, that radial motion also differs from static dots in other non-motion cues. For instance, the arrangement of dots (pattern) during radial motion changes over time whereas it remains stable for static displays. Although this contrast tends to overestimate the extent of motion-sensitive brain regions it adequately limits our search for 3D SFM-related areas.
In order to subdivide the MT complex (MT+) into MT and MST we adopted a method described elsewhere (Dukelow et al., 2001; Huk et al., 2002). In brief, MST was taken as the area of MT+ that responded more strongly to peripheral ipsilateral radial motion than to static dots while the remaining part of the MT+ area, responsive to contralateral stimulation only, was assumed to be MT. Accordingly, we conducted several additional runs in which moving dots were presented in the peripheral visual field only (sparing 10 deg to both sides of the midline). Although defining MST by its ipsilateral representation tends to falsely classify regions containing MST neurons with exclusively contralateral receptive fields as part of MT, the MT–MST border defined by this approach agrees relatively well with demarcations defined by other criteria such as the retinotopy of MT (Huk et al., 2002).
Image acquisition
MRI data were acquired via a 3T head-only Allegra scanner (Siemens, Iselin, NJ, USA) and a 12-channel whole-head coil. Three high-resolution [1 × 1 × 1.3 mm3, field of view (FOV) 256 × 256 mm2, 128 sagittal slices] T1-weighted structural runs [repetition time (TR) = 2530 ms, echo time (TE) = 3.28 ms, flip angle (FA) = 7 deg, inversion time (TI) = 1100 ms] of the whole brain were acquired with a magnetization-prepared rapid acquisition gradient echo sequence in a separate session. Prior to each sequence of functional runs T1-weighted echo-planar images (EPI) were acquired (TR = 8000 ms, TE = 39 ms, FA = 90 deg, TI = 1200 ms) with the same slice parameters as the functional runs. These runs assisted in co-registering (spatially aligning) functional and structural images.
Functional images were acquired with a T2*-weighted EPI sequence (TR = 2000 ms, TE = 30 ms, FA = 90 deg) using a whole-head coil. Twenty-five coronal slices (3.125 × 3.125 × 3 mm3, no interslice gap, FOV = 200 × 200 mm2) were placed perpendicular to the calcarine sulcus covering the occipital and most of the temporal and parietal lobes. The number of acquisitions varied according to the experimental condition (see above). The first four scans of each run were discarded to assure that magnetization reached equilibrium.
Image analysis
Cortical reconstruction
Cortical reconstruction was performed with Freesurfer version 4.1 (Martinos Center for Biomedical Imaging, Charlestown, MA, USA). The three T1-weighted structural volumes were motion-corrected (Cox & Jesmanowicz, 1999) and averaged. Non-brain tissue was removed using a hybrid watershed–surface deformation procedure (Segonne et al., 2004). Images were corrected for intensity nonuniformities (Sled et al., 1998) and automatically transformed into Talairach space. After segmentation of the subcortical white matter and deep gray matter volumetric structures (Fischl et al., 2002, 2004), the gray–white matter boundary was tesselated and topologic inaccuracies automatically corrected (Fischl et al., 2001; Segonne et al., 2007). Then, the surface was deformed following intensity gradients to optimally place the gray–white and gray–cerebrospinal fluid borders at the location where the greatest shift in intensity defines the transition to the other tissue class (Dale et al., 1999; Fischl & Dale, 2000). Once the cortical models were complete, the surface was inflated (Fischl et al., 1999a). Finally, an occipital flat patch of the inflated surface posterior to the sylvian fissure (cut along the calcarine sulcus) was created.
Pre-processing
All functional volumes were analyzed with the FSFAST tools of Freesurfer. All functional volumes were motion-corrected to the first volume of each session (Cox & Jesmanowicz, 1999). The first volume of each session was manually co-registered to the structural volume using blink comparison. The T1 EPI volumes served as an intermediate reference. All functional volumes were corrected for intensity nonuniformities (Sled et al., 1998) and spatially smoothed by a three-dimensional Gaussian kernel. The full-width at half-maximum of the Gaussian kernel spanned 5 mm for the ROI analyses but was set to 8 mm for the whole-brain analysis (see below).
Labeling of ROIs
In order to label the ROIs we calculated statistical parametric maps for all localizer tasks (retinotopy, motion) using the general linear model approach with a blocked design. In particular, the design matrix consisted of the stimulation protocol convoluted with a cumulative gamma function (delta = 2.25, tau = 1.25, alpha = 2) and a linear and cubic predictor to compensate for BOLD signal drifts. For retinotopic localizer tasks we contrasted horizontal vs. vertical meridian stimulation and upper vs. lower visual field stimulation. For motion localizer tasks we contrasted radial motion stimulation vs. static dots. In order to reduce false positives significance maps were adjusted for multiple comparisons by setting the false-discovery rate to 0.001. Significance maps for each contrast were then overlaid on the inflated or flattened cortical surface of each individual hemisphere (see above). ROI labels defined by these localizer runs were then saved for the subsequent ROI analysis (see below).
In order to define retinotopic areas (V1d/v, V2d/v, V3, VP, V3A, V4v) the borders of upper and lower visual field representations and the center of the horizontal and vertical visual field representations were marked on the occipital flat patch. These demarcations defined the borders between neighboring visual brain areas. Motion-sensitive ROIs were defined by overlaying significance maps showing stronger BOLD signals for whole field moving than for static dots on the inflated cortical surface. Brain areas (V3A, MT+, LOS, FG, STS, PIC, POIPS, VIPS and DIPS) were labeled as described in the literature (Orban et al., 1999, 2003; Sunaert et al., 1999). The following criteria were applied in order to distinguish separate regions of interests: only activities outside of retinotopic areas were classified as additional motion-sensitive regions. Separate regions had to show spatially distinct activity patterns. Significant activity had to encompass at least five functional voxels in order to be considered for the subsequent ROI analysis. Subdivisions in the DIPS (anterior, lateral and medial DIPS) were not distinguishable in all participants and, hence, were not labeled separately. Note that we restricted data acquisition to the posterior part of the brain and excluded frontal areas such as the frontal eye fields which have also been shown to be motion-sensitive. The representation of peripheral ipsilateral motion stimulation was used to separate MST from MT. In particular, the proportion of MT+ that responded to ipsilateral motion was defined as putative MST while the reminder of MT+ was classified as putative MT.
ROI analysis
BOLD signal changes in response to 3D COR and RND stimuli were calculated by modeling each stimulation epoch with a finite impulse response function that represented 20 s relative to stimulus onset (16 s stimulation and 4 s after stimulus end). Additionally, a linear and cubic predictor was added to the general linear model to compensate for BOLD signal drifts. Rather than analyzing statistical parametric maps we restricted our data analysis to the predefined ROIs. For each hemisphere the mean BOLD signal change (given as percentage signal change) of all functional voxels falling within (minimum of 20% overlap) each ROI was calculated. Mean signals of the left and right hemisphere as well as dorsal and ventral representations of V1 and V2 were pooled. Finally, the average signal falling within 6–16 s after stimulus onset was submitted to t-tests or used for correlating BOLD signal changes with behavioral measures.
Whole-brain group analysis
Although a ROI analysis is a powerful method for revealing task-related BOLD signal changes, it bears the risk that relevant regions that have not been defined a priori are overlooked. Therefore, we conducted an additional whole-brain group analysis. In order to reduce the possibility that normalizing individual brains onto a template brain may obscure small but relevant regions, we applied a surface-based (Fischl et al., 1999b) rather than volumetric normalization procedure. In brief, cortical surface reconstructions of the hemispheres were registered to a spherical atlas using individual folding patterns to match the cortical geometry across subjects.
For individual statistical parametric maps (first-level analysis) epochs of 3D COR and RND were modeled by box cart predictors (6–16 s after stimulus onset). Additionally, a linear and cubic predictor was added to the general linear model to compensate for BOLD signal drifts. Group statistical parametric maps (second-level analysis) were calculated using a weighted random-effects analysis by which each subject’s data was weighted by the inverse of its noise. The analysis was restricted to the cortical surfaces and intersubject normalization was performed on surfaces (see above) rather than volumes. As the whole-brain analysis served to identify possible additional regions that had been ignored by the ROI analysis, activity maps were thresholded to P = 0.05 (no correction for multiple comparisons). Group activity maps were overlaid on the MNI average surface provided by Freesurfer.
Results
Percept of a corrugated surface
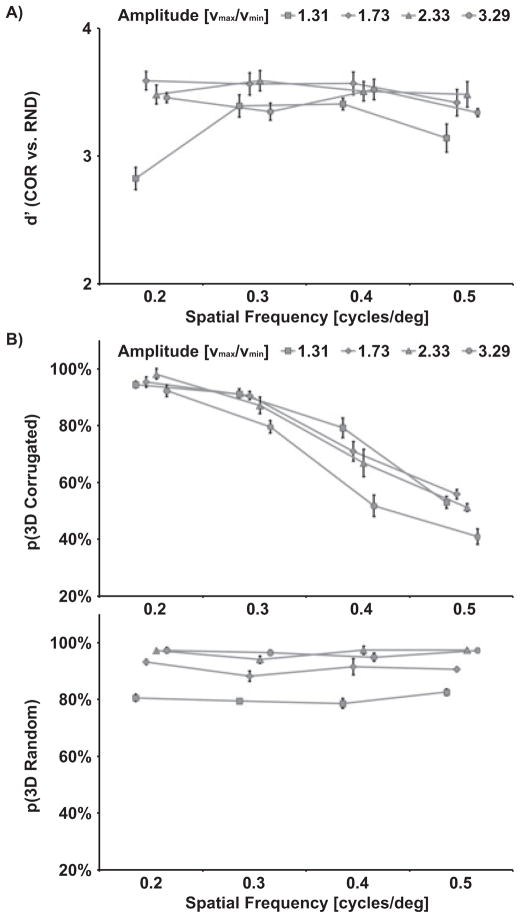
One goal of Experiment 1 was to identify parameters that elicit a compelling percept of a corrugated surface by motion and to assess individual differences in the perception of corrugated surfaces. Participants were confronted with either a COR or RND stimulus of varying amplitude (or vmin/vmax ratio) and spatial frequency and were asked to identify whether the display composed of moving dots appeared to be structured (corrugated) or uniform (volume). As illustrated in Fig. 2A, discrimination performance as measured by d′ (Swets, 1973) was uniformly high for most amplitude and frequency conditions, but decreased for small amplitude conditions (vmax/vmin = 1.31) and low and high spatial frequencies. This result pattern was confirmed by a significant main effect of Amplitude (F3,18 = 5.7, P = 0.007) and significant interaction of Amplitude × Spatial Frequency (F9,54 = 2.1, P = 0.044).
Fig. 2.
Group mean results of Experiment 1. Performance measures are shown for each level of spatial frequency (f) and amplitude (v = vmax/vmin). (A) Discrimination performance of COR (structured) vs. RND (uniform) stimuli is indicated in terms of sensitivity (d′). (B) Percentage of 3D surface responses (vs. 2D) are based on correctly identified COR stimuli. Percentage of 3D volume responses (vs. 2D) are based on correctly identified RND stimuli.
Participants were further asked to indicate whether they perceived the dots as moving along a 2D plane or along a 3D surface or within a volume. Consistent with previous findings (Andersen, 1996), the impression of a 3D surface (Fig. 2B) was determined by the amplitude (e.g., velocity ratio vmax/vmin) and the spatial frequency of the COR stimulus. In particular, the proportion of perceived 3D surface responses increased with higher velocity ratios (amplitudes) (F3,18 = 6.3, P = 0.004) and decreased with higher spatial frequencies of the COR stimuli (F3,18 = 17.9, P < 0.001). Furthermore, a significant interaction of Amplitude × Spatial Frequency (F3,18 = 2.1, P = 0.041) indicated that the percept of a surface decreased with higher velocity ratios only for high spatial frequencies (0.4 cycles/deg and 0.5 cycles/deg).
As expected, spatial frequency had no effect on the 3D percept of RNDs. However, RNDs were perceived to be three-dimensional more often with higher velocity ratios (Fig. 2B; F3,18 = 3.9, P = 0.025).
Based on this assessment, parameters were chosen for subsequent experiments that yielded a compelling percept of a corrugated surface in each individual. Accordingly, the mean amplitude factor a was 0.419 (corresponding to vmax/vmin = 2.44) and the mean spatial frequency was 0.29 cycles/deg.
Speed change detection
The goal of Experiment 2 was to find parameters for the speed change detection task in order to equalize task difficulty. The mean 75% thresholds for speed change detection as measured by bestPEST (Lieberman & Pentland, 1982) were 3.10 dB for COR stimuli and 3.17 dB for RND stimuli, corresponding to an increase in dot speed by the factors 2.05 and 2.10, respectively.
During the brain imaging session (Experiment 3) observers’ performance for detecting speed changes as well as their response times were indistinguishable between COR (83%, 559 ms) and RND (79%, 560 ms) stimuli (P > 0.1) suggesting that CORs and RNDs were equally attended.
ROI definition
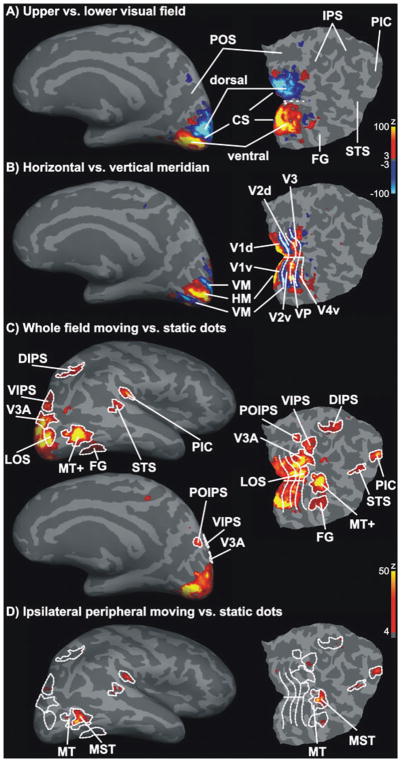
Figure 3 illustrates statistical parametric maps of the BOLD response of a representative individual hemisphere overlaid on the corresponding inflated gray matter surface and occipital flat patch. Upper and lower visual field stimulation resulted in clear activity patches ventral and dorsal to the calcarine sulcus (Fig. 3A) in all examined hemispheres. In addition, horizontal and vertical meridian stimulation (Fig. 3B) resulted in several activity stripes parallel to the calcarine sulcus. Representations of the horizontal meridian and the vertical meridian alternated and separated neighboring retinotopic visual areas (V1, V2, VP/V3 and V4v).
Fig. 3.
Definition of ROIs. Statistical parametric maps for the ROI definition localizer runs are shown for one representative hemisphere. Activity maps were overlaid on the inflated gray matter surface and a flat occipital patch that was cut along the calcarine sulcus (CS). False positives were reduced by adjusting significance maps by a false-discovery rate of 0.001. Significance maps were spatially smoothed for illustration only. (A) Representations of the lower (blue) and upper (yellow–red) visual field demarcated dorsal (d) and ventral (v) parts of early visual areas. (B) Horizontal (HM, yellow-red) and vertical (VM, blue) meridian respresentations separated early visual areas (V1d/v, V2d/v, V3, VP and V4v). (C) Statistical parametric maps for high-contrast radially moving vs. static dots were used to define motion-sensitive areas MT+, LOS, V3A, VIPS and DIPS, POIPS, FG (motion-sensitive fusiform gyrus), STS and PIC. (D) The MT+ was further subdivided into MT and MST. MST was defined as the region of MT+ that responded to visual motion in the peripheral ipsilateral visual field (Dukelow et al., 2001; Huk et al., 2002).
The contrast of whole-field moving vs. static dots revealed a large network of regions that were more active while observers viewed moving dots than static dots (Fig. 3C). The site of activated regions corresponded with motion-sensitive regions known from the literature (Orban et al., 1999; Sunaert et al., 1999). This network included, besides early retinotopic regions, areas V3A, VIPS, POIPS, DIPS, a region on the LOS, area MT+, a region overlapping with the FG, a small region in the STS and in the PIC. Figure 3D illustrates the activity pattern elicited by the contrast motion vs. static dots when only the peripheral ipsilateral visual field was stimulated. Consistent with previous research (Dukelow et al., 2001; Huk et al., 2002), only an anterior subpart of MT+ showed significant activity. This part was considered to be MST for the subsequent ROI analysis, while the remainder was labeled MT.
Similar activity patterns were obtained for all examined hemispheres. However, for some subjects the threshold had to be lowered (P = 0.05, no correction for multiple comparisons) for the contrast ipsilateral moving vs. static dots. This liberal thresholding may have resulted in an overestimation of MST. Similarly, areas STS and PIC were not visible on all hemispheres when a conservative threshold was applied. If so, these areas were defined using a reduced threshold. Table 1 lists the mean size and mean Talairach location for each ROI. Note that for some hemispheres the ROIs did not exceed the minimum requested size (five functional voxels) to be considered for the ROI analysis. Further note that higher-level visual areas (e.g. STS) showed a larger variability in their Talairach coordinates across subjects than early visual areas (e.g. V1).
Table 1.
ROI sizes and coordinates
| ROI | Left hemispheres |
Right hemispheres |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | Size | x | y | z | n | Size | x | y | z | |
| V1d | 7 | 107.0 ± 35.6 | −10.2 ± 3.2 | −93.7 ± 5.0 | 6.9 ± 4.7 | 7 | 110.9 ± 46.3 | 12.5 ± 3.0 | −89.7 ± 5.0 | 7.3 ± 6.0 |
| V1v | 7 | 90.4 ± 22.1 | −8.3 ± 2.4 | −86.2 ± 7.9 | −1.7 ± 3.9 | 7 | 85.6 ± 14.4 | 9.9 ± 2.4 | −82.7 ± 5.5 | −0.7 ± 4.9 |
| V2D | 7 | 87.3 ± 17.7 | −12.2 ± 3.3 | −96.8 ± 4.0 | 13.0 ± 6.1 | 7 | 89.0 ± 14.9 | 14.0 ± 4.2 | −93.2 ± 4.9 | 13.9 ± 6.3 |
| V2v | 7 | 104.9 ± 15.2 | −12.2 ± 2.3 | −82.8 ± 7.2 | −5.5 ± 3.3 | 7 | 92.0 ± 24.7 | 12.6 ± 2.8 | −82.4 ± 7.0 | −5.3 ± 4.4 |
| V3 | 7 | 65.0 ± 25.5 | −22.0 ± 5.7 | −93.6 ± 4.0 | 11.4 ± 6.8 | 7 | 63.0 ± 26.7 | 22.2 ± 4.7 | −92.8 ± 4.5 | 15.6 ± 4.5 |
| VP | 7 | 57.3 ± 17.3 | −21.2 ± 6.0 | −84.6 ± 5.7 | −7.2 ± 3.6 | 7 | 67.4 ± 25.2 | 21.5 ± 4.6 | −81.8 ± 5.4 | −6.7 ± 3.9 |
| V4v | 7 | 43.6 ± 17.1 | −29.3 ± 6.0 | −83.4 ± 6.2 | −9.7 ± 3.7 | 7 | 43.7 ± 19.0 | 30.3 ± 5.2 | −82.4 ± 3.9 | −8.0 ± 4.5 |
| V3A | 7 | 49.7 ± 19.7 | −19.9 ± 7.2 | −91.2 ± 5.1 | 19.5 ± 3.6 | 7 | 48.3 ± 22.2 | 20.7 ± 5.2 | −88.3 ± 4.0 | 22.6 ± 5.9 |
| POIPS | 7 | 22.0 ± 7.9 | −15.6 ± 5.1 | −81.8 ± 9.0 | 34.7 ± 8.7 | 7 | 25.3 ± 15.3 | 19.8 ± 5.0 | −78.1 ± 5.6 | 36.4 ± 5.5 |
| VIPS | 7 | 35.4 ± 16.8 | −23.8 ± 4.5 | −82.9 ± 6.8 | 26.7 ± 9.3 | 7 | 45.9 ± 16.8 | 26.2 ± 7.4 | −79.2 ± 5.4 | 30.8 ± 5.8 |
| DIPS | 7 | 54.3 ± 38.7 | −26.4 ± 3.3 | −57.4 ± 4.3 | 54.0 ± 3.4 | 7 | 70.0 ± 62.5 | 29.9 ± 3.6 | −52.9 ± 8.1 | 52.7 ± 4.2 |
| FG | 5 | 20.0 ± 5.2 | −36.4 ± 5.3 | −73.6 ± 5.8 | −12.3 ± 2.3 | 6 | 17.7 ± 8.4 | 34.7 ± 6.2 | −68.2 ± 4.3 | −11.7 ± 3.6 |
| LOS | 7 | 24.0 ± 8.1 | −31.6 ± 6.6 | −86.7 ± 6.0 | 7.3 ± 5.7 | 7 | 31.1 ± 15.8 | 31.2 ± 2.1 | −85.8 ± 6.2 | 8.1 ± 4.9 |
| STS | 7 | 22.0 ± 7.2 | −47.1 ± 4.6 | −53.1 ± 7.6 | 15.0 ± 8.7 | 5 | 18.2 ± 10.9 | 49.3 ± 6.2 | −45.5 ± 6.3 | 14.7 ± 6.3 |
| MT | 7 | 50.4 ± 25.7 | −42.7 ± 3.6 | −74.4 ± 5.6 | 0.7 ± 3.5 | 7 | 76.7 ± 34.8 | 45.4 ± 1.9 | −70.6 ± 4.9 | 1.7 ± 5.4 |
| MST | 7 | 45.7 ± 11.4 | −44.8 ± 3.1 | −69.6 ± 5.2 | 6.7 ± 4.5 | 7 | 40.1 ± 11.3 | 44.8 ± 3.6 | −65.0 ± 6.4 | 6.6 ± 3.5 |
| PIC | 7 | 11.7 ± 4.0 | −46.4 ± 8.1 | −41.0 ± 4.4 | 23.8 ± 4.5 | 6 | 18.3 ± 7.2 | 51.0 ± 7.3 | −36.7 ± 5.9 | 22.5 ± 5.8 |
The table shows the mean Talairach coordinates (x, y, z) of the center of mass for each ROI. Sizes are given in functional voxels (3.125 × 3.125 × 3 mm3). The sample included n = 7 brains but in some hemispheres the criteria for ROI definition were not met. Mean values are shown ± SD. V4v, visual area V4 (only ventral representation).
ROI analysis
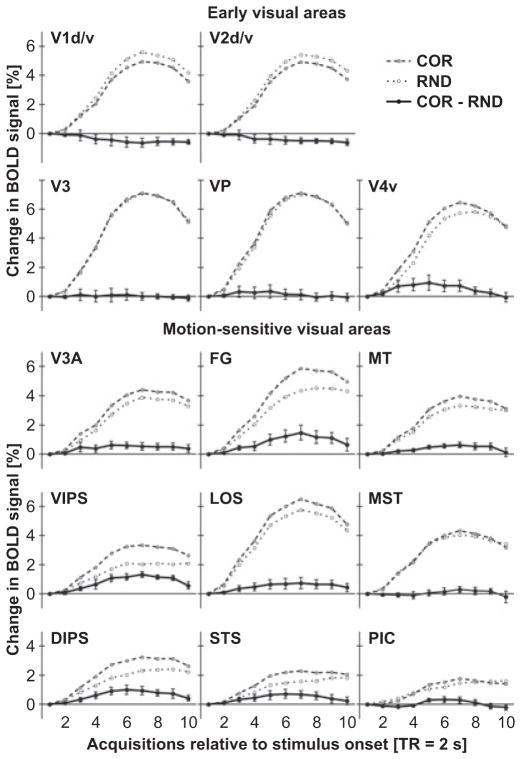
Figure 4 illustrates the time course of the BOLD signal in response to COR or RND epochs (contrasted to fixation only) separately for early retinotopic and motion-sensitive ROIs. The BOLD signal increased in all ROIs after a delay of about two TRs (4 s) and slowly decreased after the stimulation epoch (at 16 s, i.e. eight TRs). No reliable difference between COR and RND epochs were observed at early visual areas V1, V2, V3, VP and V4v. By contrast, several motion-sensitive regions showed a stronger BOLD signal increase for COR than for RND stimuli. This difference started to become reliable at about the fourth TR after epoch onset and lasted until about the end of the stimulation period.
Fig. 4.
Mean BOLD signal changes to COR and RND epochs for each ROI. The time course of the BOLD signal (percentage signal change) was calculated using the general linear model using a finite impulse response function to model ten acquisitions (TRs). The time window extended from the onset of the 16-s stimulation epoch to 4 s after the end of the epoch. Baseline differences at stimulation onset (first TR) were corrected. Signals for both COR and VOL stimulation epochs were contrasted with fixation epochs. The solid line depicts the difference COR minus VOL. Error bars reflect SEMs across subjects. Note that differences in the BOLD signal were most evident between the fourth and eighth acquisition. ROI labels as above (see Fig. 3 or Table 1).
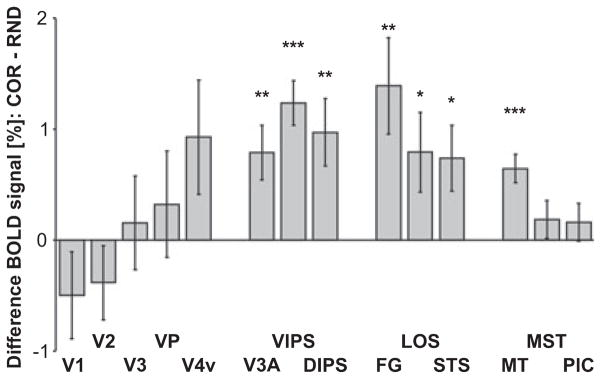
The BOLD response to motion stimuli contrasted with fixation does not necessarily reflect activity specific to motion processing. However, the difference in the responses to COR and RND stimuli may be considered a correlate of 3D SFM perception. Therefore, Fig. 5 plots the mean difference in BOLD signal for the period from the fouth to the eighth TR separately for each ROI. One-sample t-tests that compared this difference across subjects indicated that COR stimuli elicited stronger BOLD signal increases than RND stimuli in areas V3A (t6 = 3.2, P = 0.008), VIPS (t6 = 6.1, P < 0.001), DIPS (t6 = 3.2, P = 0.008), FG [t(5) = 3.2, P = 0.009], LOS (t6 = 2.2, P = 0.032), STS (t6 = 2.5, P = 0.021) and MT (t6 = 5.0, P < 0.001). A marginal significant difference was found in area V4v (t6 = 1.8, P = 0.057) and area POIPS (t6 = 1.8, P = 0.057; not shown in Figs 4 and 5). BOLD signals in early visual areas (V1, V2, V3 and VP) and the motion-sensitive regions MST and PIC did not differ (P > 0.1).
Fig. 5.
Mean difference in the BOLD signal of COR minus VOL for each ROI. BOLD signals reflect the mean signal (percentage signal change) for the period from the fourth to the eighth acquisition after epoch onset (see Fig. 4). Error bars reflect SEMs across subjects. Note that stronger BOLD signals were observed for COR than for VOL stimuli in motion-sensitive regions V3A, VIPS, DIPS, FG, LOS, STS and MT. ROI labels as above (see Fig. 3 or Table 1). ***P < 0.001, **P < 0.01, *P < 0.05.
Whole-brain analysis
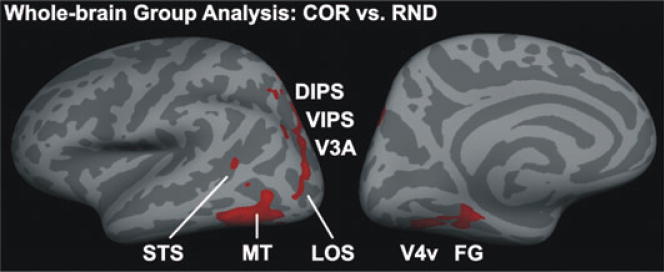
In order to test for brain areas relevant for 3D SFM perception that might have been overlooked by our ROI analysis we performed an additional whole-brain surface-based group analysis (Fig. 6). Despite some distortions and image blurring due to the normalization procedure and the extended spatial smoothing (8 mm rather than 5 mm) the significance maps of this group analysis showed several clusters of activity in occipital, temporal and parietal areas. These clusters of activity correspond relatively well with the regions identified by the ROI analysis: V4v, FG, V3A, VIPS, DIPS, FG, LOS, STS and MT. No relevant activity was observed in posterior and medial occipital lobe that would correspond to early visual areas. No additional areas that were not analyzed by the ROI approach could be identified.
Fig. 6.
Whole-brain group analysis. The group mean statistical parametric maps for the contrast 3D COR vs. RND were overlaid on the inflated left hemisphere (left, lateral view; right, medial view) of the MNI average brain of Freesurfer. Significance maps were thresholded to P = 0.05 (not corrected for multiple comparisons) and spatially smoothed. Note that data acquisition was limited to the posterior half of the brain. Labels (STS, MT, V4v, FG, LOS, V3A, VIPS and DIPS) refer to the ROI regions (see Fig. 3, Table 1) but are only approximate.
Correlation of BOLD signal and percept of a corrugated surface
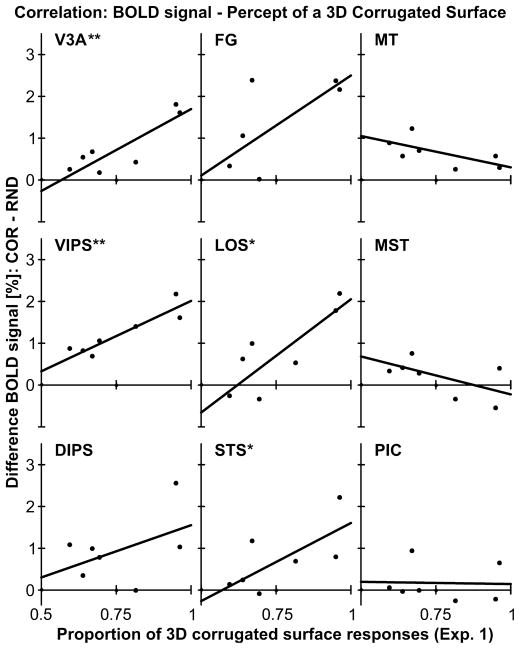
As reported above (Experiment 1), all observers were able to perceive a 3D surface defined by moving dots. However, we also noticed substantial interindividual differences regarding how strongly observers perceived the moving dots as a 3D surface. We were interested in whether these interindividual differences were also reflected in the strength of the BOLD signal. Therefore, we correlated the mean proportion of 3D surface responses from Experiment 1 with the BOLD signal difference between COR and RND stimuli of Experiment 3. These correlations are displayed in Fig. 7. Even though our sample size was small we found significant positive correlations between the perception of 3D corrugatedness and the difference in BOLD signal for several motion-sensitive regions including area V3A [r(5) = 0.86, P = 0.006], VIPS [r(5) = 0.92, P = 0.002], LOS [r(5) = 0.83, P = 0.011] and STS [r(5) = 0.69, P = 0.044]. Interestingly, BOLD signal differences in MT (and MST) were not (or were even negatively) correlated with the behavioral measures of perceived 3D corrugatedness.
Fig. 7.
Correlation of BOLD signal difference and the percept of a 3D surface. For each ROI the mean percentage of 3D surface responses (Experiment 1) was correlated with the BOLD signal difference (COR minus VOL; see Figs 4 and 5) across subjects. ROI labels as above (see Fig. 3 or Table 1). **P < 0.01, *P < 0.05.
Discussion
Our results showed that viewing a 3D surface defined by motion elicited stronger BOLD responses than viewing a 3D volume in several motion-sensitive brain regions including area V3A, VIPS and DIPS, area MT, FG, LOS and a motion-sensitive region in the posterior STS. The BOLD signal differences in these areas may not be attributed to low-level stimulus attributes (Heeger et al., 1999) as both COR and RND stimuli were composed of identical local velocity vectors. Furthermore, the BOLD signal differences in these areas were probably not due to attention, which is known to enhance visual motion perception and BOLD signals even at early cortical processing stages (Watanabe et al., 1998; Beer & Röder, 2004, 2005). In our study, BOLD signals in early visual brain areas (V1, V2 and V3/VP) were about equally strong for COR and their control stimuli. It might be argued that attention only (or primarily) affected higher-level brain areas. However, observers’ speed-change detection performance while viewing 3D CORs did not differ from their performance while viewing RNDs. If observers had attended to the 3D CORs more than to RNDs, we would expect either enhanced or (due to a trade-off) impaired speed-change detection performance.
We verified that our COR stimuli as shown during the fMRI task were indeed perceived as a 3D surface. Consistent with previous findings (Andersen, 1996), the results of Experiment 1 showed that the strength of the percept of the 3D corrugatedness varied as a function of the velocity ratio and the spatial frequency of the corrugation. By choosing stimulus attributes for the fMRI task that gave the strongest percept of a 3D surface we assured that our stimuli were optimal for examining 3D SFM. Although all observers were able to perceive a 3D surface defined by the moving dots, the strength of this percept varied across observers. Interestingly, the strength of the perceived 3D corrugatedness was positively correlated with the strength of the BOLD signal changes in areas V3A, VIPS, LOS and STS but not in MT.
Temporal brain areas
Previous findings have suggested that the perception of 3D SFM in humans primarily involves an occipital–parietal network (Orban et al., 1999, 2003; Paradis et al., 2000; Vanduffel et al., 2002; Klaver et al., 2008) whereas nonhuman primate research suggested an occipital–temporal network including motion-sensitive regions in the STS (Vanduffel et al., 2002; Anderson & Siegel, 2005; Nelissen et al., 2006). However, most previous studies focused on dorsal brain areas rather than examining a potential temporal stream in human SFM perception (Vanduffel et al., 2002; Orban et al., 2003). Our results showed that a motion-sensitive region in the STS, which is distinct from MT and MST, is also involved in the perception of 3D surfaces by motion. The BOLD signal in this area was enhanced when observers viewed 3D CORs as compared to RND. Moreover, the difference in BOLD signals correlated with observer’s report of perceiving a 3D corrugated surface, suggesting a relatively strong link between this STS region and the phenomenology of perceiving a 3D structure.
In macaques several distinct regions along the superior temporal lobe, in particular MT, MSTd, MSTv and FST, were more active during perception of moving lines that defined 3D objects than during perception of lines moving along a 2D plane (Nelissen et al., 2006). In monkeys, FST seems to be the only area along this temporal pathway outside MT+ that is specialized for 3D SFM perception (Sereno et al., 2002; Vanduffel et al., 2002). Our results suggest that a motion-sensitive region in human STS distinct from MT+ is specialized for extracting SFM information. With that regard the STS region reported here is functionally similar to the FST region in monkeys.
Other studies have not reported activity related to 3D SFM perception in the human STS. One possibility is that methodological aspects have obscured this area in previous studies. For instance, the STS region is relatively small and shows more intraindividual variability than other areas (Sunaert et al., 1999; see also Table 1). Group analyses with volumetric normalization to an average brain tend to underestimate the role of small brain areas. Alternatively, the STS may be specifically involved in the type of SFM analysis required by our COR stimuli. Optic flow may be decomposed into four basic components: translational, radial, rotational and shear motion (Koenderink, 1986). The 3D surface in our study was defined by sinusoidally varying speed gradients of moving dots and, therefore, strongly relies on the analysis of shear components (Andersen, 1996). Previous studies used more complex SFM stimuli such as moving lines that were primarily composed of radial or rotational optic flow components.
Some previous human fMRI studies have associated MT+ with processing 3D SFM (Orban et al., 1999, 2003; Vanduffel et al., 2002; Murray et al., 2003) whereas other studies have not found related activity in this area (Paradis et al., 2000; Klaver et al., 2008). We distinguished between subdivisions of MT+ such as MT and MST and found stronger activity for 3D CORs than for RND in area MT but not in MST. Note that we defined MST based on its responsiveness to visual motion in the peripheral ipsilateral visual field and MT as the remainder of MT+. This definition bears the risk that putative area MT contains MST neurons with exclusively contralateral receptive fields. However, the 3D SFM-related activity observed in area MT probably does not reflect the response of misclassified MST neurons as in this case we would expect an equally strong or even stronger response in MST than in MT, the opposite of what was observed.
Neurons in area MT are involved in depth perception by motion (Bradley et al., 1998; Nadler et al., 2008) as well as by other binocular and monocular depth cues (Nguyenkim & DeAngelis, 2003; Welchman et al., 2005; Chandrasekaran et al., 2007). The question arises whether the activity related to 3D SFM perception observed in area MT reflects motion-specific or cue-invariant 3D structure processing (similar to the IPS). According to the latter notion we would expect that the activity observed in MT would vary with the strength of the perceived 3D corrugatedness of our COR stimuli. However, we found no correlation between the BOLD signal in MT and the reported 3D percept. Accordingly, our results suggest that MT is involved in analyzing optic flow patterns as an intermediate step in the process of deriving 3D SFM rather than encoding the 3D structure itself.
In monkeys, the analysis of optic flow patterns such as radial or rotational motion involves area MST (Tanaka et al., 1989; Duffy & Wurtz, 1997). Other aspects of optic flow such as speed gradients seem to be encoded in area MT (Treue & Andersen, 1996; Martinez-Trujillo et al., 2005). The optic flow pattern defining the 3D structure of our CORs primarily consisted of smoothly varying speed gradients. Our finding of stronger 3D SFM-related activity in MT than in MST is consistent with the notion that certain optic flow patterns such as speed gradients are analyzed in MT (rather than MST).
Occipitoparietal brain areas
Several brain areas located along an occipitoparietal stream were more active during perception of motion-defined 3D surfaces than during random motion. This stream includes area V3A as well as the VIPS and DIPS subdivisions of the IPS. Moreover, BOLD signals in these areas accounted for interindividual differences in the perception of 3D CORs, suggesting a close link between these areas and the 3D percept of the stimuli. The IPS is well known to be involved in the perception of 3D structure that is derived from motion cues (Orban et al., 1999, 2003; Paradis et al., 2000; Vanduffel et al., 2002; Klaver et al., 2008). However, it also encodes the 3D structure of objects that are defined by binocular and other monocular depth cues (Shikata et al., 2001) such as disparity (Orban et al., 2006; Durand et al., 2007), shading (Taira et al., 2001) or perspective (Murray et al., 2003). Hence, it is possible that the ventral intraparietal sulcus processes cue-invariant information of 3D structures or surfaces rather than being specific to motion-defined structures. Consistent with this notion, the superior parietal lobe is thought to be involved in binding multiple cues (Zeki, 2001).
Our results further showed that both the LOS and the motion-sensitive region in the FG were involved in 3D SFM perception. Similar activity foci have been reported previously (Orban et al., 1999, 2003; Vanduffel et al., 2002). Area LOS seems to overlap or be adjacent to the kinetic occipital area (Van Oostende et al., 1997), known for its role in processing 2D structures, such as boundaries, defined by motion. However, the LOS activity reported here does not seem to reflect processing of 2D structures. The BOLD signal in LOS correlated with interindividual differences in perceiving the 3D structure of the CORs but we found no correlation between the BOLD signal and the performance (d′) for discriminating between structured (COR) and uniform (RND) motion displays. The lateral occipital cortex was also associated with the perception of shapes based on disparity cues (Chandrasekaran et al., 2007) or perspective cues (Murray et al., 2003). Therefore, it is possible that the LOS activity found in our and previous fMRI studies examining SFM does not reflect processes specific to motion processing but instead reflects processing of cue-invariant 3D structures.
Neither our ROI analysis nor our whole-brain analysis provided evidence for 3D SFM processing in early visual cortex (V1, V2, V3/VP). Although both motion stimuli (when compared to fixation only) elicited a prominent BOLD signal, the response to 3D CORs was not enhanced compared to the response to RND. In fact, BOLD signals in V1 tended (not significant) to be even weaker for 3D CORs than for RND. This finding seems to be inconsistent with previous fMRI studies that reported enhanced activity even in early visual cortex (V2 and V3) in response to 3D SFM stimuli (Vanduffel et al., 2002; Orban et al., 2003). However, our findings are in line with other studies that either reported no (Orban et al., 1999; Paradis et al., 2000; Klaver et al., 2008) or decreased (Murray et al., 2003) SFM-related activity in early visual cortex. Murray et al. (2003) attributed the reduction in V1 activity to grouping effects. In particular, they proposed that motion signals in early visual cortex that can be grouped together in higher object areas are suppressed. Alternatively, the stronger activity in V1 for RND stimuli may be the result of local interactions. Many V1 neurons show stronger responses to discontinuities in the speed array as compared to homogenous field motion (Cao & Schiller, 2003). On a local scale, speed vectors varied smoothly for CORs whereas RND stimuli were characterized by relatively pronounced discontinuities of speed vectors.
Conclusion
Perception of 3D SFM involved several occipital and parietal brain areas including area V3A, the IPS, the LOS and the FG. Moreover, area MT seems to be involved in the analysis of optic flow patterns associated with SFM perception whereas area MST seems to be less relevant. Interestingly, the superior temporal lobe in humans seems to play a greater role in the analysis of 3D SFM than previously thought.
Acknowledgments
This work was supported by grant BCS-0345746 of the National Science Foundation and grant NIH-NEI R01EY015980-04A2 of the National Institutes of Health.
Abbreviations
- 2D
two-dimensional
- 3D
three-dimensional
- BOLD
blood oxygen level-dependent
- COR
corrugated surface (stimulus)
- CS
calcarine sulcus
- d (suffix)
dorsal
- d′
unbiased measure of discrimination
- DIPS
dorsal subdivision of IPS
- FG
fusiform gyrus
- fMRI
functional magnetic resonance imaging
- FST
fundus of STS
- IPS
intraparietal sulcus
- LOS
lateral occipital sulcus
- MST
medial superior temporal (cortex)
- MT
middle temporal area
- MT+
MT complex (also known as V5), consisting of MT and satellite areas
- PIC
parietoinsular cortex
- POIPS
junction of POS and IPS
- POS
parietooccipital sulcus
- RND
random motion volume (stimulus)
- ROI
region of interest
- SFM
structure-from-motion
- STS
superior temporal sulcus
- TR
repetition time
- v (suffix)
ventral
- V3A
visual area located near dorsal V3
- V4v
visual area V4
- VIPS
ventral subdivision of IPS
- VP
ventral posterior area (ventral V3)
References
- Andersen GJ. Detection of smooth three-dimensional surfaces from optic flow. J Exp Psychol Hum Percept Perform. 1996;22:945–957. doi: 10.1037//0096-1523.22.4.945. [DOI] [PubMed] [Google Scholar]
- Anderson KC, Siegel RM. Three-dimensional structure-from-motion selectivity in the anterior superior temporal polysensory area, STPa, of the behaving monkey. Cereb Cortex. 2005;15:1299–1307. doi: 10.1093/cercor/bhi013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beer AL, Röder B. Attention to motion enhances processing of both visual and auditory stimuli: an event-related potential study. Cogn Brain Res. 2004;18:205–225. doi: 10.1016/j.cogbrainres.2003.10.004. [DOI] [PubMed] [Google Scholar]
- Beer AL, Röder B. Attending to visual or auditory motion affects perception within and across modalities: an event-related potential study. Eur J Neurosci. 2005;21:1116–1130. doi: 10.1111/j.1460-9568.2005.03927.x. [DOI] [PubMed] [Google Scholar]
- Bradley DC, Chang GC, Andersen RA. Encoding of three-dimensional structure-from-motion by primate area MT neurons. Nature. 1998;392:714–717. doi: 10.1038/33688. [DOI] [PubMed] [Google Scholar]
- Cao A, Schiller PH. Neural responses to relative speed in the primary visual cortex of rhesus monkey. Vis Neurosci. 2003;20:77–84. doi: 10.1017/s0952523803201085. [DOI] [PubMed] [Google Scholar]
- Chandrasekaran C, Canon V, Dahmen JC, Kourtzi Z, Welchman AE. Neural correlates of disparity-defined shape discrimination in the human brain. J Neurophysiol. 2007;97:1553–1565. doi: 10.1152/jn.01074.2006. [DOI] [PubMed] [Google Scholar]
- Cox RW, Jesmanowicz A. Real-time 3D image registration for functional MRI. Magn Reson Med. 1999;42:1014–1018. doi: 10.1002/(sici)1522-2594(199912)42:6<1014::aid-mrm4>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- DeYoe EA, Carman GJ, Bandettini P, Glickman S, Wieser J, Cox R, Miller D, Neitz J. Mapping striate and extrastriate visual areas in human cerebral cortex. Proc Natl Acad Sci USA. 1996;93:2382–2386. doi: 10.1073/pnas.93.6.2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy CJ, Wurtz RH. Multiple temporal components of optic flow responses in MST neurons. Exp Brain Res. 1997;114:472–482. doi: 10.1007/pl00005656. [DOI] [PubMed] [Google Scholar]
- Dukelow SP, DeSouza JFX, Culham JC, van den Berg AV, Menon RS, Vilis T. Distinguishing subregions of the human MT+ complex using visual fields and pursuit eye movements. J Neurophysiol. 2001;86:1991–2000. doi: 10.1152/jn.2001.86.4.1991. [DOI] [PubMed] [Google Scholar]
- Durand JB, Nelissen K, Joly O, Wardak C, Todd JT, Norman JF, Janssen P, Vanduffel W, Orban GA. Anterior regions of monkey parietal cortex process visual 3D shape. Neuron. 2007;55:493–505. doi: 10.1016/j.neuron.2007.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999a;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RB, Dale AM. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum Brain Mapp. 1999b;9:195–207. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Liu A, Dale AM. Automated manifold surgery: constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Trans Med Imaging. 2001;20:70–80. doi: 10.1109/42.906426. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, van der Kouwe AJ, Makris N, Segonne F, Quinn BT, Dale AM. Sequence-independent segmentation of magnetic resonance images. Neuroimage. 2004;23(Suppl 1):S69–S84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- Heeger DJ, Boynton GM, Demb JB, Seidemann E, Newsome WT. Motion opponency in visual cortex. J Neurosci. 1999;19:7162–7174. doi: 10.1523/JNEUROSCI.19-16-07162.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huk AC, Dougherty RF, Heeger DJ. Retinotopy and functional subdivision of human areas MT and MST. J Neurosci. 2002;22:7195–7205. doi: 10.1523/JNEUROSCI.22-16-07195.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaver P, Lichtensteiger J, Bucher K, Dietrich T, Loenneker T, Martin E. Dorsal stream development in motion and structure-from-motion perception. Neuroimage. 2008;39:1815–1823. doi: 10.1016/j.neuroimage.2007.11.009. [DOI] [PubMed] [Google Scholar]
- Koenderink JJ. Optic flow. Vision Res. 1986;26:161–179. doi: 10.1016/0042-6989(86)90078-7. [DOI] [PubMed] [Google Scholar]
- Lieberman HR, Pentland AP. Microcomputer-based estimation of psychological thresholds: the best PEST. Behav Res Methods Instrum Comput. 1982;14:21–25. [Google Scholar]
- Martinez-Trujillo JC, Tsotsos JK, Simine E, Pomplun M, Wildes R, Treue S, Heinze HJ, Hopf JM. Selectivity for speed gradients in human area MT/V5. Neuroreport. 2005;16:435–438. doi: 10.1097/00001756-200504040-00004. [DOI] [PubMed] [Google Scholar]
- Murray SO, Olshausen BA, Woods DL. Processing shape, motion and three-dimensional shape-from-motion in the human cortex. Cereb Cortex. 2003;13:508–516. doi: 10.1093/cercor/13.5.508. [DOI] [PubMed] [Google Scholar]
- Nadler JW, Angelaki DE, DeAngelis GC. A neural representation of depth from motion parallax in macaque visual cortex. Nature. 2008;452:642–645. doi: 10.1038/nature06814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelissen K, Vanduffel W, Orban GA. Charting the lower superior temporal region, a new motion-sensitive region in monkey superior temporal sulcus. J Neurosci. 2006;26:5929–5947. doi: 10.1523/JNEUROSCI.0824-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyenkim JD, DeAngelis GC. Disparity-based coding of three-dimensional surface orientation by macaque middle temporal neurons. J Neurosci. 2003;23:7117–7128. doi: 10.1523/JNEUROSCI.23-18-07117.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orban GA, Sunaert S, Todd JT, Van Hecke P, Marchal G. Human cortical regions involved in extracting depth from motion. Neuron. 1999;24:929–940. doi: 10.1016/s0896-6273(00)81040-5. [DOI] [PubMed] [Google Scholar]
- Orban GA, Fize D, Peuskens H, Denys K, Nelissen K, Sunaert S, Todd J, Vanduffel W. Similarities and differences in motion processing between the human and macaque brain: evidence from fMRI. Neuropsychologia. 2003;41:1757–1768. doi: 10.1016/s0028-3932(03)00177-5. [DOI] [PubMed] [Google Scholar]
- Orban GA, Janssen P, Vogels R. Extracting 3D structure from disparity. Trends Neurosci. 2006;29:466–473. doi: 10.1016/j.tins.2006.06.012. [DOI] [PubMed] [Google Scholar]
- Paradis AL, Cornilleau-Pérès V, Droulez J, Van de Moortele PF, Lobel E, Berthoz A, Le Bihan D, Poline JB. Visual perception of motion and 3D structure from motion: an fMRI study. Cereb Cortex. 2000;10:772–783. doi: 10.1093/cercor/10.8.772. [DOI] [PubMed] [Google Scholar]
- Rogers B, Graham M. Motion parallax as an independent cue for depth perception. Perception. 1979;8:125–134. doi: 10.1068/p080125. [DOI] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22:1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Segonne F, Pacheco J, Fischl B. Geometrically accurate topology-correction of cortical surfaces using nonseparating loops. IEEE Trans Med Imaging. 2007;26:518–529. doi: 10.1109/TMI.2006.887364. [DOI] [PubMed] [Google Scholar]
- Sereno ME, Trinath T, Augath M, Logothetis NK. Three-dimensional shape representation in monkey cortex. Neuron. 2002;33:635–652. doi: 10.1016/s0896-6273(02)00598-6. [DOI] [PubMed] [Google Scholar]
- Shikata E, Hamzei F, Glauche V, Knab R, Dettmers C, Weiller C, Buchel C. Surface orientation discrimination activates caudal and anterior intraparietal sulcus in humans: an event-related fMRI study. J Neurophysiol. 2001;85:1309–1314. doi: 10.1152/jn.2001.85.3.1309. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Sunaert S, Van Hecke P, Marchal G, Orban GA. Motion-responsive regions of the human brain. Exp Brain Res. 1999;127:355–370. doi: 10.1007/s002210050804. [DOI] [PubMed] [Google Scholar]
- Swets JA. The relative operating characteristic in psychology: a technique for isolating effects of response bias finds wide use in the study of perception and cognition. Science. 1973;182:990–1000. doi: 10.1126/science.182.4116.990. [DOI] [PubMed] [Google Scholar]
- Taira M, Nose I, Inoue K, Tsutsui K. Cortical areas related to attention to 3D surface structures based on shading: an fMRI study. Neuroimage. 2001;14:959–966. doi: 10.1006/nimg.2001.0895. [DOI] [PubMed] [Google Scholar]
- Tanaka K, Fukada Y, Saito HA. Underlying mechanisms of the response specificity of expansion/contraction and rotation cells in the dorsal part of the medial superior temporal area of the macaque monkey. J Neurophysiol. 1989;62:642–656. doi: 10.1152/jn.1989.62.3.642. [DOI] [PubMed] [Google Scholar]
- Treue S, Andersen RA. Neural responses to velocity gradients in macaque cortical area MT. Vis Neurosci. 1996;13:797–804. doi: 10.1017/s095252380000866x. [DOI] [PubMed] [Google Scholar]
- Van Oostende S, Sunaert S, Van Hecke P, Marchal G, Orban GA. The kinetic occipital (KO) region in man: an fMRI study. Cereb Cortex. 1997;7:690–701. doi: 10.1093/cercor/7.7.690. [DOI] [PubMed] [Google Scholar]
- Vanduffel W, Fize D, Peuskens H, Denys K, Sunaert S, Todd JT, Orban GA. Extracting 3D from motion: differences in human and monkey intraparietal cortex. Science. 2002;298:413–415. doi: 10.1126/science.1073574. [DOI] [PubMed] [Google Scholar]
- Watanabe T, Harner AM, Miyauchi S, Sasaki Y, Nielsen M, Palomo D, Mukai I. Task-dependent influences of attention on the activation of human primary visual cortex. Proc Natl Acad Sci USA. 1998;95:11489–11492. doi: 10.1073/pnas.95.19.11489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welchman AE, Deubelius A, Conrad V, Bülthoff HH, Kourtzi Z. 3D shape perception from combined depth cues in human visual cortex. Nat Neurosci. 2005;8:820–827. doi: 10.1038/nn1461. [DOI] [PubMed] [Google Scholar]
- Zeki S. Localization and globalization in conscious vision. Annu Rev Neurosci. 2001;24:57–86. doi: 10.1146/annurev.neuro.24.1.57. [DOI] [PubMed] [Google Scholar]