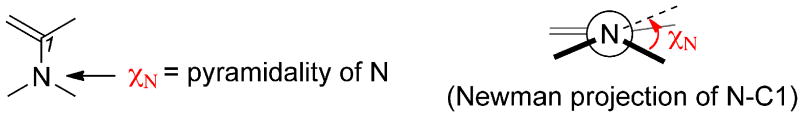Computational investigations of the stereoselectivities of proline-related catalysts for aldol reactions

Abstract

Computational investigation of the aldol reaction of benzaldehyde with acetone catalyzed by various proline derivatives and 2-azetidine carboxylic acid reveal the origins of stereoselectivities of these reactions. Structural differences between catalysts and transition states were analyzed with density functional theory geometries in order to establish the key factors that will help in the design of new catalysts.

1. Introduction

The aldol reaction is one of the most important synthetic tools for carbon-carbon bond formation. Since the work of List, Barbas, and Lerner,¹ direct aldol reactions catalyzed by small organic molecules like proline have attracted considerable attention. Despite the efficiency of proline as a catalyst, there is still a need to develop organocatalysts that achieve higher enantioselectivity, diastereoselectivity, and yield, and which can be used in less than the 30% molar equivalence that is often required for proline catalysis.

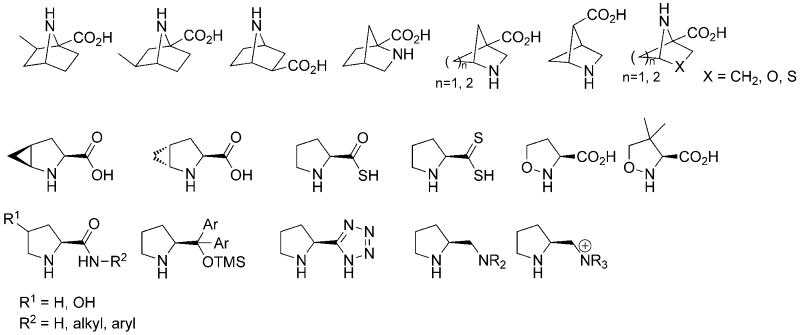
The mechanism of the proline catalyzed aldol reaction has been studied by Boyd,² Houk,³ and other groups.⁴ The reaction takes place through an enamine intermediate. In that model, hydrogen bonding and the geometry for proton transfer play important roles and determine the stereoselectivity of the reaction. Catalysis of the aldol reaction by proline analogs, including bicyclic prolines,⁵ heteroatom-substituted prolines,^4c prolinamides,⁶ prolinol ethers⁷, and amine-, ammonium-, and tetrazole-functionalized pyrrolidines⁸ (Figure 1), have also been studied computationally. Computational investigations of the Mannich,⁹ Michael addition,^{6e, 7b, 10} and Morita-Baylis Hillman¹¹ reactions by proline catalysts have also been reported.

Figure 1.

Proline analogs computationally studied in the aldol reaction.

In the present work, the same mechanistic model has been applied to study transition states for the aldol reaction of benzaldehyde with acetone catalyzed by proline, 2-azetidine carboxylic acid, 3,3-dimethyl-pyrrolidine-2-carboxylic acid (DMC), thiazolidine-4-carboxylic acid (TC), 5-methyl-thiazolidine-4-carboxylic acid (MTC), and 5,5-dimethyl-thiazolidine-4-carboxylic acid (DMTC). The focus in this paper is on the subtle differences in the structures of these catalysts, and how these differences influence reaction stereoselectivities. We also explore the suitability of B3LYP density functional calculations for reliable predictions of geometries and trends in stereoselectivity. Understanding why one catalyst performs better than another will help to design better catalysts, and the applications of a relatively well-known and economical computational method like B3LYP will permit general use of quantum mechanics for the design of catalysts.

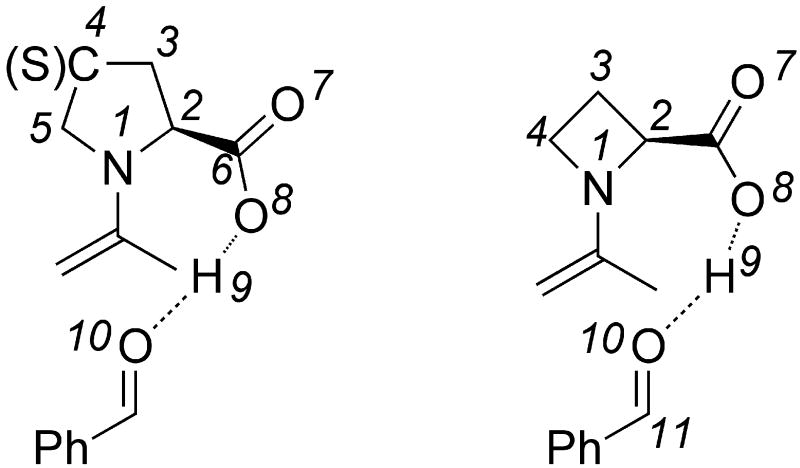
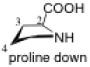
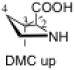
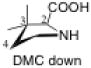
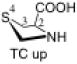
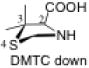
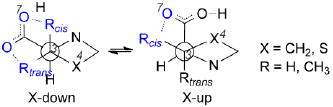
The pyrrolidine ring can adopt two stable conformations depending on the relative positions of C4 or S4 (in the thiol compounds TC, MTC, and DMTC) and the plane defined by N1-C2-C3. When C4 or S4 is below this plane, the ring conformation is called down or sometimes exo (Figure 2). When C4 or S4 is above this plane, the ring conformation is called up or sometimes endo. The conformations of prolines and N-acetyl proline dipeptides¹² as well as fluorinated prolines¹³ have been studied. The numbering shown in Figure 3 is used in this article.

Figure 2.

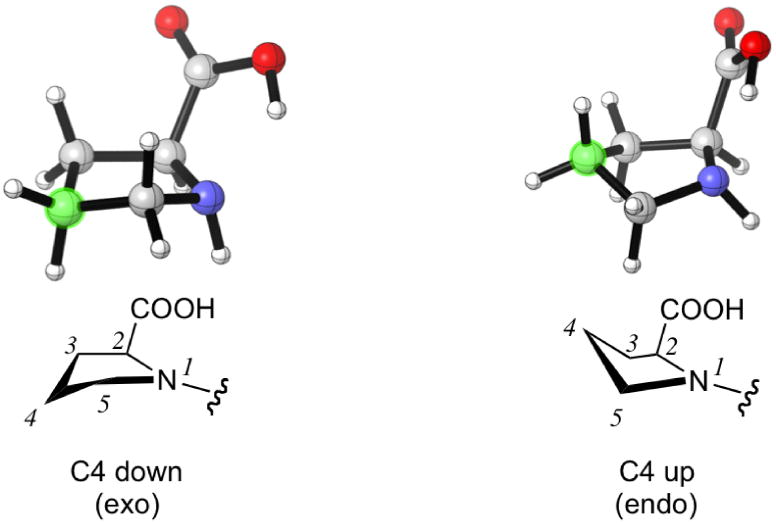
Up and down conformations of the pyrrolidine ring. C4 is labeled with green.

Figure 3.

Numbering of the catalysts and transition states.

2. Computational methods

Transition states for the aldol reaction of benzaldehyde with acetone catalyzed by proline, 2-azetidine carboxylic acid, DMC, TC, MTC, and DMTC were located with density functional theory (DFT) with the B3LYP/6-31G(d,p) functional and basis set¹⁴ for both geometries and energies¹⁵ as implemented in Gaussian 98^16a and Gaussian 03.^16b All stationary points were verified by vibrational frequency analysis.

3. Results and Discussions

3.1 Basis set effects on prediction of stereoselectivity trends with DFT

The absolute accuracy of hybrid density functional theory methods such as B3LYP¹⁴ is only moderate (mean average error ≈ 3 kcal/mol; maximum error ~ 20 kcal/mol).^14d However, the method can be used to compute relative activation energies of diastereomeric transition states on reactions involving around twenty-five heavy atoms with accuracies of a few kcal/mol and stereoselectivities with errors of less than 0.5 kcal/mol.^{3c, 3d} Previous calculations involving proline as catalyst have shown that accurate stereoselective prediction can be made with the 6-31G(d) basis set. ^3c When DMTC is used as the catalyst, this basis set gives less give accurate predictions (Table 1: calculation performed with TSs having an endo ring conformation (position 4 down)). As proton transfer plays an important role in the transition state, addition of a polarization function on hydrogen improves the predictions. The resulting basis set 6-31G(d,p) gave satisfactorily results, and was retained as basis set of choice. Other basis sets (diffuse function and large basis sets) were tested on same cases, but none of them gave better results than 6-31G(d,p). Moreover, use of solvent (DMSO, SCRF) did not improve gas phase calculations. List and coworkers recently reinvestigated the enantioselectivity of the reaction catalyzed by proline and found variable ee’s (private communication with Benjamin List) depending on the exact conditions. Our results are closer to the original value of 60%.^{1, 17, 18}

Table 1.

Influence of basis set on enantioselectivity prediction (relative energies).

Basis seta
	ΔΔH‡ (re–si, kcal/mol)	ΔΔG‡ (re–si, kcal/mol)	ΔΔH‡ (re–si, kcal/mol)	ΔΔG‡ (re–si, kcal/mol)
6-31G(d)//6-31G(d)	1.4	1.9	3.6	3.7
6-31G(d,p)//6-31G(d)	1.2	1.7	1.8	1.9
6-311+G(2df,p)//6-31G(d)	1.9	2.3	2.4	2.6
6-31G(d,p)//6-31G(d,p)	1.3	1.9	1.6	1.7
6-311+G(2df,p)//6-31G(d,p)	1.9	2.1	2.3	2.4
Experimental	1.2 (76% ee)b / 0.8 (60% ee)c		1.5 (86% ee)c

^aB3LYP method.

^bPrivate communication with B. List.

^cref. ¹, ¹⁷.

In previous studies about aldol reactions catalyzed by amino acid derivatives, predictions based on enthalpy were more accurate than predictions based on free energy, most likely due to lack of accuracy in entropy calculations involving low frequency vibrations in transition states. This is also observed with the catalysts discussed in this paper (Tables 1 and 2).

Table 2.

Experimental and calculated^a enantioselectivity.^b Influence of pyrrolidine conformation on % ee prediction.

catalyst	experimental % ee (ΔΔG‡)	predicted % ee (ΔΔH‡, ΔΔG‡)
		8TS	4TS (up)	4TS (down)
	40 (0.5)c		68 (1.0) 74 (1.1)
	72 (1.1)	69 (1.0) 81 (1.3)	65 (0.9) 76 (1.1)	79 (1.3) 92 (1.9)
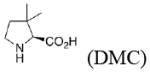	unknown	75 (1.2) 80 (1.3)	53 (0.7) 63 (0.9)	82 (1.4) 86 (1.5)
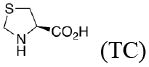	73 (1.1)	82 (1.4) 93 (1.9)	77 (1.2) 87 (1.6)	86 (1.6) 95 (2.2)
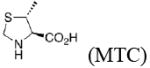	unknown	86 (1.5) 95 (2.1)	76 (1.2) 82 (1.4)	87 (1.6) 95 (2.2)
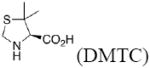	86 (1.5)	87 (1.6) 91 (2.8)	67 (1.0) 78 (1.2)	87 (1.6) 92 (1.9)

^aB3LYP 6-31G(d,p).

^bEnergy difference in parentheses. Enthalpies in bold; free energies in italics.

^cAldehyde is paranitrobenzaldehyde.

3.2 Transition states and the effect of ring puckering on stereochemistry prediction

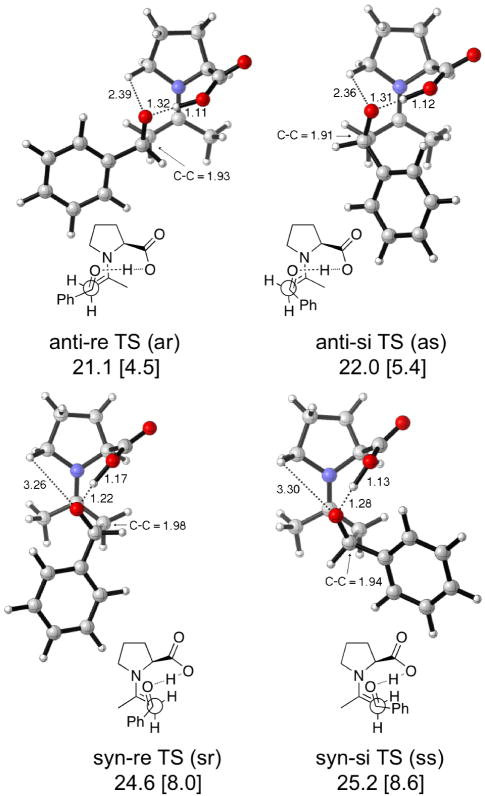
The enantioselectivity is explained with a transition state related to the Zimmermann-Traxler type model for aldol reactions involving metal enolates. The enamine can be either syn or anti to the carboxylic acid, and the nucleophilic attack of the aldol acceptor can occur from the re or si face of the aldehyde. This gives four transition states (Figure 4). In each transition state, intramolecular acid catalysis by the proton of the carboxylic acid occurs; all four transition structures have similar extents of proton transfer from acid to alkoxide. The anti-re transition state has the phenyl in an ideal equatorial position in the Zimmerman-Traxler transition state. This transition state also includes electrostatic stabilization due to the ^δ+N-C5- H^⋯O10^δ− interaction described earlier.³ The steric hindrance and non-ideal arrangement for proton transfer is obvious in the syn transition states shown in Figure 4.^3b–c

Figure 4.

Transition states and activation enthalpies (with respect to separated reactants) for proline catalyzed aldol reaction between acetone and benzaldehyde. Barriers with respect to anti enamine are in brackets. All proline conformations are C4-up.

Predictions have sometimes been attempted without considering the different conformers that can arise from proline ring puckering. Consideration of the ring conformation is necessary in order to obtain quantitative predictions, although the qualitative predictions are the same. Table 2 shows the predicted selectivities if only “up” or “down” conformers of the catalysts are included. Table 3 shows the relative energies of all eight transition states. Transition states with the less favorable ring conformation do contribute to the Boltzmann population, and influence the stereochemical outcome. As a consequence, the enthalpy of 8 TSs for each catalyst will be considered in this paper, except for 2-azetidine carboxylic acid (4 TSs), where only a single conformer is located. Syn transition states are nearly unpopulated, so exclusion of these will not cause major errors. The following trend for enantioselectivity was calculated: azetidine = proline < DMC < TC < MTC ≤ DMTC.

Table 3.

Relative B3LYP/6-31G(d,p) enthalpies and Boltzmann populations^a of aldol transition states.

catalyst	ring conformation	Relative TS enthalpies (kcal/mol) and % Boltzmann populations
		anti-re	anti-si	syn-re	syn-si
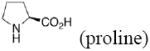	C4 up C4 down	0.0 (62.0) 0.6 (22.2)	0.9 (13.0) 1.9 (2.6)	3.5 (0.2) 5.7 (0.0)	4.2 (0.0) 6.7 (0.0)
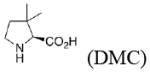	C4 up C4 down	0.8 (17.2) 0.0 (70.5)	1.5 (5.3) 1.4 (7.0)	4.4 (0.0) 5.5 (0.0)	6.6 (0.0) 5.3 (0.0)
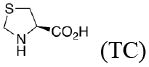	C4 up C4 down	0.0 (44.0) 0.0 (46.8)	1.3 (5.7) 1.5 (3.4)	4.1 (0.1) 5.3 (0.0)	4.3 (0.0) –
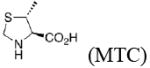	C4 up C4 down	1.5 (6.6) 0.0 (86.3)	2.7 (0.9) 1.6 (6.2)	5.3 (0.0) 5.4 (0.0)	5.5 (0.0) –
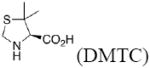	C4 up C4 down	2.5 (1.3) 0.0 (92.2)	3.5 (0.3) 1.6 (6.2)	7.3 (0.0) 5.8 (0.0)	7.9 (0.0) 6.5 (0.0)

^aBold numbers show transition state having ≥5% Boltzmann population. Percent Boltzmann populations are shown in parentheses.

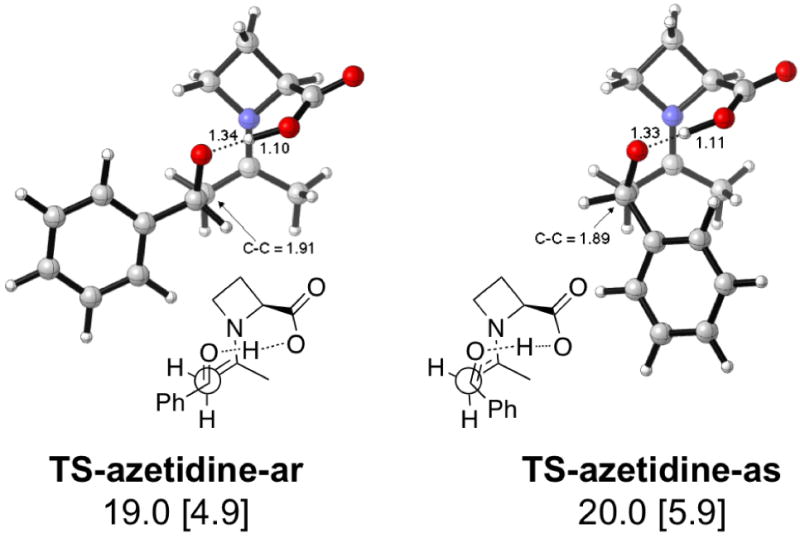
The lowest energy transition structures for re- and si-face addition of benzaldehyde to the enamines formed by the reactions of azetidine, DMC, TC, MTC, and DMTC with acetone are shown in Figures 5-9. All of the favored transition states arise from the anti conformation of the enamine. Catalyst TC favors an up conformation for the lowest si-face transition state. Proline favors the up conformation in the anti transition states, while the other catalysts favor the down conformations (Figure 4 and Table 3).

Figure 5.

Lowest energy TSs and activation enthalpies (with respect to separated reactants) for the azetidine-catalyzed aldol reaction. Barriers with respect to the anti enamine are in brackets.

Figure 9.

Lowest energy TSs and activation enthalpies (with respect to separated reactants) for the DMTC-catalyzed aldol reaction. Barriers with respect to the anti enamine are in brackets.

The azetidine-2-carboxylic acid catalyst gives calculated transition states (Figure 5) that are approximately 2 kcal/mol lower in energy than the most favored anti-re and anti-si transition states of proline (anti-re TS and anti-si TS, Figure 4). The predicted stereoselectivity is similar to that of proline (68—69% ee). Experimentally, the same reaction—but with paranitrobenzaldehyde instead of benzaldehyde—gives higher selectivity with proline (76% ee) compared to azetidine-2-carboxylic acid (40%).

The DMC transition states (Figure 6) favor conformations with C4-down in both cases. The discrimination between up and down (0.8–1.1 kcal/mol) is similar to that of proline (0.6–1.0 kcal/mol), but in favor of the down conformation. TS-DMC-ar and TS-DMC-as have similar activation barriers as the anti-re and anti-si transition states of proline, respectively.

Figure 6.

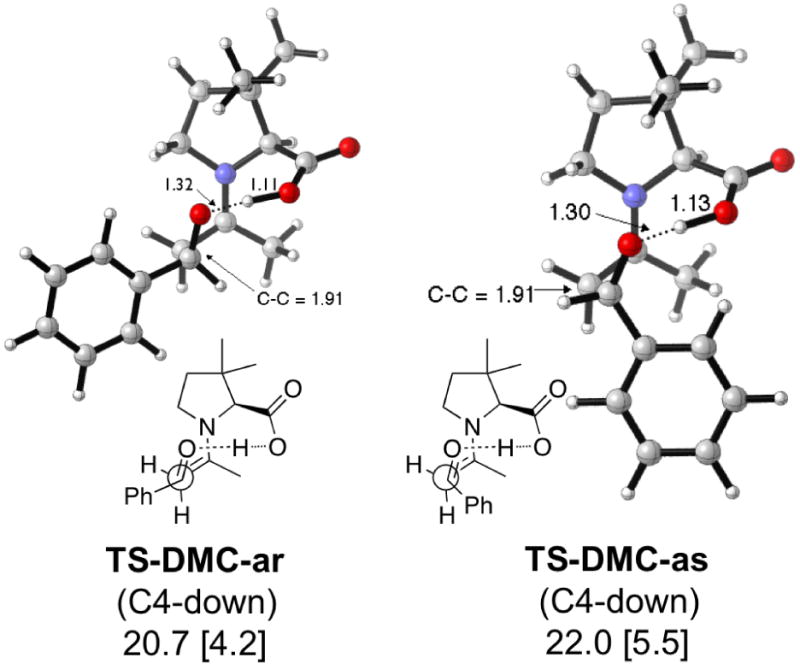
Lowest energy TSs and activation enthalpies (with respect to separated reactants) for the DMC-catalyzed aldol reaction. Barriers with respect to the anti enamine are in brackets.

The activation barriers for the aldol reaction catalyzed by TC (Figure 7) increase significantly compared to proline. This is due to the necessity to distort the thiazolidine ring in the transition states. The anti transition states show virtually no preference for either the up or down conformation.

Figure 7.

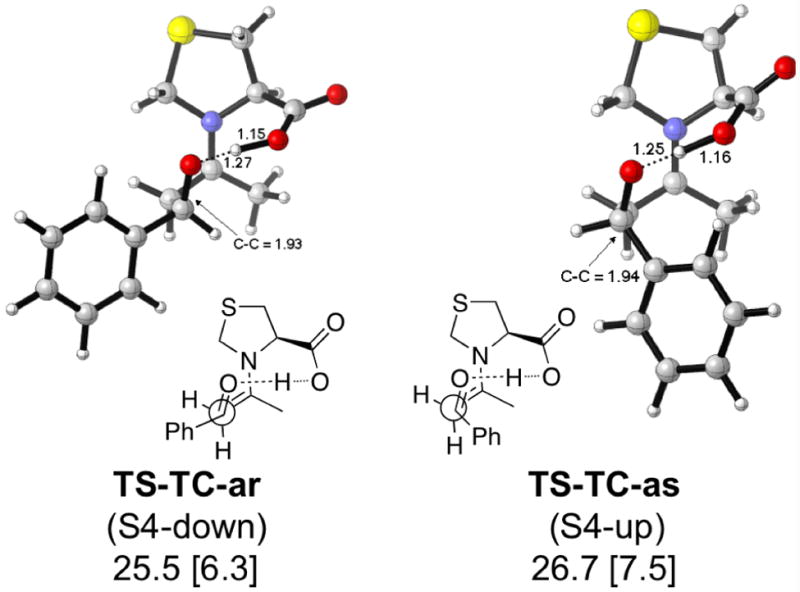
Lowest energy TSs and activation enthalpies (with respect to separated reactants) for the TC-catalyzed aldol reaction. Barriers with respect to the anti enamine are in brackets.

Both MTC and DMTC (Figures 8 and 9) give increased selectivity according to the calculations. In both cases, this appears to be related to the fact that the conformation of the thiazolidine prevents the transition states for the minor products from relaxing to a lower energy conformation.

Figure 8.

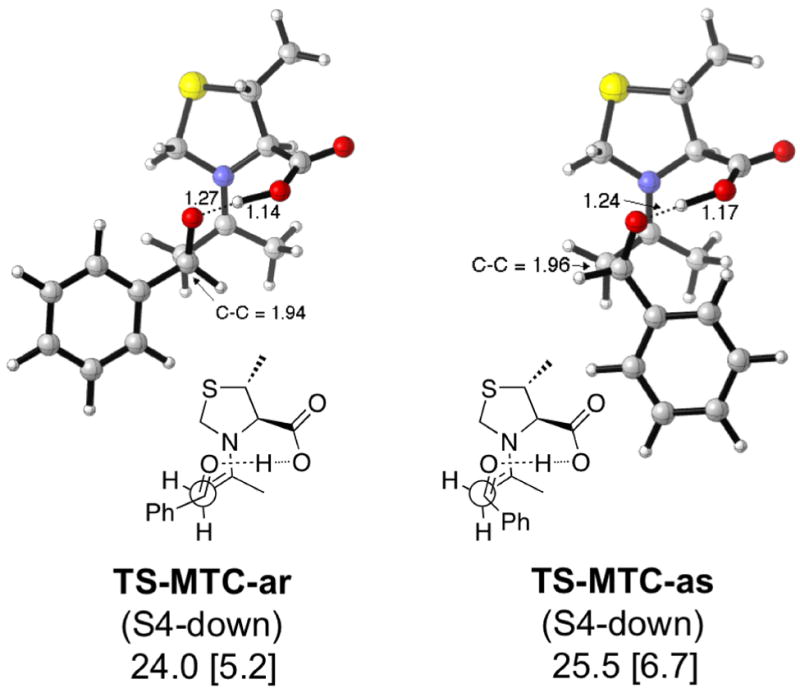
Lowest energy TSs and activation enthalpies (with respect to separated reactants) for the MTC-catalyzed aldol reaction. Barriers with respect to the anti enamine are in brackets.

3.3 Preference for the up or down ring conformation

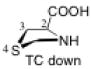
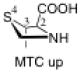
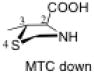
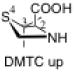
The preferred conformation of the pyrrolidine ring depends on the presence of substituent(s) on C3. A methyl substituent at C3 that is cis to the carboxylic acid group at C2 (as in DMC and DMTC) exerts steric repulsion with the acid. The torsion angle ∣Φ∣ between the cis substituent(s) at C3 and the carboxylic acid (Table 4) is an indication of the degree of repulsion. This torsion angle is significantly larger when the conformation of the ring is down (DMC: Φ = -34°, DMTC: Φ = -38°) versus up (DMC: Φ = 30° DMTC: Φ = 30°), making the down conformations more stable.

Table 4.

Influence of C3 substituents on ring conformation^a.

catalyst	Φ(°)	Δ(arup–ardown) (kcal/mol)
	32	-0.6
	-32
	28	+0.8
	-34
	31	0.0
	-35
	27	+1.5
	-39
	30	+2.5
	-38

^aRing conformation in the anti-re (ar) TS.

^bExperimental % ee in parentheses.

When one methyl group is present on C3 (trans to the carboxylic acid) as in MTC, the down conformation is favored. In the down conformation, the trans methyl group is equatorial and gauche to the developing carboxylate, whereas in the up conformation, the trans methyl group is axial and anti to the carboxylate. In the absence of a methyl group at C3, a hydrogen at C3 can also stabilize the forming carboxylate, although to a minor extent (Table 5). Thus, the up conformation is generally favored for catalysts that are unsubstituted at C3.

Table 5.

Distances between the carboxylate oxygen O7 and the proton of methyl group at C3

	TS O⋯H distances (Å)				Interaction type
	ar	as	sr	ss
azetidine	3.32	3.35	2.87	2.83	1 H
proline up	2.60	2.63	2.48	2.43	1 H
proline down	3.21	3.28	3.12	3.02	1 H
DMC up	2.74	2.69	2.72	2.69	1 Me
DMC down	2.73	2.75	2.56	2.59	2 Me
TC up	2.44	2.45	2.27	2.25	1 H
TC down	3.08	3.13	2.25	2.26	1 H
MTC up	2.41	2.40	2.24	2.23	1 H
MTC down	2.53	2.55	2.49	2.24	1 Me (anti) or 1 H (syn)
DMTC up	2.59	2.57	2.60	2.54	1 Me
DMTC down	2.59	2.60	2.53	2.55	2 Me

The presence of two methyl substituents on C3 (DMTC, DMC) also favors the down conformation. Both methyl groups are nearly gauche with the carboxylic acid. In the up conformation, the position of the methyl groups change: one methyl group becomes anti to the forming carboxylate. As a consequence, only one methyl group can stabilize the carboxylic acid through electrostatic stabilization.

The presence of sulfur at the 4-position of the five-membered ring decreases the selectivity for the up conformation and increases the selectivity for the down conformation. Analysis of the anti-re and anti-si transition states in Table 3 shows that the up conformation is favored for proline in both transition states by 0.6–1.0 kcal/mol, but for TC, this selectivity decreases to 0.0–0.2 kcal/mol. Similarly, the anti-re and anti-si transition states of DMC favor the down conformation by 0.1–0.8 kcal/mol, while the corresponding transition states for DMTC favor the down conformation by 1.9–2.5 kcal/mol.

In summary, catalysts with one or two methyls at the C3 position (MTC, DMC, and DMTC) are lowest in energy when C4 or S4 is down (Table 3). In the absence of a methyl group at C3, there is less stabilization of the carboxylic acid by the C3 substituent. Thus, catalysts without methyl at C3 have either no preference for either conformation of the ring (eg. TC), or they tend to favor C4 up (eg. proline). These unsubstituted catalysts have lower experimental and calculated enantioselectivities.

3.4 Influence of sulfur and ring size on transition states

The sulfur atom at the 4 position has no electrostatic effect on the transition states, since this atom is far from the reacting site (Figures 7-9). However, the presence of sulfur in the pyrrolidine ring does change the catalyst geometry. The C-S bond length is longer than a C-C bond: the average C-S bond length in DMTC is 1.84 Å, while the average C-C bond length in proline is 1.53 Å. In azetidine this bond length varies from 1.55 Å to 1.56 Å. In addition, the C-S-C angle is more acute than a C-C-C angle. In DMTC this angle is on average 90°, while this angle is on average 103° in proline. Thus, the presence of a sulfur atom in the five-membered ring slightly increases stereoselectivity (Table 3) due to the geometrical differences.

The catalyst ring size determines angles α and β, shown in Figure 10. The 4-membered ring azetidine has an α angle of 88° and a β angle of 132°. Angle α is larger in 5-membered rings (104° ≤ α ≤ 109°) than in azetidine, but angle β in 5-membered rings is smaller (123° ≤ β ≤ 125°) compared to azetidine. This difference moves the carbonyl function of the aldol acceptor farther away from the carboxylic acid in 4-membered rings. Stabilization of the forming alkoxide becomes less efficient as the oxide is farther away from the carboxylic acid. (Compare OH^⋯O=C distances in Figure 5 with all other transition states).

Figure 10.

Changes in ring size influence catalyst efficiency.

3.5 Pyramidality of enamine

Methyl groups at C3 influence not only the conformation of the pyrrolidine ring, but also the pyramidality of the enamine. The degree of pyramidality of the amine is defined by χn (Figure 11), where χn is measured by the out-of-plane dihedral of the amine groups [19]. The amines of 5-membered ring catalysts are almost planar in the transition states (χn = -2° to 4°, Table 6), whereas in azetidine the amine group is less planar (χn approximately 12°). Favored transition states have a planar amine due to delocalization of the nitrogen lone pair as it evolves into an iminium in the transition state.²⁰ With the exception of proline, the conformation of the ring has a very small influence on enamine planarity. In general, the amines of transition states in the down conformation are more planar than the amines of corresponding transition states in the up conformation by 1–4°.

Figure 11.

Pyramidality of enamines.

Table 6.

Pyramidality of enamines in major (ar) and minor (as) aldol transition states.

catalyst	χn-down	χn-up	(χn-down) – (χn-up)
azetidine, ar	12		0
azetidine, as	12		0
proline, ar	2	2	0
proline, as	2	1	1
DMC, ar	-1	4	-4
DMC, as	0	3	-3
TC, ar	0	3	-3
TC, as	0	3	-3
MTC, ar	0	4	-4
MTC, as	0	3	-3
DMTC, ar	-2	4	-6
DMTC, as	-2	3	-5

4. Conclusion

The trends in stereoselectivity can be predicted by using DFT at the B3LYP-6-31G(d,p) level. The conformation of the pyrrolidine ring (up and down) must be considered for accurate predictions because stabilization of the carboxylic acid and forming alkoxide changes as the pyrrolidine ring flips. Moreover, the position of the incoming carbonyl relative to the carboxylic acid, and pyramidalization of the enamine also change. A sulfur atom at the 4 position causes increased ring strain and a decreased selectivity for the up conformation. Substituents at C3 also cause the down conformation of the ring to be favored. Alteration of the proline geometry by substitution, alteration of ring size, or inclusion of a heteroatom in the ring causes small changes in selectivity. Anti transition states are always favored due to minimization of strain, maximization of interaction of the carboxylic acid and developing alkoxide, and electrostatic stabilization. Conformational changes in the catalysts are shown to be reflected in changes in stereoselectivity. The calculations indicate the multitudes of variables, some subtle, that influence stereoselectivites and show the importance of a thorough search of conformations of transition states necessary for prediction of stereoselectivities.