Genome Pool Strategy for Structural Coverage of Protein Families

Abstract

As noticed by generations of structural biologists, closely homologous proteins may have substantially different crystallization properties and propensities. These observations can be used to systematically introduce additional dimensionality into crystallization trials by targeting homologous proteins from multiple genomes in a “genome pool” strategy. Through extensive use of our recently introduced “crystallization feasibility score” (Slabinski et al., 2007a), we can explain that the genome pool strategy works well because the crystallization feasibility scores are surprisingly broad within families of homologous proteins, with most families containing a range of optimal to very difficult targets. We also show that some families can be regarded as relatively “easy”, where a significant number of proteins are predicted to have optimal crystallization features, and others are “very difficult”, where almost none are predicted to result in a crystal structure. Thus, the outcome of such variable distributions of such crystallizability' preferences leads to uneven structural coverage of known families, with “easier” or “optimal” families having several times more solved structures than “very difficult” ones. Nevertheless, this latter category can be successfully targeted by increasing the number of genomes that are used to select targets from a given family. On average, adding 10 new genomes to the “genome pool” provides more promising targets for 7 “very difficult” families. In contrast, our crystallization feasibility score does not indicate that any specific microbial genomes can be readily classified as “easier” or “very difficult” with respect to providing suitable candidates for crystallization and structure determination. Finally, our analyses show that specific physicochemical properties of the protein sequence favor successful outcomes for structure determination and, hence, the group of proteins with known 3D structures is systematically different from the general pool of known proteins. We, therefore, assess the structural consequences of these differences in protein sequence and protein biophysical properties.

Introduction

Anecdotal observations suggesting that certain physicochemical features of proteins strongly correlate with successful structure determination have been well known since the beginning of structural biology. However, with the cumulative information on such successful attempts scattered throughout thousands of publications and negative data seldom recorded, it is difficult to move beyond such anecdotal accounts in a statistically significant manner. Structural genomics (SG) has substantially changed this situation, where large numbers of proteins are now routinely subjected to similar protein production and structure determination protocols and, importantly, failures (and the exact cause and stage of the failures), as well as successes, are recorded in the publicly available NIGMS Protein Structure Initiative (PSI) database TargetDB (http://www.targetdb.pdb.org) (Chen et al., 2004). By data mining of the information currently available in TargetDB, we have identified or confirmed several properties, such as sequence length, gravy index (Kyte and Doolittle, 1982), instability index (Guruprasad et al., 1990), isoelectric point (Creighton, 1984), average number of insertions in the alignment, predicted secondary structure, predicted structural disorder, predicted coiled-coil regions, and predicted transmembrane helices, that strongly correlate with success of protein crystal structure determination (Slabinski et al., 2007a). These analyses and correlations have allowed us to derive empirical rules that were used to classify proteins into five crystallizability classes with predicted success rates progressively decreasing from optimal to the most difficult class. Further analyses with our crystallizability score also confirmed the highly complementary nature of X-ray crystallography and NMR structure determination that result in different criteria being applied for selection of optimal targets by these different methods (Slabinski et al., 2007a).

The Protein Structure Initiative (PSI), a US-based Structural Genomics effort supported by the NIH NIGMS, currently focuses on providing structural representatives of protein families with no or limited coverage (http://www.nigms.nih.gov/Initiatives/PSI/Background/MissionStatement). This approach has arisen from the realization that, despite many years of continuous effort by structural biologists, 60% of known protein families, as described for instance in the PfamA database (Finn et al., 2008), still do not include any proteins with a solved structure. Structure determination of the first protein in a family is a major milestone since it can be used as a blueprint or template to understand or narrow down the function of all, or a large subset of, the proteins in this family. We can then construct models for other members of the family using comparative modeling (Sali, 1995), (Lutfullah et al., 2008). Additional protein structures solved in a particular family bring a better understanding of the diversity/conservation within the family and improve the quality of models that can be constructed for the remaining proteins in the family (Fernandez-Fuentes et al., 2007).

For the PSI, screening of multiple homologs is a natural strategy for tackling the protein crystallization problem because of its focus on protein families rather than on individual structures and because the high-throughput approach used by the centers is particularly amenable to this strategy. In individual structural biology labs, the crystallization bottleneck is typically tackled by systematic trials of different crystallization conditions and expression constructs. Many academic and commercially available crystallization screens that were successfully developed some years ago (e.g., Carter and Carter, 1979) facilitate this approach. Crystallization screening is usually extended to homologs only if the original target fails to crystallize. In structural genomics, protein production and crystallization screening are usually attempted at the outset for multiple members of a protein family of interest. The gain from the use of multiple genomes as the source of structure determination targets has been commented on in the early years of structural genomics (Savchenko et al., 2003). This approach can be termed a “genome pool strategy” since it involves using many genomes as the pool of targets for protein expression and structure determination.

The most fundamental question concerning the genome pool strategy is whether it really works and, if yes, why. Other practical questions could be asked such as: what level of sequence similarity of homologous proteins, in fact, represents independent crystallization trials? Are some genomes better than others as sources of structure determination targets? To what extent is a protein's statistical chance to be solved determined by the family it belongs to versus the genome it comes from, or are both immaterial compared to individual features and properties of the protein itself? What is the optimal number of genomes that should be used as sources of targets (i.e. size of the genome pool), and are there any genomes (or groups of genomes) that do not provide sufficient benefits for their inclusion? As one of the four PSI production centers participating in the coordinated effort of targeting protein families for structure determination, we have both a strong motivation and a unique opportunity to address these fascinating and very pertinent questions for the entire structural biology community.

We show here that the genome pool approach significantly increases the success rate of structure determination per protein family. In trivial cases, some domains—typically linked to transmembrane regions, to regions of structural disorder, or to fragments of low complexity—may, in some organisms, be present as single-domain proteins that are more amenable for expression, purification and crystallization. In other more complex situations, many, but not all, members of a protein family may show some combination of features that are detrimental to protein expression or crystallization. In both situations, structure determination attempts are likely to benefit from screening multiple homologs and, only if that fails, should design and production of new constructs be the next best choice.

The four PSI production centers have adopted this genome pool strategy as a systematic approach to the problem of improving structural coverage of protein families. Groups of protein families without any solved structures were assigned to the PSI centers in a centrally coordinated process. It is now 2+ years after the first assignment of target families to the PSI centers and, while additional structures from these families are still being solved, it is already possible to analyze and evaluate the initial results of the first formal application of this strategy. We present this report and analysis here.

Materials and Methods

Analysis of the correlation of structure determination success in pairs of homologous proteins

In our recent publication (Slabinski et al., 2007a), we described a learning set extracted from TargetDB that was used to derive statistics and parameters on success and failure in protein structure determination. Here, we have updated this learning set and used it to analyze the relationships between sequence similarity, family assignment, and/or genome of origin and success in structure determination. The learning set contains a positive subset composed of protein sequences that led to successful structure determinations and a negative subset composed of proteins that failed for some reason. The learning set was prepared from TargetDB version March 2007 as follows:

A total of 3,140 protein structures determined by X-ray crystallography and deposited in the PDB by all PSI SG centers were included in the positive subset. As we described before, identifying meaningful criteria for the negative subset is far less obvious since, in many cases, “stopped” targets were not failures, but had been stopped for other reasons, such as solution of a similar structure by another group. In defining the criteria for the selection of the negative subset, we used our experience of how targets that failed in our own production pipeline (JCSG) were reported in TargetDB and informally consulted other PSI centers. Thus, the negative subset is composed of two groups of targets (n.b. target categories from TargetDB are shown in boldface):

• all stopped targets listed as purified, but not crystallized, and not assigned to NMR

• all targets that were purified more than 18 months before March 2007 and were not crystallized and not assigned to NMR and did not show any progress since then

A total of 5,819 proteins were included in the negative subset.

The group of proteins that were crystallized, but did not have solved structures, was excluded from both the negative and the positive learning sets because it is difficult to establish appropriate reasons for their failure. Many of them may represent inferior-quality crystals that did not lead to structure determination. Others might have been stopped before the crystallization stage because a close homolog was deposited in the PDB. The latter category would inappropriately skew the composition of the negative subset. However, PSI centers usually avoid targeting very close homologs of targets that are already targeted by other centers, so such situations were relatively rare, as compared to the number of targets that simply failed to crystallize.

Subsequently, we identified all pairs of similar proteins in the learning set using the BLAST program (Altschul et al., 1990). Pairs with BLAST e-value < 0.001, sequence identity > 20%, and alignment covering at least 75% of both proteins were regarded as similar. Positive (crystallized targets) and negative (targets that failed to crystallize) subsets were prepared as described above. For each protein, we identified the closest homolog from the negative subset and the closest homolog from the positive subset. Each protein was assigned to the appropriate bin, according to its distance (as measured by sequence identity) to the closest crystallized homolog, and to another bin, according to its distance (again measured by sequence identity) to the closest homolog that failed to crystallize. The bins correspond to the following ranges of sequence identity: 99–90%, 89–60%, 59–50%, 49–40%, 39–30%, and 29–20% (n.b. we chose a larger range for the second bin since smaller bins did not amass sufficient data). The crystallization successes and failures were then counted for each bin, and the success rate was calculated. Results are presented separately as a function of sequence identity to the closest crystallized homolog (Figure 1A) and as a function of sequence identity to the closest homolog that did not crystallize (Figure 1B).

Figure 1.

(A) The probability of crystallization is shown as a function of sequence identity to the closest crystallized, homologous target (see Materials and Methods). Each protein was assigned to the appropriate bin, according to its distance (as measured by sequence identity) to the closest crystallized homolog, and to another bin, according to its distance (again measured by sequence identity) to the closest homolog that failed to crystallize. The bins correspond to the following ranges of sequence identity: 99–90%, 89–60%, 59–50%, 49–40%, 39–30%, and 29–20% (n.b., the second bin is larger since smaller bins did not amass sufficient data). The crystallization successes and failures were then counted for each bin, and the success rate was calculated. In each bin, the number of crystallized proteins is shown as a blue bar, and the number of proteins that failed to crystallize is shown as a gray bar. The success rate (right vertical axis) was calculated directly from the histograms as a percentage of crystallized targets per bin and is shown as a black line.

(B) The probability of crystallization shown as a function of sequence identity to the closest homologous target that failed to crystallize. Prepared as in A (see Materials and Methods).

(C) The probability of crystallization shown as a function of two variables: sequence identity to the closest homologous target that crystallized and the sequence identity to the closest homolog that failed to crystallize. Figures A and B are one-dimensional projections of the figure shown here; see the detailed explanation of Figure A above and in the body of the manuscript.

In order to learn more about situations where a protein has significant homology simultaneously to both crystallized and non-crystallized targets, we calculated a two-dimensional distribution of crystallization probability as a function of sequence identity to the closest homolog in the negative and positive sets. In the learning set, we found a total of 2,034 targets with homologs in the negative and positive sets. In the two-dimensional graph, we used bins larger than in one-dimensional graphs in order to collect a sufficient number of targets in each bin (Figure 1C).

Distribution of crystallization feasibility classes in complete microbial genomes

We downloaded sequences of all proteins from the 487 completed microbial genomes (representing a total of 1,549,504 protein sequences) from the NCBI database (http://www.ncbi.nlm.nih.gov/genomes/lproks.cgi). For each protein, we calculated its crystallizability class using crystallizability score (Slabinski et al., 2007a). We then calculated the average percentages of optimal and very difficult targets in each genome. The distribution of protein crystallizability classes in 487 microbial genomes is illustrated in Figure 2. Based on information available from the NCBI Web site, we divided the genome pool into non-overlapping groups in two different ways:

• Division 1: Thermophiles, pathogens, symbionts, and all other organisms

• Division 2: Bacteria and Archaea

Figure 2.

The distribution of protein crystallization feasibility classes in known microbial genomes. Genomes of thermophilic organisms, host-associated organisms, and others are shown separately. Inside each group, genomes are sorted by the percentage of proteins in the very difficult class (magenta graph).

The average percentages of targets from optimal and very difficult classes were calculated for these groups of genomes (Table 1).

Table 1.

Average percentages of optimal and very difficult targets in different groups of organisms

Selected group	Average % optimal	Average % very difficult
Archaea	13	39
Bacteria	11	45
Thermophiles and hyperthermophiles	13	40
Host-associated	11	46
Other	11	44

Coverage of PfamA families by microbial targets from different crystallizability classes

The PfamA database (Finn et al., 2008) version 2.1 from July 2007 contains alignments and Hidden Markov Models for 8,961 protein families. For all 1,549,504 protein sequences from 487 microbial genomes, we performed HMMER (Eddy, 1998) searches against the PfamA database. A total of 5,407 PfamA families had at least one representative in microbial genomes on our list. More detailed statistics on PfamA families are given in Table 2. To assess the increase in family coverage brought by each newly sequenced genome, we calculated an incremental coverage of all PfamA families when microbial genomes were added in random order (Figure 3A). Separately, we calculated similar incremental coverage of PfamA families that still do not contain any solved structures (Figure 3B).

Table 2.

Statistics of PfamA families covered by microbial genomes

Total PfamA families (ver. 21).	8,961
PfamA families with representatives in 487 microbial genomes	5,407
PfamA families with more than 50 representatives in 487 microbial genomes	2,981
PfamA families with more than 50 proteins in microbial genomes with more than 90% of targets in the very difficult crystallizability class	739
PfamA families with more than 50 proteins in microbial genomes with all targets in the very difficult crystallizability class	427

Figure 3.

Increasing coverage of known PfamA families from sequencing of microbial genomes. The color coding reflects the different crystallizability scoring classes. Green curve—the number of PfamA families with at least one target in the optimal crystallizability class; light-green curve—the cumulative number of PfamA families with members in the two top crystallizability classes (optimal and suboptimal); yellow curve—the three top classes; and red curve—all but the fifth crystallizability class (very difficult). The magenta graph shows the number of PfamA families covered by proteins from all crystallization classes (optimal to very difficult). The differences and transitions for one color to the next then indicate the sequential additions of Pfam families covered from considering optimal through to very difficult in 5 steps of the classifications. The statistics are shown separately for all PfamA families (A) and for families that still do not contain any solved structures (B). As might be anticipated, there are fewer optimal targets and more very difficult targets in Pfam families with no solved structures.

Distribution of crystallization feasibility classes, and solved structures in protein families

The crystallizability score is calculated for individual proteins and, hence, is not directly applicable to scoring of protein families. However, we can assess the “difficulty” of a protein family by calculating the percentage of very difficult targets (i.e., the fifth class in our crystallizability score) in this family and, in this way, assess relative difficulty of any given family.

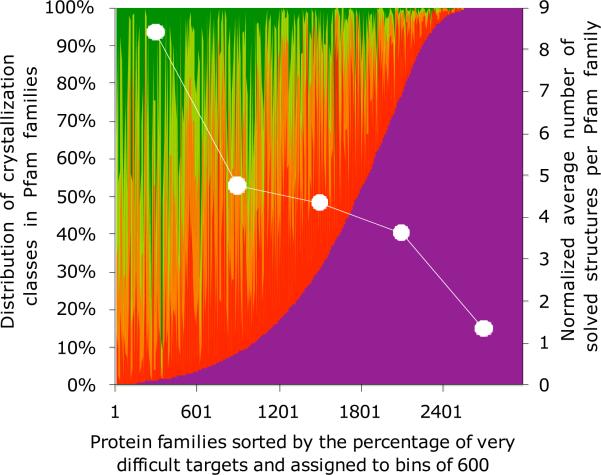
All PfamA families that contained at least one solved structure were sorted by the calculated percentage of very difficult targets and then divided into 5 bins with 600 families each. After sorting, the first bin contains families with the lowest percentage of very difficult targets, and the last bin contains families consisting mostly of very difficult targets. The first bin contains families 1–600 in the sorting order, the second bin contains families 601–1200, the third contains families 1201–1800, the fourth contains families 1801–2400, and the fifth contains families 2401–3000. The average number of solved structures per protein family was calculated for families in each bin and is shown together with the distribution of crystallizability classes in those families (see Figure 4). The average size of the family (i.e., number of members) in the five bins was 381, 689, 634, 519, and 420 (from the “easiest” to the “most difficult” bin). To eliminate the effect of different average family sizes on the number of solved structures, we normalized the number of solved structures per family in each bin by multiplying the average number of structures by the ratio of the average family size in all five bins (equal to 529) to the average family size in a given bin.

Figure 4.

The distribution of solved structures in protein families assigned with different levels of difficulty. The families were first sorted by the percentage of the very difficult targets (crystallizability class 5) and then split into six bins of 500 families corresponding to different levels of difficulty. After sorting, the first bin contains families with the lowest percentage of very difficult targets, and the last bin contains families consisting almost exclusively of very difficult targets, i.e., akin to the five relative scoring classes from optimal (green) to very difficult (magenta) as colored on the graph. The distributions of crystallizability classes (green to magenta) are shown for all protein families (left y axis). The normalized average number of structures per protein family has been calculated for each bin (right y axis). By using normalization, we are taking into account differences in family sizes—the average number of solved structures per family has been multiplied by the ratio of the average family size in all five bins to the average family size in a given bin.

Assessment of trends in solved structures from protein families

To evaluate any systematic trends in crystallized versus non-crystallized proteins, we compared average physicochemical features of solved structures from protein families with average features of all members of those families. For each PfamA family, we identified solved structures by comparing full protein sequences of all family members (downloaded from GeneBank) with sequences of PDB structures using BLAST. To be counted as a “solved structure,” the protein sequence of a family member had to be at least 95% identical to a sequence from the PDB SEQRES record, and the alignment of its sequence with the sequence from the PDB SEQRES record had to cover at least 80% of both sequences. Then, for each protein family, we calculated average values of several physicochemical features, with three types of averages calculated for each: average over full protein sequences of all family members, average over family members with solved structures, and average over sequences of constructs of solved structures (retrieved from SEQRES records of PDB entries). Then, we collected these average values for all PfamA families with solved structures and calculated their distributions (green, blue, and black graphs in Figure 5, respectively). In this analysis, we included all features identified previously as having a significant impact on protein crystallization (Slabinski et al., 2007a), such as sequence length, isoelectric point (Creighton, 1984), gravy hydropathy index (Kyte and Doolittle, 1982), number of residues in the longest disordered region as predicted by DISOPRED2 (Ward et al., 2004), protein instability index (Guruprasad et al., 1990), percentage of the coil structure as predicted by PSIPRED (Jones, 1999), number of residues in the coiled-coil structure as predicted by COILS (Lupas et al., 1991), and percentage of insertions in the sequence when aligned with its homologs. We also performed analogous calculations for PfamA families without any solved structures. Again, average parameters were calculated for each family and then presented as distributions (red graphs in Figure 5).

Figure 5.

Distributions of parameters describing various features (length, gravy index, pI, instability index, length of disordered fragment, and percentage of coil structure) of protein sequences calculated for: full sequences of microbial members of PfamA families with at least one solved structure (green graphs), full sequences of all solved structures from PfamA families (blue graphs), sequences of actual constructs of solved structures from PfamA families (black graphs), and full sequences of microbial members of PfamA families without any solved structures (red graphs). For more details, see Results and Discussion section.

Progress in structure determination of PfamA families 30 months after the first target draft

In November 2005, the four PSI production centers selected a list of the largest 1,369 PfamA protein families that had no solved structures, and were not membrane or eukaryotic-only families, to become targets for the PSI. As the crystallizability score was not used in their selection, it is possible to directly compare progress in structure determination in those families with respect to their crystallizability ranking. In 2005, the JCSG used the earlier version of our crystallizability score to prioritize all 1,369 families. Families were sorted by the number of targets from the optimal and suboptimal crystallizability class, and the top 750 families were assigned to 3 categories, each containing 250 families. The remaining 619 families formed the fourth category, regarded as very difficult because of the low number of suitable targets. Thirty months later, we calculated the percentage of families solved in each of these categories (see Table 3). While structure determination of these families is still ongoing, results already available provide a striking example of the value of using the crystallizability score in a predictive manner. For our top classification, a resounding 51% of these families have a structure determined for at least one, if not several members, whereas for our lowest `very difficult' category only 16% of these families have a structure representative to date. Interestingly, one quarter of these 16% were solved by NMR and, hence, were not categorized by our scoring system for NMR success or failure in structure determination. In the top group of families, NMR produced only 4% of the structures in this category, that, when combined with the previous analysis of the `very difficult' category, indicates the truly complementary nature of these methods and the inverse relationship in the scoring and, hence, suitability of targets for each method (Slabinski et al., 2007a).

Table 3.

Current progress in structure determination in families originally assigned to the four PSI production centers in 2005. At that time, JCSG ranked those families by the numbers of optimal to very difficult targets.

Group (category) of families in the original ranking by JCSG	Average number of class 1–3 targets per family	Percentage of families solved by X-ray and NMR in each category (X-ray+NMR)
Optimal (1–250)	45	49+2%
Suboptimal (251–500)	14	29+4%
Difficult (501–742)	10	26+5%
Very difficult (743–1369)	7	12+4%

Results and Discussion

As expected, the ability of a protein to crystallize is correlated for pairs of highly similar sequences. Close homologs of crystallized proteins are more likely to crystallize, but, interestingly, this positive correlation drops rapidly for sequence identities below 90% (see Figure 1A). As expected, close homologs of proteins that did not crystallize have significantly lower chances for crystallization, but this negative correlation does not drop so rapidly—even relatively remote homologs still have a decreased probability of crystallization (Figure 1B). In other words, it is easier to inherit a tendency for failure than for success. These trends can be rationalized by the fact that there are well-defined global physicochemical features of proteins that have a negative impact on protein crystallization (extreme values of hydropathy index, isoelectric point, predicted structural disorder, etc.), while features of proteins that strongly promote crystallization are very idiosyncratic and can rapidly change with even small sequence modifications. Therefore, features that have a negative impact on crystallization (such as long regions of structural disorder) are often conserved in groups of similar sequences, even if sequence similarity is relatively low. In contrast, the features that promote protein crystallization are conserved only for proteins with almost identical sequences. It is well known that protein crystallization can be facilitated by mutating even one or a few residues on the protein surface, while a long fragment of a structurally disordered backbone present in all homologous sequences can make crystallization impossible for all of them. We are well aware that the correlation plots presented in Figure 1 may, to some extent, be influenced by the target selection process itself. Nevertheless, to the best of our knowledge, these correlation plots represent the first examples of such statistics, the compilation of which was impossible before the PSI centers initiated a systematic collection of all protein production and crystallization data. These results confirm that features that correlate with difficulties in crystallization and structure determination are, indeed, possible to predict, while the factors that promote protein crystallization remain, to a much greater extent, unpredictable. This observation is in agreement with the fact that crystallizability score, (Slabinski et al., 2007a), is largely based on elimination of sequences with negative features rather than on selecting sequences with positive features. Many others are now emulating or this study or have independently come to similar conclusions (Overton and Barton, 2006).

The graphs presented in Figures 1A and 1B do not describe the entire complexity of the problem since most proteins in the learning set are homologous to many other proteins, whereas the histograms and resulting success rates are presented as a one-dimensional function of sequence identity to the closest crystallized homolog (Figure 1A) and (separately) as a function of sequence identity to the closest non-crystallized homolog (Figure 1B). These graphs are based on the assumption that, to the first approximation, the correlation with crystallizability should be observed between a protein and its closest homolog from each set. Of course, this does not have to be the case, especially for targets with homologs in both the negative and positive sets. In order to gain some intuition into the distribution of probability of crystallization success in such cases, we calculated a two-dimensional distribution where the crystallization success rate is plotted as a function of sequence identity to the closest crystallized homolog and sequence identity to the closest non-crystallized homolog (Figure 1C). The left horizontal axis corresponds to four ranges of sequence identity to the closest, not-crystallized homolog (sequence identity ranges 0–25%, 25–50%, 50–75%, 75–100%). In an analogous way, the right horizontal axis is sub-divided into four ranges of sequence identity to the closest crystallized homolog. Each bin is defined by a sequence identity range on the left axis and a sequence identity range on the right axis. The vertical axis corresponds to the crystallization probability calculated from the proportion of crystallized and not-crystallized targets found in each bin. The distribution shows that, indeed, the crystallization success rate is mostly correlated with crystallization success or failure of the closest homolog. For instance, targets with more than 75% sequence identity to any crystallized target have a very high success rate, even if they are also 50% identical to a protein that failed to crystallize (upper-right region of Figure 1C). In a similar fashion, targets with high sequence identity to any target that failed to crystallize are unlikely to crystallize, even if they also show some homology to a target that was crystallized (middle-left region of Figure 1C)

In our previous publication (Slabinski et al., 2007a), we presented data-mining analysis of the protein production data that are deposited in TargetDB. This analysis indicates that ranges of protein properties that are optimal for protein crystallization lie within parameter ranges that are optimal for protein production (i.e., the process consisting of cloning, expression, and purification) (Slabinski et al., 2007a), although substantially more parameters can be correlated with crystallization than with protein production. In the same publication we showed that, indeed, the OB-score (Overton and Barton, 2006) does much better for protein production than crystallization. Because of that, and since protein crystallization remains the most important bottleneck in protein structure determination, we decided to use only protein crystallization scoring in our current analysis.

Our ability to estimate the likelihood of crystallization makes it possible to define crystallization classes from 1 (optimal) to 5 (very difficult) and to analyze the distribution of different classes in microbial genomes used as sources of targets for protein families. Surprisingly, the distributions of these crystallization classes in genomes as a whole do not show large differences, with some groups, such as pathogenic and symbiotic bacteria, having only a slightly higher content of difficult targets and thermophilic organisms a slightly higher content of promising crystallization targets (Figure 2 and Table 1). These results suggest that it is not possible at present to identify any particular set of genomes that is “best” for choosing targets for protein crystallization and structure determination. It is very likely that systematic problems with protein expression are the main reason for differences in the suitability of specific genomes for structure determination reported by many labs. On the other hand, some specific genomes clearly show a lower content of optimal targets (Figure 2). It should be noted that this analysis was performed, and therefore all the observations apply, only for microbial genomes.

From the structure determination perspective, the distribution of crystallization classes in protein families is more interesting. Surprisingly, most protein families show a relatively even distribution of crystallization classes with significant percentages of both optimal and very difficult proteins (Figure 4) (n.b. we focus here on these two classes since their relative crystallizability scores have the greatest predictive power).

Despite the availability of almost 500 completed microbial genomes, the number of proteins that can be assigned to the optimal target group in individual families is still in the linear growth phase (Figure 3). It is still very encouraging that, with every 10 newly sequenced microbial genomes, promising targets (i.e. targets from classes 1–4, excluding class 5) for protein structure determination are provided for about 7 new PfamA families. Therefore, increasing the size of the genome pool to find a more suitable family member is a simple strategy for increasing the success rate, and all PSI centers adopt this strategy. Similarly, as more genome sequences are added to the database, it is valuable to go back and reassess whether a family now contains more `optimal' targets that should be considered.

As one would expect from what we have reported here, the number of solved structures from a protein family is highly correlated with the number of predicted optimal targets for crystallization and structure determination (Figure 4). This result indicates that the uneven distribution of the representation of protein families in the PDB may, to some extent, be caused by technical difficulties in protein production and crystallization rather than by research interest alone. It is important to note that these statistics are based on the entire PDB and, thus, are dominated by results from traditional structural biology labs, as PSI centers only started to contribute significantly to the PDB in the last 5–6 years.

Since certain specific protein features are so strongly correlated with likelihood for a given protein to crystallize, it is natural to ask to what extent proteins with solved structures are representative of all proteins within each family. Even for protein families which have structures of multiple members in the PDB, process itself might information may be systematically absent from the database on subfamilies of proteins within these families with features that are detrimental to protein production and crystallization. Our results (Figure 5) demonstrate that this is, indeed, the case. Within each family, proteins with solved structures are shorter, more hydrophobic, and more acidic. They also show lower structural instability and contain less structural disorder. These tendencies are not particularly strong, but are in good agreement with the propensities used to define our crystallization classes despite the fact that the latter were calculated from a small subset of TargetDB. The distributions in Figures 4 and 5 were, on the other hand, derived from all microbial representatives of PfamA families and the entire PDB, i.e. a much larger dataset by over two orders of magnitude. The distributions of protein features were also calculated for actual protein constructs used in structure determination in order to assess the impact of construct design, such as truncations, deletions, and mutations (black graphs, Figure 5). It seems that, in most cases, the impact of construct design is not readily apparent in our distributions since the differences between plots representing average parameters of all members of families with a structural representative (green graphs, Figure 5) versus plots representing only the solved proteins from those families (blue graphs, Figure 5) are much larger than the differences between full sequences of solved proteins (blue graphs, Figure 5) and protein constructs (black graphs, Figure 5). In short, this means that, statistically, the bias resulting from crystallization tendencies, albeit not very large, is still larger than the effect of minor modifications introduced in order to improve crystallization probability. This does not hold for individual cases where the construct properties are radically changed by truncation. In such instances, long fragments of disordered regions, or entire trans-membrane domains, when removed may then move the target from a very difficult to an optimal class. However, such construct design procedures require correct and precise identification of boundaries of structural domains, and this issue is not reflected by our crystallizability score. Therefore, a good crystallizability class of the designed protein construct is a necessary, but not sufficient condition for successful crystallization.

As an example of successful construct design and how it is reflected by crystallization score, we can cite the first structure determined for the NDR family (Pfam PF03096), that is related to cell differentiation and metastasis (Kovacevic and Richardson, 2006). After initial unsuccessful crystallization trials, several constructs were prepared in the JCSG, and the construct that was truncated at both the N- and C-termini was successfully crystallized and solved. The original full protein sequence was predicted to be in the most difficult crystallization class (i.e. 5), whereas the truncated constructs, including the construct that was eventually crystallized was assigned to crystallizability classes 2 and 3. Thus, this improvement in crystallizability was clearly reflected by the crystallizability score. Thus, the crystallizability score can often, but not always, differentiate between more-promising and less-promising constructs, but does not necessarily enable accurate prediction of the exact boundaries of the structural domains, which is often critical for successful construct design. It means that a good crystallizability class assignment is a positive indicator of, but is not sufficient for, crystallization success. Domain boundaries can be often predicted based on the alignment with homologous structures, multiple sequence alignment of all homologs, secondary structure prediction, and structural disorder prediction. All this information is available from the XtalPred server (Slabinski et al., 2007b).

Distributions of average sequence parameters were also calculated for protein families that still remain unsolved (red graphs, Figure 5) in order to address the question of whether there are fundamental differences between families with solved structures and families without any solved structures. The distributions illustrated in Figure 5 demonstrate that families without solved structures are, on average, considerably different from families with solved structures. The unsolved families are significantly more hydrophilic (gravy index, Figure 5), and contain more structural disorder than the successful ones. These two features clearly stand out, confirming the observation that a significant groups of proteins contain long disordered regions and that this feature, albeit detrimental to crystallization and structure determination, must be essential for protein function and, hence, conserved in the entire protein family (Romero et al., 1998) (Romero et al., 2004).

In November 2005, the four PSI production centers proposed a list of 1,369 PfamA protein families that lacked any solved structures as targets for the PSI. As the crystallizability score was not used to select these families, and the results of their structure determination were not used in the derivation of the score, they provide an independent and predictive test of the score (see Table 3). Of these families, at least one representative of 393 families is now solved (254 by four large PSI centers). We originally sub-divided the 1,369 families into four `crystallizability' groups, as described in the Methods section. The structure determination success rate per protein family reaches 51% in the top-ranking group, goes down to 33% in the next group, falls to 31% in the next group, and finally drops to 16% in the bottom–ranking group (Table 3). These results provide a very approximate, but important, illustration of the success of the crystallization feasibility score and the genome pool strategy, since the ranking was calculated in a prospective manner before any protein production and structure determination process was initiated.

We also have to stress here that the effort to determine structures of these families is still ongoing and that the number of solved families is increasing. Because the process is not finalized, it is not possible yet to accurately calculate accurate success rates per individual target in different groups of families but, from the data in Table 3, it is obvious that success rate per family is at least 3 times higher in the group of families with the highest percentage of optimal crystallization targets (top ranking group in Table 3) and this difference increases to over 10 if we further subdivide into smaller bins. Thus, these preliminary data provide a simple, but compelling illustration of the effectiveness of the genome pool approach for targeting protein families.

Despite the sequencing now of almost 500 microbial genomes, every genome still contributes valuable new targets for structure determination and brings good targets into some “difficult” families that, therefore, increase the chances for successful structural coverage. Assuming that the present trends hold up, we would need to sequence an additional 500 genomes to find targets for classes 1–4 for all 400+ PFAM families that currently do not contain such classes of targets.

The genome pool approach then is a simple strategy to improve the success rates of structure determination for protein families by targeting multiple members of a given protein family for structure determination. Similar approaches have been used in structural biology for some time, but the PSI centers have been able to apply them on a much larger scale. This strategy can be applied at random, but is much more effective when proteins with features that favor crystallization are selected or, probably more importantly, proteins with features that are disfavored are eliminated, since this approach avoids the high cost of almost certain failures. Our recently developed XtalPred server provides such a service for the entire structural biological community as it aids in selection of optimal targets for structure determination and, in addition, provides suggestions on homologs that are more suitable for crystallization and structure determination than the original sequences supplied by the user (Slabinski et al., 2007b).