Abstract
Explicit solvent molecular dynamics (MD) simulations were carried out for three RNA kissing–loop complexes. The theoretical structure of two base pairs (2 bp) complex of H3 stem–loop of Moloney murine leukemia virus agrees with the NMR structure with modest violations of few NMR restraints comparable to violations present in the NMR structure. In contrast to the NMR structure, however, MD shows relaxed intermolecular G-C base pairs. The core region of the kissing complex forms a cation-binding pocket with highly negative electrostatic potential. The pocket shows nanosecond-scale breathing motions coupled with oscillations of the whole molecule. Additional simulations were carried out for 6 bp kissing complexes of the DIS HIV-1 subtypes A and B. The simulated structures agree well with the X-ray data. The subtype B forms a novel four-base stack of bulged-out adenines. Both 6 bp kissing complexes have extended cation-binding pockets in their central parts. While the pocket of subtype A interacts with two hexacoordinated Mg2+ ions and one sodium ion, pocket of subtype B is filled with a string of three delocalized Na+ ions with residency times of individual cations 1–2 ns. The 6 bp complexes show breathing motions of the cation-binding pockets and loop major grooves.
INTRODUCTION
Loop–loop interactions between RNA hairpins represent an important class of RNA–RNA recognition motifs. These ‘kissing–loop’ complexes participate in antisense regulation of a variety of cellular processes in prokaryotic cells and in bacteriophages (1). One of the most important events in the life cycle of retrovirus is encapsidation (2). Kissing–loop complexes are involved in dimerization of retroviral RNA genomes such as HIV-1 and Moloney murine leukemia virus (3,4). The genomic RNA molecules of the viruses dimerize through non-covalent interactions at the 5′ end (2). Stem–loops of both genomic RNAs are important in this process (5). Kissing–loop complexes can be formed by self-complementary as well as non-self-complementary segments with varied number of the intermolecular base pairs usually complemented by additional structural elements such as unpaired and stacked bases.
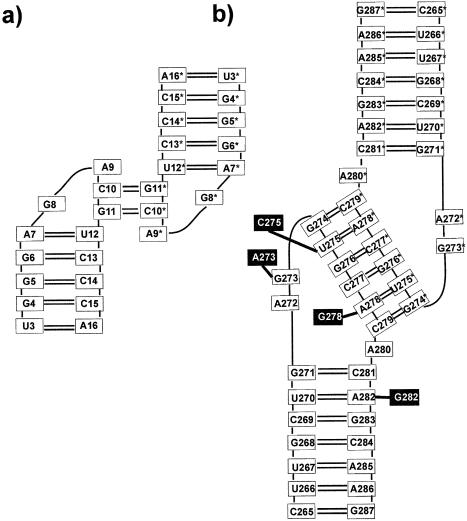
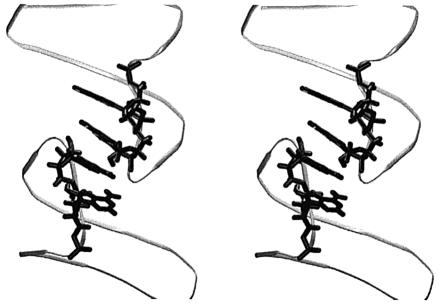
In Moloney murine leukemia virus, there are three stem–loops, H1, H2 and H3 (4,6). The H1 initiates the dimerization process and forms dimerization initiation site (DIS), which is a kissing–loop complex. The H2 and H3 stem–loops are involved in dimerization and they also form kissing complexes. They likely facilitate recognition between the two genomic RNAs. Structure of the H3 stem–loop has been solved using two-dimensional NMR (Fig. 1a) and shows a formation of a stable homo-dimeric kissing–loop complex stabilized by only two G-C Watson–Crick base pairs (7). The NMR structure suggests previously unobserved distorted non-planar and mutually interacting G-C base pairs accompanied with cross-strand stacking interactions with the adjacent adenines and unusual electrostatic interbase interactions (Fig. 2).
Figure 1.
Scheme of (a) 2 bp H3 stem–loop kissing–loop complex of the Moloney murine leukemia virus and (b) 6 bp kissing–loop complex of HIV-1 DIS subtype A. Changes in loop sequence corresponding to HIV-1 DIS subtype B are represented by black boxes and are symmetrical (see ref. 8). The intermolecular base pairs and the adjacent unpaired bases will be called the central part of the kissing–loop complex in the following.
Figure 2.
Central part of the 2 bp kissing complex as seen in the NMR structure. Note the deformed intermolecular G-C base pairs.
Other kissing–loop complexes characterized at atomic resolution level involve six base pairs (6 bp). Crystal structures are available for the RNA DIS of HIV-1 subtypes A (mal) and B (lai) (8). Both molecules adopt a hairpin conformation, with loop sequences consisting of 272-AGGUGCACA-280 and 272-AAGCGCGCA-280. The six-base self-complementary stretch (underlined) allows homodimerization through the kissing–loop complex. The conserved purines A272 and R273 are stacked in a bulged-out conformation while A280 is left unpaired within the helical stack. The HIV-1 DIS crystal structure differs in important aspects from earlier NMR study (9). Namely, the NMR structure has a distorted kissing–loop helix deviating from A-RNA geometry, bulged-in conformation of the A272/A273 bases and the G271-G281 base pair is not formed. A kissing–loop motif was observed in the anticodon–anticodon interaction of tRNAAsp crystals (10) and in 50S ribosomal subunit (11). NMR structures were reported for the ColE1 kissing complex (12) and HIV Tar hairpin loop and its complement (Tar–Tar* complex) (13). Kissing–loop complexes were studied by a variety of other experimental and molecular modelling approaches (14–18). Pattabiraman et al. (16) reported molecular modelling and MD simulations of two major subtype isolates (mal and lai) of HIV-1 kissing–loop structures investigated also in the present study. They proposed a possible mechanism of conversion of the kissing–loop structure into the extended duplex structure without unwinding the stems. Their explicit solvent simulations were extended to ∼0.5 ns while hydration and ions were not studied. Thus a direct comparison with our considerably longer simulations is not possible as most changes and important events occur after 1 ns into the simulations. Further, the model structures simulated by Pattabiraman et al. differ somewhat from the crystal geometries by Ennifar et al. (8).
Here we complement the atomic resolution experimental studies on RNA kissing–loop complexes using explicit solvent MD simulations. Although the accuracy of simulations is limited by force field approximations and simulation time scale, explicit solvent MD simulations were successfully used to analyze important aspects of RNA structure and dynamics (17,19–32). We provide insights into nanosecond dynamics of the kissing–loop complexes, cation binding, hydration and base pairing. We first analyze the kissing complex formed by two H3 stem–loops of Moloney murine leukaemia virus due to its unique intermolecular interactions with only two base pairs. The theoretical structure is in overall agreement with the NMR structure with modest violations of few loose NMR restraints comparable to violations present in the NMR structure. In contrast to the NMR structure, MD shows relaxed conventional intermolecular G-C base pairing. The central part of the 2 bp kissing complex (refer to Fig. 1a for definition) forms a pocket which is occupied by one or two sodium cations and this cation-binding pocket shows significant nanosecond-scale breathing motions. The 6 bp kissing complexes of the DIS HIV-1 subtypes A and B (Fig. 1b) show a similar dynamical cation-binding pocket and thus the 2 and 6 bp kissing–loop complexes utilize similar intermolecular interactions. The simulations suggest that in the absence of the crystal contacts the four bulged-out adenines of the subtype B kissing complex may form a four-adenine stacking stem.
MATERIALS AND METHODS
Starting structures
The starting structure of the H3 stem–loop of Moloney murine leukaemia virus kissing complex was taken from NMR data (PDB file 1F5U) (7) (36 bases). Each loop contains four unpaired bases with a non-self-complementary sequence 5′-G8A9C10G11-3′. Two bases (underlined) form highly deformed intermolecular C-G base pairs (Figs 1a and 2). Further, A9 stacks with C10 base and C13* ribose, G8 stacks with A7 and G11 base stacks with U12* ribose. Unusual electrostatic interactions were suggested to occur between C10(H41) and G11(O6), as well as between G8(H22) and G11(N7) (7). We carried out two molecular dynamics simulations, ‘kiss1’ (16 ns) and ‘kiss1b’ (5 ns) with modified initial cation distribution. Kiss1 simulation was carried out with two terminal base pairs at each end omitted. Due to the lack of any structural information regarding divalent cations the simulations were carried out in the presence of Na+.
Starting structures of the 6 bp kissing motifs of DIS HIV-1 were taken from the X-ray data (subtype A, NDB ID: UR0016, 2.76 Å resolution; subtype B, NDB ID: UR0015, 2.6 Å resolution) (8). The following simulations were carried out: for subtype A the first simulation ‘mal’ (6.5 ns) was run with 14 Mg2+ cations suggested in the crystal while the Na+ ions were added to complete the neutralization. In the second simulation ‘mal_Na’ (6.6 ns) only Na+ ions were used. For subtype B we carried out two simulations: ‘lai’ (7.5 ns) with 12 Mg2+ ions and ‘lai_Na’ (5.8 ns) with only Na+. Another short simulation (3 ns) was carried out for the NMR structure of subtype B (PDB code 1BAU) (9) in the presence of Na+.
The simulations were carried out using the AMBER-6.0 program (33) and the Cornell et al. force field (34). The RNA molecules were neutralized with sodium counterions placed by the Xleap module of AMBER-6.0 at the most negative positions close to the RNA while Mg2+ ions were placed based on the X-ray structures. The following parameters were used: Na+ radius 1.868 Å and well depth 0.00277 kcal/mol, Mg2+ radius 0.7926 Å and well depth 0.8947 kcal/mol (35). A cubic box of the TIP3P water molecules was added around the RNA to a depth 10 Å on each side of the solute. The Sander module of AMBER-6.0 was used for all minimizations, equilibrations and molecular dynamics simulations. For the 2 bp complex the system was first minimized (500 steps) with all RNA H-bonds restrained at experimental values with harmonic force constants of 5 kcal/mol for H-bond compression and 15 kcal/mol for H-bond extension. Ions, water and the rest of the RNA were allowed to relax. For the 6 bp complexes possessing the bulged-out bases we used a slightly different protocol. All residues were restrained by force constants gradually reduced from 500 to 0 kcal/mol in a course of 5000 steps while the rest of the system was allowed to relax. Both protocols were followed by 100 ps of dynamics, maintaining constraints on the H-bonds in the case of the first protocol. The systems were then heated from 50 to 300 K in 100 ps. The production runs were carried out at 300 K with constant-pressure boundary conditions and particle mesh Ewald (PME) method (36) using the Berendsen temperature coupling algorithm (with a time constant of 0.2 ps). The center of mass velocity was periodically removed during the production dynamics (37). Trajectories were analyzed using the Carnal module of AMBER and structures were visualized using VMD (molecular visualization program, http://www.ks.uiuc.edu/Research/vmd/) (38). Figures were prepared using VMD, the Chem3D and the ChemDraw Pro programs (CambridgeSoft, Cambridge, MA). Hydration and distribution of ions were calculated with the ptraj module of the AMBER-6.0 and graphics using UCSF MidasPlus (University of California, San Francisco, CA) (39). Systematic monitoring of the solute-to-water distances was carried out using the Carnal module of AMBER. All direct solute–solvent contacts were detected for the whole trajectory and then analyzed in detail. All cation-binding sites with occupancies >5% were analyzed. Molecular electrostatic potentials were calculated using the program DELPHI (40), solving the non-linear Poisson–Boltzmann equation. Visualization of the potential maps was carried out using the program Insight II (Biosym/MSI, San Diego, CA).
RESULTS
Molecular dynamics of the kissing–loop complex of H3 stem–loop of Moloney murine leukemia virus
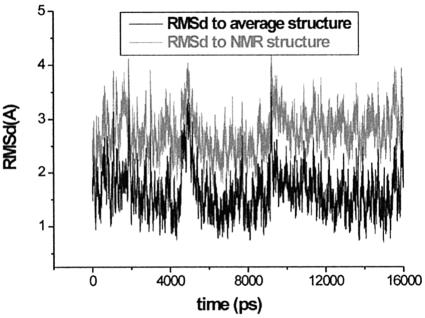
Both trajectories reveal similar behaviour, thus, in the following we describe data for the longer simulation. Figure 3 shows the time course of the RMSD value of the simulated molecule with respect to the starting NMR structure and with respect to the averaged MD structure. During the equilibration period the simulated molecule deviates modestly from the starting NMR structure. The propeller twist of the two intermolecular G-C base pairs drops from approximately –27 to –14° and remains at this value throughout the whole simulation. Swift loss of the non-planarity during the equilibration suggests that the starting structure is rather high in energy. The RMSD value with respect to the starting geometry does not further increase during the simulation.
Figure 3.
Time course of the RMSD value for the 2 bp kissing complex with respect to the starting NMR structure and the average (5–16 ns) MD structure.
Central cation-binding pocket
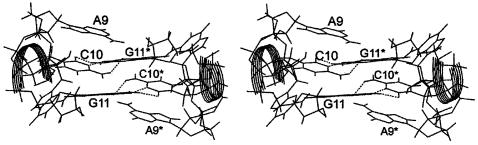
MD simulations suggest that the pocket in the central part of the molecule is permanently occupied by monovalent cations (Fig. 4, Table 1). Five different cations occurred in this pocket in the course of the 16 ns simulation, with binding times in the range of 0.5–10.0 ns. In the periods of 6.1–11.5 and 13.5–16 ns two closely spaced cations hovered in the pocket.
Figure 4.
Stereo view of the average MD structure of the simulated 2 bp kissing complex with a tightly bound Na+ cation (black) in the central cation-binding pocket (highlighted).
Table 1. Occurrence of individual Na+ ions inside the cation-binding pocket in the course of the 16 ns simulation of the H3 stem–loop kissing–loop complex.
| Cation | Presence of Na+ in the pocket (ns) |
|---|---|
| First Na+ | 0–0.5 |
| Second Na+ | 0.8–2.4 |
| Third Na+ | 2.4–3.4 |
| Fourth Na+ | 4.0–11.5 and 13.5–16.0 |
| Fifth Na+ | 6.1–16.0 |
The first Na+ cation was initially placed by Xleap at the edge of the pocket near A7*(O2′) and after equilibration it moved inside the pocket. (Note that the control simulation kiss1b was initiated with all cations moved away from this area and still the behaviour of the simulation was close to identical.) The first cation left the pocket at ∼0.5 ns and in the period of 0.5–0.8 ns the ion cross-linked the opposite loops, specifically G8*(O5′) (direct contact) and A7(O2′) (indirect contact), being just outside the pocket entrance. This cation was then released to the solvent and replaced by another Na+ ion occupying the pocket from 0.8 to 2.4 ns. This ion fluctuated and was not bound to any atom for more than 200 ps. The third Na+ was bound from 2.4 to 3.2 ns to A9(N7). After this the ion shifted to the centre of the pocket for 200 ps, then it left the pocket and fluctuated (3.4–3.9 ns) at the edge of the pocket. During this period the distance between opposite loops relaxed and at 4.0 ns increased to 10.3 Å (open state, see below). The inter-loop pocket distance can be characterized by the G8(P)-G8*(P) separation (see below). Then the fourth ion arrived at the edge of the pocket and after 100 ps it moved into the centre of the pocket. The inter-loop pocket distance decreased to 8 Å. The fourth ion fluctuated inside the pocket in the periods 4.0–11.5 and 13.5–16 ns. From 4.0 to 6.1 ns it fluctuated in the centre of the pocket with no inner-shell binding to solute atoms. The fifth ion arrived to the edge of the pocket at 6.1 ns while the fourth ion was shifted to the opposite part of the pocket close to A9*(N7) where it stayed from 6.1 to 11.5 ns. Then it was released for 2 ns into solvent but returned and was bound to A9(N7) until the end of the simulation. The fifth ion occupied the A9(N7) position in the period 8.2–9.8 ns, then it relocated across the pocket to A9*(N7) where it fluctuated until the end of simulation (16 ns).
In summary, the kissing motif is accompanied by a cation-binding pocket almost permanently occupied by one or two long-residing and fluctuating Na+ cations. These cations affect the inter-loop distance and interact with a number of solute atoms inside the pocket. The most frequent Na+ binding site is the A9(N7)/A9*(N7) position. The Na+ binding pocket is characterized by extended negative electrostatic potential (ESP) region (Fig. 5). The minimum ESP value is –20.9 kcal/mol. There are two negative regions inside the pocket at contour level of –18 kcal/mol, symmetrically positioned near atoms N7 of G11 and G11* while we see a very broad area of negative potential at –15 kcal/mol. The negative ESP region is significant and is comparable with that reported recently for 5S rRNA Loop E deep groove (29).
Figure 5.
Stereo view of the 2 bp kissing complex with an electrostatic potential map calculated at contour levels –18 (black) and –15 kcal/mol (dark gray).
Structural dynamics of the 2 bp kissing complex
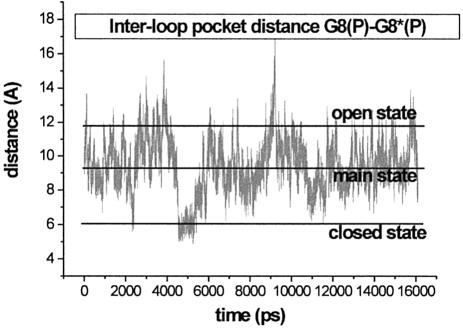
The G8(P)-G8*(P) inter-loop pocket distance is 15.2 Å in the starting NMR structure, it relaxes to 11.1 Å at the end of the equilibration and adopts an averaged value of ∼9.2 Å in the course of the simulation. The pocket shows substantial dynamics (Fig. 6). We observed its significant opening three times and its closing (compression) once, compared to the averaged structure. The closed state occurs in the period of 4530 to 5300 ps and is characterized by inter-loop G8(P)-G8*(P) distance of ∼6 Å. This leads to a formation of inter-loop H-bonds: A7(O2′)-G8*(O1P) (duration 700 ps, followed by 200 ps fluctuation, see Supplementary Material, Fig. S1) and A7(O2′)-A7*(O2′) (200 ps, see Supplementary Material, Fig. S2). The formation of the closed state is initiated by presence of a cation near the pocket entrance. The cation is essentially bridging the two strands. The above-described H-bonds keep the closed state for several hundreds of ps after the cation release to the solvent. The pocket relaxes when no Na+ ions are in proximity of its entrance and then the G8(P)-G8*(P) distance can increase even >10 Å (open state pocket).
Figure 6.
Inter-loop pocket distance of the 2 bp kissing complex characterized by the G8(P)-G8*(P) separation in the course of the simulation.
The simulated complex shows a modest asymmetry of the Na+ binding pocket. There is a difference between the molecular interactions of A9 and A9*. While A9 forms two stable H-bonds, the A9* residuum is involved in only one fluctuating H-bond, A9*(N6)-U12(O2′) (Fig. S3). Table S1 also shows only weak stacking interaction between A9* and C13 ribose. The unstable molecular interactions of A9* appear to contribute to the dynamics of the whole pocket (Fig. 7). Such asymmetry is not surprising on the nanosecond time scale for molecules that are flexible and capable to adopt substates. The control simulation kiss1b shows no asymmetry with fluctuations of both A9*-C13 and A9-C13* base-sugar stacks during the first 4 ns. Then asymmetry emerges, similar to that seen for the kiss1 simulation.
Figure 7.
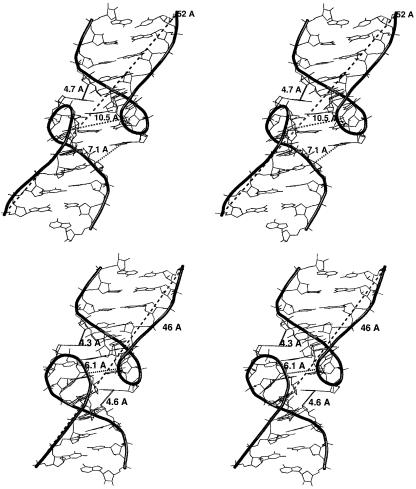
Stereo views of open (top) and closed (bottom) substates of the 2 bp kissing complex. The figure shows the inter-loop pocket distance G8(P)-G8*(P) (10.5 Å in the open state, 6 Å in the closed state), distance between the most distant phosphates P3*-P4 and the A9-C13* ribose/A9*-C13 ribose distances.
The dynamics and asymmetry of the pocket lead to inter-stem bending motions localized at the central pocket. The two stem segments are rather rigid with no groove width oscillations. This explains variation of the distance between the most distant phosphates P3*-P4. This distance is 46 Å in the NMR structure, 44 Å after the equilibration and 51 Å in the averaged MD structure. This distance varies, however, within 46–52 Å in the course of the simulation (Fig. 7). This picture is confirmed by Principal Component Analysis (PCA) showing two leading components (34 and 16%) representing different pocket motions coupled with a bending between two rigid stems (29,41). Formation of the pocket and its breathing are not affected by the asymmetry while the bending motion and length changes occur primarily when some pocket asymmetry develops.
Hydration
Figure S4 shows the main hydration sites in the simulated molecule. All sites show common water residency times around 50 ps, thus, in contrast to 5S rRNA Loop E (29) and RNA frameshifting pseudoknot (32) no tightly bound waters are present in this molecule. Except for the central sodium-binding pocket, no major Na+ binding site has been found (refer to data in Table S2).
Additional interactions
The residues A9, A9* and G8, G8* show no H-bonding in the starting structure and participate only in stacking (see above). During the first 2 ns of MD simulation several H-bonds were established that stabilize the central part of the kissing complex and anchor both loops together (Fig. S3): A9(N6)-U12*(O2), A9(N1)-U12*(O2′), A9*(N6)-U12(O2′), bifurcated G8*(N1,N2)-G11*(O2P), G8*(N2)-G11*(N7), bifurcated G8(N1,N2)-G11(O2P) and G8(N2)-G11(N7). All these H-bonds are essentially stable in the rest of the simulation. The central part of the complex is further stabilized by stacking that improves in the course of the simulation (Table S1).
Comparison with the NMR data
The MD structure satisfies the vast majority of the NMR restraints. The only significant violation is seen for A9(H2)-G11(H8) intramolecular and A9(H2)-G11*(H8) intermolecular restraints. In fact, these restraints affect the structure of the pocket and likely substantially contribute to the deformation of the kissing G-C base pairs in the NMR structure. The restraints imposed on the mutual positions of A9, A9* and G11 bases perturb the G11-C10* base pair. It is important to note that these particular NMR restraints are poorly defined (3–7 Å) and both are violated also in the NMR structure. Thus the two particular restraints appear to be somewhat incompatible with the global topology suggested for the molecule. The complete comparison of the NMR restraints with the NMR refined structure and the averaged MD structure is given in the Supplementary Material. We suggest that the MD structure remains in a quite acceptable agreement with the NMR data.
Quantum chemical calculations
The NMR study reports unusual non-planar G-C base pairs with a close mutual contact between the cytosine amino groups. It was suggested that the kissing region is stabilized by novel electrostatic interactions. However, such interactions appear unlikely and, in addition, would be reproduced by the force field. An alternative option is that the deformed base pair region could be stabilized by partial sp3 pyramidalization of the cytosine amino groups. Such interactions are not properly described by the force field (42–44). We have carried out quantum-chemical calculations that are suitable to detect such interactions (42–44), however, no stabilization due to amino group pyramidalization was achieved (see Supplementary Material).
Molecular dynamics of DIS HIV-1
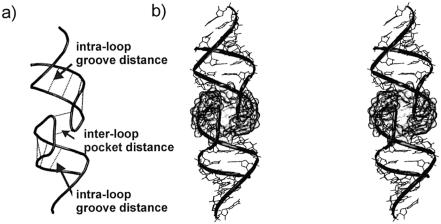
We carried out a set of simulations of subtypes A and B of DIS HIV-1 (Fig. 1b). The global structure of the 6 bp kissing complexes can be described by inter- and intra-loop distances as shown in Figure 8a.
Figure 8.
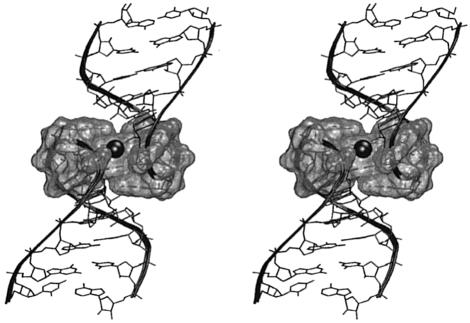
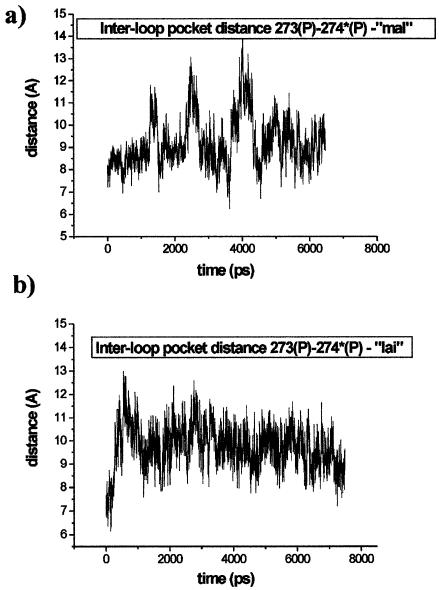
Structure of the 6 bp kissing complex. (a) Definition of the intra-loop groove distances between opposite phosphates of one loop outside of the kissing region and the inter-loop ‘pocket’ distance. The following distances (and the symmetry-related ones) are monitored: 276(P)-271(P), 277(P)-270(P), 278(P)-269(P), 279(P)-268(P) and 273(P)-274*(P). (b) Stereo view of the whole kissing complex (subtype A), the central pocket is highlighted.
Subtype A. Simulation ‘mal’ of subtype A with crystallographic Mg2+ ions shows periodic changes of the structure with instantaneous RMSD value with respect to the starting geometry in the range of 2.5 to 4 Å and instantaneous RMSD value with respect to the averaged MD structure of 2.0 ± 0.4 Å. The averaged MD structure is fairly close (RMSD value is 2.0 Å) to the X-ray structure.
The X-ray structure of subtype A shows a pocket in its central part resembling the 2 bp kissing motif above (see Figs 4 and 8b). The pocket of the 6 bp kissing motif is obviously longer in comparison to the 2 bp motif. In the X-ray structure, the pocket is occupied by three Mg2+ ions. Two Mg2+ cations remain inside the pocket in the simulation, modestly fluctuate inside the pocket and mostly bind to phosphate atoms O1P and O2P for several nanoseconds through water molecules. The third Mg 2+ ion leaves the pocket and then binds at the edge of the pocket alternatively to U270(O2P), A278(O2P) and C277(O2P) via outer-shell binding. Another Mg2+ ion is positioned at the edge of the pocket and binds permanently to U275*(O1P) via inner-shell binding while additional Mg2+ ion is at the entrance of the pocket permanently bound to G274(O2P) via inner-shell binding. The remaining Mg2+ ions are bound far from the pocket in the major grooves of the loops. The central cation-binding pocket shows dynamic behaviour with three observed opening events during 6.5 ns (Fig. 9a). The inter-loop pocket distance oscillates in the range of 8.5–11.5 Å while the intra-loop groove distances fluctuate in the range of 10–15 Å during the simulation (refer to Fig. 8a). The dynamic behaviour of the 6 bp kissing DIS HIV-1 subtype A motif thus resembles the dynamics of the 2 bp kissing motif of the H3 stem–loop of Moloney murine leukemia virus. The dynamic behaviour of the subtype A structure is influenced by stacked bulged-out purines A272* and G273*. The stacked base dimer A272*/G273* fluctuates in the absence of the crystal lattice and is temporarily partly buried inside the pocket (turned towards the interior of the structure). The two bases then establish H-bonds with phosphates or bases (Fig. S5) of the opposite loop. Nevertheless these interactions do not affect the inter-loop pocket distance 273(P)-274*(P). Further, the A280*-G273* distance is reduced to ∼7 Å. In contrast, the A272/G273 base stack remains close to its initial X-ray geometry. In the X-ray structure, G273* and G273 adopt syn and anti orientation, respectively. This difference in starting geometries explains the outcome of the simulation. There is a H-bond between G273*(N2) and G273*(O2P) that shifts the G273* base towards the pocket. This interaction is not possible with the anti orientation of guanine G273. The origin of the crystal asymmetry is not known.
Figure 9.
Time development of inter-loop (pocket) distances for (a) oscillating subtype A—simulation ‘mal’ and (b) subtype B—simulation ‘lai’ with inter-loop pocket distance stabilized at 9.5 Å by four bulged-out adenines forming a four-base stack. The base stack is not seen in the crystal possibly due to crystal packing (see Fig. 10).
The simulation ‘mal_Na’ without crystallographic Mg2+ cations shows an increase of the inter-loop pocket distance 273(P)-274*(P) from 7.7 (X-ray) to 12 Å after 1.3 ns. This is accompanied with the opening of the central cation-binding pocket. Then the inter-loop pocket distance fluctuates in the range of 10–12 Å. The intra-loop groove distances (refer to Fig. 8a) oscillate in the range of 10 to 15 Å. The instantaneous RMSD value with respect to the starting geometry is 4.5 ± 1.1 Å and with respect to average MD structure 2.3 ± 0.6 Å. The central open pocket is occupied simultaneously by three Na+ cations and the individual ions show ∼1 ns residency times in the area. While the position of the bulged-out guanines remains quite stable the bulged-out adenines A272 and A272* fluctuate with their χ angles oscillating in the range 30–190°. Thus the stacking between bulged-out adenines and guanines is partly reduced.
Subtype B. Sequence of subtype B differs from subtype A in three base positions in the hairpin part. We performed 7.5 ns simulation of subtype B-‘lai’ with 12 crystallographic Mg2+. The RMSD value along the trajectory with respect to the crystal structure is 3.6 ± 0.5 Å while the averaged MD structure is 3.0 Å away from the X-ray structure. Subtype B identically as subtype A shows a structural pocket in its central part. Crystal structure of subtype B, however, does not indicate the presence of any Mg2+ ion inside the central pocket. One Mg2+ is present close to the pocket entrance and is permanently bound to A272*(O1P) via inner-shell binding. Another Mg2+ is positioned at the edge of the pocket and binds alternately to A273(O1P) and C275(O2P) via outer-shell binding. Other Mg2+ cations bind far from the kissing part in the major grooves and interact with various O1P and O2P atoms. It follows from the experiments that Mg2+ cations are probably not important in the dimerization process of subtype B (18). During the simulation ‘lai’ no Mg2+ ion occupies the pocket. It is not surprising, as nanosecond-scale simulations do not allow significant relocations of the hydrated divalent cations. However, two or three fluctuating Na+ ions are always present in the central pocket, with residency times 0.5–1 ns.
After 1.2 ns the four bulged-out adenines (A272, A273, A272* and A273*) form four-base stacked stem, bulged-out of the central pocket and different from the arrangement in the crystal structure (Fig. 10). This stacking segment contributes to the RMSD values and its formation may reflect the lack of crystal contacts in the simulation. Note also that the rather non-polar adenines tend to form self-stacking complexes (45,46). This pulls together the loops, closes the pocket and stabilizes the inter-loop pocket distance at ∼9.5 Å (Fig. 9b). The space inside the pocket decreases so that it optimally fits the size of Na+ cations while hexacoordinated Mg2+ would be too large. This geometry of the pocket was stable over the rest of the simulation. The intra-loop groove distances fluctuate in the range of 10–14 Å.
Figure 10.
Detail of the 6 bp kissing complex, simulation ‘lai’. Four bulged-out adenines A272, A273, A272* and A273* (highlighted) create a stable bulged-out stacking stem in the course of the simulation. These bases are involved in lattice interactions in the crystal.
Simulation of subtype B ‘lai_Na’ without the crystallographic Mg2+ shows similar behavior as the mal_Na simulation. The RMSD value with respect to the starting geometry is ∼3.2 ± 0.7 Å. The intra-loop groove distances of both loops considerably fluctuate in the range 10–16 Å while the inter-loop pocket distance fluctuates in the range 9–12 Å. The central pocket is again occupied by three Na+ ions; however, the bulged-out adenines remain close to their X-ray positions.
In order to complete the investigation, we carried out 3 ns simulation of the NMR structure of subtype B (PDB code 1BAU) (9) in presence of Na+. The simulation suggests that the NMR structure is rather unstable and swiftly deviates essentially towards the X-ray geometry. All details are provided in the Supplementary Material section.
DISCUSSION
We carried out explicit solvent MD simulations to investigate nanosecond-scale dynamics, structure, hydration and cation binding of three RNA kissing–loop complexes.
H3 stem–loop kissing complex of Moloney murine leukemia virus shows conventional base pairing
Simulations of 2 bp kissing–loop complex of H3 stem–loop of Moloney murine leukemia virus show local conformational changes in the central kissing part of the structure compared to the NMR data. The deformed G-C base pairs seen in the NMR structure are unstable and the MD structure predicts conventional G-C base pairs. The MD structure shows modest violation of two NMR restraints while comparable violations are seen also in the NMR structure. Importantly, the MD simulation brings the base pairing of the 2 bp kissing complex to a close agreement with the X-ray structures of 6 bp kissing–loop complexes. Actually, the NMR structure shows base pairing different compared with the base pairing seen in 6 bp kissing complexes and such unusual pairing does not resemble any pairing pattern in available X-ray structures of RNA. We are nevertheless aware of the fact that the force fields available for MD simulations are not perfect and may affect the MD structure. However, the initial NMR structure is high in energy (marked structural changes during the equilibration) and this qualitative result should not be affected by force field approximations. Further, ab initio quantum chemical calculations carried out assuming the NMR interbase geometries do not indicate any unusual interaction that could stabilize the deformed base pairs.
DIS HIV-1 kissing complexes
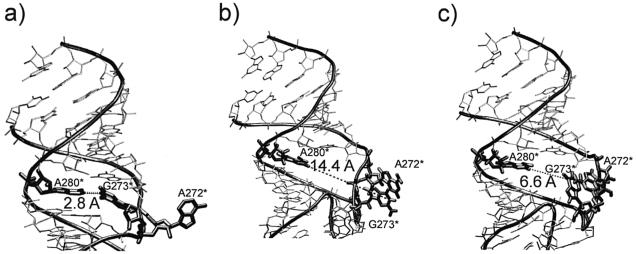
DIS of HIV-1 subtypes A and B form homodimeric kissing complexes through 6 bp. The crystal structures of both A and B subtypes simulated in presence of the X-ray Mg2+ cations are stable and in a good agreement with the crystal data, despite fluctuations and rearrangements of some unpaired bases. For subtype A, the bulged-out G273* which is in syn conformation shows substantial movements towards the interior of the kissing motif bringing this base very close to the unpaired adenine A280*. These two bases form G/A base pair in crystal structure of the extended duplex (Fig. 11a) (47) and the simulation of the kissing complex reduces their distance from 14.4 to 6.6 Å (Fig. 11b and c). Although we did not see formation of the G/A pair in the simulation we suggest that G273* motion can possibly facilitate the conversion of the kissing complex to the more stable extended duplex by forming the G/A base pair before the cleavage. The approach of G273* towards A280* also significantly reduces the 273*(O2′)-274*(P) distance to 3.2 ± 0.2 Å. The X-ray value is 3.9 Å and the 273(O2′)-274(P) MD distance is 4.1 ± 0.2 Å. The 273*(O2′)-274*(P)-274*(O5′) angle oscillates in the range of 127 ± 12° which is close to the crystal value of 137° (8). It is to be noted that the equivalent A272/G273 stack remains essentially in its initial X-ray position because the G273 base adopts anti orientation in the X-ray structure.
Figure 11.
HIV-1 DIS subtype A, positions of residues A280*, G273* and A272* with the distance between A280* and G273* highlighted. (a) X-ray structure of the extended duplex with non-planar cis-Watson–Crick A280*/G273* base pair and bulged-out A272*, (b) X-ray structure of the kissing complex with unpaired A280* and bulged-out stack of G273* and A272*, (c) intermediate MD structure of the kissing complex. The bulged-out G273* substantially approaches the unpaired adenine A280*.
In absence of Mg2+ cations the simulation shows oscillating behaviour of A272 and A272* adenines with partial unstacking of the bulged-out dimers. Thus, substantially more extended simulations would be needed to obtain a more complete insight into the flexibility of the bulged-out region, which evidently can adopt multiple geometries.
The simulation of subtype B kissing–loop complex reveals a formation of a four-adenine stack formed by bulged-out adenines (Fig. 10). This four-adenine stack is not seen in the crystal structure possibly due to the involvement of the adenines in crystal molecular interactions. The A280 bases remain stable in their initial positions in all 6 bp kissing–loop complex simulations.
Cation-binding pocket in kissing complexes
The 2 bp kissing complex of H3 stem–loop of Moloney murine leukemia virus shows a structural pocket with highly negative electrostatic potential occupied permanently by one or two fluctuating Na+ cations with nanosecond-scale residency time inside the pocket. The pocket is formed by G8, G8*, A9, A9*, C10, C10*, G11 and G11* bases and the cations may adopt several positions in the pocket with most contacts to A9(*)(N7). The deformed NMR geometry is likely not compatible with a cation binding as the A9(*) adenines partly obstruct the space of the pocket. Since this base arrangement is unstable in the simulations we could not study its ability to interact with cations.
The 6 bp kissing complexes show central cation-binding pocket very similar to that seen in the 2 bp kissing complex. In subtype A, the pocket is occupied by Mg2+ cations that are visible in the crystal structure and stay stable in the simulation. In subtype B the pocket is continuously occupied by three Na+ ions (with multiple exchange events with the bulk). Subtypes A and B simulated entirely in absence of Mg2+ cations have central binding pockets occupied by three Na+ ions and the pockets are slightly widened.
In summary, the present MD study and the X-ray structures show extensive binding of cations to the core part of the kissing–loop complexes. This indicates that the cations could stabilize the kissing–loop complexes; however, as we have only structural information the actual contribution of the ions to the stability of the structures is unknown.
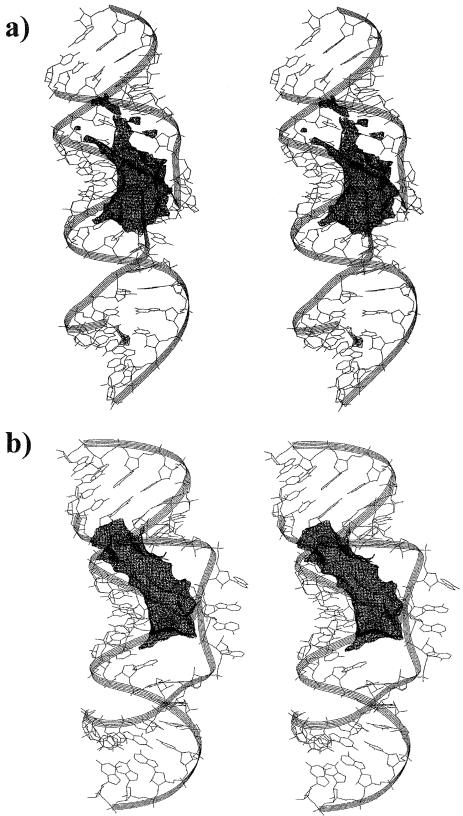
The extensive cation binding is due to several contributions. The six intermolecular Watson–Crick base pairs orient their U(O4) and G(O6) atoms into the interior of the pocket. Further, there is a high local concentration of phosphate groups at the junction that also contributes to the negative potential. The pocket itself is a small area, with a length of ∼15 Å and width ∼10 Å. The apical phosphates of both loops are oriented towards the pocket area. We calculated the molecular electrostatic potential for the averaged MD structures (simulated in the presence of Mg2+) by solving the non-linear Poisson–Boltzmann (PB) equation. The minimum electrostatic potential emerges at –30 kcal/mol contour level for subtype A and –35 kcal/mol for subtype B (Fig. 12a and b). The extended areas of very negative electrostatic potential explain binding of cations in the pockets. Note that the calculated 5 kcal/mol difference between subtypes A and B is probably not significant and may be caused by quite subtle geometry differences between the structures utilized for the calculations. For example, in the case of subtype B structure the pocket is gated by four bulged-out adenines and the absence of Mg2+ cations inside the pocket leads to a narrowing of the pocket compared to subtype A, thus strengthening the negative potential.
Figure 12.
Stereo views of the 6 bp kissing complexes with electrostatic potential (ESP) maps obtained for average MD structures taken from simulations carried out in the presence of Mg2+. (a) Subtype A, the ESP map is calculated at contour level –25 kcal/mol (black). The minimum of the negative potential is –30 kcal/mol. (b) Subtype B, the ESP map is calculated at contour level –30 kcal/mol (black). The minimum potential is –35 kcal/mol. No salt is included in the PB calculations.
Both subtypes show in the absence of Mg2+ cations increase of the inter-loop pocket distance, widening of intra-loop groove distances and increased fluctuations. The important role of Mg2+ cations in folding of RNA structures is well established (48). It cannot be ruled out that some structural perturbations and fluctuations seen in the absence of Mg2+ result from the initial impact caused by the sudden removal of numerous X-ray Mg2+ cations.
MD studies of binding of divalent cations are severely limited due to the total neglect of major polarization and charge transfer contributions by the force field and insufficient time scale for magnesium relocations (29,49,50). Thus our simulations are based on Mg2+ positions suggested by crystallographers and the simulations cannot be used to predict new Mg2+ binding positions. It is therefore not surprising that magnesium ions at the junction of the subtype A remain there while none is going to occupy the binding sites of subtype B if not initially placed there. This does not mean that, in vivo, magnesium ions could not be located nearby. Alternatively, magnesium ions located at the junction of the subtype A have been observed as a result of crystallization conditions. An excellent overview of advantages and limitations of crystallographic studies of metal cations has been written by Ennifar et al. (51). Nevertheless, Jossinet et al. (18) carried out chemical modification interference, lead-induced cleavage and three-dimensional modeling to compare dimerization of subtype A and B HIV-1 RNAs. The data indicate that unlike subtype B, subtype A requires binding of a divalent cation in the loop to promote RNA dimerization. This appears to be in agreement with Mg2+ positions reported in the X-ray structures by Ennifar et al. (8), which were utilized as starting structures for our simulations. In contrast, 10-ns scale simulations are sufficient to reproducibly locate major sodium-binding sites in RNA (29).
Nanosecond-scale dynamics of the kissing complexes
The 2 bp kissing complex shows dynamic changes of the geometry with fluctuations of its cation-binding pocket that further initiate asymmetrical bending fluctuations of the molecule (Fig. 7). The HIV-1 DIS complexes also show dynamic change of geometry during simulation: periodic oscillations (opening) of the central pocket (subtype A) and considerable fluctuations of intra-loop groove distances (both subtypes). The motions appear to be independent. Both complexes in the absence of Mg2+ ions show increased fluctuations as Mg2+ ions rigidify the molecules. In summary, kissing–loop complexes are dynamical and show substantial nanosecond-scale fluctuations. Although details of the fluctuations may certainly be affected by the force field approximations it is evident that the kissing complexes are more flexible than canonical A-RNA duplexes or for example rigid RNA molecules such as the 5S rRNA Loop E and RNA frameshifting pseudoknot (29,32).
SUPPLEMENTARY MATERIAL
The Supplementary Material provides PDB files of key MD structures and additional information as specified above and is available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENTS
We thank the Brno Supercomputer Center for a generous allotment of computer time. We are very grateful to Professor Vladimir Sklenar and Dr Petr Padrta for helpful discussion regarding the difference between NMR and MD data of the H3 stem–loop kissing complex of Moloney murine leukemia virus. This work was supported by grants LN00A016 by MSMT and Senior Wellcome Trust International Research Fellowship for Biomedical Science in Central Europe 067507 (J.S., N.S.).
REFERENCES
- 1.Wagner E.G. and Simons,R.W. (1994) Antisense RNA control in bacteria, phages and plasmids. Annu. Rev. Microbiol., 48, 713–742. [DOI] [PubMed] [Google Scholar]
- 2.Bender W. and Davidson,N. (1976) Mapping of poly(A) sequences in the electron microscope reveals unusual structure of type C oncornavirus RNA molecules. Cell, 7, 595–607. [DOI] [PubMed] [Google Scholar]
- 3.Muriaux D., Fosse,P. and Paoletti,J. (1996) A kissing complex together with a stable dimer is involved in the HIV-1Lai RNA dimerization process in vitro. Biochemistry, 35, 5075–5082. [DOI] [PubMed] [Google Scholar]
- 4.Tounekti N., Mougel,M., Roy,C., Marquet,R., Darlix,J.L., Paoletti,J., Ehresmann,B. and Ehresmann,C. (1992) Effect of dimerization on the conformation of the encapsidation Psi domain of Moloney murine leukemia virus RNA. J. Mol. Biol., 223, 205–220. [DOI] [PubMed] [Google Scholar]
- 5.Clever J.L., Wong,M.L. and Parslow,T.G. (1996) Requirements for kissing–loop-mediated dimerization of human immunodeficiency virus RNA. J. Virol., 70, 5902–5908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.DeTapia M., Metzler,V., Mougel,M., Ehresmann,B. and Ehresmann,C. (1998) Dimerization of MoMuLV genomic RNA: redefinition of the role of the palindromic stem–loop H1 (278–303) and new roles for stem–loops H2 (310–352) and H3 (355–374). Biochemistry, 37, 6077–6085. [DOI] [PubMed] [Google Scholar]
- 7.Kim C.H. and Tinoco,I.,Jr (2000) A retroviral RNA kissing complex containing only two GC base pairs. Proc. Natl Acad. Sci. USA, 97, 9396–9401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ennifar E., Walter,P., Ehresmann,B., Ehresmann,C. and Dumas,P. (2001) Crystal structures of coaxially stacked kissing complexes of the HIV-1 RNA dimerization initiation site. Nat. Struct. Biol., 8, 1064–1068. [DOI] [PubMed] [Google Scholar]
- 9.Mujeeb A., Clever,J.L., Billeci,T.M., James,T.L. and Parslow,T.G. (1998) Structure of the dimer initiation complex of HIV-1 genomic RNA. Nat. Struct. Biol., 5, 432–436. [DOI] [PubMed] [Google Scholar]
- 10.Westhof E., Dumas,P. and Moras,D. (1985) Crystallographic refinement of yeast aspartic acid transfer RNA. J. Mol. Biol., 184, 119–145. [DOI] [PubMed] [Google Scholar]
- 11.Ban N., Nissen,P., Hansen,J., Moore,P.B. and Steitz,T.A. (2000) The complete atomic structure of the large ribosomal subunit at 2.4 angstrom resolution. Science, 289, 905–920. [DOI] [PubMed] [Google Scholar]
- 12.Lee A.J. and Crothers,D.M. (1998) The solution structure of an RNA loop–loop complex: the ColE1 inverted loop sequence. Structure, 6, 993–1005. [DOI] [PubMed] [Google Scholar]
- 13.Chang K.Y. and Tinoco,I.,Jr (1997) The structure of an RNA kissing hairpin complex of the HIV TAR hairpin loop and its complement. J. Mol. Biol., 269, 52–66. [DOI] [PubMed] [Google Scholar]
- 14.Laughrea M. and Jette,L. (1996) Kissing–loop model of HIV-1 genome dimerization: HIV-1 RNAs can assume alternative dimeric forms and all sequences upstream or downstream of hairpin 248–271 are dispensable for dimer formation. Biochemistry, 35, 1589–1598. [DOI] [PubMed] [Google Scholar]
- 15.Lodmell J.S., Ehresmann,C., Ehresmann,B. and Marquet,R. (2001) Structure and dimerization of HIV-1 kissing loop aptamers. J. Mol. Biol., 311, 475–490. [DOI] [PubMed] [Google Scholar]
- 16.Pattabiraman N., Martinez,H.M. and Shapiro,B.A. (2002) Molecular modeling and dynamics studies of HIV-1 kissing loop structures. J. Biomol. Struct. Dyn., 20, 397–412. [DOI] [PubMed] [Google Scholar]
- 17.Beaurain F., Primo,C., Toulme,J.J. and Laguerre,M. (2003) Molecular dynamics reveals the stabilizing role of loop closing residues kissing interactions: comparison between TAR-TAR* and TAR-aptamer. Nucleic Acids Res., 31, 4275–4284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jossinet F., Paillart,J.C., Westhof,E., Hermann,T., Skripkin,E., Lodmell,J.S., Ehresmann,B., Ehresmann,C. and Marquet,R. (1999) Dimerization of HIV-1 genomic RNA of subtypes A and B: RNA loop structure and magnesium binding. RNA, 5, 1222–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Auffinger P. and Westhof,E. (2000) RNA solvation: A molecular dynamics simulation perspective. Biopolymers, 56, 266–274. [DOI] [PubMed] [Google Scholar]
- 20.Guo J., Daizadeh,I. and Gmeiner,W.H. (2000) Structure of the Sm binding site from human U4 snRNA derived from a 3ns PME molecular dynamics simulation. J. Biomol. Struct. Dyn., 18, 335–344. [DOI] [PubMed] [Google Scholar]
- 21.Hermann T. and Westhof,E. (1998) Exploration of metal ion binding sites in RNA folds by Brownian-dynamics simulations. Structure, 6, 1303–1314. [DOI] [PubMed] [Google Scholar]
- 22.Hermann T., Auffinger,P. and Westhof,E. (1998) Molecular dynamics investigations of hammerhead ribozyme RNA. Eur. Biophys. J., 27, 153–165. [DOI] [PubMed] [Google Scholar]
- 23.Sarzynska J., Kulinski,T. and Nilsson,L. (2000) Conformational dynamics of a 5S rRNA hairpin domain containing Loop D and a single nucleotide bulge. Biophys. J., 79, 1213–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schneider C. and Suhnel,J. (2000) A molecular dynamics simulation study of coaxial stacking in RNA. J. Biomol. Struct. Dyn., 18, 345–352. [DOI] [PubMed] [Google Scholar]
- 25.Schneider C., Brandl,M. and Suhnel,J. (2001) Molecular dynamics simulation reveals conformational switching of water-mediated uracil-cytosine base-pairs in an RNA duplex. J. Mol. Biol., 305, 659–667. [DOI] [PubMed] [Google Scholar]
- 26.Norberg J. and Nilsson,L. (2002) Molecular dynamics applied to nucleic acids. Acc. Chem. Res., 35, 465–472. [DOI] [PubMed] [Google Scholar]
- 27.Auffinger P., Louise-May,S. and Westhof,E. (1999) Molecular dynamics simulations of solvated yeast tRNA. Biophys. J., 76, 50–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Giudice E. and Lavery,R. (2002) Simulations of nucleic acids and their complexes. Acc. Chem. Res., 35, 350–357. [DOI] [PubMed] [Google Scholar]
- 29.Reblova K., Spackova,N., Stefl,R., Csaszar,K., Koca,J., Leontis,N.B. and Sponer,J. (2003) Non-Watson-Crick base pairing and hydration in RNA motifs: Molecular dynamics of 5S rRNA Loop E. Biophys. J., 84, 3564–3582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nagan M.C., Beuning,P., Musier-Forsyth,K. and Cramer,C.J. (2000) Importance of discriminator base stacking interactions: molecular dynamics analysis of A73 microhelix (Ala) variants. Nucleic Acids Res., 28, 2527–2534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nagan M.C., Kerimo,S.S., Musier-Forsyth,K. and Cramer,C.J. (1999) Wild-type RNA microhelix (Ala) and 3:70 variants: Molecular dynamics analysis of local helical structure and tightly bound water. J. Am. Chem. Soc., 121, 7310–7317. [Google Scholar]
- 32.Csaszar K., Spackova,N., Stefl,R., Sponer,J. and Leontis,N.B. (2001) Molecular dynamics of the frame-shifting pseudoknot from beet western yellows virus: The role of non-Watson-Crick base pairing, ordered hydration, cation binding and base mutations on stability and unfolding. J. Mol. Biol., 313, 1073–1091. [DOI] [PubMed] [Google Scholar]
- 33.Pearlman D.A., Case,D.A., Caldwell,J.W., Ross,W.S., Cheatham,T.E.,III, De Bolt,S., Ferguson,D., Seibel,G. and Kollman,P.A. (1995) AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecule. Comput. Phys. Commun., 91, 1–41. [Google Scholar]
- 34.Cornell W.D., Cieplak,P., Bayly,C.I., Gould,I.R., Merz,K.M., Ferguson,D.M.,Jr, Spellmeyer,D.C., Fox,T., Caldwell,J.W. and Kollman,P.A. (1995) A 2nd generation force-field for the simulation of proteins, nucleic-acids and organic molecules. J. Am. Chem. Soc., 117, 5179–5197. [Google Scholar]
- 35.Ross W.S. and Hardin,C.C. (1994) Ion-induced stabilization of the G-DNA quadruplex—free-energy perturbation studies. J. Am. Chem. Soc., 116, 6070–6080. [Google Scholar]
- 36.York D.M., Darden,T.A. and Pedersen,L.G. (1993) The effect of long-range electrostatic interactions in simulations of macromolecular crystal—a comparison of the ewald and truncated list methods. J. Chem. Phys., 99, 8345–8348. [Google Scholar]
- 37.Harvey S.C., Tan,R.K.Z. and Cheatham,T.E.,III (1998) The flying ice cube: velocity rescaling in molecular dynamics leads to violation of energy equipartition. J. Comput. Chem., 19, 726–740. [Google Scholar]
- 38.Humphrey W., Dalke,A. and Schulten,K. (1996) VMD—Visual Molecular Dynamics. J. Mol. Graph., 14, 33–38. [DOI] [PubMed] [Google Scholar]
- 39.Ferrin T.E., Huang,C.C., Jarvis,L.E. and Langridge,R. (1988) The MIDAS display system. J. Mol. Graph., 6, 13–27. [Google Scholar]
- 40.Gilson M.K., Sharp,K.A. and Honig,B.H. (1998) Calculating the electrostatic potential of molecules in solution—method and error assessment. J. Comput. Chem., 9, 327–335. [Google Scholar]
- 41.Harris S.A., Gavathiotis,E., Searle,M.S., Orozco,M. and Laughton,C.A. (2001) Cooperativity in drug-DNA recognition: A molecular dynamics study. J. Am. Chem. Soc., 123, 12658–12663. [DOI] [PubMed] [Google Scholar]
- 42.Vlieghe D., Sponer,J. and Van Meervelt,L. (1999) Crystal structure of d(GGCCAATTGG) complexed with DAPI reveals novel binding mode. Biochemistry, 38, 16443–16451. [DOI] [PubMed] [Google Scholar]
- 43.Luisi B., Orozco,M., Sponer,J., Luque,F.J. and Shakked,Z. (1998) On the potential role of the amino nitrogen atom as a hydrogen acceptor in macromolecules. J. Mol. Biol., 279, 1123–1136. [DOI] [PubMed] [Google Scholar]
- 44.Sponer J., Mokdad,A., Sponer,J.E., Spackova,N., Leszczynski,J. and Leontis,N.B. (2003) Unique tertiary and neighbor interactions determine conservation patterns of cis Watson-Crick A/G base pairs. J. Mol. Biol., 330, 967–978. [DOI] [PubMed] [Google Scholar]
- 45.Spackova N., Berger,I. and Sponer,J. (2000) Nanosecond molecular dynamics of zipper-like DNA duplex structures containing sheared G.A mismatch pairs. J. Am. Chem. Soc., 122, 7564–7572. [Google Scholar]
- 46.Cai L., Chen,L.Q., Raghavan,S., Ratliff,R., Moyzis,R. and Rich,A. (1998) Intercalated cytosine motif and novel adenine clusters in the crystal structure of the Tetrahymena telomere. Nucleic Acids Res., 26, 4696–4705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ennifar E., Yusupov,M., Walter,P., Marquet,R., Ehresmann,B., Ehresmann,C. and Dumas,P. (1999) The crystal structure of the dimerization initiation site of genomic HIV-1 RNA reveals an extended duplex with two adenine bulges. Structure, 7, 1439–1449. [DOI] [PubMed] [Google Scholar]
- 48.Misra V.K. and Draper,D.E. (2002) The linkage between magnesium binding and RNA folding. J. Mol. Biol., 317, 507–521. [DOI] [PubMed] [Google Scholar]
- 49.Auffinger P., Bielecki,L. and Westhof,E. (2003) The Mg2+ binding sites of the 5S rRNA Loop E motif as investigated by molecular dynamics simulations. Chem. Biol., 10, 551–561. [DOI] [PubMed] [Google Scholar]
- 50.Sponer J., Sabat,M., Gorb,L., Leszczynski,J., Lippert,B. and Hobza,P. (2000) The effect of metal binding to the N7 site of purine nucleotides on their structure, energy and involvement in base pairing. J. Phys. Chem. B, 104, 7535–7544. [Google Scholar]
- 51.Ennifar E., Walter,P. and Dumas,P. (2003) A crystallographic study of the binding of 13 metal ions to two related RNA duplexes. Nucleic Acids Res., 31, 2671–2682. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.