Contrast detection in fluid-saturated media with magnetic resonance poroelastography

Abstract

Purpose: Recent interest in the poroelastic behavior of tissues has led to the development of magnetic resonance poroelastography (MRPE) as an alternative to single-phase MR elastographic image reconstruction. In addition to the elastic parameters (i.e., Lamé’s constants) commonly associated with magnetic resonance elastography (MRE), MRPE enables estimation of the time-harmonic pore-pressure field induced by external mechanical vibration.

Methods: This study presents numerical simulations that demonstrate the sensitivity of the computed displacement and pore-pressure fields to a priori estimates of the experimentally derived model parameters. In addition, experimental data collected in three poroelastic phantoms are used to assess the quantitative accuracy of MR poroelastographic imaging through comparisons with both quasistatic and dynamic mechanical tests.

Results: The results indicate hydraulic conductivity to be the dominant parameter influencing the deformation behavior of poroelastic media under conditions applied during MRE. MRPE estimation of the matrix shear modulus was bracketed by the values determined from independent quasistatic and dynamic mechanical measurements as expected, whereas the contrast ratios for embedded inclusions were quantitatively similar (10%–15% difference between the reconstructed images and the mechanical tests).

Conclusions: The findings suggest that the addition of hydraulic conductivity and a viscoelastic solid component as parameters in the reconstruction may be warranted.

INTRODUCTION

Linear poroelastic media are generally described as being composed of two separate phases consisting of a solid elastic matrix and an infiltrating pore fluid. Unlike purely elastic materials, which are strain-rate independent, the deformation of a poroelastic solid is governed by the rate at which fluid can leave the matrix under an applied pressure gradient. Originally developed as a means of describing the deformation behavior of hydrated soils, consolidation theory¹ or poroelasticity has been used to characterize the quasistatic deformation of the brain through finite element modeling of edema,^{2, 3, 4} hydrocephalus,^{5, 6} and surgery.^{7, 8, 9, 10, 11} Biphasic theory has also been used extensively in modeling the deformation of articular cartilage.^{12, 13}

MR elastography (MRE)^{14, 15} is another venue where poroelastic modeling of tissue may be of interest. In general, elastographic techniques strive to characterize tissues noninvasively by assessing their resistance to deformation, a physical phenomenon which can be related to mechanical parameters such as the elastic modulus through application of the appropriate constitutive relations. To date, in vivo investigations with MRE have relied upon single-phase descriptions of tissue to recover estimates of the desired mechanical parameters. Most notable has been the assumption of linear elasticity,^{16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30} though considerable effort has been exerted more recently to characterize the viscoelastic properties of tissue.^{31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41} In 2009, studies by Perriñez et al.⁴² showed the presence of a poroelastic effect for some tissuelike materials under conditions experienced during time-harmonic MRE. The results indicated that purely elastic mechanical models are inadequate in describing the deformation behavior of fluid-saturated media and suggest that poroelastic constitutive relations may more adeptly describe the biphasic nature of in vivo tissues.

Magnetic resonance poroelastography (MRPE) (Ref. ⁴³) is a recent development in MR elastographic imaging whereby estimates of the mechanical properties of tissue are obtained by separating the mechanical response of the solid matrix from that of the free extracellular fluid. While this technique has been shown to significantly improve the image quality of the recovered elastic parameters of the solid matrix when compared to those obtained from a purely elastic model,⁴³ little is known about the quantitative accuracy of these parameters. Further, application of the technique requires a priori estimates of mechanical parameters, which may be difficult to determine experimentally. Thus, an investigation of the model sensitivity to changes in the assumed parameters is required. The purpose of this study is (1) to determine the most influential parameters assumed in the reconstruction through a sensitivity analysis performed using numerical experiments in a model-validated rectangular column undergoing confined harmonic excitation and (2) to assess quantitatively the values of the matrix shear modulus recovered with MRPE from three poroelastic tofu phantoms compared to independent measurements recorded during both quasistatic and dynamic mechanical testing of the same materials.

METHODS

Forward problem

Assuming tissue to be fully saturated (i.e., that any change in volume of the poroelastic material must result in an equivalent volume of fluid exudate) and composed of isotropic, incompressible fluid and nearly incompressible solid material constituents, the dynamic poroelasticity equations can be expressed in partial differential equation form⁴⁴ as

$$\nabla \cdot \mu \nabla \overline{\mathbf{u}}+\nabla \left(\lambda +\mu \right)\left(\nabla \cdot \overline{\mathbf{u}}\right)-\left(1-\beta \right)\nabla \overline{p}=-{\omega }^2\left(\rho -\beta {\rho }_f\right)\overline{\mathbf{u}},$$ (1a)

$$\frac{{\omega }^2{\rho }_f\left(1-\beta \right)}{\beta }\left(\nabla \cdot \overline{\mathbf{u}}\right)+{\nabla }^2\overline{p}=0,$$ (1b)

where μ and λ represent Lamé’s constants, $\overline{\mathbf{u}}$ is the time-harmonic displacement field with components u, v, and w, and $\overline{p}$ is the time-harmonic pore pressure field. Further, ω is the excitation frequency and ρ and ρ_f are the bulk material and pore-fluid densities, respectively. The parameter β can be expressed as

$$\beta =\frac{\omega {\varphi }^2{\rho }_f\kappa }{i{\varphi }^2+\omega \kappa \left({\rho }_a+\varphi {\rho }_f\right)},$$ (2)

where ϕ is the matrix porosity or volume fraction, κ is the hydraulic conductivity, and ρ_a is the apparent mass density.

Inverse problem

A three-dimensional (3D) finite element reconstruction algorithm based on the equations of linear poroelasticity⁴³ has recently been presented for the estimation of the solid matrix elastic properties (μ,λ) and the time-harmonic pore-pressure field $\left(\overline{p}\right)$ in fluid-saturated tissues. In this formulation, estimates of Lamé’s constants (Δθ) are calculated iteratively using the regularized Gauss–Newton update equation,

$$\left[\text{Re}\left({\mathbf{J}}^{\ast T}\mathbf{J}\right)+\alpha \mathbf{I}\right]\left\{\Delta \mathbf{\theta }\right\}=-\left\{{\mathbf{J}}^{\ast T}\left({\mathbf{u}}_m-{\mathbf{u}}_c\right)\right\},$$ (3)

where J^∗TJ is the Hermitian or self-adjoint Hessian, α is the regularization parameter described in Ref. 45, J is the Jacobian or sensitivity matrix, and u_m and u_c are the measured and computed displacement fields, respectively.

Simulated data

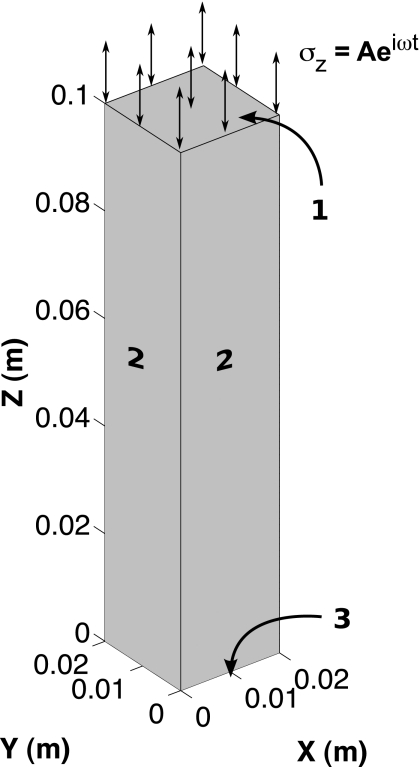
A study was performed to identify the sensitivity of the computed displacement field to the assumed poroelastic material constants (ϕ,κ,ρ_a) required for the reconstruction algorithm discussed in Sec. 2B. A 3D finite element mesh comprised of linear tetrahedral elements was generated for a 0.02×0.02×0.10 m³ rectangular poroelastic column (84 541 nodes and 480 000 elements) subjected to confined time-harmonic excitation at a frequency of 100 Hz. The displacement and pore-pressure fields obtained from the forward problem were validated against the analytic solution presented in Ref. 46 for the model parameters in Table 1. The physical properties used in the model validation, which are assumed to be isotropic and spatially uniform, are comparable to those presented in Refs. ^{42, 43} and are representative of the values for tofu reported in literature. Figure 1 contains a drawing of the rectangular column and highlights three different surfaces for which the applied boundary conditions on displacement and pressure are detailed in Table 2. As described in Ref. 46, the largest absolute error on displacement and pore pressure between the finite element model and the analytic solutions was found to be less than 1% and 6%, respectively, over the range of frequencies considered.

Table 1.

Model parameters.

Parameter	E (kPa)	ν	ϕ	κ (m3 s∕kg)	ρ (kg∕m3)	ρf (kg∕m3)	C
Model validation	10	0.45	0.20	1×10−8	1020	1000	0.75
Sensitivity analysis	10	0.45	0.1–1	1×10−4–1×10−13	1020	1000	0–1

Figure 1.

A drawing of a 0.02×0.02×0.10 m³ poroelastic column undergoing confined time-harmonic excitation. The boundary conditions on displacement and pore-pressure applied to surfaces 1–3 are summarized in Table 2.

Table 2.

Applied boundary conditions.

Surface	x,y	z	p
1	σx,y=0 (Pa)	σz=Aeiωt (Pa)	p=0 (Pa)
2	u=v=0 (m)	σxz=σyz=0 (Pa)	$\frac{\partial p}{\partial n}=0\left(\text{Pa}∕\text{m}\right)$
3	u=v=0 (m)	w=0 (m)	$\frac{\partial p}{\partial n}=0\left(\text{Pa}∕\text{m}\right)$

Among the parameters of interest is the apparent mass density ρ_a, which is a coefficient related to the work done by the solid matrix on the pore fluid due to the relative motion between their phases that can be calculated through the relation,

$${\rho }_a=C\varphi {\rho }_f,$$ (4)

where C is an experimentally determined coupling factor ranging between 0 and 1. Given that ρ_f is assumed to be very close to 1000 kg∕m³, the porosity ϕ, hydraulic conductivity κ, and coefficient C were varied incrementally across the range of values presented in Table 1 and the forward problem was solved for each subsequent combination. The porosity is defined as the ratio of the fluid volume to the total volume (V_f∕V). Therefore, as ϕ approaches 0, the fluid volume (i.e., the pore volume) approaches zero. Similarly, as ϕ approaches 1, the fluid volume approaches that of the total volume. The values for ϕ used in the sensitivity analysis were chosen to reflect the physical range of values that are allowable. The magnitude of the variation in κ employed reflects the variation observed in nature (i.e., approximately six orders of magnitude variation in κ is observed between sand∕sandstone and granite∕shale).⁴⁷ Thus, the set of values for κ presented in Table 1 was chosen to reflect a range of values that might be observed in vivo (i.e., a spectrum between highly edematous soft tissue and cortical bone).

The difference between the displacement and the pressure solutions obtained from the model validation and those determined by perturbing ϕ, κ, and ρ_a was calculated using the following relations:

$${\Psi }_{\text{displacement}}={\left[\frac{{\sum }_{i=1}^n\left({\mathbf{u}}_v-{\mathbf{u}}_p\right)\cdot {\left({\mathbf{u}}_v-{\mathbf{u}}_p\right)}^{\ast }}{{\sum }_{i=1}^n{\mathbf{u}}_v\cdot {\mathbf{u}}_v^{\ast }}\right]}^{1∕2},$$ (5)

$${\Psi }_{\text{pressure}}={\left[\frac{{\sum }_{i=1}^n\left(p_v-p_p\right){\left(p_v-p_p\right)}^{\ast }}{{\sum }_{i=1}^n{p}_v{p}_v^{\ast }}\right]}^{1∕2},$$ (6)

where n is the number of nodal locations within the finite element mesh, u_v and u_p represent the validated and perturbed displacement vector fields, p_v and p_p represent the validated and perturbed pore-pressure distributions, and “∗” indicates the complex conjugate of a given complex-valued quantity.

Poroelastic phantoms

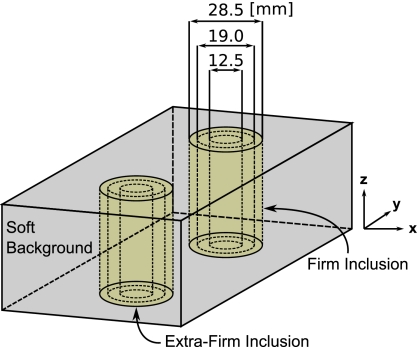
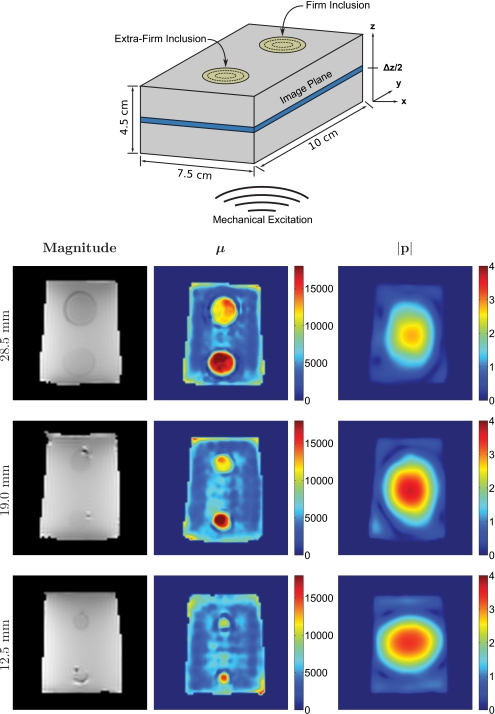
To assess the accuracy of the shear modulus estimates obtained from the reconstruction algorithm, three poroelastic phantoms (10×7.5×4.5 cm³) were constructed from three different grades of commercially available silken tofu (soft∕firm∕extra firm). Each individual phantom was composed of a soft tofu background containing two cylindrical inclusions (one firm and one extra firm) with diameters equaling 28.5, 19, or 12.5 mm. The inclusions were generated by first removing a core from the soft tofu slab and then replacing it with a core extracted from a separate firm or extra firm slab. Approximately 8 h were allowed postconstruction for the phantoms to reach temperature equilibrium (∼20 °C). Each phantom was housed in a sealed plastic container to prevent desiccation. Figure 2 contains a drawing of the tofu phantom construction. MRE motion data were recorded for each phantom in three orthogonal directions using a spin-echo phase contrast pulse sequence with added motion encoding gradients (TR=480 ms and TE=40 ms). The phantoms were excited in the z direction using a pneumatic actuator at a frequency of 100 Hz. Sixteen coronal image slices (x-y plane, 128 mm FOV) were acquired with 2×2×1.8 mm³ voxels and a 0.2 mm slice gap. The total imaging time was approximately 10 min per encoding direction.

Figure 2.

A drawing of the tofu phantom construction; each composed of multiple tofu grades (soft/firm/extra firm) and varying inclusion diameters (28.5/19.0/12.5 mm).

Poroelastic reconstructions were performed using the algorithm discussed in Sec. 2B and presented in detail in Ref. 43. A zero-flow pressure boundary condition (∂p∕∂n=0 Pa∕m) was assumed for the tofu phantoms at the actuation surface (z=0 m) with free-flow conditions (p=0 Pa) specified on all other surfaces.

Mechanical testing

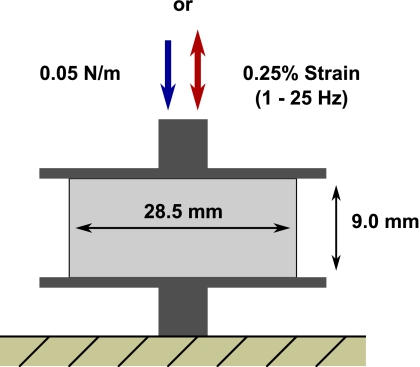
To compare the MRPE shear modulus estimates obtained for the poroelastic phantoms with values recorded during independent mechanical measurements, quasistatic and dynamic experiments were performed on 28.5 mm diameter×9.0 mm thick cylindrical tofu samples (for each grade, soft∕firm∕extra firm, n=6) compressed between two impermeable plates using a Q800 dynamic mechanical analyzer (TA Instruments, New Castle, DE). Figure 3 presents a drawing of the experimental setup. Given that hydration and temperature can be significant factors influencing the mechanical measurements, the samples were enclosed during the experiments to minimize desiccation and were maintained at a constant temperature with an automated liquid nitrogen cooling system.

Figure 3.

A drawing of the experimental setup employed during quasistatic and dynamic mechanical testing.

Since classical mechanical testing of materials assumes that only a solid phase exists, both quasistatic and dynamic measurements were acquired in order to bracket the shear modulus estimates for the solid matrix returned through MRPE. Specifically, the slow exudation of fluid is not expected to contribute to the bulk material stiffness during quasistatic compression, and thus the resulting stress-strain curves will reflect the mechanical properties of the solid matrix alone but at low frequency (essentially zero), providing a lower bound on the shear modulus expected at frequencies commonly used in MRPE. Dynamic testing, on the other hand, extracts the shear modulus at frequencies commonly used in MRPE but partitions the solid material stiffening and associated mechanical losses resulting from the presence of fluid into an effective storage (shear) and loss modulus that is expected to overestimate the actual matrix shear modulus by assuming the material under investigation is purely viscoelastic. The methods used to collect the quasistatic and dynamic measurement data on the tofu samples are briefly summarized here.

Quasistatic

The quasistatic measurements were performed as described in Ref. 42. Each sample was subjected to unconfined compression at a rate of 0.05 N∕min until 12% strain was achieved. The compression was assumed to be sufficiently slow that the influence of the pore fluid leaving the material on the measured displacements could be neglected.

Dynamic

At the conclusion of each quasistatic test, the load was removed and each sample was allowed to relax for 10 min. A viscoelastic analysis was then performed on each sample for frequencies ranging between 1 and 25 Hz (0.01 N preload and 0.25% strain). Excitation of the drained samples was intended to yield measurements which minimized the effects of the pore fluid on the composite solid∕fluid response. The dynamic tests were conducted under isothermal conditions between 20 and 5 °C with a temperature increment of −5 °C. Each sample was held at the prescribed temperature for 10 min before beginning measurements to ensure that equilibrium had been reached. Because unconfined dynamic actuation of soft materials is known to yield unreliable measurements at excitation frequencies above about 30 Hz with this experimental setup, time-temperature superposition (TTS)^{48, 49} was applied to produce a composite curve which enabled estimation of the storage and loss moduli at 100 Hz. For thermorheolologically simple materials such as tofu, TTS assumes that the entire relaxation spectrum is affected equally by a change in temperature, i.e., relaxation times increase with a reduction in temperature and decrease with elevated temperature, allowing the superposition of data sets obtained over a range of discrete temperatures to extend the dynamic range of the experiments.

RESULTS

Numerical simulation

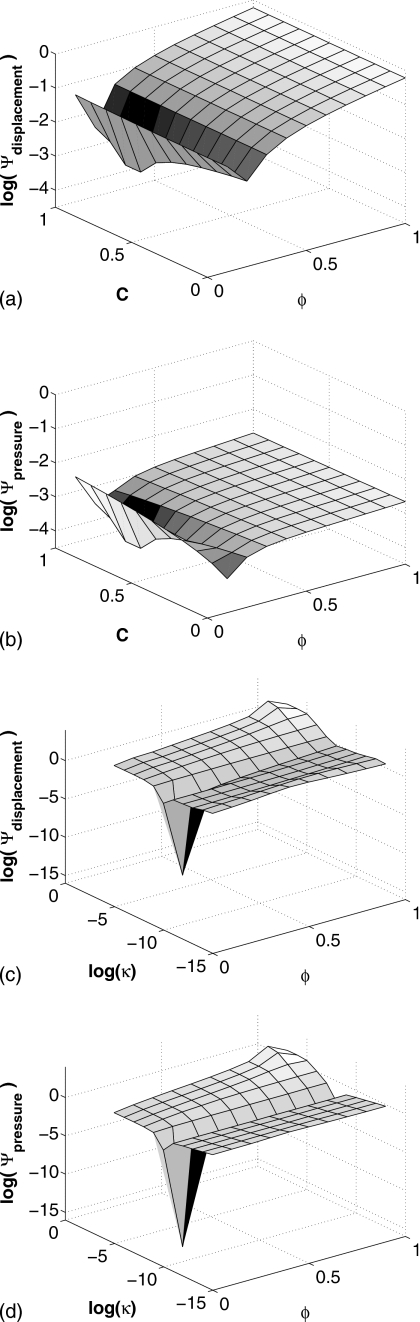
Figure 4 contains surface plots that show the relative differences between the displacement and the pore-pressure fields determined from the model validation and those obtained from solutions to the forward problem in which the porosity ϕ, experimental coefficient C, and material hydraulic conductivity κ were varied incrementally. Figures 4a, 4b depict the displacement and pressure differences computed with κ held constant at 10⁻⁸ m³ s∕kg. Similarly, Figs. 4c, 4d contain the displacement and pressure differences computed with C held constant at a value of 0.75.

Figure 4.

Surface plots showing the variation in log(Ψ) for displacement and pore-pressure fields computed by incrementally changing the model parameters C, ϕ, and κ, compared against those computed with the parameter set used during model validation: (a) and (b) compare the effect of C and ϕ while κ is held constant at 10⁻⁸ m³ s∕kg, whereas (c) and (d) compare κ and ϕ while C is held constant at 0.75.

The plots for Ψ_displacement and Ψ_pressure presented in Figs. 4a, 4b show that the calculated differences between the validated fields and those computed with the perturbed set of parameters are relatively invariant over the range of values for C. However, significant difference reduction was observed as the value of ϕ approaches 0.2. Conversely, for the plots presented in Figs. 4c, 4d, the calculated difference was observed to be relatively invariant over the range of values for ϕ for a given level of κ, showing that significant difference reduction occurs only when κ approaches 10⁻⁸ m³ s∕kg.

Poroelastic phantoms

Reconstructions performed on the experimentally acquired data employed a total of 16 processors (2× AMD Quad-Core Opteron nodes) for 60 global iterations. The average runtime for the reconstruction was approximately 5 h. A single global iteration consisted of approximately 200–300 individual iterative subzone calculations containing an average of 550–600 nodes∕subzone. In addition, a global forward solution was performed at the end of each global iteration upon completion of all subzone calculations to obtain an estimate of the internal pore-pressure distribution. A more complete description of the poroelastic algorithm and the iterative subzone reconstruction process can be found in Ref. 43.

Figure 5 shows an MRE magnitude image as well as the corresponding recovered matrix shear modulus and pore-pressure amplitude distributions from the center (z direction) of each of the three tofu phantoms described in Sec. 2D. Also included is an illustrative drawing depicting the phantom construction, reference image plane, length scales, and the location of the applied mechanical excitation. The shear modulus images reveal good recovery of the expected spatial variation in shear modulus across each phantom. The soft background was found to be relatively uniform, reflecting the expected homogeneity of the processed material. Interestingly, a dark blue ring is visible around each inclusion, regardless of the inclusion diameter. This observed drop in shear modulus at the inclusion∕background interface can be attributed to excess fluid which accumulated around the inclusions during phantom construction. Each inclusion was manually segmented from the background and each material was subsequently analyzed for mean and standard deviation. The computed values are summarized in Table 3 for each phantom and specific tofu grade. In addition, contrast ratios were calculated by dividing the average shear modulus for each individual inclusion by the average shear modulus of their respective backgrounds. Figure 6 displays the computed averages graphically. All three reconstructions produced similar estimates of the shear modulus for the soft tofu background, yielding a maximum variation in the mean of less than 6.5%. Further, the maximum variation in the mean shear modulus of the 19 and 28.5 mm diameter inclusions was determined to be less than 11.5% for both the firm and extra firm tofu grades, with the mean shear modulus estimates for the extra firm inclusions found to be statistically equivalent (p>0.05). The mean shear modulus values for the 12.5 mm diameter firm and extra firm inclusions appeared to be underestimated by about a factor of 2.

Figure 5.

MRE magnitude images and the corresponding reconstructed matrix shear modulus and pore-pressure distributions from the center of three soft tofu phantoms containing cylindrical tofu inclusions of varying diameter (28.5/19.0/12.5 mm) and grade (firm/extra firm). Images are shown on common scales and are given in units of pascals.

Table 3.

Summary of the experimentally determined values.

Experiment	Soft		Firm		Extra firm		Contrast ratios
	$\overline{\mu }$ (kPa)	σ (kPa)	$\overline{\mu }$ (kPa)	σ (kPa)	$\overline{\mu }$ (kPa)	σ (kPa)	Firm∕soft	Extra firm∕soft
MRPE (28.5 mm dia.)	4.614	2.264	10.611	3.058	14.153	2.606	2.30	3.07
MRPE (19.0 mm dia.)	4.477	2.080	9.396	3.420	14.109	4.142	2.10	3.15
MRPE (12.5 mm dia.)	4.782	2.437	5.127	2.934	7.119	3.645	1.07	1.49
Quasistatic	0.887	0.053	1.985	0.110	2.339	0.195	2.24	2.64
Viscoelastic (100 Hz)	6.368	0.390	16.051	0.663	21.889	1.846	2.52	3.44

Figure 6.

Bar graph comparing the mean and standard deviation of the recovered matrix shear modulus of the background and inclusions for each of the three tofu phantoms.

Mechanical testing

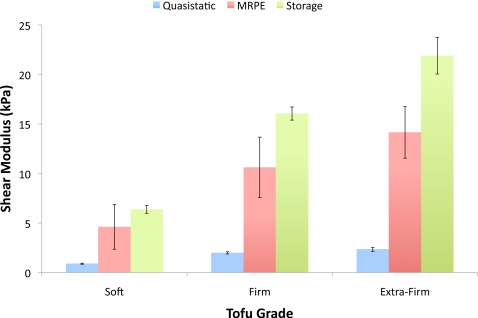
A summary of the results from the quasistatic and dynamic mechanical tests for each tofu grade is provided in Table 3. In general, the real part of the complex shear modulus or storage modulus determined during the dynamic tests (100 Hz) was found to be 7.1–9.5 times greater than that observed from the quasistatic tests, suggesting considerable frequency dependence of the modulus of the tofu matrix (although a portion of the increase is also likely due to the effects of the residual fluid remaining in the sample after the initial quasistatic compression tests). Figure 7 compares the results obtained from the mechanical tests with those from the reconstruction of the poroelastic phantom with the 28.5 mm diameter inclusions. The results from this phantom were used in the comparison as the larger inclusion diameters enabled more accurate boundary segmentation. They also included the most nodal values in the calculation of the mean.

Figure 7.

Bar graph comparing the mean and standard deviation of the matrix shear modulus obtained from the quasistatic and dynamic mechanical tests with the values reconstructed for the poroelastic phantom with 28.5 mm diameter inclusions.

DISCUSSION

Analysis of the sensitivity of the computed displacement and pore-pressure fields to changes in the a priori estimates of the experimentally derived poroelastic parameters C, ϕ, and κ has shown hydraulic conductivity (κ) to be the most influential. This result is consistent with expectations given that, in the absence of a complex-valued shear modulus, any frequency dependence observed in the deformation behavior must be attributed to the rate at which fluid movement can occur under the applied gradient in pressure. The finding also implies that the values for C and ϕ assumed in the reconstruction are less likely to influence the minimization between the measured and the computed displacement fields. Therefore, the accuracy of Lamé’s constants and the subsequent pore-pressure distribution recovered from the experimental data is likely to benefit from spatial variation in κ either through tissue-type classification (e.g., enforced through segmented MR images) or by estimating κ as an independent parameter. Implementation of the latter may be possible by reformulating Eq. 3 to incorporate β in the set of parameter updates Δθ, enabling estimation of κ indirectly. However, further study is required to determine the sensitivity and stability of the reconstruction process to estimates of κ computed on the nodal, element, or subzone levels.

Experimental results obtained for the three tofu phantoms indicate high quality recovery of the expected spatial variation in shear modulus between the soft background, firm, and extra firm tofu inclusions. Also, the estimated pore-pressure amplitude distributions appear consistent and reasonable, given knowledge of the assumed boundary conditions on pressure. The pore pressure is expected to be greatest toward the center of the actuation surface where ∂p∕∂n=0 Pa∕m and smallest in proximity to all other free surfaces where a condition of p=0 Pa is prescribed. Stress concentrations arising from the presence of the different cylindrical inclusions may account for some of the variation observed in the shape of the pore-pressure distribution at the center of the images. Elevated matrix shear modulus estimates at the slab boundary (especially in the corners) are artifacts that can likely be attributed to the assumptions surrounding the global boundary conditions on pressure. Specifically, the boundary condition p=0 was applied to the air∕tofu interface on all free surfaces. However, generation of the finite element mesh and subsequent interpolation of the measured motion data requires that the computational volume be slightly reduced (∼1–2 mm), thereby forcing the condition on pressure to be applied inside the actual phantom boundary, which has its largest impact at the corners of the phantom. The contrast ratios computed for the 19.0 and 28.5 mm diameter inclusions were found to be 2.10 and 2.30, respectively, between the firm and soft tofu regions and 3.15 and 3.07, respectively, between the extra firm and soft tofu regions. The contrast ratios determined for the 12.5 mm diameter inclusion phantom were significantly lower at 1.07 for the firm inclusion and 1.49 for the extra firm inclusion. One explanation for this observation is the smoothing effect that occurs during image reconstruction from the spatial filtering process,⁵⁰ which will have a larger impact on features with a smaller spatial footprint. Further, this process is likely to be exacerbated by the presence of excess fluid around the inclusions which will artificially decrease the value of the recovered matrix shear modulus in the adjacent regions.

The tofu matrix shear modulus values determined from mechanical testing bracketed those obtained from MRPE as expected. Specifically, a significant decrease was observed in the quasistatic shear moduli relative to values recovered with the reconstruction because of the substantial stiffening effects of the fluid at frequency. Referring to Table 3, the average matrix shear modulus at 100 Hz of the soft tofu background for all three phantoms was found to be approximately 5.2 times the quasistatic value. Not surprisingly, the average recovered MRPE shear modulus was less than but much closer to (∼75%) the storage modulus determined during dynamic testing because a substantial portion of the complex deformation behavior interpreted as viscous effects from the solid∕fluid interactions can be attributed to poroelastic damping. Similar trends in these properties were observed for the firm and extra firm inclusions as well. Interestingly, while the reconstructed values were quantitatively different from the shear moduli determined through quasistatic or dynamic testing (i.e., the relative differences between the recovered moduli and those determined from mechanical testing were observed to be 322%–421% for the qusistatic measurements and 27%–47% for the dynamic measurements), the shear modulus contrast ratios for the phantoms with 19 and 28.5 mm inclusions were much closer and very similar to those determined from the mechanical tests (10%–15% difference).

CONCLUSIONS

The goal of MRPE is to provide a more representative analysis of the mechanical properties of fluid-saturated tissues through the implementation of a mechanical model which can adequately describe poroelastic deformation and ultimately enable separation of the solid matrix response from that of the pore fluid. In this study, the sensitivity of the poroelastic model to perturbations in the a priori estimates of three unknown parameters was investigated. In addition, a quantitative assessment of the accuracy of the matrix shear modulus estimates obtained from the poroelastic reconstruction was performed on three poroelastic phantoms by comparing the reconstructed values with those obtained from quasistatic and dynamic mechanical tests.

Of the experimentally derived parameters C, ϕ, and κ, hydraulic conductivity (κ) was the most influential in terms of changes in the displacement and pore-pressure fields computed by solving the forward problem. The potential for error in the recovered matrix shear moduli due to variation in κ across the image volume indicates the need for a spatially distributed a priori estimate of κ guided by segmented MR images or an algorithm capable of recovering estimates of κ as an independent parameter on the nodal, elemental, or subzone level.

Although the MRPE matrix shear moduli recovered from different grades of tofu were different from the values recorded during mechanical testing, the technique accurately reproduced the expected spatial variation along with relative changes in its magnitude associated with the firm and extra firm inclusions. Reasonable estimation of the pore-pressure amplitude distributions was also observed. Thus, poroelastic damping accounted for much of the complex (time-dependent) behavior resulting from the interactions between the solid and the liquid material phases.

In summary, the degree to which MRPE can separate the mechanical responses of the solid and fluid compartments in tofu is encouraging. While the contribution of in vivo tissue-matrix viscoelasticity to the total deformation behavior remains largely unknown, consideration of frequency-dependent or complex matrix shear moduli may improve quantitative accuracy. In addition, future studies should include an exploration of the relationship between poroelastic damping and tissue hydraulic conductivity as well as the potential for a spatially distributed estimate of the latter.