Minimal Size of Coffee Ring Structure

Abstract

A macroscopic evaporating water droplet with suspended particles on a solid surface will form a ring-like structure at the pinned contact line due to induced capillary flow. As the droplet size shrinks, the competition between the time scales of the liquid evaporation and the particle movement may influence the resulting ring formation. When the liquid evaporates much faster than the particle movement, coffee ring formation may cease. Here, we experimentally show that there exists a lower limit of droplet size, D_c, for the successful formation of a coffee ring structure. When the particle concentration is above a threshold value, D_c can be estimated by considering the collective effects of the liquid evaporation and the particle diffusive motion within the droplet. For suspended particles of size ~100 nm, the minimum diameter of the coffee ring structure is found to be ~10 µm.

Introduction

The drying of a liquid droplet with suspended particles on a solid surface leaves a ring-shaped structure along the droplet perimeter, which is commonly known as the coffee ring phenomenon.^1,2 This phenomenon can be observed in everyday life whenever liquid droplets with suspended particles evaporate, such as ring stains left behind from spilled coffee droplets. Although the formation of these coffee ring structures is a commonly observed phenomenon, the physical mechanisms behind it are rather complex and were not elucidated until recently. Deegan et al.^1–3 were among the first to propose a plausible physical model, which showed that capillary flow, induced by droplet evaporation at a pinned contact line (CL), is the main cause for the coffee ring phenomenon. The physics of induced capillary flow within liquid droplets was further investigated by Fisher⁴ and Hu and Larson,^5,6 who described the precise flow field within evaporating droplets using lubrication theory and numerical methods. In addition, conditions for effective CL pinning have recently been studied by Sangani et al.,⁷ who showed that CL pinning is highly contingent upon the suspended particle size and the particle concentration. To further enhance the coffee ring formation, Hu and Larson showed that the suppression of Marangoni flow in a drying droplet is necessary, particularly for solvents that exhibit strong Marangoni effects.⁸

Understanding the transport mechanisms of micro- and nanoparticles within evaporating liquid droplets has important technological applications, such as nanostructure self-assembly,^9,10 particle and biomolecule separation and concentration,^7,11 functional particle coating^12,13 and lithography patterning,¹⁴ as well as device assembly.¹⁵ These capabilities offer many interesting avenues for the development of novel electronics¹³ and biological transducer systems.¹⁶ Although many of these potential applications are on the scale of micro- and nanometers, recent scientific investigations on the coffee ring phenomenon were predominately restricted to the study of macroscopic liquid droplets (i.e., on the order of millimeters) ^1–8,17 due to the various experimental challenges at the micro- and nanoscale. To address these limitations, we recently developed an experimental technique that allows for the formation of water droplets with sizes encompassing a broad range of length scales (i.e., from ~2 mm down to ~100 nm in wetting radius) with well-characterized local contact angles.¹⁸ Enabled by this technique, we can further explore the relationship between the time scales of liquid evaporation¹⁹ and the particle movement within the droplets and their affects on the formation of ringlike structures. Here, we experimentally investigate the formation of coffee ring structures for liquid droplets with sizes ranging from millimeters down to a few micrometers and explore the minimum droplet size required to form a coffee ring structure.

Experimental Section

Materials

Colloidal solution of polystyrene latex beads (surfactant-stabilized) with a particle diameter of 113 ± 11 nm (m = 20, where m is the number of independent measurements from images obtained from a scanning electron microscope, SEM) and solid content of 10% (W/W, or equivalent to a particle concentration of 1.828×10 ¹⁴ particles/mL) was purchased from Sigma-Aldrich. Carboxyl latex beads colloidal solution (surfactant-free charge-stabilized) with three different average particle diameters and concentrations were purchased from Molecular Probes (28 ± 5 nm, 3.3×10¹⁵ particles/mL; 62 ± 6 nm, 3.1×10¹⁴ particles/ml; 140 ± 13 nm, 2.7×10¹³ particles/mL, where the specifications were provided by the manufacturer). Purified deionized water with a resistivity of ~18.3 MΩ/cm was used for the dilutions of the particles. Surfactants, such as sodium dodecyl sulfate (SDS) (Fluka, Switzerland, diluted to < 0.01%), were added when necessary.

Chemically Heterogeneous Surfaces

Following the published experimental protocol,¹⁸ an engineered surface with patterned hydrophilic structures (platinum, Pt) on a relatively nonwetting surface (i.e., hexamethyldisilazane (HMDS) coated on a silicon/silicon dioxide substrate) was utilized to control the size of the liquid droplets (Supporting Information). The diameters of the hydrophilic structures ranged from ~1 mm to ~3 µm, and the thickness of the structures was ~20 nm, as confirmed by atomic force microscopy (AFM) measurements.

Formation of Nanoparticle Deposits

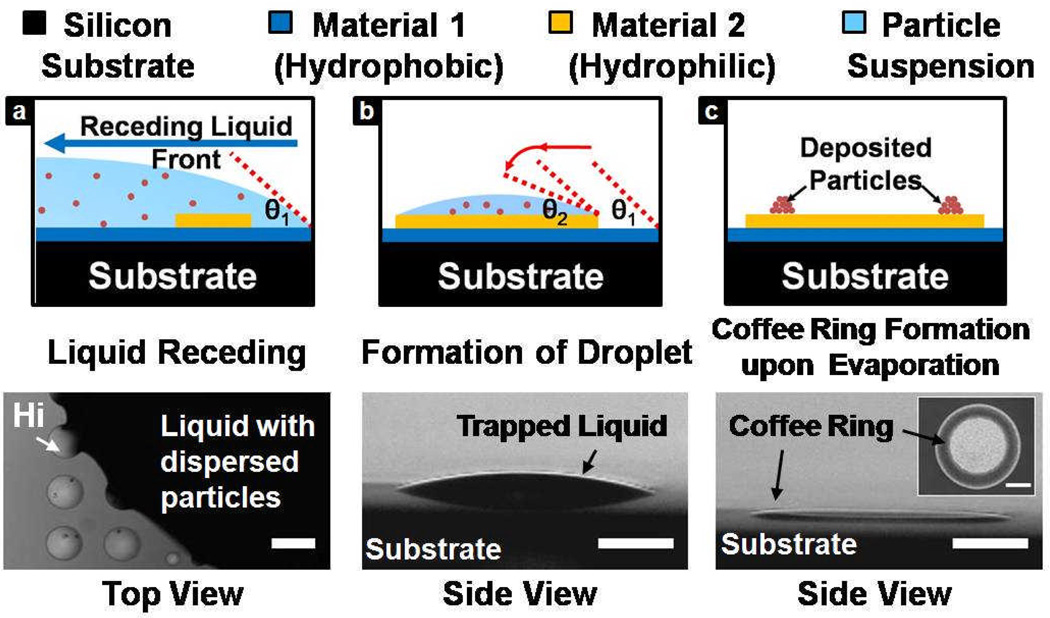
A colloidal solution, with known particle size and concentration, receded from the nonwetting surface onto the hydrophilic structures. Liquid droplets were retained on the structures as a result of pinning to the solid edge. Nanoparticle deposits were formed on the hydrophilic surfaces upon solvent evaporation under a humidity-controlled environment at room temperature (Figure 1).

Figure 1.

Schematic diagram showing the trapping of a colloidal liquid droplet on a hydrophilic surface during macroscopic liquid receding process. Upon solvent evaporation, particles deposit on the surface and form coffee ring structures. Optical images indicate the occurrence of pinning at the edges of the hydrophilic structures (indicated as Hi) and the corresponding droplet formation. Scale bars indicated in all of the figures are equivalent to 300 µm.

Surface Characterization

Both Pt and HMDS surfaces were characterized against all the colloidal solutions used in the experiments (Supporting Information). Contact angle measurements of the colloidal solutions on both surfaces were conducted by a drop shape analysis system (FTA 4000). In particular, the initial contact angles of the colloidal droplets trapped on the millimeter-sized hydrophilic structures were measured to be ~20°, which are consistent with our previous measurements (Supporting Information).¹⁸ The same system was used to study the droplet evaporation history (Supporting Information). SEM and AFM were utilized to study the nanoparticle deposits. The images obtained were further analyzed with an image processing software, ImageJ (developed by the National Institutes of Health), to extract the quantitative information of the nanoparticle deposits.

Results

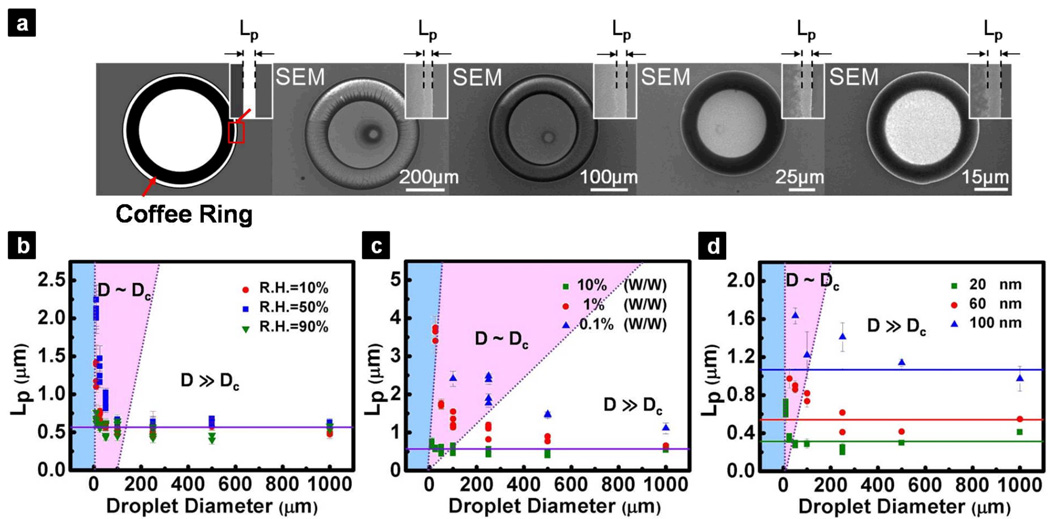
We investigated the nanoparticle deposits formed by evaporating liquid droplets (with diameters from 1 mm down to 3 µm) using surfactant-stabilized nanoparticles ~100 nm in diameter. At a constant relative humidity and particle concentration, we observed two distinct regimes for the nanoparticle deposits with cutoff at a critical length scale, D_c (Figure 2). When the droplet wetting diameter is larger than D_c, suspended nanoparticles are transported to the droplet perimeter and form a ringlike structure; for droplets with diameters smaller than D_c, the suspended nanoparticles are dispersed homogeneously on the surface of the patterned hydrophilic surfaces.

Figure 2.

Different nanoparticle deposits on hydrophilic Pt structures with diameters ranging from 3 µm to 100 µm. Representative SEM images showing the deposit patterns at different droplet diameters: (left to right) 3 µm, 5 µm, 10 µm, 25 µm, 50 µm, and 100 µm. Two different regimes of the deposit patterns are clearly distinguishable. It is important to note that the image contrast of the SEM images is dependent on the local thickness of the coffee ring structure. Therefore the region of the coffee ring structures appear to be darker as the number of the nanoparticles layers increase, which is evident in the 25 µm, 50 µm, and 100 µm structures.

On the basis of our experimental observations, we studied the effects of several critical parameters, such as the relative humidity of the evaporation environment, particle concentration, and particle size, on the formation of coffee ring structures. On the basis of our results, we observed that D_c is dependent on the relative humidity of the evaporating environments (i.e., from 10 to 90% at room temperature); at a higher relative humidity and constant particle concentration, D_c was found to decrease. In addition, we observed that D_c decreases with increasing particle concentration (i.e., from 0.1 to 10% weight fraction). To exclude any effects caused by surfactants on the observed results, we repeated the experiments using a surfactant-free charge-stabilized ~100 nm particle suspension. For colloidal solution of the same particle size (~100 nm), similar nanoparticle deposits were observed, indicating that the phenomenon is not due to the presence of surfactants (Supporting Information). From these experiments, the minimum diameter of the coffee ring structure for ~100 nm particles was ~10 µm.

Furthermore, to examine whether smaller particle sizes can lead to a smaller D_c, we investigated the formation of nanoparticle deposits using 20, 60, and 100 nm charge-stabilized nanoparticles. Interestingly, we found that a well-defined coffee ring structure can be clearly formed for 100 nm nanoparticles, but not with those of the 20 nm and 60 nm. In particular, when the 20 nm colloidal solution evaporates, the nanoparticles distribute uniformly onto the surface and form a pancake pattern instead of a ring-like structure (Supporting Information). At the same time, we observed stick-slip patterns for the 60 nm particles, indicating that the CL repeatedly pins and depins as the droplet evaporates (Supporting Information).²⁰ These experimental observations suggest that the pinning effect reduces with the particle size, which is consistent with a recent experimental study by Ondarcuhu and Piednoir,²¹ showing that pinning vanishes when the characteristic length of the solid edge is on the order of the molecular length scale of the liquid.

Under the conditions that the coffee ring structure is well-formed (i.e., D ≫ D_c),⁷ we consistently observed the existence of a monolayer formation near the coffee ring perimeters (Supporting Information). This observation is in line with the recent work of Park and Moon,²² who provided experimental evidence demonstrating the importance of this monolayer structure near the CL for coffee ring formation. Specifically, we found that a small number of concentric rings (i.e., less than five rings) in this monolayer is sufficient to maintain a pinned CL (Supporting Information). As Huang et al.²³ also pointed out, that a single line of nanoparticles is not sufficient to pin a CL, our observations further highlight that particle-to-particle contact is fundamental for the CL pinning process, which directly influences the successful formation of a coffee ring structure.

For well-formed coffee ring structures, we also noticed a finite distance, usually on the order of a few hundred nanometers, between the initial CL and the boundary of the ring structure (Figure 3a). Although this finite distance was noticed in previous investigations,^17,24 systematic studies have yet to be carried out to understand the quantitative nature of the observation. Surprisingly, we found that this finite distance, denoted as L_p, is relatively constant over a broad range of droplet length scales where the coffee ring structures were formed (i.e., from a few tens of micrometers up to 1 mm), given the same nanoparticle size and solvent type. We also measured L_p for coffee ring structures formed from droplets whose D > D_c (i.e., from a few tens of micrometers to 1 mm) by varying different conditions, such as relative humidity, particle concentration, and particle size (Figure 3b – d). We found that L_p strongly depends on the nanoparticle size, but is a weak function of particle concentration and is nearly independent of the relative humidity when D ≫ D_c. By simple geometry, we derived a relationship that correlates L_p to the particle sizes of the colloidal suspension (Supporting Information),

$$L_p=\frac{r}{\text{tan}({\theta }_{\mathit{local}}/2)}$$ (1)

where r is the radius of the nanoparticles, and θ_local is the local contact angle between the three-phase CL at the particle surface and the horizontal Pt surface. Notice that eq 1 is derived under the conditions that D ≫ D_c and r ≪ D. On the basis of eq 1 and our experimental measurements of L_p, we found that θ_local lies between ~10° to ~20°, where the upper and lower limits are close to the initial contact angle of the colloidal droplet, θ_initial, and the receding contact angle of water on Pt surface, θ_receding, respectively (i.e., θ_initial < θ_local < θ_receding).

Figure 3.

Existence of a finite distance, L_p, between the initial pinning point and the boundary of the coffee ring. (a) SEM images showing the formation of coffee ring structure on hydrophilic structures of varying diameters (left to right: 500 µm, 250 µm, 100 µm, and 50 µm). Insets show the magnified region at the edge of the coffee ring structures, indicating the existence of L_p. Quantitative measurements of L_p were performed at different (b) relative humidity, (c) particle concentrations, and (d) particle sizes, respectively. For D < D_c, the coffee ring structure is not well-defined, therefore no L_p can be measured (blue region). When D ~ D_c, L_p is found to be dependent on relative humidity and the particle concentration (red region). For D ≫ D_c, L_p converge to constant values (i.e., indicated by the solid lines), where the values are strongly dependent on the particle size. Each data point was obtained from at least 10 independent experimental measurements and the error bars represent standard deviations. In these SEM images, the darker region at the perimeters is the coffee ring structures which consist of multiple nanoparticle layers, whereas the lighter region at the center is the Pt surface covered by dispersed nanoparticle.

Discussion

Summarizing from our experimental observations, we proposed two important time scales that are central to the successful formation of coffee ring structures near the CL. The first time scale is related to the evaporation of the liquid droplet, denoted as τ_evap, which dictates the time allowed for the particle to form the initial monolayer within the droplet. The importance of this time scale is supported by our experimental observations for the nanoparticle deposits formed in the small liquid droplets (i.e., D < D_c). In these droplets, there was an adequate number of nanoparticles to form coffee ring structures, yet these nanoparticles were dispersed homogeneously on the surface (Supporting Information). This indicates that the particles did not have sufficient time to form a monolayer and maintain a pinned CL due to the fast evaporation of the liquid.²⁵ The second time scale is related to the time for two adjacent particles near the CL to meet each other, denoted as τ_particle, which is supported by our observations that only a small number of concentric rings of nanoparticles are sufficient to pin a CL. On the basis of these time scales, we further define a dimensionless number, C_R, to quantify their competition,

$$C_{\mathrm{R}}=\frac{{\tau }_{\mathit{\text{particle}}}}{{\tau }_{\mathit{\text{evap}}}}$$ (2)

To correlate the coffee ring formation phenomena to C_R, it is necessary to express both τ_particle and τ_evap in the forms of their respective intrinsic parameters of the colloidal droplet (e.g., particle size and concentration) and the evaporation environments (e.g., relative humidity).

According to our experimental measurements from L_p, the formation of the monolayer structure occurred in the time period when the local contact angle of the droplets changed from θ_initial to θ_receding. If the monolayer structure cannot be formed before the contact angle reaches θ_receding, the CL starts to recede and move the particles inward. Therefore, the evaporation time required for this contact angle change provides a representative time scale for τ_evap. To model the evaporation time, we employed the macroscopic evaporation model to evaluate τ_evap,^19,26 which is justified in our experimental situation, since the characteristic lengths of the smallest droplets (i.e., ~3 µm) are still much greater than the mean free path of the vapor molecules under ambient conditions (i.e., ~70 nm).^27–29

On the basis of the constant contact diameter evaporation model proposed by Popov,²⁶ one can express the evaporation time for the contact angle change (Supporting Information) as

$${\tau }_{\mathit{\text{evap}}}=\frac{{\theta }_{\mathit{\text{initial}}}-{\theta }_{\mathit{\text{receding}}}}{4K}\pi {(\frac{D}{2})}^2$$ (3)

where K is a characteristic parameter representing the droplet evaporation rate. Specifically, K can be further expressed as

$$K=\frac{4D_v(c_0-c_{\infty })}{{\rho }_L}$$ (4)

where D_v is the molecular diffusion coefficient of the vapor in air; c₀ and c_∞ are the densities of the saturated vapor in close proximity above the liquid-air interface and the ambient vapor density, respectively; and ρ_L is the liquid density.

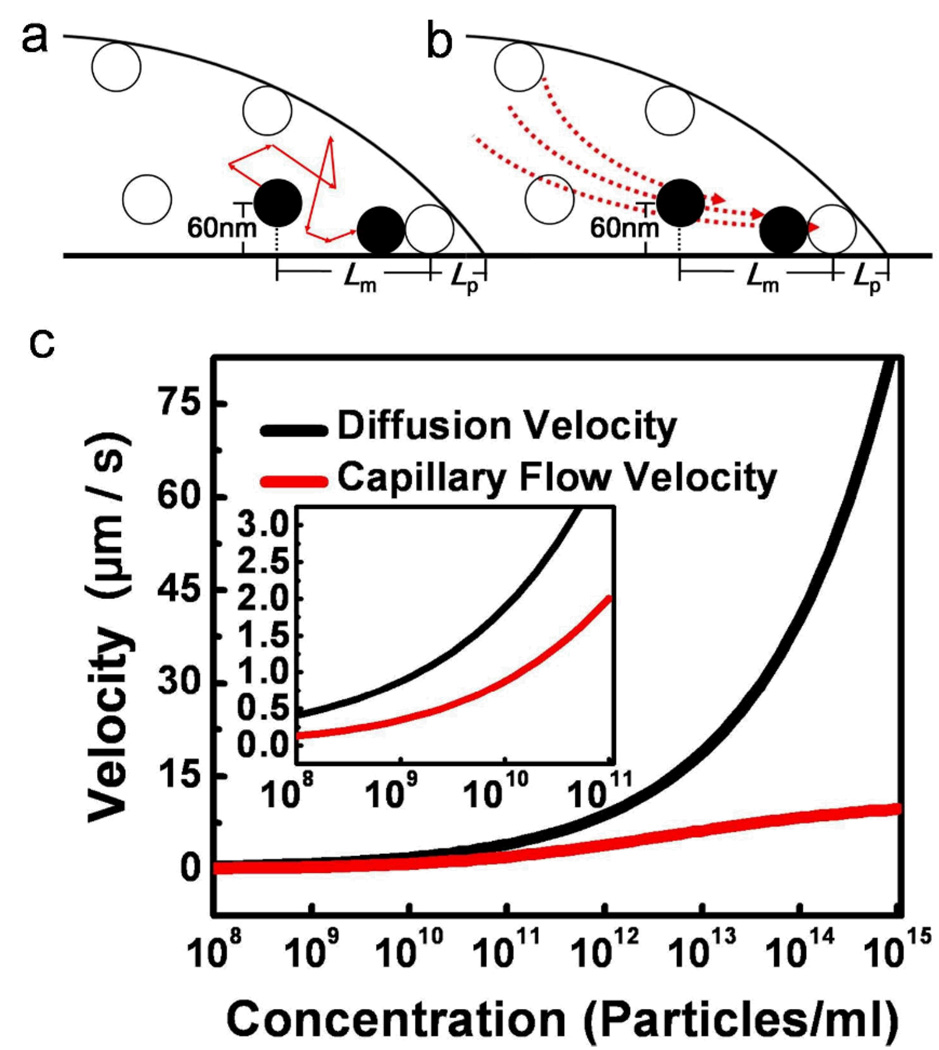
To formulate τ_particle, it is important to determine the dominating transport mechanism responsible for bringing the nanoparticles into contact and forming the initial monolayer structure. During the initial monolayer formation, the nanoparticles can be transported to the CL region by the induced capillary flow, diffusion, or by a combination of these two mechanisms. Before we compare these two transport mechanisms quantitatively, two important assumptions are made. First, we assume that the monolayer formation is initiated from the particles very close to the surface (i.e., on the order of the particle size). This assumption is supported by the fact that in all of our experimental observations in which the coffee rings were well-formed, there existed monolayer structures close to the CL (Supporting information). In addition, taking into account the size of the nanoparticles used in our experiments (i.e., order of 50 nm), we calculate the velocity of capillary flow ~60 nm above the solid surface. Second, we assume that the particles are homogeneously distributed in the liquid droplet so that the mean distance between two particles within the liquid droplet, L_m, can be estimated as

$$L_m=\sqrt[3]{V_{\mathrm{d}}/n}$$ (5)

where V _d is the volume of the droplet and n is the number of nanoparticles within the droplet. Considering the particle concentrations used in our experiments (~1 × 10¹² to ~1 × 10¹⁵ particles/mL), L_m is on the order of 100 nm – 1 µm. Since the monolayers are initiated at a distance of L_p (i.e., 600 nm – 1 µm) away from the CL according to our observations, we compared the nanoparticle velocities contributed by the capillary flow and the diffusion at a distance of ~800 nm + L_m from the CL (Figure 4a – b). The induced capillary flow within the droplet was computed by the models developed by Hu and Larson,⁶ whereas the particle diffusion velocity is defined as the ratio between the diffusion distance for two adjacent particles to meet (i.e., L_m), and the diffusion time that is estimated by the Einstein diffusion equation.³⁰

Figure 4.

Comparison of the nanoparticle velocities contributed by the capillary flow and the diffusion. (a, b) Schematic showing the contact line region of a liquid droplet with suspended particles. The particle movement could be influenced by both of the (a) particle diffusive motion and (b) induced capillary flow at this region near the surface, or either of these transport mechanisms. The velocity of the particle is calculated at the distance determined by the interparticle distance (L_m) and the distance between the contact line and the nearest particle (L_p). (c) Simulation result of the nanoparticle velocities by the diffusion (black line), and the capillary flow at ~60 nm above the surface and ~800 nm + L_m from the CL (red line, based on the model of Hu and Larson⁶). It is important to note that as the particle concentration changes within the droplet, the diffusion length will be altered correspondingly which will affect the time for particle-to-particle contact. In the simulation, the contact diameter of the droplet is 1 mm with a contact angle of 20°.

From the comparison between these two transport mechanisms, we found that for a particle concentration above a threshold value, the nanoparticle velocity contributed by the capillary flow is very small as compared with the particle diffusion velocity (Figure 4c). At the highest particle concentration in our experiments (i.e., ~1 × 10¹⁵ particles/mL), the particle diffusion velocity is ~10 times higher than that of the capillary flow. This strongly supports the assumption that for particles very close to the surface and near the CL, diffusion is the dominant mechanism to bring the particles into contact. This diffusion-dominated transport mechanism remains valid for particle concentrations higher than ~1 × 10¹⁰ according to the simulation results (i.e., diffusion velocity is ~3 times higher than that of the capillary flow velocity). Following the quantitative arguments, particle diffusion time can be used as a representative time scale to model τ_particle in our experimental concentration regime (i.e., ~1 × 10¹² to ~1 × 10¹⁵ particles/mL). Therefore, we can express τ_particle in the form of the Einstein diffusion equation,³⁰

$${\tau }_{\mathit{\text{particle}}}=\frac{\overline{{L_m}^2}}{2D_p}$$ (6)

where $D_p=\frac{k_{B}T}{6\pi \eta r}$ is the diffusion constant of the particle in a low-viscosity liquid medium.³⁰

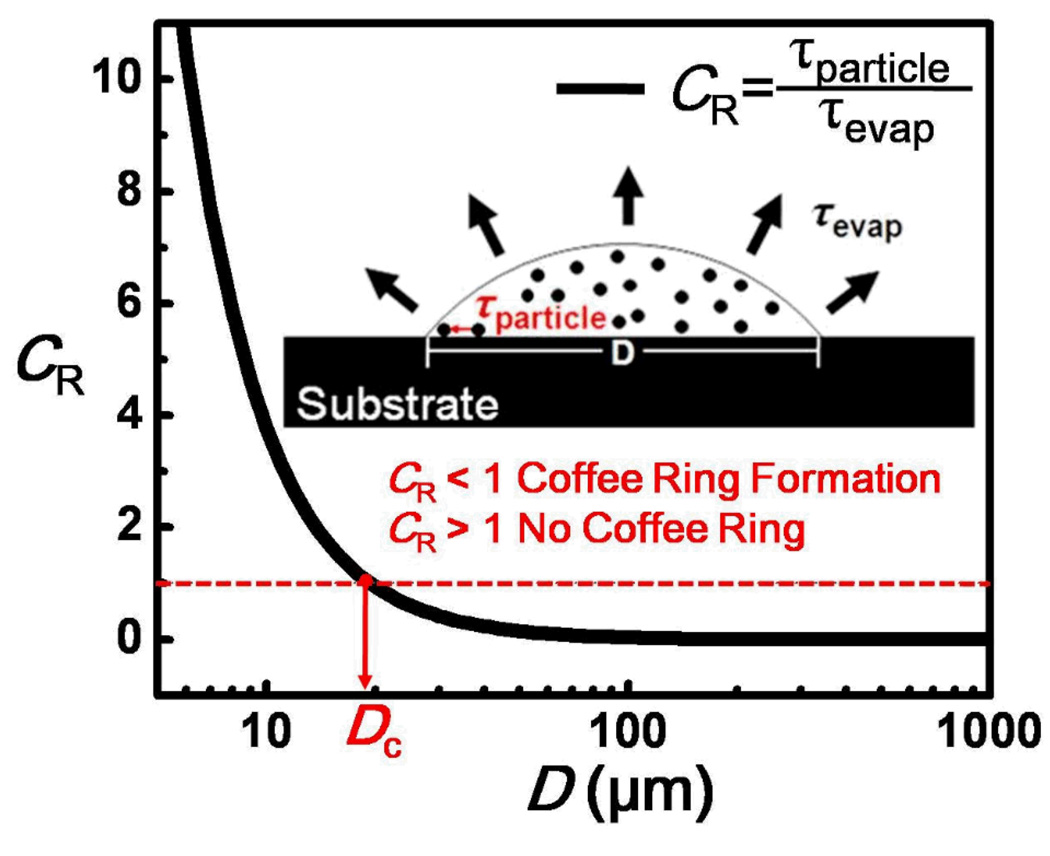
With the quantitative forms of τ_evap and τ_particle, we can further compute the critical droplet diameter, D_c, by equating these time scales (i.e., C_R = 1, Figure 5). This can be expressed as

$$D_c=\sqrt{\frac{8K}{\pi ({\theta }_{\mathit{\text{initial}}}-{\theta }_{\mathit{\text{receding}}})D_p}}{L}_m\text{\hspace{1em}for }r\ll D_c$$ (7)

Figure 5.

A semi-log plot showing the dependence of C_R with the droplet diameter. Two important time scales dictating the formation of the nanoparticle deposits near the CL. τ_evap indicates the time scale for liquid droplet evaporation, whereas τ_particle indicates the time scale for particles near the CL to meet each other, which is critical for the initial monolayer formation. The red dotted line indicates when C_R = 1 (i.e., τ_particle = τ_evap). When C_R > 1, the evaporation time is not sufficient for coffee ring formation, and the nanoparticles will be dispersed on the surface. On the other hand, when C_R ≪ 1, the nanoparticles have sufficient time to migrate to the CL and form a monolayer to maintain a pinned CL, facilitating the formation of a coffee ring structure. The parameters used in the plot refer to a particle size of 100 nm and concentration of 1.828×10¹⁴ particles/ml.

From eq 7, a number of important physical insights can be deduced. First, D _c increases with decreasing relative humidity (at a constant temperature), which in turn will affect the evaporation rate of the liquid (i.e., K). Second, D_c reduces with increasing in particle concentration (i.e., L_m decreases when particle concentration increases). These predictions are qualitatively consistent with our experimental observations. We further compared the computed D_c with that obtained experimentally, and these values agreed for large particle sizes (Table 1). Discrepancies were found for particle size smaller than 100 nm. It is important to note that although eq 7 predicts that D_c reduces with particle size (i.e., D_p increases when the particle size is reduced), the relationship is more subtle than that expressed by eq 7, because the particle size will also influence the pinning behaviors of the CL,¹⁸ which is not accounted for by the equation. With a large particle size (i.e., r > 50 nm), D _c given by eq 7 can provide a good estimation to predict the minimum size of a colloidal droplet to form a coffee ring structure. This also supports that the proposed dimensionless number, C_R, can be used as a quantitative measure for successful coffee ring formation (i.e., coffee ring forms when C_R ≪ 1, whereas no coffee ring formation for C_R > 1, Figure 5).

Table 1.

Summary of the Experimental Observations and the Theoretical Predictions by Eq 7.

Particle Type	Particle Size (nm)	Concentration (particles/ml)	R.H.	Theoretical Dc (µm)	Experimental Dc (µm)	Observed Trend
Surfactant -stabilized Particles			10 %	13.7	~10 – 25	R.H.↑
	~100	1.828×1014	50 %	10.2	~10	Dc↓
			90 %	6.6	~10
		1.828×1014		10.2	~10	Concentration↑
	~100	1.828×1013	50 %	22.0	~25	Dc↓
		1.828×1012		47.4	~50
Surfactant -free Particles	~100	2.7×1013		19.3	~25 – 50	Particle Size↓
	~60	3.1×1014	50 %	6.6	~10 – 25	If Lm↑, Dc↑
	~20	3.3×1015		---------	---------	If Lm const, Dc↓

Conclusions

In summary, we experimentally showed that there exists a lower limit of droplet size, D_c, for well-defined coffee ring formation. Under the conditions that the CL pinning is strong and the particle concentration is above a threshold value (i.e., > 10¹⁰ particles/mL), the lower limit of droplet size can be estimated by the competition between two intrinsic physical time scales related to the liquid evaporation and the diffusive particle movement within the droplet. Our experimental findings provide an important boundary condition necessary for the coffee ring formation (i.e., C_R ≪ 1), which can serve as a guideline to understand the particle transportation within evaporating micro- and millimeter-sized liquid droplets.