Shape and Individual Variability of the Blur Adaptation Curve

Abstract

We are interested in clinical implications of adaptation to blurred and sharpened images. Therefore, we investigated repeatability, individual variability and characteristics of the adaptation curves in normally-sighted individuals (n=39). The point of subjective neutrality (PSN – the slope of the spatial spectrum of the image that appears normal) following adaptation was measured for each adaptation level and was used to derive individual adaptation curves for each subject. Adaptation curves were fitted with a modified Tukey biweight function as the curves were found to be tumbled-S shaped and asymmetrical for blur and sharp in some subjects. The adaptation curve was found to be an individual characteristic as inter-subject variability exceeds test-retest variability. The existence of individual variability may have implications for the prescription and clinical success of optical devices as well as image enhancement rehabilitation options.

1. Introduction

The appearance of the visual world is affected by previous visual experience, as our visual perception is continuously modulated by adaptation to the visual environment. Blur adaptation refers to the change in the perceived level of blur following a period of exposure to blur. Webster, Georgeson & Webster (2002) reported that following a short period (3 to 6sec) of exposure to sharpened images, subsequent normal images appear to be blurred. Similarly, after viewing computationally blurred images, subsequent images appear sharpened. Aftereffects of adaptation to blur are also reported by myopic patients who describe decreased blur perception after a prolong period without their glasses (Pesudovs & Brennan, 1993; George & Rosenfield, 2004). Further, improved visual acuity and contrast sensitivity at high frequencies has been reported following periods (0.5 to 3 hours) of induced myopic blur (Pesudovs & Brennan, 1993; Mon-Williams, Tresilian, Strang, Kochhar & Wann, 1998; George & Rosenfield, 2004; Rosenfield, Hong & George, 2004; Wang, Ciuffreda & Vasudevan, 2006; Cufflin, Mankowska & Mallen, 2007; Rajeev & Metha, 2010).

Adaptation to blur and sharpness may influence practical aspects of vision care; from clinical management to rehabilitation options for visual diseases and disorders. For example, adaptation to enhanced, sharpened, images may influence low vision rehabilitation options such as computerized image enhancement for patients with reduced contrast sensitivity (Fullerton, Woods, Vera-Diaz & Peli, 2007; Fullerton & Peli, 2008; Leat & Mei, 2009; Peli & Woods, 2009). If patients adapt to the level of enhancement in a display, the perceived benefits of the enhancement could be diminished, as they may no longer appreciate it as enhanced. On the other hand, there are potentially beneficial effects of adaptation to sharpness. If patients adapt to the enhancement, the displayed images could appear more natural, so it would be more likely that they, as well as others with normal vision that may be using the enhanced television at the same time, may accept the enhancement.

Similarly, adaptation to blur may affect the subjective perception of blur and therefore the individual’s tolerance of blur (Legge, Mullen, Woo & Campbell, 1987). Tolerance of blur is crucial for the clinical success of certain ophthalmic devices, such as progressive addition lenses, multifocal contact lenses and intra ocular lenses (IOLs) used to replace the crystalline lens following cataract surgery. The designs of these devices are based on technological compromises that induce blur, by creating significant astigmatism in the periphery of progressive addition lenses, or by simultaneous refractive correction for distance and near vision in multifocal contact lenses or IOLs (Peli & Lang, 2001). Patients that adapt better to blur may perceive blurred images as more similar to best-focused images and therefore may be more tolerant of the blur induced by such ophthalmic devices.

To determine whether, and to what extent, adaptation to blur and sharpness plays a role in these or other clinical aspects of vision, the characteristics of the previously described adaptation curve need further evaluation. Webster and colleagues (Webster et al., 2002; Elliott, Hardy, Webster & Werner, 2007) have demonstrated the aftereffects of adaptation to various levels of computationally-induced blur (low-pass filtering) and sharpness (high-pass filtering). Using a forced-choice paradigm, they measured the aftereffects of adaptation by finding the filtered image that was perceived as best-focused following a period of adaptation (point of subjective neutrality, PSN). Their results show that adaptation modulates the blur or sharpness level of the image that is perceived as best-focused. They found that the level of the aftereffects increased when the magnitude of blur or sharpness of the adapting image increased. Increasing the magnitude of blur (or sharpness) of the adapting image increased the level of blur (or sharpness) of the image perceived as best-focused until it reached a level where the effect saturated. Adaptation curves, therefore, were described as sigmoidal shaped. In those studies, Webster and colleagues measured the effects of image filtering on up to three levels of blur and three levels of sharpness (Webster et al., 2002; Elliott et al., 2007). Thus only two levels of adaptation were tested along the increasing non-saturating portion of the range. To better understand the nature of the adaptation function, adaptation measurements to more finely sampled levels of blur and sharpness may be needed. Repeatability of the adaptation measurements using the procedure described by Webster et al. (2002) have not been reported yet.

Individual differences in adaptation to blur and sharpness have not been reported. Knowledge on whether there is individual variability in adaptation may affect the design of studies investigating the potential clinical or other applied aspects of blur adaptation. Subjective perception of image quality and image blur varies among people (Legras, Chateau & Charman, 2004; Chen, Artal, Gutierrez & Williams, 2007). Similarly, studies evaluating image enhancement devices found that there is individual variability in the preferred level of enhancement of the displayed images (Fullerton et al., 2007; Peli & Woods, 2009). The individual differences in preference for enhancement levels may be a consequence of differences in adaptation to sharpness.

Individual differences in the level of tolerance of blur have also been shown, and some people seem to be willing to cope with levels of blur much higher than their depth of focus limit (Atchison, Fisher, Pedersen & Ridall, 2005; Ciuffreda, Selenow, Wang, Vasudevan, Zikos & Ali, 2006; Woods, Colvin, Vera-Diaz & Peli, 2008; Woods, Colvin, Gambacorta, Vera-Diaz & Peli, 2009). Individual differences in tolerance of blur may be a consequence of individual differences in adaptation to blur. Individuals that adapt more to blur may subsequently perceive less blur and hence be more tolerant.

Investigating individual differences may also help explain the mechanism underlying adaptation, to define the normal range of adaptation, and to validate the measures as useful in other comparison studies (Wilmer, 2008). We hypothesized that adaptation measurements are repeatable and that there is individual variability in adaptation to blur and sharpness. In this study, we investigated the shape and individual variability of the adaptation curve to image blur and sharpness. We replicated the general findings of Webster et al. (2002) in a larger population, confirmed the continuous nature of the adaptation curve, characterized the adaptation curves as being tumbled-S shaped instead of sigmoid shaped function, and found individual variability.

2. Methods

The aftereffects of adaptation, i.e. the PSN (filtered image that is perceived as best-focused following a period of adaptation, to various levels of digitally induced blur and sharpness), were measured using the same original face image and a forced-choice procedure similar to Webster et al. (2002).

Image Processing

The original image used in these experiments was a grayscale image of a face provided by Michael Webster (2002) (Fig 1). The level of blur or sharpness - the relative slope (Δs) - describes the change, relative to the original image, of the slope of the image’s spatial frequency spectrum. Slope refers to the slope of the linear fit to the radially averaged amplitude of the spatial frequency spectrum on a log-log plot (Field, 1987). Images were digitally blurred or sharpened by varying the slope of the spatial frequency spectrum by up to Δs=±1.00 relative to the slope of the original image. The original amplitude spectral slope (α = −1.39 for the image used in this study) was modified by scaling the log of the spatial frequency coefficients of the Fourier transformed images proportionally to their log frequency. To accomplish this, a Fourier transform was performed on the original image, I(x,y).

Figure 1.

Examples of low-pass and high-pass filtered images used in the study. Negative Δs values represent those images that have been blurred and positive Δs values represent those that have been sharpened. There was no change in slope, Δs is zero, for the original images. These images were presented on a luminance-calibrated display, so the appearance in this figure may differ from that seen by the subjects.

$$f(u,v)=\mathfrak{J}[I(x,y)]$$ (1)

In the frequency domain, the amplitudes of each component were multiplied by ω^Δs, where

$$\omega =\sqrt{u^2+v^2},$$ (2)

Where u and v are the horizontal and vertical spatial frequencies, respectively. Hence the Fourier transform of the modified images was defined as

$$m\mathrm{\Delta }(u,v)=f(u,v)·{(u^2+v^2)}^{\mathrm{\Delta }\text{s}/2},$$ (3)

thus m_Δs (0,0), the dc component, is set to zero and then reset as stated in equation (4).

The modified spectrum was inversed-transformed back to the spatial domain to obtain the modified-slope image, M_Δs(x,y).

Following Webster et al. (2002) procedure, to ensure matching RMS contrast across all versions of the modified and original images, the RMS luminance of each filtered image was adjusted to that of the original image. Each pixel of the modified-slope image, M_Δs(x,y), was contrast-adjusted so that, the mean and standard deviation (std) of pixel values were the same as the original image, as follows:

$$P_{\mathrm{\Delta }s}(x,y)=\frac{M_{\mathrm{\Delta }s}(x,y)·\mathit{std}\left(I(x,y)\right)}{\mathit{std}\left(M_{\mathrm{\Delta }s}(x,s)\right)}+\mathit{mean}\left(I(x,y)\right)$$ (4)

Where P_Δs is the final modified image, and I is the original image. Without this RMS adjustment, subjects might use image contrast as a cue to discern the level of sharpness or blur in the stimuli (high-pass filtering increases RMS contrast and low-pass filtering decreases RMS contrast). This RMS adjustment results in changes to the spatial frequency content in ways that are not described strictly by the slope modification. The impact of these changes on adaptation may be important to understanding the phenomenon but is not addressed in this paper, where we strictly replicated the approach taken by Webster et al. (2002).

As a result of the image processing described above, sharpened images had pixels with values falling outside of the displayable range (0 to 255). When presenting these images, these pixel values were truncated to the displayable range. Fewer than 2.5% of image pixels were saturated for any modified image; and for images with Δs<+0.50 fewer than 1.6% of pixels were saturated. Prior to RMS adjustment, up to 17% of image pixels were saturated for the modified images between +0.01<Δs<+1.00, thus the RMS contrast adjustment also allows more of the pixels to be displayed veridically. Two-hundred such modified images were created from the original image by varying the global amplitude spectra slope from Δs=+1.00 to Δs=−1.00; in Δs=0.01 steps (Fig 1). These steps are sufficiently small as the JND for perception of blur and sharpness in these images was found in a small control study (n=3) to be on the order of Δs=+0.10 for sharp images and Δs=−0.05 for blurred images.

We implemented some modifications to Webster et al. (2002) procedure. We extended the range of processed images to Δs=±1.00 in steps of Δs=0.01 and tested adapting images with relative slopes of only up to Δs=±0.75, so that during the staircase procedures there was a wide range of images available above and below the adapting-image-Δs. We added a restriction to the allowed time to respond, so that responses were not accepted if entered after the adapting image had reappeared, to avoid unintended comparison to the adapting image. Trials that were rejected due to this restriction were repeated as the next trial in that staircase (due to the interleaving of the two staircases, as described later, that repeat may be shown at the next trial or later).

The images (250×250 pixels) were presented on a 17-inch-diagonal (36.1 × 27.3 cm; 800×600pixels) CRT monitor (Sony FD Trinitron) running at a frame rate of 100Hz controlled by a Cambridge Research System VSG 2/5 graphics card. The test and adapting images were presented in the center of a gray background (mean luminance of 20cd/m²). At the viewing distance of 160 cm, the images subtended 4×4deg. Monitor calibration, including gamma correction, is handled by the VSG software driver and was performed prior to experimental set up and repeated at frequent intervals thereafter.

Psychophysical Procedures

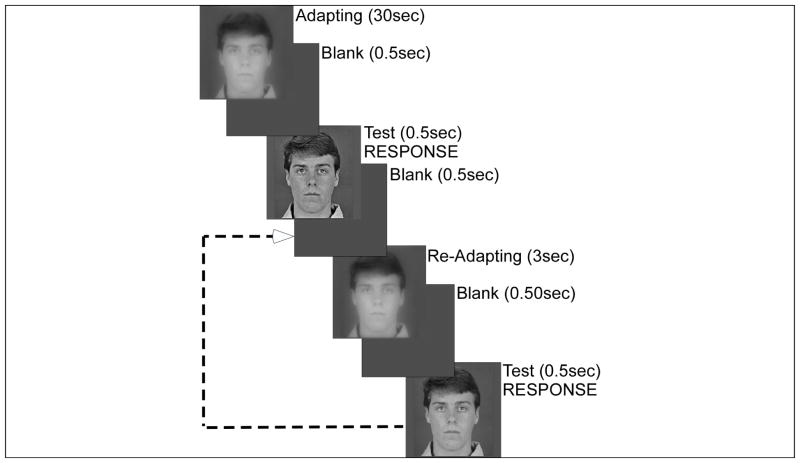
During a forced-choice task, subjects were asked to decide whether a briefly presented (500ms) test image was perceived to be “too blurred or too sharp compared to what you think is normal”. Subjects adapted to a blurred or sharpened image, “the adapting image” initially for 30s, followed by 3s re-adaptation periods (top-up time) after each test image (Fig 2). Subjects were shown examples of the original, sharpened and blurred images before testing began. Adapting and test images were separated by a 500ms “blank” period in which the stimulus was replaced with gray level matching the surround. Subjects were given instructions to respond to the 500ms “test image” with “too blurry” or “too sharp” using two keys on a keyboard number pad. Responses were to be made as quickly as possible, and before the reappearance of the top-up image, resulting in a response window of one second (500ms “test image” followed by 500ms “blank” period). This was done to decrease the probability of a potential limitation of this paradigm: that the subjects may inadvertently compare the test image to the following adaptation image rather than to what they internally perceive as the “normal” image. If the response was given before the adapting image reappears, the risk of comparison to the adapting image should be reduced. In addition, consistent and repeated instructions were given to not compare the test image with the adapting image. Most observers informed the experimenter that they believed they were not comparing to the adapting image, although they did report it was a difficult task to avoid such comparison. Therefore, a control experiment with modified instructions was conducted. The subject was told to compare the “test image” with the “long-standing” adapting image. Unlike the results for the adaptation curves shown below, there was a nearly perfect match (linear response, gain=0.96) between the relative slope of the adapting image and the relative slope of the PSN image. This suggests, at least for the more highly processed images (i.e. |Δs|>0.25), that subjects did not compare with the adapting image when instructed to determine if images were “too blurry” or “too sharp” based on their internal metrics. No feedback was given, as there was no correct answer in the task.

Figure 2.

Psychophysical procedure. Two-interleaved staircases began with one longer period of adaptation (30sec) to an image that had been either blurred or sharpened, followed by a blank (0.5sec) and a briefly presented test image (0.5sec). The observers answered whether the test image was too blurred or too sharp compared to their internal reference for image focus. Top-up, readapting images were shown between the brief test images presentations. In this example, the observers adapted to an image which had been blurred by a relative slope of −0.50 in both staircases. Only the starting level of the test target differed between the two staircases.

Each adaptation level was tested in a block consisting of 2 interleaved staircases of presentations to find the level of blur (or sharpness) appearing “normal” (PSN) for a single adapting stimulus. For each block, the spectral slope of the adapting image was modified relative to the original image by either Δs=±0.75; Δs=±0.50; Δs=±0.25; or Δs=0.00. One staircase started at a random high (sharpened) level and the other started at a random low (blurred) level. The mean of the last 10 reversals from each staircase was computed as the PSN and the values from the 2 staircases were averaged to derive the relative slope of the image that appears normal. Typically, there were about 100 trials per adapting level. The PSN was calculated for each subject at each of the 7 adaptation levels tested, to generate individual adaptation curves. Note that for some subjects there were fewer than 7 adaptation levels available as the data were not used if the upper and lower staircase differed in more than Δs=0.10; also a staircase was discarded if it appeared to not converge. A subgroup of subjects (n=16) participated in a test-retest condition, in which adaptation was tested again in a second session. In a separate control experiment, a subgroup of subjects (n=8) was tested at additional intermediate levels of blur and sharpness: Δs=±0.2; Δs=±0.15; Δs=±0.10; Δs=±0.05.

Subjects

Thirty nine subjects (21 female, median 32 years, range 19 to 71 years) with normal vision participated in the study. Subjects were screened for habitual visual acuity (VA) prior to enrollment (median 20/15) to ensure compliance with inclusion criteria (corrected VA of 20/20 or better). Three subjects were hyperopic (refractive error > +0.75D) (Mean refraction=+4.81±1.83), 18 were myopic (refractive error < −0.25D) (Mean refraction=−3.78±1.92), 17 were functionally emmetropic (−0.25D ≤ refractive error ≤ +0.75D) (Mean refraction=+0.03±0.13), with refractive error information unknown for one subject. Subjects wore their own spectacles or contact lenses during testing. An additional +0.50D was added in a clip-on to the correction of presbyopic subjects to compensate for the viewing distance. The study protocol was approved by the Schepens IRB. All subjects consented to participate in the study after explanation of the nature and possible consequences of the study.

Data analyses

Internal consistency was evaluated comparing the output values (averages of the last 10 reversals) from the 2 interleaved staircases for each run. There was no significant difference between the two staircases (repeated-measures ANOVA, F_1,34=0.022, p=0.88). In addition, Spearman rank correlations between the two staircases were high and significant (ρ≥0.82, p<0.001). This result indicates that the two staircases were converging to the same level even though the start levels were different. Therefore, the averaged raw data output for both staircases (i.e. the PSN for each adaptation level) was used to plot individual adaptation curves.

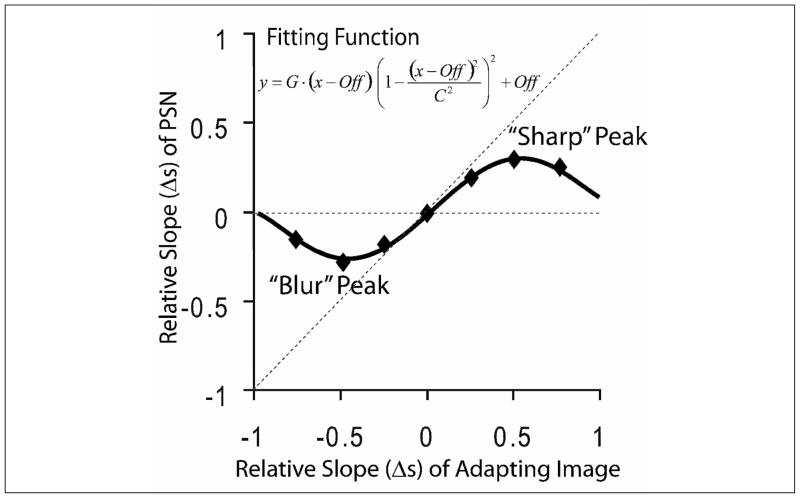
Individual variability was evaluated using the raw data for the entire adaptation curve, as described in Appendix A and the Results section. In addition, and in order to perform quantitative analyses of adaptation, raw data adaptation curves were fitted with a Tukey biweight function modified to describe our data (Fig 3). Initially, we attempted to fit adaptation curves with a logistic function, based on previous reports of adaptation curves being sigmoidally shaped (Webster et al., 2002) and our preliminary observations of the data. However, we soon noted that, although adaptation curves do show a peak, or plateau of PSN-Δs (the blurred or sharp level after which the subject will not adapt any more even if the images were made blurrier or sharper), PSN-Δs begins to return to zero for higher values of adapting-image-Δs. For several subjects, within the range of blurred and sharp images we tested (−0.75 to +0.75), the PSN-Δs gradually diminished, reaching a point after which adaptation no longer occurred (Fig 4). Three different zones may be observed in each side (blur and sharp) of the adaptation curves: an ascending zone (|PSN-Δs| increased as |adapting-image-Δs| increased), a plateau, and a redescending zone (|PSN-Δs| decreased as |adapting-image-Δs| increased, i.e. returned towards zero). Thus, an alternative fitting function was used to fit the data from the 39 subjects separately, and the adaptation function was defined as:

$$y=G·(x-\mathit{Off}){\left(1-\frac{{(x-\mathit{Off})}^2}{C^2}\right)}^2+\mathit{Off},$$ (5)

where y represents the relative slope (Δs) of the image chosen as the PSN and x represents the relative slope of the adapting image. G is the slope of the function in the region near x = 0, Off is the diagonal offset of the function, and C is related to the peaks of the function. Note that in preliminary analyses we used a 4 parameter function with independent horizontal and vertical offsets: G, C, x-offset and y-offset. However, we found the horizontal and vertical offset values to be highly correlated (ρ=0.80, p<0.001), so we subsequently simplified the fitting function and reduced the number of fitting parameters to three (G, C, Off) with minimal impact on the quality of the fit. For our purposes, equation 5 describes the data over the range −C+Off ≤ x ≤ C+Off, after these points there are further inflexions in the function (not shown in Figure 3).

Figure 3.

For the purpose of characterizing the individual adaptation functions, a modified Tukey biweight function was fitted to the individual adaptation data using a nonlinear least squares method. The following adaptation values were derived from the fittings: (1) XPeaks (X values for blurred and sharp images); (2) YPeaks (Y values for blurred and sharp images); (3) The slope of the function at adapting-image-Δs = 0, or Gain of adaptation; and (4) the intercept with the Y axis, YIntercept, at adapting-image-Δs = 0, which indicates asymmetry between adaptation to blur and sharpened images.

Figure 4.

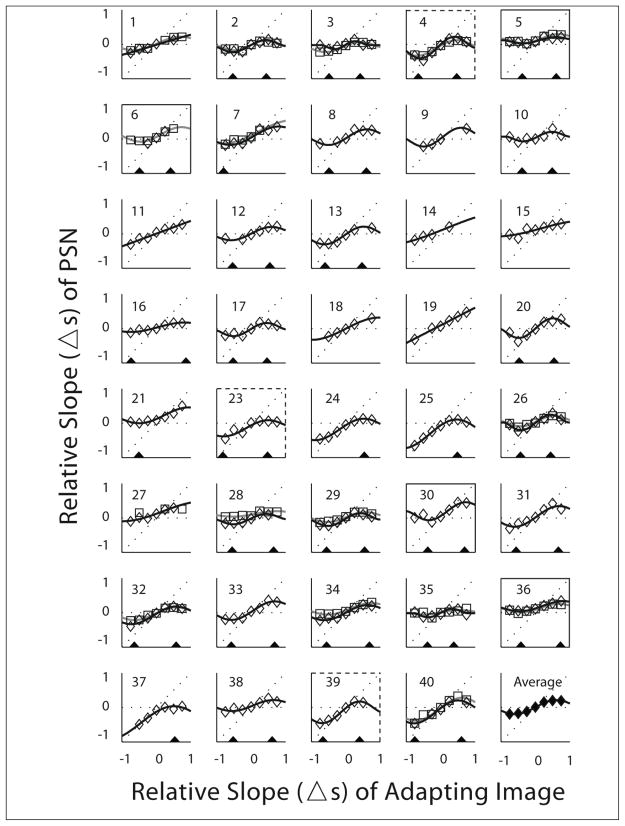
Blur adaptation raw data (diamonds) and fits (thin black curves) for the 39 subjects and repeated blur adaptation raw data (squares) and fits (thick grey curves) for 16 subjects (subject numbers 1–7, 26–29, 32, 34–36, 40). The final panel shows the average of the data for the 39 subjects (first sessions only if there was repeated data) and the associated fit. The adaptation curves were fit with a modified Tukey biweight function as described in the text. There was insufficient data (3 data points) to fit the first session of subject 6 and the second session of subject 27, note the criteria for using the fitting data was more strict (minimum of 6 data points, see text). This figure illustrates individual variability in the shape of the adaptation function. Black triangles were drawn to indicate the x-location (adapting-image-Δs) of the blur (left of zero in panel) and sharp (right of zero) peaks for those subjects that met the fitting data criteria. Note that peak locations were determined using all available data, so they may not match the peaks of the two session fits when the subject participated in the second session. Peaks were determined when there was data for at least six adapting-image-Δs levels (i.e. not for subjects 9, 14, 18). For some subjects (#11, 15, 19, 27) there was no peak within the measured range, while others had no blur peak (#24, 25, 37) and others had no sharp peak (#7, 21). For 7 subjects the level of adaptation to blur and sharpness was asymmetric; some showed more adaptation to sharpness (solid panel border) and others more adaptation to blur (dashed border).

This fitting function was chosen as it adequately described the empirical adaptation data. The function was derived from the theoretical influence curve of a robust estimator (Hampel, 1974). Since this function fits the measured blur adaptation so well, the visual system seems to be acting in the manner of a robust estimator, as discussed later. The function was fit using a non-linear least squares method in Matlab. Adaptation functions (Fig 3) may be characterized by the following adaptation values:

1. the X values of the peaks for the blurred and sharpened images, or breakdown points of the estimator. The X values of the “blurred” and “sharp” peaks, where the functions reached its maximum and its minimum, were computed as:

   $$X_{“\mathit{Sharp}”\mathit{Peak}}=\frac{C}{\sqrt{5}}+\mathit{Off},$$ (6)

   and

   $$X_{“\mathit{Blur}”\mathit{Peak}}=\frac{-C}{\sqrt{5}}+\mathit{Off}.$$ (7)

2. The Y values of the peak for blurred and sharp images, which describe the maximum and minimum values of adaptation for the subject, was defined as:

   $$Y_{“\mathit{Sharp}”\mathit{Peak}}=\frac{{0.8}^2}{\sqrt{5}}G·C+\mathit{Off}$$ (8)

   and

   $$Y_{“\mathit{Blur}”\mathit{Peak}}=-\frac{{0.8}^2}{\sqrt{5}}G·C+\mathit{Off}.$$ (9)

3. The slope of the function, or Gain of adaptation (G). (4) The vertical position of the adaptation curve, which related to the asymmetry of adaptation to blur and to sharpness. The Y axis intercept was defined as:

   $$Y_{\mathit{Intercept}}=\mathit{Off}\left(1-G{\left(1-\frac{{\mathit{Off}}^2}{C^2}\right)}^2\right).$$ (10)

Statistical analyses, described in results section, were performed using SPSS software (SPSS, Chicago, IL) version 11.5 for PC and Statistics Toolbox in Matlab (version 7.5.0.342 - 2007b).

3. Results

Despite some procedural differences, our adaptation data were largely in agreement with those reported by Webster et al. (2002). While all subjects (n=39) adapted to blur or sharpness, individual differences were apparent from the raw data adaptation curves (Fig 4). Within-subject variability of the adaptation curves (prior to fittings) was evaluated in a subgroup of subjects who repeated the adaptation measures during a second session (both measurements are shown in Fig 4 for these 16 subjects).

The three potential measurement error sources that may be expect to contribute significantly to the observed variance of the measures are: specific factor error, transient error, and random response error (Schmidt, Le & Ilies, 2003). In order to determine individual variability, we need to account for these potential sources of measurement error. The use of two interleaved staircases in each run allowed for a limited test of internal consistency over time. As described in the data analyses section, data from the two staircases (mean of the last 10 reversals) were not significantly different and were highly correlated, suggesting that this source of measurement error did not have a significant contribution. Subsequently, we evaluated reliability using test-retest repeatability, which is commonly used to assess the magnitude of transient error and random response measurement error sources (Schmidt et al., 2003), and we performed a novel analysis to investigate individual variability, as described in the Appendix. That analysis tested the hypothesis that within-subject variability would be greater than between-subject variability if there were individual differences in the shapes of the adaptation functions. In brief, the distribution of the within-subjects differences in the adaptation curves between the test and retest sessions (median 0.028; range 0.017 to 0.070) was compared with a distribution of all the between-subjects pairs of differences (median 0.055; range 0.012 to 0.166). Those two distributions were significantly different (Kolmogorov-Smirnov, z₁₃₅ = 2.30, p < 0.001). Thus, adaptation curves are repeatable and individual variability is demonstrated.

For further analyses we used the parameters obtained from the fittings made to all available data for each subject. We used two inclusion criteria: (1) only those parameters obtained from adaptation curves with a minimum of 6 raw data values were used (36 of the 39 subjects met this criterion); and (2) peak values were only used if they are within relative amplitude spectra slopes between −0.875 < adapting-image-Δs < +0.875 (these values are no more than half a Δs step of 0.25 outside the measured data range of adapting-image-Δs= ±0.75 that was examined in 0.25 increments). Both peak values were available for 26 subjects, only the sharp peak value was available for 3 subjects (#24, 25, 37) and only the blur peak value was available for 2 subjects (#7, 21). The adaptation values are summarized in Table 1.

Table 1.

Median, minimum and maximum values obtained from the fittings as described in the text.

parameter	Median	Min	Max	n
Gain	+0.52	+0.24	+0.90	36
Y Intercept	+0.01	−0.13	+0.14	36
X “Sharp” Peak	+0.53	+0.36	+0.82	29
Y “Sharp” Peak	+0.20	+0.03	+0.45	29
X “Blur” Peak	−0.53	−0.80	−0.34	28
Y “Blur” Peak	−0.16	−0.46	+0.03	28

Analyses of the repeatability and individual variability were also performed on the parameters obtained from the fitted functions for 11 of the 16 subjects who participated in a second session (those 11 that met the criteria described above). Spearman correlations between the test and retest sessions were significant for most parameters (Table 2). The coefficients of repeatability (twice the standard deviation of the observed differences between test and re-test scores) for each of the parameters were calculated with the repeated measures method suggested by Bland & Altman (1986). The coefficients of repeatability ranged from 28% to 47% of the range of all measured values for the fit parameters (Table 2), indicating that differences in these parameters between conditions may be found (i.e. not so noisy as to provide no value). Coefficients of repeatability were used in our study to evaluate asymmetry in the adaptation curves and will be useful in the design of future studies as they provide information for determination of sample size.

Table 2.

For the parameters of the adaptation curve fits from the test and retest sessions, the test and retest sessions (n=11) were significantly correlated (Spearman rank correlations) for all variables except X “Blur” Peak; the within-subject and between-subject distributions of difference scores were different for all except Gain and approached significance for Y Intercept (Kolmogorov-Smirnoff test), indicating that all but Gain were individual characteristics of the fits; and the coefficients of repeatability ranged from 0.28 to 0.47 of the measured range. Measured range is the difference between the maximum and minimum parameter values found for all fits.

Parameters	Spearman Correlations	Individual Characteristic	Coefficients of Repeatability	Measured Ranges
Gain	ρ10=0.86, p=0.001	z278=0.52, p=0.95	0.30	0.80
Y Intercept	ρ10=0.52, p=0.10	z278=1.32, p=0.06	0.09	0.27
X “Sharp” Peak	ρ10=0.73, p=0.01	z278=1.37, p=0.046	0.24	0.55
Y “Sharp” Peak	ρ10=0.73, p=0.01	z278=2.07, p<0.001	0.12	0.42
X “Blur” Peak	ρ10=0.45, p=0.17	z278=1.79, p=0.003	0.21	0.47
Y “Blur” Peak	ρ10=0.70, p=0.02	z278=1.45, p=0.03	0.17	0.50

To assess whether there were individual differences in these parameters, an analysis similar to that described for the raw data (see Appendix) was conducted. Here, the within-subject difference score was calculated as the absolute value difference between the parameter value for test 1 from that for test 2 (i.e. not Equation A1) and the between-subject difference scores were calculated for test 1 between all subjects (i.e. not Equation A3). A significant difference between the within-subject and between-subject difference distributions was found for all fit parameters except Gain and approached significance for Y_intercept (Kolmogorov-Smirnoff, z₂₇₈=1.32, p=0.06), which suggests that, apart from Gain, the fit parameters represent an individual characteristic of the fits.

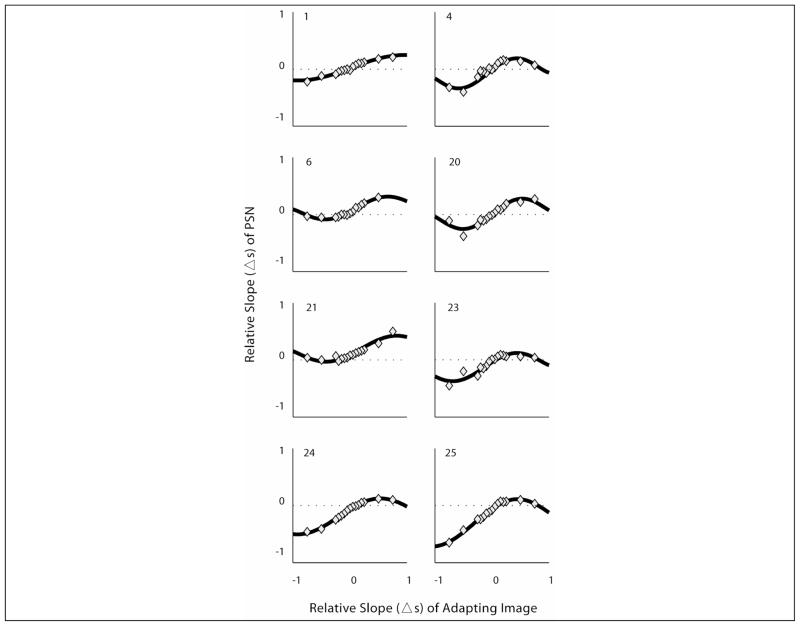
Adaptation had not been tested previously to levels on the central rising portion of the function in the range 0.25 < adapting-image-Δs < +0.25 (apart from the original image, Δs = 0). To investigate the shape of the adaptation function in that range, a subgroup of subjects (n=8) were tested at 10 additional relative slopes levels between −0.25 < adapting-image-Δs< +0.25, in steps of Δs=0.05. Adaptation functions obtained at these intervals were found to be smooth and continuous between the levels tested, confirming the presumed shape of the function (Fig 5). In these subjects, no differences were found in any of the parameters, including Gain, when adaptation functions were fitted with or without the additional adaptation levels (Wilcoxon signed-rank: z≤1.48, p≥0.14). Thus, adding adaptation levels on the ascending portion of the curve increases precision of the measurement but does not reveal additional information about the general shape of the adaptation function. However, for some subjects (e.g. 6, 21, 23) the additional points illustrate that the function is not linear in the −0.25 to +0.25 range (Fig. 5), with some saturation, consistent with the general behavior noted outside that range. Since testing at all these additional levels was not feasible (testing of one run at each level took 8min on average), we continued testing 7 levels of adaptation to characterize the adaptation curves.

Figure 5.

Blur adaptation curves for the 8 subjects who were tested at additional intermediate levels of adaptation between −0.50 and +0.50. Some saturation of the adaption function was apparent for subjects 23 and 25 for sharp adapting stimuli in this range, and for subject 6 in the blur adapting stimuli in this range.

About a third of the subjects showed lower peak levels to blur than to sharpness or vice versa (Fig 4), suggesting asymmetries between adaptation to blur and sharpness and different patterns of adaptation between individuals. Of the 26 subjects whose fitting data met all inclusion criteria (6 data points per adaptation curve and both peaks within adapting image Δs ± 0.87), 7 individuals (which included 4 of the 16 that participated in the repeatability study) showed differences between the blur and sharpness peak y values that were larger than the average of the coefficients of repeatability (>0.15, Table 2).

Our study was not designed to investigate whether adaptation effects were modulated by refractive error. With that proviso, and in response to a reviewer’s request, we analyzed the data and found that subject age and refractive error were not significantly correlated with the any of the fit parameters. Binocular visual acuity was significantly correlated with X_{“Sharp” Peak} (Spearman, ρ₂₈ = −0.43, p =0.02) and Y_{“Sharp” Peak} (ρ₂₈ = −0.37, p =0.05). No differences in the fit parameters were found between the 17 emmetropes and the 18 myopes (Mann-Whitney: z<0.97, p>0.35). As this post-hoc analysis comprised 24 comparisons (multiple comparison problem), the level of significance required for acceptance of a relationship may need adjustment. Though our study was not designed to investigate relationships between refractive error and blur adaptation, the relationships examined here suggest that any such relationships are modest, if at all.

4. Discussion

We replicated the main findings of Webster et al. (2002), illustrating the robustness of the phenomenon of adaptation and of their procedure to measure adaptation. We have shown for the first time that individual adaptation curves are repeatable, therefore further demonstrating their value. We confirmed the characteristics of the curves by measuring adaptation to smaller steps on the central rising portion of the curve and showed that the adaptation curve is indeed a continuous and dose dependent phenomenon. The adaptation curve data is well described in all subjects by a modified Tukey biweight function, and in most subjects (29 out of 39) it reaches the maximum levels of adaptation (peaks) within the range of relative slopes of the adapting images used in this study.

Our ultimate goal is to translate these findings to clinical applications; to investigate how adaptation to blur and sharpness may affect individuals’ visual experiences and patients’ clinical management and rehabilitation options. Many such practical questions in vision are questions of relation (Wilmer, 2008). For example, how does adaptation affect the perception of blur through ophthalmic devices such as multifocal lenses? How does adaptation affect the perception of blur during the emmetropization process? Or, how does adaptation to enhanced images affect the perception of image enhancement for patients with visual impairment? Inter-individual differences need to be demonstrated to investigate any such relations. Our study demonstrated that blur adaptation is a repeatable individual characteristic and documented individual variation in a context of qualitative similar adaptation behavior (Wilmer, 2008).

The magnitude of adaptation to blur in an individual may modulate their perception and therefore their tolerance of blur. Particularly, the peak or saturation of the adaptation response may be directly related to tolerance of blur; since increasing the blur content of the image does not elicit greater levels of adaptation, it is expected that individuals would not tolerate amounts of blur beyond that limit. Therefore, the level of a patient’s tolerance of blur may have important implications for the prescription and clinical success of ophthalmic devices. We have demonstrated in this study that there is individual variability in the magnitude of adaptation to blur which may modulate a person’s perception of blur in every day activities. Individual variability in tolerance of blur was previously demonstrated (Atchison et al., 2005; Ciuffreda et al., 2006; Woods et al., 2008; Woods et al., 2009). We have also previously shown evidence of a relationship between certain personality traits and tolerance of blur (Woods et al., 2008; Woods et al., 2009). Others have shown that variability in optical aberrations may also be related to tolerance of blur (Legras et al., 2004; Chen et al., 2007; Benard, Rouger & Legras, 2009). We hypothesize that a person’s magnitude of adaptation to newly induced blur, such as that induced by multifocal lenses, along with their personality traits and physiological characteristics, such as the amount and characteristics of ocular aberrations and the pupil size, could determine the person’s tolerance of blur. Individuals that perceive less induced blur would be more tolerant. Adaptation to blur may, thus, influence refractive error correction and development, and other clinical choices made when presented with degraded images.

Adaptation to sharpened images may also have significant implications in image enhancement rehabilitation options for people with visual impairments, as we discussed earlier. The individual variability found in the magnitude of adaptation to sharpened images should be considered when designing studies that evaluate the potential effect of image enhancement devices. Individual variability in the preferred level of enhancement of the displayed images has been found (Fullerton et al., 2007; Peli & Woods, 2009). Individual differences in preference for enhancement levels may be a consequence of differences in adaptation to various sharpness levels. Since blur adaptation has not been studied in visually impaired populations, further work is needed to understand the role adaption plays when people with visual impairments view enhanced images. In a separate study, we (Vera-Diaz & Peli, 2009) are investigating adaptation in patients with decreased vision due to central field loss caused by diseases such as macular degeneration.

Adaptation curves were previously described as sigmoid, with a middle linear response and two ends approaching saturation, i.e. the adaptation response would not increase even if the presented adapting images were blurrier (or sharper). However, we propose that the adaptation effect reaches a maximum level and then it begins to taper off until it disappears when the adapting images exceed certain level of blurriness or sharpness. The fitting function used in this study described the empirical data well but, more importantly; it conceptually described the phenomenon of adaptation. The fitting function used is similar in shape to the theoretical influence curve of a robust estimator (Hampel, 1974), when the adapting image is similar in appearance to the original image, the visual system "uses" this adapting image and adapts to it, whereas when the adapting image is perceived as looking very different from a normal image, it ceases to adapt, disregarding it. Similar response was previously noted for other visual behaviors, i.e., the induced effect (Landy, Maloney, Johnston & Young, 1995; Backus, Banks, van Ee & Crowell, 1999).

For 29 out of 39 individuals the adaptation curves begin to redescend within the range of blur and sharpness in the adapting images used in this study. For some of those (n=6), the adaptation curves completely taper off, i.e. no longer showing adaptation, at the highest level of adapting stimuli used in this study (Δs=±0.75). However, for two other individuals, the adaptation curves remained in the ascending zone within the range of blurred and sharp images tested in this study, failing to reach the peak, further emphasizing that there is individual variability. The fitting function used in this study described all these adaptation behavior options.

Subjectively, the appearance of the extreme blur and sharpened images used in this study is highly distorted. We suggest that the adaptation would eventually disappear in all subjects if they were shown “adapting” images that were sufficiently blurred or sharpened (as occurs with a robust estimator; Hampel, 1974). Subjects number 2–8, 12–13, 16–17, 20–25, and 28–40 appeared to demonstrate this behavior within the tested range of adapting images, at one or both ends (Fig 4). In addition, when adapting to images with larger angular sizes, a similar drop in the adaptation response may occur with images that are blurred or sharpened by amounts smaller than the Δs=±0.75 used in this study, as suggested by Vera-Diaz & Peli’s (2009) data. We hypothesize that the difference in the spatial frequency content of the (modified) adapting images compared to the (original) normal image may, therefore, be a determinant for the magnitude of the adaptation response. A drop in the adaptation response may occur earlier in the adaptation curves (i.e. with images that have lower levels of induced blur or sharpness), when the spatial frequency content of the adapting image is shifted towards lower spatial frequencies by magnification (Vera-Diaz & Peli, 2009), as distortions may be more visible and images appear further from normal with low levels of filtering. The spatial content of the extremely processed images may not even overlap with the spatial content of the original image, therefore adapting to those images will no longer modify the perception of the original image as the original image is no longer contained in the processed image.

A number of individuals (7out of 26) showed asymmetric adaptation to blur and sharpness, in either direction (Fig 4). Until now, adaptation to blur and sharpness were evaluated together under the implied assumption that they reflect the same underlying mechanism (Webster et al., 2002). The asymmetries found in this study may represent differences in the mechanisms underlying adaptation to blur and adaptation to sharpness. However, a more plausible explanation is that adaptation may be driven by a limited range of spatial frequencies, i.e. mid-spatial frequencies, and the range of spatial frequencies that drive adaptation may be different for each individual (Haber, Ballardini & Webster, 2007). Another potential reason for the asymmetry we found may be that the assumed symmetry in the stimulus appearance between the low-pass and the high-pass filtered images may only hold for a limited range of blur and sharpness (i.e. a level of induced blur (e.g. Δs=−0.25) may not be equivalent to the same level of induced sharpness (e.g. Δs=+0.25)), hence inducing asymmetries in adaptation to the blurred and sharpened images, particularly at the extremes. Asymmetries between the extremely sharp and blurred images could be a consequence of the RMS normalization process used in this experimental paradigm, as the extremely sharpened images have relatively more contrast attenuation at lower frequencies compared to the attenuation at high frequencies found in the blurred images. However, the average grouped data shows no asymmetry in these responses (Fig 4 and Table 2).

Some subjects informally said that they had used specific features in the image, such as hairline, eye, mouth, or the collar of the shirt, to decide whether the test image is blurred or sharp. Other subjects said that they had used the entire image, rather than details of the image, to make their decision. And others said that they used the “brightness” of the image, or even the “colors” to make the decision (even though the images were monochrome). The use of the “brightness” of the image by some subjects suggests that the adjustment of RMS may have not prevented the existence of cues in differentiating the processed images. It is important to realize that equating of the RMS, as done in this procedure, does not prevent residuals in the image that may provide such clues. In addition, as mentioned in the methods section, values falling outside of the displayable range were truncated (in sharpened images). The number of points truncated was small, particularly in the images with +0.01<Δs<+0.50. However, many of those points were around the eyes (the rest mostly in the lowest part of the image, which was unlikely to influence perception). A number of subjects used the eyes to make their decision. These subjects may have used the reduced contrast in the eyes area, which makes the eyes look sharper overall, found in the extremely sharpened images as a cue to make their decision. In control studies, we found similar adaption curves when the adapting image was rotated 180 degrees relative to the test image (Vera-Diaz, Goldstein & Peli, 2008), suggesting that local adaptation is not the cause of this phenomenon, and thus not an effect that is used by subjects.

Appendix

A novel method was developed to test whether the apparent between-subject differences (i.e. Fig 4) found in this study represent true individual differences in the adaptation curves. Even though there are available techniques to evaluate individual differences in single scores, to our knowledge there is no technique that evaluates individual differences in an entire function. We propose this technique whereby a single score is represented through an error score, a root mean square error.

For the 16 subjects who had the adaptation curves measured twice, we compared the within-subject difference, D_jj to the between-subject difference, D_jk, where j and k are subjects’ numbers. Within-subject differences were a test-retest estimate of the measurement noise. Between-subject differences estimate the variability of the adaptation curves of different subjects. If the apparent between-subject difference in adaptation curves were due only to measurement noise, the between-subject difference and the within-subject difference would be no different. We hypothesized that, in general, the within-subject difference would be smaller than the between-subject difference.

The within-subject difference (D_jj), the differences between the test and retest adaptation values calculated for the entire adaptation curve of each of the 16 subjects, was defined as:

$$D_{jj}=\sqrt{\frac{{\displaystyle \sum _{i=1}^{n_{jj}}}{(y_{j1i}-y_{j2i})}^2}{n_{jj}}},$$ (A1)

where i was the adaptation level or relative slope of the adapting image (e.g. Δs=+0.50); n_jj was the number of paired adaptation levels available for this subject; y_j1i was the adaptation response or PSN (Fig 3) for subject j in the first session (test) at adaptation level i; and y_j2i was the PSN in the second session (retest). Hence, the adaptation values for the test (y_j1i) session are compared to the adaptation values for the retest (y_j2i) session. This produced 16 D_jj estimates.

The between-subject difference (D_jk), calculated as all possible pairs of between-subject differences in the adaptation curves of the same 16 subjects, was defined as:

$$D_{jk}=\sqrt{\frac{{\displaystyle \sum _{i=1}^{n_{jk}}}{(y_{j1i}-y_{k2i})}^2}{n_{jk}}},$$ (A2)

for j ≠ k

for j = 1 to 15

for k = j+1 to 16

where y_k2i was the PSN of subject k in the second session at adaptation level i and n_jk was the number of paired adaptation levels available for this comparison of subjects j and k. This compares the response function at the first session of subjects to the response function at the second session of other subjects, with each subject only compared to each other subject once. Such combinations of pairs of these 16 individuals were computed for each adaptation level, resulting in 120 D_jk estimates.

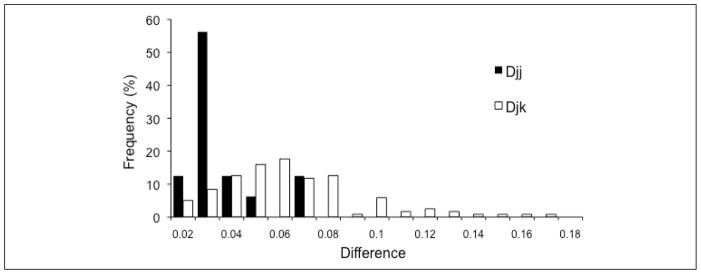
The distributions of within- (D_jj) and between- (D_jk) subject differences are shown in Fig 6. Consistent with our hypothesis, between-subject differences (median 0.055; range 0.012 to 0.166) were larger (Mann Whitney U, z₁₃₅=4.13, p<0.001) than the within-subject differences (median 0.028; range 0.017 to 0.070) and the distributions had different shapes (did not come from the same population, Kolmogorov-Smirnov two-sample test, z₁₃₅ = 2.30, p < 0.001).

Figure 6.

Frequency distributions (normalized to percentages) for the within-subject (D_jj) and between-subject (D_jk) differences. The two distributions were significantly different (p=0.001).

In addition, for the remaining 23 subjects that did not participate in the test-retest aspect of the study, between-subject differences (D_lm) were also calculated. Those differences were defined as:

$$D_{lm}=\sqrt{\frac{{\displaystyle \sum _{i=1}^{n_{lm}}}{(y_{l1i}-y_{m1i})}^2}{n_{lm}}},$$ (A3)

for l ≠ m

for l = 1 to 22

for m = l+1 to 23

as there was only one session for each of these subjects, this compares the response function of each subject to the response function of every other subject. This produced 253 D_lm estimates. Equation A3 was also used to calculate between-subject differences for the 16 subjects from the retest component using only data from their first sessions, producing 120 D_lm estimates. The between-subject differences of the 23 subjects (median 0.0.062; range 0.009 to 0.181) were larger (Mann Whitney U, z₃₇₂=3.18, p=0.001) than the between-subject differences of the 16 subjects who participated in the two sessions (median 0.054; range 0.013 to 0.132), and those distributions were of different shape (Kolmogorov-Smirnov two-sample test, z₃₇₂ = 1.53, p =0.018). This result does not pertain to the test-retest repeatability (within-subject differences) of those 23 subjects.