Abstract
Conformational transitions are functionally important in many proteins. In the enzyme adenylate kinase (AK), two small domains (LID and NMP) close over the larger CORE domain; the reverse (opening) motion limits the rate of catalytic turnover. Here, using double-well Gō simulations of E. coli AK, we elaborate on previous investigations of the AK transition mechanism by characterizing the contributions of rigid-body (Cartesian), backbone dihedral, and contact motions to the transition state (TS) properties. In addition, we compare an apo simulation to a pseudo-ligand-bound simulation to reveal insight into allostery. In Cartesian space, LID closure precedes NMP closure in the bound simulation, consistent with prior coarse-grained models of the AK transition. However, NMP-first closure is preferred in the apo simulation. In backbone dihedral space, we find that as expected, backbone fluctuations are reduced in the O to C transition in parts of all three domains. Among these “quenching” residues, most in the CORE, especially residues 11-13, are rigidified in the TS of the bound simulation, while residues 42-44 in the NMP are flexible in the TS. In contact space, in both apo and bound simulations, one nucleus of closed state contacts includes parts of the NMP and CORE; CORE-LID contacts are absent in the TS of the apo simulation but formed in the TS of the bound simulation. From these results, we predict mutations that will perturb the opening and/or closing transition rates by changing the entropy of dihedrals and/or the enthalpy of contacts. Furthermore, regarding allostery, the fully closed structure is populated in the apo simulation, but our contact results imply that ligand binding shifts the preferred O/C transition pathway, thus precluding a simple conformational selection mechanism. Finally, the analytical approach and the insights derived from this work may inform the rational design of flexibility and allostery in proteins.
Keywords: Allosteric transition, adenylate kinase, coarse-grained model, transition state ensemble, enthalpy-entropy compensation
Introduction
In most allosteric proteins, ligand-binding events at two distant sites are thermodynamically coupled.1 Conceptually, allostery is typically described by the conformational selection model or the induced fit model. In the conformational selection model, which is based on the classical Monod-Wyman-Changeux model,2 the allosteric effector (e.g. protein or ligand) selects a small population of the bound protein conformation from the apo ensemble, driving the equilibrium toward the bound conformation.3,4 In the induced fit model, originally proposed by Koshland,5 the effector binds to the apo conformation and nucleates a conformational transition from the binding site; this mechanism may be more common for protein-macromolecule interactions.
While these conceptual models provide a starting point to understand allostery, many questions remain regarding physical allosteric mechanisms in real proteins.6 Recent works are building evidence to support the hypothesis that evolution has selected precisely controlled motions in allosteric proteins. For example, motions in apo-proteins tend to parallel closure pathways associated with ligand binding.7-9 In addition, dynamics at different timescales appear to be intimately linked.10 Furthermore, in large allosteric proteins, both localized motions and large-scale rigid-body motions appear to be organized into dense cyclic networks for long-range structural and dynamic coupling.11 A full understanding of allostery requires detailed experimental and computational characterization. For example, transition path sampling and free energy calculations of CheY have revealed a mechanism intermediate between the conformational selection and induced fit extremes,12,13 and src kinase appears to follow two different transition pathways, one involving substantial unfolding and refolding and another “direct” path involving mainly contacts unique to the inactive and/or active structures.14 In addition, it is important to note that sampling of the bound conformation in the absence of ligand does not guarantee that conformational selection is the fastest pathway in the presence of ligand.15
In this work, we investigate the mechanism of the structural transition of adenylate kinase (AK). While AK lacks an allosteric site remote from the substrate sites, the gating of product release by the opening conformational transition16 is analogous to allostery. This reflects the fact that flexibility can be important to both catalysis and allostery in proteins.17 Specifically, we investigate how different types of motion in the O/C transition, as well as ligand binding, cooperate to determine the allosteric mechanism and the rate of the conformational transition. To do this, we simultaneously analyze multiple small- and large-scale motions in coarse-grained AK simulation trajectories with hundreds of independent transitions.
Previously, crystal structures of apo and bound AK revealed that upon substrate binding, two small domains (LID and NMP) close over the larger CORE domain; that is, the two predominant states are open (O) and closed (C).18 The substrates ATP and AMP bind at the CORE-LID and CORE-NMP interfaces, respectively. NMR experiments have shown that the reverse (C to O) transition limits the catalytic turnover rate.16 Regarding the allosteric mechanism, single-molecule FRET19 and unbiased all-atom MD simulations20 show that closed and/or near-closed conformations are populated in the absence of ligand. In addition, both experiments and computations support the hypothesis that apo-AK dynamics parallel the O ⇔ C pathway.21,22 Concerning the order of domain closure, various works support strict LID-first closing20,23 and utilization of both LID-first and NMP-first closing pathways.24,25
In addition, previous works have sought to identify key residues or contacts that facilitate or resist the O ⇔ C transition. For example, dynamic importance sampling has suggested that a few contacts in the LID-NMP interface region progressively ‘zip’ in the closing transition and thus determine the O/C rate.25 In addition, normal mode analysis26 and an earlier mixed Gō model23 have suggested that a few residues must locally unfold or ‘crack’ to relieve strain associated with the LID and NMP domain motions. By contrast, recent experiments have suggested a different (but not exclusive) mechanism wherein functionally important dynamics are distributed among many residues. For example, swapping the entire LID and NMP domain sequences (but not just the CORE-LID hinges) between homologous mesophilic and thermophilic AKs interconverts the catalytic properties (and thus presumably the O/C rate).27 In addition, hydrogen exchange has revealed that ligand binding quenches local unfolding in most of LID and in parts of CORE and NMP,28 and mutations perturbing LID unfolding have suggested that functional LID dynamics are cooperative.29 Furthermore, fast dihedral fluctuations important to the O ⇔ C rate are distributed broadly among LID, NMP, and the interdomain hinges.10 In this work, we elaborate upon previous investigations of the conformational transition mechanism. By simultaneously characterizing rigid-body motions, fast and slow (unfolding) dihedral motions, and protein-protein and protein-ligand contact breaking/formation events in coarse-grained simulations of the AK conformational transition, we identify a range of functionally important degrees of freedom. From this, we develop a qualitative framework to explain how the different motions cooperate to modulate conformational transition rates and functional properties. A similar detailed characterization of motions for protein kinase A suggested a mechanism in which local rigidification associated with ligand binding nucleates the closing transition of the entire molecule in a dynamic hierarchy.30
To simulate the AK transition, coarse-grained models provide a useful first approximation. While they lack the rigor of atomistic simulations,20,25 Coarse-grained approaches can simulate large-scale conformational transitions without constraints so that the trajectory can be meaningfully projected onto any arbitrary reaction coordinate representing a particular motion in Cartesian, dihedral, or contact space. We employ the double-well Gō model, which mixes single-well potentials based on the native contacts of the O and C crystal structures, respectively, of E. coli AK. According to one interpretation, coarse-grained models such as the double-well Gō model successfully capture gross features of large-scale structural transitions in proteins because structural topology determines the global properties of biomolecules.31-33 To mix the O and C potentials, we use the exponential averaging approach of Best et al.34 to calibrate the relative population of the O and C states and the frequency of transitions between them. To assess the kinetic contributions of different motions, we first partition the simulation data into O, C, and approximate transition state (TS) sub-ensembles using a contact-based reaction coordinate. For any given reaction coordinate, we characterize the position of the TS ensemble relative to the average position of the O and C sub-ensembles. We characterize rigid-body motions by interdomain distances among CORE, LID and NMP domains. In addition, we assess backbone dihedral fluctuations for each residue by calculating the O, C, and TS ensemble probabilities of the native Cα-scale dihedral conformation. Furthermore, we analyze contact motions at both the level of entire domain and interface contact sets and at the level of individual contacts. To assess the impact of ligand upon the conformational transition mechanism, we compare two variants of the AK double-well Gō model: an “apo” model including only the protein-protein residue contacts in the O and C crystal structures, and a “bound” model with selected ligand-mediated interactions added to the C potential. Based on the results, we qualitatively describe the enthalpic and entropic characteristics of the TS, predict residues and contacts that facilitate or resist the opening and/or the closing transitions, and postulate a general allosteric mechanism. Our general analytical approach may be useful to elucidate structural transition mechanisms for other allosteric proteins toward guiding the engineering or modification of allosteric properties.
Results
Calibrating the model
To construct the bound model, we add selected ligand-mediated interactions to the C potential. We calibrate our double-well Gō model so that the stability of the closed state is reasonable in the presence of ligand and the relative population of O and C states in the bound and apo simulations is comparable to experimental measurements. In addition, we compare several independent simulations of the bound model to ensure that the simulation is converged and the uncertainties of motional statistics are small enough to be useful.
Regarding stability, we calibrate the distance to the C crystal structure in single-well simulations using the C Gō potential (including ligand-mediated interactions) and with the generic bond angle potential,35 which will be used in double-well simulations, turned on. We use C as the reference since it is more compact than O. In previous atomistic simulations of the closed structure of AK,20 the native basin is located at about 2.0 Å rmsC (Cα rmsd to the closed crystal structure). In addition, for prior double-well Gō models of other proteins,34,36 the fraction of native contacts was calibrated to about 0.9. By rescaling all contacts from the raw O and C potentials by a factor of 2.5, we achieved similar values of rmsC and QC,all (the fraction of closed state native contacts) in the closed state single-well simulation (Figure S1A-B). Previous double-well Gō models of other proteins typically use a scaling factor of 1.7; this produces rmsC ~ 4 Å for the closed state single-well simulation of AK (data not shown). Figure S1C-D shows that in single-well Gō simulations of the O state, the contact energy scale of 2.5 produces rmsO ~ 2.5Å, and QO,all ~ 0.88. Interestingly, even though the O single-well simulation contains no information about C, it also samples to within 4 Å of the C crystal structure. Likewise, we use the scaling factor of 2.5 for the contacts in the apo simulation.
In addition, we calibrate the exponential averaging35 parameters for mixing O and C single-well Gō potentials so that in the bound simulation, the equilibrium slightly favors the closed over the open basin, as observed experimentally,16,19 resulting in an approximate Keq(O ⇒ C) of 3.32. For a given simulation, we define Keq as the ratio between the number of structures in the closed and open basins. To reflect the slight stabilization of C upon ligand (ATP and AMP) binding measured by single-molecule FRET,19 we calibrate the apo simulation to a slightly smaller Keq of 1.32. We do not calibrate the frequencies of closing and opening transitions to the slow experimental values (on the order of ms−1), but we calibrate the barrier height so that the protein occupies the O or the C basin approximately 99% of the time. The precise simulation setup and parameters for bound and apo forms are described in the methods.
Furthermore, we compare independent 750-ns (50 million time step) simulations of the bound model to determine an appropriate simulation time (Table S1). The 8 simulations include Oxtal and Cxtal, which start from the O and C crystal structures, respectively, and O1-3 and C1-3, which start from randomly chosen structures from the O and C basins, respectively, of the initial Oxtal simulation. Among these 8 simulations, the standard deviation of Keq is less than 1, and the O/C transition frequency varies by about 10%. Most strikingly, as discussed later in the results, motional properties of individual residues and contacts are highly consistent (≤ 5% standard deviation) among simulations. Thus, we choose 750 ns for the length of simulations in this work and rely primarily on the Oxtal simulation data for later presentation and discussion of the bound form.
Overview of double-well simulations
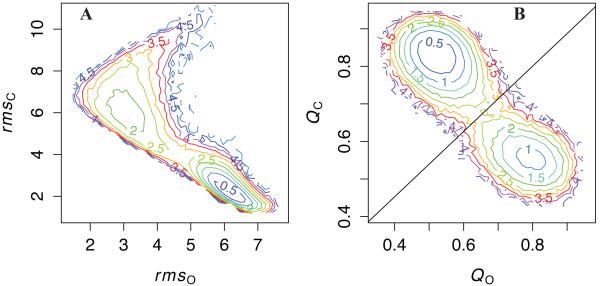
Figure 1 projects the bound simulation data (Figure S2) onto two pairs of reaction coordinates. The estimated potential of mean force PMF(rmsO, rmsC) reveals AK’s global behavior in Cartesian space, and PMF(QO, QC) reveals AK’s behavior in contact space. By contrast to QO,all and QC,all, we calculate QO and QC based on native contacts unique to the O and C crystal structures, respectively, in order to more readily separate the O and C free energy minima. Figure 1A shows that in this simulation, AK samples configurations within about 1.5 Å rmsd to both the O and C crystal structures. The closed well is narrowly defined in Cartesian space, sampling a range of about 2-2.5 Å rmsd from the C crystal structure, consistent with the single-well simulations (Figure S1). By contrast, the O well is centered about 3 Å from the open crystal structure, and configurations up to 4-5 Å away from the crystal structure are sampled; that is, conformations more open than the O crystal structure are populated. In addition, panel B shows two distinct wells in contact space: the open well near (0.8,0.55) and the closed well near (0.5,0.85), separated by a free energy barrier of about 2.25 kcal/mol. The maximum of either QO or QC is around 0.85(0.90), slightly lower than the typical values for QO,all and QC,all observed in the single-well simulations (Figure S1); however, Figure S3 shows that the double-well simulations are consistent with the single-well simulations in PMF(QO,all, QC,all). Thus, the distinct contacts of O and C are slightly less stable than the common contacts. Finally, Figure S4 shows that the uncertainty of PMF energies in both Cartesian and contact space is < 0.05 kcal/mol in the native basins and ~0.1 in the transition region.
Figure 1. The bound AK transition in global Cartesian and contact reaction coordinates.
A: Estimated potential of mean force (PMF) based on projection of simulation data onto rmsO and rmsC reaction coordinates, where rmsO(C) is the Cα root mean square distance to the O(C) crystal structure. B: Estimated PMF(QO, QC), where QO(C) is the fraction of native contacts unique to the O(C) crystal structure. The diagonal line shows the calculated transition separatrix, QC = 0.87QO + 0.335. Contours are spaced at 0.5 kcal/mol intervals in both PMFs. Uncertainties in the energies of these PMFs are shown in Figure S4.
By comparison to the bound simulation, the apo simulation (Figure S5) samples similar ranges of configurations in (rmsO, rmsC) and (QO, QC) spaces as the bound simulation. The C well is centered near 2 Å rmsd, just as in the bound simulation. That is, these results suggest that even in the absence of ligand, the closed structure is a populated state, which is consistent with the single-molecule experimental result that C is the favored state in solution.19 However, more detailed residue-level comparisons are needed to differentiate the conformational transition mechanisms under apo and bound conditions.
Since the contact energy scale required to achieve a stable closed state is higher than the factor of 1.7 typically used in previous Best/Hummer Gō models,34,36 we briefly examine the results of a 750-ns “bound-1.7” simulation with the contact energies scaled by this factor in Figure S6. Panel A shows that relative to the bound-2.5 simulation, the bound-1.7 simulation shows substantially larger excursions from both O and C crystal structures, with the C well typically 3.5 Å away from its crystal structure and the open well commonly sampling “super-open” configurations 6 Å or farther from its crystal structure. In addition, panel B shows that the bound-1.7 simulation conditions reduce the values of QO and QC in the O and C wells to about 0.65 and 0.75, respectively. We comment further on the relevance of simulations with different energy scales in the discussion.
Defining the O, C, and transition state (TS) ensembles
To quantify the kinetic contributions of different kinds of motions, we separate a simulation trajectory into ensembles of structures representing O, C, and TS dynamics and compare these three ensembles. While O and C ensembles are readily identifiable based on the minima in Figure 1B, the separatrix (dividing line) between them is less obvious. As discussed in the works of Hummer et al.,35,37 a separatrix between two states should have an optimal selectivity for structures that lie along “reactive” transitions that cross between the O and C wells (defined by the peaks (near 0.85) in histograms for QO and QC, respectively) without re-crossing. We define a separatrix s simply as the line
and optimize w and b to maximize pTP(w,b), that is, the probability of capturing reactive configurations;
where Nr is the number of reactive configurations in a given (w,b) bin and Neq is the corresponding number for the equilibrium distribution. Bin sizes are 0.01 in the w direction and 0.025 in the b direction. As expected, Figure S7A shows a sharp peak for pTP along the b coordinate separating O and C wells at a given w, but the maximum of pTP varies by 0.05 or less over a wide range of w. That is, pTP is weakly sensitive to the relative weights of O and C contacts; pTP,max = 0.34 at (w,b) = (0.87,0.10). Figure 1B indicates that the separatrix (diagonal line) cleanly divides the O and C wells. Given an optimized w and b, we define initial open and closed ensembles by s - b < −0.1 and s - b > 0.1, respectively.
We further optimize pTP by refining the sets of contacts used to define s. We choose a new separatrix (s’ = Q’C − w’Q’O) = b’, where Q’O and Q’C are defined based on “characteristic” contacts of the O and C ensembles, respectively. For each contact, we calculate pO and pC, the probability of the contact being formed in the O and C ensembles, respectively. Figure S8 shows that some of the contacts unique to the O and C crystal structures (x and +, respectively) are approximately equiprobable in O and C ensembles, probably because their interresidue distances differ little between the O and C crystal structures; thus, correcting for these contacts should improve the capturing of O/C transitions. We then define the O-characteristic and C-characteristic sets by contacts for which pO-pC ≥ 0.2 and pC-pO ≥ 0.2, respectively, corresponding to the lower and upper triangles of Figure S8.
Indeed, when s’ is used to optimize pTP, we obtain, a higher pTP,max of 0.42 at (w’,b’) = (0.47,0.28) (Figure S7B), which is comparable to pTP values of ~0.4 obtained in double-well Gō models of other proteins. Though the O and C ensembles are only weakly sensitive to the precise separatrix, we redefine them based on s’, and for all calculations in this work, we define the transition state ensemble (TSE) as structures that occupy a reactive transition path and for which s’ = b’ ± 0.05. The resultant TSE comprises 255 structures from 117 closing transitions and 224 structures from 116 opening transitions; thus, opening transitions may cross the barrier more quickly (and thus have fewer frames per transition) than closing transitions. Furthermore, for the apo simulation, we obtain pTP,max = 0.35 at (w’,b’) = (0.91,0.07).
Finally, we characterize the fractional progress of different reaction coordinates between O and C ensembles to assess the TSE properties. For a reaction coordinate x, we define
| (1) |
where ⟨x⟩E is the average value of x in ensemble E. fTS,x ~ 0 indicates that x is O-like in the TSE, while fTS,x ~ 1 indicates that x is C-like in the TSE.
Cartesian space
Table 1 applies fractional progress analysis (Eq. 1) to reaction coordinates representing AK motions in Cartesian space. For example, a typical TS structure has rmsC ~ 3.76 Å, which is about 64% closed relative to the 3.97 Å contraction of rmsC from the O to the C ensemble. rmsO behaves similarly; it is about 61% increased in the TS relative to the O to C change. In addition, interdomain distances contract substantially from O to C. In the TS, CORE-LID center of mass distance has contracted 83% of the way from O to C, while the corresponding CORE-NMP and NMP-LID distances have each contracted only 29%. Finally, we find that for each of the Cartesian variables in Table 1, the closing and opening transition sub-ensembles differ by less than 0.02 in fTS, suggesting that AK follows structurally similar paths in the two different directions; that is, there is good microscopic reversibility.
Table 1. Kinetic properties of Cartesian reaction coordinates.
| progress | ensemble-averaged value (Å) |
||||
|---|---|---|---|---|---|
| variable | O | TS | C | C-O | fTS |
| rms O | 3.26 ± 0.63 | 5.01 ± 0.49 | 6.13 ± 0.37 | 2.88 | 0.61 |
| rms C | 6.32 ± 1.21 | 3.76 ± 0.53 | 2.35 ± 0.47 | −3.97 | 0.64 |
| r CM,core-nmp | 22.50 ± 0.47 | 21.94 ± 0.57 | 20.53 ± 0.37 | −1.97 | 0.29 |
| r CM,core-lid | 27.94 ± 1.95 | 23.02 ± 1.20 | 21.99 ± 0.53 | −5.96 | 0.83 |
| r CM,nmp-lid | 32.90 ± 3.12 | 27.67 ± 1.61 | 23.67 ± 1.65 | −9.23 | 0.29 |
rCM,dom1-dom2 refers to the distance between the centers of mass of domains dom1 and dom2. Standard deviations reveal the variability of each reaction coordinate in each ensemble. fTS is an average of the values for the closing and opening transitions.
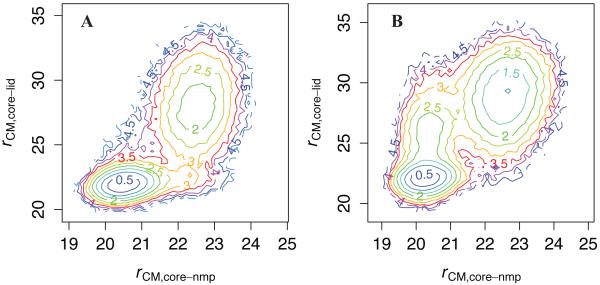
Figure 2 further illuminates the relationship between NMP and LID Cartesian motion. As suggested by Table 1, panel A shows that the preferred transition pathway in the bound simulation involves LID-first closure, passing through the region of (22.5,22). By contrast, panel B suggests that in the TSE of the apo simulation, NMP is more fully closed than LID. That is, ligand binding appears to substantially influence the closure mechanism. Through more detailed residue-scale analyses, especially of interdomain contacts, we will further investigate the molecular origin of the differential closure pathways in the presence versus the absence of ligand. In addition, as with the PMFs along global reaction coordinates (Figure 1), the uncertainty of the PMF energies in Figure 2 is less than 0.05 kcal/mol in the native basins and ~0.1 in the transition region (Figure S9).
Figure 2. NMP vs. LID motions in Cartesian space in bound and apo simulations.
PMF along rCM,core-nmp and rCM,core-lid. A: bound simulation. B: apo simulation. Uncertainties are shown in Figure S9.
Backbone dihedral dynamics
Figure 3 quantifies the contributions of large-scale dihedral dynamics of individual residues to the TSE. Large-scale dihedral fluctuations correspond to local unfolding measured by hydrogen exchange.28 We assess large-scale fluctuations with the simple metric pfolded,i, the probability that pseudodihedral angle αi-1,i is in the same rotamer (within 60°) as the native value. It is important to note that the statistical dihedral potential from Karanicolas and Brooks,38 which is used in this work, depends on the native sequence at positions i-1 and i but not upon the native structure of either O or C.
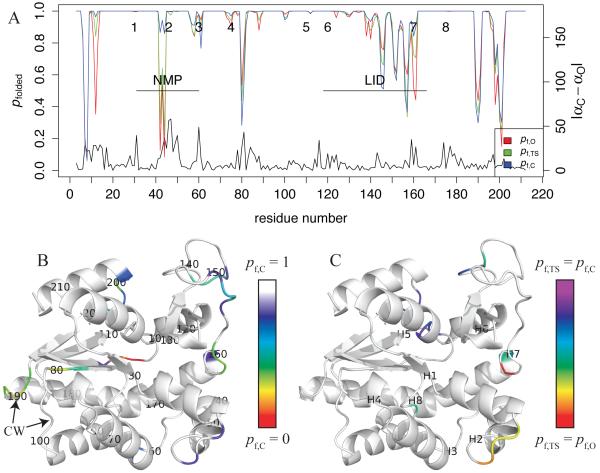
Figure 3. Unfolding dynamics in open, closed, and transition state ensembles of the bound simulation.
A: pfolded,E for the pseudodihedral angle αi-1,i is defined as fraction of structures in ensemble E for which α is in the same rotamer (within 60°) as the “reference value,” which is the average of the O and C native state values if |Δα| < 20°, where Δα = αC-αO. To simplify the calculation for residues with Δα ≥ 20°, three reference values are used (O, C, and the midpoint), and the highest probability among those three is defined as pfolded. The black curve shows |Δα| for reference. Numbers 1-8 at the top mark the positions (respective central residues) of the 8 hinges of Kern et al.10 pfolded,TS is the average of the values for the closing and opening transitions. B: pfolded in the C ensemble is contoured on a rainbow scale from red (0) to dark blue (0.9); white indicates residues for which pfolded ≥ 0.9. Labels indicate residue numbers for every 10th position; ‘CW’ indicates the counterweight loops.39 C: Fractional progress of folding in the TSE relative to the O and C ensembles. For residues for which pfolded,C−pfolded,O ≥ 0.1, fTS of pfolded (see Eq. 1) is contoured on a rainbow scale from red (0) to purple (1). Labels H1-H8 indicate the respective central residues of the 8 Kern hinges.
Figure 3A shows pfolded profiles for AK in the open, closed, and transition state ensembles. The magnitude of Δα between O and C crystal structures (black) is always less than 60°; that is, most differences between the crystal structures are intra-rotameric. For most residues, the red, blue, and green curves, respectively, show that O, C, and TS ensembles have similar pfolded. Where pfolded differs among the ensembles, C usually has the highest pfolded and thus the lowest conformational entropy. The exceptions are residues 80-81 and the “counterweight loop” 189-191, the B-factors of which increase upon ligand binding, possibly partially counterbalancing entropy loss elsewhere.39 In addition, in the LID, decreased flexibility in residues 138-140 and 158-161 upon closing is partially balanced by increased flexibility in residues 145-146 and 156-157. Four hinge regions (2-4 and 7) have some unfolding in at least one ensemble, but only two (2 and 7) have substantial differences in pfolded between O and C ensembles. Consistent with hydrogen exchange experiments,28 NMP and the LID are less folded than the CORE in all three ensembles, and the largest quenching of local unfolding upon closing occurs in the NMP domain (especially residues 42-44) and to a lesser extent, the LID domain. This is also consistent with the protein engineering experimental result that the CORE determines the thermal stability of AK.27 The CORE is also locally stabilized significantly in loop 11-13. For reference, Figure 3B maps pfolded,C onto the C crystal structure.
For “quenched” dihedrals with pfolded,C - pfolded,O ≥ 0.1, panel C characterizes dynamics in the TSE with fractional progress analysis of pfolded (see equation 1). Except for residue 88, quenched dihedrals in the CORE (residues 11-13, 198, 199, and 201) have fTS ≥ 0.5; that is, pfolded,TS is closer to pfolded,C than to pfolded,O. By contrast, the quenched dihedrals in NMP have fTS < 0.3. The CORE-LID junction near hinge 7 has one partially rigidified residue (158) and two C-like residues (160 and 161), plus two residues (156 and 157) that relative to O, increase in flexibility in both TS and C. Surprisingly, we do not observe any residues with cracking behavior, that is, fTS < 0, as seen in a few residues of AK by Whitford et al.23 Rather, in most places, dihedral dynamics of individual residues likely make smaller free energy contributions to the TS character. That is, regions with C-like (lower entropy) unfolding dynamics in the TSE will likely resist O ⇔ C transitions, while O-like (higher entropy) regions will likely facilitate O ⇔ C transitions. For most dihedrals, Figure S10 shows that pfolded is similar between opening and closing transition sub-ensembles. Finally, Figure S11 shows that among the 8 independent bound simulations, the standard deviations of all pfolded curves, including pfolded,TS, are consistently less than 0.05, which is much less than any of the noted differences among O, C, and TS ensembles.
The residues most important to the TS, and thus the best targets for mutations to perturb the opening and/or closing rates, are those for which O and C ensemble dynamics differ substantially and fTS is close to either 0 or 1. According to these criteria, in the bound simulation, the residues which most strongly facilitate O ⇔ C transitions (Δpf = pfolded,C - pfolded,O ≥ 0.2 and fTS ≤ 0.25) are G42 and E44; the residues which most strongly resist O ⇔ C transitions (Δpf ≥ 0.2 and fTS ≥ 0.75) are G12, K13, G198, and T199. Other notable residues that narrowly miss these cutoffs are for O mutants S43 (Δpf = 0.41, fTS = 0.26) and D158 (Δpf = 0.15, fTS = 0.06), and for C mutants A11 (Δpf = 0.19, fTS = 0.89). Interestingly, a surprisingly high number of glycines display important dihedral dynamics. We detail possible mutational strategies in the discussion.
By comparison, the apo simulation shows interesting differences with the bound simulation both in the location and TS properties of important dihedral residues (Figure S12). For example, loop 11-13 in the apo simulation is unfolded in all three ensembles, suggesting that its foldedness in C and TS in the bound simulation may result from the ligand contacts made by residues 10,12, and 15. In addition in the apo simulation, loop 42-44 is more rigidified in the TS than it is in the bound simulation; this rigidification may be coupled to NMP-first closure in the apo simulation. While D158 is flexible in the bound TS and residues 161-162 are rigidified, the reverse pattern exists in the apo TS. Furthermore, residues 198-199, which are near ligand-contacting residue 202, are rigidified in the bound TS but flexible in the apo TS. Thus, as with domain closure order, the presence of ligand appears to significantly influence the pattern of backbone flexibility shifts associated with the O/C transition. These backbone dynamic differences between apo and bound simulation predictions provide another opportunity to experimentally test the model.
Contact space
In Figure 4, we map O, C, and TS ensemble probabilities of individual contacts onto the three-dimensional open and closed structures of AK. Specifically, we examine the previously described O-ensemble- and C-ensemble-characteristic contact sets (Figure S8), which will be referred to in the rest of this section simply as “O-contacts” and “C-contacts,” respectively. Panels A and B of Figure 4 show that the TSE comprises more C-contacts (blue and purple) than O-contacts (orange and red); this is expected since more contacts are characteristic to the C ensemble than to the O ensemble (Figure S8). In addition, to examine consistency of contact probabilities; we compared these among the 8 independent simulations; the standard deviations are ≤ 0.04 for pO, ≤ 0.01 for pC, and ≤ 0.05 for probability in the TS ensemble (pTS). In addition, Table S2 shows the distribution of common, O-unique (to the crystal structure), C-unique, and ligand-mediated interactions among the domains and interfaces.
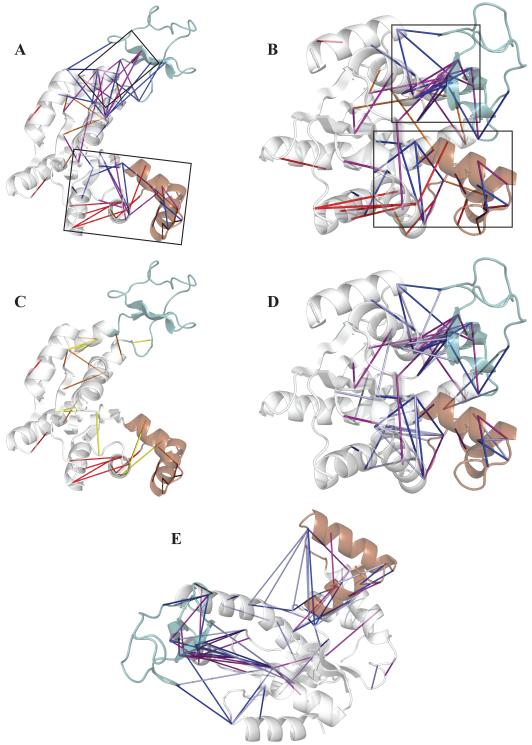
Figure 4. Important O-characteristic and C-characteristic contacts in the transition state ensemble of the bound simulation.
CORE, LID and NMP domains are colored white, green, and brown, respectively. Only contacts with max(pO, pC) ≥ 0.5 are plotted. For O-characteristic contacts (pC-pO ≤ −0.2), red, orange, and yellow indicate pTS ≥ 0.7, 0.5 ≤ pTS < 0.7, and pTS < 0.5, respectively. For C-characteristic contacts (pC-pO ≥ 0.2), purple, blue, and light blue indicate pTS ≥ 0.7, 0.5 ≤ pTS < 0.7, and pTS < 0.5, respectively. A: TSE contacts (pTS ≥ 0.5) mapped onto the O crystal structure (4AKE). B: TSE contacts mapped onto the C crystal structure (1AKE). Boxes on panels A and B indicate the two proposed transition state contact nuclei. C: All O-characteristic contacts. D: All C-characteristic contacts. E: C-characteristic contacts mapped onto O crystal structure.
The largest cluster of C-contacts includes portions of the CORE-LID interface and the CORE-LID connector helices. A larger but sparser network comprising both O-contacts and C-contacts includes a few contacts in NMP and more from the CORE-NMP interface and the lower CORE domain (see boxes on panels A and B). We define the lower CORE as the region of the CORE below the β-sheet on panel B. The two nuclei are more clearly separated in the O crystal structure (panel A) than in the C structure (panel B). Two small clusters of O contacts, one between helices 4 and 5 in the CORE adjacent to the larger C-contact network and one within helix 3 of NMP, also facilitate the O/C transition. Panel C compares O-contacts with probability in the TSE (pTS) ≥ 0.5 (red and orange) to those with pTS < 0.5 (yellow). Notably, some backbone helical O-contacts near hinges 6 and 8 appear to melt in the TSE, which may contribute some strain enthalpy to both TS and C. Panels D and E compare C-contacts present in the TS (purple and blue) to those absent in the TS (light blue). Most contacts absent in the TSE occupy the NMP domain and CORE-NMP interface. Panel E shows that late-forming (pTS < 0.5) CORE-NMP C-contacts typically have large distance differences (Δrij) between O and C crystal structures. This effect likely arises because the diffusional barrier to form a contact is presumably proportional to Δrij. CORE-LID contacts, while they too have a large distance difference between O and C, may form in the TS because enough of them exist to overcome the diffusional entropy cost of CORE-LID closure. We do not find closure of the LID-NMP interface as has been seen in dynamic importance sampling,25 in either the TS or C. The lack of formation of that interface may result from the high entropy cost relative to the small number of contacts (3) at the interface.
Figure S13 shows that by comparison to the bound simulation, the TSE of the apo simulation has a similar nucleus of contacts in the NMP and lower CORE domains, but there is no CORE-LID contact formation. To explain this difference, we compare the apo and bound contact sets. Table S2 shows that not including ligand-mediated interactions, there are 11 C-unique contacts apiece at the CORE-LID and CORE-NMP interfaces. In apo, the preference for NMP-first closure may arise from a broader range of rigid-body motions of the LID than of the NMP in the O well (see Figure 2); that is, the entropy cost to close NMP is likely less than the cost of closing LID. However, when ligand-mediated interactions are added, there are 22 contacts at the CORE-LID interface but only 14 at the CORE-NMP interface (see also Figure 5); that is, in the bound simulation, CORE-LID closure is much more enthalpically favorable than CORE-NMP closure. This may drive the conversion from an NMP-first closing mechanism without ligand to a LID-first closing mechanism in the presence of ligand.
Figure 5. Ligand-mediated interactions mapped onto the closed E. coli AK crystal structure (1AKE).
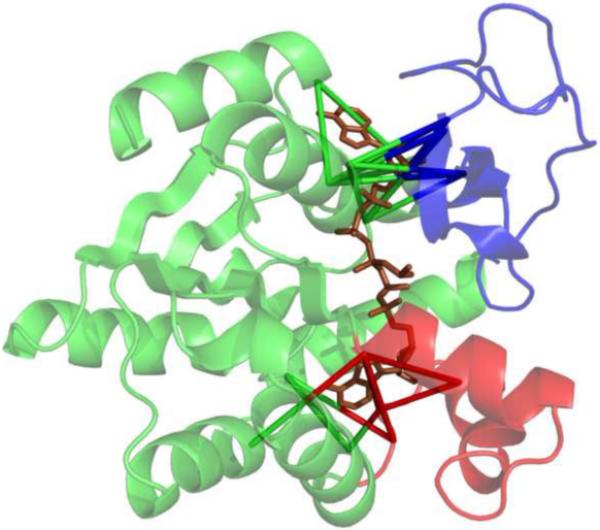
CORE, LID, and NMP domains are shown in green, blue, and red, respectively. Ligand-mediated interactions are indicated by pseudo-bonds between the Cα atoms of involved residues.
Discussion
What determines the closing and opening rates?
The adenylate kinase open ⇔ closed transition has been heavily studied experimentally and computationally at both coarse-grained and atomistic levels. We have distinguished this work by systematically analyzing many degrees of freedom and by precisely quantifying the transition state ensemble position relative to the difference between the O and C ensembles, within the framework of a coarse-grained model. The analysis reveals multiple degrees of freedom in dihedral and contact space that are important to the transition state; thus, it is unlikely that a few key residues or contacts alone determine the rate of the transition.
In addition, our results suggest a qualitative thermodynamic framework where many local entropic and enthalpic contributions combine to determine the relative free energy of the TS to the native states and hence the closing and opening rates. We infer that in the presence of ligand, CORE-LID closing in Cartesian space (ΔS < 0) and rigidification of a few CORE backbone dihedrals (ΔS < 0) resist the closing transition, while CORE-LID contact formation (ΔH < 0) facilitates the closing transition. We infer that CORE-NMP contact rupture and cooperative free energy loss (ΔH > 0) resist the opening transition, while increased freedom for NMP rigid-body motions and some NMP backbone dihedral motions (ΔS > 0) facilitates the opening transition. Thus, there appears to be substantial entropy-enthalpy compensation in both the closing and opening transitions.
In turn, the thermodynamic framework may guide experiments to identify residues critical to the closing and/or opening rates. In the context of AK, the principles of φ-value analysis from protein folding40,41 suggest that the impact of a mutation upon the relative free energy of the TS to the two native states, and hence upon the opening and/or closing rates, depends on whether the TSE structure and dynamics of that residue more closely resemble the structure/dynamics in the O or the C ensemble. For example, according to the bound model, increasing the intrinsic flexibility of dihedrals that are C-like (rigidified) in the TSE (e.g. residues 11-13 and 198-199) will slow the closing rate by stabilizing O (ΔS > 0), while increasing the intrinsic rigidity of such residues will accelerate closing. By contrast, our model predicts that rigidification of dihedrals (e.g. residues 42-44) that are O-like (flexible) in the TSE will slow the opening rate by destabilizing O and TS (ΔS < 0) while changing C less. As applicable, switching to a β-branched amino acid (thr or val), or even to pro, should reduce a residue’s intrinsic flexibility, while switching to gly or ala should increase its intrinsic flexibility. Furthermore, removal of C-characteristic contacts absent in the TS, such as those at the CORE-NMP interface, will likely accelerate opening by destabilizing C (ΔH > 0), while weakening of CORE-LID contacts formed in the TS will likely slow closing by raising (ΔH > 0) the enthalpy of both C and TS while raising the enthalpy of O less. In addition, deletion of O-contacts in the TS (e.g. between helices 4 and 5 in CORE) would raise the free energies of both O and TS, thus slowing the opening rate. Recently, several solvent-exposed val to gly mutants in the AK LID were shown to reduce the O ⇒ C equilibrium constant,29 which demonstrates that perturbation of flexibility can alter allostery. Along these lines, we suggest that the combination of coarse-grained conformational transition simulations with this type of thermodynamic framework may more efficiently and rationally identify sites to perturb the rates of allosteric-like transitions.
Allostery
Our results also illuminate the AK allosteric mechanism. While atomistic simulations20 suggest that C can be sampled from O with little free energy barrier in the absence of ligand and single-molecule O and C population measurements19 suggest that C is favored without ligand, we elaborate on the previously proposed conformational selection descriptions here by comparing apo and bound coarse-grained simulations with equivalent contact energy scales. While this is not a rigorous approach, it enables inferences about the effect of ligand on the distribution of conformations and the preferred O/C pathway.
For example, the fraction of C-characteristic CORE-LID contacts (Q’C,core-lid) in the C ensemble of the apo simulation (69%) approaches the Q’C,core-lid = 83% observed in the C ensemble of the bound simulation. This is consistent with the single-molecule result that the fully closed state can form without ligand and implies that protein-ligand contacts are not required for the stability of C.
Most interestingly, however, our results suggest that binding of ligand substantially alters the preferred transition pathway between O and C. Prior approaches including normal mode analysis,26 coarse-grained simulations,23,42 and atomistic simulations20 have supported the prevalence of a LID-first closing pathway. While the bound simulation results (Figure 2A) support a LID-first pathway, the apo simulation (Figure 2B) shows higher flux along the NMP-closing pathway; that is, LID-first closure requires the presence of ligand. The observation that ATP binding creates more contacts to stabilize the CORE-LID interface than AMP binding creates to stabilize the CORE-NMP interface provides a simple explanation for this “mechanistic switch.”
This observed mechanistic switch has theoretical implications for allostery. That is, a pre-existing equilibrium between a flexible and a rigid state without ligand, as seen in the apo simulation, AK experiments,19 and other allosteric proteins,3,4 is not sufficient evidence for a purely entropic allosteric mechanism where rigidification and/or closure precedes ligand binding. Rather, ligand can catalyze (lower the free energy barrier of) the allosteric transition by binding to partially closed conformations (e.g. the LID-closed transition state of AK) in a mechanism that fits neither the conformational selection model nor the induced fit model. Indeed, closure of a substrate-binding lid has been observed in the crystal structure of the enzyme-substrate encounter (Michaelis) complex of another enzyme, PEPCK, with a lid-gated active site.43 Furthermore, provided that the ligand does not also stabilize the O state, the allosteric selectivity of the ligand for C over O is not reduced relative to a conformational selection mechanism.
Why is there no cracking in this AK model?
It has previously been hypothesized that cracking44 facilitates the transition in AK23,26 and other proteins30,45 by enabling the protein to detour around high-free-energy states, especially in regions with rigid structure in the native state.45 However, to accurately assess cracking, the dihedral potential needs to realistically estimate the barriers to local unfolding and the resultant strain energy. For example, in the bound model, Figure 3 shows that by contrast to the model of Whitford et al,23 no residues crack. That is, in the TSE of our model, for all dihedral degrees of freedom, folding probability lies approximately within the interval [pfolded,O, pfolded,C]. This difference in results probably arises from differences between the dihedral potential in this work and that used by Whitford and co-workers. Compared to the Karanicolas and Brooks potential used here,38 which is sequence-specific but generic to the native structures (see Methods for more details), the potential of Whitford et al. is specific to the O structure. Thus, Whitford’s potential may impose unrealistically high barriers to local refolding, especially for dihedrals that are more rigidified in the TS than in O. Our model also predicts that strain may arise from the loss of O-unique helical contacts in the TS in some regions (Figure 4).
Dynamic effects of the contact energy scale
Relative to double-well Gō models of other proteins,34,36 the unusually high contact energy scale required to stabilize the open and closed crystal structures in the AK Gō model suggests that AK may be more dynamic than proteins in general. Some solution experimental evidence supports this alternative view. For example, hydrogen exchange,28 which suggests that LID and NMP are at least partially unfolded under apo conditions but become stabilized upon ligand binding. In addition, NMR relaxation experiments10 have found that fast (ps-ns) fluctuations coupled to the O/C transition are broadly distributed among LID, NMP, and the interdomain hinges. Future comparison between experiments and computations, for example, testing mutants predicted by double-well Gō models with different contact energy scales, may more clearly illuminate this issue and provide guidance for calibrating future allosteric simulations.
Beyond this work
A more quantitative thermodynamic and kinetic model might facilitate more accurate prediction of critical residues. For example, a hierarchical model connecting local motions to global dynamics could better explain the effects of multiple motions on the rate. Important contacts which co-form and/or dihedrals which co-fold could be clustered to identify a smaller number of cooperative degrees of freedom. We suggest the clustering strategy (rather than a simple breakdown of dihedrals and contacts by domains or secondary structures) since one of the two key contact nuclei includes parts of two domains (Figure 4) and since LID includes both flexible and rigid dihedrals in the TSE (Figure 3).
In addition, atomistic simulations may more accurately quantify the importance of motions that our coarse-grained simulations identify as important to the TS ensemble. Combined with the application of multi-motional analysis to simulation data from other (e.g. microscopic) coarse-grained models, atomistic simulations could discriminate factors genuinely important to the rate from those that may be artifactual to the use of a macroscopic or microscopic Gō model. For example, umbrella sampling20,46 along (dihedral) coordinates identified in coarse-grained simulations could more accurately characterize the thermodynamics of important motions proposed by our coarse-grained model. In addition, atomistic simulations using the milestoning approach of Elber et al.,47 starting with transition paths identified from coarse-grained simulations, may efficiently distinguish realistic from unfavorable transition pathways.
Conclusions
By analyzing many degrees of freedom in coarse-grained simulations of the adenylate kinase open ⇔ closed conformational transition, we have provided a qualitative mechanistic framework. Local enthalpic and entropic effects sum to determine the relative free energy of the transition state to the native states and by extension, the opening and closing transition rates, but no individual dihedral or contact appears to make a large positive or negative free energy contribution to the TS. Using detailed multi-motional analysis, we have predicted multiple residues and contacts that could be mutated to alter the opening and/or closing rates. Regarding the allosteric mechanism, comparison of simulations with and without ligand included suggests that closure can occur without ligand, but ligand binding alters the preferred closure pathway from NMP-first without ligand to LID-first in the presence of ligand. This ligand-driven reshaping of the energy landscape indicates a mechanism intermediate between conformational selection and induced fit. Finally, this work’s general analytical approach may complement structural analysis and protein dynamics experiments toward identifying structural features for allosteric design in proteins.
Methods
Gō model implementation
For each of two (O and C) conformations, the algorithm of Karanicolas & Brooks38,48 creates a single-well Gō potential with the aid of the MMTSB server (www.mmtsb.org). We combine the potentials for open and closed structures into a double-well potential using the exponential averaging approach and generic pseudo-bond angle potential of Best and Hummer.34 The mixed potential E(R) takes the form:
where R is a given conformation, Ei are the single-well potentials to be mixed, β is a mixing parameter, not to be confused with 1/kBT, and εi is an energetic offset applied to Ei. β calibrates the barrier height and thus the conformational transition rate, and εi calibrates the relative stability of the two states. For all simulations, we calibrate β to obtain approximately the smallest value for which the population of “intermediate” conformations not in a series of frames for which max(QO, QC) < 0.8 is O(0.01) or less, resulting in β=0.0185 for the bound simulation, 0.0277 for the apo simulation, and 0.0330 for the ligand-bound simulation with the contacts scaled by 1.7. We calibrate εO so that Keq between O and C forms is slightly greater than 1 (for the bound simulations) and about 1 (for the apo simulations) as found experimentally,19 which results in εO = 97.5 kcal/mol for the ligand-bound simulation, 53.00 for the apo simulation, and 51.3 for the bound simulation with the contacts scaled by 1.7. Simulations are carried out with the molecular dynamics program CHARMM49,50 for 750 ns (50 million 15 fs time steps) per independent simulation.
For each residue, we use the minimum non-bonded radius between the O and C potentials for the repulsive energy of non-native contacts. In addition, for native contacts common to the O and C crystal structures, the respective contact distances from the O and C single-well potentials are averaged to avoid excessive roughness in the energy landscape. If the difference between O and C in the Cα distance for a common contact is less than 1.5 Å, the Cα radii from the two structures are averaged and the contact is kept in both O and C potentials. Otherwise, the common contact is kept only for the structure with the smaller Cα distance. Out of 404 common contacts, only 4 are excluded from C and only 5 from O for this reason. There are also 72 contacts unique to O and 101 unique to C. As described in the results, we scale contact energies by a factor of 2.5 to compensate for the extra conformational entropy caused by the generic bond angle potential. In addition, O and C contact energy scales are equalized to the average of the original scales calculated by the Karanicolas algorithm38 for the O and C single-well potentials. This ensures that contacts with the same two residue types are given equal weights in the mixed potential.
An important feature of the Karanicolas model used here is a generic statistical pseudodihedral potential which is specific to the sequence but not to the native structure. Compared to other double-well models that explicitly include the native-state dihedral values,23,51 the Karanicolas potential supports freer sampling of backbone dihedral conformations, which is important for accurate assessment of folding dynamics in O, C, and TS ensembles.
Ligand-mediated interactions
We introduce a pseudo-ligand into the bound simulation by adding selected ligand-mediated interactions to the C Gō potential, an approach that has been used before in double-well coarse-grained simulations.42,51 An explicit coarse-grained ligand representation was previously used for a Gō model of irreversible ligand dissociation in myosin,52 but such a representation is not appropriate in our double-well simulation, where multiple O ⇔ C transitions are required.
We seek interactions across the ligand binding site according to several criteria for the vector rij between the Cα atoms of two ligand-binding residues (4.5 Å protein-ligand atomic contact distance cutoff) i and j. First, we exclude local contacts (|j-i| < 5 residues). We select residues for which |rij| ≤ 12.2 Å, which is approximately the width of the ligand-binding site. In addition, we select vectors which pass near ligand atoms, as defined by the following constraints: rij passes within 2.5 Å of at least one ligand atom, and for at least one ligand atom A, the angle Cα,i-A-Cαj is at least 120°. Using these criteria, 22 ligand-mediated interactions were identified based on the interaction of bisubstrate analog AP5A with 1AKE (Figure 5). The interactions mainly involve the two adenosine rings and avoid the bridging phosphate of AP5A, thus providing a realistic simulation of independent “binding” of the two natural ligands ATP and AMP.
We calibrate the contact energies for the ligand-mediated interactions to ensure CORE-LID and CORE-NMP interface formation (Qcore-lid/nmp ~ 0.9) at 300K in single-well simulations of the closed form that include the generic bond angle potential. 20 kcal/mol of energy is spread evenly among the 22 contacts.
Error calculations for PMFs
The PMF is calculated from a two-dimensional histogram of the data in any two reaction coordinates (e.g. (rmsO, rmsC)). For a given bin,
where nbin is the number of trajectory structures occupying that bin, and nmax is the maximum value of nbin in the histogram, and RT is 0.596 at 300K.
For each histogram bin, the sampling error ε can be estimated as for random sampling from a heterogeneous set, . Then, the error in energy of that bin is calculated as
since the error of ln(x) = dx/x, where dx is the error of x.
Supplementary Material
Acknowledgements
MDD acknowledges funding from the Computation and Informatics in Biology and Medicine Training Program at University of Wisconsin - Madison (NLM training grant 5T15LM007359). In addition, we thank Robert Best for providing the exponential averaging CHARMM package and instructing us in its use. We thank Jejoong Yoo for helpful discussions and the reviewers of our initial submission for helpful comments about improving the quality of the double-well Gō simulation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Monod J, Changeux JP, Jacob F. Allosteric proteins and cellular control systems. J Mol Biol. 1963;6:306–29. doi: 10.1016/s0022-2836(63)80091-1. [DOI] [PubMed] [Google Scholar]
- 2.Monod J, Wyman J, Changeux JP. On The Nature Of Allosteric Transitions: A Plausible Model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 3.Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allosteric behavior in a single-domain signaling protein. Science. 2001;291:2429–33. doi: 10.1126/science.291.5512.2429. [DOI] [PubMed] [Google Scholar]
- 4.Boehr DD, Nussinov R, Wright PE. The role of dynamic conformational ensembles in biomolecular recognition. Nat Chem Biol. 2009;5:789–96. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Koshland DE. Application of a Theory of Enzyme Specificity to Protein Synthesis. Proc Natl Acad Sci U S A. 1958;44:98–104. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cui Q, Karplus M. Allostery and cooperativity revisited. Protein Sci. 2008;17:1295–307. doi: 10.1110/ps.03259908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Beach H, Cole R, Gill ML, Loria JP. Conservation of mus-ms enzyme motions in the apo- and substrate-mimicked state. J Am Chem Soc. 2005;127:9167–76. doi: 10.1021/ja0514949. [DOI] [PubMed] [Google Scholar]
- 8.Yang L, Song G, Jernigan RL. How well can we understand large-scale protein motions using normal modes of elastic network models? Biophys J. 2007;93:920–9. doi: 10.1529/biophysj.106.095927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tobi D, Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc Natl Acad Sci U S A. 2005;102:18908–13. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–6. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 11.Daily MD, Gray JJ. Allosteric communication occurs via networks of tertiary and quaternary motions in proteins. PLoS Comput Biol. 2009;5:e1000293. doi: 10.1371/journal.pcbi.1000293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Formaneck MS, Ma L, Cui Q. Reconciling the “old” and “new” views of protein allostery: a molecular simulation study of chemotaxis Y protein (CheY) Proteins. 2006;63:846–67. doi: 10.1002/prot.20893. [DOI] [PubMed] [Google Scholar]
- 13.Ma L, Cui Q. Activation mechanism of a signaling protein at atomic resolution from advanced computations. J Am Chem Soc. 2007;129:10261–8. doi: 10.1021/ja073059f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yang S, Roux B. Src kinase conformational activation: thermodynamics, pathways, and mechanisms. PLoS Comput Biol. 2008;4:e1000047. doi: 10.1371/journal.pcbi.1000047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhou HX. From induced fit to conformational selection: a continuum of binding mechanism controlled by the timescale of conformational transitions. Biophys J. 2010;98:L15–7. doi: 10.1016/j.bpj.2009.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wolf-Watz M, Thai V, Henzler-Wildman K, Hadjipavlou G, Eisenmesser EZ, Kern D. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 17.Goodey NM, Benkovic SJ. Allosteric regulation and catalysis emerge via a common route. Nat Chem Biol. 2008;4:474–82. doi: 10.1038/nchembio.98. [DOI] [PubMed] [Google Scholar]
- 18.Schulz GE, Müller CW, Diederichs K. Induced-fit movements in adenylate kinases. J. Mol. Biol. 1990;213:627–630. doi: 10.1016/S0022-2836(05)80250-5. [DOI] [PubMed] [Google Scholar]
- 19.Hanson JA, Duderstadt K, Watkins LP, Bhattacharyya S, Brokaw J, Chu JW, Yang H. Illuminating the mechanistic roles of enzyme conformational dynamics. Proc Natl Acad Sci U S A. 2007;104:18055–60. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Arora K, Brooks CL., 3rd. Large-scale allosteric conformational transitions of adenylate kinase appear to involve a population-shift mechanism. Proc Natl Acad Sci U S A. 2007;104:18496–501. doi: 10.1073/pnas.0706443104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Henzler-Wildman KA, Thai V, Lei M, Ott M, Wolf-Watz M, Fenn T, Pozharski E, Wilson MA, Petsko GA, Karplus M, Hubner CG, Kern D. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–44. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 22.Cukier RI. Apo adenylate kinase encodes its holo form: a principal component and varimax analysis. J Phys Chem B. 2009;113:1662–72. doi: 10.1021/jp8053795. [DOI] [PubMed] [Google Scholar]
- 23.Whitford PC, Miyashita O, Levy Y, Onuchic JN. Conformational transitions of adenylate kinase: switching by cracking. J Mol Biol. 2007;366:1661–71. doi: 10.1016/j.jmb.2006.11.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chu JW, Voth GA. Coarse-grained free energy functions for studying protein conformational changes: a double-well network model. Biophys J. 2007;93:3860–71. doi: 10.1529/biophysj.107.112060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Beckstein O, Denning EJ, Perilla JR, Woolf TB. Zipping and unzipping of adenylate kinase: atomistic insights into the ensemble of open<-->closed transitions. J Mol Biol. 2009;394:160–76. doi: 10.1016/j.jmb.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maragakis P, Karplus M. Large amplitude conformational change in proteins explored with a plastic network model: adenylate kinase. J Mol Biol. 2005;352:807–22. doi: 10.1016/j.jmb.2005.07.031. [DOI] [PubMed] [Google Scholar]
- 27.Bae E, Phillips GN., Jr. Roles of static and dynamic domains in stability and catalysis of adenylate kinase. Proc Natl Acad Sci U S A. 2006;103:2132–7. doi: 10.1073/pnas.0507527103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rundqvist L, Aden J, Sparrman T, Wallgren M, Olsson U, Wolf-Watz M. Noncooperative folding of subdomains in adenylate kinase. Biochemistry. 2009;48:1911–27. doi: 10.1021/bi8018042. [DOI] [PubMed] [Google Scholar]
- 29.Schrank TP, Bolen DW, Hilser VJ. Rational modulation of conformational fluctuations in adenylate kinase reveals a local unfolding mechanism for allostery and functional adaptation in proteins. Proc Natl Acad Sci U S A. 2009;106:16984–9. doi: 10.1073/pnas.0906510106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hyeon C, Jennings PA, Adams JA, Onuchic JN. Ligand-induced global transitions in the catalytic domain of protein kinase A. Proc Natl Acad Sci U S A. 2009;106:3023–8. doi: 10.1073/pnas.0813266106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: the energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 32.Levy Y, Wolynes PG, Onuchic JN. Protein topology determines binding mechanism. Proc Natl Acad Sci U S A. 2004;101:511–6. doi: 10.1073/pnas.2534828100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hills RD, Brooks CL. Insights from coarse-grained go models for protein folding and dynamics. Int J Mol Sci. 2009;10:889–905. doi: 10.3390/ijms10030889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Best RB, Chen YG, Hummer G. Slow protein conformational dynamics from multiple experimental structures: the helix/sheet transition of arc repressor. Structure. 2005;13:1755–63. doi: 10.1016/j.str.2005.08.009. [DOI] [PubMed] [Google Scholar]
- 35.Best RB, Hummer G. Reaction coordinates and rates from transition paths. Proc Natl Acad Sci U S A. 2005;102:6732–7. doi: 10.1073/pnas.0408098102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Turjanski AG, Gutkind JS, Best RB, Hummer G. Binding-induced folding of a natively unstructured transcription factor. PLoS Comput Biol. 2008;4:e1000060. doi: 10.1371/journal.pcbi.1000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hummer G. From transition paths to transition states and rate coefficients. J Chem Phys. 2004;120:516–23. doi: 10.1063/1.1630572. [DOI] [PubMed] [Google Scholar]
- 38.Karanicolas J, Brooks CL., 3rd. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002;11:2351–61. doi: 10.1110/ps.0205402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Müller CW, Schlauderer GJ, Reinstein J, Schulz GE. Adenylate kinase motions during catalysis: an energetic counterweight balancing substrate binding. Structure. 1996;4:147–156. doi: 10.1016/s0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- 40.Matouschek A, Kellis JT, Jr., Serrano L, Fersht AR. Mapping the transition state and pathway of protein folding by protein engineering. Nature. 1989;340:122–6. doi: 10.1038/340122a0. [DOI] [PubMed] [Google Scholar]
- 41.Fersht AR, Matouschek A, Serrano L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J Mol Biol. 1992;224:771–82. doi: 10.1016/0022-2836(92)90561-w. [DOI] [PubMed] [Google Scholar]
- 42.Lu Q, Wang J. Single molecule conformational dynamics of adenylate kinase: energy landscape, structural correlations, and transition state ensembles. J Am Chem Soc. 2008;130:4772–83. doi: 10.1021/ja0780481. [DOI] [PubMed] [Google Scholar]
- 43.Sullivan SM, Holyoak T. Enzymes with lid-gated active sites must operate by an induced fit mechanism instead of conformational selection. Proc Natl Acad Sci U S A. 2008;105:13829–34. doi: 10.1073/pnas.0805364105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Miyashita O, Onuchic JN, Wolynes PG. Nonlinear elasticity, proteinquakes, and the energy landscapes of functional transitions in proteins. Proc Natl Acad Sci U S A. 2003;100:12570–5. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tripathi S, Portman JJ. Inherent flexibility determines the transition mechanisms of the EF-hands of calmodulin. Proc Natl Acad Sci U S A. 2009;106:2104–9. doi: 10.1073/pnas.0806872106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Faraldo-Gomez JD, Roux B. On the importance of a funneled energy landscape for the assembly and regulation of multidomain Src tyrosine kinases. Proc Natl Acad Sci U S A. 2007;104:13643–8. doi: 10.1073/pnas.0704041104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Faradjian AK, Elber R. Computing time scales from reaction coordinates by milestoning. J Chem Phys. 2004;120:10880–9. doi: 10.1063/1.1738640. [DOI] [PubMed] [Google Scholar]
- 48.Karanicolas J, Brooks CL., 3rd. Improved Go-like models demonstrate the robustness of protein folding mechanisms towards non-native interactions. J Mol Biol. 2003;334:309–25. doi: 10.1016/j.jmb.2003.09.047. [DOI] [PubMed] [Google Scholar]
- 49.Brooks B, Bruccoleri R, Olafson B, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. 1983. [Google Scholar]
- 50.Brooks BR, Brooks CL, 3rd, Mackerell AD, Jr., Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: the biomolecular simulation program. J Comput Chem. 2009;30:1545–614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Okazaki K, Koga N, Takada S, Onuchic JN, Wolynes PG. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: Structure-based molecular dynamics simulations. Proc Natl Acad Sci U S A. 2006;103:11844–9. doi: 10.1073/pnas.0604375103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Takagi F, Kikuchi M. Structural change and nucleotide dissociation of Myosin motor domain: dual go model simulation. Biophys J. 2007;93:3820–7. doi: 10.1529/biophysj.106.103796. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.