FINDING UNIQUE FILTER SETS IN PLATO: A PRECURSOR TO EFFICIENT INTERACTION ANALYSIS IN GWAS DATA

Abstract

The methods to detect gene-gene interactions between variants in genome-wide association study (GWAS) datasets have not been well developed thus far. PLATO, the Platform for the Analysis, Translation and Organization of large-scale data, is a filter-based method bringing together many analytical methods simultaneously in an effort to solve this problem. PLATO filters a large, genomic dataset down to a subset of genetic variants, which may be useful for interaction analysis. As a precursor to the use of PLATO for the detection of gene-gene interactions, the implementation of a variety of single locus filters was completed and evaluated as a proof of concept. To streamline PLATO for efficient epistasis analysis, we determined which of 24 analytical filters produced redundant results. Using a kappa score to identify agreement between filters, we grouped the analytical filters into 4 filter classes; thus all further analyses employed four filters. We then tested the MAX statistic put forth by Sladek et al. ¹ in simulated data exploring a number of genetic models of modest effect size. To find the MAX statistic, the four filters were run on each SNP in each dataset and the smallest p-value among the four results was taken as the final result. Permutation testing was performed to empirically determine the p-value. The power of the MAX statistic to detect each of the simulated effects was determined in addition to the Type 1 error and false positive rates. The results of this simulation study demonstrates that PLATO using the four filters incorporating the MAX statistic has higher power on average to find multiple types of effects and a lower false positive rate than any of the individual filters alone. In the future we will extend PLATO with the MAX statistic to interaction analyses for large-scale genomic datasets.

1. Introduction

1.1. Dissecting the Genetic Architecture of Complex Traits in GWAS

In the quest for disease susceptibility genes, genome-wide association studies (GWAS) have become the standard approach utilized by many investigators, with the promise of finding genes. Innovation is needed for the analysis and interpretation of GWAS data, as we are headed for a calamity. In the past, there have been problems replicating single-locus candidate genes studies². Soon, we will be faced with many 500K and 1M (1-million) SNP datasets with failure to replicate, as well as a flood of publicly available data that could be a gold mine, if the appropriate analysis strategy is utilized. Currently, no single analytical method will allow us to extract all information from a GWAS; in fact, no single method can be optimal for all datasets, especially when the genetic architecture for a given disease is not well understood. Therefore, an integrative platform is needed to accommodate the multitude of sophisticated analytical methods being developed in the field for analysis as we learn more about the genetic architecture as well as which methodologies are successful for GWAS analyses. As a resolution to this crisis, we have developed a system, the Platform for the Analysis, Translation, and Organization of Large Scale data (PLATO), for the analysis of GWAS data that will incorporate numerous analytic approaches as filters. The use of multiple filters that can be used in a modular way will allow a flexible analytical strategy that can be tailored to each investigation. In particular, these filters will be critical in the search for complex interactions among genes and/or the environment. It is already feasible to search all individual effects on even 1M single nucleotide polymorphisms (SNPs); however, once interactions between SNPs are considered, the problem becomes much less tractable. Most GWAS contain at least 500,000 or 1M SNPs and sometimes include environmental or clinical factors. Many common diseases are believed to be multifactorial, having multiple genetic and/or environmental disease susceptibility factors that may or may not have statistically detectable main effects ^3,4. Interaction effects have been discovered as influential in conditions such as hypertension ⁵, Hirschsprung’s disease ⁶, and cystic fibrosis^7,8; examples such as these demonstrate the importance of considering interactions during analysis of GWAS data. Efficiently exploring the search space when considering interactions in GWAS data becomes challenging very quickly, considering that looking for an interaction between just two variables among 500,000 requires the analysis of about 1.25×10¹¹ models. It is nearly infeasible to exhaustively search a space that large, much less the space that results from searching for interactions between three or more variables out of 500,000 or 1M SNPs. Since exhaustive approaches are intractable, alternative strategies must be employed.

1.2. PLATO

PLATO is a computational framework that analyzes SNPs and other independent variables using a variety of filters in an effort to identify a subset of interesting SNPs from a much larger set. A filter in this case is defined as an analytical method or knowledge-based approach which mediates a reduction in the number of SNPs to a smaller subset. PLATO allows the flexibility of applying filters in series, parallel, or individually and also allows the specification of filters for different disease models (additive, dominant, etc). Furthermore, PLATO is extensible, allowing users to easily implement their own analytical methods as filters using a modular C++ library. By narrowing down the number of SNPs using various filters, looking for interactions between the remaining variables may be feasible.

An important consideration when applying multiple analytical filters to a dataset is the potential for redundancy among the filters. It is well known that many analytical methods are similar and follow the same underlying principles. Still, in many studies, several similar methods are often used and the results compared. Within PLATO, many of the filters are highly correlated; however, the different filters are options for analysis to accommodate user preferences. Since some of the filters are correlated, it is not necessary to analyze datasets with all of them. By grouping filters into classes according to their tendency to identify overlapping subsets of putatively important SNPs, and subsequently running filters from these distinct classes, it may be possible to remove the most SNPs with the fewest number of filters, and subsequently reduce computation time. It is also possible that by running multiple distinct filters, “noise” SNPs can be removed and the truly significant effects can be found by singling out SNPs that repeatedly appear highly ranked across multiple filters.

To determine which of the PLATO filters yield unique results, a simulation study was performed. Simulations, where the true location and size of the genetic effect are known, prove indispensible for evaluating new analytical techniques. Genomic data with a known effect was simulated, specifying disease prevalence and a disease variant. The resulting data was then analyzed using all twenty-four PLATO filters individually. A kappa statistic was used as a measure of comparison to provide a mechanism for grouping filters into subsets that yield similar results. One filter from each resulting group was chosen as a representative filter for the group based on ease of use and interpretation. These filter sets were then further subset into filter classes by their tendency to rank embedded genetic effects similarly. Once a set of filter classes had been determined, we implemented a MAX statistic in an additional simulation. Here, one filter from each of the four filter classes was performed on the simulated data for each SNP in the dataset, taking the lowest p-value among the four tests for each SNP. Permutation was then performed on the entire analysis procedure to create an empirical null distribution and the results were compared with those found from running the four filters individually. The PLATO approach utilizing the MAX statistic (PLATO_MAX) out-performed all of the individual filters alone and demonstrates promise for future applications to multiple types of analyses, in particular the search for epistasis.

2. Methods

2.1. Data Simulation

The genomeSIMLA software ^9,10 was used to conduct the data simulations. Simulation was performed by first generating a population of 100,000 chromosomes containing 1000 bi-allelic polymorphisms. For each chromosome, all polymorphisms with exception of the disease polymorphism(s) were initialized randomly with respect to allele frequency within a range of minor allele frequency between 10% and 50%. We conducted a two-stage simulation study. In the initial phase of the simulation study, the goal was to determine the redundancy among the PLATO filters. For these simulations, the disease minor allele frequency was fixed at 25%. In the second phase simulations, the goal was to evaluate the approach whereby the correlated filters were clustered into filter classes and the MAX statistic was evaluated. Here, the disease polymorphisms were allowed to vary freely in allele frequency. Once the population of chromosomes was initialized, a penetrance function describing the size of the disease effect and the location of the disease locus was applied and random sampling theory was utilized in order to choose datasets of 1000 cases and 1000 controls. In all simulations for the estimation of power, 100 datasets were used; however, to test the Type 1 error rate of the PLATO_MAX approach, 1000 datasets were simulated.

A number of different disease models were simulated for the different elements of this study. Table 1 lists the different genetic models simulated. First, to determine the agreement between filters, single-locus additive, dominant, and recessive genetic effects with an odds ratio of 1.2, 1.5, 1.8, and 2.0 were simulated independently. In addition, a null model with no genetic effect was simulated separately. The simulated data used to further subset these filters into filter classes included six genetic effects: 2 each of additive, dominant, and recessive effects with one effect of each pair having an odds ratio of 1.2 and the other an odds ratio of 1.5. Finally, the data simulated to test the PLATO_MAX approach was evaluated using three effects, each exhibiting an odds ratio of 1.5 under additive, dominant, and recessive models.

Table 1.

Simulation Design

	Model type (effect size)
Experiment	Additive	Dominant	Recessive	Null
Agreement between filters (Kappa comparison)	OR = 1,2, 1.5, 1.8, 2.0	OR = 1,2, 1.5, 1.8, 2.0	OR = 1,2, 1.5, 1.8, 2.0	X
Creation of filter classes	OR = 1.2 and 1.5	OR = 1.2 and 1.5	OR = 1.2 and 1.5	N/A
PLATO_MAX Power analysis	OR = 1.5	OR = 1.5	OR = 1.5	N/A
Type I error analysis (null data)	N/A	N/A	N/A	X

2.2. PLATO Filters

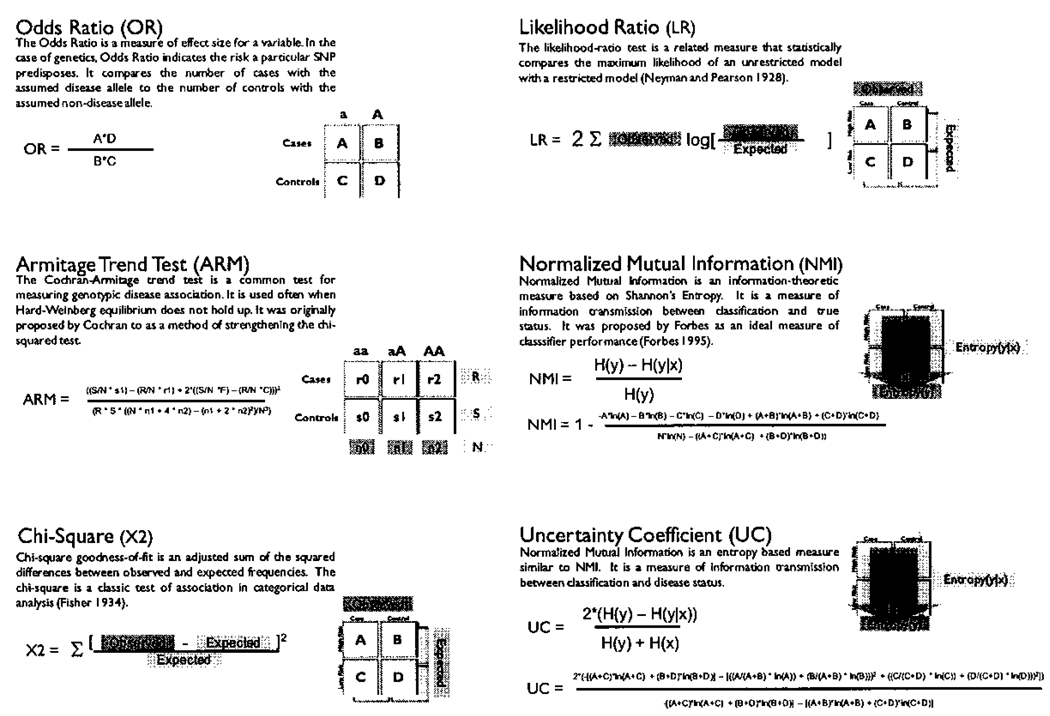
The datasets generated were analyzed individually using each of 24 different filters making up the comprehensive set of filters currently available for PLATO (Table 2). There are several of these filters that are subsets of filters with different data encodings. For example, the LIKELIHOODRATIO (G) filter is a LIKELIHOODRATIO filter that uses a genotypic data encoding while LIKELIHOODRATIO (A) is a LIKELIHOODRATIO filter that uses an allelic data encoding. Each filter type is summarized below, including how it functions as well as the meaning of different data encodings. The contingency table analytical methods utilized by the filters are further illustrated in Figure 1.

Table 2.

Filters implemented in current PLATO analyses. A-Allelic; G-Genotypic; ADD-Additive; D-Dominant; R-Recessive.

ARMITAGE (ADD)	MDR
ARMITAGE (G)	NMI (A)
CHISQUARE (A)	NMI (ADD)
CHISQUARE (G)	NMI (D)
LIKELIHOODRATIO (A)	NMI (G)
LIKELIHOODRATIO (ADD)	NMI (R)
LIKELIHOODRATIO (D)	ODDSRATIO
LIKELIHOODRATIO (G)	UNCERTAINTYCOEFF (A)
LIKELIHOODRATIO (R)	UNCERTAINTYCOEFF (ADD)
LOGISTICREGRESS (ADD)	UNCERTAINTYCOEFF (D)
LOGISTICREGRESS (D)	UNCERTAINTYCOEFF (G)
LOGISTICREGRESS (R)	UNCERTAINTYCOEFF (R)

Figure 1.

Six contingency table based filters used in PLATO. Adapted from (Bush, 2008)¹¹.

The ODDSRATIO filter utilizes a 2×2 table with the minor and major allele types as the columns and case and control status as the rows. To calculate the statistic, the product of cases with the minor allele (A) and controls with the major allele (D) is divided by the product of the cases with the major allele (B) over the controls with the minor allele (C). The ARMITAGE filter uses a Cochran-Armitage trend test to find the probability that a particular genotype is disease-associated by fitting the case-control distribution to a linear predictor equation of the form p_i = a + B_xi where i is the genotype being tested and B is the effect being attributed to the genotype ^12–15. Statistically speaking, testing disease association is looking for rejection of the null hypothesis that B=0. The CHISQUARE filter uses a chi-square ¹² test to look for differences between observed and expected numbers of cases and controls for each genotype. LIKELIHOODRATIO filters use an analytical method that is very similar to the CHISQUARE filters. The difference between these methods is that in calculating the statistic, a log ratio of the difference between observed and expected is used as opposed to the squared deviation from expected ¹². The NMI and UNCERTAINTYCOEFFICIENT filters are quite similar, both functioning on the entropy in the data ¹⁶. They examine the amount of information any particular genotype provides about the disease status. The main difference is that NMI (Normalized Mutual Information) is a normalized measure, as reflected in the name ^12,17.

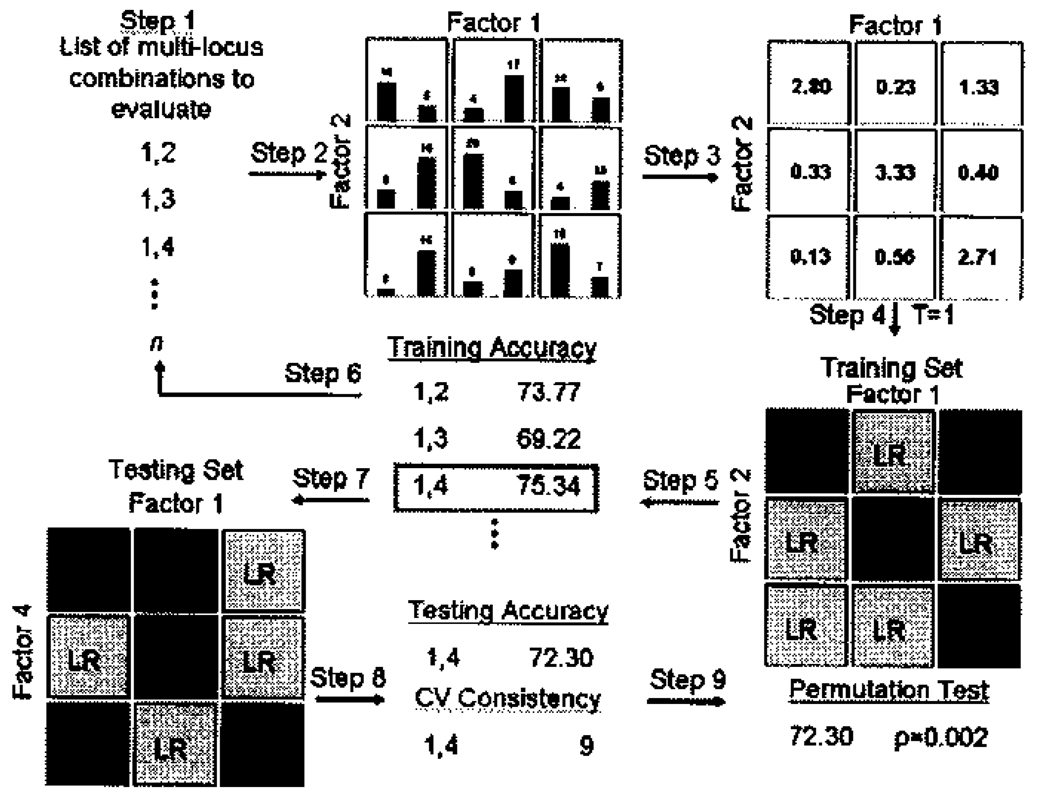
The LOGISTICREGRESS filters are one of the few types of filters - along with the Multifactor Dimensionality Reduction (MDR) filter - which do not use a contingency table measure to calculate the statistic used for comparison. LOGISTICREGRESS refers to logistic regression analysis. Logistic regression is a standard method used by epidemiologists when looking for disease association with both genetic and environmental factors ¹⁸. Logistic regression uses a logistic equation to fit the pattern of cases and controls with respect to genotype and then determines if the genotype classes are predictive of disease. This equation is of the form p(x)=exp(a + Bx)/(1 + exp(a + Bx)), where p(x) is the probability of getting the disease and B is the coefficient describing the effect of the genotype x ¹². MDR is an analytical method initially developed to analyze interactions between variables such as SNPs involved in disease susceptibility, although it can also identify single-locus effects ¹⁹. The underlying method of the MDR filter takes a specified number of polymorphisms and looks at the intersection of genotypes to determine if, for a particular single- or multi-locus genotype, there are more cases than controls with that genotype combination (Figure 2). MDR utilizes a cross-validation measure to divide the data into N equal-sized partitions, looking for high risk genotypes in N-1 partitions –the training set– and then examining the predictive value of those high risk genotypes in the remaining partition of the data – the testing set. The process is then repeated N times until all of the partitions have been used as the testing set. The result is two measures of accuracy for each model MDR evaluates, the classification accuracy and the prediction accuracy. The classification accuracy describes the number of cases and controls the particular model classifies correctly in the training set while the prediction accuracy describes the same measure in the testing set. In this PLATO study, MDR was run with 10-fold cross validation analyzing single-locus models only.

Figure 2.

The MDR method. MDR partitions data into N parts and then uses N-1 of those to do the association test and the other part to look at the predictive accuracy of the models found. Adapted from (Ritchie and Motsinger, 2005)²⁰.

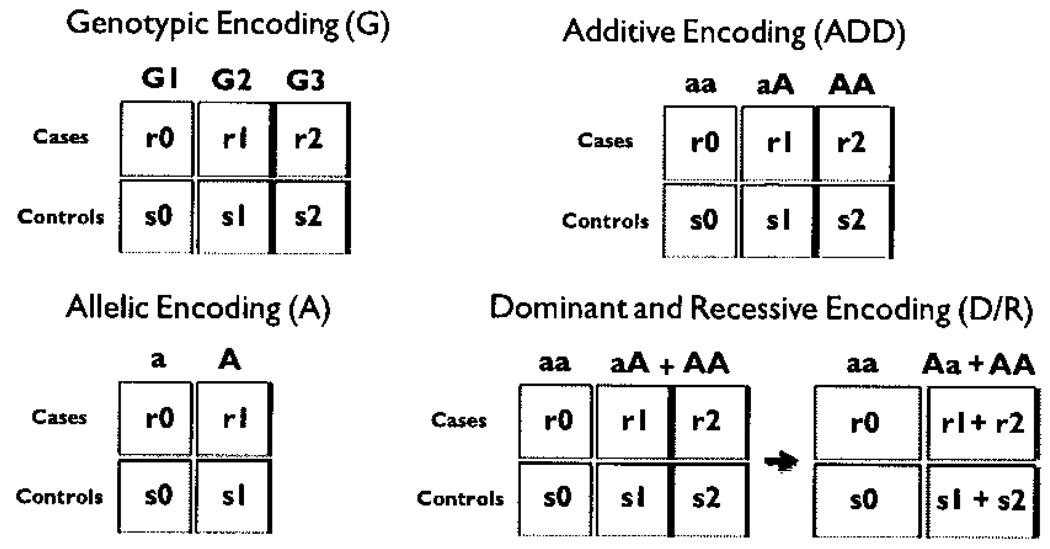
Most of the filters implemented in PLATO utilize multiple different data encodings, as shown in Table 1. There are 5 different data encodings: additive, dominant, recessive, allelic, and genotypic (Figure 3). The additive encoding assumes that the addition of each disease allele results in increased disease risk. Dominant and recessive encodings are very similar, the only difference being where the disease is assumed to reside. In both cases, a 2×2 table is made in which the cases and controls for the dominant homozygote and heterozygote from the 3×2 genotypic table are condensed into one column and the cases and controls for the recessive homozygote reside in the other column. The genotypic encoding is very similar to the additive encoding, with each genotype possessing one column. The only difference is that the genotypic encoding is not necessarily ordered. Where the additive encoding assumes an order to the genotypes in the model, the genotypic encoding does not necessarily possess order in the columns. The allelic encoding simply makes a 2×2 table with the cases and controls that have a major allele and minor allele. Having multiple encodings such as these allows the user to bias a test for a specific disease model which might be present.

Figure 3.

The five different data encodings available in using the PLATO filters are depicted. The r0, r1, r2 values correspond to the number of cases with the particular genotypes while s0, s1 and s2 refer to the controls with those genotypes.

2.3. The Kappa Statistic

The kappa statistic has been suggested as a good measure to determine agreement between classifiers ²¹. It is a way of examining how well two ranking systems – in this case, filters – classify data in the same way. The idea is to build a 1000×1000 matrix corresponding to the rankings for the 1000 loci by each filter. In the matrix, tallies are placed according to the rankings for each filter (see example in Table 3). If two filters agree on a ranking, the tally will lie directly on the diagonal. The kappa statistic (Eq 1.) looks at the degree to which these tallies group around the diagonal and awards a score of 1 for a perfect agreement at all rankings for two filters. In our method, a weighting measure is used to score tallies closer to the diagonal higher than those that occur further away. Based on suggestions from Landis and Koch ²², a kappa score of 0.60 was used as the cutoff to group filters with similar results. Some of the filters run in this comparison were previously known to have correlated results but were included as a proof of concept for using the kappa statistic.

$$K_w=\frac{x_{++}{\displaystyle \sum _{\mathit{\text{cells}}}{w}_{\mathit{\text{ij}}}{x}_{\mathit{\text{ij}}}-{\displaystyle \sum _{\mathit{\text{cells}}}{w}_{\mathit{\text{ij}}}{x}_{i+}{x}_{+j}}}}{x_{++}^2-{\displaystyle \sum _{\mathit{\text{cells}}}{w}_{\mathit{\text{ij}}}{x}_{i+}{x}_{+j}}}$$ Eq(1)

Table 3.

An example of a kappa statistic matrix. First, the rankings for the two filters are aligned to create a matrix which is then populated by tallies for each agreement in rankings in each filter. The kappa statistic then measures the degree to which the tallies fall on the diagonal.

		Filter 1 Rankings
	Rank	1	2	3	4	5	Sum
Filter 2 Rankings	1	6	.	3	1	.	10
	2	2	8	.	.	.	10
	3	1	1	5	.	3	10
	4	1	.	.	8	1	10
	5	.	1	2	1	6	10
	Sum	10	10	10	10	10	100

2.4. Implementing the PLATO_MAX approach

The MAX statistic is a measure utilizing multiple data encodings to maximize the power for finding a genetic effect. Sladek et al.¹ originally utilized this statistic with a combination of the additive, dominant, and recessive encodings in logistic regression. We have extended the statistic to include the genotypic encoding of the chi-square test, which is shown in our results to be uncorrelated with logistic regression. To implement the PLATO_MAX approach¹ and test its efficacy, a simulation study was performed. First, 100 datasets with 1000 cases and 1000 controls were simulated to find the power of the method. Three genetic effects with an odds ratio of 1.5 – one additive model, one recessive model, and one dominant model – were embedded in these datasets. To find the MAX statistic for each SNP, four filters – LOGISTICREGRESS (ADD/D/R) and CHISQUARE (G) – were run and the minimum p-value between the four was kept as the best solution. These four filters represented one filter from each of the four filter classes identified (as described in the results below). We selected one filter per class based on ease of use and interpretation. In order to deal with multiple testing issues, a set of 1000 permutations was performed, building a null distribution for each SNP. Here, the disease status was randomized to create 1000 null datasets where the genotype matrix was held constant but the association between genotype and phenotype was removed. The full PLATO_MAX analysis was performed on each null dataset and the lowest p-value was obtained from each dataset and collected in the empirical null distribution. The original lowest p-value was then compared to the permutation null distribution to find a corrected p-value. The power was calculated for each of the three effects at α=0.01 and 0.05 levels as the number of times out of the 100 datasets that the SNP in question was found to be significant after permutation testing. The false positive rate was calculated as the average number of incorrect loci found to be significant for each dataset divided by the number of SNPs in the dataset. We also investigated the Type 1 error rate of the PLATO_MAX approach by simulating 1000 datasets with no genetic effect. The PLATO_MAX approach was then run with permutation and the number of times which SNPs were found to be significant with the null model was examined.

3. Results

3.1. Kappa Comparisons

The kappa score was used to do pair-wise comparisons between all 24 filters that are used in the current version of PLATO. This created a set of 276 comparisons which were repeated for all 13 models tested. To do the comparisons, the raw results from each filter were first sorted into a list of rankings that were suitable for making an ordered matrix (Table 3). For each filter comparison, the 1000 rankings were lined up so that one filter’s rankings made up the columns and the other’s made up the rows. Then, tallies were placed in the matrix corresponding to instances in which the rankings from the two filters agreed. The kappa statistic weighs the degree to which these tallies fall on the diagonal, as perfect agreement will be demonstrated by all tallies falling on the diagonal. A kappa statistic score of 1 is given in the case of perfect agreement between two filters. The score of 0.60 was used as significant based on literature about the statistic²².

Using the cutoff stated above, the filters were grouped into sets that provided non-redundant results. By grouping the filters for all 13 models, it became apparent that the same groups appeared regardless of the type or size of the effect simulated, including a null model. The result of this experiment is a set of 14 groups in which all filters within each group had a kappa score of at least 0.60 with each other (Table 4). Once we arrived at these 14 groups, we chose one filter from each group as the representative filter based on the number of assumptions the method made and/or the commonality of its use. We then ran these 14 filters on 10 datasets simulated with 6 genetic effects to determine the remaining correlation between filter rankings present even after kappa statistic comparison. On the basis of these results, we grouped these 14 filters into four filter classes with correlated findings (Table 5). For future analyses, we propose using a single analytical filter from each filter class. This filter is chosen based on interpretability and ease of implementation.

Table 4.

The list of filter groups that resulted from kappa statistic comparisons.

Group 1	Group 2	Group 3	Group 4
LIKELIHOOD (ADD)	CHISQUARE (A)	ARMITAGE (A)	LIKELIHOODRATIO (D)
LIKELIHOOD (G)	LIKELIHOODRATIO (A)	ARMITAGE (G)	NMI (D)
NMI (ADD)	NMI (A)	LOGISTICREGRESS (ADD)
NMI (G)
Group 5	Group 6	Group 7	Group 8
LIKELIHOODRATIO (R)	UNCERTAINTYCOEFF (ADD)	CHISQUARE (G)	LOGISTICREGRESS (D)
NMI (R)	UNCERTAINTYCOEFF (G)
Group 9	Group 10	Group 11	Group 12
LOGISTICREGRESS (R)	MDR	ODDSRATIO	UNCERTAINTYCOEFF (A)
Group 13	Group 14
UNCERTAINTYCOEFF (D)	UNCERTAINTYCOEFF (R)

Table 5.

Filter Classes found to display correlation in analysis results. Highlighted in bold italics is the selected filter for the PLATO_MAX experiment.

Filter Class 1	Filter Class 2	Filter Class 3	Filter Class 4
CHISQUARE (A)	CHISQUARE (G)	LIKELIHOODRATIO (D)	LIKELIHOODRATIO (R)
LOGISTICREGRESS (ADD)	LIKELIHOODRATIO (ADD)	LOGISTICREGRESS (D)	LOGISTICREGRESS (R)
UNCERTAINTYCOEFF (A)	UNCERTAINTYCOEFF (ADD)	UNCERTAINTYCOEFF (D)	UNCERTAINTYCOEFF (R)
ODDSRATIO	MDR

3.2. The PLATO_MAX Approach

The PLATO_MAX approach was implemented to examine its power to identify multiple types of genetic effects while controlling the false positive and Type 1 error rates of the method. The power of the PLATO_MAX approach (using the four filter class filters) is compared to using each of the four filters individually for each effect in Table 6. In addition, the false positive and Type 1 error rates are given in Table 6.

Table 6.

Power, False positive and Type 1 error rate of the PLATO_MAX approach compared to each individual filters.

	MAX	LOGISTIC (ADD)	LOGISTIC (D)	LOGISTIC (R)	CHISQUARE (G)
Power (0.05)
Additive	75	83	78	56	71
Dominant	97	96	97	23	97
Recessive	45	28	7	57	47
AVG POWER	72.3	69.0	60.7	45.3	71.7
False Positive	0.04795	0.05795	0.06039	0.06735	0.0537
Type 1 Error	0.054473
Power (0.01)
Additive	52	63	59	34	49
Dominant	92	85	97	11	91
Recessive	24	13	2	37	23
AVG POWER	56	53.7	52.7	27.3	54.3
False Positive	0.00954	0.01458	0.01482	0.01739	0.01308
Type 1 error	0.01254

Here the false positive rate is the average number of incorrect loci found to be significant for each dataset divided by the number of SNPs in the dataset where an actual genetic model was simulated. On the contrary, the Type 1 error rate is the average number of incorrect loci found to be significant for each dataset divided by the number of SNPs in the dataset where no genetic effect was simulated. The PLATO_MAX approach had power of 75%, 97% and 45% to find the additive, dominant, and recessive effects respectively at an alpha level of 0.05 and power of 52%, 92%, and 24% at the 0.01 level. The average power of the PLATO_MAX approach over the three effects at the 0.05 level was 72.3% as opposed to the average power of the four individual filters which was 69.0% for LOGISTICREGRESS (ADD), 60.7% for LOGISTICREGRESS (D), 45.3% for LOGISTICREGRESS (R), and 71.7% for CHISQUARE (G). The false positive rate of the PLATO_MAX was lower than the individual filters at 0.04795 and 0.00954 for an alpha of 0.05 and 0.01 respectively. Finally, the Type 1 error rate of the method was well controlled at 0.054473 at an alpha of 0.05 and 0.012541 at an alpha of 0.01.

4. Discussion

GWAS analyses have thus far been fairly straightforward single locus tests of association such as logistic regression, chi-square tests, or Cochran-Armitage trend tests. These tests have been successful in many situations. Clearly, the optimal test is highly dependent on the type of effect being detected. Since we do not know a priori what type of effect we are looking for, some groups, such as Sladek et al.¹ have proposed using multiple analyses simultaneously and taking the maximum statistic as the final solution. Using multiple analysis approaches (as filters) and employing a maximum statistic allows one to test for many known types of effects and have power to detect them while controlling the Type I error rate.

The motivation for PLATO is twofold. First, the fact that any single underlying analytical scheme will reveal only some important results and that multiple filters will reveal different subsets of important results. However, once results are obtained these results can be viewed in light of the results from other filters to best understand the full meaning of the genetic data. The potential to use multiple filters forces no a priori assumptions about the mode of action of the genetic components of a phenotype allowing the most general possible analysis and interpretation. This is critical as it is rare that we know what type of effect we are attempting to detect in disease gene association studies. Thereby the ability to evaluate the association in the context of many different models and select the optimum solution for the dataset at hand, while controlling Type I error rate is a great success. Second, it is hypothesized that the genetic architecture of complex disease will include interactions between many genes as well as the environment. In GWAS scale datasets, searching for interactions is a computational challenge; thus filtering the full set of GWAS SNPs to a smaller subset will be critical in the quest for detecting interactions. PLATO accomplishes both of these goals.

There are a large number of possible filters that one can envision for the PLATO framework. Currently, PLATO has the following tests implemented: Cochran-Armitage trend test, chi-square, likelihood ratio, logistic regression, MDR, normalized mutual information, odds ratio, and uncertainty coefficient as well as a thorough quality control filter including sample and SNP efficiency, HWE, allele frequency, rates of homozygosity, concordance checks, gender errors, and Mendelian errors. In addition, PLATO currently has the following filters under development: the Biofilter²³, data transformations, conditional logistic regression, MDR-PDT, generalized MDR, Cochran-Mantel-Haenszel analysis, linkage disequilibrium (r^2), linear regression, and TDT.

PLINK is another currently available software package for GWAS data²⁴. PLATO differs from PLINK in two significant ways. First, PLINK is primarily for performing one test of association for each single SNP across the genome; whereas PLATO performs multiple single locus tests and uses a MAX statistic with permutation testing to determine statistical significance. Second, while PLINK has a few regression-based tests for interaction, that is not the focus; whereas, the primary goal of PLATO is to provide a mechanism for searching for complex gene-gene and gene-environment interactions in GWAS data. With multiple interaction filters integrated with tests for main effects as well as biological knowledge, PLATO will provide a powerful framework to elucidate the genetic architecture of complex disease.

This study examined the redundancy among filters currently available for PLATO, the creation of filter classes based on these correlations, and the utility of the PLATO_MAX approach in the context of one filter from each class. We simulated case-control data for a number of effects and then compared results from each filter after running them on this data. The kappa statistic provided a means of comparison between these results, allowing for the grouping of filters into sets based on similar results. From 276 filter-filter comparisons, 14 groups of filters with kappa statistic scores greater than 0.60 were obtained. As expected based on the numerical formulas, these 14 groups were then filtered down through elimination of some filters and grouping of correlated entities to form 4 filter classes. The primary motivation for this research was finding an effective way to filter GWAS data to determine an interesting subset of SNPs and therefore reduce the number of model comparisons during interaction analysis. This was accomplished through selection of an informative group of filters to achieve reduced computational time during a PLATO run. In addition to reducing the number of filters, we have implemented a useful analysis tool in the form of the MAX statistic. Although the PLATO_MAX approach only offers a small power gain for individual genetic effects, it has shown that it has higher power to detect all types of genetic effects than the individual filters composing it. The PLATO_MAX approach also has a lower false positive rate than any of the other filters alone.

The current study offers multiple avenues for future exploration. Now that a set of filter groups has been proposed, it must be determined which filter from each group provides the most accurate results. While it is possible that the best filter from each group could vary for different effects, this will supply a default PLATO filter set to achieve the largest degree of filtering with the smallest computational obligation in most cases. In addition, we can use this new default filter set to test the idea that looking for an intersection between results from multiple filters can filter out background noise. By running several filters that each provide different results and then selecting for SNPs which receive high scores in all filters, it should be possible to sift out the uninformative background noise of SNPs that are significant in one filter only. Power and type I error studies must be performed to test this notion.

In addition to realizing an increase in power for single-locus genetic analysis, this exercise in implementing the MAX statistic has demonstrated an important point which was introduced by the computational optimization field: “No Free Lunch” (NFL)²⁵. The NFL theory states that no one method run alone is best in all situations. Although we have demonstrated this theory in the search for single-locus genetic models, it is likely to be an even more important consideration when analyzing epistatic models. This concept is supported also by previous research in the field. Upon testing a number of interaction-searching analysis methods, it was found that the performance of each was dependent on the context of the interaction or genetic effect being searched for²⁶. When a single-locus effect was presented, the methods that condition on main effects out-performed those which look specifically for epistasis. On the other hand, when two-locus and three-locus models were imparted to these methods, different interaction-searching methods surpassed both those conditioning upon main effects as well as each other depending on the particular context of the multi-locus effect. In addition, when MDR and FITF were applied to look for gene-environment interactions involved in the etiology of pancreatic cancer, the researchers found that a combination of methods was necessary to mine the data effectively and identify the important multi-locus models²⁷. In the future we will extend the PLATO_MAX approach to include methods designed for interaction searching.

PLATO is a very flexible analytical method with promise as a major component of association studies. With its ability to run filters individually, in series or in parallel as well as the opportunity for users to implement their own filters, PLATO can be easily customized for any study. Future work will likely introduce a study design that takes advantage of this customization to use PLATO as both an analytical method and a prior to performing interaction analysis.