Abstract
Accurate, nonintrusive, and inexpensive techniques are needed to measure energy expenditure (EE) in free-living populations. Our primary aim in this study was to validate cross-sectional time series (CSTS) and multivariate adaptive regression splines (MARS) models based on observable participant characteristics, heart rate (HR), and accelerometer counts (AC) for prediction of minute-by-minute EE, and hence 24-h total EE (TEE), against a 7-d doubly labeled water (DLW) method in children and adolescents. Our secondary aim was to demonstrate the utility of CSTS and MARS to predict awake EE, sleep EE, and activity EE (AEE) from 7-d HR and AC records, because these shorter periods are not verifiable by DLW, which provides an estimate of the individual's mean TEE over a 7-d interval. CSTS and MARS models were validated in 60 normal-weight and overweight participants (ages 5–18 y). The Actiheart monitor was used to simultaneously measure HR and AC. For prediction of TEE, mean absolute errors were 10.7 ± 307 kcal/d and 18.7 ± 252 kcal/d for CSTS and MARS models, respectively, relative to DLW. Corresponding root mean square error values were 305 and 251 kcal/d for CSTS and MARS models, respectively. Bland-Altman plots indicated that the predicted values were in good agreement with the DLW-derived TEE values. Validation of CSTS and MARS models based on participant characteristics, HR monitoring, and accelerometry for the prediction of minute-by-minute EE, and hence 24-h TEE, against the DLW method indicated no systematic bias and acceptable limits of agreement for pediatric groups and individuals under free-living conditions.
Introduction
Accurate, nonintrusive, and inexpensive methods are needed to measure energy expenditure (EE)5 in free-living populations, especially in children and adolescents. Direct and indirect calorimetric methods that measure EE can be intrusive, confining and expensive and thus impractical for large-scale studies. The stable isotope method, doubly labeled water (DLW), is considered the “gold standard” for free-living measurements of 24-h total EE (TEE) (1). Due to the considerable cost of 18O and mass spectrometry measurements, alternative approaches based on physiological correlates of EE using small, relatively inexpensive wearable devices such as heart rate (HR) monitors and accelerometers have been sought and validated against DLW.
HR monitors have been used to predict EE based on the linear relationship between HR and EE above a given threshold. In children, HR predictions of TEE were evaluated against DLW (2,3). Predicted TEE did not differ significantly from DLW-derived TEE at the group level, but substantial differences were seen for individuals (2). The HR method did not completely address either the poor predictive power of HR during sedentary and light activities or the fact that HR can be influenced by other factors such as stress, hydration, and environmental factors. Despite individual calibration, the HR method provides only a close estimation of TEE among population groups (2,3).
Accelerometer-based predictions of EE also have been evaluated against the DLW method in a number of pediatric studies (4–9). Significant correlations were observed between accelerometer counts (AC) and TEE, activity EE (AEE), and physical activity level (PAL) (4–9). None of these studies presented differences between methods, SE, or limits of agreement. These and other studies demonstrated that accelerometers discriminate levels of physical activity but are inaccurate for the prediction of TEE or AEE in individual children (10–12).
To overcome these limitations, a number of investigators have combined HR and AC to improve estimates of free-living TEE (13–22). In general, the combination of HR and AC provided more precise estimates of TEE than either used independently. However, the models relied on individual laboratory calibration of the HR:EE and AC:EE relationships. Using room respiration calorimetry, a miniaturized HR/accelerometer monitor, and advanced mathematical techniques, we developed 2 population-specific models for the prediction of minute-by-minute EE, and hence 24-h TEE, in children and adolescents that do not require individual laboratory calibration. First, we applied cross-sectional time series (CSTS) modeling for the prediction of EE from HR and AC (23). This approach accounts for the interdependence of EE, HR, and AC over time. Second, we applied multivariate adaptive regression splines (MARS) modeling, a nonparametric regression method that approximates a complex nonlinear relationship by a series of spline functions on different intervals of the independent variable (24). Both models were developed (n = 109) and validated (n = 61) within the confines of a room respiration calorimeter using independent cohorts of children and adolescents. In this manuscript, we present further validation of the CSTS and MARS models (23,24) in the validation cohort of children and adolescents under free-living conditions using DLW (1).
Our primary aim in this study was to validate 24-h EE and Combined Awake and Sleep EE CSTS and MARS models based on observable participant characteristics, HR, and AC for the prediction of minute-by-minute EE and, hence 24-h TEE, against the 7-d DLW method in children and adolescents. Because the DLW method provides an estimate of the individual's mean TEE over a 7-d interval, our secondary aim was to demonstrate, not verify, the utility of the CSTS and MARS models to predict awake EE, sleep EE, and AEE from 7-d HR and AC records.
Materials and Methods
Study design.
CSTS and MARS models based on HR and AC for the prediction of minute-by-minute EE, and hence 24-h TEE, were validated in 60 normal-weight and overweight children (ages 5–18 y) against the stable isotope DLW method. The DLW method was executed simultaneously with HR and AC monitoring under free-living conditions for 7 d. Inclusion criteria required the children to be healthy and free from any medical condition that would limit participation in physical activity. The Institutional Review Board for Human Subject Research for Baylor College of Medicine and Affiliated Hospitals approved the protocol. All parents gave written informed consent to participate in this study.
Participants.
The characteristics of the children who took part in the DLW validation study are presented in Table 1. Participants represented white, black, Hispanic, and Asian children in the age range of 5–18 y. Twenty-four children were classified as overweight by the CDC growth charts (25). This is the same cohort of children and adolescents enrolled in the calorimeter validation (23,24), except for 1 participant who was eliminated due to failure of the Actiheart device in the field.
TABLE 1.
Description of the children and adolescents in the validation study1
| Boys | Girls | All | |
|---|---|---|---|
| n | 32 | 28 | 60 |
| Age, y | 11.9 ± 4.1 | 11.4 ± 3.9 | 11.6 ± 4.0 |
| Race/ethnicity, % white/black/Hispanic/Asian | 22/31/47/0 | 21/21/54/4 | 22/27/50/1 |
| Weight, kg | 57.6 ± 29.4 | 50.0 ± 19.5 | 54.1 ± 25.3 |
| Height, m | 1.52 ± 0.25 | 1.45 ± 0.19 | 1.49 ± 0.22 |
| BMI, kg/m2 | 23.0 ± 6.8 | 22.9 ± 5.7 | 22.9 ± 6.3 |
| BMI Z-score | 0.93 ± 1.20 | 1.02 ± 1.24 | 0.97 ± 1.21 |
| Overweight (BMI ≥ 95th percentile), % | 31 | 50 | 40 |
| FFM, kg | 42.5 ± 20.0 | 33.1 ± 11.1 | 38.2 ± 17.1 |
| FM, kg | 15.8 ± 12.1 | 18.5 ± 9.8 | 17.0 ± 11.1 |
| FM, % weight | 25.4 ± 9.0 | 34.7 ± 7.9 | 29.6 ± 9.8 |
Data are mean ± SD.
Anthropometry and body composition.
Body weight to the nearest 0.1 kg was measured with a digital balance and height to the nearest 1 mm was measured with a stadiometer. BMI was calculated as weight/height2 (kg/m2). Total body estimates of fat-free mass (FFM), fat mass (FM), and percent FM were measured by dual-energy X-ray absorptiometry using a Hologic Delphi-A whole-body scanner (Delphi-A, Hologic).
HR/accelerometer device.
The Actiheart (MiniMitter, a Respironics company) monitor was secured to the chest of each participant with 2 electrodes. Actiheart is a compact (7 mm thick, 33 mm diameter, 10 g total weight), ambulatory device equipped with an omnidirectional accelerometer and ECG signal processor. The accelerometer contains a piezoelectric transducer, whose motion sensitivity is greatest along the preferred axis (vertical, when worn as prescribed) but which will produce lesser signals when the motion is perpendicular to the preferred axis. The memory capacity of 128 kb allows data storage for 11 d for the 15-s epoch setting. The dynamic range of the accelerometer is ±25 m/s2 and its sensitivity per bit is approximately 1 count per 0.23 m/s2. Actiheart digitizes the ECG signal and calculates the HR from the inter-beat interval (IBI). It detects the QRS complex by identifying the location of the R-wave line of steepest descent. The logger firmware applies a digital threshold for this differential value that compensates for variation in the signal level due to physiological changes, noise, and physical movement. Sixteen consecutive IBI intervals are measured and the mean of the 16 intervals is calculated. Any of the IBI values that are >37.5% of the mean are identified and discarded. The mean IBI is recalculated and its inverse is multiplied by 60 to obtain the HR. The activity counts output of the MiniMitter Actiheart and CamNtech Actiheart (CamNtech) differ slightly. To utilize the CSTS or MARS equations in this paper, the activity counts from the CamNtech unit should be multiplied by 5/6 to achieve the same value as the MiniMitter unit.
Occasionally, HR values were lost due to outside electronic interference, including strong sources of electromagnetic radiation, physical artifacts, or poor electrode adhesion. For missing values during sleep, HR was replaced with the participant's mean sleeping HR. For missing values during awake periods, we developed the following CSTS equation to predict HR from AC:
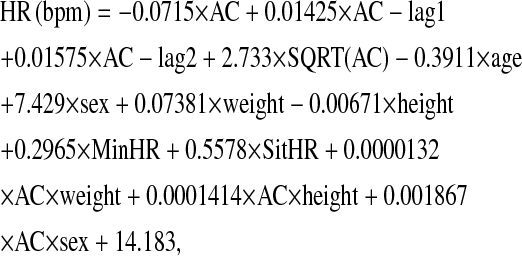 |
where AC is activity counts (cpm); age (y); sex is coded 0 = male, 1 = female; weight (kg); height (cm); MinHR is minimal 20-min mean of HR during sleep; and SitHR is the 10-min mean of HR while sitting upright.
Prior to each test, the calibration of the Actiheart device was confirmed using the Motion Performance Verification System (MiniMitter). Variability of AC measurements both within and between Actiheart monitors was tested using repeated measurements on the Motion Performance Verification System. Intra-monitor CV was 1.3% and inter-monitor CV was 4.3%. HR measurements of the Actiheart monitors were in perfect agreement with an ECG Simulator (Dale Technology) operating at rates of 60 and 120 bpm.
The Actiheart was affixed on the chest using electrodes (Skintact Premier, Leonhard Lang). The main sensor was attached left of the sternum and the lead was attached parallel along the mid-clavicular line at the level of the third intercostal space (upper position) or just below the left breast (lower position). Prior to discharge from the Children's Nutrition Research Center Metabolic Research Unit, the participant and parent(s) were given a supply of electrodes and instructed in the care of the Actiheart and electrode replacement if there was poor adhesion.
HR and AC data acquisition by Actiheart was set at 15-s intervals. Actiheart data were collapsed into 60-s intervals. HR data were filtered with an upper cutoff of 240 bpm and a lower cutoff set at 10% below the participant's minimal sleeping HR. MinHR was determined to be the lowest 20-min mean of HR during sleep. SitHR was the mean HR for a 10-min period while the participant was sitting in the upright position.
DLW method.
Free-living TEE was measured over a 7-d period using the DLW method (1). After collection of the baseline urine samples, each participant received by mouth 0.086 g/kg body weight of 2H2O at 99.9 atom %2H and 1.38 g/kg body weight of H218O at 10 atom %18O (Isotec). The bottle holding the 2H218O was rinsed 3 times with ∼5–10 mL of drinking water and the children were instructed to finish drinking all the rinses. Participants were given instructions on the proper procedure to collect a daily urine sample at home in the evening, record the date and time of the sample collection, and transfer a 1-mL urine sample each into 2 o-ring cryovials. Seven postdose urine samples were collected at home on d 1–7. The urine samples were stored frozen prior to transfer for analysis in the Gas-Isotope-Ratio Mass Spectrometry (GIRMS) Laboratory at the Children's Nutrition Research Center.
Urine samples were analyzed for stable hydrogen and oxygen isotopic enrichment by GIRMS (26). For stable hydrogen isotope ratio measurements, 10 μL of urine without further treatment were reduced to hydrogen gas with 200 mg zinc reagent at 500°C for 30 min (27). The 2H/1H isotope ratios of the hydrogen gas were measured with a Finnigan Delta-E gas-isotope-ratio mass spectrometer (Finnigan MAT). For stable oxygen isotope ratio measurements, 100 μL of urine was allowed to equilibrate with 300 mbar of CO2 of known 18O content at 25°C for 10 h using a VG ISOPREP-18 water-CO2 equilibration system (VG Isogas). At the end of the equilibration, the 18O/16O isotope ratios of the CO2 were measured with a VG SIRA-12 gas-isotope-ratio mass spectrometer (VG Isogas).
The isotopic results were normalized against 2 international water standards: Vienna-Standard Mean Ocean Water and Standard Light Antarctic Precipitation (28). The isotope dilution spaces for 2H (NH) and 18O (NO) were calculated as follows:
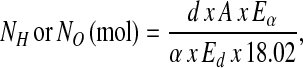 |
where d is the dose of 2H2O or H218O in grams, A is the amount of laboratory water in grams used in the dose dilution, α is the amount of 2H2O or H218O in grams added to the laboratory water in the dose dilution, Eα is the rise in 2H or 18O abundance in the laboratory water after the addition of the isotopic water, and Ed is the rise in 2H or 18O abundance in the urine samples at time zero obtained from the zero-time intercepts of the 2H and 18O decay curves in the urine samples. Carbon dioxide production rates (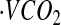 ) were calculated from the fractional turnover rates of 2H (kH) and 18O (kO) as follows:
) were calculated from the fractional turnover rates of 2H (kH) and 18O (kO) as follows:
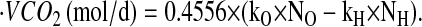 |
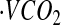 was converted to TEE using the Weir equation (29) as follows:
was converted to TEE using the Weir equation (29) as follows:
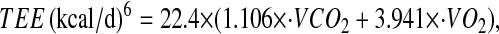 |
where 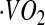 was calculated using the relationship
was calculated using the relationship 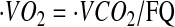 , assuming a food quotient (FQ) (30) equal to 0.86. PAL was calculated as the ratio of TEE to basal metabolic rate (BMR). AEE was calculated as the difference between TEE and BMR and thermic effect of food, which was assumed to be equal to 10% of TEE, as follows:
, assuming a food quotient (FQ) (30) equal to 0.86. PAL was calculated as the ratio of TEE to basal metabolic rate (BMR). AEE was calculated as the difference between TEE and BMR and thermic effect of food, which was assumed to be equal to 10% of TEE, as follows:
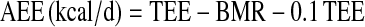 |
Room respiration calorimetry.
Oxygen consumption (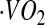 ) and
) and 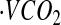 were measured continuously over a 24-h period in a 30-m3 room calorimeter. The performance of the respiration calorimeters has been described previously (31). EE was computed using the Weir equation (29). EE was averaged at 1-min intervals and used to develop the CSTS and MARS models, reported in our previous publications (23,24). In this study, the BMR was used to compute AEE and PAL. BMR was measured under thermoneutral conditions (22–24°C) upon awakening after a 12-h fast for 30 min.
were measured continuously over a 24-h period in a 30-m3 room calorimeter. The performance of the respiration calorimeters has been described previously (31). EE was computed using the Weir equation (29). EE was averaged at 1-min intervals and used to develop the CSTS and MARS models, reported in our previous publications (23,24). In this study, the BMR was used to compute AEE and PAL. BMR was measured under thermoneutral conditions (22–24°C) upon awakening after a 12-h fast for 30 min.
CSTS.
The field of CSTS analysis provides a body of techniques for analyzing the dynamics of the dependent structure of observations, i.e. repeated measurements taken from a cross section of participants (32,33). In this framework, the key idea of the application is that by pooling information from a large number of time series, we can obtain more accurate estimates of the parameters instead of evaluating a single time series. In general, the heterogeneity among the participants or cross-sectional units is modeled as a random coefficient, i.e. individual specific effects are treated as random. CSTS is a parametric approach to model a collection of correlated data, taking into account within-individual changes and between-individual heterogeneity.
The development and initial validation of our CSTS models were fully presented in our previous publication (23). Here, we briefly review the theory of CSTS modeling and present the basic structure of our models. Our final CSTS or mixed-effects regression models with random intercepts and random slopes for HR and AC with unstructured variance-covariance matrix are described by the following equation: let yij denote the minute-by-minute EE measures on the ith individual at consecutive time points j:
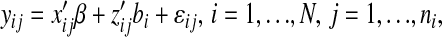 |
where β is a vector of regression coefficients associated with the covariates xij (i.e. HR, AC, etc.) and contains population-specific parameters describing average trends; bi are independent vectors of random effects associated with covariates zij and contain participant-specific parameters describing how the response of the ith individual deviates from the mean response over time; and εij is the random noise for the ith individual at time j. We assume that bi and εij are mutually independent. The term x′ijβ comprises the fixed-effects portion of the model and the term z′ijbi comprises the random effects, and zij is a subset of xij, i.e. some subset of the regression parameters that varies randomly from one child to another, accounting for sources of heterogeneity in the population.
The final CSTS models are based on time varying variables, i.e. HR and AC, participant-specific variables, and appropriate interaction terms among HR, AC, and other variables. Significant covariates included weight, height, minHR, and SitHR. Inclusion of the time-dependent variables, HR and AC, and the lagged covariates, namely lagged HR and AC, and lead values of HR substantially improved the prediction of EE. CSTS modeling was performed using STATA (release 8.2, StataCorp).
MARS model.
The MARS procedure is a nonparametric, spline-based method and makes no assumptions about the underlying functional relationship between the dependent and independent variables (34,35). Splines are generally defined to be piecewise polynomial functions of some degree q > 0, the highest power defining the polynomial. The breakpoints marking the transition from one polynomial to the next are referred to as knots (or joint points). Spline-based models require consideration of the degree of polynomials, the number of knots, and the location of knots. The fundamental idea of MARS is to use the combination of the linear truncated basis functions to approximate the model. Thus, the functions of MARS consist of single spline functions or the product of 2 or more of the truncated power functions to allow for the interactions. This allows both the additive and the interactive effects of the predictors in determining the response variable. The MARS estimate of the unknown regression function f(x) can be written as an additive function of the product basis functions:
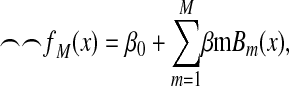 |
where β0 is the coefficient of the constant basis function B0(x) = 1, Bm(x) is the mth basis function, which may be a single spline function or product of 2 or more, βm is the coefficient of the basis function, and M is the number of basis functions in the model.
In our final MARS models (24), the basis functions utilized participant characteristics, HR and AC, 1- and 2-min lag and lead values of HR and AC, and appropriate interaction terms. Participant-specific variables included age, gender, weight, height, minHR, and SitHR. The final MARS models are based on linear combinations of 28, 28, 26, and 23 basis functions for 24-h EE, awake EE, AEE, and sleep EE, respectively. MARS was implemented using R programming language [Hornik (2009), “The R FAQ”, http://CRAN.R-project.org/doc/FAQ/R- FAQ.html, ISBN 3-900051-08-9] and Salford System (Salford Software).
Statistical analysis.
Concordance between 2 methods indicates the extent to which measurements made by one of the methods can serve as a surrogate for the other. Bland and Altman (36) recommend a graphical method to assess concordance or agreement between 2 methods. Bland and Altman plot displays the difference between methods versus the mean of the 2 methods and the “limits of agreement,” which are horizontal lines indicating mean ± 2 SD intervals encompassing intra-individual differences.
Although the Bland-Altman diagnostic plot of the difference versus the mean can provide insight into the measurement differences between 2 methods, it does not provide a single measure of agreement. Krippendorff (37) and Lin (38,39) advocate the concordance correlation coefficient (CCC) that is appropriate for measuring agreement when the data are measured on a continuous scale. The CCC consists of a precision component, the Pearson correlation coefficient, which measures how closely observations lie on the line fit to the data, and an accuracy component, which measures how closely the fitted line deviates from the 45-degree line through the origin. Therefore, when the concordance correlation is high, confidence about the similarity of the 2 methods is substantiated. Using linear regression analysis, differences between methods were also examined as a function of participant characteristics including age, sex, body weight, and composition.
Data are summarized as means ± SD. Descriptive statistics were calculated using STATA (release 11, StataCorp) and SPSS (release 17.0).
Results
A description of the 60 children and adolescents who participated in the DLW validation study is presented (Table 1). By design, participants represented both sexes and ages 5–18 y. Weight was 54.1 ± 25.3 kg with a range from 15.5 to 118.7 kg. Forty percent of the participants were classified as overweight, defined as ≥95th BMI percentile (25). By dual-energy X-ray absorptiometry, the %FM was 25.4 ± 9.0% in boys and 34.7 ± 7.9% in girls.
Actiheart monitors were worn for 6.9 ± 0.5 d, 1419 ± 34 min/d, of which 1333 ± 125 min or 94% had valid HR values. In the remaining 6%, HR values were predicted from AC. Participants slept 538 ± 50 min/d. HR and AC for the 24-h, awake, and sleep periods, as well as discrete HR values used in the models, are summarized (Table 2).
TABLE 2.
Observations from 7-d HR and accelerometry monitoring of children and adolescents enrolled in the validation study1
| Variable | |
|---|---|
| Monitor worn, min/d | 1419 ± 34 |
| Valid minutes of HR, min/d | 1333 ± 125 |
| Sleep time, min/d | 538 ± 50 |
| 24-h HR, bpm | 88 ± 10 |
| Awake HR, bpm | 97 ± 11 |
| Sleep HR, bpm | 71 ± 10 |
| MinHR, bpm | 62 ± 10 |
| SitHR, bpm | 86 ± 11 |
| 24-h AC, cpm | 40 ± 19 |
| Awake AC, cpm | 63 ± 30 |
| Sleep AC, cpm | 1 ± 1 |
Data are mean ± SD, n = 60.
Parameters generated by the DLW method are presented (Table 3). The ratio of the isotope dilution spaces (NH/NO) was 1.04 ± 0.01. The fractional turnover rates were −0.097 ± 0.024 and −0.129 ± 0.030, with R2 for the isotopic enrichments regressed on time (d) equal to 0.992 ± 0.014 and 0.994 ± 0.012 for 2H and 18O, respectively. TEE was 2153 ± 625 (range 1118–3924 kcal/d). Calculated using measured BMR, PAL was 1.54 ± 0.16 (range 1.30–2.08), indicating a range of PAL from sedentary to vigorous.
TABLE 3.
Isotope dilution spaces, fractional turnover rates, total body water, carbon dioxide production, and TEE derived from the DLW method of children and adolescents enrolled in the validation study1
| Variable | |
|---|---|
| 2H dilution space, kg | 27.9 ± 12.5 |
| 18O dilution space, kg | 26.8 ± 11.9 |
| NH/NO | 1.04 ± 0.01 |
| 2H turnover rate, d−1 | −0.097 ± 0.024 |
| 18O turnover rate, d−1 | −0.129 ± 0.030 |
| Total body water, 2H, kg | 26.8 ± 12.0 |
| Total body water, 18O, kg | 27.6 ± 12.3 |
| CO2 production, mol/d | 17.0 ± 4.9 |
| TEE, kcal/d | 2153 ± 625 |
Data are mean ± SD, n = 60.
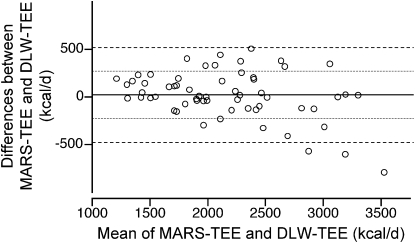
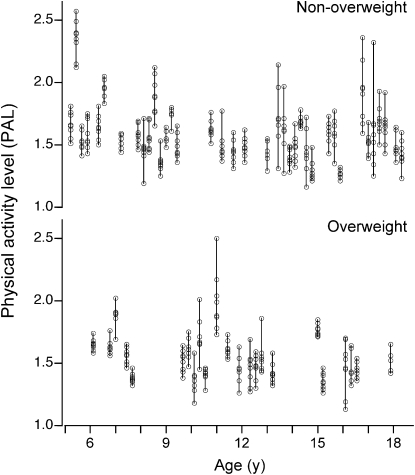
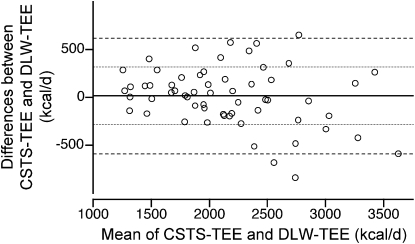
TEE values predicted by the CSTS and MARS 24-h EE models were 2163 ± 545 and 2171 ± 535 kcal/d, respectively (Table 4). Corresponding PAL values were 1.57 ± 0.22 by CSTS and 1.57 ± 0.19 by MARS. Individual PAL values for 7 d are illustrated (Fig. 1). Concordance between the predicted TEE from CSTS and MARS models and the DLW-derived TEE were evaluated by CCC and Bland Altman plots. The CCC between the CSTS and DLW methods was 0.863 (SE = 0.032; 95% CI = 0.799–0.926). The CCC between the MARS and DLW methods was 0.906 (SE = 0.022; 95% CI = 0.862–0.949). Bland-Altman plots for the comparison of the CSTS and MARS models with DLW-derived TEE are depicted (Figs. 2 and 3). Neither the CSTS nor MARS model demonstrated an absolute bias relative to DLW. The Bland-Altman plots indicated a negative trend with increasing TEE (r = −0.27–0.37; P = 0.04–0.004), due to 3 extreme observations with high TEE values. Exclusion of these observations attenuated the negative tendency such that it was no longer significant (r = −0.10–0.13; P > 0.35). TEE values predicted by the CSTS model were within ± 1 SD (307 kcal/d) of DLW-TEE for 75% of participants. TEE predicted by the MARS model were within ± 1 SD (252 kcal/d) of DLW-TEE for 75% of participants. For the combined Awake+Sleep EE models, there was a slight reduction in root mean square error (RMSE) (286 and 243 kcal/d for CSTS and MARS models, respectively). The CCC between the combined Awake+Sleep CSTS and DLW methods was 0.880 (SE = 0.028; 95% CI = 0.825–0.936). The CCC between the combined Awake+Sleep MARS and DLW methods was 0.912 (SE = 0.021; 95% CI = 0.871–0.952).
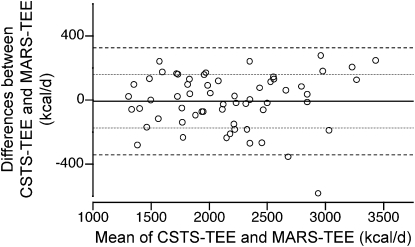
FIGURE 3 .
Bland-Altman plot of the differences in TEE predicted by the MARS and DLW methods versus the mean of the 2 methods in 60 children and adolescents enrolled in the validation study. Horizontal lines indicate mean differences, mean ± 1 SD and mean ± 2 SD intervals (1 kcal = 4.184 kJ).
TABLE 4.
EE predicted using CSTS and MARS models relative to DLW method of children and adolescents enrolled in the validation study1
| Method | DLW2 | CSTS2 | MARS2 | CSTS3 | MARS3 | CSTS4 | MARS4 |
|---|---|---|---|---|---|---|---|
| kcal/d | |||||||
| TEE | 2153 ± 625 | 2163 ± 545 | 2171 ± 535 | 10.7 ± 307 | 18.7 ± 252 | 305 | 251 |
| Combined awake+sleep EE | 2136 ± 551 | 2160 ± 541 | −16.5 ± 288 | 7.4 ± 245 | 286 | 243 | |
| Awake EE | 1643 ± 453 | 1671 ± 451 | |||||
| Sleep EE | 493 ± 118 | 489 ± 113 | |||||
| AEE | 607 ± 251 | 587 ± 194 | 608 ± 198 | −20.3 ± 228 | 0.8 ± 197 | 227 | 195 |
Data are mean ± SD, n = 60.
Measured or predicted EE.
Mean absolute error.
RMSE.
FIGURE 1 .
y-axis: individual PAL (TEE/BMR) values for 7 d predicted from the MARS model in nonoverweight (n = 36) and overweight (n = 24) children and adolescents enrolled in the validation study shown as a function of age (x-axis).
FIGURE 2 .
Bland-Altman plot of the differences in TEE predicted by the CSTS and DLW methods versus the mean of the 2 methods in 60 children and adolescents enrolled in the validation study. Horizontal lines indicate mean differences, mean ± 1 SD and mean ± 2 SD intervals (1 kcal = 4.184 kJ).
Prediction errors for the CSTS and MARS models for TEE were examined as a function of participant age, sex, body size (weight, height, BMI, BMI Z-score, FFM, FM, and %FM) and PAL. There was no evidence of bias associated with participant characteristics, except for age and FFM. Scatter plots of method differences against age and FFM indicated some heterogeneity along the horizontal axis for higher values of age and FFM. As mentioned above, there were 3 extreme observations in the data set; these individuals were teenage males with high values for FFM and TEE. Not surprisingly, age, FFM, and TEE values were intercorrelated (r = 0.72–0.92; P < 0.001). Exclusion of these 3 extreme observations eliminated the error heterogeneity.
Prediction models for rates of EE (kcal/min) also were developed for awake and sleep periods and AEE during the awake period. Because DLW provides only an estimate of TEE, these models cannot be verified directly. AEE was calculated taking a factorial approach by subtracting BMR and thermic effect of food from DLW-derived TEE. Absolute errors and RMSE for the AEE were slightly lower than the 24-h models (RMSE = 227 and 195 kcal/d for the CSTS and MARS models, respectively).
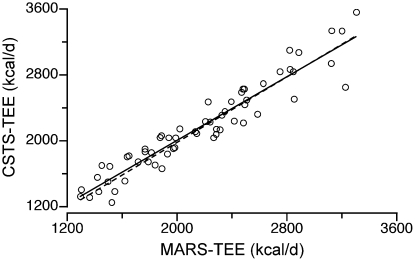
Concordance between the CSTS and MARS prediction models was also explored (Fig. 4). The CCC between the CSTS and MARS TEE models was 0.951 (SE = 0.013; 95% CI = 0.926–0.975). The Bland Altman plot revealed no systematic bias between methods (r = 0.058; P = 0.66) (Fig. 5). The CCC for the combined Awake+Sleep EE models was 0.957 (SE = 0.011; 95% CI = 0.935–0.978). The Bland Altman plot revealed no systematic bias between methods (r = 0.065; r = 0.62).
FIGURE 4 .
Concordance plot between TEE predicted by the CSTS and MARS methods in 60 children and adolescents enrolled in the validation study (CCC = 0.951, P = 0.001, SE = 0.013, 95% = CI 0.926–0.975) (1 kcal = 4.184 kJ).
FIGURE 5 .
Bland-Altman plot of the differences in TEE predicted by the CSTS and MARS methods versus the mean of the 2 methods in 60 children and adolescents enrolled in the validation study. Horizontal lines indicate mean differences, mean ± 1 SD and mean ± 2 SD intervals (1 kcal = 4.184 kJ).
Discussion
This study validated the use of CSTS and MARS models for the prediction of TEE in free-living children and adolescents. CSTS and MARS models for the prediction of TEE were developed and validated in independent cohorts across a wide range of ages, body sizes, levels of EE, and physical activity and therefore should be robust for populations of children and adolescents. Relative to the DLW method, the bias and limits of agreement indicate that the models are acceptable for groups and individuals. The high degree of concordance (CCC = 0.86–0.91) for the CSTS and MARS models with DLW method reconfirms our earlier validation of the models against room respiratory calorimetry (23,24).
Participant compliance was excellent in this field study; participants wore the Actiheart monitor continuously for nearly 7 d and urine collections and records for the DLW method were complete. The 18O and 2H isotope measurements by GIRMS were very accurate and precise (26). DLW parameters such as NH/NO and the high R2 for 2H and 18O turnover rates are indicative of high quality DLW experiments.
Although DLW is considered the gold standard for measuring TEE under free-living conditions, its application does involve several assumptions and potential sources of error (40). Validations of near-continuous respiratory gas exchange have demonstrated that the method is accurate and has a precision of 2–8%, depending on the loading dose, length of metabolic period, and number of samples (41). The principal of the method is that after dosing with water labeled with the stable isotopes 2H and 18O, 2H is lost as water and 18O is lost as water and CO2. The difference in the turnover rates of the 2 isotopes provides an estimate of 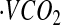 , which is converted to TEE. Across 9 human studies with small sample sizes, the agreement between respiratory gas exchange and DLW was 0.78%, with a range of SDs from 2 to 8%, indicating individual errors encompassed within the 95% CI (±2 SD) could be much higher (41).
, which is converted to TEE. Across 9 human studies with small sample sizes, the agreement between respiratory gas exchange and DLW was 0.78%, with a range of SDs from 2 to 8%, indicating individual errors encompassed within the 95% CI (±2 SD) could be much higher (41).
Based on the Bland-Altman plots and CCC, CSTS and MARS proved to be powerful statistical methods for prediction of EE from HR, physical activity, and other physiological characteristics of individuals. Predicted TEE values were within 11–14% of DLW-derived TEE in 75% of participants. Given the potential errors of the DLW, methods agreement would not be expected to be better than the precision observed in DLW validation studies (i.e. 2–8%) (41). High concordance (CCC = 0.951) between these different statistical methods affirms the validity of both models.
In contrast to the DLW method, both MARS and CSTS models provide minute-by-minute predictions of EE and thus information about patterns of EE throughout the day. Although the CSTS and MARS models performed comparably, there are inherent differences in the 2 approaches and the choice of models may depend on the research question. Our results lend strong support to the view that both CSTS and MARS methodologies produced stronger prediction equations with substantially smaller error than existing methods. Both methods provide interpretable results and are easily implemented in a straightforward manner using standard software. Both methods are strong contenders for prediction of EE. In some respects, the difference between CSTS and MARS is similar to the difference between global and local regression models. Methodologically, MARS is a simpler automated way to develop nonlinear regression models and should be especially useful in settings where complex interactions may exist among variables.
In the development and validation of the CSTS and MARS models, we intentionally enrolled children across a wide range of ages (5–18 y), body sizes (15.5–118.7 kg), and PAL (1.30–2.08) in order to produce robust prediction models. We found that method bias was not influenced by sex, weight, height, BMI, BMI Z-score, FM or %FM, or PAL. There was a negative bias with age and FFM. The slight heterogeneity reflective of the large variability in the data was attributed to 3 extreme observations in teenaged males with high TEE. While the large differences were most likely due to errors in both prediction and DLW, heterogeneity in prediction errors for larger values is not uncommon and no model can totally account for extreme observations without compromising the overall fit of the model. CSTS and MARS models can be extended to incorporate other features; however, the performance of the models in the presence of other covariates would require further validation.
Validation of CSTS and MARS modeling for the prediction of EE in children and adolescents represents a significant advancement in the field of ambulatory, physiological monitoring, because these population-specific models are laboratory calibration-free, and prediction errors are acceptable at the level of the individual. CSTS and MARS modeling successfully captured the complex dynamics among EE, HR, and physical activity in a wide array of children and adolescents.
Acknowledgments
We thank Mercedes Alejandro for contributing to study coordination, Nitesh Mehta, Lucinda Clarke, and William Chun Liu for the stable isotope ratio measurements, and Sopar Seributra and Theresa Wilson for nursing and dietary support. N.F.B. designed and conducted research, analyzed data, wrote the paper, and had primary responsibility for the final content; W.W.W. conducted the GIRMS analysis of DLW; A.L.A. and M.R.P. conducted research and analyzed data; F.A.V. conducted research and oversaw biomedical engineering; and I.F.Z. designed research, analyzed data, and wrote the paper. All authors read and approved the final manuscript.
Supported by federal funds from the NIH (DK-74387) and by the USDA/Agricultural Research Service under Cooperative Agreement number 6250-51000-037. The contents of this publication do not necessarily reflect the views or policies of the NIH or USDA, nor does mention of trade names, commercial products, or organizations imply endorsement by the U.S. Government.
Author disclosures: N. F. Butte, W. W. Wong, A. L. Adolph, M. R. Puyau, F. A. Vohra, and I. F. Zakeri, no conflicts of interest.
Abbreviations used: AC, accelerometer count; AEE, activity energy expenditure; BMR, basal metabolic rate; CCC, concordance correlation coefficient; CSTS, cross-sectional time series; DLW, doubly labeled water; EE, energy expenditure; FFM, fat-free mass; FM, fat mass; GIRMS, Gas-Isotope-Ratio Mass Spectrometry; HR, heart rate; IBI, inter-beat interval; MinHR, minimal HR; MARS, multivariate adaptive regression spline; PAL, physical activity level; RMSE, root mean square error; SitHR, sitting HR; TEE, total energy expenditure; 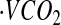 , carbon dioxide production rate;
, carbon dioxide production rate; 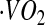 , oxygen consumption.
, oxygen consumption.
To convert kcal to kJ, the conversion factor of 1 kcal = 4.184 kJ may be used.
References
- 1.Abrams SA, Wong WW. Stable isotopes in human nutrition. Laboratory methods and research applications. London: CABI Publishing; 2003.
- 2.Livingstone MBE, Coward WA, Prentice AM, Davies PSW, Strain JJ, McKenna PG, Mahoney CA, White JA, Stewart CM, et al. Daily energy expenditure in free-living children: comparison of heart-rate monitoring with the doubly labeled water (2H2 18O) method. Am J Clin Nutr. 1992;56:343–52. [DOI] [PubMed] [Google Scholar]
- 3.Ekelund U, Yngve A, Westerterp K, Sjostrom M. Energy expenditure assessed by heart rate and doubly labeled water in young athletes. Med Sci Sports Exerc. 2002;34:1360–6. [DOI] [PubMed] [Google Scholar]
- 4.Ekelund U, Yngve A, Westerterp K, Sjostrom M. Physical activity assessed by activity monitor and doubly labeled water in children. Med Sci Sports Exerc. 2001;33:275–81. [DOI] [PubMed] [Google Scholar]
- 5.Hoos MB, Plasqui G, Gerver WJ, Westerterp KR. Physical activity level measured by doubly labeled water and accelerometry in children. Eur J Appl Physiol. 2003;89:624–6. [DOI] [PubMed] [Google Scholar]
- 6.Montgomery C, Reilly JJ, Jackson DM, Kelly LA, Slater C, Paton JY, Grant S. Relation between physical activity and energy expenditure in a representative sample of young children. Am J Clin Nutr. 2004;80:591–6. [DOI] [PubMed] [Google Scholar]
- 7.Abbott RA, Davies PSW. Habitual physical activity and physical activity intensity: their relation to body composition in 5.0–10.5-y-old children. Eur J Clin Nutr. 2004;58:285–91. [DOI] [PubMed] [Google Scholar]
- 8.Johnson RK, Russ J, Goran MI. Physical activity related energy expenditure in children by doubly labeled water as compared with the Caltrac accelerometer. Int J Obes Relat Metab Disord. 1998;22:1046–52. [DOI] [PubMed] [Google Scholar]
- 9.Lopez-Alarcon M, Merrifield J, Fields DA, Hilario-Hailey T, Franklin FA, Shewchuk RM, Oster RA, Gower BA. Ability of the Actiwatch accelerometer to predict free-living energy expenditure in young children. Obes Res. 2004;12:1859–65. [DOI] [PubMed] [Google Scholar]
- 10.Chen KY, Bassett DR Jr. The technology of accelerometry-based activity monitors: current and future. Med Sci Sports Exerc. 2005;37:S490–500. [DOI] [PubMed] [Google Scholar]
- 11.Westerterp KR. Assessment of physical activity: a critical appraisal. Eur J Appl Physiol. 2009;105:823–8. [DOI] [PubMed] [Google Scholar]
- 12.Corder K, Brage S, Ekelund U. Accelerometers and pedometers: methodology and clinical application. Curr Opin Clin Nutr Metab Care. 2007;10:597–603. [DOI] [PubMed] [Google Scholar]
- 13.Moon JK, Butte NF. Combined heart rate and activity improve estimates of oxygen consumption and carbon dioxide production rates. J Appl Physiol. 1996;81:1754–61. [DOI] [PubMed] [Google Scholar]
- 14.Treuth MS, Adolph AL, Butte NF. Energy expenditure in children predicted from heart rate and activity calibrated against respiration calorimetry. Am J Physiol. 1998;275:E12–8. [DOI] [PubMed] [Google Scholar]
- 15.Eston RG, Rowlands AV, Ingledew DK. Validity of heart rate pedometry, and accelerometry for predicting the energy cost of children's activities. J Appl Physiol. 1998;84:362–71. [DOI] [PubMed] [Google Scholar]
- 16.Rennie K, Rowsell T, Jebb SA, Holburn D, Wareham NJ. A combined heart rate and movement sensor: proof of concept and preliminary testing study. Eur J Clin Nutr. 2000;54:409–14. [DOI] [PubMed] [Google Scholar]
- 17.Strath SJ, Bassett DR Jr, Thompson DL, Swartz AM. Validity of the simultaneous heart rate-motion sensor technique for measuring energy expenditure. Med Sci Sports Exerc. 2002;34:888–94. [DOI] [PubMed] [Google Scholar]
- 18.Strath SJ, Bassett DR Jr, Swartz AM, Thompson DL. Simultaneous heart rate-motion sensor technique to estimate energy expenditure. Med Sci Sports Exerc. 2001;33:2118–23. [DOI] [PubMed] [Google Scholar]
- 19.Brage S, Brage N, Franks PW, Ekelund U, Wong MY, Andersen LB, Froberg K, Wareham NJ. Branched equation modeling of simultaneous accelerometry and heart rate monitoring improves estimate of directly measured physical activity energy expenditure. J Appl Physiol. 2004;96:343–51. [DOI] [PubMed] [Google Scholar]
- 20.Brage S, Brage N, Franks PW, Ekelund U, Wareham NJ. Reliability and validity of the combined heart rate and movement sensor Actiheart. Eur J Clin Nutr. 2005;59:561–70. [DOI] [PubMed] [Google Scholar]
- 21.Corder K, Brage S, Wareham NJ, Ekelund U. Comparison of PAEE from combined and separate heart rate and movement models in children. Med Sci Sports Exerc. 2005;37:1761–7. [DOI] [PubMed] [Google Scholar]
- 22.Crouter SE, Churilla JR, Bassett DR Jr. Accuracy of the Actiheart for the assessment of energy expenditure in adults. Eur J Clin Nutr. 2008;62:704–11. [DOI] [PubMed] [Google Scholar]
- 23.Zakeri I, Adolph AL, Puyau MR, Vohra FA, Butte NF. Application of cross-sectional time series modeling for the prediction of energy expenditure from heart rate and accelerometry. J Appl Physiol. 2008;104:1665–73.24. [DOI] [PubMed] [Google Scholar]
- 24.Zakeri IF, Adolph AL, Puyau MR, Vohra FA, Butte NF. Multivariate adaptive rregression splines (MARS) models for the prediction of energy expenditure in children and adolescents. J Appl Physiol. 2010;108:128–36. [DOI] [PubMed] [Google Scholar]
- 25.Kuczmarski RJ, Ogden CL, Grummer-Strawn LM, Flegal KM, Guo SS, Wei R, Mei Z, Curtin LR, Roche AF, Johnson CL. CDC growth charts: United States. Advance data from vital and health statistics. Hyattsville (MD): U.S. Department of Health and Human Services; 2000. [PubMed]
- 26.Wong WW, Lee LS, Klein PD. Deuterium and oxygen-18 measurements on microliter samples of urine, plasma, saliva, and human milk. Am J Clin Nutr. 1987;45:905–13. [DOI] [PubMed] [Google Scholar]
- 27.Wong WW, Clark LL, Llaurador M, Klein PD. A new zinc product for the reduction of water in physiological fluids to hydrogen gas for 2H/1H isotope ratio measurements. Eur J Clin Nutr. 1992;46:69–71. [PubMed] [Google Scholar]
- 28.Gonfiantini R. Standards for stable isotope measurements in natural compounds. Nature. 1978;271:534–6. [Google Scholar]
- 29.Weir JB. New methods for calculating metabolic rate with special reference to protein metabolism. J Physiol. 1949;109:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Black AE, Prentice AM, Coward WA. Use of food quotients to predict respiratory quotients for the doubly-labelled water method of measuring energy expenditure. Hum Nutr Clin Nutr. 1986;40:381–91. [PubMed] [Google Scholar]
- 31.Moon JK, Vohra FA, Valerio Jimenez OS, Puyau MR, Butte NF. Closed-loop control of carbon dioxide concentration and pressure improves response of room respiration calorimeters. J Nutr. 1995;125:220–8. [DOI] [PubMed] [Google Scholar]
- 32.Diggle PJ. An approach to the analysis of repeated measurements. Biometrics. 1988;44:959–71. [PubMed] [Google Scholar]
- 33.Hsiao C. Analysis of panel data. Cambridge (UK): Cambridge University Press; 2004.
- 34.Eubank RL. Nonparametric and spline smoothing. New York: Marcel Dekker; 1999.
- 35.Venables WN, Ripley BD. Modern applied statistics with S. New York: Springer-Verlag; 2002.
- 36.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–10. [PubMed] [Google Scholar]
- 37.Krippendorff K. Bivariate agreement coefficients for reliability of data. San Francisco: Jossey Bass; 1970.
- 38.Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–68. [PubMed] [Google Scholar]
- 39.Lin LI. Correction: A note on the concordance correlation coefficient. Biometrics. 2000;56:324–5. [Google Scholar]
- 40.Schoeller DA. Energy expenditure from doubly labeled water: some fundamental considerations in humans. Am J Clin Nutr. 1983;38:999–1005. [DOI] [PubMed] [Google Scholar]
- 41.Schoeller DA. Measurement of energy expenditure in free-living humans by using doubly labeled water. J Nutr. 1988;118:1278–89. [DOI] [PubMed] [Google Scholar]