Abstract
The USDA's Healthy Eating Index-2005 (HEI-2005) is a tool to quantify the quality of diet consumed by individuals in the U.S. It comprises 12 components expressed as ratios of a food group or nutrient intake to energy intake. Components are scored on a scale from 0 to M, where M is 5, 10, or 20. Ideally, the HEI-2005 is calculated on the basis of the usual, or long-term average, dietary intake of an individual. In recent cycles of the NHANES, intake data have been collected via 24-h recalls for more than 1 d on most participants. We present here a statistical method to estimate a population's distribution of usual HEI-2005 component scores when ≥2 d of dietary information is available for a sample of individuals from the population. Distributions for the total population and for age-gender subgroups may be estimated. The method also yields an estimate of the population's mean total HEI-2005 score. Application of the method to NHANES data for 2001–2004 yielded estimated distributions for all 12 components; those of total vegetables (range 0–5), whole grains (range 0–5), and energy from solid fats, alcoholic beverages, and added sugars (range 0–20) are presented. The total population mean scores for these components were 3.21, 1.00, and 8.41, respectively. An estimated 30% of the total population had a score of <2.5 for total vegetables. This is the first time, to our knowledge, that estimated distributions of usual HEI-2005 component scores have been published.
Introduction
The USDA Healthy Eating Index-2005 (HEI-2005)7 is a tool to quantify and evaluate diet quality in terms of its conformity to the 2005 Dietary Guidelines for Americans (1,2). It comprises 12 components that are scored on a scale from 0 to M, where M is 5, 10, or 20, according to the component. The maximum total score is 100. Each component is expressed as a ratio of an individual's intake of a specific food or nutrient to their intake of energy, before scoring.
The HEI-2005 can be applied to individual diets or to the food environment (3). At the individual level, the HEI-2005 ideally should be calculated on the basis of the usual dietary intake of each individual, i.e. their mean daily intake over a specified period (often 1 y). This is in line with the Institute of Medicine's emphasis on assessing usual diets. Both the Institute of Medicine and the Dietary Guidelines for Americans 2005 point out that recommendations are to be met over the long term (4,5). In practice, when only 1 d of food intake, collected via a 24-h recall (24HR), is available for each individual, the HEI-2005 component and total scores of each individual's 1-d intake can be calculated, but this will lead to a biased measure of the individual's HEI-2005 score of usual intake, because the scoring system is truncated at 0 on one end and at 5, 10, or 20 at the other.
One of the most important uses of the HEI is to monitor the dietary intake of the population over time. For this purpose, the natural measures of the quality of the population's diet are the population's distributions of HEI component and total scores, based on the usual intake of each component. Of special interest are the means of these distributions. A previous report showed that when only one 24HR per individual is available, the population's mean HEI-2005 scores could not be estimated without bias but that the method with least bias was the score of the population ratio (6). Furthermore, in these circumstances, no satisfactory method of estimating the full population distribution exists.
In this paper, we describe a method of estimating the population's distribution of HEI-2005 component scores of usual intake when data are available on a sample of individuals, of which a substantial subsample supply 2 24HR. We apply the method to data from the 2001–2004 NHANES and present distributions of selected HEI components. In addition, we compare the estimates of the population means derived from this method with those derived from the score of the population ratio, based on the first 24HR.
Methods
Data
The data for this study were 24,963 recalls obtained from 17,311 participants in the 2001–2004 NHANES. All recalls obtained from individuals aged ≥2 y were included, except those deemed unreliable by survey staff (268 recalls from 268 individuals).
Dietary intakes were assessed via computer-assisted, interviewer-administered 24HR. For the 9036 individuals representing the 2001–2002 NHANES, only 1 recall was available. Of the 8275 individuals representing the 2003–2004 NHANES, 2 recalls were available for 7652 individuals and 623 individuals supplied a single recall. Overall, for the combined 2001–2004 data set, 44% of the participants completed 2 24HR. The first dietary recall was conducted in a mobile examination center and the second one was conducted 3–10 d later via telephone.
The NHANES has a complex, multistage, probability design. For this study, replicate weight sets suitable for the Balanced Repeated Replication method of variance estimation (7) were obtained from the USDA Agricultural Research Service. The replicate weights were based on the dietary survey weights accompanying the NHANES data files, which adjust for survey design, nonresponse, and day of week.
The NHANES 2001–2004 surveys were approved by the NHANES Institutional Review Board under protocol 98–12. Further information about the NHANES is available elsewhere (8).
Estimating the population distribution of an HEI component
Seven of the 12 HEI dietary components [total grains; total vegetables; meat and beans; oil; saturated fat; sodium; solid fats, alcoholic beverages, and added sugars (SoFAAS)] are consumed nearly every day by nearly everyone in the U.S. population, and 5 (total fruit, whole fruit, whole grains, dark-green/orange vegetables and legumes, milk) are episodically consumed.
Methods for estimating the distribution of the ratio of usual intakes of 2 foods or nutrients consumed every day (e.g. total grains:energy) have been described previously (9). Extending the method to estimate the distribution of the HEI-2005 score for such components involves an extra calculation that translates the ratio to the HEI-2005 score in the Monte-Carlo step of the procedure.
Joint statistical model for the intake of an episodically consumed food and energy
The method for estimating the distribution of the scores for the 5 HEI components that are episodically consumed requires using a new method, described here, that is based on a joint model for the numerator (episodically consumed food/nutrient) and denominator (energy). A more precise and technical description of the method is provided in Supplemental Appendix A.
The model is an extension of that described by Tooze et al. (10). They described a 2-part model that comprises, in the first part, a model of the probability to consume the episodically consumed food on a particular day and, in the second part, a model for the amount consumed on a consumption day. The method used in this paper extends this to a 3-part model, where the third part is a model for the amount of energy consumed (on any day).
The first part of the model is a logistic regression model for the probability to consume the food group, with an intercept (fixed effect), an indicator for whether the reported day was a weekday or a weekend (fixed effect), an indicator for the sequence number (first vs. second) of the report (fixed effect), indicators for age group (fixed effects), and a subject-specific term (random effect). The 2nd and 3rd parts of the model are linear mixed-effects models for a mathematically transformed amount of the food group (or energy) consumed, with the same terms as in the logistic regression model together with a within-subject error term (random error). In practice, a Box-Cox (power) transformation was used, and the power was chosen to minimize the mean squared error around a straight line fit to a weighted QQ plot of the reported amounts of the food group consumed on consumption days (or of energy), using the survey sampling weights of each participant.
The weekday/weekend indicator was included in the model to accommodate the difference in intake that often occurs between the weekend (Friday through Sunday) and the rest of the week. The sequence number indicator was included to accommodate the possibility that participants report less fully on the second recall than on the first. The first recall was taken to be the unbiased report.
The age-group indicator, which is a factor with several levels, was included to allow estimation of the distribution within specific age groups. Including such indicators in the model allows estimation of distributions in subpopulations and results in much greater precision than running the model on only the subset of data from that subpopulation (10). For the analysis of the diets of children aged 2–8 y, an extra indicator for gender (fixed effect) was included. For older age groups, males and females were analyzed separately.
The 3 subject-specific terms in the model were assumed to have a trivariate normal distribution with the variances and covariances estimated from the data. Likewise, the 2 within-subject terms were assumed to be bivariate normal and independent of the subject-specific terms and required another 2 variances and a covariance to be estimated. The model parameters could be estimated, because many participants completed more than one 24HR. If there are no repeated determinations, then within-subject variance parameters cannot be estimated. The 3 parts of the model are linked by having common covariates, by the covariances between the subject-specific effects, and by the covariances between the within-subject effects.
There are 2 important implicit assumptions of this 3-part model. First, it is assumed that an individual's 24HR-reported intake is an unbiased estimate of true usual intake. In particular, it is assumed that the probability to report consumption is equal to the true probability to consume and that the average reported amount on a consumption day is equal to the true average amount on a consumption day. We note that this is a strong assumption that may not be exactly true.
Second, it is assumed that intake of an episodically consumed food group on a given day can be zero, but usual intake of that food group is assumed to be always greater than zero, although it could be very small. There may be foods that some people never consume (e.g. alcoholic beverages). Kipnis et al. (11) described an extension of the present model that allows usual intake to be zero, but with only 2 24HR/person, it is difficult in practice to distinguish never consumers from infrequent consumers, and estimation of the model parameters becomes unstable.
Execution of the method
The method was executed in 2 steps. In the first step, the data from the survey were used to estimate the parameters of the statistical model. In the second step, the estimated parameter values were used in Monte-Carlo simulations to generate a pair of usual intakes of the HEI component in question and energy for “pseudo-individuals” representative of the population. In the 3rd step, the HEI-2005 component score was calculated for each pseudo-individual and the population distribution constructed from these scores.
Step 1.
The model was fitted to the data using the NLMIXED procedure in the statistical software package SAS, with the sampling weights of each participant incorporated into the analysis. The output yielded estimates of the regression coefficients of the fixed effects and the variances and covariances of the random effects. Three runs of the NLMIXED procedure for each HEI component were performed: for children aged 2–8 y, males aged ≥9 y, and females ≥9 y.
Step 2.
Monte Carlo simulations were then run using the parameter values estimated from the model. These simulations generated pairs of usual intakes of the food group and energy for a large number of pseudo-individuals, each set of 100 pseudo-individuals corresponding to a participant in the sample. The details of these simulations are described in the online Supplemental Appendix A.
Step 3.
The ratio of usual HEI component intake:usual energy was calculated for each pseudo-individual and the HEI-2005 score was calculated from the ratio. Using the sampling weights for each pseudo-individual, the percentiles of the distribution of HEI-2005 scores were then estimated. SE of the distribution mean and percentiles were estimated using balanced repeated replication, which accounted for the stratification and clustering of the NHANES sampling design.
Output from the Monte-Carlo Simulations
These procedures were used to estimate distributions for 10 age-gender subgroups. The distributions for men and women ≥19 y were estimated by combining the distributions of 4 finer age groupings, according to the population proportion in each subgroup. Results are shown for the following 3 HEI components: total vegetables, whole grains, and SoFAAS. Proportions of the population who consumed the recommended levels of vegetables or more, i.e. achieved the maximum score of 5 for total vegetable consumption, and proportions who consumed less than one-half the recommended level, i.e. had scores <2.5, were also estimated.
Comparison of estimated population means with those obtained from approximate methods
As part of the estimation of the full distribution of HEI-2005 component scores, the 3-part model method yields an estimate of the population mean score. We recently recommended that, when only one 24HR is available per individual, the score of the population ratio be used to estimate the population mean in preference to the mean score or the score of the mean ratio (6). The definitions of these methods follow.
Score of the population ratio.
On the basis of the individual 24HR reports, calculate the population's mean intake of the HEI component and the population's mean energy intake and take the ratio of these. Then calculate the HEI-2005 component score based on this ratio of the means.
Mean score.
Calculate each individual's HEI-2005 component score on the basis of the single 24HR. Then, take the (arithmetic) mean of the score over individuals.
Score of the mean ratio.
For each individual, calculate the ratio of the 24HR reported intake of the HEI component to the 24HR reported energy intake. Take the mean of these ratios over individuals. Then, calculate the HEI-2005 component score based on this mean ratio.
None of these approximate methods can account for daily variation, because there are no repeat 24HR and they are therefore expected to be biased. In this paper, we computed each of these 3 measures for each component, using the first 24HR, and compared these estimates with those derived from the 3-part model. Because the latter estimate is based on more than one 24HR and takes proper account of the daily variation, we regard it as the gold standard. Our interest is in how close the score of the population ratio comes to the gold standard estimate and whether it performs better than the other 2 approximate methods.
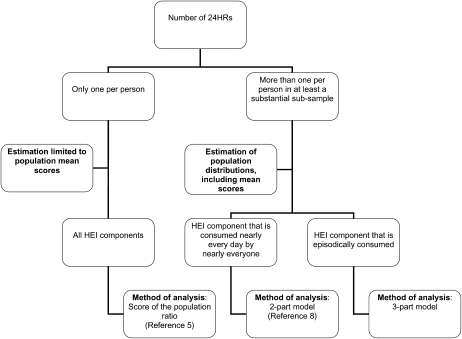
Figure 1 displays the estimates that can be obtained and the analytic approaches required, showing how they vary by the number of 24HR available per person and the nature of the dietary components under study.
FIGURE 1 .
Recommended methods for estimating population-level HEI-2005 scores with 24HR.
Values in the text are means or proportions ± 1 SE or estimated percentiles. The documented SAS code for performing these analyses is available online (12).
Results
The estimated mean HEI-2005 score for total vegetables (range 0–5) in the total population was 3.2 ± 0.03 and the median 3.1 (Table 1). The 5th and 95th percentiles were 1.5 and 5.0, respectively. There was substantial variation with age and gender, with older persons and women tending to have higher scores.
TABLE 1.
Distribution of the HEI-2005 score for total vegetables (range 0–5) in the total U.S. population and selected age-gender subgroups, 2001–20041
| Percentiles |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Subpopulation | n | Mean ± SE | 5% | 10% | 25% | 50% | 75% | 90% | 95% |
| Males and females | |||||||||
| 2–3 y | 937 | 2.18 ± 0.07 | 1.07 | 1.26 | 1.62 | 2.10 | 2.65 | 3.21 | 3.57 |
| 4–8 y | 1701 | 2.17 ± 0.07 | 1.13 | 1.31 | 1.66 | 2.11 | 2.60 | 3.12 | 3.44 |
| Males | |||||||||
| 9–13 y | 1061 | 2.44 ± 0.10 | 1.11 | 1.30 | 1.72 | 2.32 | 3.02 | 3.75 | 4.26 |
| 14–18 y | 1424 | 2.50 ± 0.09 | 1.17 | 1.39 | 1.83 | 2.39 | 3.06 | 3.75 | 4.22 |
| 19–30 y | 1100 | 2.86 ± 0.07 | 1.44 | 1.70 | 2.18 | 2.78 | 3.47 | 4.19 | 4.66 |
| 31–50 y | 1466 | 3.22 ± 0.07 | 1.70 | 1.97 | 2.49 | 3.15 | 3.92 | 4.69 | 5.00 |
| 51–70 y | 1252 | 3.64 ± 0.08 | 1.93 | 2.26 | 2.87 | 3.66 | 4.57 | 5.00 | 5.00 |
| ≥71 y | 832 | 3.64 ± 0.09 | 1.86 | 2.18 | 2.82 | 3.65 | 4.66 | 5.00 | 5.00 |
| ≥19 y | 4650 | 3.28 ± 0.05 | 1.67 | 1.96 | 2.50 | 3.22 | 4.06 | 4.96 | 5.00 |
| Females | |||||||||
| 9–13 y | 1112 | 2.62 ± 0.09 | 1.19 | 1.42 | 1.88 | 2.50 | 3.24 | 4.03 | 4.57 |
| 14–18 y | 1362 | 2.72 ± 0.10 | 1.25 | 1.49 | 1.97 | 2.61 | 3.37 | 4.18 | 4.74 |
| 19–30 y | 1325 | 3.23 ± 0.09 | 1.62 | 1.91 | 2.44 | 3.15 | 3.99 | 4.87 | 5.00 |
| 31–50 y | 1595 | 3.58 ± 0.07 | 1.87 | 2.18 | 2.79 | 3.57 | 4.51 | 5.00 | 5.00 |
| 51–70 y | 1284 | 4.01 ± 0.06 | 2.22 | 2.60 | 3.28 | 4.19 | 5.00 | 5.00 | 5.00 |
| ≥71 y | 860 | 4.03 ± 0.09 | 2.17 | 2.55 | 3.29 | 4.26 | 5.00 | 5.00 | 5.00 |
| ≥19 y | 5064 | 3.67 ± 0.05 | 1.88 | 2.21 | 2.84 | 3.69 | 4.72 | 5.00 | 5.00 |
| All persons | |||||||||
| ≥2 y | 17,311 | 3.21 ± 0.03 | 1.47 | 1.75 | 2.34 | 3.13 | 4.11 | 5.00 | 5.00 |
| Observed2 | 17,311 | 2.95 ± 0.02 | 0.18 | 0.72 | 1.67 | 2.92 | 4.64 | 5.00 | 5.00 |
Estimated from data on 17311 participants in NHANES.
Empirical distribution of 24HR-based HEI-2005 score.
The estimated mean HEI-2005 score for whole grains (range 0–5) in the total population was 1.0 ± 0.03 and the median 0.7 (Table 2). The 5th and 95th percentiles were 0.1 and 2.9, respectively. Older persons tended to have a higher score than younger persons and women tended to higher scores than men. Adolescent males (14–18 y) appeared to have a lower score than preadolescents (9–13 y) and the score for males rose gradually with increasing age after 18 y. Among females, the mean score was similar between the ages of 9 and 30 y and increased with age thereafter.
TABLE 2.
Distribution of the HEI-2005 score for whole grains (range 0–5) in the total U.S. population and selected age-gender subgroups, 2001–20041
| Percentiles |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Subpopulation | n | Mean ± SE | 5% | 10% | 25% | 50% | 75% | 90% | 95% |
| Males and females | |||||||||
| 2–3 y | 937 | 0.95 ± 0.05 | 0.13 | 0.21 | 0.41 | 0.77 | 1.29 | 1.93 | 2.40 |
| 4–8 y | 1701 | 0.85 ± 0.05 | 0.12 | 0.18 | 0.36 | 0.69 | 1.16 | 1.73 | 2.15 |
| Males | |||||||||
| 9–13 y | 1061 | 0.95 ± 0.06 | 0.05 | 0.10 | 0.27 | 0.67 | 1.33 | 2.18 | 2.85 |
| 14–18 y | 1424 | 0.56 ± 0.04 | 0.02 | 0.04 | 0.11 | 0.33 | 0.77 | 1.41 | 1.90 |
| 19–30 y | 1100 | 0.65 ± 0.07 | 0.02 | 0.05 | 0.14 | 0.40 | 0.90 | 1.61 | 2.17 |
| 31–50 y | 1466 | 0.79 ± 0.05 | 0.04 | 0.07 | 0.20 | 0.53 | 1.10 | 1.85 | 2.43 |
| 51–70 y | 1252 | 1.24 ± 0.07 | 0.08 | 0.16 | 0.41 | 0.92 | 1.75 | 2.77 | 3.53 |
| ≥71 y | 832 | 1.84 ± 0.10 | 0.20 | 0.36 | 0.78 | 1.53 | 2.60 | 3.90 | 4.91 |
| ≥19 y | 4650 | 0.97 ± 0.04 | 0.04 | 0.08 | 0.24 | 0.64 | 1.35 | 2.31 | 3.06 |
| Females | |||||||||
| 9–13 y | 1112 | 0.80 ± 0.06 | 0.06 | 0.11 | 0.27 | 0.60 | 1.11 | 1.74 | 2.23 |
| 14–18 y | 1362 | 0.83 ± 0.07 | 0.05 | 0.10 | 0.25 | 0.59 | 1.17 | 1.91 | 2.42 |
| 19–30 y | 1325 | 0.79 ± 0.06 | 0.06 | 0.10 | 0.25 | 0.58 | 1.11 | 1.78 | 2.28 |
| 31–50 y | 1595 | 0.99 ± 0.06 | 0.08 | 0.14 | 0.34 | 0.74 | 1.39 | 2.17 | 2.73 |
| 51–70 y | 1284 | 1.44 ± 0.06 | 0.17 | 0.29 | 0.62 | 1.19 | 1.98 | 2.94 | 3.61 |
| ≥71 y | 860 | 1.64 ± 0.08 | 0.22 | 0.36 | 0.74 | 1.37 | 2.28 | 3.32 | 4.08 |
| ≥19 | 5064 | 1.14 ± 0.04 | 0.09 | 0.16 | 0.39 | 0.87 | 1.60 | 2.50 | 3.14 |
| All persons | |||||||||
| ≥2 y | 17,311 | 1.00 ± 0.03 | 0.06 | 0.11 | 0.30 | 0.72 | 1.39 | 2.27 | 2.94 |
| Observed2 | 17,311 | 1.00 ± 0.03 | 0.00 | 0.00 | 0.00 | 0.37 | 1.52 | 3.06 | 4.50 |
Estimated from data on 17,311 participants in NHANES.
Empirical distribution of 24HR-based HEI-2005 score.
The estimated mean HEI-2005 score for SoFAAS (range 0–20) in the total population was 8.4 ± 0.2 and the median 8.4 (Table 3). The 5th and 95th percentiles were 0 and 17.1, respectively. Scores varied substantially with age and gender, with older persons and women tending to have higher scores. Scores were higher among infants and children (up to 8 y) than preadolescents and adolescents (9–18 y). Note that, unlike the vegetable and grain components of HEI-2005, a higher SoFAAS score indicates a lower intake.
TABLE 3.
Distribution of the HEI-2005 score for SoFAAS (range 0–20) in the total U.S. population and selected age-gender subgroups, 2001–20041
| Percentiles |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Subpopulation | n | Mean ± SE | 5% | 10% | 25% | 50% | 75% | 90% | 95% |
| Males and females | |||||||||
| 2–3 y | 937 | 9.75 ± 0.33 | 2.28 | 4.04 | 6.97 | 9.96 | 12.71 | 15.05 | 16.33 |
| 4–8 y | 1701 | 8.41 ± 0.36 | 1.00 | 2.80 | 5.64 | 8.58 | 11.27 | 13.59 | 14.88 |
| Males | |||||||||
| 9–13 y | 1061 | 7.39 ± 0.32 | 0.00 | 0.00 | 3.42 | 7.38 | 11.02 | 13.99 | 15.75 |
| 14–18 y | 1424 | 6.67 ± 0.31 | 0.00 | 0.00 | 2.75 | 6.56 | 10.07 | 13.03 | 14.75 |
| 19–30 y | 1100 | 6.00 ± 0.37 | 0.00 | 0.00 | 2.07 | 5.75 | 9.25 | 12.24 | 13.93 |
| 31–50 y | 1466 | 7.07 ± 0.33 | 0.00 | 0.00 | 3.34 | 7.03 | 10.44 | 13.34 | 15.00 |
| 51–70 y | 1252 | 9.00 ± 0.33 | 0.00 | 1.75 | 5.36 | 9.14 | 12.62 | 15.54 | 17.26 |
| ≥71 y | 832 | 10.32 ± 0.41 | 0.57 | 2.94 | 6.68 | 10.61 | 14.14 | 17.12 | 18.73 |
| ≥19 y | 4650 | 7.61 ± 0.21 | 0.00 | 0.05 | 3.70 | 7.56 | 11.20 | 14.30 | 16.11 |
| Females | |||||||||
| 9–13 y | 1112 | 7.83 ± 0.35 | 0.00 | 0.00 | 3.79 | 7.82 | 11.56 | 14.70 | 16.49 |
| 14–18 y | 1362 | 7.36 ± 0.25 | 0.00 | 0.00 | 3.21 | 7.26 | 11.05 | 14.20 | 16.05 |
| 19–30 y | 1325 | 7.56 ± 0.43 | 0.00 | 0.00 | 3.55 | 7.54 | 11.20 | 14.29 | 16.03 |
| 31–50 y | 1595 | 8.69 ± 0.30 | 0.00 | 0.99 | 4.84 | 8.80 | 12.46 | 15.51 | 17.23 |
| 51–70 y | 1284 | 11.40 ± 0.29 | 1.72 | 4.15 | 7.94 | 11.75 | 15.26 | 18.14 | 19.82 |
| ≥71 y | 860 | 11.49 ± 0.36 | 1.51 | 4.00 | 7.87 | 11.86 | 15.52 | 18.59 | 20.00 |
| ≥19 y | 5064 | 9.49 ± 0.26 | 0.00 | 1.56 | 5.53 | 9.67 | 13.47 | 16.65 | 18.46 |
| All persons | |||||||||
| ≥2 y | 17,311 | 8.41 ± 0.18 | 0.00 | 0.74 | 4.51 | 8.45 | 12.12 | 15.29 | 17.12 |
| Observed2 | 17,311 | 9.06 ± 0.15 | 0.00 | 0.00 | 3.64 | 8.93 | 13.81 | 18.70 | 20.00 |
Estimated from data on 17,311 participants in NHANES.
Empirical distribution of 24HR-based HEI-2005 score.
Supplemental tables providing SE for the individual percentile estimates for these HEI components may be found at the Web site riskfactor.cancer.gov/usualintakes; the Web site also presents the estimated distributions for the other 9 components.
The last row in Tables 1–3 show the observed distribution of HEI-2005 scores based on a single 24HR or the mean of 2 24HR. These distributions include day-to-day dietary variation and consequently are wider than our estimates of the usual intake distributions. For example, in Table 1, the estimated 5th percentile for the total vegetables HEI-2005 component score was much lower (0.18) in the observed distribution than in the usual intake distribution (1.47). Likewise, the 75th percentile in the observed distribution was higher (4.64) than in the usual intake distribution (4.11).
The methodology described also allows estimation of the proportion of the population whose HEI-2005 scores fall within a chosen interval. Only 12 ± 1% of the total population achieved a maximum score of 5, reflecting total vegetable consumption at or above the recommended level [≥1.1 cup equivalents/1000 kcal (≥63.1 mL/1000 kJ)] (Table 4). However, 30 ± 1% had scores <2.5 [0.55 cup equivalents/1000 kcal (31.5 mL/1000kJ)], reflecting consumption at less than one-half the recommended level. Among those aged ≤18 y, a particularly high percentage of the population (46–71%) had scores <2.5.
TABLE 4.
Proportions in the total U.S. population and selected age-gender subgroups with total vegetable HEI-2005 score below 2.5 and equal to 5, 2001–20041
| Subpopulation | n | Proportion <2.5 ± SE | Proportion = 5 ± SE |
|---|---|---|---|
| Males and females | |||
| 2–3 y | 937 | 0.69 ± 0.04 | 0.00 ± 0.00 |
| 4–8 y | 1701 | 0.71 ± 0.04 | 0.00 ± 0.00 |
| Males | |||
| 9–13 y | 1061 | 0.57 ± 0.04 | 0.02 ± 0.01 |
| 14–18 y | 1424 | 0.55 ± 0.04 | 0.01 ± 0.01 |
| 19–30 y | 1100 | 0.38 ± 0.03 | 0.03 ± 0.01 |
| 31–50 y | 1466 | 0.25 ± 0.03 | 0.07 ± 0.01 |
| 51–70 y | 1252 | 0.15 ± 0.02 | 0.17 ± 0.03 |
| ≥71 y | 832 | 0.17 ± 0.03 | 0.19 ± 0.02 |
| ≥19 y | 4650 | 0.25 ± 0.02 | 0.10 ± 0.01 |
| Females | |||
| 9–13 y | 1112 | 0.50 ± 0.04 | 0.03 ± 0.01 |
| 14–18 y | 1362 | 0.46 ± 0.04 | 0.04 ± 0.01 |
| 19–30 y | 1325 | 0.27 ± 0.03 | 0.09 ± 0.02 |
| 31–50 y | 1595 | 0.17 ± 0.02 | 0.16 ± 0.02 |
| 51–70 y | 1284 | 0.09 ± 0.02 | 0.30 ± 0.02 |
| ≥71 y | 860 | 0.09 ± 0.02 | 0.33 ± 0.03 |
| ≥19 y | 5064 | 0.16 ± 0.02 | 0.20 ± 0.02 |
| All persons | |||
| ≥2 y | 17,311 | 0.30 ± 0.01 | 0.12 ± 0.01 |
Estimated from data on 17,311 participants in NHANES, 2001–2004.
Of the 3 methods for estimating the mean HEI-2005 score when only one 24HR is available, the score of the population ratio was the closest to the estimate obtained from the 3-part model (that uses 2 24HRs) for the majority of components for both men and women (Tables 5 and 6). It was also the closest of the 3 methods to the 3-part model estimate for HEI-2005 total score summed over the 12 components.
TABLE 5.
Comparison of the results of 4 methods for estimating the mean HEI-2005 component and total scores for U.S. males aged ≥19 y, 2001–20041
| HEI Component (maximum score) | Mean Score2 ± SE | Score of Mean Ratio2 ± SE | Score of Population Ratio2 ± SE | Three-part Model Estimate3 ± SE |
|---|---|---|---|---|
| Total fruit (5) | 1.98 ± 0.06 | 2.86 ± 0.12 | 2.62 ± 0.12* | 2.34 ± 0.08 |
| Whole fruit (5) | 1.74 ± 0.05 | 3.34 ± 0.14 | 2.89 ± 0.14* | 2.34 ± 0.08 |
| Total vegetables (5) | 2.94 ± 0.04 | 3.45 ± 0.06 | 3.30 ± 0.06* | 3.28 ± 0.05 |
| DOL vegetables (5) | 1.07 ± 0.04 | 1.37 ± 0.05 | 1.28 ± 0.05* | 1.30 ± 0.05 |
| Total grains (5) | 4.14 ± 0.02 | 5.00 ± 0.00* | 5.00 ± 0.02* | 4.60 ± 0.03 |
| Whole grains (5) | 0.93 ± 0.03 | 1.02 ± 0.04 | 0.94 ± 0.04* | 0.97 ± 0.04 |
| Milk (10) | 2.77 ± 0.06* | 3.07 ± 0.08 | 3.03 ± 0.10 | 2.89 ± 0.07 |
| Meat/beans (10) | 8.39 ± 0.06 | 10.00 ± 0.00* | 10.00 ± 0.00* | 9.38 ± 0.05 |
| Oil (10) | 5.48 ± 0.08 | 6.76 ± 0.15* | 6.85 ± 0.16 | 6.71 ± 0.13 |
| Saturated fat (10) | 5.95 ± 0.07* | 6.68 ± 0.14 | 6.37 ± 0.14 | 6.15 ± 0.11 |
| Sodium (10) | 4.29 ± 0.06 | 3.72 ± 0.07 | 4.02 ± 0.08* | 3.94 ± 0.07 |
| SoFAAS (20) | 8.24 ± 0.17 | 7.52 ± 0.26* | 6.70 ± 0.27 | 7.61 ± 0.21 |
| Total Score (100) | 47.91 ± 0.38 | 54.79 ± 0.59 | 52.99 ± 0.61* | 51.50 ± 0.41 |
Estimated from data on 4650 participants in NHANES, 2001–2004.
Estimate based on the first 24HR.
Estimate based on 2 24 HR.
*The closest of the 3 estimates to that from the 3-part model.
TABLE 6.
Comparison of the results of 4 methods for estimating the mean HEI-2005 component and total scores for U.S. females aged ≥19 y, 2001–20041
| HEI Component (maximum score) | Mean Score2 ± SE | Score of Mean Ratio2 ± SE | Score of Population Ratio2 ± SE | Three-Part Model Estimate3 ± SE |
|---|---|---|---|---|
| Total fruit (5) | 2.31 ± 0.07* | 3.58 ± 0.14 | 3.31 ± 0.13 | 2.80 ± 0.09 |
| Whole fruit (5) | 2.09 ± 0.06* | 4.58 ± 0.18 | 4.03 ± 0.16 | 2.89 ± 0.10 |
| Total vegetables (5) | 3.15 ± 0.04 | 4.04 ± 0.07 | 3.79 ± 0.06* | 3.67 ± 0.05 |
| DOL vegetables (5) | 1.27 ± 0.05 | 1.82 ± 0.08 | 1.68 ± 0.08* | 1.69 ± 0.07 |
| Total grains (5) | 4.25 ± 0.03 | 5.00 ± 0.00* | 5.00 ± 0.00* | 4.67 ± 0.04 |
| Whole grains (5) | 1.07 ± 0.03 | 1.21 ± 0.04 | 1.12 ± 0.04* | 1.14 ± 0.04 |
| Milk (10) | 3.12 ± 0.08 | 3.50 ± 0.09 | 3.46 ± 0.10* | 3.32 ± 0.08 |
| Meat/beans (10) | 7.89 ± 0.06 | 10.00 ± 0.00* | 10.00 ± 0.00* | 9.13 ± 0.11 |
| Oil (10) | 5.80 ± 0.06 | 7.46 ± 0.15* | 7.68 ± 0.17 | 7.35 ± 0.13 |
| Saturated fat (10) | 6.01 ± 0.10* | 6.69 ± 0.20 | 6.33 ± 0.17 | 6.08 ± 0.14 |
| Sodium (10) | 4.16 ± 0.08 | 3.51 ± 0.11 | 3.78 ± 0.10* | 3.74 ± 0.10 |
| SoFAAS (20) | 9.82 ± 0.21 | 9.54 ± 0.28* | 8.81 ± 0.26 | 9.49 ± 0.26 |
| Total score (100) | 50.93 ± 0.47 | 60.92 ± 0.82 | 58.97 ± 0.75* | 55.97 ± 0.64 |
Estimated from data on 5064 participants in NHANES, 2001–2004.
Estimate based on the first 24HR.
Estimate based on 2 24HR.
*The closest of the 3 estimates to that from the 3-part model.
Discussion
The HEI-2005 component scores are based upon ratios of reported intakes of food groups or nutrients to that of total energy. In this way, the HEI-2005 evaluates the appropriateness of the mix of foods, i.e. the quality, rather than the quantity, of the diet. Estimating distribution properties of ratios is always more challenging than estimating those of single variables. For example, special methods are required to estimate the population distribution of usual intake of a ratio such as the percentage of energy from saturated fat (9).
Such complications are compounded by 2 other features of HEI components. First, several of the components involve foods that are episodically consumed, i.e. they are not consumed every day by everyone in the population. The basic quantity of interest is a ratio of usual intake of that food:usual total energy intake. Analysis of the ratio of an episodically consumed food:a nutrient (or a nonepisodically consumed food), such as energy, requires extension of the methods of Tooze et al. (10) to a 3-part model. Second, the HEI-2005 component scores are nonlinear functions of a ratio due to the truncation imposed at the minimum and maximum scores. In our method, this is dealt with at the Monte Carlo simulation stage (see Supplemental Appendix A).
The method described in this paper has provided for the first time, to our knowledge, estimates of the distribution of HEI-2005 component scores, based on usual intakes for the U.S. population and age-gender subgroups. These component scores give direct information on the quality of the composition of the diet consumed by the U.S. population.
For the 3 examples given (total vegetables, whole grains, and SoFAAS), differences between men and women were quite substantial, with women tending to have higher scores in each case. This result differs from that in the examples of distributions of nutrient ratios that we recently reported (9), where there was little difference between men and women in ratios of total fat, saturated fat, and sodium to energy. Substantial differences in HEI-2005 scores according to age were also seen, with older adults tending to have higher scores. One notably low score was the whole grains score for boys aged 14–18 y (0.6 of a possible 5.0), which was considerably lower than that of boys aged 9–13 y. Such differences highlight the value of estimating the distribution of HEI-2005 scores in age and gender subgroups, another feature that is afforded by the 3-part model that we used.
The method described is an extension of the 2-part model, which has been validated by extensive computer simulations (10). If there is doubt over whether the model provides a good fit to the data, then graphical methods similar to those described by Kipnis et al. (11) may be used as a check. The method is intended for use on quite large datasets with sample sizes of at least 1000 or more, especially if distributions in population subgroups are to be estimated. If one is interested in the distribution of scores in a total population only, then a sample of several hundred may suffice. The method requires data be gathered by repeated 24HR for a large number of the individuals. Information on individuals with only one 24HR can be included and will add to the precision of estimation, but several hundreds of individuals with repeat assessments are still required.
If the available data include only one 24HR assessment per person, and no (or few) individuals provide a second assessment, then the usual intake estimation would be limited to means. In such cases, we have previously recommended estimating the population's mean HEI-2005 score using the score of the population ratio (6). The comparison of our estimates from the 3-part model with those from 3 candidate methods that require only one 24HR, shown in Tables 5 and 6, reinforces that recommendation. These tables also confirm that the score of the population ratio is a slightly biased estimate, usually, but not always, in the direction of overestimation.
In conclusion, the method we describe allows examination of the distribution of HEI-2005 component scores in the U.S. population, both for the total population and for population subgroups. Its use will enhance the monitoring of the quality of the U.S. population's dietary intakes.
Supplementary Material
Acknowledgments
We thank Victor Kipnis and Raymond J. Carroll for contributions to developing the underlying statistical methodology used in this application. We also thank Joseph Goldman of the USDA Agricultural Research Service for providing the replicate weight sets used by us for the Balanced Repeated Replication method of variance estimation. D.M. played a major part in developing the statistical methodology, L.S.F., P.M.G., and S.M.K-S. designed the research; D.M. and K.W.D. performed the statistical analysis; L.S.F., P.M.G., and S.M.K-S. wrote the paper. L.S.F. had primary responsibility for final content. All authors read and approved the final manuscript.
Supported by a contract held by Information Management Services Inc with the US National Cancer Institute (to L.S.F.); the remaining authors were supported by their respective institutions, the USDA, and the National Cancer Institute.
Author disclosures: L. S. Freedman, P. M. Guenther, K. W. Dodd, S. M. Krebs-Smith, and D. Midthune, no conflicts of interest.
A technical description of the statistical method is included in Supplemental Appendix A that is available with the online posting of this paper at jn.nutrition.org.
Abbreviations used: HEI-2005, Healthy Eating Index 2005; SoFAAS, solid fats, alcoholic beverages, and added sugars; 24HR, 24-hour dietary recall.
References
- 1.Guenther PM, Reedy J, Krebs-Smith SM. Development of the Healthy Eating Index-2005. J Am Diet Assoc. 2008;108:1896–901. [DOI] [PubMed] [Google Scholar]
- 2.Guenther PM, Reedy J, Krebs-Smith SM, Reeve BB. Evaluation of the Healthy Eating Index-2005. J Am Diet Assoc. 2008;108:1854–64. [DOI] [PubMed] [Google Scholar]
- 3.Reedy J, Krebs-Smith SM, Bosire C. Evaluating the food environment: application of the Healthy Eating Index-2005. Am J Prev Med. 2010;38:465–71. [DOI] [PubMed] [Google Scholar]
- 4.Institute of Medicine. Dietary Reference Intakes: applications in dietary assessment. Washington, DC: National Academy Press; 2000.
- 5.US Department of Health and Human Services and USDA. Dietary guidelines for Americans 2005. US Government Printing Office, Stock Number: 001–000–04719–1, 2005 [cited 2009 Oct 8]. Available from: http://www.healthierus.gov/dietaryguidelines.
- 6.Freedman LS, Guenther PM, Krebs-Smith SM, Kott PS. A population's mean Healthy Eating Index 2005 scores are best estimated by the score of the population ratio when one 24-hour recall is available. J Nutr. 2008;138:1725–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kish L, Frankel MR. Balanced repeated replications for standard errors. J Am Stat Assoc. 1970;65:1071–94. [Google Scholar]
- 8.NHANES. National Center for Health Statistics. NHANES Homepage. [cited 2010 14 Jun]. Available from: http://www.cdc.gov/nchs/nhanes.htm.
- 9.Freedman LS, Guenther PM, Dodd KW, Krebs-Smith SM, Midthune D. The population distribution of ratios of usual intakes of dietary components that are consumed every day can be estimated from repeated 24-hour recalls. J Nutr. 2010;140:111–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tooze JA, Midthune D, Dodd KW, Freedman LS, Krebs-Smith SM, Subar AF, Guenther PM, Carroll RJ, Kipnis V. A new statistical method for estimating the usual intake of episodically consumed foods with application to their distribution. J Am Diet Assoc. 2006;106:1575–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kipnis V, Midthune D, Buckman DW, Dodd KW, Guenther PM, Krebs-Smith SM, Subar AF, Tooze JA, Carroll RJ, et al. Modeling data with excess zeros and measurement error: application to evaluating relationships between episodically consumed foods and health outcomes. Biometrics. 2009;65:1003–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.US National Cancer Institute website at: http://riskfactor.cancer.gov/diet/usualintakes/.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.