Spatiotemporal Temperature Distribution and Cancer Cell Death in Response to Extracellular Hyperthermia Induced by Gold Nanorods

Abstract

Plasmonic nanoparticles have shown promise in hyperthermic cancer therapy, both in vitro and in vivo. Previous reports have described hyperthermic ablation using targeted and non-targeted nanoparticles internalized by cancer cells, but most reports do not describe a theoretical analysis for determining optimal parameters. The focus of the current research was first to evaluate the spatiotemporal temperature distribution and cell death induced by extracellular hyperthermia in which gold nanorods (GNRs) were maintained in the dispersion outside human prostate cancer cells. The nanorod dispersion was irradiated with near infrared (NIR) laser and the spatiotemporal distribution of temperature was determined experimentally. This information was employed to develop and validate theoretical models of spatiotemporal temperature profiles for gold nanorod dispersions undergoing laser irradiation, and the impact of the resulting heat generation on the viability of human prostate cancer cells. A cell injury/death model was then coupled to the heat transfer model to predict spatial and temporal variations in cell death and injury. The model predictions agreed well with experimental measurements of both, temperature and cell death profiles. Finally, the model was extended to examine the impact of selective binding of gold nanorods to cancer cells compared to non-malignant cells, coupled with a small change in cell injury activation energy. The impact of these relatively minor changes results in a dramatic change in the overall cell death rate. Taken together, extracellular hyperthermia using gold nanorods is a promising strategy and tailoring the cellular binding efficacy of nanorods can result in varying therapeutic efficacies using this approach.

Introduction

Cancer diseases are among the leading causes of death in the United States, accounting for approximately 1 in every 4 deaths. Hyperthermia is the use of local heating (temperatures above 42-43°C) for tumor ablation¹ and is receiving increased attention as an adjunctive treatment option for cancer.² Cellular injury/death at temperatures above 43°C is thought to be caused by protein denaturation triggered by these elevated temperatures,^{3, 4} and previous work has utilized microwaves and radio waves,^{5, 6} magnetic heating,⁷ or ultrasound⁸ to achieve the required level of heating.

The ability to generate high temperatures at a desired site with externally tunable control, as opposed to whole-body hyperthermia, holds significant promise for cancer therapy. Nanoparticles can be targeted to the tumor in vivo and subjected to laser irradiation from an external source, leading to the selective localization of hyperthermic treatment.⁹ The photothermal response of gold nanoparticles, including nanorods, nanoshells, nanoclusters, and nanocages, has been exploited for the hyperthermic destruction of cancer cells.^10-12 In addition to gold nanoshells, nanoclusters, and nanocages, gold nanorods (GNRs) demonstrate an aspect-ratio dependent tunable photothermal response to near infrared (NIR) light.^{13, 14} The transverse absorption of gold nanorods is at a wavelength of 520 nm, but the longitudinal peak can be tuned to different regions of the absorption spectrum, including the NIR region, as a function of the nanorod length. Consequently, gold nanorods have been employed in diagnostics,^{15, 16} therapeutic / delivery systems,^17-20 including small-molecule drugs^21-26 and exogeneous nucleic acids,^27-32 imaging,³³ sensing,^34-36 and responsive advanced materials / assemblies.^{37, 38} Properties such as biocompatibility, ease of functionalization, and near infrared optical imaging make gold nanorods promising in novel theranostic platforms.

Most previous reports focus on nanoparticle-mediated ‘intracellular’ hyperthermia in which, plasmonic nanoparticles are first internalized by cells followed by exposure to laser irradiation which induces a temperature increase leading to cell death. In this approach, hyperthermic temperatures are generated inside cancer cells by the internalized nanoparticles. However, efficient homogeneous delivery of macromolecular and nanoscale therapeutics throughout the tumor tissue is hindered by high interstitial pressures, slow diffusion in the extracellular region, non-specific binding and lymphatic leakage.³⁹ A recent investigation of macromolecular (dextran) therapeutics found localization of >10kDa dextran in the vicinity of the tumor vasculature with poorer penetration with increasing macromolecular size.⁴⁰ These transport limitations can hinder transport of nanoparticles to cancer cells away from the vasculature and can therefore limit the effective administration of nanoparticle-induced hyperthermia in tumors.

An alternate approach is to use plasmonic nanoparticles in the extracellular space of the cancer cells, mimicking their extravasation from the leaky tumor vasculature and localization in this region, particularly in cases of poor or sluggish flow in vivo. Laser irradiation of nanoparticles in the extracellular space leads to generation of heat outside the cancer cell (extracellular hyperthermia) which can be employed for cancer cell ablation. While the use of intracellular hyperthermia has been extensively explored, we asked whether the gold nanorods present in the extracellular space of cultured cancer cells could result in effective cancer cell death following laser irradiation of the nanoparticles, and sought to characterize the spatiotemporal temperature distribution and cell death efficacy using this approach.

Various mathematical models have been developed to study the different physical and transport mechanisms that play a role in using nanoparticles for hyperthemic cancer treatment. Heat transport in tissues has been studied for a number of decades and is now largely based on the use of on the Pennes' bio-heat equation.⁴¹ The heat transport equation has been used by a number of researchers for the specific problem of laser induced heat generation/transport from gold nanoparticles.^{2, 42-44} The spatial transport of nanoparticles, which is governed by nanoparticle diffusion and binding, has also been modeled previously.⁴⁵ Finally, hyperthermal cell injury/death has been modeled using the Arrhenius rate model, isoeffective dose model, and other models.⁴⁶

The objective of the current work is to present a mathematical model and experimental results for heating, heat transport, and cellular injury/death for the laser induced heating of gold nanorods (GNRs) present in a dispersion outside cultured cancer cells. Spatiotemporal profiles of temperature increase following laser irradiation of gold nanorods were determined experimentally following laser irradiation and were used to evaluate the mathematical model. The validated temperature model was then used to predict cell death following gold nanorod induced extracellular hyperthermia and the model predictions were quantitatively compared to experimental results. Finally, the model was used to predict how selective binding of gold nanorods to cancer cells might influence the efficacy of extracellular hyperthermia.

Results and Discussion

The first set of model validation results focuses on the comparison of the heat transfer model (Equation 1) with experimental temperature measurements with different ODs (i.e., different GNR concentrations) and different laser irradiation levels. The first experimental conditions used a 24-well plate and 4 different ODs (0.065, 0.148, 0.285, and 0.50). The temperature was measured at 4 different locations within a well, and two different samples at each OD were employed. The experimental measurements and simulation predictions at three radially spaced points in the domain are shown in Figure 3.

Figure 3.

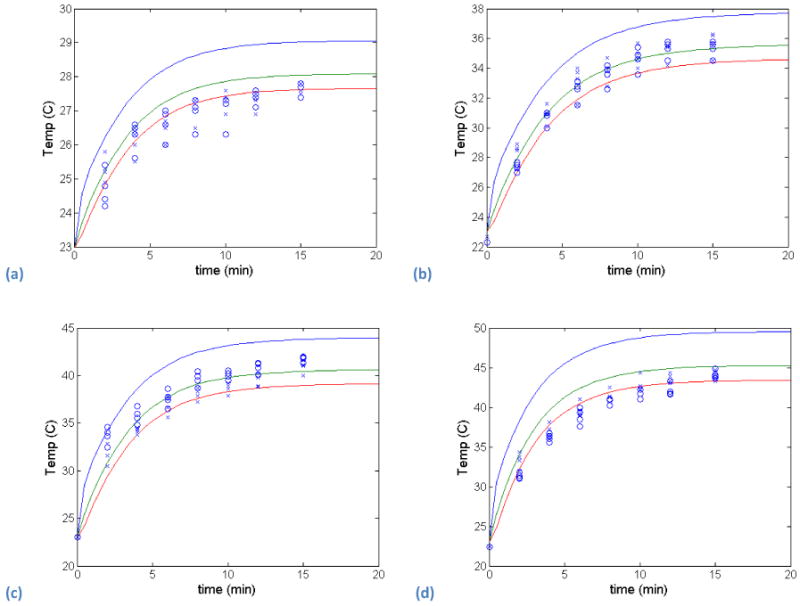
Experimental temperature measurements (2 samples, circles and crosses) and heat transfer model predictions (solid lines for three radial points in the domain) for 4 different ODs - (a) 0.065, (b) 0.148, (c) 0.285, and (d) 0.50.

Significant spatial differences were not seen in the current set up indicating that even though the laser diameter was only 2 mm in a well of approximately 16 mm diameter, the heat transfer was rapid throughout the gold nanorod dispersion. The model predictions are in good agreement with the experimental measurements for all optical densities, and the largest errors occur at the lowest optical density. However, even at the lowest optical density, the experimental measurement and model prediction agree once steady-state is achieved. The model simply predicts a slightly faster heating rate than is measured experimentally. The model predicts the temperature distribution throughout the well being irradiated with the laser. Figure 4 shows the temperature contours within the well, and as expected, the highest temperatures occur along the well axis where the laser is focused, and the coolest temperatures occur near the wall at the surface of the fluid.

Figure 4.

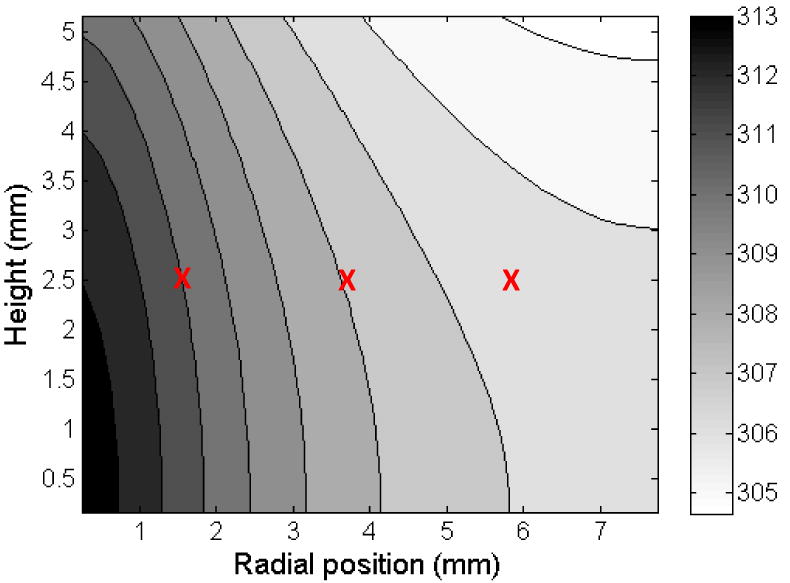
Temperature distribution within the well for an OD=0.45. The temperature is reported in K, and approximate locations of the thermocouples are shown by ‘X’.

The second set of comparisons between experimental measurements and the heat transfer model (Equation 1) uses GNR dispersons in a 96-well plate and different laser energy levels (0.008 W/mm³, 0.016 W/mm³, and 0.032 W/mm³). The results are summarized in Figure 5 and show good agreement at the lower two laser energy levels (0.008 W/mm³ and 0.016 W/mm³). At the highest laser energy level (0.032 W/mm³), the model predicts a higher temperature than is measured experimentally, especially at steady-state. The most likely cause for this difference is the assumptions behind Newton's law of cooling for the upper boundary. This boundary condition lumps radiative cooling, evaporative cooling, and convective cooling into a single parameter that is independent of temperature. In other words, it assumes that all these energy loss mechanisms are (linearly) proportional to the temperature. In reality, none of these energy loss mechanisms are linear with temperature changes, and these nonlinear effects become important at temperatures above 50°C or 60°C.⁴⁷

Figure 5.

Heat transfer model prediction at different radial locations (solid lines) and experimental temperature measurements (open circles and crosses) at three different laser energy levels -- (a) 0.008 W/mm³, (b) 0.016 W/mm³, and (c) 0.032 W/mm³.

Once acceptable agreement between the heat transfer model and experimental measurements was achieved, the next set of validation experiments focused on the cell death model (Equations 3 and 4). The GNR dispersion with cells attached to the bottom of the well was then irradiated for 0, 4, 8, 12, or 20 minutes, and the temperature was also monitored immediately after switching the laser off. A cell viability assay was conducted 24 hours after irradiation, and the viability measurements were compared to model predictions. Figure 6 shows the temperature and cell viability results for a GNR solution with an OD of 0.15. The model predictions of the temperature are slightly lower than the experimental measurements for lower laser exposure times, and are slightly higher for exposure times greater than five minutes. The 24 hour cell death predictions deviate slightly from experimental measurements, but these differences can be expected from the temperature predictions. Lower values of temperature at the initial laser exposure times (< 5 minutes) result in predictions of high cancer cell viability. Conversely, higher temperature predictions lead to modest over-estimations of cell death predictions (or lower predictions of cell viability values). The model and experimental results for a GNR solution with an OD=0.2, shown in Figure 7, are similar to the OD=0.15 results. Here, the temperature agreement and cell viability agreement are improved, with the largest errors being in the early cell viability results. The temperature within the well varies both temporally and spatially.

Figure 6.

(a) Temperature measurements and model predictions for a GNR solution with OD=0.15. (b) Cell Viability measurements after 24 hrs and predictions for different laser irradiation times.

Figure 7.

(a) Temperature measurements and model predictions for a GNR solution with OD=0.20. (b) Cell Viability measurements after 24 hrs and predictions for different laser irradiation times.

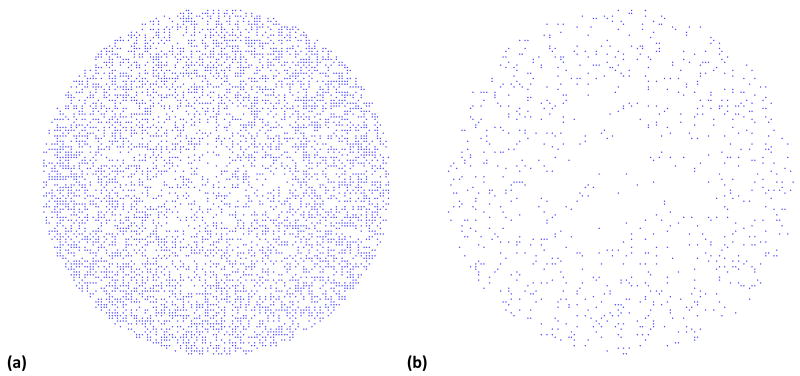
To help visualize the impact of the spatial temperature variation on cell viability, the well bottom in the model was covered with a monolayer consisting of approximately 13,000 cells. Each cell was assigned a random number between 0 and 1, and when the cell viability, F_D, dropped below that random number, the cell was removed from the model. Figure 8 shows the viable cells after 10 minutes and after 18 minutes of laser irradiation. The solution in the well above the cells contained GNR with an OD=0.2. Despite the small spatial temperature differences, there is a lower loss of cell viability for the outer regions of the well. The higher temperatures at the center result in a higher rate of cell death.

Figure 8.

Cell viability predictions after 24 hrs for approximately 13,000 cells along the bottom of the well after laser irradiation for (a) 10 minutes and (b) 18 minutes with GNR solution at OD=0.20. The cells disappear when their cell viability level falls below a randomly assigned threshold.

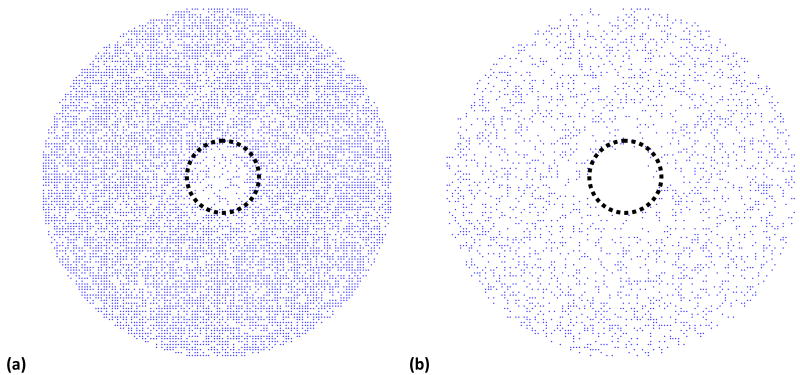
The final model prediction is speculative in nature, and was carried out to elucidate the role of nanoparticle binding to cell surface on hyperthermia. Some evidence has shown that cancer cells are more susceptible to damage from elevated temperatures than healthy cells due to the hypoxic environment.⁴⁸ To model this impact, it was assumed in the model that the inner 1.2 mm (in diameter) of a 6mm well was cancerous cells, and for these cells, E_a = 198kJ/mol was used instead of E_a = 200kJ/mol in equation 3 to simulate the increased heat sensitivity. Further, GNRs can be conjugated with cancer cell targeting antibodies that will increase their potential for binding to malignant cells versus healthy cells. To model the impact of this change, the GNR concentration was increased by 20% near the cancer cells versus the healthy cells, which represents an assumed increase of 20% in the number of binding sites for cancerous versus healthy cells. It is important to remind the reader that the targeted nanorods in this case are still external to the cell and have not been internalized. The predicted living cell populations at the bottom of the well are once again shown for ten and eighteen minutes of laser irradiation in Figure 9. At the ten-minute point, 31% of the healthy cells have been killed, and 65% of the cancer cells have died. At the eighteen-minute point, 71% and 96% of the healthy and cancer cells, respectively, have died.

Figure 9.

Cell viability predictions for approximately 13,000 cells along the bottom of the well after laser irradiation for (a) 10 minutes and (b) 18 minutes with GNR solution at OD=0.17. The inner 1.2 mm has cancerous cells with a lower activation energy for cell injury and an increased number of GNR binding site (simulating targeting delivery of GNRs to cancer cells). The cells disappear when their cell viability level falls below a randomly assigned threshold.

The model parameters were changed only a small amount between the results shown in Figures 8 and 9. However, the impact on cell death over the tumor region in the model was far greater, overall, than the small individual changes to cell injury activation energy and GNR concentration. This dramatic change is simply a result of the impact of these two parameters being multiplicative (or geometric) instead of additive (or arithmetic). Multiplicative interactions can cause multiple small changes to result in a large change overall, much larger than simply adding up the small changes. Ideally, the cancer cells could be individually identified, and the laser could be focused directly on those cells to maximize cancer cell death and minimizing normal cell death. Since it is not possible to easily identify individual cancer cells, the approach described above, which utilizes preferential binding of gold nanorods to enhance local temperature elevations near cancer cells, provides a potential alternative.

Conclusions

The use of gold nanoparticles in hyperthermal therapy continues to be an important area of research and therapeutic development. It is important to develop theoretical models of this treatment option so that the many parameters (e.g., laser power, irradiation time, nanoparticle concentration, etc.) can be optimized and the treatment can be as effective as possible. Most previous models have focused on gold nanoshells, but the theoretical model presented here is based on experimental measurements of gold nanorods and their use in extracellular hyperthermal therapy for human prostate cancer cells. The heat transfer model (equation 1) accurately predicted the temperature distribution for various optical density and laser irradiation levels. The cell death model (equations 3 and 4) predicted cell death levels that were highly consistent with experimental measurements.

Previous theoretical analyses have shown that ‘intracellular hyperthermia’ with cells loaded with magnetic nanoparticles and exposed to AC magnetic heating effects, is not superior for killing cancer cells compared to ‘extracellular hyperthermia’ in which cells are surrounded by nanoparticles.⁴⁹ We have demonstrated that extracellular hyperthermia, in which gold nanorods are maintained in the extracellular space can be an effective method of inducing cell death in cancer cells. Presumably, this approach can overcome limitations associated with transport in the tumor tissue following extravasation through the leaky vasculature. The efficacy of this approach can be further enhanced by using nanorods conjugated with cancer cell targeting antibodies for specific localization at cancer cells. The model demonstrated the small differences in GNR-cell binding combined with small differences in hyperthermal cell sensitivity between cancer cells and healthy cells could lead to significant differences in cell death with cancer cells being eliminated much more rapidly than nearby healthy cells, strengthening the case for targeted plasmonic nanoparticles. While the current work was able to demonstrate the utility of plasmonic nanoparticles in the extracellular space as a potential alternative for hyperthermia administration using cell culture experiments, further work is required for investigating nanoparticle transport, concomitant laser-induced heat transport, cellular death and responses, in model three-dimensional systems (e.g. tumor spheroids) and in animal models. Future work will need to investigate the effects heterogeneous distribution of plasmonic nanoparticles in tumors following extravasation from the leaky vasculature, diffusion through the extracellular matrix⁵⁰, and the effect of these heterogeneities on temperature distribution and cancer cell death.

Methods - Experimental

Preparation of Gold Nanorods (GNRs)

Cetyltrimethyl ammonium bromide (CTAB) gold nanorods were synthesized via seed growth method as described previously.^{51, 52} The seed solution was prepared by vigorously mixing 0.3 ml iced water-cooled sodium borohydride (0.01 M) in order to reduce a solution of 2.5 ml CTAB (0.2 M) in 2.5 ml auric acid (0.0005 M) (HAuCl_4·3H₂O). The growth solution was prepared by reducing 10 ml CTAB (0.2 M) in 10 ml auric acid (0.001M) (HAuCl_4·3H₂O) containing 560 μl silver nitrate (0.004 M) with 140 μl L-ascorbic acid (0.0788 M) solution. Seed solution (24 μl) was added to a 20 ml growth solution which resulted in the generation of gold nanorods after 4 h of continuous stirring at 28°C. Gold nanorods that possessed an absorbance maxima (λ_max) at 800 nm were centrifuged once and at 6,000 rcf (relative centrifugal force) for ten minutes in order to remove excess CTAB molecules, and resuspened in different volumes of deionized (DI) water to form dispersions with varying optical densities (ODs) with a maximum OD = 0.5 at peak absorption wavelength (λ_max) of 800nm (Figure 1).

Figure 1.

Absorbance spectrum of gold nanorods employed in the current study indicated different concentrations as determined using optical densities (left). Schematic of the laser experiment which shows approximate positions (a,b,c) of the thermocouple used for determining spatiotemporal temperature distribution.

Preparation of PEGylated Nanorods

Thiolated poly(ethylene glycol) (mPEG-SH, 5000 MW) was obtained from Creative PEGworks. The polymer (3 mg/ml) was added to GNR (optical density 0.5 at λmax = 800 nm) and the dispersion was sonicated for thirty minutes. After sonication, the mPEG-SH-GNR mixture were centrifuged at 6,000 rcf for ten minutes in order to remove excess mPEG-SH molecules, followed by resuspension in serum-free media, resulting in stock mPEG-GNR dispersions with final optical densities of 0.15 and 0.2.

Photothermal Response of GNR and Determination of Spatiotemporal Temperature Profiles

The photothermal response of gold nanorods (CTAB-GNRs) to laser irradiation was determined using a titanium CW sapphire (Ti:S) laser (Spectra-Physics, Tsunami) pumped by a solid state laser (Spectra-Physics, Millennia). The experiment was carried out in a 24 well plate (15.6 mm internal diameter of the well). The laser excitation source was tuned to 800 nm (2 mm diameter) in order to coincide with the longitudinal absorption maximum of the CTAB-GNR dispersions (1 ml) with various optical densities (O.D. = 0.065, 0.148, 0.285, and 0.50). A fixed laser power density of 20 W/cm² was employed for fifteen minutes. The dispersion temperature was monitored using a FLUKE 54 II (Type J) thermocouple immediately after laser irradiation at three different locations, (1) center, (2) 4 mm from center, (3) at the edge of the well (Figure 1).

Cell Culture

The human prostate cancer cell line (PC3-PSMA)⁵³ was a generous gift from Dr. Michel Sadelain of the Memorial Sloan Cancer Center, New York, NY. RPMI 1640 with L-glutamine and HEPES (RPMI-1640 medium), Pen-Strep solution: 10,000 units/mL penicillin and 10,000 μg/mL streptomycin in 0.85% NaCl, and fetal bovine serum (FBS) were purchased from Hyclone. In these experiments, serum-free medium (SFM) was RPMI-1640 medium plus 1% antibiotics, while serum-containing medium was SFM plus 10% FBS. Cells were cultured in a 5% CO₂ incubator at 37 °C using RPMI-1640 medium containing 10% heat-inactivated fetal bovine serum (FBS) and 1% antibiotics (10000 units/mL penicillin G and 10000 μg/mL streptomycin). Prostate cancer cells were seeded in 96 well plates (well diameter 6.4 mm) with a density of 15,000 cells / well and allowed to attach for 24 h at 37°C, in a 5% CO₂ incubator.

Photothermal Cell Ablation

The laser irradiation experiment was carried out with a titanium CW sapphire (Ti:S) laser (Spectra-Physics, Tsunami) pumped by a solid state laser (Spectra-Physics, Millennia). Prior to laser irradiation, serum-containing media in PC3-PSMA cell cultured 96 well plates were replaced by 200 μl of mPEG-GNR (O.D. 0.15 and 0.2, in serum free media). PEGylated nanorods were used in cell ablation studies in order to minimize adhesion to the cell surface and maintain them in dispersion in the extracellular space. As before, the laser excitation source was tuned to 800 nm (2 mm diameter) in order to coincide with the longitudinal absorption maximum of the mPEG-GNR; a fixed laser power density of 20 W/cm² was used for different exposure times (4, 8, 12, and 20 min), while monitoring the dispersion temperature using a FLUKE 54 II (Type J) thermocouple immediately after laser exposure. The mPEG-GNR dispersion was immediately removed and replaced by fresh serum containing media after laser exposure.

Cell Viability Assay (MTT)

Cell viability was assayed 24 h after laser irradiation, using the 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT) cell proliferation assay kit (ATCC CA#30-1010k). This assay involves the enzymatic conversion of the MTT substrate to purple-colored formazan in metabolically active cells. This activity is widely employed as an indicator of cell viability and proliferation;⁵⁴ loss of metabolic activity is used as an indirect indicator of loss of cell viability using this assay. We used the MTT assay as a reporter for cell viability following GNR-induced hyperthermia and did not carry out secondary analyses of cell viability.

Following addition of the MTT reagent (6 h at 37°C), cells were treated with a lysis buffer from the kit and kept at room temperature in the dark for 4 h in order to carry out complete lysis and solubilization of the MTT product. The absorbance of each well was measured using a plate reader (Bio-Tek Synergy 2) at 570 nm. For data analysis, absorbance readouts were normalized to the live (untreated) and dead (5 μl of 30 % hydrogen peroxide-treated) controls.

Methods - Theoretical Model

The modeling of GNR use in hyperthermal cancer treatment requires a three part model: (1) a heat transport (or energy balance) equation, (2) a cell death model, and (3) a GNR spatial distribution model. Each of the three parts is described below.

1. Heat Transport Model

The temperature distribution model for either a fluid or tissue containing GNRs is based on the Pennes' bio-heat equation ^{41, 44} with an additional term to account for energy released by the GNRs:

$$\frac{\partial T}{\partial t}=\alpha {\nabla }^2\text{T}+\frac{\text{Q}}{{\rho \text{C}}_{\text{p}}}(1-{10}^{-\text{OD}}),$$ (1)

where the first term on the right side is heat conduction (diffusion), the second is plasmonic heating by the GNRs from laser irradiation, and the heat transfer due to blood flow is omitted because all of the experimental results presented below are conducted in vitro. The parameters used in the model are defined in Table 1. The incident laser power (5 to 20 W/cm²) was divided by the sample depth to obtain Q, the laser power per volume required in equation 1. The value used for each parameter is consistent with values used previously by others except for the thermal diffusivity, which is approximately twice the value for pure water. The thermal diffusivity value utilized in the model was chosen because it gave the best agreement with the experimental data as described later in the results section. It is also reasonable to assume that the presence of a high concentration of GNR in the solution would significantly increase the thermal diffusivity of the solution ⁵⁵.

Table 1.

Heat transport model parameters based on ⁴³, ⁵⁹

Parameter	Description	Value
ρ	Tissue or fluid density	1000 kg/m3
Q	Laser energy	0.008 - 0.038 W/mm3
Cp	Tissue or fluid heat capacity	3.4 kJ/(kg K)
OD	Optical density	0 to 0.5
$\alpha =\stackrel{k}{}/\underset{\left(\rho ·C_p\right)}{}$	Tissue or fluid thermal diffusivity with GNRs	3.0 × 10-7 m2/s

Three types of boundary conditions are commonly used during the solving of the heat transfer model. First, if the surrounding fluid or tissue is held at a fixed temperature, a Dirichlet condition can be applied, which specifies the temperature along the boundary. Second, a heat flux or Neumann boundary condition can be used in conjunction with Newton's law of cooling to give:

$$k\frac{\partial T}{\partial n}=U\left(T-T_0\right).$$ (2)

Here, U is the overall heat transfer coefficient for the region adjacent to the model boundary, and T₀ is the bulk temperature of the surroundings. The final type of boundary condition is a symmetry condition, which is equivalent, in practice, to a zero temperature gradient boundary condition. The model domain and boundary conditions are shown in Figure 2. For the in vitro cell culture based system described here, $U_{\mathit{\text{air}}}=0.08\frac{\text{W}}{m^2·°C}$, $U_{\mathit{\text{wall}}}=1\times {10}^{-5}\frac{\text{W}}{m^2·°C}$, and $k=1.0\frac{W}{m·°C}$ were used in the model, and T_air and T_wall were measured to be 23°C.

Figure 2.

The model domain (grey) represents a symmetrical cross-section of a well in a plate. The top boundary is the air-solution interface, the right and bottom boundaries are plate-solution interfaces, and the left boundary (dotted line) is the symmetry axis.

2. Cell Death Model

Cell injury and death is predicted using the Arrhenius injury model^{43, 56}. The cell injury rate is calculated by

$$k={\mathit{\text{Ae}}}^{\frac{-E_{\text{a}}}{R·T}},$$ (3)

where E_a is the activation energy, R is the gas constant, T is the temperature, and A is a scaling factor. The values for E_a and A were determined for the experimental cell line studied here using isothermal cell viability tests, and the values used in the model are A = 6 × 10²⁹ s⁻¹, and E_a = 200kJ/mol. These values are consistent with the values measured for similar cell lines and tissues.^57,58 Finally, the cell injury rate is integrated over time to account for injury accumulation, and the fraction of tissue that is injured over time is given by

$$F_D=1-e^{-{\int }_{\text{o}}^t\mathit{\text{kdt}}}$$ (4)

so healthy tissue has F_D = 0 and dead tissue has F_D =1.

3. GNR Spatial Distribution

The distribution of GNRs in the extracellular dispersion is governed by diffusion, binding, unbinding, and cell internalization events. Initial studies on tumor spheroids have established the potential for mathematical models to accurately model the spatial distribution of nanoparticles,⁴⁵ but the general applicability of these models to other tissues and nanoparticle systems is still unknown. It is, in general, difficult to estimate the diffusivity of the nanoparticles in the tissues, and the rate of particle binding, unbinding, and internalization within the cell are challenging to measure.

It is possible to obtain a simplified model for the problems of interest here using scaling analysis. The diffusivity of nanoparticles in water is very small (< 10^-8 cm²/s), and the diffusivity within a tissue is even smaller.⁴⁵ The result of the small diffusivity is that diffusion through only a 100 μm of tissue requires a number of hours depending on the concentration and temperature.⁴⁵ The internalization of particles into cells is also relatively small for the time scales of interest here because the internalization rate is typically an order of magnitude less than the unbinding rate. This means that a GNR attached to a cell surface is 10 times more likely to go back into solution than to be internalized. Of course, internalization is largely irreversible, so given sufficient time many particles will be internalized, but this can take a few hours.

For the systems of interest here, it is valid to assume that most GNRs do not diffuse into tissue and are not internalized by the cells, but they remain in the extracellular dispersion or bound to the surface of the tissue. The concentration of bound particles is governed by the equation

$$\frac{\partial C_b}{\partial t}=k_a{C}_{bs}C-K_d{C}_b$$ (5)

where C_b is the concentration of bound particles, C_bs is the concentration of open binding sites, C is the concentration of free particles in solution, and k_a and k_d are the association (binding) and disassociation (unbinding) rates, respectively. If sufficient time has elapsed before turning on the laser, equilibrium is achieved so the binding model can be simplified using a pseudo-steady-state assumption. The concentration of bound particles then becomes

$$C_b=K_{eq}{C}_{bs},$$ (6)

where $K_{eq}=\stackrel{k_a^{\prime }}{}/\underset{k_d}{}$ and k_a′=k_aC. The particle contrast (i.e., the ratio in bound particles between health and cancerous tissues) is determined by the ratio of binding site concentration between healthy and cancerous tissues.