Accelerated Hazards Mixture Cure Model

Abstract

We propose a new cure model for survival data with a surviving or cure fraction. The new model is a mixture cure model where the covariate effects on the proportion of cure and the distribution of the failure time of uncured patients are separately modeled. Unlike the existing mixture cure models, the new model allows covariate effects on the failure time distribution of uncured patients to be negligible at time zero and to increase as time goes by. Such a model is particularly useful in some cancer treatments when the treat effect increases gradually from zero, and the existing models usually cannot handle this situation properly. We develop a rank based semiparametric estimation method to obtain the maximum likelihood estimates of the parameters in the model. We compare it with existing models and methods via a simulation study, and apply the model to a breast cancer data set. The numerical studies show that the new model provides a useful addition to the cure model literature.

1 Introduction

Statistical models for survival data with a surviving or cure fraction, often called cure models, have received a great deal of attention in the last decade. There are a variety of cure models proposed in the literature based on different assumptions or different perspectives of the cure mechanism. In this paper, we focus on the popular mixture cure models where the population is considered as a mixture of cured patients and uncured patients. Let Y be the indicator variable for an uncured patient with Y = 1 if the patient is uncured and 0 if cured, T be the failure time of a patient. Define π = P(Y = 1), S(t) = P(T > t) and S_u(t) = P(T > t|Y = 1). That is, π is the probability of being uncured, and S(t) and S_u(t) are the survival functions of the failure time of a patient and the failure time of an uncured patient respectively. The mixture cure model is given by

$$S(t|x,z)=\pi (z)S_u(t|x)+1-\pi (z)$$ (1)

where x and z are two sets of covariates that have effects on π and S_u(t). The use of the mixture cure model dates back to Berkson and Gage [1]. The advantage of the mixture cure model is that the proportion of cured patients and the survival distribution of uncured patients are modeled separately and the interpretation of the parameters of x and z in the model is straightforward.

The most common method to specify the effects of z on π is via a logit link function:

$$\pi (z)=\frac{\text{exp}({\gamma }^{T}z)}{1+\text{exp}({\gamma }^{T}z)}$$ (2)

where γ is a vector of unknown parameters. Other link functions may be considered, such as the complementary log-log and the probit link functions in the generalized linear models for binary data. In this paper, we will use the logit link function only because of its simplicity and popularity.

Similar to the classical survival models, there are a number of methods to specify the effects of x on S_u(t). Let S_u0(t) be an arbitrary baseline survival function. Similar to the proportional hazards model in survival analysis, one can assume

$$S_u(t|x)=S_{u0}{(t)}^{\text{exp}({\beta }^{T}x)}$$

or equivalently

$$h_u(t|x)=h_{u0}(t)\text{exp}({\beta }^{T}x)$$ (3)

where h_u(t) and h_u0(t) are the corresponding hazard functions of S_u(t) and S_u0(t). This model is referred to as the proportional hazards mixture cure (PHMC) model. The model can be easily estimated if the baseline survival function S_u0(t) is specified up to a few unknown parameters. However, verifying a parametric assumption for the baseline distribution can be a challenging task. A semiparametric estimation method based on the partial likelihood approach becomes a well accepted method after the work of Kuk and Chen [2]; Peng and Dear [3]; Sy and Taylor [4]. Large sample properties of estimators from the semiparametric PH mixture cure model were investigated in Fang et al. [5].

An alternative to the proportional hazards assumption (3) is the accelerated failure time (AFT) assumption to model the effects of x on S_u(t). That is

$$S_u(t|x)=S_{u0}({\mathit{\text{te}}}^{{\beta }^{T}x})$$

or equivalently

$$h_u(t|x)=h_{u0}({\mathit{\text{te}}}^{{\beta }^{T}x})e^{{\beta }^{T}x}$$ (4)

This model is referred to as the accelerated failure time mixture cure (AFTMC) model. A parametric distribution with a few unknown parameters is often assumed for the baseline distribution and the parameters in the model is estimated by the maximum likelihood approach ([6, 7, 8]). Recently several authors investigated semiparametric estimation methods. Li and Taylor [9] employed the M-estimation method [10] to estimate the unknown parameters in the AFTMC model. Zhang and Peng [11] further adapted a rank estimation method [12] to improve the semiparametric estimation method for the AFTMC model.

An unstated assumption of the two models is that the covariate effects on the hazard rate of uncured patients are immediate. Considering a case with a single covariate equal to 1 if a new treatment is used and 0 if a standard treatment is used for a cancer study, the covariate is considered in both x and z in the mixture cure model (1), and the hazard of patients in the standard treatment group satisfies h_u0(0) > 0. For uncured patients, it is obvious to see that in the PHMC model (3) the hazard ratio of patients in the new treatment group versus that in the standard treatment group is e^βTx at t = 0 and it remains the same for any t > 0. In the AFTMC model (4), even though the hazard ratio is no longer constant over time, it still starts with e^βTx at t = 0. This immediate effect assumption may not be desirable in some cancer studies when a treatment effect increases gradually over time from zero. For example, in testing antidepression drugs, it is sometimes not practical to assume that the drug is effective at the early stage of the treatment but rather to assume no effect at t = 0 and a gradual effect at the later stage of the treatment.

To model a gradual treatment effect for data without a cure fraction, Chen and Wang [13] and Chen [14] proposed an accelerated hazard (AH) model

$$h(t|x)=h_{u0}({\mathit{\text{te}}}^{{\beta }^{T}x}).$$ (5)

For the binary treatment covariate defined above, it is easy to see that the hazard functions of the new and the standard treatments are h_u0(te^β) and h_u0(t) respectively, and the difference of the two hazard functions starts at 0 when t = 0. Thus the AH model assumes that the hazard does not change at time 0 and then change gradually with time. Unless h_u0(t) ≡ constant or lim_t→0+ h_u0(t) = 0, the AH model provides a useful way to model the gradual effect of a treatment that other existing models cannot handle properly.

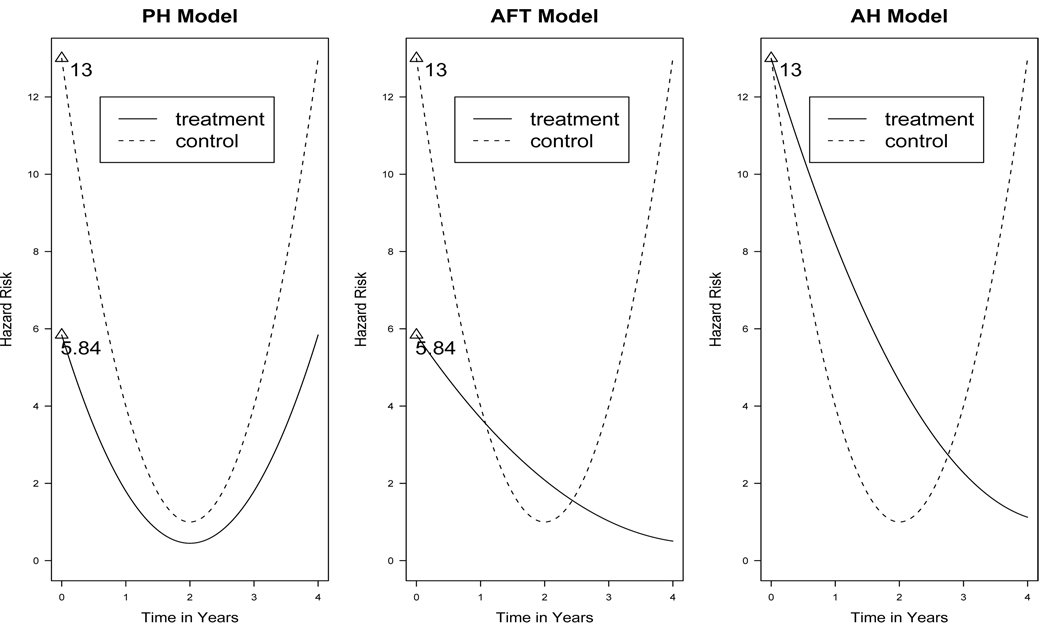
To better demonstrate the differences, we plot the hazard curves based on the three models in Figure 1. We consider two groups with x = 0 for the control (baseline) group and x = 1 for the treatment group. The baseline hazard function is a U-shape function, which is often employed in health research. The value of β is set to −0.8. Comparing the hazard curves from the two groups, we can see that the PH model implies that the treatment decreases the hazard rate by e^−0.8 = 0.45 for the whole period. In the AFT model, the relationship of hazard rates in the two groups is more complicated: the treatment has a smaller hazard rate at beginning, larger hazard rate in the middle and then smaller hazard rate after the two periods. The AH model, on the other hand, provides a simple scenario: the treatment starts at the same hazard rate as the control group, it has a higher hazard rate than the control group at the early period due to, say, the toxicity of the treatment. However, after certain time point, the positive effect of the treatment is demonstrated with a smaller hazard rate than the control group.

Figure 1.

Hazard curves from the PH model, AFT model, and AH model

Chen and Wang [13] proposed estimating equations to estimate the parameters semiparametrically in the AH model (5). When there is a cure fraction in the data, the model (5) is clearly not appropriate. It is unclear whether the model and the semiparametrically estimation method can be easily adapted to incorporate the cure fraction. This motivates the work in this paper on a cure model that allows a gradual effect of covariates on the hazard of uncured patients. In this paper, we propose a new mixture cure model that employs a AH model to model the effects of x on S_u(t) in the mixture cure model (1). A semiparametrically method is proposed to estimate the parameters in the cure model. We demonstrate the performance of the proposed model and estimation method via simulation and apply the model and estimation method to a data set from Surveillance, Epidemiology, and End Results (SEER) Program of the National Cancer Institute [15].

The remaining paper is organized as follows. Section 2 presents an accelerated hazard mixture cure model. A semiparametric estimation method for the proposed model is also discussed in this section. Section 3 reports a simulation study to investigate the performance of proposed model and estimation method. Section 4 describes an application of the model to the breast cancer data set of Polk, Iowa from SEER. Finally conclusions and some discussions are given in Section 5.

2 Accelerated Hazard Mixture Cure Model

To allow a gradual effect of covariates on the failure time of uncured patients, we propose to model S_u(t) in the mixture cure model (1) by the AH model proposed by Chen [14]. That is,

$$h_u(t|x)=h_{u0}({\mathit{\text{te}}}^{{\beta }^{T}x})$$

or

$$S_u(t|x)=S_{u0}{({\mathit{\text{te}}}^{{\beta }^{T}x})}^{\text{exp}(-{\beta }^{T}x)}$$ (6)

where h_u0(t) is an arbitrary unspecified baseline hazard function and S_u0(t) is the corresponding survival function. We refer to the model specified by equation (1), (2), and (6) as the AH mixture cure (AHMC) model.

If h_u0(t) is specified up to a few unknown parameters in the AHMC model, the parameters in the model can be estimated by the maximum likelihood approach. We will skip details of this parametric approach in this paper and focus on a semiparametric estimation approach where h_u0(t) is not parametrically specified. This approach is more attractive in application because it does not rely on a parametric assumption that may be difficult to verify.

Chen [14] proposed a semiparametric method to estimate the parameters in the AH model (5). Due to the presence of cured patients, their method is no longer applicable in this situation and a new estimation method is required. We propose a semiparametric method to estimate the parameters in the AHMC model based on the EM algorithm.

Let (t_i, δ_i, z_i, x_i) denote the observed data for the ith individual i = 1,…, n, where t_i is the observed survival time of T for the ith patient (may be censored), δ_i is a censoring indicator with δ_i = 1 for uncensored t_i and δ_i = 0 for censored t_i, and z_i, x_i are observed values of z and x for the ith patient. The value of Y for the ith patient is denoted as y_i with y_i = 1 if the ith individual is not cured and y_i = 0 if cured. Clearly for a censored patient, Y is a latent variable and its value is not observable. Denote y = (y₁,…,y_n). The complete log likelihood in the EM algorithm when assuming all values of y are available is given by l(β, h_u0(t), γ; y) = l_c1(γ; y) + l_c2(β, h_u0(t); y), where

$$\begin{array}{cc}\hfill l_{c_1}(\gamma ;y)& ={\displaystyle \sum _{i=1}^n{y}_i\text{ log}[\pi (z_i)]+(1-y_i)\text{ log}[1-\pi (z_i)],}\hfill \\ \hfill l_{c_2}(\beta ,h_{u0}(·);y)& ={\displaystyle \sum _{i=1}^n{y}_i{\delta }_i\text{ log}[h_{u0}(e^{{\beta }^T{x}_i}{t}_i)]+(y_i)\text{ log}[S_{u0}{(e^{{\beta }^T{x}_i}{t}_i)}^{\text{exp}(-{\beta }^T{x}_i)}].}\hfill \end{array}$$

The E-step computes E[l_c(γ, β, h_u0(t); y)|Θ^(m)], the conditional expectation of the complete log-likelihood with respect to y, given the current estimates ${\mathrm{\Theta }}^{(m)}=\{{\gamma }^{(m)},{\beta }^{(m)},h_{u0}^{(m)}(t)\}$. It is not difficult to see that

$$w_i^{(m)}=E(y_i|{\mathrm{\Theta }}^{(m)})={\delta }_i+(1-{\delta }_i)\frac{\pi (z_i)S_{u0}{(e^{{\beta }^T{x}_i}{t}_i)}^{e^{-{\beta }^T{x}_i}}}{1-\pi (z_i)+\pi (z_i)S_{u0}{(e^{{\beta }^T{x}_i}{t}_i)}^{e^{-{\beta }^T{x}_i}}}{|}_{\mathrm{\Theta }={\mathrm{\Theta }}^{(m)}}.$$ (7)

Let $w^{(m)}=(w_1^{(m)},\dots ,w_n^{(m)})$. Then

$$E[l_c(\gamma ,\beta ,h_{u0}(t);y)|{\mathrm{\Theta }}^{(m)}]=l_c[\gamma ,\beta ,h_{u0}(t);w^{(m)}]=l_{c1}[\gamma ;w^{(m)}]+l_{c2}[\beta ,h_{u0}(t);w^{(m)}].$$

The M-step maximizes l_c1(γ;w^(m)) and l_c2(β, h_u0(t);w^(m)) with respect to the unknown parameters γ, β and h_u0(t). Maximizing l_c1(γ;w^(m)) with respect to γ can be easily carried out using the Newton-Raphson algorithm. Maximizing l_c2(β, h_u0(t);w^(m)) with respect to β and h_u0(t) is a challenge task. We propose a rank-like estimation method to update β and h_u0(t). Since δ_i log $w_i^{(m)}\equiv 0,l_{c2}(\beta ,h_{u0}(·);w^{(m)})$ can be written as

$${\displaystyle \sum _{i=1}^n{\delta }_i\text{ log}[w_i^{(m)}{h}_{u0}(t_i{e}^{{\beta }^T{x}_i})]}+[\text{log}(S_{u0}{(e^{{\beta }^T{x}_i}{t}_i)}^{w_i^{(m)}\text{exp}(-{\beta }^T{x}_i)})]$$

which can be treated as the log-likelihood function of the AH model considered by Chen [14] with the hazard function $w_i^{(m)}{h}_{u0}(t_i{e}^{{\beta }^T{x}_i})$. Following Chen [14] and Zhang and Peng [11], a rank-type estimation equation of β can be written as

$$\mathrm{\Psi }(\beta ;k(·))={\displaystyle \sum _{i=1}^n{\delta }_{i}k(t_i{e}^{{\beta }^T{x}_i})}(x_i-\frac{{\displaystyle {\sum }_{j=1}^n{x}_j{w}_j^{(m)}{e}^{-{\beta }^T{x}_j}I(t_j{e}^{{\beta }^T{x}_j}\ge t_i{e}^{{\beta }^T{x}_i})}}{{\displaystyle {\sum }_{j=1}^n{w}_j^{(m)}{e}^{-{\beta }^T{x}_j}I(t_j{e}^{{\beta }^T{x}_j}\ge t_i{e}^{{\beta }^T{x}_i})}}),$$

where k(·) is a general (predictable) weight function. We choose a Gehan type weight

$$k(u)=\frac{1}{n}{\displaystyle \sum _{j=1}^n{w}_j^{(m)}{e}^{-{\beta }^T{x}_j}I(t_j{e}^{{\beta }^T{x}_j}\ge u)}$$ (8)

and the corresponding estimating equation can be written as

$$\mathrm{\Psi }(\beta )=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\delta }_i(x_i-x_j)w_j^{(m)}{e}^{-{\beta }^T{x}_j}I(t_j{e}^{{\beta }^T{x}_j}\ge t_i{e}^{{\beta }^T{x}_i})}}$$ (9)

The advantage of using the Gehan type weight function (8) is that the estimating equation (9) is a discontinuous but monotone function of β. Other weight functions may be considered for k(·). However, the corresponding estimating equation Ψ(β; k(·)) may not be a monotone function of β, and finding its root may be difficult.

Given β^(m+1), the updated estimate of β, a nonparametric estimate of H_u0(t) can be obtained based on the residuals t_ie^β(m+1)Tx_i [16, 17]. For example, let τ₁ < τ₂ < … < τ_k be the distinct uncensored residuals, d_τj denote the number of uncensored residuals equal to τ_j, and R(τ_j) denote the risk set at τ_j. An estimate of H_u0(t) in the current M-step is

$${\widehat{H}}_{u0}^{(m+1)}(t)=\text{exp }(-{\displaystyle \sum _{j:{\tau }_j<t}\frac{d_{{\tau }_j}}{{\displaystyle {\sum }_{i\in R({\tau }_j)}{w}_i^{(m)}\text{exp}(-{\beta }^{{(m)}^T}{x}_i)}}})$$

and ${\widehat{S}}_{u0}^{(m+1)}(t_i{e}^{{\beta }^{{(m+1)}^T}{x}_i})=\text{exp}[-{\widehat{H}}_{u0}^{(m+1)}(e^{{\beta }^{{(m+1)}^T}{x}_i}{t}_i)]$ and 0 if t_ie^β(m+1)Tx_i > τ_k. With β^(m+1) and ${\widehat{S}}_{u0}^{(m+1)}(t_i{e}^{{\beta }^{{(m+1)}^T}{x}_i})$, w_i in the E-step (7) can be updated and the EM algorithm will proceed until convergence.

Obtaining the variances of the estimated parameters in the proposed AHMC model is not straightforward because the complete log-likelihood function corresponding to (9) is not available. The standard methods proposed for the EM algorithm [18, 19] cannot be used to obtain estimates of the variances. A bootstrap method can be used to estimate the variances of the estimates in the model before a computationally light method is available.

3 Simulation Study

To evaluate the performance of the proposed method, we conduct a simulation study. The study will show the bias and variation of the parameter estimates under small samples and how they change when the sample size increases. The semiparametric estimation method is compared to a parametric estimation method when the baseline distribution is assumed to be from a parametric distribution family. The study also demonstrates the validity of bootstrap method in estimating the variance of parameter estimates.

In the simulation study, we assume a single binary covariate indicating a standard treatment and a new treatment. The data sets are generated from the AHMC model (1), (2), and (6). The binary covariate has effects on both S_u(t) and π with the corresponding β = log(0.5) and (γ₀, γ₁) = (2, −1). These coefficient values indicate that the cure rates are about 12% for the standard treatment and 27% for the new treatment. For uncured patients, the hazard of a patient at time t in the new treatment is equal to the hazard of a patient in the standard treatment at time 2t. The baseline hazard function h_u0(t) is assumed to be either 6t² (the hazard function of the Weibull distribution) or ϕ(log(t))/[t(1 − Φ(log(t)))] (the hazard function of the lognormal distribution with mean 1.65 and variance 4.67, where ϕ(·) and Φ(·) denote the density function and cumulative density function of the standard normal distribution). The censoring time is generated from a uniform distribution between 0 and a and the value of a is chosen so that the corresponding censoring rate is about 25%. The sample size is assumed to be 250, 500 and 800.

Under each case above, we generate 1000 data sets and fit each generated data set with the semiparametric method proposed in the last section and two parametric models assuming Weibull and lognormal baseline distributions. The biases and variances of results of β̂ and γ̂ from these models/methods are computed and summarized in Table 1 and Table 2. A bootstrap estimate of the parameter variance is obtained for each data set and the average of the bootstrap estimates (reported in the column Var* in the table) is compared to the variances of the 1000 estimates (reported in the column Var in the table) to verify the bootstrap method. The coverage probabilities of 95% confidence intervals based on the bootstrap variance estimates are also reported in the tables (reported in the column CP).

Table 1.

Bias and variance of β̂₁, γ̂₀, γ̂₁ from 1000 simulated data sets under Weibull distribution. The variances under Var* are the average of the bootstrap variances from simulated data in the AHMC model, and CP is coverage probability.

		Parametric				Semiparametric
		Weibull		Lognormal		Logrank		Gehan
n		Bias	Var	Bias	Var	Bias	Var	Bias	Var	Var*	CP
250	γ̂0	0.027	0.114	0.164	0.107	0.036	0.083	0.036	0.083	0.118	0.972
	γ̂1	−0.018	0.126	−0.111	0.169	−0.019	0.140	−0.019	0.140	0.166	0.967
	β̂1	0.008	0.011	−1.333	0.015	0.005	0.006	0.005	0.008	0.008	0.959
500	γ̂0	0.008	0.038	0.132	0.052	0.008	0.041	0.008	0.041	0.044	0.958
	γ̂1	−0.006	0.056	−0.098	0.076	−0.009	0.063	−0.009	0.063	0.067	0.942
	β̂1	0.004	0.001	−1.336	0.008	0.003	0.003	0.003	0.004	0.004	0.947
800	γ̂0	0.005	0.018	0.128	0.033	0.009	0.028	0.009	0.028	0.027	0.948
	γ̂1	−0.004	0.036	−0.094	0.050	−0.009	0.043	−0.009	0.043	0.041	0.944
	β̂1	0.003	0.001	−1.338	0.005	0.004	0.002	0.000	0.003	0.002	0.950

Table 2.

Bias and variance of β̂₁, γ̂₀, γ̂₁ from 1000 simulated data sets under lognormal distribution. The variances under Var* are the average of the bootstrap variances from simulated data in the AHMC model, and CP is coverage probability.

		Parametric				Semiparametric
		Weibull		Lognormal		Logrank		Gehan
n		Bias	Var	Bias	Var	Bias	Var	Bias	Var	Var*	CP
250	γ̂0	0.144	0.105	0.025	0.077	0.038	0.088	0.038	0.088	0.102	0.972
	γ̂1	−0.101	0.154	−0.009	0.117	−0.027	0.134	−0.027	0.134	0.148	0.973
	β̂1	−1.241	0.014	0.002	0.021	−0.002	0.020	0.001	0.013	0.013	0.945
500	γ̂0	0.142	0.054	0.021	0.043	0.037	0.046	0.037	0.045	0.046	0.962
	γ̂1	−0.104	0.078	−0.008	0.065	−0.031	0.069	−0.031	0.070	0.069	0.952
	β̂1	−1.230	0.006	0.002	0.001	0.003	0.009	0.001	0.006	0.006	0.964
800	γ̂0	0.111	0.030	0.003	0.025	0.010	0.026	0.010	0.026	0.027	0.954
	γ̂1	−0.071	0.042	0.012	0.037	−0.003	0.038	−0.003	0.038	0.041	0.960
	β̂1	−1.239	0.004	0.003	0.002	0.002	0.006	0.002	0.004	0.004	0.944

Comparing to the parametric estimation method, the proposed semiparametric method produces estimates with reasonable biases and variances. It is obvious that the estimation error in the estimates from the proposed estimation method decreases when the sample size increases from 250 to 800. It demonstrates that the proposed estimators have a good consistency property. The parametric method works well only when the baseline distribution assumption of the fitted model agrees with the true model that generated the data sets. When the two do not agree, the parametric method suffers large biases or variances. The results in the table also demonstrate that the bootstrap method produces good variance estimates of the estimated parameters in the model.

We also examined whether the distributions of the proposed estimators can be approximated well by the normal distribution. Q-Q plots of γ̂₀, γ̂₁ and β̂ (not shown) under different sample sizes and different baseline hazard distributions clearly indicate that the larger the sample size the better the approximation of the normal distribution to the distributions of the estimators.

4 SEER Breast Cancer Data

Breast cancer is the most common non-skin cancer in women and the second most common cause of cancer-related death in U.S. women. It is estimated that 182,460 women will be diagnosed with and 40,480 women will die of cancer of the breast in 2008. Therefore, the data in breast cancer from the SEER program are important for researchers, clinicians, policy makers, and citizens in understanding this disease. The SEER program has 17 registries (including San Francisco-Oakland, Connecticut, Detroit, Hawaii, Iowa, New Mexico and Utah for period 1973–2004, Seattle for period 1974–2004, Atlanta for period 1975–2004, Alaska, San Jose-Monterey, Los Angeles and Rural Georgia for period 1992–2004, Great California, Kentucky, Louisiana and New Jersey for period 2000–2004).

As an application of the proposed model and estimation method, we consider a breast cancer data of Polk, Iowa from the SEER program, which includes 1584 patients diagnosed between 1995–2004. The maximum follow-up is near 10 years. The purpose of our study is to investigate impact of stage of breast cancer to cancer survival. In SEER data, there has four categories for stage: local, regional, distant and unstaged. Unstaged means information is not sufficient to assign a stage for the cancer. Thus, we exclude the unstage cases when we extracted data from the SEER cancer incidence public-use data base. Observations with missing values on stage are excluded also in this analysis.

We consider the AHMC model to assess the effect of the stage on the cure rate and the survival probability of uncured breast cancer patients. Stage is classified by two dummy indicators, denoted by z₁ and z₂, where z₁ = 1 indicates the distant stage and 0 otherwise; z₂ = 1 represents the regional stage and 0 otherwise. Same definition for x₁ and x₂. We fit the model with the proposed semiparametric estimation method and estimate the variances of the parameters via 500 replications. The results of the model fitting are listed in Table 3. As a comparison, we also fit the data with the PHMC model [3].

Table 3.

Estimates and variances of β̂₁, γ̂₀, γ̂₁ for breast cancer data set from the AHMC model. The estimated variances are from bootstrap method with 500 replications.

	AHMC		PHMC
	Estimate	Variance	Estimate	Variance
γ̂0	−0.831	0.028	−0.903	0.217
γ̂1	1.671	0.461	3.036	1.405
γ̂2	0.431	0.086	0.722	1.212
β̂1	1.212	0.057	0.382	0.298
β̂2	0.412	0.104	0.006	0.116

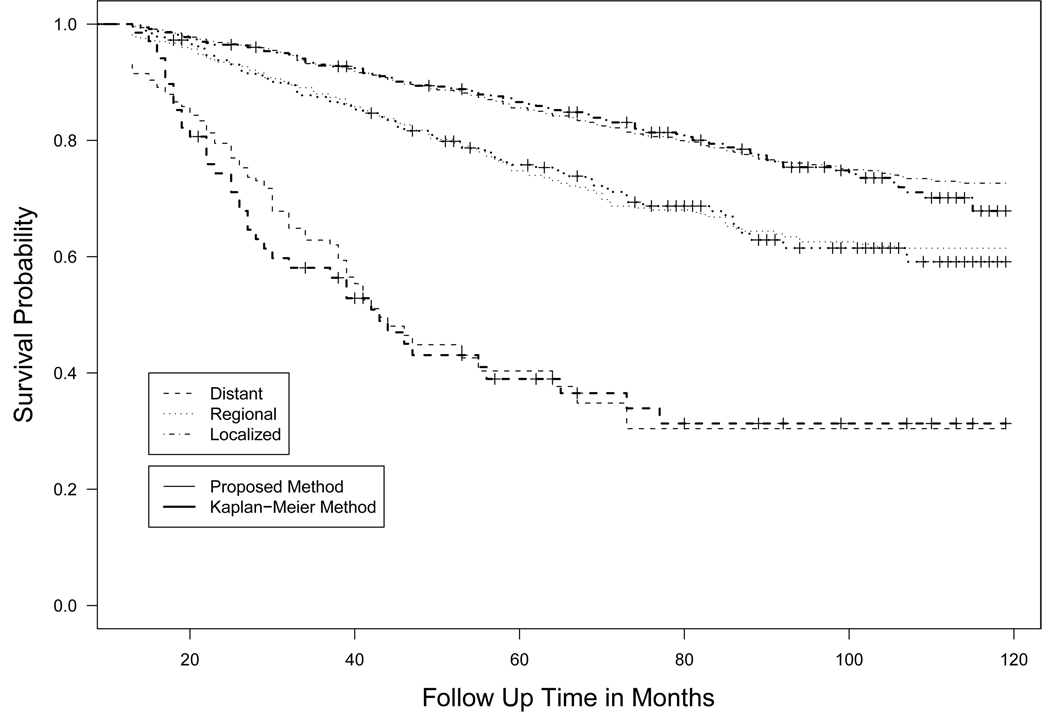
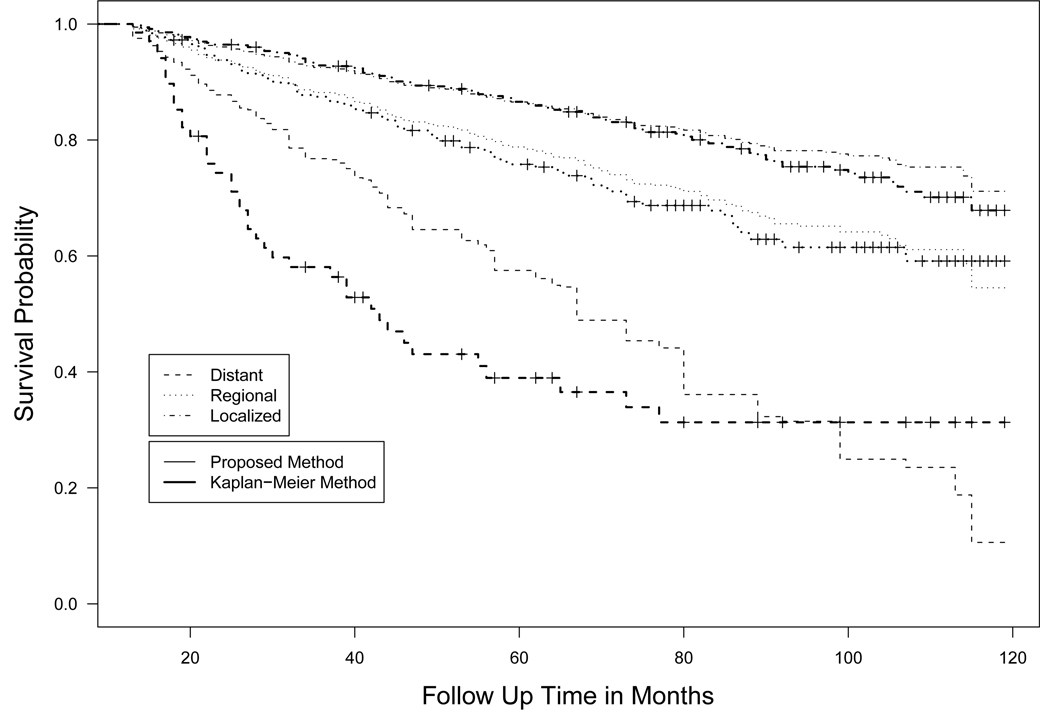
The two models lead to different results. In the AHMC model, the stage has significant effects both on the hazard rate of uncured patients and on the cure rates. The estimated cure rate are 0.700 for localized stage, 0.602 for regional stage and 0.304 for distant stage from the proposed method, while they are 0.741, 0.584, 0.079 from the PHMC model. For illustration, we calculated the marginal survival probability Ŝ(t|x, z) and plotted them in Figure 2 for the AHMC model and in Figure 3 for the PHMC model along with the Kaplan-Meier survival curve. It can be seen that the estimated survival curves from the AHMC model are closer to those from the Kaplan-Meier survival estimator than the PHMC model. It provides further evidence that the AHMC model is an appropriate choice for analyzing the data.

Figure 2.

Estimated survival curves for three stages based on the proposed method and the Kaplan-Meier survival estimator

Figure 3.

Estimated survival curves for three stages based on the PHMC model and the Kaplan-Meier survival estimator

5 Conclusions and Discussions

In this paper, we proposed an accelerated hazard mixture cure model. It is an extension of the accelerated hazard model to allow a fraction of cured patients. It extends the existing cure models by allowing a treatment to have no effect at time t = 0 and a gradual effect at t > 0 on the hazard function of uncured patients. To estimate the parameters in the model, we developed a semiparametric estimation method based on the EM algorithm and rank like estimating equation. The finite sample performance of the estimation method was examined via a simulation study. We observed that the proposed semiparametric estimation method is comparable to the parametric estimation method with correctly specified baseline distribution. When the baseline distribution in the parametric estimation method is misspecified, the semiparametric estimation method outperforms the parametric estimation method.

A limitation of the estimation method is that the variances of the estimated parameters in the model have to be estimated via the bootstrap method. Despite its validity, the bootstrap method is computationally intensive method and may not be desired in practice. Further study is still needed to develop a simple method to estimate the variances of the estimated parameters.

Comparing to the PHMC model, the AHMC model allows nonproportionality in hazard functions. There are other approaches in the literature to accommodate non-proportionality of hazard functions. However, the AH assumption in the AHMC model is conceptually simple. It may be easier to justify than other approaches, which makes it attractive to practitioners. Together with the proposed semiparametric estimated method, the AHMC model provides a viable alternative way to model survival data with a cure fraction and nonproportional treatment effects.

One referee pointed out that the Gehan-type weight function in (8) is essentially a predictable version of the estimated baseline survival function and it is usually more efficient when used in a model with converging hazard functions, such as the proportional odds model. The referee wonders whether such a weight function will result in efficiency loss when used in a model with diverging hazard functions, such as the AHMC model. We investigated this issue via simulation. In the simulation study, we compared the parameter estimates with the Gehan-type weight function and the estimates with a simple weight function k(u) ≡ 1 when data are generated from the AHMC model. We did not notice any obvious efficiency loss with the Gehan-type weight function. However, using k(u) ≡ 1 did increase the computing burden as we expected.