Analysis of enzyme kinetic data for mtDNA replication

Abstract

A significant amount of experimental data on the reaction kinetics for the mitochondrial DNA polymerase gamma exist, but interpreting that data is difficult due to the complex nature of the function of the polymerase. In order to model how these measured kinetics values for polymerase gamma affect the final function of the polymerase, the replication of an entire strand of mitochondrial DNA, we implement a stochastic simulation of the series of reaction events that the polymerase carries out. These reactions include the correct and incorrect polymerization events, exonuclease events which may remove both incorrectly and correctly matched base pairs, and the disassociation of the polymerase from the mitochondrial DNA template. We also describe other reactions which may be included, such as the addition of nucleoside analog tri-phosphates as substrates. The simulation analysis of the kinetics data is implemented through a standard Gillespie algorithm. We describe the methods necessary to define, code and test this algorithm, as well as describing the hardware and software options that are available.

1. Introduction

1.1 The Function of Polymerase Gamma

Mitochondrial polymerase gamma is the sole DNA polymerase active in mitochondria [1] and is responsible for the replication of mitochondrial DNA (mtDNA). Vertebrate polymerase gamma is composed of two subunits: a catalytic core, Pol γ-α, that contains the DNA polymerase and 3’-5’ exonuclease activities, and an accessory subunit, Pol γ-β, which enhances catalytic activity and serves as a processivity factor during DNA synthesis [2].

The function of polymerase gamma is far more complicated than the function of a typical enzyme which converts a substrate into a product. For that reason, the analysis of the enzyme kinetics of polymerase gamma must also be far more complicated. The function of polymerase gamma is the replication of a complete mitochondrial DNA molecule, while the enzyme kinetics data for polymerase gamma are at the level of individual reactions at the base-pair level. One tool that can be used to bridge that large gap between the enzyme kinetics data and the final product of a replicated DNA molecule is simulation. A computational simulation can reproduce each individual reaction of the polymerase activity, at the lowest level for which we have experimental data on the relevant reaction kinetics of the polymerase. The simulation can tirelessly repeat this process for the several tens of thousands of reactions necessary for the replication of a single strand of human mtDNA. Since mutations introduced through polymerase errors are of great practical interest, we need to use a stochastic simulation approach that will allow such replication errors to occur with probabilities that are calculated from the experimentally measured enzyme kinetics.

1.2 The Gillespie Algorithm

The “Gillespie algorithm” (or “Stochastic Simulation Algorithm”) is a well-known Monte Carlo simulation method for chemical reactions [3]. This algorithm takes a defined list of possible reactions and uses the reaction rates, based on the measured enzyme kinetics data and the substrate concentrations, to calculate the probability of each reaction on the list. These probabilities are then used to randomly choose the sequence of reactions which occur. The original Gillespie algorithm is particularly useful for simulating reactions involving a small number of molecules, while more elaborate and approximate versions of the basic algorithm have been created in order to handle large numbers of molecules [4].

Traditional continuous and deterministic biochemical rate equations are modeled as a set of coupled ordinary differential equations but these methods rely on bulk reactions that require the interactions of millions of molecules. In contrast, the Gillespie algorithm allows a discrete and stochastic simulation of a system with few reactants because every individual reaction is explicitly simulated. The physical basis of the Gillespie algorithm is the collision of molecules within a reaction vessel where the reaction environment is assumed to be well mixed. The general Gillespie algorithm can be summarized by the following series of steps:

Step 1, Initialization

Initialize the number of molecules in the system, the reaction kinetics constants, and the random number generators.

Step 2, Calculate Reaction Probabilities From Reaction Rates

Based on the substrate concentrations and the enzyme kinetics data, reaction rates R_i are calculated for each possible reaction, where i is an index denoting the particular reaction from the reaction list. The probability P_i for each reaction is then calculated from the list of n reaction rates through the following equation.

$$P_i=R_i/R_{\mathit{total}}$$ (1)

The parameter R_total is the sum of all of the reaction rates, as follows.

$$R_{\mathit{total}}=\sum _{j=1}^n{R}_j$$ (2)

Note that the sum of the probabilities is 1, with this definition.

Step 3, Choose A Reaction

Use a pseudo-random number generator to generate a uniform random number r_reaction in the range [0,1] and use this random number to choose the one reaction that occurs from the list of n possible reactions. The reaction number j is chosen if it satisfies the following condition.

$$\sum _{i=1}^{j-1}{P}_i<r_{\mathit{reaction}}\le \sum _{i=1}^j{P}_i$$ (3)

Then a second uniform random number r_time, also in the range [0,1] is chosen. This random number is used to set the time τ required for this reaction by the following equation.

$$\tau =-(1/R_{\mathit{total}})\ln (r_{\mathit{time}})$$ (4)

It is important to note here that the sum of all of the reaction rates is used in defining the time τ, not just the rate of the one particular reaction that was chosen.

Step 4, Update the Variables

Increase the time by τ. Update the molecule count based on the reaction that occurred.

Step 5, Iterate the Process

Check to see if any stopping condition has been met. If not, return to step 2 to recalculate the reaction rates, which may have changed due to the reaction chosen and carried out in steps 3-4.

These five steps define the basic Gillespie method for stochastic simulation. For applications of the stochastic simulation that involve large numbers of interacting molecules this basic method is inefficient in many ways, though it is an exact solution of the relevant stochastic master equation. In those cases more advanced and efficient methods should be used [4]. However, for modeling polymerase gamma activity we are generally concerned with only a single enzyme molecule, the one molecule of polymerase gamma that is replicating a particular strand of mtDNA. In this special case, the simple Gillespie algorithm outlined above is the preferred simulation method.

2. Applying the Gillespie Algorithm to Polymerase Gamma

The Gillespie algorithm is fundamentally a way of analyzing the outcome of a set of defined reactions which are competing with each other. The heart of this method is the definition of the reaction list. As we stated above, the function of polymerase gamma is complicated, and the reaction list could conceivably be defined in many different ways. However, our purpose is the analysis of the measured enzyme kinetics data, and for that purpose the available kinetics data are the primary determinant of the level of the reaction that can be modeled. There is no doubt that many of these kinetics values actually represent the cumulative effect of a number of subreactions. But unless there are enzyme kinetics data available for these subreactions, it is futile to attempt to model the subreactions. The available experimental kinetics data determine the lowest level of reactions which can be modeled reasonably.

Some DNA polymerases, such as the bacterophage T7 DNA polymerase, have had their kinetics examined in great detail by transient-state analysis of single nucleotide incorporation [5]. However, the kinetics of the mitochondrial DNA polymerase gamma have not been measured in that high level of detail. A series of papers from the Johnson group [6-9] have reported kinetic parameters for polymerase gamma at the level of polymerization, exonuclease and the disassociation of the polymerase gamma holoenzyme from the mtDNA molecule. Based on these experiments, we have developed a stochastic model to simulate the replication of an individual strand of mtDNA based on the Gillespie algorithm [10]. This model operates at the level of individual nucleotide insertions in the new DNA strand, using a reference mtDNA sequence (generally the human reference sequence) for the template strand.

Of course, polymerase gamma does not operate in a vacuum. It uses deoxyribonucleoside triphosphates (dNTPs) as substrates and these chemicals are created through some combination of a salvage pathway within mitochondria and the transport of substrates or their precursors into mitochondria from the cytoplasm [11, 12]. One must choose an artificial boundary for every computational model and events outside of that boundary are ignored in the model. In the following description we will assume that only the actions of polymerase gamma are modeled and that the concentrations of the dNTPs within the mitochondria are held constant. Alternatively, one could reasonably extend the model to include the reactions of the salvage pathway. A practical limitation on this extension of the model is our current lack of knowledge of the correct transport kinetics of deoxyribonucleotides between the cytoplasm and the mitochondrial matrix [13]. Another alternative would be to extend the model to include the function of other proteins critical to mtDNA replication, such as the helicase [14]. All such extensions of the model are limited by the availability of kinetics data for the relevant enzymes.

2.1 Definition of the Reaction List for Polymerase Gamma

In this model, polymerase gamma carries out four basic classes of reactions: DNA polymerase activity (inserting a correct or incorrect nucleotide into the new DNA strand), exonuclease activity (removing a nucleotide from the new DNA strand), disassociation of the polymerase from the DNA, and reassociation of the polymerase with the DNA molecule. In the DNA polymerase reaction a single nucleotide is added to the new DNA strand. This nucleotide may be the correct base indicated by the template strand, or it may be an incorrect one which does not complement the template. In the exonuclease reaction one nucleotide is removed from the new DNA strand. Again the removed nucleotide may be either a correct match to the template strand or an incorrect match. The exonuclease reaction is an error correction mechanism, as the rate for removal of incorrectly incorporated nucleotides is faster than that for correctly incorporated nucleotides. In the disassociation reaction the polymerase holoenzyme separates from the DNA molecule. The reassociation reaction re-attaches the polymerase to the DNA molecule after a disassociation event occurs.

In our basic model of polymerase gamma function at each position on the replicating mtDNA strand polymerase gamma will randomly undergo one of a set of six reactions; one correct polymerase reaction, three incorrect polymerase reactions, the exonuclease reaction, or disassociation (Figure 1). Which reaction polymerase gamma undergoes at each time is determined by the probability of each reaction, calculated using the reactions rates as introduced in the Gillespie algorithm [3] and described above. The probability for each possible reaction is proportional to the reaction rate, so that fast reactions occur more often than slow reactions. Currently, kinetics data for the reassociation reaction rate for polymerase gamma are not available to the best of our knowledge. For this model we assume that once disassociation occurs the only possible reaction is then reassociation of the polymerase with the DNA template. Considering the lack of kinetics for the reassociation reaction, we make the choice to immediately reassociate the polymerase to the DNA after a disassociation event. This choice neglects the time that this reassociation event requires, but without kinetics data for this reaction little else can be done.

Figure 1.

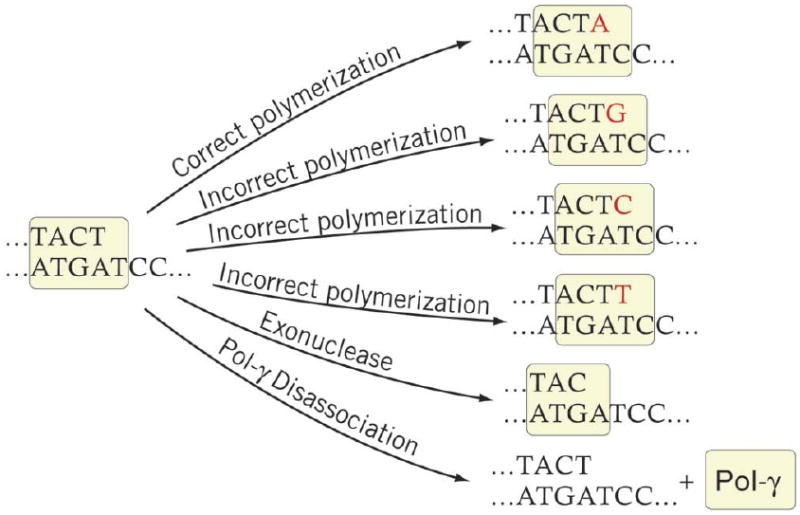
Diagram of the six basic competing reaction of the mitochondrial DNA polymerase.

Michaelis-Menten kinetics were used for all of the DNA polymerization reactions. The exonuclease reaction and the disassociation reaction were set to have constant reaction rates based on the experimental data. For the two scenarios of a correctly inserted and incorrectly inserted previous nucleotide we have separate sets of kinetic parameters from Lee and Johnson [15] and Johnson and Johnson [6, 7]. These studies have reported an increase in exonuclease and disassociation rates, but a decrease in incorporation rates by polymerase gamma following an incorrect incorporation. This is included in the simulation model by using two sets of enzyme kinetics parameters, one set for reactions following a correct incorporation and another set for reactions following an incorrect incorporation. The full set of enzyme kinetics data used in the model is listed in Tables 1-5, which are reproduced from reference [10].

Table 1.

Kinetic parameters k_cat (1/s) for base pairings when the previously inserted nucleotide pair is a correct Watson-Crick pair ordered by template strand (rows) and the new strand (columns).

Base pairings	T	G	C	A
A	25	0.08	0.1	0.0036
C	0.012	37	0.003	0.1
G	0.16	0.066	43	0.042
T	0.013	1.16	0.038	45

Table 5.

Reaction rates for the exonuclease and disassociation reactions of polymerase gamma when the previous base pair is a Watson-Crick pair or a non-Watson-Crick pair.

Previous base pairs	Exonuclease rate (1/s)	Disassociation rate (1/s)
Watson-Crick pair	0.05	0.02
Non-Watson-Crick pair	0.4	0.2

2.2 Modified Nucleotide Reactions

The reaction list illustrated in Figure 1 may be considered as a minimum list of reactions needed to model the activity of polymerase gamma. This list can be extended in a number of different ways. In addition to the four natural deoxyribonucleotide tri-phosphate substrates, several chemically altered forms of these substrates can also interact with polymerase gamma, albeit with altered, and generally poorer, enzyme kinetics. One important class of these chemically altered substrates are the nucleoside analogs commonly used in the treatment of HIV infection. Many of these drugs have mitochondrial toxicity [16, 17] which may be due to their interaction with polymerase gamma [8, 10, 18, 19] and their subsequent incorporation into mtDNA, generally causing the disruption of the mtDNA replication event. Due to this toxicity, which is very important in the long-term treatment of HIV infection, the kinetics data for the interaction of many nucleotide analog drugs have been measured [8, 18, 20, 21] (see Table 6, reproduced in part from reference [10]). Based on these data, we have included these alternate substrates in a model of polymerase gamma function [10]. Other naturally occurring alternative substrates could also be modeled. The most important of these are arguably ribonucleotide tri-phosphates [22] or oxidatively damaged substrates such as 8-oxo-dGTP [23]. The only practical limitation to the additional reactions that could be modeled is the availability of the reaction kinetics data for the new reaction.

Table 6.

Enzyme kinetics parameter values used for polymerase gamma reactions with clinically relevant nucleoside analog drugs.

NRTI	Km (μM)	Kcat (1/s)	Exonuclease rate (1/s)	Disassociation rate (1/s)
ddC	0.041	0.660	<0.00002	0.02
ddA	0.022	0.310	0.0005	0.02
FIAU	2.9	24	0.06	0.02
d4T	0.045	0.24	0.0004	0.02
FTC(+)	0.79	0.84	0.0048	0.02
3TC(-)	9.2	0.125	0.015	0.02
3TC(+)	1.5	0.35	0.02	0.02
Acyclovir	6	1.03	0.0021	0.02
ddI	6.3	0.15	0.0007	0.02
TDF	40.3	0.21	0.0007	0.02
ABC	13	0.0018	0.0016	0.02
AZT	280	0.001	Not reported	0.02
FTC(-)	62.9	0.0086	0.0048	0.02

3. Enzyme Kinetics Data

3.1 Michaelis-Menten kinetics for incorporation rates after a matched or an unmatched base pair

The reaction kinetics for polymerization reactions are given in Tables 1-4. The reaction rates for the polymerization are calculated using a standard Michaelis-Menten equation, using assumed values for the four dNTP substrate concentrations. The dNTP concentrations are the major parameters for the simulation, and the results of the simulation depend greatly on the pattern of these four concentrations.

Table 4.

Estimated K_m (μM) kinetic parameters for base pairings when the previously inserted nucleotide forms a non-Watson-Crick pair. The array order is the same as in Table 1.

Base pairings	T	G	C	A
A	404	40400	40400	40400
C	40400	404	40400	40400
G	40400	40400	404	40400
T	40400	40400	40400	404

Given the complexity of polymerase gamma activity, it should not be surprising that even with the large set of kinetic parameters that have been measured our knowledge of the relevant enzyme kinetics parameters for this enzyme is still incomplete. For example, the data used in Tables 1-2 was measured only in the case where the previous base pair was an A:T pair. In principle the reaction rates could be different for other preceding bases, however in the absence of this data we have applied these reaction kinetics to all cases where the previous base pair is a standard Watson-Crick pairing. The data on kinetics following a non-Watson-Crick base pair are even more limited. The k_cat and K_m values reported by reference [7] for this case were only determined for the correct pairing of a C opposite to a G in the template strand, where the previous base pairing was an incorrect T:T pairing. The kinetics values for other pairings, such as an A opposite to a T, are not available, and the kinetics for any incorporations following incorrect pairings other than T:T are also not available. The last point is of perhaps great practical importance since the incorrect T:T pairing represents an A to T (or T to A) transversion, which is actually a rare event in mitochondrial DNA. It would be far more valuable to have kinetics after a G:T incorrect pairing, as this represents the very common A to G transition mutation. One important application of this analysis of the kinetics data for polymerase gamma is to discover such limitations in the experimental data.

Table 2.

Kinetic parameters K_m (μM) for base pairings when the previously inserted nucleotide is a correct Watson-Crick pair. The array order is the same as in Table 1.

Base pairings	T	G	C	A
A	0.6	800	540	25
C	180	0.8	140	160
G	200	150	0.9	250
T	57	70	360	0.8

Since there are holes in the available experimental data for polymerase gamma, we must make some practical assumptions to fill these holes. We defined an approximate model by setting the kinetic coefficients for all correct incorporations following an incorrect incorporation to be equal (Table 3-4) to the values reported for the C:G pairing. Reaction kinetics for the incorporation of an incorrect nucleotide following an incorrect nucleotide are not available at all, to the best of our knowledge. To fill this gap in our knowledge we chose to assume values for these missing parameters (Table 3, off-diagonal elements) based on the observation from Table 1 that k_cat values were approximately 1000 times less for non-Watson-Crick pairing compared to regular Watson-Crick pairings. Similarly, based on Table 2 K_m values were estimated to be approximately 100 times greater for the non-Watson-Crick pairings and this was used to estimate K_m values in Table 4 for the off-diagonal elements.

Table 3.

Estimated k_cat (1/s) kinetic parameters for base pairings when the previously inserted nucleotide forms a non-Watson-Crick pair. The array order is the same as in Table 1.

Base pairings	T	G	C	A
A	0.52	0.00052	0.00052	0.00052
C	0.00052	0.52	0.00052	0.00052
G	0.00052	0.00052	0.52	0.00052
T	0.00052	0.00052	0.00052	0.52

3.2 Reaction rates for the exonuclease and disassociation reactions

Reaction rates for the exonuclease and disassociation reactions of polymerase gamma are listed in Table 5. As with the polymerase reaction, the exonuclease and disassociation reaction rates were measured for the two DNA template conditions where the previous base pair was a Watson-Crick pair or a non-Watson-Crick pair.

3.3 Reassociation of the polymerase with the DNA

Data regarding the reassociation reaction rate is not available to the best of our knowledge. For this model we assume that once disassociation occurs the only possible reaction is reassociation of the polymerase with the DNA template. That reassociation is modeled as occurring immediately, since we lack any experimental data on this process.

4. Details of the Experiments Measuring the Enzyme Kinetics of Polymerase Gamma

One must take care to consider the idealized conditions under which the experiments measuring the enzyme kinetics of polymerase gamma were conducted. Differences between these idealized conditions and the real in-vivo conditions must always be kept in mind. In this section we summarize the conditions of the experiments as described in references [6-9, 15].

4.1 The polymerization rate kinetics

Each incorporation of a nucleotide into the new mtDNA strand by polymerase gamma under all possible 16-base pair combinations conditions was examined using synthetic DNA oligonucleotides and a recombinant holoenzyme of human mitochondrial DNA polymerase gamma. The recombinant holoenzyme consisted of a catalytic subunit containing a 29-amino acid truncation and an accessory subunit containing a His₆ tag and a 56-amino acid terminal truncation. The catalytic and accessory subunits were combined at a molar ratio of 1:5 to saturate the binding to reconstitute the holoenzyme [15]. The kinetics of incorporation for all correct nucleotides were similar, with an average K_d of 0.8 μM and an average k_pol of 37 s^-1. However, the kinetics of misincorporation varied widely. The ground state binding K_d (K_m) of incorrect bases ranged from a low of 25 μM for an A:A mispair to a high of 360 μM for a C:T mispair. The rates of incorporation of incorrect bases varied from a low of 0.0031 s^-1 for a C:C mispair to a high of 1.16 s^-1 for a G:T mispair. [15]

An exonuclease-deficient (EXO^–) catalytic subunit was created to allow examination of the polymerization reaction in the absence of proofreading. Mutagenesis of Glu-200 to alanine (E200A) produced a modified enzyme with reduced exonuclease activity of single base excision from duplex DNA but which was shown to bind DNA and to catalyze the correct base pair insertion with kinetics identical to the wild type enzyme. This mutant polymerase gamma enzyme was treated identically to the wild type for purification and experimental purposes. The wild-type polymerase was used to determine polymerization parameters for correct incorporation after a correct Watson-Crick match, for exonuclease experiments, and for the disassociation kinetics measurements following mismatched DNA. The exonuclease deficient mutant polymerase gamma was used for measuring the enzyme kinetics for the correct incorporations after a Watson-Crick mismatch and for the enzyme kinetics of incorrect incorporations [7].

Single nucleotide incorporation assays were performed at various concentrations of the nucleotide substrates to examine the effects of nucleotide concentration on the incorporation rate. Burst conditions and a range of deoxyribonucleoside tri-phosphate (dNTP) concentrations were used to examine the enzyme kinetics for correct nucleotide incorporations. A reaction time course was determined for each concentration of nucleotide, and the product formation rate was plotted against time and fit to a burst equation. The burst rates (k) were then plotted against dNTP concentration and fit to a hyperbola to obtain the K_d and the maximum rate of polymerization, k_pol, for each correct dNTP [7].

Because the rate of incorporation after a non-Watson-Crick pair was comparable to the rate of exonuclease by polymerase gamma, the EXO⁻ polymerase was used to perform the experiment to determine the enzyme kinetics of a correct polymerization following an incorrect pairing. Incorporation of a dCTP was examined opposite a template G, following a T:T mismatch. The rate of the single turnover correct incorporation of dCTP was measured and the data were fit to a hyperbola, providing a K_d of 404 ± 51 μM and maximum incorporation rate of k_pol = 0.52 ± 0.03 s^-1 [7].

The wild-type human polymerase gamma cannot be used to measure the enzyme kinetics for incorrect polymerizations because the misincorporation is almost always corrected by the efficient exonuclease function. Therefore, EXO^– polymerase gamma was used to measure the kinetics of incorrect polymerizations. In order to limit the effects of disassociation these experiments were carried out with high polymerase gamma concentrations in excess of the template concentrations so that whenever disassociations did occur a rapid reassociation of another polymerase molecule was likely to occur, “canceling out” the disassociation event [7]. The reaction product formation was plotted against time and fit to a single exponential. Rates of polymerization determined from the single exponential were plotted against nucleotide concentration and fit to a hyperbola to determine the disassociation constant, K_d, and the maximum rate of polymerization, k_pol, for each incorrect nucleotide. [15]

4.2 The exonuclease rate kinetics

To measure the exonuclease reaction rate, the wild-type polymerase gamma holoenzyme was reconstituted by mixing catalytic and accessory subunits in a 1:5 ratio. To quantify the excision reaction, the loss of full-length substrate primer due to exonuclease hydrolysis was plotted against time and fit to a single exponential [6]. To measure the exonuclease rate of polymerase gamma following a Watson-Crick matched base pair excision of the 3’-end base from the primer strand of correctly base-paired DNA was examined. The rate was obtained by fitting to a single exponential defining the kinetics of excision of the first base from the 3’-terminal of the primer and yielded a rate of 0.05 s^-1 [6].

To determine the effect of a mismatched non-Watson-Crick base pair on the exonuclease rate, three DNA substrates (containing a T:T, C:T or G:T mismatch) were used under conditions of excess polymerase concentration compared to template concentration. The decreases in concentrations of DNA were fit to single exponential curves. Excision of DNA containing the T:T, C:T and G:T mismatches occurred at rates of 0.40 ± 0.04 s^-1, 0.31 ± 0.01 s^-1, and 0.57 ± 0.03 s^-1 respectively [6]. Since these values are similar and kinetics data were not available for all possible mismatched pairs, in our simulations we have chosen the value 0.4 s^-1 to represent the exonuclease rate for all mismatched base pairs.

4.3 The disassociation rate kinetics

The rate-limiting step of single nucleotide incorporation is presumably the disassociation of the polymerase enzyme from the DNA. The steady-state rate is determined by the slowest step during polymerization, which must occur after the chemical reaction to account for the observation of a pre-steady-state burst. Therefore the DNA disassociation rate of polymerase gamma holoenzyme is assumed to equal its steady-state rate of polymerization. The reported disassociation rate of polymerase gamma after a correct Watson-Crick base pair is 0.02 ± 0.001 s^-1 [9].

To examine the rate of release of polymerase gamma from a mismatched DNA substrate, the EXO^– polymerase was used. The data was fit to a single exponential and yielded a k_off of 0.18 ± 0.02 s^-1 for DNA containing a 3’ T:T mismatch [7]. This value is very close to the data listed in [6] that gave the disassociation rate of polymerase gamma after an incorrect non-Watson-Crick base pair as 0.2 s^-1.

4.4 Kinetics for nucleoside analogs substrates

To measure K_d and k_pol for each nucleoside analog triphosphate, an exonuclease-deficient (E200A) was used to reconstitute the human polymerase gamma holoenzyme. As in the previous sections, an excess of the polymerase was used in comparison to the template concentration. The kinetics of incorporation of nucleoside analog triphosphates were measured using this mutant, which was selected based upon studies showing that this single point mutation did not alter the kinetics of normal nucleotide incorporation [8]. To measure the exonuclease kinetics of polymerase gamma for nucleoside analog triphosphates, the wild-type polymerase holoenzyme was preincubated with DNA containing a 3’-terminal nucleoside analog to initiate the hydrolysis reaction [8]. No published study that we are aware of has been done to measure the disassociation rate of polymerase gamma following the incorporation of an analog triphosphate into the new mtDNA strand. With no experimental data available, we assumed that the disassociation rates following an incorporated nucleoside analog were equal to the disassociation rates after a matched Watson-Crick pair.

The lack of experimental data on the disassociation rate of polymerase gamma following the incorporation of a nucleoside analog into the mtDNA may seem like a trivial limitation, but the analysis of the enzyme kinetics data through the stochastic simulation shows that this rate is actually critical to our understanding of the mitochondrial toxicity of these drugs [10]. Since the chemical alteration of these drugs prevents further polymerization after the nucleotide analog is incorporated into the DNA strand (“chain termination”), only two competing reaction are left, the exonuclease reaction which removes the nucleoside analog and the disassociation reaction which ends the mtDNA replication and defines the chain termination event. Therefore the disassociation rate following the analog is a fundamental determinant of the chain termination probability of the drug.

5. Problems

As the previous two sections illustrate, the primary problem with using a stochastic simulation to analyze the enzyme kinetics of polymerase gamma is the incomplete reaction kinetics data. The function of the polymerase, as represented in this simulation model, depends on the competition between different reactions which have different reaction rates. The outcome of that competition depends on the complete set of reaction rates. A change in the reaction rate of any single reaction alters the probability of all of the reactions (see equation 1). While this is an explicit feature of the simulation method, it is also a very realistic one and we should expect that the same principle should hold for the function of the real polymerase enzyme. Lack of knowledge about one reaction does not just affect that one aspect of the polymerase function. It can in principle affect the balance between all of the other reactions which compete with that reaction. One very important practical exception to this problem is if the reaction with missing enzyme kinetics data is expected to have a very slow reaction rate in comparison to the reactions competing with it. In that case, uncertainty in the reaction kinetics of that relatively very slow reaction may cause negligible alterations in the probabilities of the competing reactions.

One important example of the limited kinetics data is that there is little data on how the template sequence may affect the reaction kinetics of polymerase gamma. As discussed earlier in section 3.1, the kinetics data that are currently available were taken from a very limited template of either a A:T pair or a T:T pair (to represent kinetics following a non-Watson-Crick pair). The lack of experimental data for other templates limits the ability of the model to analyze the potential effect of flanking sequences on mtDNA mutation rates, for example.

6. Equipment

No specialized hardware is required for carrying out these simulations. We have run the simulation code on both a relatively standard desktop PC under LINUX with a 4400 Intel CPU (dual core, 2.0 GHz with 2.0 GB of RAM) and on a central server (Intel Xeon CPU, 2.33 GHz). Typically, we simulate the replication of a single strand of mtDNA and repeat that simulate 10,000 times in order to gather statistics on rare events, such as specific point mutations. On the central server a set of 10,000 simulated mtDNA strand replications would take approximately 10 minutes of CPU time, and on the desktop PC would take approximately 20 minutes. The simulation that we wrote requires less than 7 MB of virtual memory to run.

For software, anyone wishing to carry out this model is faced with the basic choice of coding the algorithm in a standard programming language, or using one of several packages that exist for developing stochastic biochemical simulations. Two examples of these packages are StochKit [24] and StochSim [25]. The advantage of using a prepared package such as these is that the basic algorithm is already written and debugged for you and that no programming knowledge is needed. However, much of the capabilities of the advanced packages, such as the relatively new StochKit, are aimed at developing approximate methods to handle simulations with large numbers of reacting molecules or to include spatial effects. These capabilities are not needed for a model of the polymerase gamma enzyme kinetics. Anyone using these packages must be careful to use the options which are relevant to this particular simulation, which will require at least some familiarity with the principles of stochastic simulations. We made the choice to write our own simulation code in C++. The decision to write our own code was based on the need for maximum flexibility in our definition of the model and in controlling the data output.

The Gillespie algorithm yields a series of reaction events, chosen from the reaction list of the model. For complete information about the simulation, one can choose to save this data in a number of ways. One simple choice of format is illustrated in Table 7. Each line in the file represents one reaction event. Column 1 gives the event number. Column 2 gives the sequence position of the polymerase. Column 3 gives the template base at that position, Column 4 gives the reaction event chosen by the Gillespie algorithm, where and “A”, “C”, “G”, or “T” means the insertion of that nucleotide into the new DNA strand, a “ˆ” indicates a disassociation event, and a “<” indicates an exonuclease reaction. Column 5 gives the time τ for that step, as defined by equation 4. Finally, column 6 gives the sequence context of the event in the format “template / new strand”. The total space needed for the file varies depending on the number of incorrect polymerization events which occur, but is generally in the range 0.5 to 1.0 MB.

Table 7.

Example format for output file of the simulation.

Event number	Sequence position	Template	Reaction	Reaction time, τ (s)	Sequence context
1012	990	T	A	0.017525	AGT/TC
1013	991	T	G	0.0809195	GTT/CA
1014	992	G	ˆ	3.73018	TTG/AG
1015	992	G	ˆ	0.491668	TTG/AG
1016	992	G	<	0.82397	TTG/AG
1017	991	T	A	0.0055691	GTT/CA
1018	992	G	C	0.0246826	TTG/AA

Carefully controlling the IO (the storage of data from the program onto the physical hard drive of the computer) is an important factor in the final speed of the code. This is a basic point, but it is also a common error. We chose to save in the RAM memory a time ordered list of every single reaction event that occurred in the simulation of the mtDNA strand, and then we analyzed that list for specific properties with a different analysis code, separate from the simulation code. It is a mistake to save each reaction event to a file on the hard drive as it is calculated in the simulation, as that process of initiating access to the file on the hard drive repeatedly a large number of times takes a very substantial amount of time. Instead, the list of reactions that occurred in a simulated mtDNA replication should be kept within the memory of the program and either downloaded to the hard drive in one piece at the end of the complete simulation run of a single strand replication or analyzed at the end of the simulation so that only summary statistics are saved to the hard drive.

In order to generate reliable statistics on rare events we run large numbers of repeated replications of a full mtDNA strand, typically 10,000 repetitions. Since a set of 10,000 mtDNA strand replications only takes about 10 minutes to run, and the disk space necessary for saving the 10,000 output files would be approximately 10 GB, we analyze the output of each simulated strand replication as it finishes, and then we save only the summary statistics for the specified quantity of interest for the full set of 10,000 simulated strand replications. These analysis programs were written in Perl, as the best choice for programs handling character data.

7. Troubleshooting

It is necessary to have quantitative and qualitative predictions against which the simulation output can be compared. There are statistical properties which the output data of the simulation must have, based on the assumptions of the algorithm. These properties should be used as checks to see if the algorithm has been properly implemented.

7.1 The distribution of reaction times

The simplest property to check is the distribution of the reaction times. From equation 4, the Gillespie algorithm assumes that the reaction times have an exponential distribution with a mean value of 1/R_total, where R_total is the sum of all of the competing reaction rates. If you have chosen to keep the dNTP concentrations constant, then the R_total will also be constant and the distribution of the reaction times calculated by the simulation should have an exponential distribution with a mean value of 1/R_total. We actually have two sets of reaction rates in this model, depending on whether the previous base was a correct Watson-Crick pairing or an incorrect Watson-Crick pairing. So for this test the reaction times should be separated into two lists depending on whether the previous pairing was a Watson-Crick pairing or not. Each list of reaction times should have an exponential distribution with different means corresponding to the correct 1/R_total for that list, which can be calculated.

7.2 The mutation pattern under equal dNTP concentrations

When the four substrate dNTP concentrations are equal, it is easy to see from the experimental kinetics data in Table 1 and 2 that the incorrect polymerization event with the highest rate (and thus the greatest probability) is the polymerization of a G opposite to a T, forming an A to G transition mutation in the new strand. The second most common polymerization error should be the insertion of a T opposite to a G, forming the C to T transition on the new strand. All of the transversion mutations should occur at far lower rates than these two transition mutations, under equimolar dNTP concentration conditions. This can serve as a qualitative test of the accuracy of the simulation of the rare mutation events. Of course, if a different set of kinetics values are used than those given in Tables 1-2, then the prediction of the mutation pattern should change based on that data.

8. Using the Simulation to Analyze Polymerase Gamma Enzyme Kinetics Data

The process of the complete replication of a single strand of mitochondrial DNA by polymerase gamma is the result of tens of thousands of individual reactions. The exact sequence of reactions that occurs, the number and pattern of the point mutations introduced through polymerase errors, the number of exonuclease events and the number of disassociation events all have strong random components. The dependence of all of these important quantities on the basic measured kinetics of polymerase gamma is complex, and a direct stochastic simulation of the polymerase activity, as described in this paper, is a thorough way of determining the end consequences of the measured kinetics values. This simulation should be thought of simply as an ordered way of determining the end result of a set of competing reaction rates. This process is of particular importance when one is considering the measured kinetics of a variant form of the polymerase gamma protein, which may be pathogenic. Many polymerase gamma variants are likely to have altered kinetics for more than one of the reactions illustrated in Figure 1. The ultimate effect of multiple changes in the kinetic parameters of the polymerase may be quite difficult to predict correctly without the use of a simulation as a tool to organize our analysis, and our thinking.