Multimodal Functional Neuroimaging: Integrating Functional MRI and EEG/MEG

Abstract

Noninvasive functional neuroimaging, as an important tool for basic neuroscience research and clinical diagnosis, continues to face the need of improving the spatial and temporal resolution. While existing neuroimaging modalities might approach their limits in imaging capability mostly due to fundamental as well as technical reasons, it becomes increasingly attractive to integrate multiple complementary modalities in an attempt to significantly enhance the spatiotemporal resolution that cannot be achieved by any modality individually. Electrophysiological and hemodynamic/metabolic signals reflect distinct but closely coupled aspects of the underlying neural activity. Combining fMRI and EEG/MEG data allows us to study brain function from different perspectives. In this review, we start with an overview of the physiological origins of EEG/MEG and fMRI, as well as their fundamental biophysics and imaging principles; it is followed by a review of major progresses in understanding and modeling the neurovascular coupling, methodologies for the fMRI-EEG/MEG integration and EEG-fMRI simultaneous recording; finally, important remaining issues and perspectives (including brain connectivity imaging) are summarized.

I. Introduction

Neuroimaging plays a critically important role in neuroscience research and management of neurological and mental disorders. Modern neuroimaging techniques rely on various “source” signals that change across different spatial and temporal scales in accompany with neuronal activity. For instance, neuronal activity intensifies electrophysiological signals, such as action potentials and post-synaptic potentials, which serve as the primary messengers for communication among neurons. It is generally agreed that neural activity is well-characterized by electrophysiological processes which tightly correspond with neuronal dynamics. In addition, neural activity is also coupled with metabolic and hemodynamic processes. As brain function requires sustained blood flow to supply oxygen to compensate for cerebral metabolic energy consumption, changes in neural activity often induce cascaded changes in cerebral metabolic rate of oxygen (CMRO₂), cerebral blood flow (CBF), oxygen extraction fraction (OEF), cerebral blood volume (CBV), etc. In contrast to electrophysiological signals, metabolic and hemodynamic responses are much slower and reflect the indirect and secondary effects of neural activity.

All noninvasive neuroimaging modalities are based on biophysical signals related to either brain electrophysiology or hemodynamics/metabolism. Electroencephalography (EEG) [1] and magnetoencephalography (MEG) [2] are based on electrophysiological principles. Functional magnetic resonance imaging (fMRI) [3–5], positron emission tomography (PET) [6, 7], single-photon emission computed tomography (SPECT) and near-infrared spectroscopy (NIRS) are based on hemodynamic and/or metabolic principles. Strengths and limitations of these modalities depend largely upon the spatiotemporal characteristics of the measured “source” signals in relation to neuronal activity, as well as many diverse sensing and imaging methods applied to individual modalities.

EEG and MEG measure external electrical potentials and magnetic fluxes, respectively, which arise collectively from mass neuronal responses within the brain. Such electromagnetic signals propagate (virtually) instantaneously from the activated neuronal tissues via volume conduction to the recording sites on/above the scalp surface [8–11]. The instantaneous nature of EEG/MEG indicates an intrinsically high temporal resolution and precision, which make them well suited for studying brain functions on the neuronal time scale. The collective nature suggests low spatial resolution and specificity, which impede mapping brain functions in great regional details [12]. This is regardless of recent advancements in electromagnetic source imaging (ESI) [13–15], which has led to great strides in improving the EEG/MEG spatial resolution to a centimeter scale or even smaller.

The strength and limitation of fMRI are almost precisely the obverse of those of EEG and MEG. As neural activity elevates, the concomitant alternation of local oxyhemoglobin vs. deoxyhemoglobin content gives rise to a so-called blood oxygen level dependent (BOLD) magnetic resonance (MR) signal [16]. Since its advent in the early 1990's [3–5], the BOLD-contrast fMRI has rapidly gained a dominant position in neuroscience research [17]. The merits of fMRI include its whole brain coverage, relatively uniform sensitivity, high spatial resolution and specificity. These advantages are primarily attributable to well-established MR imaging techniques (e.g. echo-planar imaging) that allow for the frequency and phase encoding of spatially distributed MR signals. However, fMRI is also limited by its poor temporal resolution as well as its indirect nature with respect to neuronal activity. These limitations often pose concerns to any simple interpretation of the BOLD signal as a surrogate index of neural activity.

For an illustrative overview, we graph the existing noninvasive neuroimaging methodologies, in comparison with relevant invasive recording/imaging techniques, with respect to their spatial and temporal resolution, as shown in Fig. 1. Typical invasive techniques include intracranial electrophysiological recordings of the single-unit activity (SUA), multi-unit activity (MUA) and local field potential (LFP). In addition, intrinsic light optical imaging, which can be applied to exposed brain surface, is also capable of imaging the hemodynamic signals [18,19]. Noticeably, none of existing noninvasive modalities can alone achieve high resolution in both spatial and temporal domains. One technique may have merits in the temporal aspect but limitations in the spatial aspect (such as EEG/MEG), or vice versa (such as fMRI). These complementary features have motivated recent developments in integrating multiple neuroimaging modalities, particularly EEG/MEG and fMRI [20–24]. As illustrated in Fig. 2, such a multimodal functional neuroimaging approach is based on the fundamental relationships between electromagnetic signals generated by neuronal activity via volume conduction, and BOLD-contrast fMRI signals related to the hemodynamic responses. A number of efforts in recording technology, multimodal data fusion and the neurovascular modeling, have collectively led to a promising fMRI-EEG/MEG integrated functional neuroimaging approach, which holds the potential to reach millimeter spatial resolution and millisecond temporal resolution, thereby opening a unique and noninvasive window to investigate dynamic brain activity and connectivity.

Figure 1.

Schematic illustration of the ranges of spatial and temporal resolution of various noninvasive (in blue) imaging techniques and invasive (in red) experimental techniques.

Figure 2.

Illustration of the fMRI-EEG/MEG integrated multimodal neuroimaging (part of figure adapted from Fig. 1 of [46] with permission).

However, the integration of fMRI and EEG/MEG also faces great challenges, which arguably compromise its intuitive promise and benefits to neuroimaging and neuroscience fields. To list a few most critical ones, what is the physiological and physical relationship between hemodynamic and electrophysiological responses? How can EEG be reliably recorded during concurrent fMRI scans without affecting the signal quality for both modalities? How should we fuse the recorded fMRI-EEG/MEG data in a principled way for integrative imaging with enhance spatiotemporal resolution?

The past decade has witnessed significant progresses in both fundamental and technical aspects related to these questions. Most of them are still under active research or remain poorly understood. In this review, we start with an overview of the physiological origins of EEG/MEG and fMRI, as well as their fundamental biophysics and imaging principles; it is followed by a review of major progresses in understanding and modeling the neurovascular coupling, methodologies for the fMRI-EEG/MEG integration and EEG-fMRI simultaneous recording; finally, important remaining issues and perspectives are summarized. Although some of the points we make in this review might be speculative or even controversial, we hope they serve to identify important scientific elements that would help to stimulate future discussion and research.

II. Overview of Electromagnetic Source Imaging and fMRI

A. Origin of EEG/MEG

As the mass responses from all activated neural tissues, EEG/MEG signals can be regarded as a weighted sum of instantaneous neuronal currents throughout the entire brain volume. In other words, EEG/MEG reflects the synchronized electrical behavior of an assembly of neurons within a certain brain region or even across regions. Asynchronized electrical activities have little contribution to EEG/MEG, because their random consequences are virtually cancelled out when summed over locations. The large-scale synchrony serves as the major factor to identify which specific aspects of brain electrophysiology contribute to EEG/MEG.

Brain electrophysiological processes take place in a variety of spatial and temporal scales. In a microscopic scale down to a single neuron, the electrophysiological activity manifests itself as the neuronal spiking activity and the post-synaptic potential (PSP). The neuronal spiking activity refers to the action potentials that propogate along the axon. The spiking activity reaches and accumulates at the synapse through which one neuron connects to another. When the accumulated spiking activity exceeds a certain threshold, it controls the amount of chemical transmitters released from the synapse. The released neurotransmitters further control the gating of the ion channels at the post-synaptic neuron and hence modulates the PSP. For the spiking activity above the threshold, the synapse effectively behaves as a low-pass filter, owing to its accumulative effect and the delay due to the electrochemical conversion. Under such circumstances, the pre-synaptic spiking activity may be temporally correlated with the PSP. However, for the sub-threshold spiking activity, such correlation does not necessarily hold true.

EEG/MEG measurements in a macroscopic level are insensitive to action potential sources with short-duration bidirectional current flows. As action potentials propagate along an axon, the associated electrical currents flow in opposite directions (i.e. along and opposite to the direction of action potential propagation) in both intracellular and extracellular spaces. Signals generated by such action potential sources are only recordable from a sensor at a close vicinity to the neuron. At a relatively remote sensor (such as on the scalp surface), the electromagnetic signals generated by opposing currents are essentially cancelled out. Moreover, the brief duration of the action potential also requires a very strong degree of synchrony with great temporal precision in order to be observable from the scalp surface. However, high-frequency (>120Hz) components associated with neuronal spiking activity are significantly underrepresented in EEG/MEG.

In fact, the primary sources of EEG/MEG are the synaptic currents flowing through the apical dendrites of large pyramidal neurons within the cortical gray matter [8, 13, 25, 26]. The apical dendric trees extend toward the pial surface and are organized into columns – a unique structure facilitating the formation of regionally synchronized synaptic currents [12]. It has been approximated that the simultaneous activation of as few as 0.1% synapses within a cortical area of around 40 mm² would suffice to produce a detectable EEG/MEG signal [9]. Moreover, the view that the primary EEG/MEG sources are synaptic currents is also supported by a general similarity between the frequency spectra of scalp potentials and post-synapc potentials [27]. This is regardless of the fact that extracranial potentials measured with EEG have much smaller amplitudes and lower frequency than intracranial potentials, such as local field potentials (LFP) and electrocorticograms (ECoG), owing to the different spatial scale to which each recording technique is applied. In general, low-frequency signals tend to be synchronized in a larger spatial scale, whereas synchronous high-frequency activity is often confined to a smaller scale. The same relationship also holds true for MEG.

B. Origin of BOLD Signals

Most fMRI applications utilize a BOLD contrast, whose mechanism is attributable to some basic biophysical properties of hemoglobin and its susceptibility effects in nuclear magnetic resonance (NMR). Deoxyhemoglobin is paramagnetic and its concentration inversely depends on the blood oxygenation level [28]. The paramagnetic property of the blood causes the bulk susceptibility difference between a blood vessel and its surrounding neural tissue. This effect, in turn, gives rise to the inhomogeneity of the local magnetic field and introduces additional resonance frequency shifts and phase dispersion for extra-vessel molecules. The BOLD contrast is pronounced in gradient echo (i.e. T₂*-weighted) MR images where higher oxygenation level leads to larger MR signals [16]. In addition, the echo-planar imaging (EPI) technique further provides remarkable temporal resolution for recording dynamic BOLD signals in realtime [29].

In the first three pioneer studies, the BOLD-contrast fMRI has been independently demonstrated in noninvasively mapping in vivo neurophysiologic changes due to either visual stimulation [3, 4] or motor tasks [5]. In all these three experiments as well as numerous fMRI studies that followed, the brain regions engaged in performing a task or processing a stimulus demonstrate increased BOLD signals relative to the resting state, namely the positive BOLD response (PBR). The PBR is widely believed to result from the over-compensation of oxygen usage by the cerebrovascular system, which causes a regional hemodynamic influx in excess of the oxygen consumption of the activated neuronal tissue [6, 7]. In fact, the BOLD signal reflects the combined effect of CBF, CBV and CMRO₂ [30]. Several models have been proposed to describe the BOLD signal as a function of the neural activity-induced changes in CBF, CBV and CMRO₂ [30–35]. Qualitatively, the CBF contributes positively to the BOLD signal while the CBV and CMRO₂ have negative contributions; yet such relationships are not necessarily linear.

Another fundamental question concerning the interpretation of BOLD-fMRI data lies in the neurophysiological origin of BOLD signals. There have been debates regarding whether the BOLD signal arises from neuronal inputs or outputs (i.e. synaptic or spiking activities, respectively). Early studies [36, 37] suggest the dependence of the BOLD responses upon neuronal spiking activity. This conclusion was drawn from the observations that the peak magnitudes of the BOLD signals measured in human V5 [36] and V1 [37] were linearly correlated with the averaged spiking rates invasively recorded in analogous areas in primates. More recently, Mukamel et al. also found a close correlation between the BOLD signals measured from healthy subjects and the neuronal spiking activity recorded from epilepsy patients when both groups underwent identical stimuli [38]. However, questions may be raised, since these studies compared the BOLD and neuronal spiking signals acquired from different species or subjects.

In contrast, more studies have demonstrated that BOLD-fMRI reflects synaptic activity rather than spiking activity [39–42]. In a very influential and technically demanding experiment, Logothetis and his colleagues recorded the spiking activity (i.e. single-unit activity (SUA) and multi-unit activity (MUA)) and the synaptic activity (i.e. local field potential (LFP)) simultaneously with the BOLD-fMRI signals from monkeys [39]. Through linear transformation systems, the LFP was found to yield better estimates of BOLD responses than the MUA. Hence, they conclude that BOLD signals primarily reflect synaptic activities [39, 43, 44]. Following this study, similar findings were also reported in several independent studies [40–42].

Between two competing views, an agreement has been reached in general with regard to the synaptic origin of BOLD signals [17]. Hemodynamic responses are driven by metabolic energy demands, nearly all of which are imposed by synaptic activity instead of action potential firing [45, 46]. The observed correlation between the BOLD signal and the neuronal spiking rate [36, 37] might be owing to the fact that the pre-synaptic neuronal spiking activity is sometimes correlated with the synaptic current, as previously discussed in this review and elsewhere [46, 47]. However, when LFP and MUA are disassociated, the BOLD response is primarily correlated with LFP [41, 42].

C. Electromagnetic Source Imaging

Electromagnetic source imaging (ESI) is a model-based neuroimaging technique. It entails: 1) modeling the brain electrical activity, 2) modeling the head volume conduction process so as to link the modeled electrical activity to EEG/MEG, and 3) reconstructing the brain electrical activity from recorded EEG/MEG data. The first two modeling steps serve to solve the EEG/MEG forward problem; the third step is the inverse of the second step, thereby commonly known as the EEG/MEG inverse problem.

A model of brain electrical activity (in short “source model”) is composed of bioelectric units distributed within the brain volume or over the brain surface, or confined to few locations in the brain. A single source unit is often defined as a current dipole, which well-approximates the synchronized synaptic currents at a columnar level [9, 12]. Any brain electrical activity can be modeled by a distribution of current dipoles within the entire brain volume. One may further choose to confine the dipole locations to the cortical gray matter and constrain the dipole orientations to be perpendicular to the cortical surface [26]. Alternatively but less frequently, a bioelectric source unit can also be defined as a current monopole [48], current multipole [49], or extracellular potential [50–58]. Moreover, when brain electrical activity is confined to a few focal regions, one may prefer to use a source model consisting of only a few discrete dipoles, namely the equivalent current dipole (ECD) model [59–62]. As opposed to the general applicability of the distributed source models, the ECD model assumes small extents of the neural responses, which may or may not be valid depending on the particular circumstances. Even if the assumptions are valid, the appropriate number of dipoles is often difficult to be determined a priori or solely from the EEG/MEG data [63].

A linkage from the source model to the electromagnetic signals at the sensor locations on the scalp can be established by constructing a volume conductor model that resembles the human head in both geometry and conductivity. Historically, the head volume conductor is modeled as concentric three-shell [57, 64, 65] or four-shell [66] spherical models. More accurate forward solutions become possible by using numerical algorithms, such as the boundary element method (BEM) [61, 67, 68], finite element method (FEM) [69, 70, 211], and finite difference method (FDM) [71]. Such numeric models allow us to incorporate the realistic geometries of the head compartments segmented from anatomical images such as MRI. The conductivities of different head tissues, especially for the skull in EEG, may be specified according to empirical values [64], in vitro measurements [72], in vivo estimates [73, 74], or potentially the results of electrical impedance tomography (EIT) [75] or MR electrical impedance tomography (MREIT) [76]. In addition, diffusion tensor magnetic resonance imaging (DT-MRI) [77] provides a new means to obtain the anisotropic conductivity of the cerebral white matter [78–80].

Given a source model and a head volume conductor model, the EEG/MEG can be linked with the brain electric sources by

$$\mathbf{x}\left(t\right)=\mathbf{As}\left(t\right)+\mathbf{b}\left(t\right)$$ (1)

where x(t) is the vector of EEG or MEG signals, s(t) is the source vector, A is the transfer matrix, and b(t) is the noise vector, respectively.

As opposed to the well-posed forward modeling and computation, the EEG/MEG inverse problem is more challenging. Such a problem is to estimate the source signals s(t) from EEG or MEG measurements x(t). As the number of EEG/MEG sensors is in general smaller than the number of sources within the brain, the EEG/MEG inverse solution is non-unique if no constraints are given. Over the past two decades, a number of efforts have been made to tackle this challenge. Evidence has increasingly indicated that reasonable EEG/MEG inverse solutions can be obtained if appropriate constraints, as derived from brain anatomy and physiology, are placed on the source distribution. For instance, one may specify the optimal solution as the most energy efficient one among those fitting equally well with the data. In a noise-free condition, this constraint leads to the linear least-squares source estimate. In noisy conditions, this constraint can be incorporated as a minimum norm side constraint, giving rise to the minimum norm estimate (MNE) [81]. Other variations of the MNE include the lead-field normalized weighted minimum norm (WMN) [82], low-resolution brain electromagnetic tomography (LORETA) [83], and their extensions to statistical mapping [21, 84], etc. The common feature shared by these algorithms is the linearity of the inverse solution, meaning that the inverse solution can be obtained through transforming the measurements through a linear system (or inverse matrix). The linear inverse solutions return low-resolution images of current density or its statistics. Iterative algorithms have been developed to enhance the focal sources [85]. These iterative methods have been suggested to be equivalent to a nonlinear inverse solver that minimizes a cost function formulated with L-p norms for both the data fitting term and the side constraint [86]. This is in line with other nonlinear inverse algorithms that specifically utilize the solution constraint other than the L-2 norm, such as the minimum current estimation (MCE) [87], L1 norm [88–90] and L-p norm [91].

In parallel to current density imaging, dipole source localization can be approached using nonlinear optimization [59–62, 92, 93] or sub-space scanning procedures [94–99] Moreover, the beamforming techniques based on linear spatial filtering can be used to estimate the source activity at a region of interest (ROI) or every individual location in the source space [100–103]. The beamformer for a specific ROI or source location is derived in an attempt to minimize the interference from other locations.

The imaging performance of all linear and nonlinear EEG/MEG inverse algorithms varies from case to case, depending on the nature of the brain electrical activity. The methodological choice is up to the users' own judgment as to whether the activity is sparse or extended, stationary or non-stationary, etc. Although the evaluation of some typical algorithms have been done in a few experimental and simulation settings [55,104–106], a general conclusion or agreement regarding a single optimal source imaging approach, if possible at all, has not been reached.

D. fMRI Statistic Parametric Mapping

The vast majority of fMRI applications use fMRI for functional localization of the brain regions engaged in specific sensory processing or cognitive functions [107]. FMRI as a brain mapping tool depends on experimental designs, data analysis methods and an explicitly or implicitly assumed relationship between BOLD signals and neural responses. Fig. 3 summarizes the principle of fMRI.

Figure 3.

Schematical illustration of BOLD-contrast fMRI. The regional neuronal activity alters the local CBF, CBV and CMRO₂, which collectively leads to changes in the blood oxygen level. The increase of oxygen level, meaning the decrease of local field inhomogeniety, produces a longer T2 or T2* and therefore larger MR signals. The frequency-and-phase encoding technique (e.g. echo-planar imaging) allows for the fast acquisition of a so-called k-space data, which can be transformed to the original image space through Fourier transformation. The signal is most frequently analyzed voxel by voxel, yielding statistic maps indicating regions with significant hemodynamic effects related to external stimuli/tasks or internal events. These regions arguably define the activated neuronal populations.

FMRI is a comparative technique in nature. An fMRI experiment must include at least two conditions in contrast. A task (or stimulus) condition places specific demands to the brain, while a user-defined control condition may involve a “baseline” task or a resting state. The signal difference between the task and control conditions is evaluated, typically voxel by voxel, to identify the regions engaged in the task execution. Popular fMRI experimental designs define the alternation of conditions in either a block-design or event-related manner. In line with earlier PET paradigms, the block-design involves prolonged task and control periods, so as to observe sustained BOLD signal changes with a high contrast-to-noise ratio (CNR). The event-related design focuses on the averaged single-trial BOLD response in ways analogous to event-related potentials/fields (ERP/ERF) in EEG/MEG [108, 109].

For both types of study designs, the BOLD signal at an “activated” voxel is expected to change in a way related to the transitions from one condition to another. This rationale allows us to make inference about regionally specific effects in response to the task/stimulus. For experiments with only two conditions, voxel-wise statistical inference may be simply based on a Student's t-test or period cross correlation [5]. A more general and flexible approach is based on the general linear model (GLM) [110, 111]. Stimulus functions encoding the occurrence of a particular event or experimental state (e.g. boxcar-functions) are convolved with a hemodynamic response function (HRF) to form regressors in the GLM. Fitting the GLM to the data allows for the estimation of model parameters and the statistic inference against a null hypothesis (i.e. the voxel is not activated). Such inference is classic in terms of statistics, as opposed to more recent methods based on the Bayesian inference which provides the posterior probability that the voxel is activated given the data [112]. All of these methods discussed so far are model-driven in a sense that they require specific assumptions about the time courses of the processes contributing to the measured signals and/or a priori statistical distributions of the signal and the noise. To remove such model dependence, a data-driven method has been implemented using independent component analysis (ICA) [113, 114].

III. Neurovascular Coupling

Statistical inference based on fMRI data alone can only draw conclusions about regional hemodynamic effects. However, it is the neuronal effect that is of ultimate interest to neuroimaging. Interpretations of BOLD fMRI data in terms of neural responses are crucially dependent upon the neurovascular coupling, which is commonly referred to as the relationship between electrophysiological responses and BOLD signals. This relationship should also serve as the most fundamental ground for all fMRI-EEG/MEG integrated neuroimaging methods (to be discussed later).

In order to infer neural activity from fMRI, the neurovascular relationship is most frequently modeled as a linear convolution system. It means that the BOLD signal surrounding the activated neural tissue results from the local neural activity convoluted with a time-invariant HRF, which describes the hemodynamic consequence of an impulse neural response. The linear HRF serves as an approximation for the complex interactions between neuronal activity, metabolic demand and blood flow and oxygenation [47]. With approximations made at various degrees, the HRF may be simply a Gauss, gamma [115] or double-gamma function [116]. While all these functions capture the key features of hemodynamics (e.g. the sluggishness and long duration), the double-gamma HRF entails the most detailed features, including a delayed onset time, initial dip, overshoot, undershoot, etc.

A linear HRF largely simplifies the analysis and interpretation of BOLD fMRI data. It serves as the central assumption of the classic GLM analysis [110, 111] and the rapid event-related fMRI design [109]. Note that, in such fMRI analyses and designs, the linear system is specified to the relationship between BOLD responses and external stimuli (or tasks), while implicitly assuming linear, yet unknown, neural responses to the stimuli. However, a nonlinear stimulus-to-BOLD relationship has been found in a number of studies [117–123]. The observed nonlinearity may originate from neural and/or vascular sources (e.g. neuronal and vascular refractory effects), since the BOLD response is the ultimate consequence of cascaded processes involving the neural response, the neurovascular coupling and the vascular response [119, 123].

To address the linearity or nonlinearity of the neurovascular coupling, investigators need to monitor both neural activity and hemodynamic response through invasive [39, 121, 122, 124] or noninvasive measurements [125–127]. The measured electrophysiological (e.g. MUA, LFP, EEG and MEG) and hemodynamic (e.g. BOLD and CBF) signals are quantified individually before being compared against a linear function. In this regard, a critical concern lies in the variety of methods for quantifying the multimodal signals. Hemodynamic signals have been quantified as its peak height [124], steady-state height [128] or integral over time [129]. Ways for quantifying electrophysiological signals are even more diverse. No consensus has been reached so far with regard to an appropriate pair of quantitative measures for assessing the cross-modal relationship. It is likely that some reported nonlinear neurovascular coupling may be simply due to the use of mismatched quantitative measures. Additional challenges may be further appreciated by considering the highly different temporal scales of the hemodynamic and electrophysiological responses. Table 1 lists typical values related to the temporal and frequency features of the single-trial ERP/ERF and BOLD signals. A quantitative cross-modal relationship is even more obscured when the electrophysiological signal is analyzed in an event-related manner while the hemodynamic signal changes across prolonged periods as in block-design experiments.

Table 1.

For event-related potential or field and event-related fMRI, the response delay, duration, signal sampling rate and frequency.

	Delay (sec)	Duration (sec)	Sampling Rate (ms)	Frequency (Hz)
ERP/ERF	0	0.01–2	≤ 5	0.5~40
ER-fMRI	1~3	15–30	≥ 50	0~0.4

For the purpose of integrating ERP/ERF and fMRI or investigating the relationship between them, it is particularly important to develop a theoretically-driven approach to interpret the fMRI signals as certain meaningful indices in terms of ERP/ERF. In this regard, we have developed a mathematical model [24] to describe the interactions between stimuli (or tasks), neuronal synaptic currents and BOLD responses. This model allows us to derive the relationship between event-related synaptic responses and BOLD fMRI signals.

This model is composed of two cascaded linear systems. The first system is characterized by the neuronal impulse response function (NRF). The NRF varies across locations and represents the power of regional synaptic currents $\stackrel{\rightharpoonup }{r}(\mathbf{r},t)$, with a very short duration T_s up to several hundred milliseconds. The task-induced or stimulus-evoked electrophysiological response, in terms of the biophysical energy, is modeled as the convolution of the tasks or stimuli with the NRF. As the second system, the neurovascular coupling is simply modeled as a location-independent and time-invariant linear system, characterized by the hemodynamic impulse response function (HRF), denoted as h(t). Therefore, the BOLD fMRI signal f (r,t), in response to a block of sustained stimuli, can be written as Eq. (2).

$$f(\mathbf{r},t)=\sum _{n=1}^N\delta (t-n{T}_{ISI})\otimes s^2(\mathbf{r},t)\otimes h\left(t\right)+f_n(\mathbf{r},t)$$ (2)

where δ (t) is a delta function, T_ISI is the inter-stimulus-interval (ISI), f_n(r,t) is the noise, and ⊗ stands for convolution. Eq. (2) is valid when the ISI is longer than the neuronal refractory period and the linear neurovascular coupling holds true.

Since the HRF evolves much slower and lasts much longer than the NRF, Eq. (2) can be rewritten as Eq. (3).

$$f(\mathbf{r},t)=p(\mathbf{r},t)\cdot {\int }_{T_s}{s}^2(\mathbf{r},t)dt+f_n(\mathbf{r},t)$$ (3)

where $p(\mathbf{r},t)={\sum }_{n=1}^N\delta (t-n{T}_{ISI})h\left(t\right)$. As graphically illustrated in Fig. 4, Eq. (3) suggests that the BOLD signal at an activated voxel can be modeled as the product of a predictor function and a parameter proportional to the time integral of the power of the local event-related synaptic currents plus the noise. This model resembles the GLM used in the conventional fMRI analysis, except that the predictor function is defined as the convolution of the HRF with a train of delta functions (instead of a box-car function) which represent the occurence of discrete stimuli. The model parameter (or regression coefficient) can be estimated by fitting the model to voxel-specific BOLD fMRI time series. The estimated parameter, known as the BOLD effect size, represents the relative strength of the regional BOLD response, since it reflects the ratio between the measured and predicted BOLD time courses (i.e. f (r,t)/p(t)). More importantly, the model shown in Fig 4 gives the BOLD effect size a clear biophysical interpretation meaningful to EEG/MEG. That is, the BOLD effect size provides an fMRI-based estimate for the time integral of the power of the regional EEG/MEG source activity during an effective duration of the ERP/ERF. As discussed later in this review, such a biophysical implication serves as the theoretical basis for important developments in fMRI-EEG/MEG integrated neuroimaging [24].

Figure 4.

The BOLD fMRI signal at an “activated” voxel can be modeled using a linear system. The signal is the scaled version of a location-independent predictor signal, derived from the stimulus function and the hemodynamic response function (HRF). The scaling factor (called the BOLD effect size) is proportional to the time integral of the event-related synaptic power.

It is worth mentioning that the above theoretical model assumes the baseline activity remains unchanged from the resting-state or control condition to the stimulus condition. However, it is possible that the baseline activity changes by itself or in response to certain stimuli. This depends on the brain location of interest as well as the stimulus type and property. For instance, there are a number of default-mode regions that are functionally active during the resting state but are likely suppressed given certain stimuli or tasks that request attentional resources [130]. It is also possible that the baseline activity at some brain regions spontaneously modulates over time, with or without any relationship to the external stimulus. As a result, if the stimulus is given when the baseline activity modulation reaches a lower (or higher) level than during the resting-state control state, the corresponding BOLD signal change reflects not only the stimulus evoked neuronal response but also the modulation of the spontaneous baseline activity.

IV. fMRI-EEG/MEG Integrated Neuroimaging

Methods for the fMRI-EEG/MEG integrated neuroimaging are categorized into two types: the fMRI-constrained electromagnetic source imaging or localization and the EEG/MEG-informed fMRI analysis. As the names suggest, the former rests on the EEG/MEG source imaging while incorporating spatial information from fMRI; the latter utilizes the time and/or frequency specific electrophysiological information to derive regressors in the fMRI analysis.

A. fMRI-constrained electromagnetic source imaging/localization

The earliest efforts in the fMRI-constrained EEG/MEG source imaging utilize fMRI statistical parametric maps to obtain a priori information on where EEG/MEG sources are likely located. Depending on different source models, the spatial information from fMRI is typically used to constrain the locations of multiple current dipoles, namely the fMRI-constrained dipole fitting [131–133], or to constrain the distributed source distribution, namely the fMRI-constrained current density imaging [20–22, 24, 134–139].

When neural activity is confined to a few regions with small extents, the fMRI analysis should yield several fMRI foci (or hotspots). It is reasonable to model the electrical activity at each fMRI hotspot as an equivalent regional current dipole. The dipole locations are fixed to the fMRI foci, or initially seeded to the fMRI foci, yet are adjustable to best fit the EEG/MEG data. Given the dipole locations are assigned or estimated, the dipole moments can be uniquely estimated by fitting the ECD model to the EEG/MEG data. From the estimated dipole time course, one can tell the temporal dynamics of the regional neural activity. Note that the primary goal of the fMRI-seeded dipole fitting technique is not to image brain activity; rather, it aims at retrieving the time course of the brain activity at identified fMRI activation foci. However, this technique is questionable when applied to imaging extended neural responses.

In contrast, the fMRI-constrained distributed source imaging is generally applicable regardless of whether the source activity is focal or extended. Perhaps, the most straightforward approach is the fMRI-weighted current density imaging, which uses the fMRI activation map to derive weighting factors for the inverse solutions compatible with the EEG/MEG signals. This approach can be implemented in a Wiener filter [20, 21, 26] and weighted minimum norm frameworks [22, 134–136]. Although seemingly different, these implementations are fundamentally equivalent [23]. Both of them are based upon the identical core assumption that locations inside the fMRI activations are more favored than those outside in terms of the likelihood of being active current sources. The degree of preference to fMRI hightlighted areas is controlled by an fMRI weighting factor.

These methods have limitations in both technical and fundamental aspects. Technically, the fMRI weighting factor is most frequently up to users' subjective choice, although several empirical values have been suggested to be 10 [20], 3 [135] or 1.4 [134] based on results obtained in several simulation studies. This technical limitation may be solvable by using data-driven methods for choosing the fMRI weighting factor, such as the expectation maximization (EM) algorithm [137, 138, 140]. Moreover, we may bypass this uncertainty by using an alternative two-step estimation algorithm which avoids using the fMRI weighting factor [139]. In the first step, the EEG/MEG source space is strictly confined to the regions highlighted in fMRI, giving rise to an inverse solution firmly constrained by the fMRI. In the second step, the fMRI constraint is removed, and the solution obtained in the first step is re-entered as the initial solution to fit the EEG/MEG data again employing a so-called Twomey regularization [141].

These technical limitations are primarily due to the fundamental mismatches between fMRI and EEG/MEG, owing to highly different temporal scales in which fMRI and ERP/ERF data are generated and collected (see Table 1). The fMRI-EEG/MEG mismatches may be further categorized into three types, namely fMRI extra sources, fMRI invisible sources and the fMRI displacement [20, 134, 139]. The fMRI extra sources represent the source regions that are deemed as active in fMRI but do not contain the sources for the EEG/MEG at a certain time instant. During a short period of interest following the event onset, the fMRI activations are thought of as “static” (or time-invariant) while the EEG/MEG signals are variable and the source imaging is carried out instant by instant. The electrical source activity in a millisecond time scale may only involve a subset of the activated fMRI areas, whereas other areas may appear as false positives if all of the “activated” fMRI voxels are included in the prior spatial constraint [24, 139]. The fMRI invisible sources are the real EEG/MEG sources but not deemed as active by fMRI. A transient current source may generate observable EEG/MEG signals whereas it may last too briefly to induce a sustained BOLD response. In this condition, the fMRI-derived time-invariant spatial constraint includes false negatives, which often result in the underestimation of fMRI invisible sources as reported in several independent studies [20, 24, 139]. The fMRI displacement refers to the spatial difference between the vascular and electrophysiological sources [134, 139]. Because of these fMRI-EEG/MEG mismatches, it is problematic to constrain the temporally variable current source estimates to “time-invariant” fMRI spatial priors, which may entail both fMRI false positives and false negatives.

To tackle these technical and fundamental issues, we have proposed a new framework for the fMRI-EEG/MEG integrated neuroimaging. As illustrated in Fig. 5, this approach rests on a unified system underlying the signal generation and analysis for both modalities. The system assumes a common neuronal source (i.e. synaptic activity), from which fMRI and EEG/MEG signals are generated via a temporal low-pass filter and a spatial low-pass filter, respectively. The EEG/MEG inverse problems essentially deal with the spatial deconvolution – the process of reversing the head volume conduction. The inverse solutions retain the temporal source evolution even though it may fail to reconstruct the spatial source distribution. In other words, at every source location, the souce waveform estimated from EEG/MEG is much less distorted (in terms of its normalized “shape”) than its absolute magnitude, since the filtering applies to the spatial domain instead of the time domain. This feature is as opposed to the temporal regression of fMRI data (e.g. the GLM analysis), which theoretically ends up with high-resolution spatial maps of brain activations but with little or no temporal information.

Figure 5.

Flow-chart of the fMRI-EEG/MEG co-registration.

Such complementary multimodal results can be simply merged by utilizing the cross-modal relationship, derived and discussed in Section III. That is, the BOLD effect size estimated from the fMRI signal in each voxel is proportional to the time integral of the local source power underlying the ERP/ERF signals.

$${\int }_{T_s}{s}^2(r,t)dt\propto \beta \left(r\right)$$ (4)

where s² (r,t) is the source power at location r and time t, β(r) is the quantified BOLD effect size at location r. T_S is the duration of the electrophysiological response induced by a transient stimulus or task, which is referred to as the “event-related period”.

This relationship allows us to constrain, voxel by voxel, the integral of the power of the EEG/MEG source estimates in accordance with the BOLD effect size. Specifically, we can scale the source time course estimated from the ERP/ERF, so that the time integral of the power of the scaled source estimates equals the BOLD effect size [24] as illustrated in Fig. 5. Namely, this process is referred to as the fMRI-EEG/MEG co-registration.

Furthermore, we can re-fit the source estimates to the EEG/MEG data while taking the fMRI-EEG/MEG co-registered source power estimates as time-variant prior spatial constraints. This additional estimation step can be implemented by means of an adaptive Wiener filter (AWF) [24]. It ensures that the spatiotemporal source reconstruction depends primarily upon EEG/MEG measurements, and thus provides robustness against inaccurate fMRI constraints. Relative to the fMRI-EEG/MEG co-registration, the AWF represents an integrative multimodal imaging superior to simply putting together the results separately obtained from fMRI and EEG.

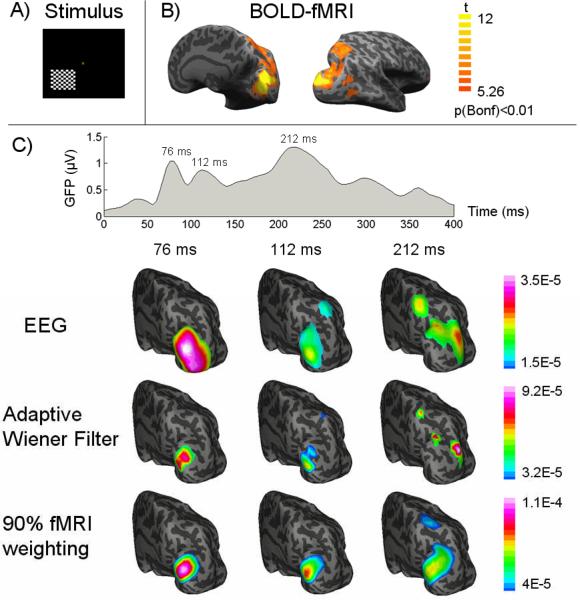
The performance of the AWF was assessed by computer simulations, wherein encouraging results were obtained in imaging multiple focal sources from simulated fMRI and EEG data [24]. Fig. 6 shows the data obtained from a pilot experiment exploring the cortical pathway specialized in processing unilateral visual stimuli [24]. The experiment included two separate sessions with the identical visual stimuli for the EEG and fMRI data collection. The visual stimulation was a rectangular checkerboard within the lower left quadrant of the visual field; the checkerboard pattern was reversed at 2 Hz. With significantly enhanced spatial resolution, the AWF algorithm revealed a pathway sequentially activating V1/V2, V3/V3a, V5/V7 and intraparietal sulcus, in general agreement with the hierarchical organization of the visual system [142]. This pathway was also observed in the low-resolution images reconstructed from the VEP alone. In contrast, a fMRI-weighted source imaging algorithm [20, 21] showed a false positive source region in and around V1/V2 at the latency of 212 ms, whereas a more likely high-tier EEG source around V5, as observed from the EEG data, was missed. This experimental result indicates the promises in dynamic neuroimaging by integrating fMRI with EEG using the model-based adaptive Wiener filter.

Figure 6.

A) The pattern-reversal checkerboard visual stimulation, B) fMRI activation map with a corrected threshold p<0.01, and C) the global field power of VEP and the dynamic cortical source distribution at three VEP latencies (76, 112, 212 ms after the visual onset) imaged from EEG alone (1st row), or fMRI-EEG integration using our proposed adaptive wiener filter (2nd row) and the conventional 90% fMRI weighted algorithm (3rd row). Both the source images and the fMRI activation map are visualized on an inflated representation of cortical surface. (From [24] with permission)

B. EEG-informed fMRI analysis

The EEG/MEG-informed fMRI analysis rests on the fMRI analysis frameworks (e.g. the GLM analysis) while incorporating temporal- or frequency-specific information available in EEG/MEG. Such a multimodal strategy differs from the conventional fMRI analysis in its unique ability to selectively localize the fMRI correlates to specific neuronal events or rhythms. This ability directly benefits from the EEG/MEG measurements which reflect the mass neural responses, whereas the analysis based on fMRI alone relies on the timing of the stimuli or tasks. Note that the approaches in this category usually prefer EEG to MEG due to the highly desired simultaneous recordings of fMRI and electrophysiological signals.

Techniques employing this strategy are particularly useful in stimulus- or task-free experimental conditions. Perhaps the most typical example is the interictal spike-related fMRI mapping, in which the interictal epilepiform events manifest themselves as spike-like discharges in EEG [143, 144]. Some other examples have been witnessed in studies exploring the neural substrates underlying the rhythmic modulations in the resting or pathological brain [145–149]. In these studies, predictors for the fMRI regression analysis are derived from frequency-specific EEG modulations. By assessing the correlation between the fMRI signals and the EEG-defined predictors, one may localize the neural regions responsible for the generation of the rhythmic modulations of interest.

A more sophisticated approach is based on parametric task manipulations and single-trial EEG-fMRI covariation [150, 151]. A range of parametrically graded experimental conditions are employed to identify cortical regions for which the BOLD response shows the same modulation across conditions as a specific single-trial ERP component. More specifically, external stimuli are designed to induce the variation of single-trial EEG responses. This single-trial variability is specific to each time point within a trial. For a specific time point, the signal varying over trials can serve as the predictor in the fMRI regression analysis, yielding a map of fMRI correlates. Repeating the analysis at multiple or potentially all latencies, one can obtain a series of fMRI maps, each of which is associated with a specific instant within the time scale of a single trial. This approach, although interesting, is theoretically demanding. The single-trial variability can result from spontaneous activity and noise that may or may not be differentiable from that driven by the external stimuli. Moreover, it requires a careful design of stimulus properties to allow for an effective control of single-trial amplitudes.

Compared to the fMRI-constrained EEG/MEG source imaging, the EEG -informed fMRI analysis appears to be wholly different. In fact, both types of methods share an important commonality in their fundamental assumption – that is, the neuronal electrophysiological response is linearly correlated with the BOLD fMRI signal. To date, it is difficult to judge which method is superior to the other, although the EEG-informed fMRI analysis is formulated in a better posed manner than the fMRI-constrained source imaging.

V. Simultaneous EEG-fMRI Measurement

In the context of multimodal neuroimaging, one unique feature of EEG, as opposed to MEG, lies in the feasibility of recording fMRI and EEG simultaneously. This feature is often desirable in studies that integrate both modalities or investigate the cross-modal relationship. For instance, simultaneous fMRI-EEG recordings are indispensable for using fMRI to localize the neural substrates underlying interictal EEG spikes. For this purpose, the fMRI response is not manipulated by user-defined external stimuli or tasks; but rather, it is driven by spontaneous biological events. The onsets of these events can be determined by detecting the interitcal spikes from the EEG recorded during concurrent fMRI scans, serving as the temporal markers necessary for carrying out the event-related fMRI analysis [143, 144]. For similar reasons, simultanoues fMRI-EEG recordings are desirable for mapping the fMRI correlates to continuous rhythmic EEG modulations during the resting state [145–147] or sleep [148, 149].

However, strong cross-modal interferences pose great challenges to simultaneous fMRI-EEG recordings. Both time-varying and static magnetic fields in the MRI/fMRI environment can introduce large artifacts to EEG recordings. During the fMRI scans, the radio-frequency (RF) excitation pulses and rapidly switching magnetic gradients result in large dB/dt, which in turn induce gradient artifacts (GA) about 1000 times larger than the normal EEG magnitude [152, 153]. The pulsatile motion of EEG leads associated with heart beats causes cardiac ballistic artifacts (CBA) [154]. In addition, subjects' safety is worth special attention, since the tissues surrounding the electrodes may be heated or damaged by large artificial currents [155]. The quality of MRI/fMRI images may also be affected by the EEG electrodes as well as other devices placed inside the scanner [156].

Active research has been conducted to resolve these practical issues (for reviews, see [157, 158]). Special efforts have been put forth upon devising MR-compatible EEG caps and amplifiers [152, 153], synchronizing the EEG sampling with fMRI pulses [159], EEG lead design and placement [155, 160, 161], cable wiring [152], signal transmitting [153, 162], subject comfort and safety [155, 163] etc. Signal processing algorithms have been developed to remove the GA [153, 164–168] and CBA [152, 154, 168–171] from the EEG simultaneously recorded with fMRI. Most of these methods are based on template matching/subtraction algorithms [153, 154, 164] or the blind source separation with principal component analysis [165–168] or independent component analysis [168, 170, 171]. Interleaved strategies are occasionally adopted to acquire fMRI data during the delayed time windows of little or no interest to EEG recordings [172, 173].

Fig. 7 illustrates a typical experimental setting for simultaneous fMRI-EEG recordings. Carbon electrodes and current-limiting resistors are often used to minimize the MR susceptibility effect and the safety concerns [155]. Short copper wires connecting electrodes should be twisted, bundled and stabilized using taps and sandbags. Local amplifiers are preferred for signal amplification and digitization. Optical fibers are used for transmitting signals to the recording devices outside the MR environment. An ECG lead is placed at the subject's back to record a temporal marker for every heart beat. The onsets of fMRI volume acquisitions are recorded by connecting the TTL output from the scanner to the EEG recording device. Both the ECG and the scanner TTL signals are useful for the artifact removal during the post-processing. It may also be desirable to synchronize the EEG sampling with the clock driving the fMRI pulse sequence to avoid any phase-asynchrony of the GA.

Figure 7.

Typical experimental setting for simultaneous fMRI-EEG recordings.

Artifact reduction algorithms are often designed according to the fact that the GA and CBA remain relatively stable and independent of the EEG signals. The most widely used (and perhaps still the most effective) algorithms for removing the GA and CBA are based on average template subtraction [153, 154, 164]. The central strategy can be briefly described as follows. A signal-free artifact template is obtained by averaging the raw (or preprocessed) data phase-locked to the fMRI volume onsets or the ECG-derived heart-beat markers. Assuming the signal and the artifacts are additive and mutually independent, the EEG signal should be retained by subtracting the averaged artifact template from the original data. Although these procedures end up with a significant artifact reduction, some artificial residuals often remain present owing to possibly non-phased-locked or drifted GA or instable CBA. These residual artifacts can be further removed by use of independent component analysis (ICA), which allows us to identify and remove the noisy and artificial components, whose spatial, temporal and frequency patterns are in accordance with those of the artifact templates [127].

As the above techniques appear promising, simultaneous fMRI-EEG recordings have proven to provide reasonable data quality for event-related potentials, frequency-specific oscillatory activities and rhythmic modulations. To attest this point, three control experiments have been conducted with the data shown in Fig. 8. In an experiment using 2-Hz full-screen visual stimuli [174], similar visual evoked potentials (VEP) were obtained from the EEG data recorded with or without concurrent fMRI scans (Fig. 8.A). No obvious distortions were found in either MRI or fMRI [174]. In another experiment with 9-Hz visual stimuli, sustained oscillatory EEG signals at the stimulus frequency, known as the steady-state visual evoked pontetials (SSVEP), were found at occipital electrodes (Fig. 8.B) [127]. The last example involved a self-paced eye-open-and-close task, which is known to change the occipital rhythmic EEG in the alpha band (8~12Hz). Such an expected rhythmic modulation was clearly observed from the time-frequency representation of the EEG data at the occipital electrodes (Fig. 8.C) [127].

Figure 8.

Examples of simultaneous fMRI-EEG data in three control experiments. A) VEP waveforms obtained inside the fMRI scanner with (blue) or without (dashed red) fMRI scans, or outside the scanner (black). The scalp potential map corresponds to the 120-ms peak latency in the VEP acquired during fMRI scans. B) SSVEP power spectrum and the spatial distribution of the power at the stimulus frequency. C) Time-frequency representation of the alpha modulation induced by self-paced eye-open and eye-close. (Panel A) from [174] with permission)

Simultaneous recording is challenging but necessary in fMRI-EEG integrated neuroimaging and neuroscience research. Advances, mainly in signal processing techniques, have allowed us to remove various MR-related artifacts from the EEG data recorded during concurrent fMRI scans. Future development of hardware and software will no doubt further improve the quality of EEG and fMRI from simultaneous recordings. Although the simultaneous fMRI-EEG recording is desirable for a variety of purposes, it is not always necessary when studying some passive sensory evoked responses. In this regard, one has to base his/her own choice on the reproducibility of the task (or stimulus) of interest vs. the possible risk of dealing with largely contaminated EEG data if recorded simultaneously with fMRI. Regardless of the theoretical efficacy of artifact reduction algorithms, the outcome of these algorithms is after all partly artificial and inevitably “worse” than artifact-free signals. For some simple paradigms only involving passive stimulus-evoked responses, it might not always be worthwhile to obtain these simultaneously-collected signals and, rather, ensure clear signals by conducting separate but highly reproducible experiments.

Efforts have also been made to develop SQUID-based instrumentation for ultralow-field MRI, which aims at ultimately potentially acquiring MEG with MRI [175]. However, achieving high quality data in an experimental setting remains elusive.

VI. Conclusions and Perspectives

Noninvasive functional neuroimaging, as an important tool for basic neuroscience research and clinical diagnosis, continues to have room for improvement of spatial and temporal resolution. While existing neuroimaging modalities might approach their limits in imaging capability mostly due to theoretical as well as technical reasons, it becomes increasingly attractive to integrate multiple complementary modalities in an attempt to significantly enhance the spatiotemporal resolution that cannot be achieved by any modality individually.

In this regard, the integration of fMRI and EEG/MEG has received the most interest. Electrophysiological and hemodynamic/metabolic signals reflect distinct but closely coupled aspects of the underlying neural activity. Combining fMRI and EEG/MEG data allows us to study brain function from different perspectives. Convergent evidence, on one hand, definitely leads to much more confident conclusions on understanding the neural mechanisms. Contradictory observations, on the other hand, also pose new hypotheses and challenges necessary to guide further investigations of the human neural system.

Our understanding of the coupling between fMRI and EEG/MEG has been substantially improved in the past decade, providing a great opportunity to combine these modalities in a more fundamental and principled way. Agreements have been reached in general regarding the neurovascular and neurometabolic coupling. Quantitative models of the cross-modal relationship, like those discussed in this review, represent important progress along this line. Although these models can at best approximate the complex interactions between hemodynamics and electrophysiology while subjected to experimental conditions and fundamental assumptions, they do serve as a sound basis for developing multimodal neuroimaging techniques, which promise to enhance the existing imaging capability, at least relative to fMRI and EEG/MEG alone.

However, this is not meant to guarantee the success of multimodal neuroimaging. Existing theories fail to explain every aspect of the explosively expanding imaging datasets documented in thousands of research articles. To date, the primary bottleneck is still more fundamental than technical. Methodologies that rest on an assumed or modeled physiological linkage between fMRI and EEG/MEG, almost certainly fail under particular circumstances when the linkage is invalid. On one hand, theoretical modeling and experimental investigation need to be performed across microscopic, mesoscopic and macroscopic scales, and proceed in parallel to further solidify the physiological and physical basis for the multimodal integration. On the other hand, careful considerations should be taken in experimental designs to justify the rationale of combining different modalities, regardless of whatever algorithms are used to fuse the multimodal datasets. Cautions have to be taken as well in the interpretation of the imaging results.

In what follows, we will discuss a few important remaining issues that deserve systematic investigations and may represent critical challenges as well as opportunities to future developments in multimodal neuroimaging.

A. Negative BOLD

Most fMRI studies rely on the task-induced positive BOLD response (PBR) as the hemodynamic index of increased neuronal activity. The negative BOLD response (NBR), commonly observed as the sustained BOLD signal decrease relative to the resting-state baseline, is occasionally observed in both humans and animals undergoing sensory [176–183] and cognitive tasks [184].

Regardless of the increasing observations of the negative BOLD, its origin and relationship to neuronal activity remains poorly understood and controversial. The NBR may originate from reduced neuronal activity [176, 180, 183, 185, 186], or vascular blood stealing [187, 188], or perhaps both [181, 182]. In addition, the NBR can be either dependent or independent upon the task or stimulus content [17, 185]. For example, in response to a particular stimulus, the NBR may be found at non-stimulated regions within the relevant sensory system [177–183]. Such a task-dependent NBR is often hypothesized to reflect neuronal suppression at regions complementary to those with increased neural activity [182]. On the other hand, decreases in BOLD (or CBF) signals are also observable at locations that change little across a wide variety of tasks [130, 176]. These task-independent NBR regions are believed to be functionally active [130, 185] and connected [189] in the resting state, collectively responsible for a default-mode brain function [130, 190]. At these regions, the NBR may be induced as a consequence of decreased default-mode activity when the resting-state brain function is interrupted by the execution of attention demanding tasks [17].

Nevertheless, how the NBR should be interpreted in the context of fMRI-EEG/MEG integration remains to be investigated.

B. Frequency-dependent Neurovascular Coupling

As discussed in this review, the vast majority of methodologies integrating fMRI and EEG/MEG are based upon a linear neurovascular coupling. However, recent studies have proposed alternative hypotheses [38, 191]. That is, a negative correlation between low-frequency (e.g. alpha-band) electrophysiological signals and BOLD fMRI signals [38, 145–147], whereas high-frequency components (e.g. gamma-band) contribute positively to the BOLD signal [38, 192]. Although this relationship remains highly controversial and often varies considerably across subjects [193], it does point to some cross-modal relationship that has been ignored or unexplained by conventional neurovascular coupling models. This alternative view, although being speculative so far, may help in revising the neurovascular model by extending the model from the spatiotemporal domain to the spatial-frequency or spatial-temporal-frequency domain. Along this line, an interesting paper deserves attentions [191]. In this analytical work, Kilner et al. propose a heuristic model suggesting that an increase in hemodynamic signals is associated with a shift of electrophysiological power spectrum from low to high frequencies (i.e. a loss in low-frequency power relative to a gain in high-frequency power). As the authors admit, the model may be oversimplified. Its value to neuroimaging also remains to be demonstrated. Moreover, the validity of this model is obviously challenged by the fact that the stimulus-driven low-frequency power increase is associated with an increase in the BOLD response. For instance, visual stimuli presented with low temporal frequency (e.g. 4~5 Hz) induce a noticeable increase in the occipital EEG/MEG power at the stimulus frequency to accompany a positive increase of the BOLD fMRI signals in the primary visual cortex.

In short, the frequency-dependent neurovascular coupling remains to be verified. Even if true, its impact on interpretation of fMRI, EEG/MEG and their combined imaging remains to be investigated.

C. Imaging Brain Functional Connectivity

One of the important applications of the multimodal fMRI-EEG/MEG imaging lies in imaging brain functional connectivity. Static images indicating brain regions responsible for the execution of particular tasks do not convey sufficient information with respect to how these regions communicate with each other. The concept of brain connectivity now plays an important role in neuroscience, as a way to understand the organized behavior of brain regions or to reveal the functional brain circuitry [194, 195].

Investigators have computed cortical connectivity patterns based on hemodynamic or metabolic measurements such as fMRI [196–199], whereas the indirect nature of fMRI signals confounds the interpretation of fMRI-derived connectivity in terms of neuronal interaction [200]. The cortical networks are formed and characterized by organized neuronal oscillations that span several orders of magnitude in frequency [201]. As discussed in this review, the neurovascular coupling behaves as a temporal low-pass filter with a cut-off frequency at around 0.4 Hz. High-frequency oscillations may be effectively excluded from the connectivity patterns estimated from fMRI. Even though the fMRI connectivity may reveal coherent low-frequency modulations of high-frequency oscillatary neural activities, the sluggishness of BOLD fMRI signals represents a significant challenge, if all possible, to imaging the full spectrum of brain functional connectivity.

EEG/MEG holds the promise to reveal dynamic connectivity since it is sensitive to transient neural activities occurring on the order of milliseconds [202–204]. A variety of techniques have been used, most of which have amounted to evaluating the cross-correlation or phase synchronization of signals between pairs of scalp electrodes or sensors [205]. Graph-theory-based tools from the study of complex network have also been developed to describe the connectivity of large-scale networks [206]. However, the relationship between the observed connectivity pattern in the sensor space and that in the source space is complicated by the dispersion of electromagnetic signals from the cortex to the sensors.

Multimodal fMRI-EEG/MEG integrated neuroimaging approaches hold the potential to greatly enhance our ability to reveal the brain functional connectivity, due to the combined high spatial and temporal resolution. The more precise is our ability to image the brain functional anatomy, the better we would be able to pinpoint neural connectivity among specific brain regions. The higher temporal resolution we can achieve, the better chance we would be able to view a wide range of dynamics in functional interactions within a local or large scale. Efforts have been made in integrating fMRI with electromagnetic source imaging [22] using the directed transfer function (DTF) approach. Other existing methods, such as structural equation modeling (SEM) [207], and Partial Directed Coherence (PDC) [208], are also applicable to fMRI-EEG/MEG imaging data [209].

Also of importance is the investigation of the relationships between the functional connectivity as derived from fMRI data and from EEG/MEG data. Due to the different time scales and spatial resolutions of these two modalities there has not been a clearly established consistency between the results obtained from fMRI or EEG/MEG alone. Perhaps, this is simply owing to the fact that these modalities reflect the different and complementary consequences of the same neurophysiological origin. Combining both modalities promises to offer a more complete conclusion on the connectivity among assemblies of neurons.

Retrieving connectivity patterns from functional neuroimaging data essentially deals with a problem of data-driven system identification. That is to find a directional or non-directional functional network that can explain or predict the relationship among the data at various brain locations. While neuronal interactions are physically enabled by anatomical connections, which may be reconstructed from diffusion tensor MRI [77], the consistency between functional and anatomical connectivity remains to be investigated. Moreover, neuronal circuitry at microscopic scales entails inhibitory and excitatory connections. The dynamic yet balanced behaviors of neuronal inhibition and excitation fulfill the regional computation, as well as the large-scale synchrony and interaction among regions. The linkage between the large-scale functional network and neuronal microcircuits remains unclear. Interpretations of functional connectivity in terms of excitation and inhibition are currently missing, but potentially important.