Understanding the Evolutionary Process of Grammatical Evolution Neural Networks for Feature Selection in Genetic Epidemiology

Abstract

The identification of genetic factors/features that predict complex diseases is an important goal of human genetics. The commonality of gene-gene interactions in the underlying genetic architecture of common diseases presents a daunting analytical challenge. Previously, we introduced a grammatical evolution neural network (GENN) approach that has high power to detect such interactions in the absence of any marginal main effects. While the success of this method is encouraging, it elicits questions regarding the evolutionary process of the algorithm itself and the feasibility of scaling the method to account for the immense dimensionality of datasets with enormous numbers of features. When the features of interest show no main effects, how is GENN able to build correct models? How and when should evolutionary parameters be adjusted according to the scale of a particular dataset? In the current study, we monitor the performance of GENN during its evolutionary process using different population sizes and numbers of generations. We also compare the evolutionary characteristics of GENN to that of a random search neural network strategy to better understand the benefits provided by the evolutionary learning process—including advantages with respect to chromosome size and the representation of functional versus non-functional features within the models generated by the two approaches. Finally, we apply lessons from the characterization of GENN to analyses of datasets containing increasing numbers of features to demonstrate the scalability of the method.

1. INTRODUCTION

The identification and characterization of genetic factors/features that are predictive of disease is an important goal in the field of human genetics [1,2]. For common human diseases, the complexity of the underlying genetic architecture presents immense analytical challenges. This is largely due to the likelihood that many disease susceptibility genes exhibit effects that are dependent partially or solely upon interactions with other genes and the environment. These interactions, known as epistasis, are difficult to detect using traditional statistical methods [3]. The development of statistical and computational methods to deal with such feature selection problems is an important and growing field [4–9].

One computational approach that has been proposed for the study of disease susceptibility genes is neural networks (NN). NN are a supervised pattern recognition method used in many fields for data mining. In genetic epidemiology, NN have been used for both linkage and association studies of common, complex disease[10–15] The success of NN methodologies for data mining is greatly influenced by the definition of NN architecture. This is a challenge, since the optimal architecture is not always apparent and can vary by dataset. As a result, a cumbersome trial and error approach is often taken.

In order to evolve appropriate NN architectures for multiple contexts, machine learning methods have been combined with NN approaches in many fields [16], including genetic epidemiology [15]. Previously, we introduced a NN approach for detecting gene-gene interactions that uses grammatical evolution (GE) as a strategy for optimization of the NN architecture [17]. The grammatical evolution optimized neural network (GENN) approach optimizes the inputs from a pool of features, the synaptic weights, and the architecture of the network. Thus, GENN automatically selects the relevant features and appropriate network architecture for a particular analysis problem. Preliminary studies with GENN show that this evolutionary optimization is more powerful than traditional NN methods and even other evolutionary computing approaches for detecting gene-gene interactions [17]. We have shown that the power of our GENN strategy to model and detect gene-gene interactions in the absence of main effects in many simulated epistatic models is higher than that of a back propagation NN [17], a genetic programming neural network strategy, or a random search neural network strategy [17].

The initial success of GENN is promising, but questions have been raised regarding the success of the evolutionary process. First, what is the impact of adjusting the parameters used in the evolutionary process, such as population size and number of generations, on the performance of the method? Also, GE is a greedy algorithm, which, in theory, should require some sort of main effect to build upon during model generation. Without any main effects, how does GENN build models with only functional loci? Finally, will GENN have power to detect gene-gene interactions in larger datasets comprised of enormous numbers of features?

In the current study, we address these questions using a range of simulated genetic datasets. First, we examine the ability of GENN to detect gene-gene interactions given different population sizes and numbers of generations during the evolutionary process. Next, we compare the performance, in terms of power, of GENN with that of the random search NN for two purely epistatic disease models. Then, in order to understand and visualize the evolutionary process during a GENN analysis and gain insight into its advantages over a random search, we monitor several evolutionary characteristics of both analysis methods. Finally, we apply knowledge gleaned from the preceding experiments to GENN analyses of datasets of increasing size to demonstrate the scalability of the method.

2. METHODS

2.1 Grammatical Evolution Neural Networks (GENN)

Grammatical Evolution (GE) is a form of evolutionary computation that uses grammars to generate computer programs [18,19]. GE uses individuals consisting of a binary genome divided into codons. Populations of such individuals undergo evolution to find the optimal solution for the problem at hand. Evolutionary operations occur at the individual level. Mutation can occur on individual bits along the genome, but crossover only occurs between codons. These codons are translated according to the grammar into a resulting phenotype (in this case, a functional NN). The resulting individual/phenotype can be tested for fitness and evolutionary operators are applied to create subsequent generations. By using the grammar to map a NN, GE separates genotype from phenotype, allowing for greater genetic diversity within a population than offered by other evolutionary algorithms. For a detailed description of GE, see O'Neill and Ryan [19].

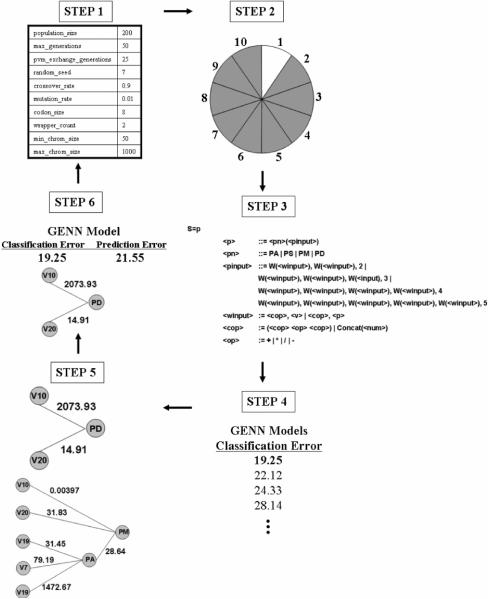
The steps of GENN have previously been described [17]. As summarized in Figure 1, GENN configuration parameters are first specified. Second, the data are divided into 10 equal parts for 10-fold cross-validation. Here, 9/10 of the data is used for training to develop a NN model. Later, the 1/10 of the data left out is used to test this model for predictive ability. Third, training of GENN begins by generating an initial population of random solutions. Sensible initialization [19] is used to ensure that the initial population creates functioning NN. In the fourth step of GENN, each NN is evaluated on the training set and its fitness recorded. Fifth, the best solutions are selected for crossover and reproduction using the selection technique specified in the configuration file (uniform, rank, roulette, and tournament are all options) [20]. This newly created generation begins the cycle again. This process continues until some criterion is met, after which GENN stops. At the end of GENN evolution, the overall best solution is selected as the optimal NN. In the sixth step, this best GENN model is tested on the 1/10 of the data left out to estimate the prediction error of the model. Steps two through six are performed ten times, each time using a different 9/10 of the data for training and 1/10 for testing.

Figure 1.

An overview of the GENN method. The steps correspond to the description of the method in Section 2.1.

GE has been implemented to optimize the inputs, architecture, and weights of a NN. Due to space limitations, the grammar cannot be presented here but is available from the authors upon request. The genetic algorithm (GA) used to evolve the binary string that is transcribed into a NN has the following parameters in the current implementation: crossover rate = 0.9, mutation = 0.01, codon size = 8, GE wrapping count = 2, minimum chromosome size (in terms of codons) = 50, maximum chromosome size = 1000, selection = tournament (can also be uniform, rank, or roulette), and sensible initialization depth = 10. The population size and number of generations were varied in the current study to find optimal values for these parameters. To prevent stalling in local minima, the island model of parallelization is used, where the best individual is passed to each of the other processes after every 25 generations [21]. The genome is derived from GAlib (version 2.4.5) which is freely available at http://lancet.mit.edu/ga/dist/, and a typical GA one-point crossover of linear chromosomes is used. The fitness metric used for the evolutionary process is the classification error in the training data. Classification error refers to the proportion of samples in the training dataset that are incorrectly classified by the network. Prediction error, which refers to the proportion of samples incorrectly classified in the test dataset using the GENN model generated during training, is used for final model selection. The overall goal of the learning process is to find genetic models that classify the data as accurately as possible. Cross-validation is used in conjunction with the learning process to produce a model that not only accurately classifies the data at hand, but generalizes to future, unseen data as well.

For the current study, additional output options were added to the configuration file. Output was generated that included information for every genome in the population, at each generation. This information included the features included in the model and the genome (chromosome) size. Two aspects of genome size were provided as output: 1. the actual physical chromosome size, and 2. the effective chromosome size (how much of the genome was actually consumed in the translation to a NN).

2.2 Random Search Algorithm

For a negative control, a random-search algorithm was implemented having identical properties to GENN in all aspects except for the evolution of individual solutions over subsequent generations. The random search algorithm uses the same fitness metric as GENN. The random search generates the initial chromosome population as described above for GENN, but this creation of random solutions occurs at every generation instead of only at the beginning of the run. Each genome is converted by the grammar into a NN and the fitness is determined just as it is for GENN. The algorithm stores the single best network from all the generations and returns that as the final model. All other networks are discarded. Other than the lack of evolutionary operators, the random search is performed in exactly the same way as GENN. Cross-validation is implemented, as described in the GENN section, and sensible initialization is used. Prediction error is used for selection of the final best model. The additional output options (features in each model and genome size) were also used for the random search analysis.

2.3 Data Simulation

Epistasis, or gene-gene interaction, occurs when the phenotype under study cannot be predicted from the independent effects of any single gene, but is the result of combined effects of two or more genes [22]. Penetrance functions are used to represent epistatic genetic models in this simulation study. Penetrance defines the probability of disease given a particular genotype combination by modeling the relationship between genetic variations and disease risk. Models lacking marginal main effects (where one gene exhibits an effect on case-control status independently) are appropriate for the goals of this study because they challenge the method to find gene-gene interactions in a complex dataset. The dimensionality involved in the evaluation of combinations of multiple variables quickly diminishes the usefulness of traditional statistical methods. As the number of genetic or environmental factors increases and the number of possible interactions increases exponentially, many cells in the resulting contingency table will be left with very few, if any, data points, referred to as the curse of dimensionality [23]. Traditional approaches using logistic regression modeling are limited in their ability to deal with models with no main effects due to the hierarchical model building process[2], leading to an increased risk of type II errors and decreased power [24].

For the current study, we simulated case-control data using two different two-locus epistatic models in which the functional loci (features) are single nucleotide polymorphisms (SNPs). The first model is based on the nonlinear XOR [25,26] function that generates an interaction effect in which high risk of disease is dependent on inheriting a heterozygous genotype (Aa) from one locus or a heterozygous genotype (Bb) from a second locus, but not both. The proportion of the trait (case-control status) variance that is due to genetics, or heritability, is low (0.053 as calculated according to [27]). In the second model, known as the ZZ model [28,29] high risk of disease is dependent upon inheriting exactly two high risk alleles (A and/or B) from two different loci. The heritability of this model is also very low (0.051). Table 1 illustrates the penetrance functions for these two models.

Table 1.

Multilocus penetrance functions used to simulate case-control data exhibiting gene-gene interactions in the absence of main effects. Each table cell gives the probability of disease associated with a particular combination of genotypes at the functional loci.

a. XOR Model
	BB	Bb	bb
AA	0	0.10	0
Aa	0.10	0	0.10
aa	0	0.10	0

b. ZZ Model
	BB	Bb	bb
AA	0	0	0.10
Aa	0	0.05	0
aa	0.10	0	0

These models were selected because they exhibit interaction effects in the absence of any marginal main effects when genotypes were generated according to Hardy-Weinberg proportions (in both models, allele frequencies of 0.5). For both models, we simulated 100 datasets consisting of 500 cases and 500 controls. Dummy variable encoding was used for each dataset, where n−1 dummy variables were used for n levels [30]. For each model, datasets of different sizes were generated. Total numbers of SNPs generated included: 25, 100, 500, 1000, and 5000. In each case, two SNPs were functional (disease-associated) and the remaining SNPs were noise features/variables. Though the biological significance of these particular models is uncertain, they are intended to represent a “worst-case scenario” in the detection of epistasis. If a method performs well under such minimal effects, it should also perform well in identifying gene-gene interactions in models with greater effect sizes. Furthermore, a method able to detect purely interactive features/terms will likely identify main effects.

2.4 Data Analysis

While the genetic models specified no marginal main effects in the data simulation, the datasets were carefully checked for any detectable main effects after each feature/SNP/variable was recoded according to the dummy encoding scheme and after division into cross-validation intervals. Any slight main effects after these two steps could explain the success of GENN over the random search, as these slight main effects could act as building blocks for model evolution. After converting to n−1 dummy SNP features/variables, χ² statistics were calculated for each individual SNP feature/variable across the entire dataset and for each cross-validation interval within a dataset. No significant main effects were found (data not shown). Additionally, the number of times one of the functional SNP features/variables had the highest χ² value within a cross-validation interval was tallied for each dataset. Even in the absence of significant main effects, we wanted to see if the functional SNP features/variables could serve as building blocks by demonstrating the strongest, even if not significant, associations when the data was divided for cross-validation. The proportion of times one of the functional SNP variables had the highest χ² value over all cross-validation intervals for all datasets was compared to the expected proportion (2/25 = 0.08%) using a binomial test of proportion, and no significant deviation from what would be expected purely by chance was detected (data not shown).

To optimally tune GENN parameters, both the population size and the number of generations were varied during analysis of the 25-SNP datasets. All combinations of the following parameter values were used: population size = {10, 20, 50, 100, 200, 500} and number of generations = {10, 20, 50, 100}.

For experiments concerned with characterizing the progress of GENN, we used both GENN and the random search NN to analyze the 25-SNP datasets of both epistatic models. The population size and number of generations were based on the ideal parameter settings from the analysis results above (population size = 200 and number of generations = 50). The other configuration parameter settings were as described in Section 2.1 and were identical for both methods (without evolutionary operators for random search). All output options were turned on to facilitate monitoring of the evolutionary characteristics as the algorithm progressed.

For experiments with the larger datasets, parameters were scaled according to the results obtained during the 25-SNP analyses. The number of generations was set to twice the number of SNP features in the particular dataset. Since the population size had minimal effect compared to the number of generations (see results), to minimize computation time while still providing an ample population size, this parameter was set to 2000.

For all analyses, prediction error was used for final model selection in both GENN and the random search, as described in Section 2.1. Power for all analyses is reported under each epistatic model as the number of times the algorithm correctly identified the functional loci (without any false-positive noise loci) over 100 datasets. If either one or both of the dummy SNP variables representing a single SNP was selected, that locus was considered present in the model.

3. RESULTS

Tables 2A and 2B show the power results of the 25-SNP data analyses for both the XOR and ZZ models—varying both the population size and number of generations. As the tables show, increasing either parameter enhances the power of GENN. An important trend seen in these tables is that while increasing both parameters improves power, increasing the number of generations has a more immediate impact than increasing population size. For both models, the combination of parameter settings that achieves 100% power with minimal computation time (since computation time scales linearly with both parameters) was a population size of 200 and 50 generations. The optimal population size of 200 corresponds to less than 10 times the number of SNP variables (features), while the optimal number of generations is twice the number of SNP loci (features) in the dataset. These optimal parameters were chosen for further exploration of the evolutionary process.

Table 2.

Power results of 25-SNP GENN analysis. Power is reported as the number of times the correct functional loci were selected (without any false-positive noise loci) over 100 datasets.

A. XOR Model
Number of Generations	Population Size
	10	20	50	100	200	500
10	0	2	5	10	17	46
20	0	2	12	10	21	34
50	19	64	78	89	100	100
100	34	100	89	97	100	100

B. ZZ Model
Number of Generations	Population Size
	10	20	50	100	200	500
10	3	0	13	8	25	50
20	2	4	6	6	17	48
50	45	31	82	99	100	100
100	32	77	94	95	100	100

Table 3 shows the power results for the 25-SNP datasets for both the XOR and ZZ models using GENN and the random search analyses with 50 generations and a population size of 200. As the table demonstrates, GENN soundly outperforms the random search for both epistatic models.

Table 3.

Power of each method to detect gene-gene interactions in the XOR and ZZ models.

Model	Power (%)
	GENN	Random Search
XOR	100	1
ZZ	100	0

To monitor the evolutionary process, several aspects of both GENN and the random search analysis were recorded over each generation. These features included the total chromosome size, the effective chromosome size, and the occurrence of both functional and non-functional SNP features included in each model. The total chromosome size is defined as the number of codons in each genome. The effective chromosome size is the number of codons that are actually translated into a NN. The occurrence of SNP features is quantified as the number of times each feature is selected for inclusion within the total populations evolving during analysis. To examine the inclusion of functional SNP features, this was quantified for all four dummy-encoded loci associated with simulated disease status. To examine the inclusion of all non-functional loci, this was recorded for all other features (simulated noise loci). Each of these properties was recorded across the ten cross-validation intervals for each dataset. These properties were then averaged for each epistasic model and analysis method. Standard errors were calculated, but are not shown since the magnitude of standard errors recorded was minimal. Figures 2 through 5 summarize the results of these analyses.

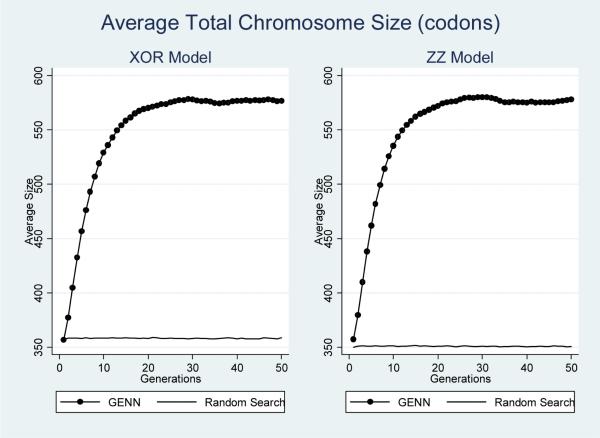
Figure 2.

Average total chromosome size at each generation for both epistatic models and analysis methods.

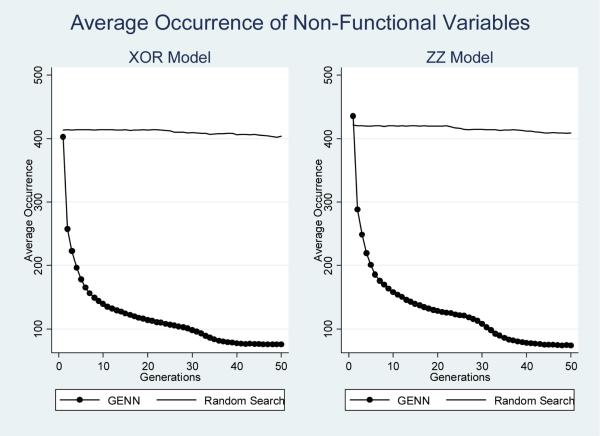
Figure 5.

Average occurrence of non-functional SNP features at each generation by epistatic model and analysis method.

Figure 2 shows the average total chromosome size across generations for both models, for both GENN and the random search analyses. As the figure shows, the average chromosome sizes remain constant during the analysis for the random search, which would be expected since each generation produced by the random search is independent of the previous generation. The figure also demonstrates that the total chromosome size expands over generations during GENN analysis.

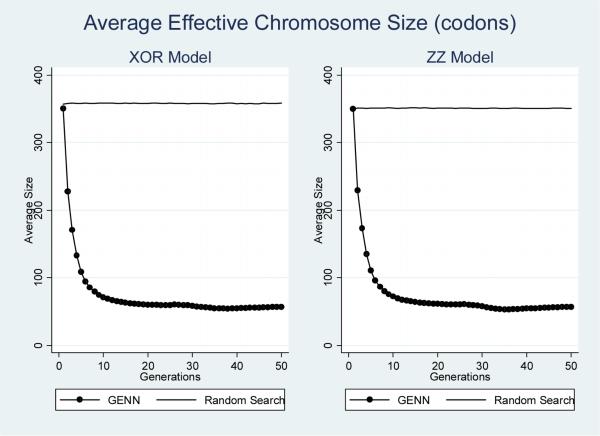
Figure 3 shows the average effective chromosome size during GENN and random search analysis of both epistatic models. Just as with the total chromosome size, the effective size does not change during the random search analysis, but changes quite substantially during the GENN analysis. While the total chromosome size dramatically increases during GENN analysis, the effective chromosome size dramatically decreases. It is important to note that the results shown in figures 2 and 3 may indicate the occurrence of bloat during the evolutionary process. This may be due to the standard one-point crossover implemented in GE [31].

Figure 3.

Average effective chromosome size at each generation for both epistatic models and analysis methods.

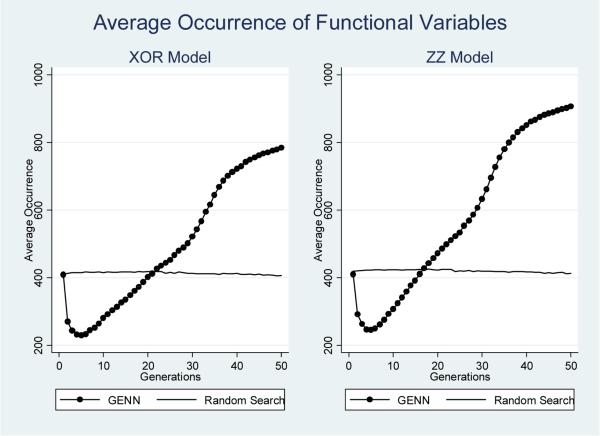
Figures 4 and 5 summarize the occurrence of both functional and non-functional SNP variables as the average number of times any of the four functional variables are included in the total populations across generations during the analysis of both models. Again, the horizontal line for random search analysis illustrates that the occurrence of both non-functional and functional SNP variables remained constant across generations. GENN, on the other hand, demonstrates a rapid decrease in the occurrence of non-functional SNP variables, and dramatic increase in the occurrence of functional SNP variables after the first few generations. As Figure 4 shows, the random search and GENN initially demonstrate the same average occurrence of functional features. However, the random search never improves over subsequent generations, while the occurrence of functional SNP variables included in GENN models increases in subsequent generations. The positive slope in inclusion of functional SNP features with respect to generations and the negative slope in inclusion of non-functional (noise) SNP features with respect to generations is evidence that GENN is learning as evolution progresses.

Figure 4.

Average occurrence of functional SNP features at each generation by epistatic model and analysis method.

Interestingly, during the GENN analyses, early generations see rapid declines in effective chromosome size, the occurrence of non-functional SNP features/variables, and the occurrence of functional SNP features/variables. In contrast, the total chromosome size is dramatically increasing during the early generations.

The results for GENN analysis of the larger datasets are given in Table 4. Table 4 lists the number of SNP features in each dataset and the GENN parameters (population size and number of generations) implemented for GENN detecting both the XOR and ZZ models in the larger datasets. GENN had 100% power for both models for each size dataset using the parameters listed. Based on the results shown in Table 2, the number of generations was scaled to be twice the number of SNPs per dataset. To minimize computation time, since the population size had less impact than the number of generations, the population size was held constant at 2000 for all datasets.

Table 4.

GENN configuration parameters lending 100% power for datasets with greater numbers of SNP features.

SNPs per dataset	Population Size	Number of Generations	Power (%)
			XOR Model	ZZ Model
100	2000	200	100	100
500	2000	1000	100	100
1000	2000	2000	100	100
5000	2000	10000	100	100

4. DISCUSSION

The results of this study demonstrate the utility of using grammatical evolution for the optimization of the architecture, inputs, and weights of NN. We optimized GENN input parameters, illustrated several aspects of the method's evolutionary process, and demonstrated its scalability to larger datasets.

Our experiments comparing GENN with a random search consider datasets containing a modest number of features. Even with such modest dataset sizes, there is a pronounced performance gap between the evolutionarily optimized algorithm and the trial-and-error random search approach. As the number of features increases, this gap is expected to widen even further.

The characterization of GENN's evolutionary progression demonstrates that, even with no main effects in the data, GENN is able to learn. Given that our simulated disease models are purely epistatic, learning the model requires that GENN include the two functional SNP loci in the NN. Without some type of a priori information, no evolutionary algorithm can create a building block by selecting both loci, since they have no independent effects. However, once GENN puts the two functional loci together, it learns that this is a good building block and all other features are not. One possible explanation for the patterns observed in Figures 2 through 5 is that GENN may be producing very large, diverse models initially, and then eliminating poorer models including non-functional loci. This would mean that the success of GENN in finding purely epistatic effects would be dependent upon randomly generating models containing both functional variables. The expansive size of the genome populations during GENN analysis would thus be an asset. Larger models will have a better chance of including all functional loci than smaller ones. It appears that GENN is then able to prune away non-functional features in subsequent generations. Applying this knowledge to analysis of larger datasets proved successful, in that GENN demonstrated 100% power to identify functional loci given a sufficiently large population size and appropriate number of generations.

It will be important to gain further insight into the relationships between the evolutionary process and other configuration parameters, such as population size, cross-over rate, and mutation frequency. Ongoing studies are aimed at understanding the configuration requirements of all parameters to scale GENN to the enormous datasets now being generated by modern experimental techniques. While this study began to dissect the evolutionary process of GENN, for a more complete understanding, further work should be done to follow the progress of individual genomes during GENN analysis.