Genotype by Environment Interaction in Adolescents’ Cognitive Aptitude

Abstract

In a replication of Turkheimer, Haley, Waldron, D’Onofrio, Gottesman II (2003, Socioeconomic status modifies heritability of IQ in young children. Psychological Science, 14:623–628), we investigate genotype–environment (G × E) interaction in the cognitive aptitude of 839 twin pairs who completed the National Merit Scholastic Qualifying Test in 1962. Shared environmental influences were stronger for adolescents from poorer homes, while genetic influences were stronger for adolescents from more affluent homes. No significant differences were found between parental income and parental education interaction effects. Results suggest that environmental differences between middle- to upper-class families influence the expression of genetic potential for intelligence, as has previously been suggested by Bronfenbrenner and Ceci’s (1994, Nature-nurture reconceptualized in developmental perspective: a bioecological model Psychological Review, 101:568–586) bioecological model.

Turkheimer et al. (2003) published a report of genotype–environment (G × E) interaction in the intelligence of young children. In a sample of 7-year old children from the National Perinatal Collaborative Project, the genetic and shared environmental influences on IQ, as measured by the Weschler Intelligence Scale for Children—Revised (WISC-R), were modified by the socioeconomic status (SES) of the children. For disadvantaged children, shared environmental influences accounted for nearly 60% of the variance in IQ, while genetic factors accounted for negligible variance. In advantaged children, the pattern was nearly the reverse.

Although the above results are congruent with some previous research (for reviews see Rowe et al. 1999 or Turkheimer et al. 2003), researchers have not always found clear evidence for G × E interaction in cognitive ability (e.g., Scarr 1981, Van den Oord and Rowe 1997), leaving open the extent to which the results Turkheimer et al. present can be generalized beyond the NCPP sample. This paper presents results of a replication of Turkheimer et al.’s (2003) investigation; however, there are several key changes in the current study. First, the demographic composition of the present sample, which includes middle to upper class adolescents, is different from the NCPP sample, which included a number of extremely disadvantaged children. We are interested in whether the expression of genetic potential for intelligence interacts with environment over the entire range of environmental experience, or whether such interactions are limited to environments of radically poor quality. Second, rather than combining indices of SES into a single measure, we examine potential differences in the magnitude of interactive effects between aspects of socioeconomic advantage, specifically between parental education and income.

In a sample of 839 adolescent twin pairs (Loehlin and Nichols 1976), we examine whether the genetic and shared environmental influences of cognitive aptitude, as measured by the National Merit Scholarship Qualifying Test (NMSQT), are modified by SES. Of the home environment measures available for the NMQST sample, mid-parent education and parental income were used. (These were chosen to be similar to the measurement of SES in Turkheimer et al. (2003), a linear combination of parental education, income, and occupational status. Parental occupational status was not available for this sample.) Our expectation is that additive genetic influences will account for a substantial portion of the phenotypic variance in the cognitive aptitude of adolescents from high income, highly educated families, while the shared environment will be more influential in less advantaged families. It is possible, however, that changes in heritability with socioeconomic status will be less marked in the present sample, because our participants have higher socioeconomic status than nearly all of the participants used by Turkheimer et al. (2003).

Method

Participants

Participants were sampled from the nearly 600,000 nationwide adolescents who completed the National Merit Scholarship Qualifying Test (NMSQT) in 1962. Virtually all adolescents were in the 11th grade at the time of the NMSQT, and most were 17 years old. Of these adolescents, 1507 prospective pairs of same-sex twins were identified and 839 pairs of twins (509 MZ, 330 DZ) ultimately participated in the study (a 56% response rate). Female twins composed 58.4% of the sample; male twins 41.6%. This sample represented approximately 5% of the live same-sex twin pairs born in the United States in 1945. Representation of the U.S. population was biased towards high-achieving adolescents. Students taking the NMQST ranked, on average, in the 79th percentile in their high schools. Zygosity was assigned by twins’ responses to questionnaire items concerning their similarity in childhood and the frequency with which they were confused by others (Nichols and Bilbro 1966). Questionnaire zygosity assignments were cross-validated with a subsample of 124 twin pairs (82 MZ, 42 DZ) and shown to be over 90% accurate. For a more detailed discussion of selection and data collection procedures see Loehlin and Nichols (1976).

Measures

The NMSQT is composed of five subtests: English Usage, Mathematics Usage, Social Science Reading, Natural Science Reading, and Word Usage/Vocabulary (means and standard deviations are shown in Table 1). The NMSQT is highly reliable, as indicated from the split-half reliability coefficients for this sample, which range from 0.83 for Natural Science to 0.96 for Vocabulary (Loehlin and Nichols 1976), and subtest scores are highly correlated with one another (see Table 2). The variance of NMSQT total scores is roughly constant across the range of total scores. Test constructors describe the NMSQT as a measure of cognitive aptitude, i.e., students’ readiness for future intellectual or educational pursuits (National Merit Scholarship Corporation, 2005). It is not, therefore, synonymous with an IQ test of the sort used in the Turkheimer et al. (2003) study. However, general cognitive ability, or g, accounts for most individual differences on various cognitive tests, regardless of the specific content of any particular test (Jensen 1998). Therefore, we can reasonably expect genotype–environment interactions for NMSQT aptitude scores to be similar to those found for IQ, although differences between cognitive ability and cognitive aptitude may have some implications for replication.

Table 1.

NMSQT subtest sample statistics and twin pair correlations by zygosity

Subtest	Twin 1		Twin 2		MZ	DZ
	M	SD	M	SD
English	19.22	4.88	19.76	4.60	0.76	0.57
Math	20.64	6.29	21.36	6.19	0.75	0.49
Social	20.34	4.87	20.85	4.89	0.77	0.52
Natural	19.45	5.88	20.16	5.70	0.69	0.55
Vocabulary	20.75	4.95	21.09	4.88	0.86	0.64
Total	101.40	22.12	103.29	21.95	0.88	0.65

Table 2.

Correlations between NMSQT subtests by member of twin pair

Subtest	English	Math	Social	Natural	Vocabulary	Total
English	1.00	0.56	0.62	0.56	0.67	0.80
Math	0.53	1.00	0.65	0.67	0.58	0.84
Social	0.64	0.57	1.00	0.67	0.77	0.88
Natural	0.59	0.64	0.66	1.00	0.60	0.85
Vocabulary	0.67	0.54	0.77	0.60	1.00	0.84
Total	0.81	0.81	0.86	0.85	0.84	1.00

Note: Twin 1 correlations are below the diagonal; Twin 2 correlations are above the diagonal

Mothers reported on both their own and the fathers’ level of education and the annual family income in a written questionnaire. Parental education was classified on a 6-point ordinal scale, from less than an 8th grade education to a graduate or professional degree. Mid-parent education was calculated as the average of maternal and paternal education (median = 3.5; variance = 1.44). Income was classified on a 7-point ordinal scale (median = 3; variance = 2.37), from less than $5000 per year to over $25,000 per year (roughly equivalent to less than $31,250 to over $156,250 in 2004 dollars). Response categories and frequency counts for the income and parental education scales are shown in Appendix A. The scaling used in the questionnaire partially adjusted for the non-normality of income and education in the population, although income did remain somewhat positively skewed and parental education negatively kurtotic. Furthermore, as might be anticipated given the bias towards high-achieving twins, the distribution of parental income was not nationally representative: less than 12% of the NMSQT families reported annual incomes less than $5000, in comparison to 42% of the U.S. population in 1960 (U.S. Department of Commerce, Bureau of the Census 1960). Parental education and income were correlated (r = 0.530). Parental education and income were equally correlated with adolescents’ total NSMQT scores (calculated separately for member of twin pair: r_{income - NMSQT1} = 0.23; r_{education - NMSQT1} = 0.21; r_{income - NMQT2} = 0.26; r_{education - NMSQT2} = 0.21). Of the 839 twin families, 777 reported income, 813 reported parental education, and 768 reported both. The twin pair average NMSQT total score for twin pairs with missing parental income data (M = 95.74) was significantly less than the average score for twin pairs with parental income data (M = 102.92, t = 2.62, P < 0.01). Twin pair average scores did not differ as a function of missing parental education data (t = 0.20, P = 0.845). Both parental education and income were centered at the median prior to structural equation modeling.

Appendix A.

Response categories and frequencies for parental education and income scales

Response	Description	Frequency (%)
Mid-parent education
1	8th grade or less	3.69
1.5		4.55
2	Part high school	7.38
2.5		9.59
3	High school graduate	17.71
3.5		15.38
4	Part college or junior college	13.78
4.5		9.23
5	College graduate	10.70
5.5		6.03
6	Graduate or professional degree	1.97
Income
1	Less than $5,000	11.84
2	$5,000 to $7,499	25.74
3	$7,500 to $9,999	21.36
4	$10,000 to $14,999	23.55
5	$15,000 to $19,999	9.4
6	$20,000 to $24,999	2.96
7	$25,000 and over	5.15

Analyses

We first conducted an exploratory factor analysis on subtest scores. In order to prevent bias due to non-independent observations, the EFA was restricted to one randomly selected twin per pair. EFA results clearly indicated a one factor model (eigenvalues = 3.84, 0.56, 0.39; root mean square error of approximation = 0.046), as also suggested by the consistently large intercorrelations among the subtests (see Table 2). For this reason, we chose to consider G × E interactions for overall cognitive aptitude, modeled as a common factor of the NMSQT subtests.

Using the cognitive aptitude factor, we fit two series of interaction models, one series for each measured indicator of SES. Each interaction model decomposed the variance of cognitive aptitude into four components: variance accounted for by the measured environment (income or education), variance due to other environmental influences shared by twins (C), variance due to additive genetic influences (A), and variance unique to each twin (E; due to environmental influences not shared by twins and measurement error). Furthermore, the paths from the additive genetic and shared environmental variance components were allowed to vary according to the measured environment. For example, for the income interaction models, aptitude scores were modeled as follows:

$$\text{NMSQT}=i\text{Income}+(a+a^{\prime }\text{Income})A+(c+c^{\prime }\text{Income})C+eE.$$ (1)

Similarly, for the parental education interaction models, aptitude scores were modeled as follows:

$$\text{NMSQT}=p\text{Education}+(a+a^{\prime }\text{Education})A+(c+c^{\prime }\text{Education})C+eE.$$ (2)

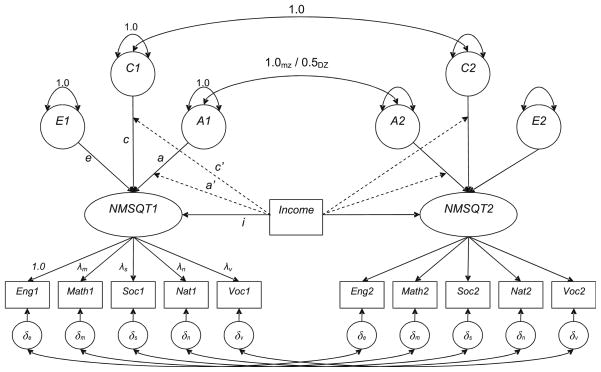
The income interaction model is illustrated in Fig. 1, where the dotted lines leading from income represent the interaction between income and the magnitude of the paths. Only the main effect of the non-shared environment was estimated, because the high MZ twin correlations for NMSQT total score suggest that non-shared influences are small. Indeed, the MZ twin correlation is only slightly smaller than the within-person split-half reliability coefficient, indicating that much of the non-genetic variance in cognitive ability not shared by twins is merely error. The residual variances of each subtest in Twin 1 were allowed to covary with the corresponding residual variances in Twin 2, separately by zygosity.

Fig. 1.

Income interaction model

Note that the inclusion of the main effects of income and education has implications for interpreting other model parameters: any interactive effects exist for variance in cognitive aptitude independent of the included measure of SES. Inclusion of the main effects of parental income and education is necessary both because we hypothesize there are such main effects and because of the possibility of genotype–environment correlation (rGE). Parents’ cognitive abilities are associated with their income and educational attainment, thus rendering the genetic influences on cognitive ability adolescents inherit related to their socioeconomic status. Purcell (2002) demonstrated that inclusion of the main effect of the measured environment prevents bias in estimation of G × E interactions resulting from unspecified rGE. We were unable to explicitly examine rGE here because such analyses require within-twin pair variation. Twin pairs in this analysis were necessarily identical for the parental variables used to index SES.

Following Button et al. (2005), the significance of the interactions between additive genetic effects and SES (a′) and between shared environmental effects and SES (c′) was tested by comparing the full model in which these were fitted with nested models in which they were dropped. Comparison of the fit of nested models used differences in chi-square distributed fit function (−2LL). All models were fit using Mplus (Muthén and Muthén 1998–2004). Mplus scripts are available from the first author upon request.

Results

The parameter estimates of the common factor model of NMSQT subtests for income and education models are shown in Tables 3 and 4. There are minor differences between them, at least in part, because they are based on two slightly different subsets of our sample (i.e., the 777 twin pairs with non-missing income data versus the 813 twin pairs with non-missing education data). It is also possible, however, that small differences between education and income in their relations to NMSQT subtests are being reflected in the measurement portion of the model. The proportion of variance not shared with the common factor differed across subtests (Tables 3 and 4). For income models, Math had the highest proportion of unique variance (approximately 53% in Twin 1; 45% in Twin 2), while Social Science Reading had the lowest (approximately 22% on both Twin 1 and Twin 2). A similar pattern was evident for education models. Overall, the residual covariances were greater in MZ than DZ twins; however, the magnitude of the MZ—DZ difference varied across subtests. This is consistent with previous analyses of the NMSQT data demonstrating both common and subtest-specific genetic effects (Martin and 1984).

Table 3.

Estimated parameters of NMSQT common factor model for income models

Parameter	Subtest
	English	Math	Social	Natural	Vocabulary
λ	1.00	1.30	1.22	1.23	1.14
δ1	10.15 (44.3%)	21.36 (53.7%)	5.40 (22.7%)	13.56 (40.4%)	6.52 (28.1%)
δ2	8.98 (43.7%)	17.57 (45.0%)	5.40 (22.7%)	12.64 (39.1%)	6.07 (26.9%)
MZσ2(1,2)	5.26	10.99	1.39	4.19	4.34
DZσ2(1,2)	4.57	6.44	0.15	3.86	2.91

Note: Factor loadings (λ) are equal for Twin 1 and Twin 2, but residual variances (δ₁; δ₁) allowed to differ. Percentages of unique variance are in parentheses. Residual covariances between Twin 1 and Twin 2 noted as σ² _(1,2). Parameters are estimated from the parental income model without either interaction term; parameter estimates from other income models differ by less than 0.1

Table 4.

Estimated parameters of NMSQT common factor model for parental education models

Parameter	Subtest
	English	Math	Social	Natural	Vocabulary
λ	1.00	1.29	1.22	1.26	1.15
δ1	9.99 (43.6%)	20.98 (52.8%)	5.73 (24.1%)	13.46 (40.1%)	6.58 (28.4%)
δ2	8.93 (43.5%)	17.52 (44.9%)	5.56 (23.4%)	13.07 (40.5%)	6.18 (27.4%)
MZσ2(1,2)	5.25	10.76	1.48	4.38	4.36
DZσ2(1,2)	4.52	6.54	0.25	3.95	2.99

Note: Factor loadings (λ) are equal for Twin 1 and Twin 2, but residual variances (δ₁; δ₁) allowed to differ. Percentages of unique variance are in parentheses. Residual covariances between Twin 1 and Twin 2 noted as σ² _(1,2). Parameters are estimated from the parental education model without either interaction term; parameter estimates from other income models differ by less than 0.1

The parameter estimates from the nested models are shown in Table 5. In the models containing interaction terms (Models 1–3, 5–7), the variance in the cognitive aptitude factor attributable to additive genetic or shared environmental influences is a function of the measured environment. (There is no interaction with the non-shared environmental component (e) or the main effects of income (i) or education (p), so e, i, and p are interpreted in the interaction models the same as in a classical twin model.) For example, additive genetic variance in Models 1–3 is calculated as:

$$V_a={(a+a^{\prime }\text{Income})}^2.$$ (3)

Table 5.

Estimated parameters of income and education interaction models

	a	c	e	iorp	a′	c′	−2LL	Δ − 2LLdf	p values
Income
1. Full	2.39 (2.14, 2.65)	2.28 (2.02, 2.55)	0.93 (0.77, 1.09)	0.58 (0.46, 0.70)	0.13 (0.02, 0.25)	0.02 (− 0.12, 0.16)	42666.90	–	–
2. Drop a′	2.43 (2.07, 2.80)	2.14 (1.68, 2.60)	0.96 (0.82, 1.10)	0.58 (0.41, 0.75)	[0]	0.13 (− 0.02, 0.28)	42672.06	5.161	0.023
3. Drop c′	2.36 (1.99, 2.73)	2.22 (1.80, 2.65)	0.96 (0.82, 1.10)	0.58 (0.41, 0.75)	0.13 (0.01, 0.26)	[0]	42670.73	3.831	0.050
4. Drop a′, c′	2.42 (2.06, 2.79)	2.19 (1.76, 2.63)	0.96 (0.83,1.11)	0.56 (0.40, 0.73)	[0]	[0]	42674.49	7.592	0.022
Parental education
5. Full	2.37 (2.11, 2.62)	2.25 (1.99, 2.51)	0.93 (0.78, 1.08)	0.86 (0.69, 1.04)	0.12 (− 0.10, 0.33)	0.004 (− 0.24, 0.25)	44682.61	–	–
6. Drop a′	2.38 (2.03, 2.74)	2.15 (1.72, 2.58)	0.95 (0.81, 1.08)	0.87 (0.65, 1.08)	[0]	0.12 (− 0.09, − 0.34)	44686.30	3.691	0.055
7. Drop c′	2.37 (2.00, 2.73)	2.16 (1.74, 2.59)	0.97 (0.90, 1.04)	0.87 (0.66, 1.07)	0.11 (− 0.06, 0.28)	[0]	44685.68	3.091	0.079
8. Drop a′, c′	2.38 (2.02, 2.73)	2.16 (1.74, 2.58)	0.96 (0.82, 1.09)	0.88 (0.68, 1.08)	[0]	[0]	44687.66	5.052	0.064

Note: Lower and upper bounds of 95% confidence intervals are in parentheses

Because parental income and education were centered such that values of zero correspond to the medians for each variable, the squared genetic (a) and shared environmental (c) main effects parameters equal the genetic and shared environmental variance in the common aptitude factor at the median level of the measured environment. Similarly, the proportion of variance attributable to a predictor in the interaction models also changes as a function of the measured environment. For example, the proportion of genetic variance (i.e., the heritability) for Model 1 is calculated as:

$$h^2=\frac{{(a+a^{\prime }\text{Income})}^2}{{(a+a^{\prime }\text{Income})}^2+{(c+c^{\prime }\text{Income})}^2+{\sigma }_{\text{inc}}^2{i}^2+e^2}.$$ (4)

The squared a and c main effects divided by the total variance equals the heritability and shared environmentality of NSMQT at the median environment. Using parameters from Model 1, additive genetic factors accounted for 45% of the variance in cognitive aptitude, shared environment 41%, unique environment 7%, and income 6% at the median level of parental income ($7500 to $9999). Using parameters from Model 5, additive genetic factors accounted for 44% of the variance in cognitive aptitude, shared environment 40%, unique environment 7%, and parental education 9% at the median level of parental education (high school graduate or part college).

Whether the observed interactions can be attributed to sampling error can be gauged by the confidence intervals around the individual interaction parameters, a′ and c′, and by differences in fit function (− 2LL) between the full model and nested models that drop one or both of the interaction parameters. In Model 1, the 95% confidence interval around a′ (0.02, 0.25) indicates that the change in genetic variance with income is significant. In contrast, the shared environmental interaction is not significantly different from zero (95% CI = −0.20, 0.16). The change in − 2LL (5.16, Δdf = 1) from Model 1 to Model 2 is significant (P = 0.023), indicating that dropping the genetic interaction worsens the fit of the model. Model 3 assessed the contribution of the shared environment interaction by fixing c′ to zero. The change in − 2LL (3.83, Δdf = 1) from Model 1 to Model 3 is not (quite) significant at the 0.05 level (P = 0.0503); i.e., dropping the shared environment interaction did not demonstrably worsen the fit of the model. Finally, Model 4 assessed the simultaneous contribution of both a′ and c′ to model fit. The change in − 2LL from Model 1 to Model 4 is significant (7.59, Δdf = 2), further suggesting that inclusion of some interaction parameter (presumably the genetic one) improves model fit. Model 3, then, represents the most parsimonious fit to the data.

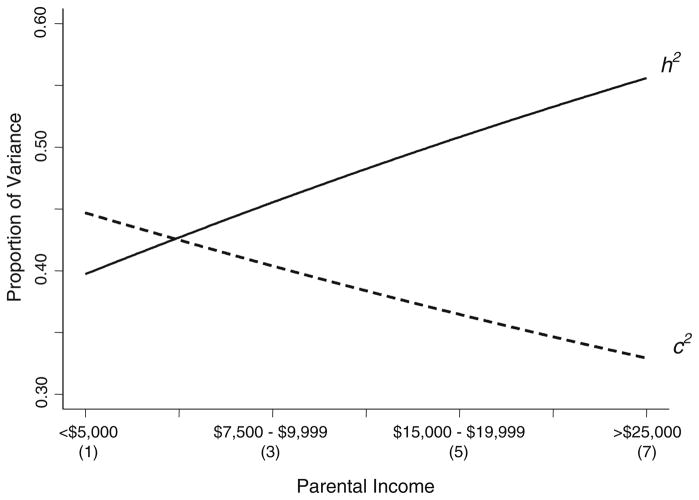
Figure 2 illustrates the relations between income and genetic and shared environmental proportions of variance, as implied by the parameters estimated in Model 3. Genetic influences accounted for about 55% of the variance in adolescents’ cognitive aptitude and shared environmental influences about 35% among higher income families. Among lower income families, the proportions were in the reverse direction, 39% genetic and 45% shared environment. Although the shared environmental proportion of variance decreased with income, shared environmental variance per se did not decrease. The interactive effect was driven entirely by the increase in genetic variance. Genetic variance in cognitive aptitude nearly doubled from 4.41 in families earning less than $5000 annually to 8.29 in families earning more than $25,000 annually.

Fig. 2.

Genetic and shared environmental proportions of variance by parental income, as implied by fitted interaction parameters.

*Note: X-axis corresponds to response categories of parental education scale

A slightly different picture emerges for the parental education models. The wide 95% CIs around both a′ and c′ in Model 5, and the non-significant worsening of fit when both are dropped in Model 8, suggest that interactions may not be necessary to explain the data. Moreover, the change in − 2LL (3.69, Δdf =1) from Model 5 to Model 6 is not quite significant (P = 0.054), suggesting that the genetic interaction may be dropped. Model 7 also did not fit the data significantly worse than Model 5 (Δ − 2LL = 3.09, Δdf=1, P = 0.079), suggesting that the shared environment interaction may be dropped. Therefore, we may not conclude that parental education interacts with genetic and shared environmental influences on cognitive aptitude beyond what may be attributed to sampling error.

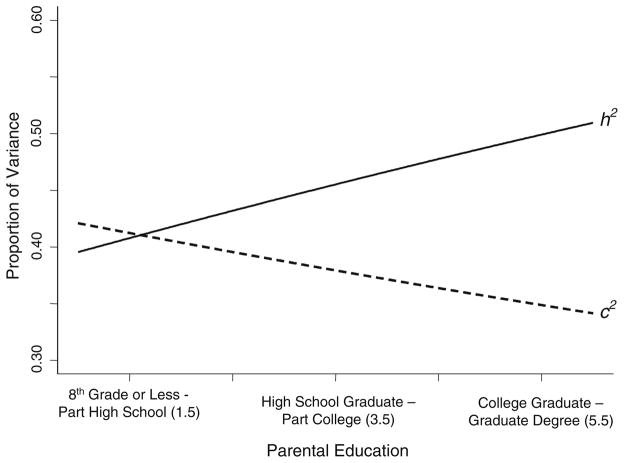
If, however, a parental education interaction was present, it appeared to be a genetic one, consistent with the results for income. For the sake of illustration, Fig. 3 graphs the relations between parental education and genetic and shared environmental proportions of variance, as implied by the parameters estimated from Model 7. Its general similarity to Fig. 2 is evident. Genetic influences accounted for about 50% of the variance and shared environmental influences about 35% among highly educated families. Among lower education families, the proportions were in the reverse direction, 39% genetic and 42% shared environment. Although the shared environmental proportion of variance decreased with increasing income, shared environmental variance per se did not decrease. The interactive effect was driven entirely by the increase in genetic variance. Genetic variance in cognitive aptitude increased from 4.39 in children whose parents had less than an 8th grade education to 7.00 in children whose parents had a graduate or professional degree.

Fig. 3.

Genetic and shared environmental proportions of variance by parental education, as implied by fitted interaction parameters.

*Note: X-axis corresponds to response categories of parental education scale

As a post-hoc test of whether income and parental education differ in their ability to modify genetic influences, we fit two additional nested models (Models 9 and 10; see Table 6). Model 9 decomposed variance in cognitive aptitude into five components: (a) variance accounted for by parental income, i; (b) variance accounted for by parental education, p; (c) variance due to additive genetic influences, a; (d) variance due to other environmental influences shared by twins, c; and (e) variance unique to each twin, e. The magnitude of genetic influences was allowed to vary with both income and parental education simultaneously (a′_i and a′_P, respectively). Because our previous models failed to indicate a shared environmental interaction effect, it was not included here. In order to directly compare their main and interactive effects, income and parental education were standardized. Also, the covariance between income and parental education was estimated. The estimated genetic interaction effect for parental income was larger (a′_i = 0.13) was than that for parental education (a′_P = 0.03), although the 95% confidence intervals around both parameters included zero.

Table 6.

Estimated Parameters of Income and Education Genetic Interactions Models.

Parameter	9. Full.	10. a′i = a′P
a	2.39 (2.02, 2.76)	2.39 (2.01, 2.77)
c	2.09 (1.64, 2.53)	2.08 (1.63, 2.53)
e	0.96 (0.82, 1.10)	0.96 (0.82, 1.10)
i	0.47 (0.18, 0.76)	0.46 (0.17, 0.75)
p	0.80 (0.50, 1.10)	0.80 (0.50, 1.10)
σ2ip	0.19 (0.17, 0.22)	0.19 (0.17, 0.22)
a′i	0.13 (− 0.08, 0.34)	0.08 (− 0.04, 0.19)
a′P	0.03 (− 0.20, 0.26)	0.08 (− 0.04, 0.19)
−2LL	46622.31	46622.56
Δ −2LLdf	–	0.251
P	–	0.617

Note: Lower and upper bounds of 95% confidence intervals are in parentheses

Next, Model 10 constrained the income interaction (a′_i) and education interaction (a′_p) to be equal. Constraining the income and education interaction effects to be equal, however, resulted in a trivial change in model fit (Δ − 2LL = 0.25; Δdf = 1; P = 0.617) and failed to indicate any significant difference between income and education in their ability to modify the magnitude of genetic influences. If the expression of genetic predispositions was indeed better facilitated by material wealth than by exposure to highly educated parents, we were unable to demonstrate such an effect with these data.

Discussion

Our investigation supports our hypothesis that the magnitude of genetic influences on cognitive aptitude varies with socioeconomic status. This partially replicates the results presented by Turkheimer et al. (2003); however, no shared environmental interaction effects were demonstrable in the current study. Genetic influences accounted for about 55% of the variance in adolescents’ cognitive aptitude and shared environmental influences about 35% among higher income families. Among lower income families, the proportions were in the reverse direction, 39% genetic and 45% shared environment. This pattern is similar to the pattern seen in Turkheimer et al. (2003), although less marked.

Differences among aspects of SES in the facilitation of genetic potential

We were unable to demonstrate directly that parental income and parental education differ in their interaction with genetic influences on cognitive aptitude; however, income and education models had different patterns of results, with a significant genetic interaction detected only for income. It is, therefore, possible that not all aspects of high socioeconomic standing equally facilitate expression of genetic potential. Guo and Stearns (2002) drew similar conclusions in their investigation of adolescent verbal intelligence, which demonstrated that the interaction between parental education and genetic influences on verbal intelligence disappeared if other environmental indices—income, parental employment, absence of a biological father, and race—were included. Most previous research investigating interactions between genetic variance in cognitive aptitude and socioeconomic advantage have used single indices of SES, including parental education (Rowe et al. 1999), parental occupational status (van den Oord and Rowe 1997), census tract characteristics (Scarr 1981), and linear combinations of the above (Turkheimer et al. 2003). With the exception of Guo and Stearns (2002), differences among indicators with regard to their ability to modify genetic expression have not been explored. Such differences may conceivably explain the inconsistency with which clear evidence for G × E interactions have been found: van den Oord and Rowe (1998) did not find evidence of a direct interaction with parental occupational status, nor did Scarr (1981) with census tract characteristics.

A difficulty with interpreting an interaction between genotype and socioeconomic status is that SES presumably reflects genetic differences between parents, in addition to differences in the quality of the environment provided for children (Turkheimer et al. 2003). The observed increase in heritability with parental income, therefore, may reflect an interaction with genetic differences between more and less affluent families (gene–gene interaction), rather than an interaction with environmental quality. Income, however, is loaded with genetic variance to a lesser extent than parental education or occupational status and is less closely related to parental IQ. Rowe, Vesterdal, and Rodgers (1998), using a nationally representative sample of adults aged 28–35 years, reported within-person correlations between education and IQ of 0.52–0.66, whereas within-person correlations between income and IQ were 0.26–0.38. Furthermore, the heritability of income was substantially lower than that of education (0.42 vs. 0.68), and the majority of the total genetic variance in education was shared with IQ (75%), while the majority of the total genetic variance in income was not shared with either education or IQ (71%). The relative independence of income from genetic influences on parental IQ raises our confidence somewhat that the observed interaction is truly a genotype by environment interaction. Ideally, we would like some knowledge of the genetic correlation between adolescents’ cognitive aptitude and parental SES. This is impossible to estimate in the current study, because twin children are not genetically informative about parental characteristics for which they are necessarily identical.

The modification of heritability within the range of “normal” environments

These results partially replicate the work of Turkheimer et al. (2003) in a sample of radically different demographic composition. The National Collaborative Perinatal Project sample over-represented children from extremely disadvantaged environments, with 33% of families on public assistance and 25% of mothers having less than a 9th grade education. In contrast, the adolescents composing the NMSQT sample are relatively advantaged in terms of intellectual ability (ranking, on average, in the 79th percentile in their high schools) and their parents’ income. Less than 12% of the NMSQT families reported annual incomes less than $5000, in comparison to 42% of the U.S. population in 1960; over 60% of the NMSQT families reported incomes over $7500, whereas only 34% of the U.S. population reported incomes over $7000 in 1960 (U.S. Department of Commerce, Bureau of the Census 1960). The socioeconomic advantage of the NMSQT adolescents may be due to two selection processes: (a) for this cohort, only adolescents with a certain level of academic achievement took the NMSQT; (b) of twins identified as potential participants, non-response may have been associated with environmental disadvantage. The modification of heritability within the NMSQT sample suggests that genotype–environment interactions in cognitive ability are not limited to severely disadvantaged environments, as has been previously suggested (Turkheimer and Gottesman 1991; Scarr 1992).

Turkheimer and Gottesman’s (1991) hypothetical reaction norm for intelligence illustrates the hypothesis that differences among “normal” environments are largely irrelevant for differences among children’s intelligence. Below a certain threshold of environmental quality, intelligence increases sharply with better environments (i.e., a steep slope across the environmental axis), and genetic differences among individuals are better expressed in better environments (i.e., the slope along the genetic axis depends on the environment). The latter reflects a gene-environment interaction. In contrast, above a certain threshold of environmental quality, the reaction plane is essentially flat: for any given genotype, better environments do not predict an increase in intelligence (a flat slope across the environmental axis), and for any given environment, genetic differences are equally well expressed (a constant linear slope along the genetic axis). Thus any gene-environment interaction disappears above a threshold of environmental quality. Scarr (1992) further elaborated on this idea, claiming that other than severe abuse and neglect, such as being “trapped in crack houses of inner cities, locked in basements and attics by vengeful crazy relatives” (p. 3), differences in family environments have no effect on children. In sum, differences among normal-range family environments have been thought to be largely irrelevant to the development of intelligence, both because shared environmental variance components are low in advantaged environments and because only extremely disadvantaged environments can suppress the expression of genetic potential.

The alleged irrelevance of differences among normal- range family environments has been challenged by Bronfenbrenner and Ceci (1994), who “take issue with the prevailing conception of the reaction range simply as a curved plane, similar to a bent piece of chicken wire …” (p. 571). Their bioecological model proposes that proximal processes, i.e., mechanisms by which genetic potential for effective or adaptive functioning are realized, differ among families in magnitude, quality, and stability, and that these differences in proximal processes “can produce substantial variation in heritability even in advantaged environments” (p. 571). Rowe et al. (1999) characterized this position as “paradoxical,” because the proportion of environmental variance must necessarily decrease as the proportion of genetic variance (i.e., heritability) increases. This characterization is inaccurate in two respects. First, although proportions of variance are constrained to sum to unity, unstandardized variance components are not. Second, by asserting that differences among normal-range family environments are relevant to children’s functioning, the bioecological model is not necessarily predicting substantial shared environmental variance in adequate environments. Rather, the bioecological model is predicting an increase in genetic variance even over the range of normal environments, a slightly different conception of what it means for environmental differences to be “relevant” for children’s functioning. Indeed, Bronfenbrenner and Ceci (1994) predict the identical pattern as Turkheimer and Gottesman (1991): high heritability estimates and low shared environmentality estimates as environmental advantage increases.

In the typology of genotype–environment interactions recently proposed by Shanahan and Hofer (2005), the “bent piece of chicken wire” view of the reaction norm for intelligence emphasizes “social context as social control”—extreme socioeconomic disadvantage enforces structural constraints on people and their choices. Beyond the constraints of poverty, the genotype–environment interaction is thought to no longer operate. In contrast, the present research, echoing Bronfenbrenner and Ceci’s (1994) formulation, emphasizes “social context as enhancement” (Shanahan and Hofer 2005, p. 69)—high quality interactions with the environment increase adaptive functioning and increase heritability, even within normal range environments. Our results suggest that differences between middle class and affluent parents affect the expression of genetic potential.

Data from a sample spanning the entire range of socioeconomic advantage—from extreme poverty to extreme wealth—would be useful in further tests of the Turkheimer and Gottesman (1991) reaction norm and Bronfenbrenner and Ceci (1994) bioecological models. By comparing results from two roughly contemporaneous samples of overlapping socioeconomic status, we have attempted to “piece together” a representation of how genetic influences interact with the home environment over a broad range of socioeconomic status. Although this comparison suggests support for the bioecological model, this approach is not without difficulty. Specifically, the heritability estimates for IQ among the most advantaged NCPP participants (h² ≈ 0.80; Turkheimer et al. 2003) are substantially higher than the heritability estimates for NMQST scores of participants with similar socioeconomic status (i.e., the low end of the NMSQT sample). As mentioned previously, NMSQT aptitude scores are not synonymous with IQ scores. The shared environment may be more influential for NMSQT scores because they also reflect, to some extent, academic achievement, rather than pure cognitive ability. Regardless of why heritability estimates differ in the two samples, these differences are indicative of the need for future research to construct a model of genotype–environment interactions from a single sample, rather than piecing together such a model from various, partially overlapping, samples.

Conclusions

Overall, these results mirror findings in other areas of behavior genetic research demonstrating that the magnitude of genetic variance is not a static characteristic of a trait but a population statistic that may be moderated by other predictors. For example, Johnson and Krueger (2005) have demonstrated that genetic variance in physical health decreases with increasing income and increasing sense of psychological control. Similarly, Button et al. (2005) have shown that genetic variance in childhood conduct problems drops dramatically with elevated levels of family dysfunction. The present research thus extends a relatively small body of behavior genetic research that has moved beyond the calculation of heritability coefficients for overall psychological outcomes to investigations of the environmental contexts facilitating or suppressing genetic expression.