CAN HIGH-FIELD MREIT BE USED TO DIRECTLY DETECT NEURAL ACTIVITY? THEORETICAL CONSIDERATIONS

Abstract

We sought to determine the feasibility of directly studying neural tissue activity by analysis of differential phase shifts in MRI signals that occurred when trickle currents were applied to a bath containing active or resting neural tissue. We developed a finite element bidomain model of an aplysia abdominal ganglion in order to estimate the sensitivity of this contrast mechanism to changes in cell membrane conductance occurring during a gill-withdrawal reflex. We used our model to determine both current density and magnetic potential distributions within a sample chamber containing an isolated ganglion when it was illuminated with current injected synchronously with the MR imaging sequence, and predicted the resulting changes in MRI phase images. This study provides the groundwork for attempts to image neural function using Magnetic Resonance Electrical Impedance Tomography (MREIT). We found that phase noise in a candidate 17.6 T MRI system should be sufficiently low to detect phase signal differences between active and resting membrane states at resolutions around 1 mm³. We further delineate the broad dependencies of signal to noise ratio on activity frequency, current application time and active tissue fractions, and outline strategies that can be used to lower phase noise below that presently observed in conventional MREIT techniques. We also propose the idea of using MREIT as an alternative means of studying neuromodulation.

INTRODUCTION

Non-invasive detection of neural activity is an area of great interest in neuroscience for its expected high impact and significance. As well as the well-established areas of fMRI, inverse MEG and EEG, methods have been proposed for detection of activity from perturbations of MR signals, including those occurring in the main magnetic field, B₀ (Bodurka et al. 1999, Xue et al. 2006, Park et al. 2006, Park and Lee 2007), phase (Petridou et al. 2006); via Lorentz effects (Truong 2008), or methods involving conventional MR in combination with application of ultra low (μT) magnetic fields (Kraus et al., 2008). Methods from direct external impedance measurement or from impedance changes related to blood flow (Bagshaw et al. 2003) have also been proposed. Methods that rely on perturbations of the main magnetic field have been found to work in small preparations (Petridou et al. 2006, Park et al. 2006) but in trials performed in bloodless whole brain preparations (Luo et al 2009), and humans in vivo (Chu et al. 2004, Tang et al. 2008) significant changes have not been found thus far.

Recently Cassarà et al. (2008) demonstrated use of NEURON software (Hines and Carnevale 1997) to determine expected B₀ and phase perturbations for a realistic model of hippocampal neurons. This paper discussed effects of changes in neuron density, imaging parameters (TE), differences in firing rates, diffusion, noise levels with averaging and the effect of dipole orientation. They found that detectability could be strongly affected by these variables, but made no concrete conclusions as to the viability of the technique.

We have been investigating MREIT (Woo and Seo 2008), which involves application of current synchronized with standard MR imaging sequences. The phase image contains scaled B_z data, that is, information about the induced magnetic flux density in the direction of the main magnetic field due to current flow within the imaged object. In Current Density Imaging (CDI) the curl of phase data can be used to directly calculate current density within the object as long as the object can be rotated twice to gather all three components of B_x, B_y, and B_z. CDI was developed by Scott et al. (1991) and subsequently extended to include conductivity imaging in MREIT by Kwon et al. (2002). MREIT without the need for object rotation was proposed by Seo et al. (2003). This method involves use of Ampere's law to relate the Laplacian of B_z data to electrical conductivity gradients. With the advent of this technique it has become practical to measure conductivity distributions at near MR resolution (Seo et al. 2003, Oh et al. 2005, Sadleir et al. 2006). The most recent MREIT applications include imaging of the canine brain in-vivo (Kim et al. 2008), demonstrating good contrast between white and gray matter. The conductivity resolution possible using MREIT depends ultimately on interdependent factors such as averaging time, system noise levels, RF coil sensitivity, current amplitude, current injection patterns and measurement resolution as well being limited by diffusion processes.

MREIT could potentially be applied to achieve direct detection of neural activity by virtue of changes in membrane conductance (G_m). MREIT is uniquely positioned compared to other contrast mechanisms designed for this purpose in that G_m can only have positive values and the phase signals resulting from fluctuations in G_m are integrated over each current application time. Although the phase signals may still be quite small, in theory it may be possible to detect neural activity via this process as long as the sample is imaged for long enough and if the intrinsic phase noise in the imaging system is low enough. Any examination of the viability of using MREIT for detection of neural activity must consider the interaction of this imaging method with the neural tissue in question against limits imposed by factors such as diffusion, habituation and the required temporal resolution. In this paper, we have performed a feasibility study of MREIT for direct detection of neural activity in a well-studied neural complex: the abdominal ganglion of aplysia (AAG). In contrast to the work presented by Cassarà et al. (2008), we have chosen to model the AAG as a bidomain (Henriquez 1993) rather than employing a core-conductor model. We believe that in the context of applying a far field to the neural complex in combination with the averaging that occurs over voxels, the bidomain representation may give a suitably realistic result. To our knowledge, this is the first model of a neural complex (as opposed to a cylindrical neural bundle (Altman and Plonsey 1990, Roth and Altman 1992) that uses a bidomain framework.

The AAG anatomy and function have been extensively studied (Frazier et al. 1967) and characterized in behavioral experiments. We have chosen the AAG gill withdrawal reflex as our model of neural activity, (Zecevic et al. 1989, Falk et al. 1993, Zochowski et al. 2000) and used data from these papers as a basis for estimating the spatially averaged extent of activity within a ganglion preparation.

In order to establish the feasibility of using MREIT to image neural activity, we must determine MR resolutions sufficient to isolate the tissue involved. If possible, we should image near cell scale (Ciobanu, Webb & Pennington 2003), or at a high enough resolution to unambiguously identify active units. At the scale of the abdominal ganglion (up to approximately 5 mm, Frazier et al. 1967), fields over 10 T must be used to give resolutions ca. 20 μm. This is the realm of MRI microscopy. Grant et al. (2000) found that they could image giant (R1) cells of aplysia at 17.6 T. While there may be advantages in precisely imaging active cells, it is conversely advantageous to use larger voxel samples as this will lead to smaller noise levels and better temporal resolution. The feasibility of the technique also depends on aspects related to system performance such as main field homogeneity, ambient noise levels and naturally, the scale of expected B_z deviations induced by membrane conductivity changes related to neural activity.

In this paper we construct a bidomain model of a neural complex similar to that of an aplysia abdominal ganglion and estimate the size of B_z perturbations that would be expected between active and rest conditions. We also analyze sample 17.6 T data to estimate signal to noise ratios and B_z noise levels at realistic imaging resolutions, and therefore the potential of MREIT as a method for imaging cellular neural activities. We determine the effects of changing voxel size, differences in levels of activity, current application time and averaging parameters on signal sizes, and compare them with measured noise levels in a candidate MR system. We also determine the possible effects of the imaging current on the ganglion complex and estimate maximum imaging currents.

METHODS

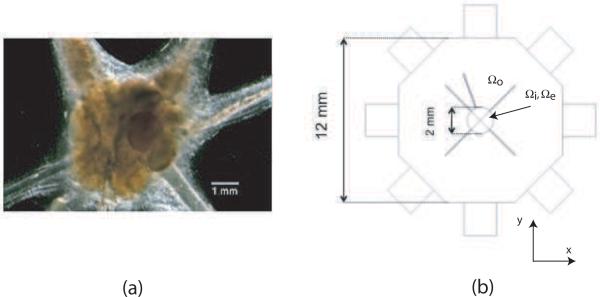
Our model is based on a simple representation of the aplysia abdominal ganglion. A typical dissected ganglion is shown in figure 1(a). The AAG is a well-characterized and easily obtained neural preparation. We modeled the AAG as comprising a central body and four radial unmyelinated neural bundles arranged in a plane transverse to the main magnetic field of an MRI system (figure 1(b)). The AAG complex was enclosed in a saline-filled sample chamber with current injection ports. Tissue conductivity and membrane characteristics were taken from the literature. This model is also similar to any simple ganglion structure.

Figure 1.

(a) Microscope image of aplysia abdominal ganglion. (b) Simple model of ganglion, showing bath and current application ports

2.1 Bidomain Model

The bidomain model (Tung 1978, Henriquez 1993) is an approximation to the quasi-static electrical behavior of active tissue. It has principally been used to model cardiac tissue (Tranquillo et al. 2005, Trayanova 1996), but can also be applied to distributed neural tissue such as axonal bundles (Altman and Plonsey 1990). It is so named because the model consists of two domains - intracellular (Ω_i) and extracellular (Ω_e) spaces - occupying the same region of space. The domains are coupled via a passive or active membrane model that determines the flow of current from one space to another. The membrane can be thought of as occupying the same volume as the intra- and extracellular spaces. Both spaces may be anisotropic and share a principal anisotropic axis. In general (and in real tissue) the degree of anisotropy, defined as the ratio of conductivity along the principal cellular axis to across it, is different in extracellular and intracellular spaces. The bidomain may be placed into an external isotropic bath (denoted `o') that couples to the extracellular space and can also share current with the bidomain structure.

The equations describing the bidomain are as follows. The intra and extracellular spaces share current density J_i and J_e, respectively, according to

$$\nabla \cdot {\mathbf{J}}_i=-\nabla \cdot {\mathbf{J}}_e=i_m$$ (1)

where i_m is the current passing through the membrane in Am⁻³. In our model, we chose to define i_m as due to passive conduction through the membrane and

$$i_m=\beta G_m{V}_m$$ (2)

where β and G_m are the surface to volume ratio of the tissue in m⁻¹ and the membrane conductance in Sm⁻², respectively. The membrane voltage V_m is the difference between intracellular and extracellular voltages, and is defined in (4) below. In general, the membrane current is defined by a time-dependent membrane model, but in this model we have chosen only to calculate differences between passive and active extremes of activity.

The current volume densities J_i and J_e are defined as

$$\begin{array}{cc}\hfill {\mathbf{J}}_i& =-{\mathbf{D}}_{\mathbf{i}}\nabla {\varphi }_i\hfill \\ \hfill {\mathbf{J}}_e& =-{\mathbf{D}}_e\nabla {\varphi }_e\hfill \end{array}$$ (3)

where ϕ_e and ϕ_i are potential distributions in the extra and intracellular spaces, respectively, and D_i,e is a conductivity tensor. The membrane voltage, V_m, is

$$V_m={\varphi }_i-{\varphi }_e.$$ (4)

The tensors D_i and D_e contain conductivities of the intra or extracellular tissues with respect to the principal model directions such that

$${\mathbf{D}}_{\mathbf{i},\mathbf{e}}={\mathbf{AD}}_{i,e}^{\prime }{\mathbf{A}}^{\mathbf{T}}.$$ (5)

where the matrix A represents rotation about the z (depth) axis by an angle α, and D′_i,e is a diagonal matrix consisting of tissue conductivities. If the model x-axis is coincident with fiber direction then

$${\mathbf{D}}_{\mathbf{i},\mathbf{e}}^{\prime }=\left[\begin{array}{ccc}\hfill g_{(i,e)L}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill g_{(i,e)T}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill g_{(i,e)T}\hfill \end{array}\right]$$ (6)

Here, g_iL, g_iT, g_eL, and g_eT are the tissue conductivities along and across the intra- and extracellular spaces, respectively, and (in this case) fibers are aligned with the x-axis and the y and z directions are perpendicular to fiber direction. Explicitly, in either the intra- or extracellular space, the components of the tensor D consist of three independent parameters k_xx, k_xy and k_yy such that (dropping i,e subscripts)

$$\mathbf{D}=\left[\begin{array}{ccc}\hfill k_{xx}\hfill & \hfill k_{xy}\hfill & \hfill 0\hfill \\ \hfill k_{yx}\hfill & \hfill k_{yy}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill g_z\hfill \end{array}\right]$$ (7)

where

$$\begin{array}{cc}\hfill k_{xx}& =g_L{\cos }^2\alpha +g_T{\sin }^2\alpha \hfill \\ \hfill k_{xy}& =k_{yx}=(g_L-g_T)\cos \alpha \sin \alpha \hfill \\ \hfill k_{yy}& =g_L{\sin }^2\alpha +g_L{\cos }^2\alpha .\hfill \end{array}$$ (8)

By means of equations (5)–(8), each tensor D_i (or D_e) may be represented by the three parameters g_L, g_T and α, where g_L, g_T are the conductivities along and across tissue, respectively and α is the fiber angle with respect to the x-axis of a coordinate system. Since the fiber angle in both (i, e) spaces is the same, there are a total of 5 parameters describing the bidomain.

The bath field is described by Laplace's equation, i.e.

$$\nabla \cdot {\mathbf{J}}_{\mathbf{o}}=0$$ (9)

subject to

$${\int }_{\partial {\Omega }_o}{I}_o=0\mathrm{and}\frac{{\sigma }_0\partial {\varphi }_o}{\partial \mathbf{n}}=J_o\mathrm{on}\partial {\Omega }_o$$ (10)

where J_o and J_o are the current density within the bath and normal to electrode surfaces, respectively, ∂Ω_o is the surface of the medium containing the neural tissue, I_o is the current passing through the bath boundary and n is a unit vector normal to its surface. The quantity ϕ_o is the bath voltage. At the extracellular-bath boundary we have

$${\varphi }_o={\varphi }_e.$$ (11)

Further, at the intracellular boundary we have

$$\frac{\partial {\varphi }_i}{\partial \mathbf{n}}=0.$$ (12)

2.2 Finite Element Model Description

2.2.1 Bidomain parameters and tissue dimensions

The AAG was approximated as a spheroidal structure with cross-sectional xy dimension of 2 mm and five radiating neural bundles (figure 1(b)). The spheroid was denoted the body and the neural bundles the arms. The spheroid had a thickness of 1 mm. Each arm had a length of 2.75 mm and a diameter of 0.1 mm. The AAG model was placed inside an octagonal prism structure with side lengths of 5.2 mm. Each octagonal face contained a recessed port for current injection (Oh et al. 2003) with dimension 2 mm × 2 mm × 2 mm. The overall size of the model was 9 mm × 9 mm × 8 mm. We considered currents applied via two orthogonal orientations because they produce two non-parallel current densities almost everywhere inside the domain, which are required for a unique conductivity image reconstruction in MREIT (Kwon et al. 2002, Seo et al. 2003, Woo and Seo 2008).

Intra- and extracellular conductivities, the fraction of intracellular space, tissue and membrane conductivities were assigned with reference to basic works in the area (Malmivuo and Plonsey 1995). Rest and active membrane conductivities were estimated from standard Hodgkin-Huxley parameters. The extracellular conductivity and bath conductivity were chosen to be the conductivity of artificial sea water (σ_ASW) of about 5.07 S/m (Foster et al. 1976). Axoplasm conductivity (σ_i) was chosen to be σ_ASW/1.4 as suggested in Foster et al. (1976). The parameters chosen are shown in Table 1. No anisotropy was assigned to the central ganglion structure, but anisotropic tensors for the five arms in each space were assigned according to (8).

Table 1.

Bidomain Parameters and Constants

Parameter	Value	Units	Description
σ i	3.63	S/m	intracellular conductivity
σ e	5.07	S/m	extracellular conductivity
σ o	5.07	S/m	bath conductivity
σ p	1	S/m	port conductivity
fi	0.7	-	intracellular filling fraction
β	20 000	m −1	surface to volume ratio
Gm,rest	6.7	S/m 2	membrane conductivity, rest
Gm,active	320	S/m 2	membrane conductivity, active

2.2.2 Model equations, source, boundary conditions and solution strategy

We used COMSOL (Comsol AB, Burlington MA) software to create a three-region coupled finite element environment. Three coupled partial differential equations were defined within the COMSOL environment; the bath equation (o) which was defined on all regions except the body and arms of the AAG; the extracellular equation (e) which was defined on the AAG body and arm subdomains; and the intracellular equation (i) which was defined on the same set of subdomains as in the extracellular equation. To solve for flux densities we used a static version of a general electromagnetic partial differential equation that solved for V (voltage), A (magnetic vector potential) and ψ (magnetic scalar potential). Electromagnetic parameters in each defined region were therefore denoted V_o, A_o, ψ_o; V_e, A_e, ψ_e; and V_i, Ai, ψ_i, respectively. In this formulation, magnetostatic equations were defined on each region as

$$-\nabla \times \left({\mu }_0^{-1}\nabla \times {\mathbf{A}}_{(i,e,o)}\right)+\sigma \nabla V_{(i,e,o)}=Q_{(i,e,o)}$$ (13)

subject to the Coulomb gauge

$$\nabla \cdot \mathbf{A}=0.$$ (14)

where Q is electrical charge density, μ₀ is the magnetic permeability of a vacuum and σ is electrical conductivity. The relations between magnetic vector potential, magnetic flux density and magnetic field strengths are given by

$$\mathbf{B}=\nabla \times \mathbf{A}\mathrm{and}\mathbf{B}={\mu }_0\mathbf{H}$$ (15)

All subdomains had no magnetic susceptibility. Components of B were calculated from A. We also defined a set of electrostatic equations on the same three regions. Results from these simulations were used to verify solutions from the magnetostatic equations. In this framework the three equations were solved for V_o, V_e, and V_i as

$$\sigma \nabla V_{(i,e,o)}=Q_{(i,e,o)}.$$ (16)

In both magnetostatic and electrostatic formulations, charge was allowed to flow between intra- and extracellular domains by specifying an additional source term to the equations. In the extracellular space the equation solved for had the source density term

$$Q_e=\beta G_m(V_i-V_e).$$ (17)

In the intracellular space the corresponding source was

$$Q_i=-Q_e=\beta G_m(V_e-V_i).$$ (18)

There were no sources inside the bath, therefore we specified Q_o = 0.

We defined the following boundary conditions. At all bath-extracellular space boundaries we had

$$V_o=V_e.$$ (19)

At all intracellular domain boundaries we specified no current flow, that is

$$\frac{\partial V_i}{\partial \mathbf{n}}=0.$$ (20)

In the bath region, fixed voltages of ±1 V were applied to two opposite ports. All other bath external boundaries were electrically and magnetically insulated.

The model described in Section 2.2.1 was meshed to 131 097 quadratic tetrahedral elements. The overall model had 1 168 197 degrees of freedom, approximately nine times the number of elements, reflecting the need to solve for V, A, and ψ within each element over the three environments. Solutions were obtained using the conjugate gradient method with an algebraic or geometric multigrid preconditioner. A relative tolerance of 1 × 10⁻¹⁰ was chosen to ensure good accuracy over all subdomains. Solutions for the electrostatic case were very fast, typically requiring around one minute on a Linux Workstation with 450 MHz processor and 16 GB RAM. Magnetostatic solutions, having many more degrees of freedom for the same mesh, were much slower and took around six hours to reach a solution to the same tolerance.

To internally verify our electric and magnetostatic models we compared voltage data (V_o, V_e and V_i) from the electrostatic model with voltage results from the magnetostatic model (V(i,e,o), A(i,e,o)). When both formulations were solved to the same error tolerance, we found that there was a maximum of 10⁻³ % difference between the voltages observed in both intracellular and extracellular environments of the two formulations.

2.3 Voxel Calculations

We calculated expected B_z values by averaging solution results over a voxel structure overlaid on the model. Dimensions of these structures were chosen to be reasonable for both detection of neural activity signals, internal structure size and SNR considerations in an environment of a 17.6 T MRI scanner. Several test resolutions were used: (128 × 128 × 16), (64 × 64 × 8), (32 × 32 × 8) and (16 × 16 × 8). In the three eight-slice structures, slice thicknesses were chosen to be 1 mm, with xy resolutions of 281, 562 and 1120 μm, respectively. The (128 × 128 × 16) voxel structure had a slice thickness of 500 μm and xy dimensions of 140 μm.

B_z values were interpolated at points on an 11 × 11 × 11 regular grid over each voxel. Since parameters were undefined on a portion of a voxel, such as on a bath-air boundary, the meshing procedure excluded these external areas. B_z values at points within bidomain regions were calculated by summing the B_z values found in intracellular and extracellular domains. The B_z values calculated within each voxel were integrated over a tetrahedral mesh defined on the 11 × 11 × 11 grid. Finally, average B_z values in each voxel were calculated by dividing integrated B_z values by voxel volume. We analyzed differences between active and rest membrane conditions using histogram representations and by making example calculations in bidomain voxels.

2.4 B_z noise levels at 17.6 T

We developed a method to determine a noise standard deviation in measured B_z data as a function of current application time, signal-to-noise ratio (SNR) of MR magnitude image (Sadleir et al. 2005a). We found that the noise standard deviation (sd) of the B_z data is given by

$$sd\left(B_z\right)=\frac{1}{\sqrt{2}\gamma T_c{\mathrm{Y}}_M}$$ (21)

where γ = 26.75 × 10⁷ rad/T/s is the gyromagnetic ratio of hydrogen, T_c is the current injection time and Y_M is the signal-to-noise ratio in MR magnitude images of the sample. This equation is different from the one in Scott et al. (1992) by a factor of $\sqrt{2}$, because of the definition of SNR used. At higher main field levels, equation (21) predicts that lower noise values should be measured because of the increased signal-to-noise ratio observed in higher fields. Noise levels depend inversely on voxel size, but using larger voxels of course results in worse localization.

From experimental analysis of phantom data, Sadleir et al. (2005a) found that the noise level in B_z data using an 11 T MRI system and four excitations was about 1.32 nT when 1 mm cubed voxels were used and averaging over four datasets. In MREIT, a phase image is obtained from two complex MR images subject to positive and negative injection currents with the same amplitude and width. This is to reject any systematic phase artifact and also to increase the phase change by a factor of 2. We assume two B_z images, ±B_z(x,y) subject to two injection currents ±I, respectively. We may denote two complex MR images as

$${\mathcal{M}}^{\pm }(x,y)=M(x,y)e^{j\delta (x,y)}{e}^{\pm j\gamma B_z(x,y)T_c}$$ (22)

where δ(x,y) is the systematic phase artifact. The phase change is

$$\Phi (x,y)=\arg \left(\frac{{\mathcal{M}}^{+}}{{\mathcal{M}}^{-}}\right)=2\gamma B_z(x,y)T_c$$ (23)

From (21) it is easy to see that a noise level of 1.32 nT is equivalent to 0.73° for a T_c of 18 ms. The 0.1° noise threshold used by Luo et al. (2009) corresponds to 0.18 nT in MREIT phase images assuming current is injected for the time period. However, the value of 0.1° quoted in Luo et al. (2009) was obtained with averaging over 140 trials (excitations) and using 0.5 mm³ voxels. Translating this value to the same resolution and the four excitations used in Sadleir et al. (2005a), the noise floor found by Luo et al. is equivalent to around $0.1∕2\times \sqrt{140∕4}\approx {0.3}^o$ or 0.54 nT.

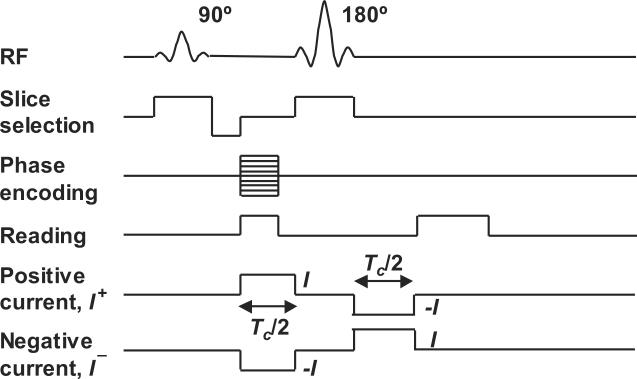
We expected that SNR values measured at 17.6 T would be higher than those found at 11 T. In order to estimate the likely noise levels in a system operating at 17.6 T and therefore the feasibility of measuring activity-related phase changes at this field strength, we prepared solutions of 1 S/m saline, doped with 1 g/l CuSO₄. We placed this solution in a small cylindrical polycarbonate tube (inside diameter 11.5 mm, outside diameter 15 mm). The tube was placed inside a 20 mm diameter linear birdcage coil and scanned in a wide bore 17.6 T MRI scanner (Oxford/Bruker) using a spin echo sequence modified for MREIT application (Figure 2) with TE = 10 or 20 ms and TR = 600 ms. Images collected at the two TE values were compared and used to estimate a T2 value for the doped saline solution of approximately 11 ms. Using TE = 20 ms, current was passed through electrodes placed at four recessed ports created by piercing the tube with a 2 mm diameter needle. Cross-sectional images of the phantom are shown in Figure 3.

Figure 2.

Spin-echo pulse sequence used in MREIT imaging

Figure 3.

(a) Phantom showing test region and SNR value, and B_z data corresponding to current injections of 200 μA between (b) ports A and C and (c) B and D. Parameters used were T_c = 18 ms, NEX = 2, TR/TE = 600/20 ms, FOV 16 × 16 mm, Δz = 250 μm. Resolution was 128 × 128 pixels (125 mm pixel scale)

The current source was a customized MREIT current source (Impedance Imaging Research Center, Kyung Hee University, Republic of Korea) that was triggered synchronously with the MR spectrometer, as shown in Figure 2. Eight slices with 250 μm thickness were captured, with the central slices closest to the plane containing the four electrode ports. The field of view was 16 mm square, with 128 pixels per side; therefore each pixel was 125 μm on a side. The current injection time T_c was 18 ms, and current amplitude was 200 μA. Total imaging time for NEX = 1 was 156 sec. To estimate the noise standard deviation in B_z using (21), we calculated Y_M from magnitude images by calculating mean signal levels in a circular region in a central image slice (shown in Figure 3) and then measuring the standard deviation in a circle having the same size, outside the phantom bounds. Y_M was then computed as the ratio of the mean to the standard deviation. Because the resolution used in test SNR data was not the same as for those used in the model, we translated SNR data from these experiments to model data by rescaling noise values by the relative voxel volumes (Haacke et al. 1999.)

2.5 Integrated membrane conductance change and active fraction estimations

Our model calculations were made assuming that a change in membrane conductivity was maintained for the entire bidomain over the total current application time. We need to account for factors such as the actual membrane conductance profile of these active cells and the fraction of tissue involved. We used spike rate data in the paper by Falk et al. (1993) as a guide to our estimation of typical firing rates and numbers of cells involved in the gill-withdrawal reflex. This paper identified six sets of neurons and presents raster diagrams and spike rates per 812 msec monitoring periods during habituation of an AAG preparation to stimulus of skin tissue (Falk et al. 1993, Figure 2). We estimated that average spike rates in the most consistently active neuron set (Group II) during control stimulation protocols were around 28 Hz averaged over 4.5 s. Thus, the number of spikes occurring in this group during our notional current application time was around 0.5. Average spike rates over all neuron groups for this time period were about 48 Hz, corresponding to a total of around 0.9 spikes during each current application period. Finally, average spike rates during the first 812 msec averaging interval were around 125 Hz, which would result in 2.3 spikes occurring during each current application period.

To estimate the total conductance change during each spike, we used NEURON (Hines and Carnevale 1997) to generate conductance profiles during activity of an 18.8 μm diameter cell body. We modeled the cell with the Hodgkin-Huxley model parameters provided by the program and calculated conductances from potassium and sodium currents and membrane voltages as

$$G_{si}=G_{Na}+G_K=\frac{i_{Na}}{V_m-E_{Na}}+\frac{i_K}{V_m-E_K}$$ (24)

where G_si is the total membrane conductance, i_Na, i_K, E_Na and E_K are the sodium and potassium membrane currents and resting voltages, respectively.

2.6 Membrane voltages and stimulation thresholds

It is desirable that activity is not initiated by the imaging current. We calculated simulated current densities at the body and bundle boundaries to determine their values and compare them with classically stimulating current densities. We also determined whether cell-firing rates should be affected by the externally applied currents (Terzuolo and Bullock 1956, Purpura and Mc Murtry 1965). We estimated the threshold for stimulation as being 1.2 A/m² at a distance of 1 mm from the complex, following Reilly (1998). We then examined current densities formed close to the AAG complex to see at what current levels this threshold would be exceeded. All B_z values were then rescaled to reflect those measured using currents just under this threshold value.

RESULTS

3.1 Measurements of B_z noise

We found that at the specified resolution and using two excitations (NEX = 2), the SNR observed in 17.6 T magnitude images was about 82. From (21), the noise standard deviation in B_z at that resolution was around 1.8 × 10⁻⁹ T. We repeated this measurement at NEX = 1 with the same current injection time and other imaging parameters, and found an SNR of 53 which was only slightly worse than the expected value of 82/√2 = 58. At an SNR of 53 the noise level expected would be 2.8 × 10⁻⁹ T. Translating these noise levels to our modeled resolutions gives the predicted noise levels shown in Table 2. Note that although these noise levels were measured with a current of 200 μA rather than the 90 μA level of our simulated data, noise levels do not depend on current amplitude (Sadleir et al. 2005a, Scott et al. 1992). Therefore, these measurements may be directly compared to simulated data if we assume that the current application time for the simulation was the same as that used in the noise measurement (18 ms).

Table 2.

Expected B_z Noise Levels (T) at different SNR levels in a 17.6 T main field

Resolution	Pixel Size μm	Δz mm	Predicted Noise (T)
			NEX=2	NEX=1
128 × 128 × 16	140	0.5	7.1 × 10−10	1.1 × 10−9
64 × 64 × 8	281	1	8.9 × 10−11	1.4 × 10−10
32 × 32 × 8	562	1	2.2 × 10−11	3.4 × 10−11
16 × 16 × 8	1120	1	5.6 × 10−12	8.6 × 10−12

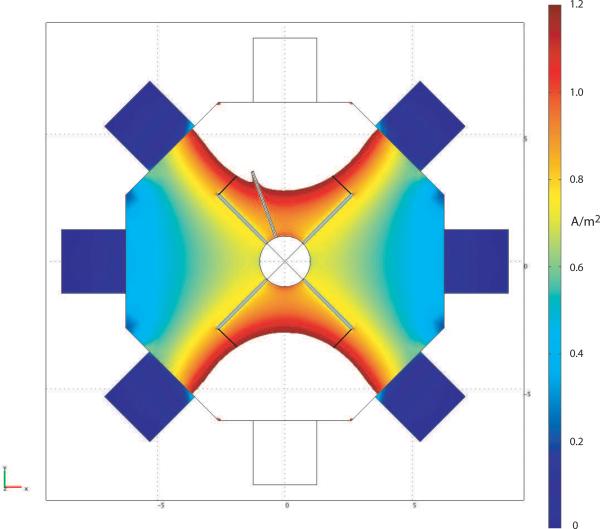
3.2 Current density distributions relative to classical neural activity thresholds

As a guide to likely current density levels near active tissue surfaces, we calculated the current density at a distance of 1 mm from the tissue boundary. As suggested by Reilly (1998), the threshold current density for initiation of activity may be around 1.2 A/m² at a distance of 1 mm. A sample plot of current density overlaid on the model geometry is shown in Figure 4, with the maximum threshold value scaled to be 1.2 A/m². With the port arrangement shown in Figure 1 (b), a reduction in applied current, and therefore of observed B_z signals, to around 0.04 that injected in our simulation (where injected current was of the order of 2.3 mA) would be required to avoid the imaging current stimulating tissue (although it may result in a change in cell firing rate). The current required to create this distribution was around 90 μA. Thus, with subthreshold currents we would expect to observe a voltage drop between opposite electrodes of 80 mV. All subsequent calculations in our analysis were performed using B_z values scaled to this current injection level.

Figure 4.

Current density cross-sectional map with maximum value set to 1.2 A/m². Distances of 1 mm from tissue are marked at the end of neural bundles, and correspond to an applied current of around 90 μA.

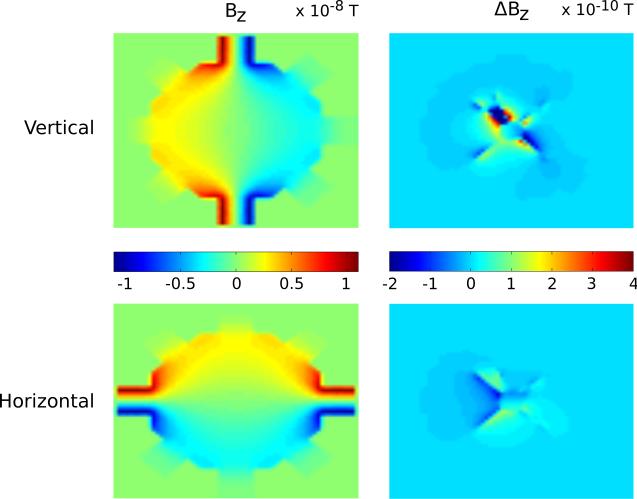
3.3 B_z values in two different orientations

Two current patterns were simulated, one for horizontal (x direction) and one for vertical (y direction) injection, as indicated in Figure 1 (b). Injected currents in our simulations were scaled to 90 μA. Simulated B_z data for a central slice (pixel size 281 μm, Δz = 1 mm) through the center of the sample and a resting membrane are shown in the left hand images of Figure 5 for (top) vertical and (bottom) horizontal current injections. The images on the right are of the differences appearing in each B_z distribution, denoted as ΔB_z, caused by an increase in membrane conductance. Note that because of the AAG geometry, the B_z differences in the vertical injection case were somewhat larger in this plane than those in the horizontal injection case.

Figure 5.

Sample central (left) B_z and (right) ΔB_z data slices at 64 × 64 × 8 resolution (281 μm × 281 μm × 1 mm) for (top) vertical and (bottom) horizontal current injections of 90 μA using bidomain model of aplysia.

3.4 Analysis of B_z changes

At an applied current of 90 μA, typical ΔB_z values were of the order of 2 × 10⁻¹¹ T, which corresponds to about 0.011° in MREIT phase images measured with a T_c of 18 ms. From examination of Figure 5 it appears that larger voxels of approximately 1 mm³ are more practical for detection of activity since they will increase signal levels. At the same time, a resolution of 1 mm³ may still provide localization on a useful scale compared to neural structures. Distributions of ΔB_z data using the `subthreshold' current of 90 μA found above for the different injection patterns and resolutions are shown in Figure 6 compared to the noise levels found at 17.6 T, extrapolated to different numbers of excitations.

Figure 6.

ΔB_z signal distributions compared to predicted noise levels at resolutions of (a) 128 × 128 × 16, (b) 64 × 64 × 8, (c) 32 × 32 × 8 and (d) 16 × 16 × 8, for `subthreshold' current of 90 μA applied along (top) vertical and (bottom) horizontal axes, with resolutions noted on each figure. Lines and excitation numbers relate to noise thresholds at 17.6 T based on the noise measurements at 17.6 T shown in figure 3 The number of excitations required to attain an SNR of 1 relative to the ΔB_z distribution for the larger and smaller spike rates are indicated by lines in green (for a spike rate of 28 Hz) and red (a spike rate of 125 Hz) overlaid on the plots.

3.5 Predicted ΔB_z values with gill withdrawal reflex

As mentioned in section 2.5 above, we have assumed that conductance changes from 6.7 S/m² to 320 S/m² during an action potential and our estimates of signal size are based on the entire ganglion bidomain complex experiencing this change. In a real preparation, discrete portions of the tissue will be active and the maximum conductance change will be experienced as a transient. We assumed currents in our noise measurement study were applied for a period of 18 msec. Assuming this value was adopted as imaging time with an AAG preparation, the integrated conductance change happening over this time would be (320-6.7) × 18 × 10⁻³ ≈ 5.6 Ssec/m². From our simulations of action potential profiles using NEURON, we found that the total integrated conductance change occurring if one spike occurred over this time was 0.18 that of the integrated membrane conductance difference and therefore that actual integrated conductance changes should be 0.18 those found using our model, or about 1 Ssec/m². Multiplying this value by estimated spike rates, the total integrated B_z change in each of the three groups described in Section 2.5 above would be 0.09, 0.16, or 0.41, respectively, those of the levels shown in Figure 6. On this basis, the number of excitations used would have to be increased by a factor between (1/0.41)² = 6 and (1/0.09)² = 125 to bring signal levels in line with the levels shown in the distributions illustrated in Figure 6. The number of excitations required to attain an SNR of 1 relative to the ΔB_z distribution for the larger and smaller spike rates are indicated by lines in green (for a spike rate of 28 Hz) and red (a spike rate of 125 Hz) overlaid on Figure 6.

DISCUSSION

In MREIT, we inject current into an imaging object. Conductivity changes related with neural activity alter internal current pathways. Internal current flows generate a distribution of magnetic flux density, which in turn produces phase changes in MR images. In functional MREIT (fMREIT), we try to capture activity-related changes in MR phase images invoked by externally injected imaging current. The main advantages of fMREIT compared to direct measurements of current flow from phase data is the positive sense of the contrast mechanism, which eliminates problems related to source orientation and cancellation, and the SNR advantage of MREIT produced by the externally injected imaging current. The signal created by changes in measured magnetic flux densities depends directly upon the magnitude of the imaging current rather than on the magnitude of endogenous currents flowing within cells. The noise level in measured magnetic flux density depends on the overall system noise level, current injection time (or phase accumulation time), voxel size, and the number of excitations.

Because of these factors, the challenges to detection become mostly dependent upon the careful design of imaging currents, current density distributions and careful management of MR pulse sequences to maximize the time for which imaging currents are applied. It is clear from the analysis in Sections 3.4 and 3.5, and from Figure 6, that that active imaging MREIT will require multiple excitations in order to reach useful SNR levels, and as in other modalities we can consider some circumstances where use of this mechanism may be unrealistic if the number of excitations and time to acquire data is very long. For example, application of many stimuli may also result in loss of signal because of habituation (Falk et al. 1993). Therefore, employment of strategies that will allow increased current application time, reduced noise levels, increased imaging current, or parallel data acquisitions with higher sensitivity are vital if this method is to be generally useful.

4.1 Overall Signal Levels

In maximizing the amount of signal available from active neural tissue we have to take into account many factors. We must consider the maximum current we can apply (which in turn depends on activity threshold and the dynamic characteristics of the imaging current); the expected spike rate; and lastly the fraction of active cells. In the sections below we examine the effects of these contributions and outline strategies for maximizing SNR. In our analysis, we have assumed that the threshold for detection is SNR = 1.

4.2 Effects of increasing current application time, T_c and spike rate

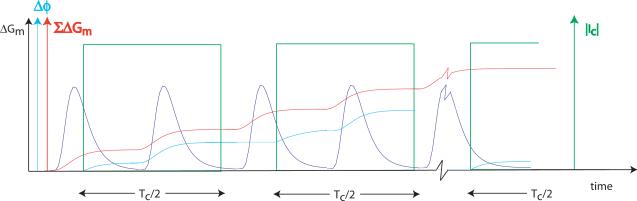
Figure 7 shows the conductance profile, integrated conductance change and phase change measured over a single spin echo MREIT pulse sequence. The beginning of a second RF pulse is shown at the right of the diagram. Phase change is integrated throughout the current application time directly following integrated conductance change. The diagram provides a simple illustration of the dependencies of activity levels on measured signal, with additional factors summarized below.

Figure 7.

Schematic showing relation between conductance changes ΔG_M, shown in blue, integrated conductance change ΣΔG_M (red) and total measured phase change ϕ (cyan) over a single current application cycle. Current I_C is injected for a total of T_c during each cycle. The start of a second RF pulse is shown at right.

Noise in B_z signals is inversely proportional to current application time (21). Thus, the SNR in measured B_z data increases directly with T_c. As long as activity occurs during T_c there will be a difference between active and resting phase images, since results of activity-related membrane conductance changes will be integrated over this period, as diagrammed in Figure 7. Of course, there will only be a differential signal present if there are differences between `active' and `resting' spike rates. Thus we have in general

$$\mathit{SNR}\propto (f_A-f_R)T_C$$ (25)

where f_A and f_R are the `active' and `resting' spike rates, respectively. SNR is also proportional to the integrated conductance change over one spike, denoted $G_M^1$, and

$$G_m^1=\kappa (G_A-G_R)$$ (26)

Here, G_A and G_R are active and resting membrane conductances, respectively, and κ is a shape factor that describes the integrated conductance profile of a single spike.

4.3 Effects of resolution and partial volume

As in other strategies, this method will suffer from partial volume effects. The volume of inactive tissue surrounding active tissue within a voxel will proportionally decrease any signal it creates. Thus SNR in B_z data is also proportional to V_f, where V_f is the fraction of active tissue within a voxel.

Combining all the relations above, we have that

$$\mathit{SNR}\propto (f_A-f_R)V_f{G}_M^1{T}_c.$$ (27)

Examining (27), it is clear that the most important factor to consider in estimating the SNR of measured B_z data is the expected differential level of activity between two sampling periods. In the section below we consider realistic SNR levels within a single model voxel containing active tissue.

4.4 Example calculation

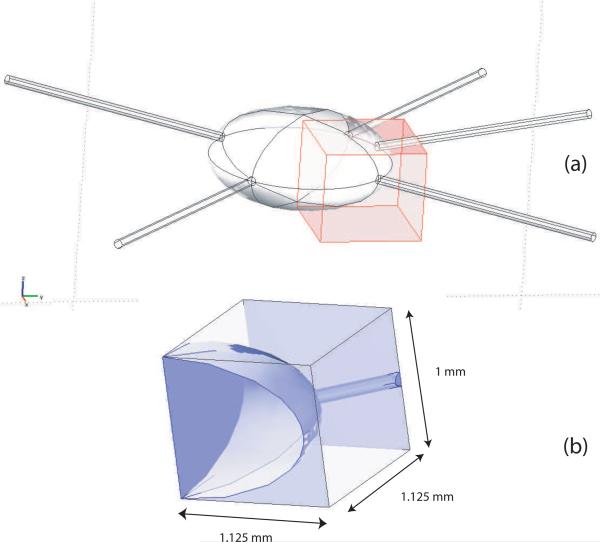
Consider the region of the model at the voxel highlighted in Figure 8, corresponding to data sampled with ΔX = ΔY = 1.125 mm and ΔZ = 1 mm. The average ΔB_z values observed within this voxel (only 40% of which consists of bidomain tissue) were 39 and 23 × 10⁻¹² T for the horizontal and vertical current application patterns, respectively. These values assume all the bidomain tissues within the voxel are active. If we now assume that 30% of the neural tissue within the voxel is active (Falk et al. 1993), we may say there is an effective partial volume V_f of 0.3. Further, if we also choose $(f_A-f_R)G_M^1{T}_C=0.16$ (corresponding to the intermediate spike rate factor in section 3.5), there will be an integrated phase change within this voxel equal to 32 × 10⁻¹² × 0.3 × 0.16 = 1.5 × 10⁻¹² T (for horizontally applied current), or 23 × 10⁻¹² × 0.3 × 0.16 = 1.1 × 10⁻¹² T (for vertically applied current). Examining the noise levels predicted at 17.6 T shown in Table 2, the SNR in this test voxel is then approximately 1.5 × 10⁻¹²/8.6 × 10⁻¹² = 0.17 or 1.1 × 10⁻¹²/8.6 × 10⁻¹² = 0.13 for horizontal and vertically applied currents respectively at this resolution for the case of one excitation (NEX = 1). Therefore, at this input current level, an SNR of 1 for this voxel would be obtained using 33 (horizontal) or 61 (vertical) excitations respectively.

Figure 8.

(a) Overlay of coarse voxel on finite element model overlapping both bath and simulated AAG. (b) Magnified view of voxel showing AAG and voxel dimensions. Voxel dimensions are the same as those shown in the data of Figure 6 (d).

4.5 Effects of axonal current flow

While we have considered the effects of interactions between externally applied current and membrane conductance changes, we have not considered the effect of axonal current flow on phase signals. We can estimate its influence by referring to the calculations in Cassarà et al. (2008). Their simulations predicted maximum phase changes of the order of 20 μ rad (1.1 × 10^{−3 o}) would be observed in a 1.2 mm side length voxel as a direct result of neuronal current flow in a single layer of dendrite-like neurons. If this phase were to be directly translated to our imaging parameters, (a current injection time of 18 ms) this corresponds to a change of 2.2 × 10⁻¹² T. This change is very close to that observed in the similarly sized voxel considered in section 4.4 above. However, we note that in an extension of their model involving several layers of different neuron types, much smaller maximum phase changes (ca. 7 μ rad) were found, because these layers were randomly rotated with respect to each other and current flows within voxels interfered destructively. We believe the unique strength of our imaging method is that as it is not possible for membrane conductance changes to cancel out, it is not subject to loss of signal because of neuronal orientation. In summary, it will be the case that axonal current flow will be a source of either increases or decreases in the signal expected from membrane conductance changes alone. More detailed modeling is necessary to determine the magnitude of these deviations.

4.6 Data collection and denoising strategies

The estimations derived above were calculated assuming standard MREIT techniques, and calculations assume that the only strategy available to reduce noise levels is to increase numbers of excitations. However, there are many alternative strategies to increase signal and decrease noise that may be implemented, for example by using modified pulse sequences or RF coils. Examples of pulse sequence variations may include multiple echo and ICNE (injection current nonlinear encoding) pulse sequences (Park et al. 2007). The basic approach of the ICNE method is to increase the current injection time within one TR to accumulate more phase change. Phantom experiments have shown that SNR levels may be increased by a factor of around 1.7 by use of this technique. We may also take advantage of the balanced SSFP (steady state free precession) pulse sequence, which is highly sensitive to small off-resonance phase changes (Minhas et al. 2009). Special care must be given to the main field inhomogeneity in this case. High-sensitivity RF coils are always beneficial in MREIT and we should emphasize the importance of an optimal design and tuning of RF coils. If quadrature coils are used instead of linear coils, we may also improve SNR up to a factor of $\sqrt{2}$ (Morris 1986). Use of parallel systems will be beneficial.

Apart from improving data collection techniques, we may also apply several denoising methods in post-processing. We may adopt the PDE-based denoising method by Lee et al. (2005) to improve B_z data SNR. Recent investigations also suggest that a ramp-preserving denoising technique is desirable for B_z signals (Lee et al. 2009), and can result in improvements in SNR by around a factor of 20 in synthetic data with added Gaussian noise, with comparable improvements demonstrated in both phantom objects and post mortem canine brain. General denoising techniques may not achieve all possible improvements, and we will need to thoroughly analyze the nature of B_z changes related to conductivity perturbations to determine an optimal denoising method for this application.

Working at high fields with small samples we also need to consider factors that have negligible effects at lower B₀ levels, such as movement of the sample caused by Lorentz forces. We have found that the presence of copper current wiring and electrodes in the magnet bore contributes to overall noise levels, an effect which can be greatly reduced by using carbon fiber wires and electrodes (Sadleir et al 2005b, Woo and Seo 2008). The port design shown in Figure 1 (b) will cause larger current density peaks than larger ports delivering the same total current, and redesign of sample vessels should also allow application of larger imaging currents before they evoke activity, therefore improving SNR.

Rather than using 750 MHz (17.6 T), an alternative is to use a higher field where noise levels are smaller (e.g. 900 MHz or 21.1 T). At high fields, signal to noise levels depend approximately linearly on main magnetic field strengths (Mansfield and Morris 1982). Therefore, increasing to this higher field magnet would result in an improvement of SNR by a factor around 1.2. Even though there exist other technical difficulties with higher field magnets, their advantages will be of use in providing proof of concept.

4.7 Increasing activity thresholds

We may chemically inactivate the cell so that it is insensible to nominally suprathreshold imaging currents. On repeating the same experiment with the inactivated cell, we may compare changes in collected B_z data with activity caused by higher independent stimulus levels. Alternatively, ramping the current may reduce tissue sensitivity to imaging currents and allow imaging and activity to continue independently.

4.8 An alternative experimental paradigm

In order to provide an initial proof of concept, we may use a relatively large imaging current enough to produce B_z signals above the noise floor. This may have the effect of evoking neural activity, but would allow us to confirm that changes in membrane conductance can be related to B_z changes. Further, it is quite likely that while our calculated subthreshold imaging currents may not induce classical stimulation, they may have an effect on activity frequency (Terzuolo and Bullock 1956, Purpura and McMurtry 1965). In MREIT we use pulse-type imaging currents with no dc component. We need further studies to thoroughly investigate effects of MREIT imaging currents on the neuron excitability. We may consider a slightly different experimental setting, therefore, where this or another type of applied current is used to study neuromodulation.

4.9 Differences between impedance-based and current-detection-based methods

In our analysis, we have assumed that activity is due to axonal spikes in unmyelinated tissue using a basic model of neural tissue. Naturally, if we extend our analysis to more complex model of neural tissue we may also examine the effect of more complex structures, including dendritic currents, on signal levels. This does not affect the basic factors that determine the signal magnitudes to be expected using this contrast mechanism. The key advantage of this method compared to other methods advanced so far is that the contrast parameter, the membrane conductance, can only assume positive values. Therefore, there is no susceptibility of this mechanism to be affected by factors that may cancel the contrast, such as dipole orientation, polarity, and the presence of nearby activity. We expect that a model of gray matter will produce similar dependencies to the model we describe here and that the signal obtained will likely be directly related to the density of cell activity inside each voxel.

4.10 Implications for imaging larger tissue volumes and in vivo imaging

Imaging neural tissue of an entire organism at 17.6 T is impractical. We intend to develop our method initially as a method of studying activity in small preparations such as the AAG, and subsequently for imaging in entire organisms and ultimately in vivo at fields of ca. 3T. Because the contrast mechanism of this method is positive, it should be possible to ultimately extend its use to lower fields and higher intrinsic noise levels by employing multiple excitations, signal denoising, careful design of imaging current patterns to accommodate sample geometry (for example, to increase current delivered through the skull), and pulse sequences. Signal denoising strategies will be particularly important as we anticipate that noise floors in vivo could be significantly higher than expected from simulations or in vitro work. Hemodynamic changes related to activity may also affect B_z data in intact specimens (Luo et al. 2009).

The relatively robust contrast mechanism of this method is potentially of great use in neurophysiological studies. Its use could lead to further developments in the design of neural prostheses and therapy as well as being a method used to investigate normal neural function. The analyses and preliminary results described in this paper will enable us to carefully design experimental protocols to investigate the feasibility of this new functional neural imaging method.