ESTIMATING MARGINAL RETURNS TO MEDICAL CARE: EVIDENCE FROM AT-RISK NEWBORNS

Abstract

A key policy question is whether the benefits of additional medical expenditures exceed their costs. We propose a new approach for estimating marginal returns to medical spending based on variation in medical inputs generated by diagnostic thresholds. Specifically, we combine regression discontinuity estimates that compare health outcomes and medical treatment provision for newborns on either side of the very low birth weight threshold at 1500 grams. First, using data on the census of US births in available years from 1983–2002, we find that newborns with birth weights just below 1500 grams have lower one-year mortality rates than do newborns with birth weights just above this cutoff, even though mortality risk tends to decrease with birth weight. One-year mortality falls by approximately one percentage point as birth weight crosses 1500 grams from above, which is large relative to mean infant mortality of 5.5% just above 1500 grams. Second, using hospital discharge records for births in five states in available years from 1991–2006, we find that newborns with birth weights just below 1500 grams have discontinuously higher charges and frequencies of specific medical inputs. Hospital costs increase by approximately $4,000 as birth weight crosses 1500 grams from above, relative to mean hospital costs of $40,000 just above 1500 grams. Under an assumption that observed medical spending fully captures the impact of the “very low birth weight” designation on mortality, our estimates suggest that the cost of saving a statistical life of a newborn with birth weight near 1500 grams is on the order of $550,000 in 2006 dollars.

I. Introduction

Medical expenditures in the United States are high and increasing. Do the benefits of additional medical expenditures exceed their costs? The tendency for patients in worse health to receive more medical inputs complicates empirical estimation of the returns to medical expenditures. Observational studies have used cross-sectional, time-series, and panel data techniques to attempt to identify patients who are similar in terms of underlying health status but who for some reason receive different levels of medical spending. The results of such studies are mixed. On one hand, time-series and panel data studies that compare increases in spending and improvements in health outcomes over time have argued that increases in costs have been less than the value of the associated benefits, at least for some technologies.¹ On the other hand, cross-sectional studies that compare “high-spending” and “low-spending” geographic areas tend to find large differences in spending yet remarkably similar health outcomes.²

The lack of consensus may not be surprising as these studies have measured returns on many different margins of care. The return to a dollar of medical spending likely differs across medical technologies and across patient populations, and in any given context the return to the first dollar of medical spending likely differs from the return to the last dollar of spending. The time-series studies often estimate returns to large changes in treatments that occur over long periods of time. The cross-sectional studies, on the other hand, estimate returns to additional, incremental spending that occurs in some areas but not others. While estimates of returns to large changes in medical spending are useful summaries of changes over time, estimates of marginal returns are needed to inform policy decisions over whether to increase or decrease the level of care in a given context.

The main innovation of this paper is a novel research design which, under explicit assumptions, permits direct estimation of the marginal returns to medical care. Implementation of our research design requires a setting with an observable, continuous measure of health risk and a diagnostic threshold (based on this risk variable) that generates a discontinuous probability of receiving additional treatment.³ In such settings, we can use a regression discontinuity framework: as long as other factors are smooth across the threshold (an assumption we investigate in several empirical tests), individuals within a small bandwidth on either side of the threshold should differ only in their probability of receiving additional health-related inputs and not in their underlying health. This research design allows us to estimate marginal returns to medical care for patients near such thresholds in the following sense: conditional on estimating that, on average, patients on one side of the threshold incur additional medical costs, we can estimate the associated benefits by examining average differences in health outcomes across the threshold. Under an assumption that observed medical spending fully captures the impact of a “higher risk” designation on mortality, combining these cost and benefit estimates allows us to calculate the return to this increment of additional spending, or “average marginal returns.”

We apply our research design to study “at risk” newborns, a population that is of interest for several reasons. First, the welfare implications of small reductions in mortality for newborns can be magnified in terms of the total number of years of life saved. Second, technologies for treating at-risk newborns have expanded tremendously in recent years, at very high cost. Third, although existing estimates suggest that the benefits associated with large changes in spending on at risk newborns over time have been greater than their costs (Cutler and Meara, 2000), there is a dearth of evidence on the returns to incremental spending in this context. Fourth, studying newborns allows us to focus on a large portion of the health care system, as child birth is one of the most common reasons for hospital admission in the US. This patient population also provides samples large enough to detect effects of additional treatment on infant mortality.

We focus on the “very low birth weight” (VLBW) classification at 1500 grams (just under 3 pounds, 5 ounces) - a designation frequently referenced in the medical literature. We also consider other classifications based on birth weight and alternative measures of newborn health. From an empirical perspective, birth weight-based thresholds provide an attractive basis for a regression discontinuity design for several reasons. First, they are unlikely to represent breaks in underlying health risk. A 1985 Institute of Medicine report, for example, notes: “…designation of very low birth weight infants as those weighing 1,500 grams or less reflected convention rather than biologic criteria.” Second, it is generally agreed that birth weight cannot be predicted in advance of delivery with the accuracy needed to change (via birth timing) the classification of a newborn from being just above 1500 grams to being just below 1500 grams. Thus, although we empirically investigate our assumption that the position of a newborn just above 1500 grams relative to just below 1500 grams is “as good as random,” the medical literature also suggests this assumption is reasonable.

To preview our main results, using data on the census of US births in available years from 1983–2002, we find that one-year mortality decreases by approximately one percentage point as birth weight crosses the VLBW threshold from above, which is large relative to mean one-year mortality of 5.5% just above 1500 grams. This sharply contrasts with the overall increase in mortality as birth weight falls, and to the extent that lighter newborns are less healthy in unobservable ways, the mortality change we observe is all the more striking. Second, using hospital discharge records for births in five states in available years from 1991–2006, we estimate a $4,000 increase in hospital costs for infants just below the 1500 gram threshold, relative to mean hospital costs of $40,000 just above 1500 grams. As we discuss in Section VIII, this estimated cost difference may not capture all of the relevant mortality-reducing inputs, but it is our best available summary measure of health inputs. Under an assumption that hospital costs fully capture the impact of the “very low birth weight” designation on mortality, our estimates suggest that the cost of saving a statistical life for newborns near 1500 grams is on the order of $550,000 - well below most value of life estimates for this group of newborns.

The remainder of the paper is organized as follows. Section II discusses the available evidence on the costs and benefits of medical care for at-risk newborns and gives a brief background on the at-risk newborn classifications we study. Section III describes our data and analysis sample, and Section IV outlines our empirical framework and bandwidth selection. Section V presents our main results, and Section VI discusses several robustness and specification checks. Section VII examines variation in our estimated treatment effects across hospital types. In Section VIII we combine our main estimates to calculate two-sample estimates of marginal returns, and Section IX concludes.

II. Background

A. Costs and benefits of medical care for at-risk newborns

Medical treatments for at-risk newborns have been expanding tremendously in recent years, at high cost. For example, in 2005 the US Agency for Healthcare Research and Quality estimated that the two most expensive hospital diagnoses (regardless of age) were “infant respiratory distress syndrome” and “premature birth and low birth weight.”⁴ Russell et al. (2007) estimated that in the US in 2001, preterm and low-birth weight diagnoses accounted for 8% of newborn admissions, but 47% of costs for all infant hospitalizations (at $15,100 on average). Despite their high and highly-concentrated costs, use of new neonatal technologies has continued to expand.⁵

These high costs motivate the question of what these medical advances have been “worth” in terms of improved health outcomes. Anspach (1993) and others discuss the paucity of randomized controlled trials which measure the effectiveness of neonatal intensive care. In the absence of such evidence, some have questioned the effectiveness of these increasingly intensive treatment patterns (Enthoven, 1980; Grumbach, 2002; Goodman et al., 2002). On the other hand, Cutler and Meara (2000) examine time-series variation in birth weight-specific treatment costs and mortality outcomes and argue that medical advances for newborns have had large returns.⁶

B. “At risk” newborn classifications

Birth weight and gestational age are the two most common metrics of newborn health, and continuous measures of these variables are routinely collapsed into binary classifications. We focus on the “very low birth weight” (VLBW) classification at 1500 grams (just under 3 pounds, 5 ounces). We also examine other birth weight classifications - including the “extremely low birth weight” (ELBW) classification at 1000 grams (just over 2 pounds, 3 ounces) and the “low birth weight” (LBW) classification at 2500 grams (just over 5 pounds, 8 ounces) - as well as gestational age-based measures such as the “prematurity” classification at 37 weeks, where gestation length is usually based on the number of weeks since the mother’s last menstrual period. Below, we briefly describe the evolution of these classifications.⁷

Physicians had begun to recognize and assess the relationships among inadequate growth (low birth weight), shortened gestation (prematurity), and mortality by the early 1900s. The 2500 gram low birth weight classification, for example, has existed since at least 1930, when a Finnish pediatrician advocated 2500 grams as the birth weight below which infants were at high risk of adverse neonatal outcomes. Over time, interest increased in the fate of the smallest infants, and “very low birth weight” infants were conventionally defined as those born weighing less than 1500 grams (United States Institute of Medicine, 1985).⁸

Key to our empirical strategy is that these cutoffs appear to truly reflect convention rather than strict biologic criteria. For example, the 1985 IOM report notes:

“Birth weight is a continuous variable and the limit at 2,500 grams does not represent a biologic category, but simply a point on a continuous curve. The infant born at 2,499 grams does not differ significantly from one born at 2,501 grams on the basis of birth weight alone…As with the 2,500 gram limit, designation of very low birth weight infants as those weighing 1,500 grams or less reflected convention rather than biologic criteria.”

Gestational age classifications, such as the “prematurity” classification at 37 gestational weeks, have also been emphasized. While gestational age is a natural consideration when determining treatment for newborns with low birth weights, applying our research design to gestational age introduces some additional complications. Gestational age is known to women in advance of giving birth, and women can choose to time their birth (for example, through an induced vaginal birth or through a C-section) based on gestational age. Thus, we would expect that mothers who give birth prior to 37 gestational weeks may be different from mothers who give birth after 37 gestational weeks on the basis of factors other than gestational age. It is thought that birth weight, on the other hand, cannot be predicted in advance of birth with the accuracy needed to change (via birth timing) the classification of a newborn from being just above 1500 grams to being just below 1500 grams; this assertion has been confirmed from conversations with physicians,⁹ as well from studies such as Pressman et al. (2000).

Of course, birth weight and gestational age are not the only factors used to assess newborn health.¹⁰ This implies that we should expect our cutoffs of interest to be “fuzzy” rather than “sharp” discontinuities (Trochim, 1984): that is, we do not expect the probability of a given treatment to fall from 1 to 0 as one moves from 1499 grams to 1501 grams, but rather expect a change in the likelihood of treatment for newborns classified into a given risk category.

Discussions with physicians suggest that these potential discontinuities are well-known, salient cutoffs below which newborns may be at increased consideration for receiving additional treatments. From an empirical perspective, the fact that we will observe a discontinuity in treatment provision around 1500 grams suggests that hospitals or physicians do use these cutoffs to determine treatment either through hospital protocols or as rules of thumb. As an example of a relevant hospital protocol, the 1500 gram threshold is commonly cited as a point below which diagnostic ultrasounds should be used.¹¹ Such classifications could also affect treatment provision through use as more informal “rules of thumb” by physicians.¹² As we discuss below, it is likely that VLBW infants receive a bundle of mortality-reducing health inputs, not all of which we can observe.¹³ Moreover, because several procedures are given simultaneously, our research design does not allow us to measure marginal returns to specific procedures. This motivates our focus on summary measures - such as charges and length of stay - that are our best available measures of differences in health inputs.

Differential reimbursement by birth weight is another potential source of the observed discontinuities in summary spending measures. For example, some Current Procedural Terminology (CPT) billing codes and ICD-9 diagnosis codes are categorized by birth weight (ICD-9 codes V21.30-V21.35 denote birth weights of 0–500, 500–999, 1000–1499, 1500–1999–1499, 1500–2000–2500, etc.). If prices differ across our threshold of interest, then any discontinuous jump in charges could in part be due to mechanical changes in the “prices” of services rather than changes in the “quantities” of the services performed. In practice, we argue that a substantial portion of our observed jump in charges is a “quantity” effect rather than a “price” effect, for three reasons. First, the limited qualitative evidence available to us suggests that prices do not vary discontinuously across the VLBW threshold for many of the births in our data.¹⁴ Second, we empirically observe a discontinuity in charges within California, a state where the Medicaid reimbursement scheme does not explicitly utilize birth weight during the time period of our study. Third, we find evidence of discontinuities in a summary quantity measure - length of stay - as well as quantities of specific procedures. These three reasons suggest that a substantial portion of our observed jump in charges is a “quantity” effect rather than a “price” effect. Furthermore, if the pricing effect were purely mechanical, we should not observe the empirical discontinuity in mortality.

III. Data

A. Data description

Our empirical analysis requires data with information on birth weight and some welfare-relevant outcome, such as medical care expenditures or health outcomes. Our primary analysis uses three data sets: first, the National Center for Health Statistics (NCHS) birth cohort linked birth/infant death files; second, a longitudinal research database of linked birth record-death certificate-hospital discharge data from California; and third, hospital discharge data from several states in the Healthcare Cost and Utilization Project (HCUP) state inpatient databases.

The NCHS birth cohort linked birth/infant death files, hereafter the “nationwide data,” include data for a complete census of births occurring each year in the US, for the years 1983–1991 and 1995–2002 - approximately 66 million births.¹⁵ The data include information reported on birth certificates linked to information reported on death certificates for infants who die within one year of birth. The birth certificate data offers a rich set of covariates (for example, mother’s age and education), and the death certificate data includes a cause of death code. Beginning in 1989, these data include some treatment variables - namely, indicators for use of a ventilator for less than or (separately) greater than thirty minutes after birth.

Our other two data sources offer treatment variables beyond ventilator use. The California research database is the same data set used in Almond and Doyle (2008). These data were created by the California Office of Statewide Health Planning and Development, and include all live births in California from 1991–2002 - approximately 6 million births. The data include hospital discharge records linked to birth and death certificates for infants who die within one year of birth. The hospital discharge data include diagnoses, course of treatment, length of hospital stay, and charges incurred during the hospitalization. The data are longitudinal in nature and track hospital readmissions for up to one year from birth as long as the infants are admitted to a California hospital. This longitudinal aspect of the data allows us to examine charges and length of stay even if the newborn is transferred to another hospital.¹⁶

The HCUP state inpatient databases allow us to analyze the universe of hospital discharge abstracts in four other states that include the birth weight variable necessary for our analysis.¹⁷ Specifically, we use HCUP data from Arizona for 2001–2006, New Jersey for 1995–2006, Maryland for 1995–2006, and New York for 1995–2000 - approximately 10.5 million births (see Table A1 in the online appendix for the number of births by state and year within our pilot bandwidth of 3 ounces of the VLBW cutoff). The HCUP data include variables similar to those available in the California discharge data, but unlike the California data are not linked to mortality records nor to hospital records for readmissions or transfers. Although we cannot link the HCUP data with mortality records directly, we can examine mortality outcomes for these newborns using a sub-sample of our nationwide data, as our nationwide data and the HCUP discharge data relate to the same births.¹⁸ In much of our analysis, we pool the California and HCUP data to create a “five-state sample.”

Both the California and HCUP data report hospital charges. These charges are used in negotiations for reimbursement and are typically inflated well over costs. We consider these charges as our best available summary of the difference in treatment that the VLBW classification affords. When calculating the returns to medical spending, we adjust hospital charges by a cost-to-charge ratio.¹⁹ The main text focuses on charges rather than costs because charges are available for all years of data, while cost-to-charge ratios are available for only a subset of years and are known to introduce noise into the results.

B. Analysis sample

Sample selection issues are minimal. In our main specifications, we pool data from all available years, although in the online appendix we separately examine results across time periods. For the main results, we limit the sample to those observations with non-missing, non-imputed birth weight information.²⁰ Fortunately, given the demands of our empirical approach, these data provide relatively large samples: over 200,000 newborns fall within our pilot bandwidth of 3 ounces around the 1500 gram threshold in the nationwide data, and we have approximately 30,000 births in the same interval when we consider the five-state sample. We discuss bandwidth selection below.

IV. Empirical framework and estimation

A. Empirical framework

To estimate the size of the discontinuity in outcomes and treatment, we follow standard methods for regression discontinuity analysis (as in, for example, Imbens and Lemieux (2008) and Lee and Lemieux (2009)).

First, we restrict the data to a small window around our threshold (85 grams) and estimate a local-linear regression. We describe the selection of this bandwidth in the next subsection. We use a triangle kernel so that the weight on each observation decays with the distance from the threshold, and we report asymptotic standard errors (Cheng et al., 1997; Porter, 2003).²¹

Second, within our bandwidth, we estimate the following model for infant i weighing g grams in year t:

$$Y_i={\alpha }_0+{\alpha }_1{\mathit{VLBW}}_i+{\alpha }_2{\mathit{VLBW}}_i\ast (g_i-1500)+{\alpha }_3(1-{\mathit{VLBW}}_i)\ast (g_i-1500)+{\alpha }_t+{\alpha }_s+\delta X_i^{\prime }+{\epsilon }_i$$ (1)

where Y is an outcome or treatment measure such as one-year mortality or costs, and V LBW is an indicator that the newborn was classified as very low birth weight (that is, strictly less than 1500 grams). We include separate gram trend terms above and below the cutoff, parameterized so that α₂ = α₃ if the trend is the same above and below the cutoff. In some specifications, we include indicators for each year of birth t, indicators for each state of birth s, and newborn characteristics, $X_i^{\prime }$. The newborn characteristics that are available for all of the years in the nationwide data include an indicator that the mother was born outside the state where the infant was born, as well as indicators for mother’s age, education, father’s age, the newborn’s sex, gestational age, race, and plurality.

We estimate this model by OLS, and we report two sets of standard errors.²² First, we report heteroskedastic-robust standard errors. Second, to address potential concerns about discreteness in birth weight, we perform the standard error correction suggested by Card and Lee (2008). In our application, this correction amounts to clustering at the gram-level. Estimation of our outcome and treatment results with quadratic (or higher order) rather than linear trends in birth weight gives similar results (see online appendix table A4).

In Section V, we report outcome and treatment estimates separately. Our reduced form estimate of the direct impact of our V LBW indicator on mortality is itself interesting and policy relevant, as this estimate includes the effects of all relevant inputs.

Under an additional assumption, we can combine our outcome and treatment estimates into two-sample estimates of the return to an increment of additional spending in terms of health benefits. In the language of instrumental variables, the discontinuity in mortality is the reduced form estimate and the discontinuity in health inputs is the first stage estimate.²³ In this framework, the instrument is the V LBW indicator. In order for our V LBW indicator to be a valid instrument, the two usual instrumental variables conditions must hold. First, there must exist a first stage relationship between our V LBW indicator and our measure of health inputs; note that this relationship will be conditional on our running variable (birth weight). Second, the exclusion restriction requires that the only mechanism through which the instrument V LBW affects the mortality outcome, conditional on birth weight falling within the bandwidth, is through its effect on our measure of health inputs. If our summary measures allow us to observe and capture all relevant health inputs, then we can argue for the validity of this exclusion restriction. However, for any given measure of health inputs that we observe, it is likely that there exists some additional health-related input that we do not observe (see Section IIB). It is unclear how important such unobserved inputs are in practice, but to the extent they are important, a violation of the exclusion restriction would occur.

We present two-sample estimates in Section VIII, using our most policy relevant available summary measure of treatment (hospital costs) as our first stage variable, but we stress that the interpretation of these estimates relies on an assumption that hospital charges capture all relevant medical inputs. We also attempt to gauge the magnitude of unobserved inputs by testing for effects on short-run mortality. To the extent that medical inputs are much more important relative to parental or other unobserved inputs in the very short run after birth (say, within twenty-four hours of birth), we can test for impacts on short run mortality measures and be somewhat assured that unobserved parental or other inputs are not likely to affect these estimates. As we will discuss in Section V, we do indeed find effects on short run mortality measures.

B. Bandwidth selection

Our pilot bandwidth includes newborns with birth weights within 3 ounces (85 grams) of 1500 grams, or from 1415 grams to 1585 grams. We chose this bandwidth by a cross-validation procedure where the relationships between the main outcomes of interest and birth weight were estimated with local linear regressions and compared to a 4-th order polynomial model. These models were estimated separately above and below the 1500 gram threshold. The bandwidth that minimized the sum of squared errors between these two estimates between 1200 and 1800 grams tended to be between 60 and 70 grams for the mortality outcomes. For the treatment measures, the bandwidth tended to be closer to 40 grams. Given that we are estimating the relationship at a boundary, a larger bandwidth is generally warranted. We chose to use a pilot bandwidth of 85 grams - 3 ounces²⁴ - for the main results. This larger bandwidth incorporates more information that can improve precision, but of course including births further from the threshold departs from the assumption that newborns are nearly identical on either side of the cutoff. That said, our local linear estimates allow the weight on observations to decay with the distance from the threshold. In addition, the results are qualitatively similar across a wide range of bandwidths (see online appendix Table A3). To give a clearer sense of how our data look graphically, our figures report means for a slightly wider bandwidth - namely, the 5 ounces above and below the threshold.

V. Results

A. Frequency of births by birth weight

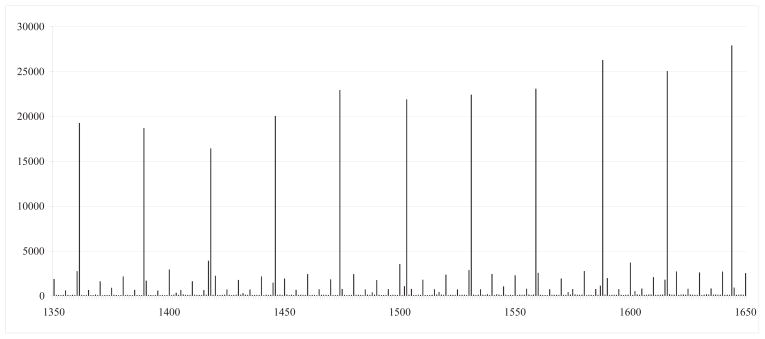
Figure I reports a histogram of births between 1350 grams and 1650 grams in the nationwide sample, which has several notable characteristics.²⁵ First, there are pronounced reporting heaps at the gram equivalents of ounce intervals. Although there are also reporting heaps at “round” gram numbers (such as multiples of one hundred), these heaps are much smaller than those observed at gram equivalents of ounce intervals. Discussions with physicians suggest that birth weight is frequently measured in ounces, although typically also measured in grams as well for purposes of billing and treatment recommendations. Given the nature of the variation inherent in the reporting of our birth weight variable, our graphical results will focus on data which has been collapsed into one-ounce bins.²⁶

Figure I. Frequency of births by gram: Population of US births between 1350–1650 grams.

Notes: NCHS birth cohort linked birth/infant death files, 1983–1991 and 1995–2003, as described in the text.

Second, we do not observe irregular reporting heaps around our 1500 gram threshold of interest, consistent with women being unable to predict birth weight in advance of birth with the accuracy necessary to move their newborn (via birth timing) from just above 1500 grams to just below 1500 grams. The lack of heaping also suggests that physicians or hospitals do not manipulate reported birth weight so that, for example, more newborns fall below the 1500g cutoff and justify higher reimbursements. In particular, the frequency of births at 1500 grams is very similar to the frequency of births at 1400 grams and at 1600 grams, and the ounce markers surrounding 1500 grams have similar frequencies to other ounce markers.

More formally, McCrary (2008) suggests a direct test for possible manipulation of the running variable. We implement his test by collapsing our nationwide data to the gram level - keeping a count of the number of newborns classified at each gram - and then regressing that count as the outcome variable in the same framework as our regression discontinuity estimates. Using this test, we find no evidence of manipulation of the running variable around the VLBW threshold.²⁷

Fetal deaths are not included in the birth records data, and hence one possible source of sample selection is the possibility that very sick infants are discontinuously reported more frequently as fetal deaths across our cutoff of interest (and are thus excluded from our sample). We test for this type of sample selection directly using a McCrary test with data on fetal death reports from the National Center for Health Statistics (NCHS) perinatal mortality data for 1985 to 2002. We would be concerned if we observed a positive jump in fetal deaths for VLBW infants, but in fact the estimated coefficient is negative and not statistically significant.²⁸ Graphical analysis of the data is consistent with this formal test.

More complicated manipulations of birth weight could in theory be consistent with Figure I. For example, if doctors re-label unobservably sicker newborns weighing just above 1500 grams as being below 1500 grams (to receive additional treatments, for example) and symmetrically “switched” the same number of other newborns weighing just below 1500 grams to be labeled as being above 1500 grams, this could be consistent with the smooth distribution in Figure I. This seems unlikely, particularly given that we will later show that other covariates (such as gestational age) are smooth across our 1500 gram cutoff - implying that doctors would need to not only “symmetrically switch” newborns but symmetrically switch newborns who are identical on all of the covariates we observe. We hold that the assumption that such switching does not occur is plausible.²⁹

B. Health outcomes

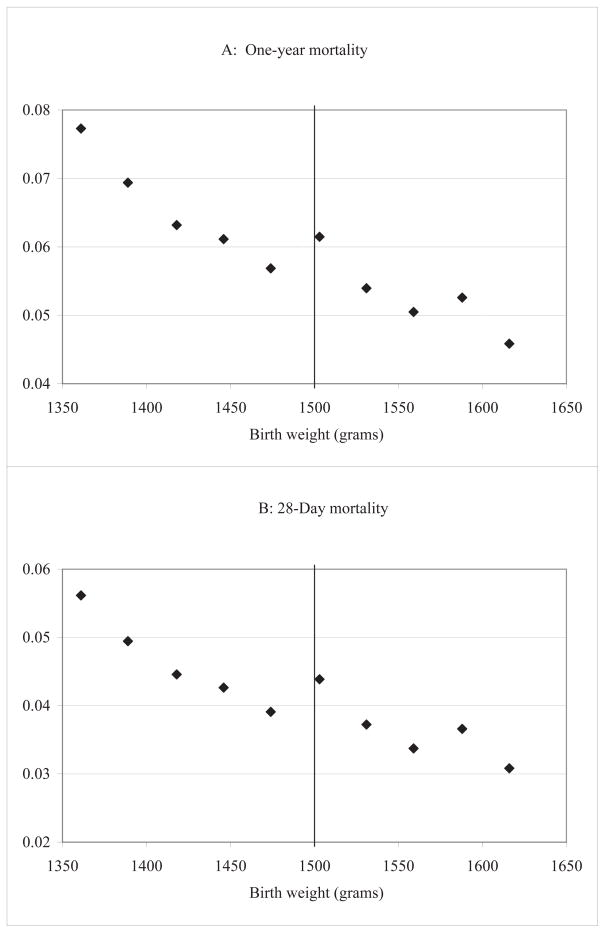
Figure II reports mean mortality for all infants in one-ounce bins close to the VLBW threshold. Note that the one-year mortality rate is relatively high for this at-risk population: close to 6%. The figure shows that even within our relatively small bandwidth, there is a general reduction in mortality as birth weight increases, reflecting the health benefits associated with higher birth weight. The increase in mortality observed just above 1500 grams appears to be a level shift, with the slope slightly less steep below the threshold.³⁰ The mean mortality rate in the ounce bin just above the threshold is 6.15%, which is 0.46 percentage points larger than mean mortality just below the threshold of 5.69%. We see a similar .48 percentage point difference for 28-day mortality - between 4.39% above the threshold and 3.91% below the threshold. This suggests that most of the observed gains in 28-day mortality persist to one year.

Figure II. One-year and 28-day mortality around 1500 grams.

Notes: NCHS birth cohort linked birth/infant death files, 1983–1991 and 1995–2003, as described in the text. Points represent gram-equivalents of ounce intervals, with births grouped into one-ounce bins radiating from 1500 grams; the estimates are plotted at the median birth weight in each bin.

Table I reports the main results that account for trends and other covariates. The first reported outcome is one-year mortality, and the local-linear regression estimate is −0.0121. This implies a 22% reduction in mortality compared to a mean mortality rate of 5.53% in the 3 ounces above the threshold (the “untreated” group in this regression discontinuity design). The OLS estimate in the second column mimics the local linear regression but now places equal weight on the observations up to 3 ounces on either side of the threshold. The point estimate is slightly smaller, but still large: −0.0095. The probit model estimate is similar.³¹

Table I.

Infant mortality by very low birth weight status, National data, 1983–2002 (available years)

Dependent variable:	one-year mortality				28-day mortality
Model:	local linear	OLS	OLS	OLS	local linear	OLS	OLS	OLS
Birth weight < 1500g	−0.0121 (0.0023)**	−0.0095 (0.0022)** [0.0048]*	−0.0076 (0.0022)** [0.0040]	−0.0072 (0.0022)** [0.0040]	−0.0107 (0.0019)**	−0.0088 (0.0018)** [0.0038]*	−0.0074 (0.0018)** [0.0031]*	−0.0073 (0.0018)** [0.0031]*
Birth weight < 1500g * Grams from cutoff (100s)		−0.0136 (0.0032)** [0.0062]*	−0.0119 (0.0032)** [0.0024]**	−0.0111 (0.0032)** [0.0018]**		−0.0114 (0.0027)** [0.0055]*	−0.0102 (0.0027)** [0.0027]**	−0.0097 (0.0027)** [0.0022]**
Birth weight >= 1500g * Grams from cutoff (100s)		−0.0224 (0.0029)** [0.0081]**	−0.0196 (0.0029)** [0.0074]**	−0.0184 (0.0029)** [0.0074]*		−0.0199 (0.0024)** [0.0060]**	−0.0179 (0.0024)** [0.0056]**	−0.0172 (0.0024)** [0.0055]**
Year controls		No	Yes	Yes		No	Yes	Yes
Main controls		No	No	Yes		No	No	Yes
Mean of dependent variable above cutoff:	0.0553				0.0383

Dependent variable:	7-day mortality				24-hour mortality
Model:	local linear	OLS	OLS	OLS	local linear	OLS	OLS	OLS
Birth weight < 1500g	−0.0068 (0.0017)**	−0.0060 (0.0016)** [0.0032]	−0.0049 (0.0016)** [0.0027]	−0.0047 (0.0016)** [0.0027]	−0.0068 (0.0017)**	−0.0043 (0.0013)** [0.0023]	−0.0036 (0.0013)** [0.0020]	−0.0035 (0.0013)** [0.0020]
Birth weight < 1500g * Grams from cutoff (100s)		−0.0078 (0.0024)** [0.0047]	−0.0068 (0.0024)** [0.0026]**	−0.0066 (0.0024)** [0.0023]**		−0.0042 (0.0019)* [0.0031]	−0.0036 (0.0019) [0.0018]*	−0.0036 (0.0019) [0.0015]*
Birth weight >= 1500g * Grams from cutoff (100s)		−0.0137 (0.0022)** [0.0049]**	−0.0120 (0.0022)** [0.0046]*	−0.0116 (0.0022)** [0.0046]*		−0.0098 (0.0017)** [0.0036]**	−0.0088 (0.0017)** [0.0034]*	−0.0086 (0.0017)** [0.0034]*
Year controls		No	Yes	Yes		No	Yes	Yes
Main controls		No	No	Yes		No	No	Yes
Mean of dependent variable above cutoff:	0.0301				0.0191
Observations	202071

Notes: Local linear regressions use a bandwidth of 3 ounces (85 grams). OLS models are estimated on a sample within 3 ounces above and below the VLBW threshold. “Main controls” are listed in online appendix Table A5, in addition to indicators for 5-year intervals of mother’s age, 5-year intervals of father’s age, gestational week, state of residence, year, as well as missing-information indicators for the prenatal, birth order, gestational age and mother’s race categories.

^*significant at 5%;

^**significant at 1%.

Local linear models report asymptotic standard errors. OLS models report heteroskedastic-robust standard errors in parentheses and standard errors clustered at the gram level in brackets.

The trend terms reflect the overall downward slope in mortality. The point estimates suggest a steeper slope after the threshold. This trend difference could result from greater treatment levels that extend below the cutoff at a diminishing rate. Our estimate of the discontinuity in models that account for trends will not take treatment of inframarginal VLBW infants into account.

In terms of the covariates, the largest impact on our main coefficient of interest is found when we introduce year indicators, likely because medical treatments, levels of associated survival rates, and trends in survival rates have changed so much over time. The estimated change in mortality around the threshold in the specification with the year indicators decreases to −0.0076. When we include the full set of covariates, the results are largely unchanged.³² To be conservative, in the rest of our analysis, we always report a specification that includes the full set of covariates.

The remaining outcomes in Table I are mortality measures at shorter time intervals. The 28-day mortality coefficient is similar in magnitude to the one-year mortality coefficient, despite a smaller mean mortality rate of 3.83%. Given different mean mortality rates, the estimate implies a 23% reduction in 28-day mortality as compared to a 17% reduction in one-year mortality. As discussed above, the similarity between the one-year and 28-day mortality coefficients implies that any effects of being categorized as very-low birth weight are seen in the first month of life - a time when these infants are largely receiving medical care (as described more below in our length of stay results). Within the first month of life, timing of the mortality gains varies, but the percentage reduction in mortality for VLBW infants relative to the rate above the threshold is consistent with that at 28 days. The 7-day and 24-hour mortality rates are 16% and 19% compared to the mean mortality rate for infants above the threshold. Finally, 1-hour mortality rates (not shown) are also lower for those born just below the threshold.³³

The following two subsections consider the extent to which newborns classified as very low birth weight receive discontinuously more medical treatments relative to newborns just above 1500 grams. While the universe of births in the natality file allows us to consider mortality effects with a large sample, these data do not include summary measures of treatment. As described above, we are able to examine summary measures of treatment in our hospital discharge data from five states (Arizona, California, Maryland, New Jersey, and New York), which appear to have broadly representative mortality outcomes.³⁴ When we replicate the results in Table I limiting our nationwide data to these five states (a sample of nearly 50,000 births), we estimate that mortality falls by 1.1 percentage points (s.e.=0.42) compared to a mean of 5.4% (as reported in online appendix Table A7).

C. Differences in summary measures of treatment

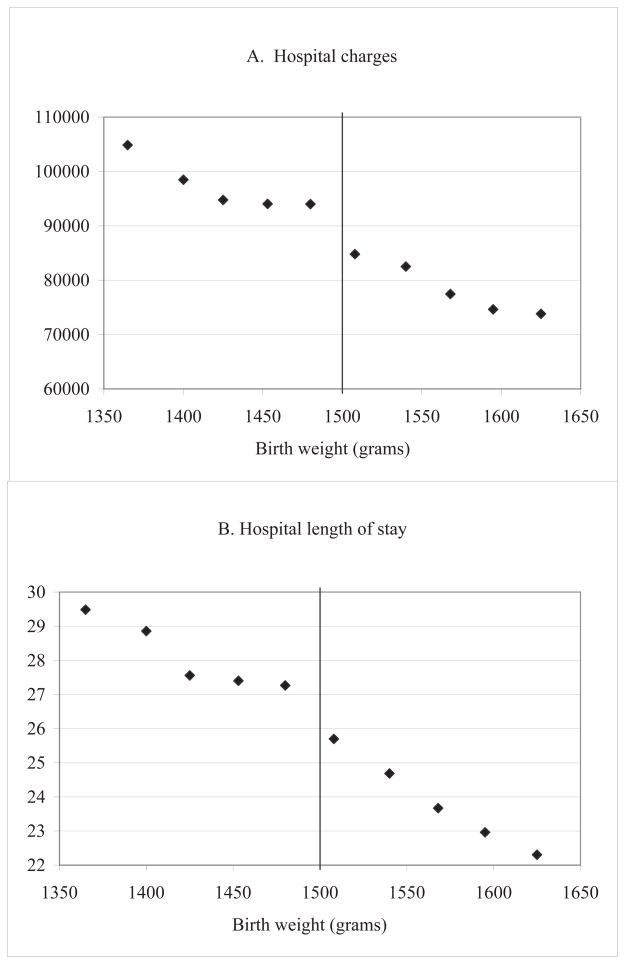
Figure IIIA reports mean hospital charges in one-ounce bins. The measure appears fairly flat at $94,000 for the three ounces prior to the threshold, then falls discontinuously to $85,000 after the threshold and continues on a downward trend, consistent with fewer problems among relatively heavier newborns.³⁵

Figure III. Summary treatment measures around 1500 grams.

Notes: Data are all births in the five-state sample (AZ, CA, MD, NY, and NJ), as described in the text. Charges are in 2006 dollars. Points represent gram-equivalents of ounce intervals, with births grouped into one-ounce bins radiating from 1500 grams; the estimates are plotted at the median birth weight in each bin.

Table 2 reports the regression results.³⁶ The first column reports estimates from the local linear regression, which suggests hospital charges are $9,450 higher just before the threshold -relatively large compared to the mean charges of $82,000 above the threshold. The remaining columns report the OLS results. Without controls, the estimate decreases somewhat to $9,022; with full controls the estimated increase in charges for infants categorized as very low birth weight is largely unchanged ($9,065, s.e.=$2,297). These estimates imply a difference of approximately 11% compared to the charges accrued by infants above the threshold.

Table II.

Summary treatment measures by very low birth weight status, five-state sample, 1991–2006

Dependent variable:	hospital charges				length of stay
Model:	local linear	OLS	OLS	OLS	local linear	OLS	OLS	OLS
Birth weight < 1500g	9450 (2710)**	9,022 (2,448)** [3,538]*	8,205 (2,416)** [3,174]*	9,065 (2,297)** [5,094]	1.97 (0.451)**	1.7768 (0.4165)** [1.0024]	1.7600 (0.4166)** [0.9775]	1.4635 (0.4107)** [0.7928]
Birth weight < 1500g * Grams from cutoff (100s)		−1,728 (3,700) [8,930]	−3,176 (3,647) [7,937]	617.4876 (3,463) [8,447]		−0.1012 (0.6482) [1.9397]	−0.1356 (0.6467) [1.8419]	−0.5766 (0.6366) [1.4858]
Birth weight >= 1500g * Grams from cutoff (100s)		−7,331 (3,018)* [5,022]	−8,684 (2,978)** [4,337]*	−7,951 (2,823)** [7,562]		−2.3130 (0.5245)** [1.4366]	−2.3779 (0.5250)** [1.4117]	−2.5993 (0.5174)** [1.1464]*
Year controls		No	Yes	Yes		No	Yes	Yes
Main controls		No	No	Yes		No	No	Yes
Mean of dependent variable above cutoff:	81566				24.68
Observations	28928				30935

Notes: Local linear regressions use a bandwidth of 3 ounces (85 grams). OLS models are estimated on a sample within 3 ounces above and below the VLBW threshold. Five states include AZ, CA, MD, NY, and NJ (various years). Charges are in 2006 dollars. “Main controls” are listed in online appendix Table A5, as well as indicators for each year. Some observations have missing charges, as described in the text.

^*significant at 5%;

^**significant at 1%.

Local linear models report asymptotic standard errors. OLS models report heteroskedastic-robust standard errors in parentheses and standard errors clustered at the gram level in brackets.

As the large mean charges suggest, this measure is right skewed. The results are similar, however, when we estimate the relationship using median comparisons and when the charges are transformed by the natural logarithm to place less weight on large charge amounts, as shown in online appendix Figure A2 and online appendix Table A6.³⁷

As noted in Section IIB, if prices differ across our threshold of interest, then any discontinuous jump in charges could in part be due to changes in prices rather than changes in quantities. One way to test whether differences in quantities of care are driving the main results is to consider a quantity measure that is consistently measured across hospitals: length of stay in the hospital.³⁸Figure IIIB shows that average length of stay drops from just over 27.3 days immediately prior to the threshold to 25.7 days immediately after the threshold. Corresponding regression results shown in Table 2 show that newborns weighing just under 1500 grams have stay lengths that are between 1.5 and 2 days longer, depending on the model, representing a difference of 6–8% compared to the mean length of stay of 25 days above the threshold. Of course, length of stay and charges are not independent measures, as longer stays accrue higher charges both in terms of room charges and as associated with a greater number of services provided. We further investigate the differences in such service provision measures below.

The first stage variables in the five-state sample could be censored from above if newborns are transferred to another hospital because we do not observe charges and procedures across hospital transfers in the HCUP data. This censoring is only problematic insofar as newborns on either side of the cutoff are more likely to be transferred to another hospital. In the discharge data, we do observe hospital transfers, and we do not find a statistically significant difference in transfers across the threshold. The first stage results are also similar when we use the longitudinal data available from California to consider treatment provided at both the hospital of birth and any care provided in a subsequent hospital following a transfer (online appendix Table A6).

It can also be argued that if treatment is effective at reducing mortality, newborns just below 1500 grams will receive more medical treatment than newborns just above 1500 grams because they are more likely to be alive. Such treatment is unlikely to drive the first stage results, however, as it is provided to only 1% of newborns below the cutoff who appear to have longer lives due to their VLBW status (as in Figure II). Nevertheless, any additional care provided to these newborns is part of the total cost of treatment. Our two-sample instrumental variable estimate of the returns to care discussed in Section VIIIB takes into account these additional costs. To the extent that some of this additional care does not contribute to an improvement in mortality, then our estimate will attribute the reduction in mortality to both care that is effective and care that is ineffective. This will lead to estimated returns that are smaller than they otherwise would be if the ineffective care were excluded.

Taken together, these results show differences in summary treatment measures of approximately 10–15% with some variation in the estimate depending on the treatment measure. In terms of charges, the difference across the discontinuity is approximately $9,000.

D. Mechanisms: Differences in types of care

The hospital discharge data include procedure codes that can be used to investigate the types of care that differ for infants on either side of the very low birth weight threshold. We explore the data for such differences, with a special focus on common perinatal procedures.³⁹ As in the mortality analysis in the smaller five-state sample, however, such differences are difficult to find. Often for the same procedures, statistically significant regression results do not correspond to convincing graphical results, and convincing graphical results do not correspond to convincing regression results. Table III and Figure IV present regression and graphical results for four common types of treatment.

Table III.

Specific treatment measures by very low birth weight status: Five-state sample, 1991–2006

Dependent variable:	Ventilation (various methods)			California: >24 hours in NICU
Model:	local linear	OLS	OLS	local linear	OLS	OLS
Birth weight < 1500g	0.0357 (0.0125)**	0.0380 (0.0115)** [0.0263]	0.0274 (0.0112)* [0.0191]	0.0372 (0.0170)*	0.0282 (0.0157) [0.0214]	0.0265 (0.0156) [0.0204]
Controls		No	Yes		No	Yes
Mean of dependent variable above cutoff:	0.511			0.444
Observations	30935			16528

Dependent variable:	Diagnostic ultrasound of infant			Operations on the heart
Model:	local linear	OLS	OLS	local linear	OLS	OLS
Birth weight < 1500g	0.0196 (0.0109)	0.0166 (0.0101) [0.0128]	0.0297 (0.0095)** [0.0125]*	0.0147 (0.0112)	0.0155 (0.0104) [0.0338]	0.0236 (0.0100)* [0.0146]
Controls		No	Yes		No	Yes
Mean of dependent variable above cutoff:	0.244			0.260
Observations	30935			30935

Notes: Local linear regressions use a bandwidth of 3 ounces (85 grams). OLS models are estimated on a sample within 3 ounces above and below the VLBW threshold, and include linear trends in grams (coefficients not reported). Five states include AZ, CA, MD, NY, and NJ (various years). “Main controls” are listed in online appendix Table A5, as well as indicators for each year. The dependent variable in the NICU models is only available in our California data, and equals one if the infant spent more than 24 hours in a NICU or died in the NICU at less than 24 hours.

^*significant at 5%;

^**significant at 1%.

Local linear models report asymptotic standard errors. OLS models report heteroskedastic-robust standard errors in parentheses and standard errors clustered at the gram level in brackets.

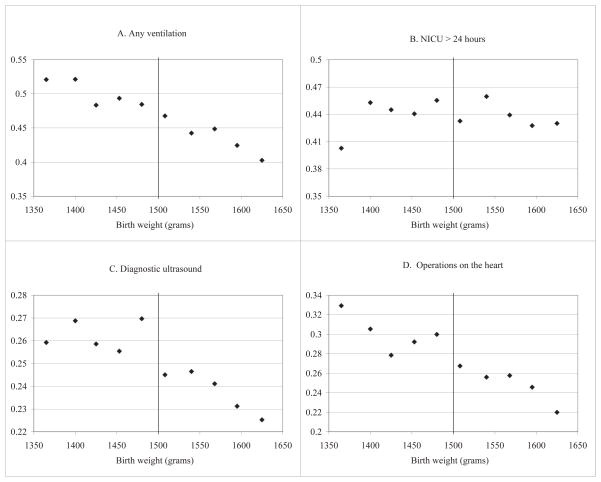
Figure IV. Specific treatment measures around 1500 grams.

Notes: Data are all births in the five-state sample (AZ, CA, MD, NY, and NJ), as described in the text. Points represent gram-equivalents of ounce intervals, with births grouped into one-ounce bins radiating from 1500 grams; the estimates are plotted at the median birth weight in each bin.

One of the most common procedures is some form of ventilation.⁴⁰ Although Table III provides some evidence of a discontinuous increase in ventilation for VLBW infants, Figure IVA does not offer compelling evidence of a meaningful difference.

Another common measure of resource utilization that we observe in our summary treatment measures is admission to a neonatal intensive care unit (NICU). Since care provided in such units is costly, it seems plausible that the threshold could be used to gain entry into such a unit. However, our data reveal little difference on this margin. First, we examine the California data, which includes a variable on whether or not the infant spent at least 24 hours in a NICU or died in the NICU in less than 24 hours. We include newborns born in hospitals that did not have a NICU for comparability to our main results, which also include such newborns. Although Table III suggests a modest increase in this NICU use measure (approximately 3 percentage points as compared to a mean just above the threshold of 44 percentage points), Figure IVB shows little evidence of a discontinuous change. Second, we examine the Maryland HCUP data, which records the number of days in a NICU, but again we find little evidence of a difference at the threshold.⁴¹ Our results are consistent with a study of NICU referrals (Zupancic and Richardson, 1998), in which very low birth weight was not listed among the common reasons for triage to a NICU.

We find some weak evidence of differences for two relatively common procedures: diagnostic ultrasound of the infant and operations on the heart. As noted above, diagnostic ultrasounds are used to check for bleeding or swelling of the brain and some physician manuals cite 1500 grams as a threshold below which diagnostic ultrasounds are suggested. Figure IVC suggests a jump in ultrasounds of roughly 2 percentage points compared to a mean of approximately 25%. Table III suggests estimates of similar size, although only the OLS estimates with controls are statistically significant at conventional levels.

The pattern of the “operations on the heart” indicator in Figure IVD shows an upward pre-trend in the procedures prior to the threshold and what appears to be a discontinuous drop after the threshold.⁴² Table III suggests that the jump is between 1.5 and 2.4 percentage points, or roughly 8% higher than the mean rate for those born above the threshold in this sample, although again only the OLS estimates with controls are statistically significant at conventional levels.

In summary, we examine several possible treatment mechanisms at the discontinuity. We find some weak evidence of differences for operations on the heart and diagnostic ultrasounds, for which we estimate an approximate 10% increase in usage just prior to the VLBW threshold.⁴³ These differences are often not statistically significant, and would be even less so if the standard errors were corrected with a Bonferroni correction to account for search across procedures. We find little evidence of differences in NICU usage or other common procedures such as ventilation. In the end, differences in our summary measures are consistent with medical care driving the mortality results, but we likely lack the statistical power to detect differences in particular procedures in our five-state sample (as evidenced by relatively noisy procedure rates across birth weight bins).

VI. Robustness & specification checks

In this section, we test for evidence of differences in covariates across our VLBW threshold (sub-section A), discuss the sensitivity of our results to alternative bandwidths (sub-section B), examine our mortality results by cause of death (sub-section C), and discuss evidence of discontinuities at alternative birth weight and gestational age thresholds (sub-sections D and E).

A. Testing for evidence of differences in covariates across 1500 grams

As discussed above, it is thought that birth weight cannot be predicted in advance of birth with the accuracy needed to change (via birth timing) the classification of a newborn from being just above 1500 grams to being just below 1500 grams. Moreover, as discussed in Section VA, most forms of strategic recategorization of newborns based on birth weight around 1500 grams should be detectable in our histograms of birth frequencies by gram of birth weight. As such, we expect that the newborns will be similar above and below the threshold in both observable and unobservable characteristics. That said, it is still of interest to directly compare births on either side of our threshold based on observable characteristics.

Online appendix Table A2 compares means of observable characteristics above and below the threshold, controlling for linear trends in grams from the threshold as in the main analysis. The table also includes a summary measure - the predicted mortality rate from a probit model of mortality on all of the controls (specifically, the newborn characteristics $X_i^{\prime }$ described above together with year indicators). Most of the comparisons show similar levels across the threshold, with few that appear to be meaningfully different. Given the large sample size, however, some of the differences are statistically significant.

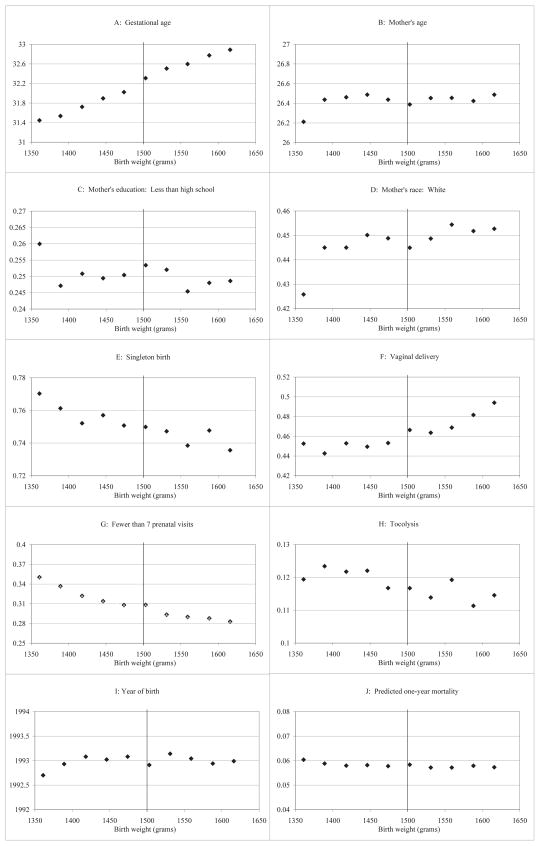
To further consider these differences, Figure V compares covariates of interest in the 5 ounces around the VLBW threshold.⁴⁴ Here, the comparisons appear even more stable across the threshold. In particular, gestational age - which is particularly related to birth weight and shows a statistically significant difference in online appendix Table A2 - is generally smooth through the threshold. Similarly, Figure VJ, which is on the same scale as actual mortality in Figure II, suggests little difference in predicted mortality across the threshold. It thus appears that newborns are nearly identical based on observable variables regardless of whether they weighed just below or just above the VLBW threshold.⁴⁵

Figure V. Covariates around 1500 grams.

Notes: NCHS birth cohort linked birth/infant death files, 1983–1991 and 1995–2003, as described in the text. Points represent gram-equivalents of ounce intervals, with births grouped into one-ounce bins radiating from 1500 grams; the estimates are plotted at the median birth weight in each bin.

B. Bandwidth sensitivity

The local-linear regression results are qualitatively similar for a wide range of bandwidths (see online appendix Table A3). The magnitude of the mortality estimates decreases with the bandwidth, suggesting that our relatively large bandwidth is conservative. When the bandwidth includes only one ounce on either side of the threshold (h = 30 grams), the difference in 1-year mortality is −2.7 percentage points; when h = 150 grams, the estimate decreases to −0.8 percentage points, which is similar to our main estimate at a bandwidth of 85 grams. In fact, we find qualitatively similar results for bandwidths as large as 700 grams. In terms of the treatment measures in the five-state sample, the discontinuity in hospital charges is largest in magnitude for our benchmark bandwidth, although qualitatively similar across the range from h = 30 grams to h = 150 grams.

C. Causes of death

If our mortality effect were driven by so-called “external” causes of death (such as accidents), this would be concerning since it would be difficult to link deaths from those causes to differences in medical inputs. Reassuringly, we find no statistically significant change in external deaths across our cutoffs of interest (see online appendix Table A8).

Examination of our mortality results by cause of death may also be of interest from a policy perspective. When we group causes of death into broad, mutually exclusive categories, we find (see online appendix Table A8) effects of the largest magnitude for perinatal conditions (such as jaundice and respiratory distress syndrome), as well as for nervous system and sense organ disorders - the latter of which is a statistically significant effect at conventional levels. We also examine a few individual causes of death, and find a modestly statistically significant reduction in deaths due to jaundice for V LBW infants.⁴⁶ These results support the notion that differences in care received in the hospital are likely driving our mortality results.

D. Alternative birth weight thresholds

A main limitation to our analysis is that the returns are estimated at a particular point in the birth weight distribution. For two reasons, we also examine other points in the birth weight distribution. First, other discontinuities could provide an opportunity to trace out marginal returns for wider portions of the overall birth weight distribution. Second, at points in the distribution where we do not anticipate treatment differences, economically and statistically significant jumps of magnitudes similar to our VLBW treatment effects could suggest that the discontinuity we observe at 1500 grams may be due to natural variation in treatment and mortality in our data.

As noted in Section IIB, discussions with physicians and readings of the medical literature suggest that other cutoffs may be relevant. To investigate other potential thresholds, we estimate differences in mortality and hospital charges for each 100 gram interval between 1000 and 3000 grams. We use local linear regression estimates because they are less sensitive to observations far from the thresholds, and our pilot bandwidth of 3 ounces for comparability.

In terms of the mortality differences, the largest difference in mortality compared to the mean at the cutoff is found at 1500 grams (23%), other than one found at 1800 grams (27%).⁴⁷ A 5% reduction in mortality (relative to the mean) is found at 1000 grams and a 16% reduction in mortality is found at 2500 grams, but graphs do not reveal convincing discontinuities in mortality at these, or other, cutoffs.

When we considered hospital charges, again 1500 grams stands out with a relatively large discontinuity, especially compared to discontinuities at birth weights between 1100 and 2500g. A 12% increase in charges (relative to the mean) is found for newborns classified as extremely low birth weight (1000 grams), with similarly large differences for 800 and 900 gram thresholds. However, differences at and below 1000 grams are not robust to alternative specifications (such as the transformation of charges by the natural logarithm), possibly because there are fewer newborns to study at these lower thresholds and the spending levels are thus particularly susceptible to outliers given the large charge amounts. In summary, we find striking discontinuities in treatment and mortality at the VLBW threshold, but less convincing differences at other points of the distribution.⁴⁸ These results support the validity of our main findings, but they do not allow us to trace out marginal returns across the distribution.

E. Gestational age thresholds

As motivated by the discussion in Section IIB, as an alternative to birth weight thresholds we also examine heterogeneity in outcomes and treatment by gestational age across the 37-week threshold. In graphical analyses using the nationwide sample, measures of average mortality by gestational week appear smooth across the 37-week threshold.⁴⁹ Corresponding regression results yield statistically significant coefficients of the expected sign, but we do not emphasize them here given the lack of a visibly discernable discontinuity in the graphical analysis.⁵⁰

We also investigated the interaction between birth weight and gestational age through the “small for gestational age” (SGA) classification: newborns below the 10th percentile of birth weight for a given gestational age. Conversations with physicians suggest doctors use SGA charts such as that established by Fenton (2003), updating the previous work of Babson and Benda (1976). On this chart, 2500 grams is almost exactly the 10th percentile of birth weight for a gestational age of 37 weeks. If physicians treat based on SGA cutoffs, we expect discontinuities in outcomes and treatment at 2500 grams to be most pronounced exactly at 37 weeks and less pronounced at other values of gestational weeks, although we are agnostic about the pattern of decline. In regression results (not shown) we do find evidence consistent with treatment being based on SGA around 2500 grams. For 1500 grams, analogous results are not clearly consistent with treatment based on the Fenton (2003) definition of SGA around 1500 grams.⁵¹

VII. Variation in treatment effects across hospital types

Our regression discontinuity design allows us to assess potential heterogeneity in outcomes and treatment across hospitals.⁵² In contexts without a regression discontinuity, an estimated relationship between hospital quality and newborn health could be biased: on one hand, a positive correlation could arise if healthier mothers choose to give births at better hospitals; on the other hand, a negative correlation could arise if riskier mothers choose to give birth at better hospitals, knowing that their infant will need more care than an average newborn. However, as discussed above, because birth weight should not be predictable in advance of birth with the accuracy needed to move a birth from just above to just below our 1500 gram threshold of interest, selection should not be differential across our discontinuity - implying that we can calculate internally valid estimates for different types of hospitals and consider how the quality of the hospital affects the results.

One natural grouping of hospitals, given our population under study, is the level of neonatal care available in an infant’s hospital of birth. For our California data, classifications of neonatal care availability by hospital by year are available during our time period due to analysis by Phibbs et al. (2007).⁵³ In the sample of newborns within our bandwidth, 10% of births occur at hospitals with no NICU, just over 12% at hospitals with a Level 0–2 NICU, and the remainder at hospitals with Level 3A-3D NICUs.⁵⁴

While we can examine our reduced form estimates by NICU quality level, it is worth noting that we expect to lack sufficient sample size within these NICU quality level sub-samples to give precise estimates of these effects for our one-year mortality outcome. Perhaps unsurprisingly, regression estimates which interact our regression discontinuity variable as well as our linear birth weight trends with indicators for the NICU quality level available in a newborn’s hospital of birth generally do not give statistically significant estimates for our one-year mortality outcome, with the exception of Level 0/1/2 NICU hospitals - for which we estimate a negative, statistically significant coefficient. Using charges as a first stage outcome in the same regression framework, we estimate economically and statistically significant positive coefficients for non-NICU hospitals as well as Level 0/1/2 and Level 3B hospitals; coefficients for the other hospitals do not produce statistically significant coefficients.

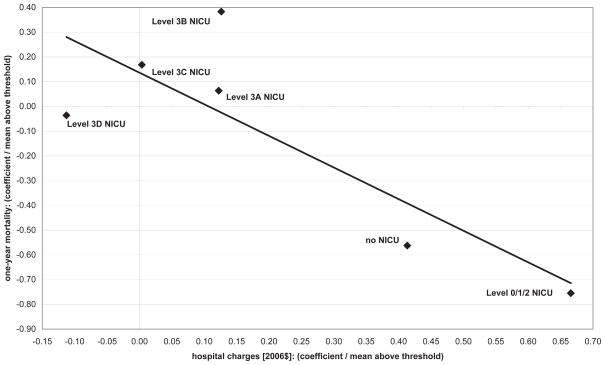
We can only offer a cautious interpretation of these results given that many of our estimates are not statistically significant at conventional levels. That said, Figure VI provides one descriptive analysis - plotting first stage estimates by hospital against reduced form estimates by hospital, normalizing each coefficient by the mean outcome for newborns above 1500 grams within our bandwidth for that type of hospital. Hospitals with larger first stage estimates have larger reduced form estimates, providing further evidence that treatment differences are driving the outcome differences. In addition, this analysis provides suggestive evidence that the non-NICU and Level 0/1/2 NICU hospitals are the hospitals where our estimated effects are largest.⁵⁵

Figure VI. First stage versus reduced form, by NICU quality level.

Notes: Plot of first stage coefficients (for 2006 charges, in levels) and reduced form coefficients (for one-year mortality) by NICU level in our California data. See text for details on the NICU classifications.

VIII. Estimating returns to medical spending

In this section, for comparability to the existing literature we present a time series estimate of the returns to large changes in spending over time for newborns in our bandwidth (sub-section A). We then combine our first stage and reduced form estimates to derive two-sample estimates of the marginal returns to medical spending for newborns near 1500 grams (sub-section B). As noted in Section IIIA, all of our spending figures in this section are hospital costs (that is, hospital charges deflated by a cost-to-charge ratio) since costs most closely approximate the true social costs of resource use.

A. Comparison to time-series estimates of returns to medical spending

As one benchmark, we can compare our marginal return estimate to the type of return estimate calculated by Cutler and Meara (2000). The spirit of the Cutler-Meara calculation is to assume that within-birth weight changes in survival over time are primarily due to improvements in medical technologies in the immediate postnatal period (Paneth, 1995; Williams and Chen, 1982), and to thus value medical improvements by looking at changes over time in within-birth weight expenditures and health outcomes. We undertake this calculation in our California data as a “long difference” in costs (in 2006 dollars) and one-year mortality from 1991 to 2002. Within our bandwidth, we estimate a $30,000 increase in costs and a 0.0295 decline in one-year mortality over this period, which implies a cost per newborn life under the Cutler-Meara assumptions of $1 million dollars. By this metric, as we will see below, our marginal return estimates appear to be similar or slightly more cost-effective than time-series returns to large changes in spending for newborns in our bandwidth.

B. Two-sample estimates of marginal returns to medical spending

As discussed in Section IVA, we can combine our results to produce two-sample estimates of the effect of treatments on health outcomes around the VLBW threshold. To do so, we need to invoke the exclusion restriction that the VLBW designation only affects mortality through treatments captured by our treatment measure - an assumption that is most plausible for costs, our best available summary treatment measure.

Because we examine health outcomes and summary treatments in different data sources, additional assumptions are required to combine our estimates. To be conservative, we can focus on mortality and cost estimates based solely on states in the five-state sample. We obtain the one-year mortality estimate on the nationwide data, restricted to newborns in the five-state sample in available years and standardize covariates across the two samples.⁵⁶ If we had the exact same newborns in the two samples, our two-sample estimate would be identical to a one-sample estimate on the complete data.⁵⁷ Coefficients are shown in the last column of online appendix Table A7, where $4,553 in additional costs are associated with a 0.74 percentage point reduction in mortality.

If we are willing to assume that costs differences in the five-state sample in the available years (1991–2006) are broadly representative of what we would observe in the full national sample in available years (1983–2002), we can compare our main results: a difference of $3,795 in costs and a one-year mortality reduction of 0.72 percentage points as birth weight approaches the VLBW threshold from above.

Equivalently, we can compute a measure of dollars per newborn life saved. In such a calculation, the numerator is our hospital costs estimate: $3,795 for each VLBW newborn in the full five-state sample. The denominator is our mortality estimate: a 0.72 percentage point reduction in mortality among VLBW newborns in the full sample. These estimates imply that the cost per newborn life saved is $527,083 ($3,795/.0072). In the five-state sample over the years that overlap with the nationwide data, we obtain a slightly larger estimate of costs per newborn life saved of $615,270 ($4,553/.0074). Following Inoue and Solon (2005), we calculate an asymptotic 95% confidence interval on this estimate of approximately $30,000 to $1.20 million. Note that this confidence interval for the estimate from the restricted sample is conservative relative to the analogous confidence interval for the more precise estimate we obtain from the full samples: $30,000 to $1.05 million.

We can compare these estimates of the cost per newborn life saved to a variety of potential benchmarks. Using data on disabilities and life expectancy, Cutler and Meara (2000) calculate a quality-adjusted value of a newborn life for newborns born in 1990 near 1500 grams to be approximately $2.7 million. If we take the less conservative view that newborns who are saved do not experience decreases in life span or quality of life, the relevant benchmark is approximately $3 to $7 million dollars (Cutler, 2004). Comparison with this benchmark suggests that the treatments that we observe are very cost-effective.

IX. Conclusion

Medical inputs can vary discontinuously across plausibly smooth measures of health risk - in our case, birth weight - inviting evaluation using a regression discontinuity design. The treatment threshold and estimated effects are relevant to a “marginally untreated” sub-population. The relatively frequent use of clinical triage criteria (as discussed in Section I) and availability of micro-level data on health treatments and health outcomes imply that this type of regression discontinuity analysis may be fruitfully applied to a number of other contexts. This approach offers a useful complement to conventional approaches to estimating the returns to medical expenditures - which have generally focused on time-series, cross-sectional, or panel variation in medical treatments and health outcomes - yet has not been widely applied in either the economics literature or the health services literature to date (Linden et al., 2006; Zuckerman et al., 2005).

In the universe of all births in the US over 20 years, we estimate that newborns weighing just below 1500 grams have substantially lower mortality rates than newborns that weigh just over 1500 grams, despite a general decline in health associated with lower birth weight. Specifically, one-year mortality falls by approximately one percentage point as birth weight crosses 1500 grams from above, which is large relative to mean one-year mortality of 5.5% just above 1500 grams. Robustness tests suggest some variation around this point estimate, but we generally find a reduction in mortality of close to 0.7 percentage points for newborns just below the threshold.

It appears that infants categorized as “very low birth weight” have a lower mortality rate because they receive additional treatment. Using all births from five states that report treatment measures and birth weight - states that have a similar mortality discontinuity to the nationwide sample - we find that treatment differences are on the order of $9,500 in hospital charges, or $4,000 when these charges are converted into costs. While these costs may not represent social costs for such care - the nurses, physicians, and capital expenditures may not be affected by the births of a small number of very low birth weight infants - they represent our best summary measurement of the difference in treatment that the VLBW classification affords. Taken together, our estimates suggest that the cost of saving a statistical life for newborns near 1500 grams is on the order of $550,000 with an upper bound of approximately $1.2 million in 2006 dollars. While the cost measures may not fully capture the additional care provided to VLBW newborns, the magnitude of the cost effectiveness estimates suggests that returns to medical care are large for this group.