Cooccupancy of the Outer Vestibule of Voltage-Gated Sodium Channels by μ-Conotoxin KIIIA and Saxitoxin or Tetrodotoxin

Abstract

The guanidinium alkaloids tetrodotoxin (TTX) and saxitoxin (STX) are classic ligands of voltage-gated sodium channels (VGSCs). Like TTX and STX, μ-conotoxin peptides are pore blockers but with greater VGSC subtype selectivity. μ-Conotoxin KIIIA blocks the neuronal subtype Na_V1.2 with nanomolar affinity and we recently discovered that KIIIA and its mutant with one fewer positive charge, KIIIA[K7A], could act synergistically with TTX in a ternary peptide·TTX·Na_V complex. In the complex, the peptide appeared to trap TTX in its normal binding site such that TTX could not readily dissociate from the channel until the peptide had done so; in turn, the presence of TTX accelerated the rate at which peptide dissociated from the channel. In the present study we examined the inhibition of Na_V1.2, exogenously expressed in Xenopus oocytes, by STX (a divalent cation) and its sulfated congener GTX2/3 (with a net +1 charge). Each could form a ternary complex with KIIIA and Na_V1.2, as previously found with TTX (a monovalent cation), but only when STX or GTX2/3 was added before KIIIA. The KIIIA·alkaloid·Na_V complex was considerably less stable with STX than with either GTX2/3 or TTX. In contrast, ternary KIIIA[K7A]·alkaloid·Na_V complexes could be formed with either order of ligand addition and were about equally stable with STX, GTX2/3, or TTX. The most parsimonious interpretation of the overall results is that the alkaloid and peptide are closely apposed in the ternary complex. The demonstration that two interacting ligands (“syntoxins”) occupy adjacent sites raises the possibility of evolving a much more sophisticated neuropharmacology of VGSCs.

INTRODUCTION

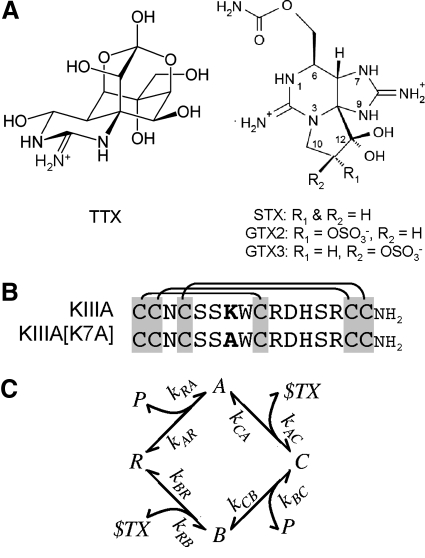
Voltage-gated sodium channels (VGSCs) are responsible for the upstroke of action potentials in excitable cells. Tetrodotoxin (TTX) and saxitoxin (STX) are guanidinium alkaloids (Fig. 1A) that block six of the nine isoforms of the pore-bearing α-subunit of mammalian VGSCs with K_d values in the nanomolar range (Catterall et al. 2005). μ-Conotoxins, which also block VGSCs, are peptides of 16 to 25 residues, including six cysteines that form a characteristic disulfide framework (see Fig. 1B) (Terlau and Olivera 2004). In contrast to the promiscuity of TTX and STX, GIIIA, the best-studied μ-conotoxin, is significantly more potent against the skeletal muscle subtype of channel Na_V1.4 (half-maximal inhibitory concentration [IC₅₀] = 19 nM), than other TTX-sensitive subtypes, such as brain Na_V1.2 (IC₅₀ ≈ 2.7 μM) (Safo et al. 2000). TTX, STX, and GIIIA competitively bind to site 1 of Na_V1.4, located at the outer vestibule of the channel's pore (Al-Sabi et al. 2006; Cestele and Catterall 2000; French and Terlau 2004; Moczydlowski et al. 1986).

Fig. 1.

Structures of guanidinium alkaloids and peptides whose activities were examined in this study. A: tetrodotoxin (TTX, left) and saxitoxin (STX) and GTX2/3 (STX congener with a net +1 charge; right). At neutral pH, TTX has a single positive charge, whereas STX has 2. GTX2/3 is a mixture of epimers GTX2 and GTX3 and differs from STX by having a sulfate group, so its net charge is +1 (Hall et al. 1990). B: aligned sequences of μ-conotoxin KIIIA and its point mutant KIIIA[K7A]. These peptides are identical except for bold residue, which is Lys7 in KIIIA and Ala7 in KIIIA[K7A]. Three disulfide bridges characteristic of all μ-conotoxins are indicated by lines linking Cys residues. Carboxyl terminals of both peptides are amidated. C: proposed reaction scheme for the syntoxin interactions between alkaloid and peptide when they bind to Na_V1.2. The channel (i.e., receptor) is represented by R and its ligands by P for μ-conopeptide and $TX for alkaloid (TTX or STX). A is the binary peptide·channel complex, B is the binary alkaloid·channel complex, and C is the ternary peptide·alkaloid·channel complex. The formation of the same ternary complex, independent of order of ligand addition, was inferred from the interactions of TTX and KIIIA or KIIIA[K7A] with Na_V1.2 (Zhang et al. 2009) and is also consistent with the results in the present experiments with STX and GTX2/3. The notation for the rate constants correspond to that in the formulae, used to numerically simulate the kinetics of the reactions, in methods.

We recently discovered μ-conotoxins KIIIA and SIIIA, which block Na_V1.2 with higher affinity than Na_V1.4 (Bulaj et al. 2005; Yao et al. 2008; Zhang et al. 2007). Single-channel analyses of brain VGSCs in planar lipid bilayers showed that KIIIA produced only a partial block (Zhang et al. 2007). In saturating concentrations of KIIIA or its mutant KIIIA[K7A], a residual sodium current (rI_Na) could be macroscopically recorded in voltage-clamped Xenopus oocytes expressing Na_V1.2 (Zhang et al. 2009). Remarkably, TTX blocked the rI_Na with either peptide, albeit 10²- to 10⁴-fold more slowly than control I_Na. When TTX was bound to the channel first, only a modest nearly 25% decrease in the rate of peptide binding was observed. The rates of recovery from block of the ternary complexes (k_off values) were the same regardless of the order of ligand addition. The k_off values for the bimolecular complex KIIIA[K7A]·Na_V and the ternary complexes KIIIA·TTX·Na_V and KIIIA[K7A]·TTX·Na_V were similar; in contrast, the k_off value for KIIIA·Na_V was 10-fold smaller, indicating that the presence of TTX decreased the stability of KIIIA·TTX·Na_V. We hypothesized that TTX and peptide bound abutting microsites (Olivera et al. 1991), within the greater confines of a macrosite synonymous with neurotoxin receptor site 1 designated by Catterall (Catterall 1980; Cestele and Catterall 2000).

In this report we tested STX, which has two positive charges (Bordner et al. 1975; Schantz et al. 1975), in contrast to TTX's single charge (Hille 1975), and GTX2/3, a naturally occurring STX congener with a net +1 charge (Fig. 1A). In view of their rather different structures, it is not surprising that STX and TTX do not bind in an identical fashion to VGSCs. For example, when Phe 385 near the selectivity filter of Na_V1.2 is mutated to Cys, the channel's affinity for TTX is reduced 3,000-fold (Zhang et al. 2009), whereas that for STX is reduced (only) 340-fold (Heinemann et al. 1992). Herein, we show that STX and GTX2/3 behave differently from each other as well as from TTX in the formation and dissociation of complexes of peptide and alkaloid with Na_V1.2. Nevertheless, the overall results are explicable in terms of the reaction scheme in Fig. 1C and support the hypothesis that in the ternary peptide·alkaloid·Na_V complex, KIIIA or KIIIA[K7A] cooccupies site 1 with alkaloid, irrespective of whether it is STX, GTX2/3, or TTX.

METHODS

Oocyte electrophysiology

Oocytes expressing rat Na_V1.2 were prepared and two-electrode voltage clamped essentially as previously described (Fiedler et al. 2008; Zhang et al. 2007). Oocytes were harvested from Xenopus frogs, following a protocol approved by the University of Utah's Institutional Animal Care and Use Committee that conforms to the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Briefly, oocytes were bathed in ND96 and sodium currents (I_Na) were recorded by holding the membrane potential at −80 mV and stepping to −10 mV for 50 ms every 20 s. The oocytes were exposed to toxin in a small (30 μl) static bath to conserve material. Recordings were done at room temperature (∼21°C).

Toxins

μ-Conopeptides were synthesized as previously described (Zhang et al. 2007). TTX was obtained from Alomone Labs (Jerusalem, Israel), STX from either Calbiochem (San Diego, CA) or the National Research Council Canada (Halifax, Nova Scotia, Canada), and GTX2/3 from the National Research Council Canada. In experiments involving high concentrations, STX and GTX2/3 were lyophilized then dissolved in ND96. All stocks were stored at −20°C in a nonfrost-free freezer until use.

Data analysis

Off-rate constants (k_off values) were determined from single-exponential fits of peak I_Na following toxin washout; observed rate constants (k_obs values) were obtained by single exponential fits of I_Na following toxin addition and on-rate constants (k_on values) were obtained from slopes of k_obs versus [toxin], all as reported previously (West et al. 2002). In particular instances (see the text immediately following), the time course of the recovery of I_Na following toxin washout was biphasic and the recovery was fit to a double-exponential curve as previously reported (Zhang et al. 2009).

Numerical simulation of the reaction scheme in Fig. 1C

To model the time-dependent changes in the concentrations of the various components, the reaction scheme in Fig. 1C was simulated by reiteration of the following formulas in a for-loop using the graphical programming language LabVIEW (National Instruments, Austin, TX)

$${\left[A\right]}_{\text{new}}={\left[A\right]}_{\text{old}}+\left(k_{RA}*\left[P\right]*{\left[R\right]}_{\text{old}}-k_{AR}*{\left[A\right]}_{\text{old}}-k_{AC}*{\left[A\right]}_{\text{old}}*\left[\$\right]+k_{CA}*{\left[C\right]}_{\text{old}}\right)*$$

$${\left[B\right]}_{\text{new}}={\left[B\right]}_{\text{old}}+\left(k_{RB}*\left[\$\right]*{\left[R\right]}_{\text{old}}-k_{BR}*{\left[B\right]}_{\text{old}}-k_{BC}*{\left[B\right]}_{\text{old}}*\left[P\right]+k_{CB}*{\left[C\right]}_{\text{old}}\right)*$$

$${\left[C\right]}_{\text{new}}={\left[C\right]}_{\text{old}}+\left(k_{AC}*{\left[A\right]}_{\text{old}}*\left[\$\right]-k_{CA}*{\left[C\right]}_{\text{old}}-k_{BC}*{\left[B\right]}_{\text{old}}*\left[P\right]+k_{CB}*{\left[C\right]}_{\text{old}}\right)*\Delta t$$

$${\left[R\right]}_{\text{new}}={\left[R\right]}_{\text{old}}-{\left[A\right]}_{new}-{\left[B\right]}_{\text{new}}-{\left[C\right]}_{\text{new}}-{\left[D\right]}_{\text{new}}$$

Pseudofirst-order kinetics was assumed; i.e., the concentration of alkaloid, denoted by [$] (representing STX, GTX2/3, or TTX), and that of μ-conopeptide, denoted by [P], remained constant. When concentrations were expressed in micromoles (μM) and time in minutes, a time increment Δt of 10⁻⁴ proved sufficiently small to accommodate the concentrations and rate constants used for the simulations used in this study. The rate constants are as denoted in Fig. 1C and their values were obtained by measuring the kinetics of block and recovery of I_Na following exposure to, and washout of, alkaloid and peptide, each alone or in combinations, as follows: k_RA and k_AR were the k_on and k_off values, respectively, of the reaction of Na_V with peptide alone; k_BR and k_RB were the k_on and k_off values, respectively, of the reaction of Na_V with alkaloid alone; and k_AC was determined from the k_on value for the block of residual current of the peptide·Na_V complex at saturating [peptide]. There was no direct means to determine k_CA, but its value could be calculated, since the product of the rate constants for the four clockwise steps equals that for the four counterclockwise steps; that is, k_CA = [k_RA*k_AC*k_CB*k_BR]/[k_RB*k_BC*k_AR]. When all of the Na_V was converted into a ternary complex by use of saturating concentrations of toxins, the time course for functional recovery after toxin washout could be fit by a single-exponential curve with a rate constant k_off, which was smaller than k_BR (and larger than k_AR), indicating that k_CB was rate-liming during toxin washout; therefore k_CB could be approximated by k_off. A more accurate value of k_CB could be estimated from the experimentally determined values for six of the rate constants, k_RA, k_AR, k_AC, k_RB, k_BR, and k_BC (see next paragraph for experimental determination of k_BC), and calculating the seventh, k_CA, as described earlier, while the value of k_CB was varied until the mean squared error between the simulated and experimental time courses of recovery from block reached a minimum. Values of k_CA and k_CB determined in this fashion are presented in Table 4.

Table 4.

Equilibrium constants (nM) of reactions in Fig. 1C

A. Kdvalues of peptides for channel alone versus channel saturated with peptide
	Channel Alone	Channel Saturated With Alkaloid
Peptide	None Kd (kBR/kRB)	KIIIA Kd (kCA/kAC)	KIIIA[K7A] Kd (kCA/kAC)
Alkaloid
TTX	38 ± 6	730 ± 800	45 ± 22
STX	8 ± 2	—	6 ± 3
GTX2/3	5 ± 1	—	7 ± 4

B. Kdvalues of peptides for channel alone versus channel saturated with alkaloid
	Channel Alone	Channel Saturated With Alkaloid
Alkaloid	None Kd (kAR/kRA)	TTX Kd (kCB/kBC)	STX Kd (kCB/kBC)	GTX2/3 Kd (kCB/kBC)
Peptide
KIIIA	5 ± 5	105 ± 25	4 (1–12) × 103†	290 ± 30
KIIIA[K7A]	115 ± 40	138 ± 30	87 ± 18	156 ± 62

Equilibrium K_d values, mean ± SD, were calculated from k_off/k_on ratios (notations of corresponding rate constants in Fig. 1C are indicated in parentheses); values for these rate constants were obtained from Tables 1–3, except for those of k_CB and k_CA, which were obtained by numerical simulation, as described in methods. Values of k_CB, in min⁻¹, were (for indicated peptide–alkaloid combinations): 0.021 (KIIIA–TTX); 0.35 (KIIIA–STX); 0.029 (KIIIA–GTX2/3); 0.022 (KIIIA[K7A]–TTX); 0.013 (KIIIA[K7A]–STX); and 0.014 (KIIIA[K7A]–GTX2/3); SDs of k_off values for corresponding ternary complexes in Table 2 served as proxies for SDs for k_CB values and these were used in calculating SDs for corresponding k_CA and K_d values. Mean values of k_CA ± SD, in min⁻¹, were (for indicated peptide–alkaloid combinations): 0.0022 ± 0.0024 (KIIIA–TTX); 0.025 ± 0.012 (KIIIA[K7A]–TTX); 0.0038 ± 0.0018 (KIIIA[K7A]–STX); and 0.004 ± 0.0021 (KIIIA[K7A]–GTX2/3).

^†Values in parentheses indicate range of uncertainty of predicted K_d, from limits of uncertainty for corresponding k_BC value in Table 3.

The value of k_BC was estimated from experiments in which alkaloid was added before peptide and exploiting the large disparity between k_CB and k_BR (except in one instance, involving KIIIA and STX; see following paragraph), which produced a double-exponential time course for the recovery of I_Na following toxin washout. The coefficients of the double-exponential fits provided the k_off values and spans of the fast and slow phases. In every case, the fast k_off had a value close (within a factor of ∼2) to k_BR (i.e., the rate constant for the recovery from block of the binary alkaloid·Na_V complex) and the slow k_off had a value close (within a factor of ∼2) to k_CB (i.e., the rate constant for recovery from block of the ternary complex formed with saturating concentrations of both alkaoid and peptide applied for sufficient time to convert all of the Na_V into a ternary complex). These results supported the notion that the span of the slow phase was likely to provide a good estimate of the fraction of the channels that were in the ternary peptide·alkaloid·Na_V complex at the start of toxin washout (Zhang et al. 2009). It was assumed that preceding toxin washout, the fraction of ternary complex formed (FTCF) as a function of time followed a single-exponential time course and therefore the estimated value for the observe rate constant k_obs was calculated from the equation k_obs = [ln (FTCF)]/time. For the sake of simplicity, data were obtained only at a single time point. This k_obs was used with the equation k_obs = k_on*[peptide] + k_off and, since k_off (i.e., ∼k_CB) was invariably about an order of magnitude smaller than k_obs, the apparent k_on (i.e., k_BC) was calculated from k_obs/[peptide].

A procedure different from that described earlier had to be used to estimate k_BC in the case of STX and KIIIA because the difference between k_CB and k_BR was only fourfold and the experimental time course of recovery of I_Na following toxin washout could not be fit by a double-exponential curve better than a single-exponential one. Instead, the experiment was simulated using different values for k_BC and the value producing simulated results that corresponded best with the experimental data was used to approximate k_BC. The remaining rate constants used in this approximation are specified in results.

Molecular modeling and docking of Na_V1.2, μ-conotoxin KIIIA, and the alkaloids TTX and STX

A model of rat Na_V1.2 was constructed using as a template the model of rat Na_V1.4 proposed by Lipkind and Fozzard (2000), which was composed of 12 parts from the four domains. Each domain was represented by three structural fragments: S5-segment, P-loop, and S6-segment. Sequence analysis of these 12 parts from Na_V1.2 and Na_V1.4 shows 91.0% identity (data not shown). We found every structural fragment for each domain of Na_V1.2 that corresponded to Lipkind and Fozzard's model of Na_V1.4. Our model of Na_V1.2 was built by introducing modifications of specific residues using PyMOL (DeLano Scientific, Palo Alto, CA); the residues of the Na_V1.4 model were replaced by corresponding backbone-dependent rotamer residues of the Na_V1.2 using the PyMOL mutagenesis function. The conopeptide KIIIA was constructed with coordinates from Khoo et al. (2009) and the coordinates of TTX and STX were from Tikhonov and Zhorov (2005).

Automated docking of TTX, STX, and KIIIA to the model of Na_V1.2 was performed using the AutoDock4.2 software package (Morris et al. 2009). Flexible torsions of ligands were assigned using AUTOTORS and a grid box defined by 60 × 60 × 60 grid points and spacing of 0.375 Å with AUTOGRID. Docking simulations were performed using a Lamarckian genetic algorithm (Morris et al. 1998), with the following parameters: population size = 300, mutation rate = 0.02, crossover rate = 0.8. The numbers of dockings per simulation were 50 and 256 for conopeptide and alkaloid, respectively. The number of dockings per simulation for conopeptide was lower than that for alkaloid due to the larger values of flexible torsions and corresponding longer simulation times. The maximum number of energy evaluations was set to 250,000 and the maximum number of generations was 27,000. One cluster-representative structure was selected from each of the docking runs. Clusters were examined for quantity of conformations and those with the greatest number were chosen for further analysis. A secondary criterion for selecting a cluster-representative structure was the value of binding energy.

RESULTS

Residual Na current (rI_Na) with KIIIA[K7A] can be blocked by both STX and GTX2/3; however, block of the rI_Na with KIIIA by either of these alkaloids could not be demonstrated

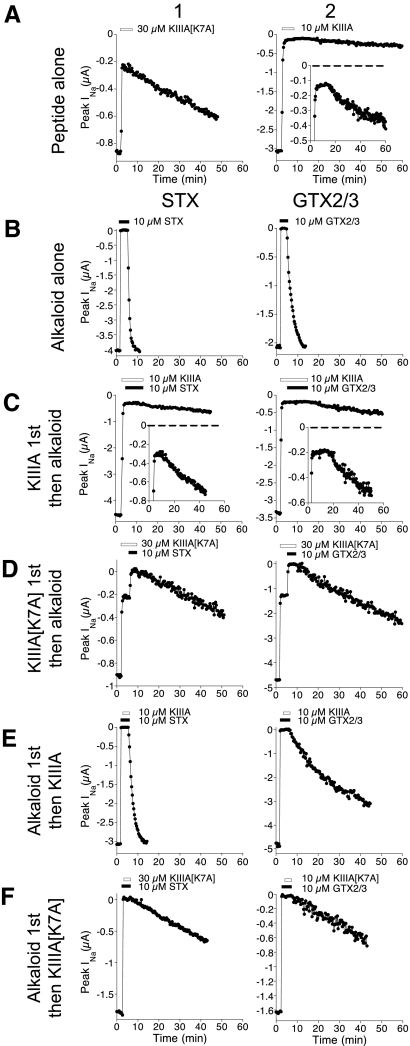
As we previously showed (Zhang et al. 2009), when oocytes expressing Na_V1.2 were voltage clamped and exposed to saturating concentrations of either KIIIA or KIIIA[K7A], a residual sodium current (rI_Na) of 5 and 23% of control I_Na, respectively, persisted (Fig. 2A). In contrast, saturating concentrations of the alkaloids STX or GTX2/3 produced essentially a complete block (>99%), which was much more quickly reversible than the block by either conopeptide alone (Fig. 2, A and B).

Fig. 2.

Block of Na_V1.2 by KIIIA, KIIIA[K7A], STX, or GTX2/3, each alone or in combination. Voltage-gated sodium currents (I_Na) of voltage-clamped oocytes expressing Na_V1.2 were measured as described in methods. Plotted are peak I_Na as a function of time during exposure to, and subsequent washout of, peptide alone (row A) or alkaloid alone (row B) or both (rows C–F). Bars above plots indicate when peptide (white bar) or alkaloid (black bar) were present. Except for row A, 1st column represents STX and 2nd column, GTX2/3. A: block by saturating concentration of either KIIIA[K7A] or KIIIA alone (30 or 10 μM, respectively). Inset in KIIIA plot shows curve with I_Na-axis expanded. Note residual current (rI_Na) persisting in the presence of each peptide. B: block by saturating concentration of STX or GTX2/3 alone (each 10 μM). C: rI_Na with KIIIA was blocked by neither STX nor GTX2/3. Insets show plots with I_Na-axis expanded; note rate of recovery following toxin washout was unaffected (cf. inset of A2). D: in contrast, STX and GTX2/3 each blocked rI_Na with KIIIA[K7A]. E and F: recovery from block during simultaneous washout of both alkaloid and peptide following exposure to alkaloid first, then KIIIA (E) or KIIIA[K7A] (F). E: with KIIIA, washout rates were much faster than those following exposure to KIIIA alone (A2) but slower than those following exposure to alkaloid alone (B), consistent with KIIIA retarding the washout of alkaloid and alkaloid reciprocating by accelerating the washout of KIIIA. F: with KIIIA[K7A], washout rates were similar to those following exposure to peptide alone (A1) and slower than those following exposure alkaloid alone (B), consistent with peptide retarding alkaloid washout. Time bases (abscissa) of all plots have the same scale. Representative experiments are shown; for quantitative summaries see Tables 1 and 2.

The rI_Na with KIIIA was not blocked by either STX or GTX2/3 at the highest concentrations tested (10 μM); i.e., ≲10%, if any, of the rI_Na was blocked (Fig. 2C). In contrast, the rI_Na with KIIIA[K7A] could be readily blocked by STX and GTX2/3 (Fig. 2D). With each alkaloid, complete block was achieved with the formation of a ternary KIIIA[K7A]·alkaloid·Na_V complex, as evident from the rate of recovery from block after toxin washout, which occurred in a single phase (Fig. 2D) without an initial fast phase that would indicate the recovery from block by alkaloid alone (also see following text).

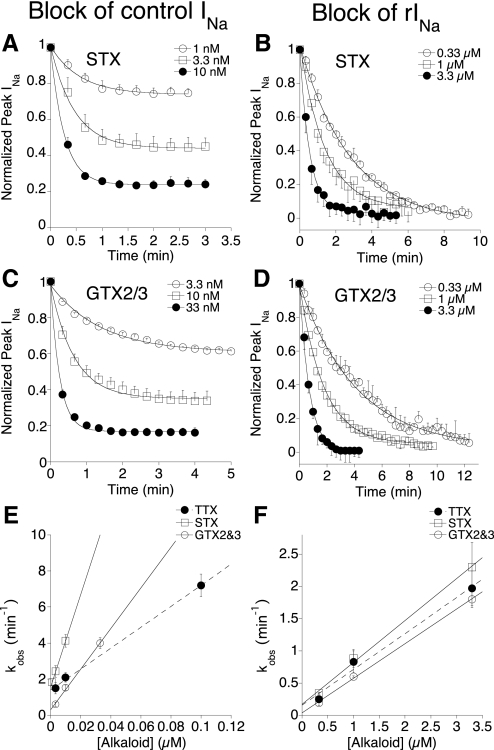
The time course of the onset of block by STX and GTX2/3 of control I_Na and rI_Na with KIIIA[K7A] could be fit with single-exponential curves (Fig. 3,A–D), and the resulting observed rate constants (k_obs values) were linearly dependent on the concentration of alkaloid (Fig. 3, E and F). For comparison, also illustrated in Fig. 3, E and F are previously acquired results with TTX (Zhang et al. 2009). The slopes of the lines yielded apparent k_on values, which are tabulated in Table 1. The presence of KIIIA[K7A] decreased the on rates of all three alkaloids by at least two orders of magnitude.

Fig. 3.

Rates of block of control I_Na and rI_Na with KIIIA[K7A] by different concentrations of STX and GTX2/3. Experiments were done as in Fig. 2, B and D. Time courses of block of control I_Na (A, C; cf. Fig. 2B) and rI_Na (B, D; cf. Fig. 2D) by various alkaloid concentrations were each fit to a single exponential (solid curve) to obtain k_obs. Dependence of k_obs on alkaloid concentration for block of control I_Na (E) or rI_Na with 30 μM KIIIA[K7A] (F) (STX, open squares; GTX2/3, open circles; or TTX, closed circles). Data for TTX are from Zhang et al. (2009) and are included for comparison. Straight lines represent linear regression slopes whose values (i.e., k_on values) are given in Table 1. Rates of block of rI_Na were significantly slower than those of control I_Na (note ∼30-fold difference in x-axis scale between E and F). Steady-state block of control I_Na at different concentrations of STX (A) and GTX2/3 (C) yielded half-maximal inhibitory concentration (IC₅₀) values of 3 ± 0.3 and 4.6 ± 1.0 nM, respectively, which are close to (within a factor of 3 of) their respective K_d values of 7.9 ± 1.7 and 5.3 ± 0.8 nM calculated from k_off and k_on values (Tables 1 and 2). In contrast, steady-state block of rI_Na is essentially complete, even at the lowest [alkaloid] tested (B, D); using lower concentrations takes too long to reach steady state, precluding determination of IC₅₀ values for this reaction. Data points represent mean ± SD (n ≥ 3 oocytes).

Table 1.

Rates of block of rI_Na and control I_Na by the various guanidinium alkaloids, corresponding to k_AC and k_RB of Fig. 1C, respectively

	Apparent kon, μM−1·min−1†
Alkaloid	rINa With KIIIA	rINa With KIIIA [K7A]	Control INa	Reference
TTX	0.003 ± 0.0004	0.56 ± 0.08	58 ± 5.3	Zhang et al. (2009)
STX	∼0‡	0.65 ± 0.10	254 ± 41.0	Thisstudy
GTX2/3	∼0‡	0.55 ± 0.03	113 ± 8.7	Thisstudy

Values are means ± SD, n ≥3 oocytes.

^†Rate constants were obtained from slopes of curves in Fig. 3.

^‡No block of the rI_Na with KIIIA was discernable at the highest alkaloid concentration tested (10 μM, Fig. 2C), indicating a k_on at least tenfold smaller than that of TTX.

Ternary complexes of KIIIA·alkaloid·Na_V and KIIIA[K7A]·alkaloid·Na_V can be formed by adding STX or GTX2/3 first, followed by peptide

Instead of adding peptide first, then alkaloid, experiments were also performed in which the order of ligand addition was reversed. Formation of a ternary complex was evident from the single-phase nature of the recovery of activity when both toxins were washed out (Fig. 2, E and F). The rates of functional recovery during dissociation of the ternary KIIIA[K7A]·alkaloid·Na_V complex after toxin washout were similar for both STX and GTX2/3. This was so regardless of whether alkaloid or peptide was added first and the off rates were essentially the same as those for the recovery from block of the binary KIIIA[K7A]·Na_V complex (Fig. 2, A, D, and F, Table 2).

Table 2.

Rates of recovery from block during washout of ligand(s) from binary and ternary complexes, corresponding to k_BR and k_AR and approximation of k_CB of Fig. 1C, respectively

	koff of complex, min−1†
Alkaloid	KIIIA·X·NaV	KIIIA[K7A]·X·NaV	X·NaV	Reference
None	0.0016 ± 0.0016	0.015 ± 0.005	—	Zhang et al. (2009)
TTX	0.020 ± 0.005 (0.017 ± 0.002)	0.024 ± 0.004 (0.025 ± 0.003)	2.2 ± 0.3	Zhang et al. (2009)
STX	0.350 ± 0.039 (NA)‡	0.014 ± 0.002 (0.015 ± 0.007)	2.0 ± 0.3	This study
GTX2/3	0.029 ± 0.001 (NA)‡	0.014 ± 0.003 (0.018 ± 0.005)	0.6 ± 0.08	This study

Values are means ± SD, n ≥3 oocytes.

^†Rate constants of recovery from block during washout of toxin(s) following exposure to: each peptide alone (top data row), or each alkaloid alone (right data column), or both alkaloid and peptide (remaining data entries). Ternary complexes were formed by exposure first to alkaloid as in Fig. 2, E and F (or exposure first to peptide as in Fig. 2D), followed by mixture of alkaloid plus peptide. Values of k_off were obtained by fitting the time course of recovery of activity after toxin(s) were washed out to a single-exponential curve, values without parentheses are those of the complex formed by exposure to alkaloid first, and values in parentheses are those of the complex formed by exposure to peptide first.

^‡NA, not available because ternary complex was not readily formed by adding peptide first.

Although we were unable to show that the rI_Na with KIIIA could be blocked by STX or GTX2/3, formation of a ternary KIIIA·alkaloid·Na_V complex could be readily demonstrated by adding STX or GTX2/3 first, followed by KIIIA: on toxin washout, the respective rates of recovery of block were >100- and >10-fold faster than that after exposure to KIIIA alone and 6- and 20-fold slower than that after exposure to the respective alkaloid alone (Fig. 2E, Table 2).

Rates of formation of ternary complexes when peptide was added after alkaloid

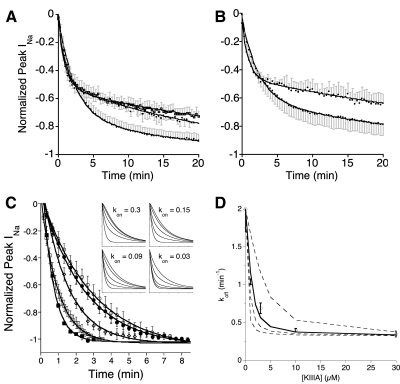
In view of the dramatic reduction by the presence of peptide in the rate of binding of alkaloid to the channel, it was of interest to see how the presence of alkaloid affected the rate of binding of peptide to the channel. After exposure to a saturating concentration of alkaloid to form the fully blocked binary alkaloid·Na_V complex, the amount of the ternary complex formed following addition of peptide was determined by analyzing the recovery from block following toxin washout as described in methods. For all but the KIIIA·STX·Na_V complex, after exposure to both alkaloid and peptide using a protocol similar to that used in Fig. 2, E and F but with tenfold lower peptide concentration, the time course of recovery of activity following toxin washout had two distinct phases that could be fit by a double-exponential curve (Fig. 4, A and B): an early fast phase attributed to the off rate of the binary alkaloid·Na_V complex and a slower phase attributed to the dissociation of the ternary peptide·alkaloid·Na_V complex—these attributions were inferred because the respective k_off values were within a factor of 2 of the expected values in Table 2. As elaborated in methods, the span of the slow component yields the fraction of ternary complex formed (FTCF) from which the apparent k_on value for the reaction peptide + alkaloid·Na_V → peptide·alkaloid·Na_V, provided in Table 3, was calculated. The approach used here was a simplified version of the protocol used to determine the apparent k_on of KIIIA and KIIIA[K7A] binding to the channel preoccupied with TTX, where a fixed concentration of peptide was used and the peptide exposure time was varied (Zhang et al. 2009); in those experiments the apparent k_on value for the reaction peptide + TTX·Na_V → peptide·TTX·Na_V was 0.13 ± 0.006 and 0.20 ± 0.008 μM⁻¹·min⁻¹ with KIIIA and KIIIA[K7A], respectively. These values are close to the corresponding k_on values obtained in the present experiments with these two peptides and TTX (Table 3) and suggest that good estimates of k_on were obtained by the simpler protocol used here.

Fig. 4.

Time course of recovery from block when toxins are washed out before all of the channels have been converted into a ternary complex. Experiments were done essentially as in Fig. 2, E and F, except a lower concentration of peptides was used and results were processed as described in methods. A and B: oocytes were exposed first to a saturating concentration (10 μM) of alkaloid for 2 min, followed by 10 μM alkaloid + 1 μM peptide for 4 min before toxin washout. Plotted are recoveries of I_Na following toxin washout (normalized mean ± SD, n = 3 oocytes). Solid lines represent data fit to double-exponential curves; in each case, fast and slow components had rate constants (see following text) within a factor of 2 of the k_off values of the corresponding alkaloid·Na_V or peptide·alkaloid·Na_V complex, respectively (Table 2). Spans of slow components (fractions of ternary complex formed [FTCFs]) are given in Table 3. A: recovery from block by KIIIA[K7A] and either GTX2/3, TTX, or STX (bottom, middle, and top traces at 20 min, respectively); fast rate constants were 0.45 ± 0.02, 1.9 ± 0.3, and 1.0 ± 0.1 min⁻¹, respectively, and slow constants were 0.025 ± 0.004, 0.04 ± 0.002, and 0.027 ± 0.002 min⁻¹, respectively. B: recovery from block by KIIIA and either GTX2/3 or TTX (bottom and top traces at 20 min, respectively); fast rate constants were 0.43 ± 0.02 and 1.1 ± 0.1 min⁻¹, respectively; slow constants were 0.031 ± 0.004 and 0.02 ± 0.002 min⁻¹, respectively. C: recovery from block following washout after oocytes were exposed to 10 μM STX for 2 min, then for 4 min to 10 μM STX + x μM KIIIA, where x was 0, 1, 3, 10, and 30 (briefest to longest-lasting curves, respectively). Data points represent normalized mean peak I_Na ± SD (n = 3 oocytes) and solid lines are data fit to single-exponential curves. Insets: simulated curves, obtained as described in methods, when k_on values for formation of ternary complex were (left to right, top to bottom) 0.3, 0.15, 0.09, and 0.03 μM⁻¹·min⁻¹ and where for each plot [KIIIA] = 0, 1, 3, 10, and 30 μM (briefest to longest-lasting curves, respectively). Ranges of x and y axes are the same as those of the main experimental plot. Note that of the simulated plots, the pattern of curves in the bottom left, where k_on was 0.09 μM⁻¹·min⁻¹, most closely resembles that of the experimental plot. D: decay constants of experimental curves in C, k_off (mean ± SD), plotted as a function of KIIIA concentration. Lines plot decay constants of simulated curves in inset of C, where (top to bottom) k_on = 0.03 (dashed), 0.09 (solid), 0.15 (dashed), and 0.3 (dashed) μM⁻¹·min⁻¹, with additional decay constants representing those with [KIIIA] of 2 and 5 μM. Correspondence of simulated and experimental data suggests a k_on of 0.09 μM⁻¹·min⁻¹, with a proposed uncertainty ranging from 0.03 to 0.3 μM⁻¹·min⁻¹.

Table 3.

Fraction of ternary complex formed (FTCF), apparent k_on for the reaction peptide + alkaloid·Na_V → peptide·alkaloid·Na_V, and k_on for the reaction peptide + Na_V → peptide·Na_V, corresponding to k_BC and k_RA of Fig. 1C, respectively

Peptide	Alkaloid	FTCF†	Apparent kon, min−1·μM−1†	kon, min−1·μM−1‡
KIIIA[K7A]	TTX	0.48 ± 0.08	0.16 ± 0.02	—
KIIIA[K7A]	STX	0.46 ± 0.07	0.15 ± 0.02	—
KIIIA[K7A]	GTX2/3	0.30 ± 0.07	0.09 ± 0.03	—
KIIIA[K7A]	None	—	—	0.13 ± 0.006
KIIIA	TTX	0.56 ± 0.03	0.20 ± 0.01	—
KIIIA	STX	—	0.09 (0.03–0.3)§	—
KIIIA	GTX2/3	0.31 ± 0.03	0.10 ± 0.01	—
KIIIA	None	—	—	0.30 ± 0.030

Values are means ± SD, n ≥3 oocytes, except for the following.

^§Values in parentheses, which span a decade, indicate proposed limits of uncertainty for k_on; see Fig. 4, C and D.

^†From results for formation of ternary complex illustrated in Fig. 4, A and B, processed as described in methods.

^‡From slope of k_obs versus [peptide] for formation of binary peptide·NaV complex, from Zhang et al. (2009).

As noted previously, with KIIIA and STX, the off rate for the recovery from block of the ternary complex was only sixfold slower than that of the binary STX·Na_V complex (Table 2). Consequently, when the experimental protocol used earlier was used with these ligands, the washout data were not fit by a double- any better than by a single-exponential curve, presumably in part because of experimental noise. Nevertheless, the formation of the ternary KIIIA·STX·Na_V complex could be discerned from the observation that the rate constant of the fit to a single-exponential curve decreased as the concentration of KIIIA increased (Fig. 4, C and D). The reaction scheme in Fig. 1C was numerically simulated for KIIIA and STX as ligands using the algorithm described in methods. The following rate constants were used in the simulation: k_RA and k_AR, 0.3 μM⁻¹·min⁻¹ and 0.0016 min⁻¹, respectively (Zhang et al. 2009); k_RB, 254 μM⁻¹·min⁻¹ (Table 1); k_BR, 2.0 min⁻¹ (Table 2); k_AC and k_CA, both 0 (since STX was unable to block rI_Na with KIIIA, as described earlier); k_CB, 0.35 min⁻¹ (from the limiting k_off value in Fig. 4D at high [KIIIA]); and, finally, k_BC (i.e., k_on for the reaction KIIIA + STX·Na_V → KIIIA·STX·Na_V) was varied over a tenfold range from 0.03 to 0.3 μM⁻¹·min⁻¹, where the latter value is that of k_RA (i.e., the k_on for the reaction KIIIA + Na_V → KIIIA·Na_V) (Zhang et al. 2009). Simulated decay curves for the recovery from block are illustrated in the inset of Fig. 4C. It is apparent by visual inspection that the pattern of the simulated curves with the k_on of 0.09 μM⁻¹·min⁻¹ most closely resembles that of the experimental curves. On fitting each of the experimental and simulated decay curves in Fig. 4C to a single-exponential time course and plotting the resulting k_off values as a function of [KIIIA], the formation of the ternary complex was reflected by the decreasing k_off value as [KIIIA] increased, until a limiting value of k_off was achieved at presumably saturating levels [KIIIA] (30 μM) (Fig. 4D). In the figure, the congruence between the experimental k_off values (circles) and those obtained by simulation (solid line) suggests that the k_on for the reaction KIIIA + STX·Na_V → KIIIA·STX·Na_V was about 0.09 μM⁻¹·min⁻¹.

Table 4 shows the equilibrium binding constants (i.e., k_off/k_on ratios or K_d values) for each of the four limbs of the reaction scheme in Fig. 1C. The table also indicates the predicted rate constants obtained by numerical simulation that were used, along with rate constants presented in previous tables, to derive the K_d values. It might be noted that direct determinations of steady-state IC₅₀ values for alkaloids, corresponding to the K_d values in saturating [peptide], were not obtained because the time it would have taken to reach steady-state block of rI_Na, using alkaloid concentrations near the anticipated IC₅₀ values (≈K_d values), was hours and outside the roughly 1-h time window of our experiments. Corresponding IC₅₀ values for peptides in saturating [alkaloid] were not obtained because, of course, no sodium currents are detectable under those circumstances.

DISCUSSION

In this study, we used two μ-conotoxins and two alkaloids and tested all four peptide–alkaloid combinations on Na_V1.2. The results, together with those obtained previously with TTX (Zhang et al. 2009), support the idea that bound conopeptide not only increases the access resistance to sodium ions, as evident by the diminutive rI_Na, but moreover also restricts the alkaloid's access to its binding site on the channel. The results also support the notion that in the ternary peptide·alkaloid·Na_V complex, the peptide traps the alkaloid at the latter's binding site and the alkaloid does not dissociate from the channel until the peptide has dissociated.

Implications of the rates of functional recovery following toxin washout of ternary complexes

A ternary complex could be formed by either order of toxin addition in four peptide–alkaloid pairs: one pair with KIIIA (in which the alkaloid was TTX) and three pairs with KIIIA[K7A] (in which the alkaloid was, respectively, TTX, STX, and GTX2/3). In each instance, essentially the same k_off value was obtained for a given pair (Table 2), suggesting that for each pair the same ternary complex was formed regardless of order of toxin addition. Thus all totaled, it appears that six unique ternary (peptide·alkaloid·Na_V) complexes can be formed with the two peptides and three alkaloids tested thus far.

Comparison of the k_off values of the six ternary peptide·alkaloid·Na_V complexes indicates that by far the least stable ternary complex was KIIIA·STX·Na_V (Table 2). The other ternary complexes had remarkably similar k_off values, as if TTX and GTX2/3 can shield Lys7 of KIIIA from the same site(s) on the channel. The presence of alkaloid destabilized the KIIIA[K7A]·alkaloid·Na_V complex minimally with TTX and hardly at all with STX and GTX2/3. Compared with TTX and GTX2/3, STX has an extra positive charge, as does KIIIA compared with KIIIA[K7A]; thus we hypothesize that charge repulsion accounts for the relatively high instability of the ternary KIIIA·STX·Na_V complex.

Implications of the on rates for the formation of the ternary complex

TTX blocked the rI_Na with KIIIA at a rate 10⁴-fold slower than it blocked control I_Na (Zhang et al. 2009) and the block of rI_Na by STX and GTX2/3 were not observed even at the highest concentrations tested (10 μM) (Table 1). Thus KIIIA bound to the channel severely restricted the access of TTX and that of STX and GTX2/3 even more so. In striking contrast, for the block of the channel preoccupied by KIIIA[K7A], the k_on values of all three alkaloids were more modestly reduced and, furthermore, to essentially the same value (Fig. 3F, Table 1). A possible mechanism for this is that the binary peptide·Na_V complex flickers between two states: a permissive state wherein an alkaloid can “sneak” by the peptide and a state in which the alkaloid cannot. The rate at which an alkaloid sneaks by would be dictated by the fraction of time the complex dwells in the permissive state and how readily the alkaloid can permeate that state. The permissive state with KIIIA may be permeable to TTX but not to STX or GTX2/3, whereas that with KIIIA[K7A] may be equally permeable to all three alkaloids. This would explain why the alkaloids have similar on rates in blocking the rI_Na with KIIIA[K7A], even though they block the control I_Na at very different rates; i.e., the rate-limiting factor for rI_Na block is the fractional dwell time of the permissive state, which is intrinsic to the peptide and independent of the specific alkaloid.

Examination of the rates of recovery from block allowed the apparent k_on for the reaction

$$\text{peptide}+\text{alkaloid}·{\text{Na}}_{\text{V}}\to \text{peptide}·\text{alkaloid}·{\text{Na}}_{\text{V}}$$

to be estimated (Fig. 4). When alkaloid was already bound to the channel, the rate at which peptide could subsequently bind to the channel appeared to be only modestly impeded, if at all. With KIIIA[K7A] and STX, GTX2/3, or TTX (Fig. 4A) and with KIIIA and GTX2/3 or TTX (Fig. 4B), the apparent k_on values were within a factor of 2 of each other (Table 3). This was consistent with previous results with KIIIA and KIIIA[K7A], where the presence of TTX on the channel was observed to reduce the apparent k_on of the peptide by only about 25% by Zhang et al. (2009). STX bound to the channel reduced the apparent k_on of KIIIA by about threefold, from 0.3 μM⁻¹·min⁻¹ under control conditions (Zhang et al. 2009) to about 0.1 μM⁻¹·min⁻¹ (Fig. 4, C and D).

Equilibrium constants derived for the proposed reaction scheme in Fig. 1C

The upper and lower limbs on the left side of the reaction scheme in Fig. 1C represent simply the binding of peptide and alkaloid, respectively, to the channel. The upper and lower limbs on the right represent binding of alkaloid and peptide, respectively, to the channel preoccupied with the opposite ligand; their convergence to form a single species of ternary complex for a given peptide/alkaloid pair, although hypothetical, is compatible with the results of our experiments. Table 4 lists the apparent binding constants of the reactions in all four limbs of the scheme. The K_d of TTX for the channel saturated with KIIIA was 20-fold larger than that without the peptide, where the presence of KIIIA decreased TTX's k_on (i.e., block of control I_Na vs. rI_Na) about 20,000-fold (Table 1) and k_off [i.e., k_off of binary (Table 2) vs. ternary complex (predicted k_CA, footnote Table 4)] about 1,000-fold. (Note that the SD of the predicted k_CA is responsible for the large SD in K_d here.) In contrast, the presence of KIIIA[K7A] only modestly altered the K_d values of TTX, STX, and GTX—the apparent k_on (Table 1) and predicted k_off (k_CA, Table 4) values for a given alkaloid were both decreased by two orders of magnitude or more. This raises the possibility that the binding site of the alkaloids per se may not have been strongly affected by KIIIA[K7A]; instead, access to and egress from the binding site was retarded by the presence of the peptide. This conjecture is compatible with the flicker mechanism for the binary peptide·Na_V complex suggested in the preceding section.

For each ternary complex, the predicted k_CB value (Table 4) was close to the measured k_off value for the recovery of I_Na during toxin washout (Table 2), consistent with the idea that the rate-limiting step in disassembly of the ternary complex is the dissociation of peptide. Likewise, k_CB was always greater than k_CA except for the KIIIA[K7A]·TTX·Na_V complex, in which the two rate constants were predicted to be similar (Table 4).

The K_d of KIIIA[K7A] binding was approximately the same irrespective of whether the channel was preoccupied with alkaloid, regardless of the alkaloid species; here, neither k_on nor predicted k_off was affected much by the presence of alkaloid (Table 4B). In stark contrast, the K_d of KIIIA was increased close to 20-, 800-, and 60-fold by TTX, STX, and GTX2/3, respectively; in each case, an increased k_off value was responsible for most of the elevation in K_d (compare k_CB values in Table 4 with the k_off, i.e., k_AR, value in Table 2).

Our overall results support the conclusion that the presence of alkaloid minimally interfered with the accessibility of peptide, whereas the presence of peptide severely occluded the accessibility of alkaloid. This striking asymmetry is consistent with the picture of the ternary complex wherein the alkaloid is sandwiched between the peptide and selectivity filter of the channel (Zhang et al. 2009). We explored the feasibility of this “sandwich” model in silico, as described in the immediately following text.

Structural models of alkaloid and peptide docked at the outer vestibule of the channel

Following the advent of the cloning of VGSCs, experiments to pinpoint the binding site for TTX and STX have been carried out by several investigators; the general consensus is that the alkaloids bind at a site deep in the outer vestibule of the channel to cork its pore (Choudhary et al. 2002, 2003, 2007; Lipkind and Fozzard 1994, 2000; Penzotti et al. 1998, 2001; Santarelli et al. 2007; Terlau et al. 1991; Tikhonov and Zhorov 2005). On the other hand, studies with GIIIA and Na_V1.4 indicate that the conopeptide binds at a more superficially located site (Chang et al. 1998; Choudhary et al. 2007; Dudley Jr et al. 1995, 2000; Hui et al. 2002; Li et al. 2001; Xue et al. 2003).

Given this background work by others, it behooved us to simply see whether both KIIIA and TTX or STX would fit in the vestibule. We present here our initial attempts to examine this by docking alkaloid and peptide in silico, as described in methods. These docking experiments are based on the sodium channel model proposed by Lipkind and Fozzard (2000). The model, which consists of the S5- and S6-fragments and P-loop present in each of the four domains of the channel, was built starting with the structural framework of the KcsA potassium channel (Doyle et al. 1998). The approach of using such models to analyze the results of electrophysiological measurements of sodium channel mutants has proven instructive (see references published after 2000 cited in preceding paragraph).

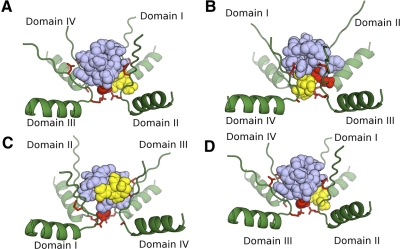
Illustrated in Fig. 5 are the pore loops at the outer vestibule of Na_V1.2, including the DEKA “ring” forming the ion selectivity filter (Hille 2001) and the more superficial EEDD ring of negative charges that are common to all mammalian Na_Vs (except Na_V1.9, where the latter ring is EEED). STX and TTX were each docked before KIIIA (Fig. 5, A and B, respectively) as well as after KIIIA (Fig. 5, C and D, respectively). Indeed, both KIIIA and alkaloid can simultaneously fit in the vestibule. Furthermore, when KIIIA was docked first, TTX could also dock close to the selectivity filter (Fig. 5D); however, this was not the case with STX (Fig. 5C). Thus these results are, to a first approximation, consistent with our experimental observations. It would be interesting to examine the docking behaviors of the alkaloids when KIIIA[K7A] is docked first, as well as the docking of other peptides and alkaloids that have yet to be tested experimentally (see following text).

Fig. 5.

Possible arrangements of KIIIA (lavender) and STX or TTX (yellow) nestled in outer vestibule of Na_V1.2 (green). Only the 4 pore loops of the channel are illustrated: backbone ribbons are alpha-helices and beta-strands, with associated red sticks representing side chains of EEDD ring at the top and DEKA ring of selectivity filter at the bottom (only 3 of the 4 side chains of residues in each ring are visible in each panel). Models were constructed using AutoDock4, as described in methods where: STX was docked before KIIIA (A); TTX was docked before KIIIA (B); KIIIA was docked before STX (C); and KIIIA was docked before TTX (D). Each panel shows the ternary complex from a perspective that provided good visibility of alkaloid, peptide, and DEKA ring. Note, alkaloid managed to dock close to DEKA ring in all panels except C.

Aside from GTX2/3, 15 other naturally occurring congeners of STX have been identified (Yasumoto and Murata 1993). Experiments with: 1) these congeners as well as possible synthetic derivatives of both STX and TTX (good progress in guanidinium alkaloid syntheses is promising in this regard; Andresen and Du Bois 2009; Mulcahy and Du Bois 2008; Nishikawa et al. 2004; Sato et al. 2008); 2) close relatives of KIIIA, such as the μ-conotoxins SIIIA and SmIIIA (Bulaj et al. 2005; West et al. 2002); and 3) mutants of the channel, such as Na_V1.2[F385C] (Zhang et al. 2009), should advance our understanding of the mechanism of action of guanidinium alkaloids and μ-conopeptides that target site 1 of VGSCs. Furthermore, if active, covalently linked alkaloid–peptide adducts can be synthesized, these should provide insights into the arrangement of the units when bound to site 1, as well as also serve as second-generation ligands for sodium channels.

We introduced the descriptor syntoxin to denote the phenomenon wherein toxins such as TTX and KIIIA can act in concert (Zhang et al. 2009). From a broader perspective, investigation of the syntoxin interactions of guanidinium alkaloids and conopeptides with VGSCs may contribute to more than just our understanding of the structure and function of sodium channels per se. For example, STX is a major active factor in paralytic shellfish poisoning, a serious public health hazard (Al-Sabi et al. 2006; Bricelj et al. 2005). KIIIA is a lead compound in the development of an antidote to STX in the form of a contratoxin; i.e., a ligand that shields the target receptor against a toxin (Zhang et al. 2009). KIIIA's ability to prevent STX binding augurs well for its development into a contratoxin, although it remains to be seen whether KIIIA can be sculpted to minimize its efficacy in interfering with sodium conductance (that is, engineered to increase its rI_Na) without excessively compromising both its affinity for the channel and its ability to interfere with STX binding. It also remains to be shown how conserved are the properties of the toxins when tested against sodium channels expressed in mammalian cells (as opposed to Xenopus oocytes). In any event, the exploration of the syntoxin and contratoxin properties of μ-conotoxins and their derivatives opens a new window through which to view the pharmacology of sodium channels.

GRANTS

This work was supported by National Institutes of Health Grants GM-48677 to G. Bulaj, B. M. Olivera, and D. Yoshikami and R21 NS-055845 to G. Bulaj and D. Yoshikami.

DISCLOSURES

G. Bulaj is a cofounder of NeuroAdjuvants, Inc. B. M. Olivera is a cofounder of Cognetix, Inc.