Magnetoencephalography Demonstrates Multiple Asynchronous Generators During Human Sleep Spindles

Abstract

Sleep spindles are ∼1 s bursts of 10–16 Hz activity that occur during stage 2 sleep. Spindles are highly synchronous across the cortex and thalamus in animals, and across the scalp in humans, implying correspondingly widespread and synchronized cortical generators. However, prior studies have noted occasional dissociations of the magnetoencephalogram (MEG) from the EEG during spindles, although detailed studies of this phenomenon have been lacking. We systematically compared high-density MEG and EEG recordings during naturally occurring spindles in healthy humans. As expected, EEG was highly coherent across the scalp, with consistent topography across spindles. In contrast, the simultaneously recorded MEG was not synchronous, but varied strongly in amplitude and phase across locations and spindles. Overall, average coherence between pairs of EEG sensors was ∼0.7, whereas MEG coherence was ∼0.3 during spindles. Whereas 2 principle components explained ∼50% of EEG spindle variance, >15 were required for MEG. Each PCA component for MEG typically involved several widely distributed locations, which were relatively coherent with each other. These results show that, in contrast to current models based on animal experiments, multiple asynchronous neural generators are active during normal human sleep spindles and are visible to MEG. It is possible that these multiple sources may overlap sufficiently in different EEG sensors to appear synchronous. Alternatively, EEG recordings may reflect diffusely distributed synchronous generators that are less visible to MEG. An intriguing possibility is that MEG preferentially records from the focal core thalamocortical system during spindles, and EEG from the distributed matrix system.

INTRODUCTION

Large-scale oscillations of cortical field potentials may play a central role in synchronizing neuronal interactions (Buzsaki 2006). Discovered 75 yr ago (Loomis et al. 1935), spindles in the sleep EEG have been explored as a prototype of thalamocortical synchronization (Andersen and Andersson 1968; Contreras et al. 1997; Spencer and Brookhart 1961). In healthy humans, spindles occur mainly in stage 2 NREM sleep, last ∼0.5–2 s, and have a frequency of 10–16 Hz (Gibbs and Gibbs 1950). Spindles may play a role in memory consolidation and regulation of arousal (Buzsaki 2006; Destexhe and Sejnowski 2003).

Spindles recorded at the scalp are generated by postsynaptic currents in cortical pyramidal cells depolarized by the rhythmic firing of thalamo-cortical neurons. This rhythmicity arises from interactions between inhibitory cells in the thalamic reticular nucleus and bursting thalamocortical neurons (Destexhe et al. 1998; Traub et al. 2005). Widespread synchrony of cortical generators has been found in cats, where it is thought to represent synchrony of the thalamo-cortical projection cells, which results from cortical feedback (Contreras et al. 1997; Destexhe and Sejnowski 2003; McCormick and Bal 1997). Spindle synchrony may also be supported by matrix thalamo-cortical cells, which project diffusely to layer 1, in contrast to core thalamo-cortical cells which project focally to layer 4 (Jones 2001).

Widespread synchrony of spindle generators has been inferred to also occur in humans from the high correlation of spindle discharges across widely dispersed scalp EEG channels (Contreras et al. 1997). However, other data have suggested that at least two spindle generators may be active. EEG spindles often have lower frequencies over frontal compared with parietal leads (Anderer et al. 2001; De Gennaro and Ferrara 2003; Gibbs and Gibbs 1950; Schabus et al. 2007). Furthermore, in simultaneous EEG and magnetoencephalogram (MEG) recordings, spindles may appear in only one or the other modality or both (Hughes et al. 1976; Manshanden et al. 2002; Nakasato et al. 1990; Yoshida et al. 1996). However, because the MEG-only spindles might be considered incomplete and unrepresentative, typical EEG spindles themselves could still reflect a synchronous cortical discharge.

Source analysis of MEG spindles has found that multiple equivalent current dipoles (ECDs) are necessary to account for the field pattern (Lu et al. 1992; Shih et al. 2000; Urakami 2008). The number of generators remains unclear; a variety of source estimation techniques find that four sources, placed in the deep parieto-central and fronto-central regions bilaterally, are adequate to explain most of the variation in spindles, including the tendency for frontal spindles to be slower (Ishii et al. 2003; Manshanden et al. 2002; Urakami 2008), although Gumenyuk (2009) estimated overlapping sources for faster and slower spindle components. Shih et al. (2000) inferred multiple distributed generators, but their subjects were sedated, and animal studies indicate that this may result in more independent spindle generators (Contreras et al. 1997).

We re-examined these issues in this study, using combined high-density EEG and MEG. Spindles were identified using standard criteria from the EEG to permit comparison with previous studies. Although EEG spindles were highly coherent across the entire scalp, simultaneous MEG signals were incoherent with each other and with the EEG. The variability of MEG spindles in phase, amplitude, topography, and frequency implies that they are recording from multiple partially independent cortical generators. Several of these generators may summate at each EEG sensor to produce more synchronous signals. Alternatively, the EEG may be dominated by a weak but widespread spindle generator.

METHODS

Participants and recordings

We recorded the electromagnetic field of the brain during sleep from seven healthy adults (3 males, 4 females; ages, 20–35 yr). Participants had no neurological problems including sleep disorders, epilepsy, or substance dependence, were taking no medications, and did not consume caffeine or alcohol on the day of the recording. We used a whole-head MEG scanner (Neuromag Elekta) within a magnetically shielded room (IMEDCO, Hagendorf, Switzerland) and recorded simultaneously with 60 channels of EEG and 306 MEG channels. MEG SQUID (super conducting quantum interference device) sensors are arranged as triplets at 102 locations; each location contains one magnetometer and two orthogonal planar gradiometers (GRAD1, GRAD2). Unless otherwise noted, “MEG” will be used here to refer to the gradiometer recordings. Locations of the EEG electrodes on the scalp of individual subjects were recorded using a three-dimensional (3D) digitizer (Polhemus FastTrack). EEG channels had impedances <10 KOhms. Referential EEG recordings are referenced to averaged mastoid; bipolar EEG recordings are differential between adjacent scalp locations using a standard clinical montage (double banana). Unless otherwise noted, “EEG” will be used here to refer to referential recordings. Head position index (HPI) coils were used to measure the spatial relationship between the head and MEG scanner. Four subjects had a full night's sleep in the scanner and three had daytime sleep recordings (2 h). Padding was provided under the arms and knees, and around the head and neck, to make the subjects more comfortable and minimize movements. Every 20 min, the recording was stopped, data were saved, HPI locations were remeasured, and recordings were restarted. Analyses were limited to epochs where the subject did not move between the beginning and end of the 20 min recording. Sampling rate was either 1,000 (downsampled by a factor of 2 for the final analysis) or 600 Hz. The continuous data were low-pass filtered at 40 Hz. An independent component analysis (ICA) algorithm was used to remove ECG contamination (Delorme and Makeig 2004). Sleep staging was confirmed by three neurologists according to Rechtschaffen and Kales' sleep classification (Rechtschaffen and Kales 1968).

Coherence and power

Spindles were selected through visual inspection of all EEG channels during stage 2 NREM sleep. Events lasting ∼1 s and containing 10–15 Hz oscillations with a crescendo-decrescendo morphology were selected. We excluded spindles that immediately preceded or followed K-complexes. These standard clinical criteria identified 183 spindles from the seven subjects with a mean duration of 721 ± 235 (SD) ms (range, 427-1,386 ms). To calculate the magnitude square coherence, we used Welch's averaged modified periodogram. For any given pair of sensors, the time series were split into eight equal overlapping sections (with 50% overlap). In the next step, magnitude square coherence calculated from periodograms were averaged over time to reach one single number representing the coherence between the two selected sensors in the spindle frequency range (7–15 Hz). This method was used to compare one sensor from EEG (Fz) and all other EEG and MEG sensors for individual spindles. In a complementary and more extensive analysis, the scalp was divided into nine regions (right and left frontal, midfrontal, right and left parietal, vertex parietal, right and left occipital, midoccipital). The number of non-noisy EEG channels in any of these divisions was calculated, and a matching set of magnetometer and one set of gradiometers with the same topographical distribution were selected. Coherence between each possible pair of sensors was calculated for each spindle. Averaging of these coherences across pairs, spindles, and subjects yielded “sensor pair coherence.”

Spectral power was calculated as the squared Morlet wavelet transform of the spindles over 10–16 Hz (Caplan et al. 2001). This power needed to be over 90% more than background for at least 5 EEG channels over at least 4 cycles (see Caplan et al. 2001). The beginnings and ends of spindles were defined as where these criteria no longer obtained. Automatic selection of the beginning and end of spindles was confirmed by visual examination.

Principal components analysis

In each subject, four 30 s long segments of recordings from stage 2 sleep containing several spindles were selected. These long segments contained a total of 85 EEG spindles. We used principal components analysis (PCA) to quantify the dimensionality of the signal variance for each sensor modality, using the EEGLAB toolbox (Delorme and Makeig 2004). To have an unbiased comparison, for each subject, an equal number of sensors from each sensor modality (referential EEG, bipolar EEG, magnetometers, and gradiometers) was used. Channels were selected at random from each modality with the restriction that the number of channels included from any given lobe and hemisphere were equal across modalities. For each subject/sensor modality/segment, using singular value decomposition (SVD), PCA was calculated on individual spindles, and the cumulative sum of variance was measured and averaged across individual spindles. This indicates the complexity of the fields of the average spindle considered separately. In a separate analysis, the individual spindles from all long segments in each subject were concatenated, and PCA was calculated on the concatenated segment. This indicates the overall complexity of all spindles in a given subject considered together. The results of PCA can be plotted as the cumulative amount of variance explained versus the number of components. To compare different curves, we fitted each individual curve with a single-coefficient two-term exponential equation [f(x) = 1 – a × exp(−x) – exp(a × x)], and the coefficient a of each curve was entered into ANOVA. The average goodness of fit across all subjects was measured as R² = 0.977 ± 0.025 and sum of square errors (SSE) of 0.026 ± 0.0243.

RESULTS

In the first half of the results, spindle synchrony is examined in sensor space, for EEG and MEG separately and together; in the second half, the complexity of the spatiotemporal patterns of EEG and MEG during spindles are compared. We begin by presenting sample spindles for which the degree of synchrony measured by EEG (referential or bipolar) or MEG (magnetometers or gradiometers) can be appreciated from visual inspection. We quantify the degree of synchrony by measuring the average coherence between pairs of sensors of different kinds. The dimensionality of the spindle fields as recorded in different modalities is quantified by applying PCA and examining the amount of variance explained by successive components. PCA also allows quantification of the regularity of successive spindles, where visual inspection suggests greater variability when measured with MEG than with EEG.

EEG recordings of spindles appear more synchronous than do MEG recordings of the same spindles

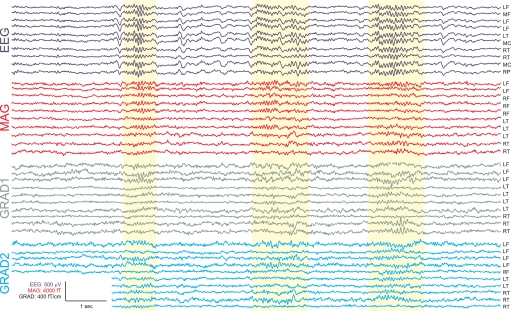
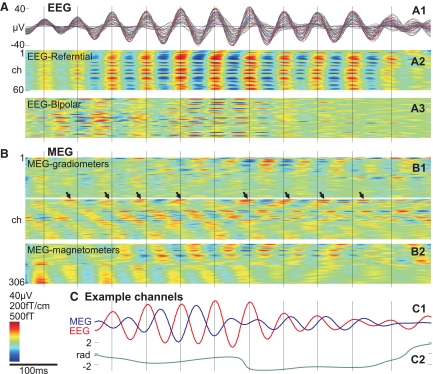
In Fig. 1, multiple spindles from representative EEG and MEG channels over different lobes and hemispheres are shown from a single subject. The complete recording profiles from all 306 MEG and all 60 EEG channels of the same epoch are portrayed in Supplementary Fig. S1.¹ In Fig. 2A1, all referential EEG channels recording a single spindle are superimposed, and in Fig. 2A2 the same data are shown with voltage color-coded. Standard referential EEG appears highly synchronous during spindles across wide areas of the scalp. In contrast, simultaneous recordings from MEG sensors show highly variable and asynchronous activity (Fig. 2B). Another example is shown in Supplementary Fig. S2.

Fig. 1.

Example spindles. Selected spindles in sample EEG and magnetoencephalogram (MEG) channels are highlighted in yellow. Complete recording profiles are shown in Supplementary Fig. S1. The greater variability in MEG spindles is obvious even in the raw recordings. L, left; M, middle; R, right; F, frontal; T, temporal; C, central; P, parietal.

Fig. 2.

Recording of a single spindle with EEG sensors (A), MEG sensors (B), and their relationship (C). A1: superimposed referential EEG waveforms from 60 scalp channels during a single spindle. A2: the same data in a time-intensity plot from referential and bipolar (A3) montages, where peaks and troughs, normalized to the largest channel, are obviously synchronous across the scalp. B: the EEG peaks, marked with vertical lines, have no regular relationship to the peaks of simultaneously recorded MEG spindles from 204 gradiometers (B1) and 102 magnetometers (B2). For this spindle, the mean coherence between Fz and the other 59 EEG ch was 0.82 and between Fz and the 306 MEG ch was 0.45. Arrows mark the peaks of an example MEG channel that initially precedes and later follows the EEG peaks (vertical lines). C1: waveforms of 2 of the largest amplitude EEG and MEG channels during the same spindle. Coherence between these 2 channels was 0.49. C2: instantaneous relative phase, calculated using the Hilbert transform, varies widely. Subject 2. For an example from another subject, see Supplementary Fig. S2.

Three kinds of variability can be observed in MEG spindles (Figs. 1 and 2). First, for a given spindle and sensor, activity may vary across time in amplitude, phase, and instantaneous frequency. Second, for a given spindle, activity may vary across sensors again in amplitude, phase-relations, or instantaneous frequency. Third, activity may vary across multiple spindles. That is, to the degree that different MEG sensors have consistent relative amplitudes, frequencies, or phase within a given spindle, those relationships may change in subsequent spindles. For example, in Fig. 1, the second spindle activates a different subset of MEG channels in comparison with the first and third spindles (see also Supplementary Fig. S1), whereas the EEG profiles are highly similar across the same spindles. The evidence for spindle synchrony has been taken from referential EEG (Contreras et al. 1997), whereas the most asynchronous spindles are recorded by the gradiometer MEG, and thus these sensor configurations are shown in Fig. 2 and Supplementary Fig. S2. Bipolar EEG and magnetometers exhibit intermediate levels of synchrony—greater than gradiometers but less than referential EEG (Fig. 2). From these figures, it is clear that both referential and bipolar EEG show a high degree of synchronization across most sensors, whereas the asynchronous MEG behavior can be seen in both magnetometers and gradiometers. In MEG recordings, some spindles showed a pattern resembling traveling waves (such a pattern can be seen in the selected spindle in Fig. 2). The more synchronous pattern of EEG compared with MEG was consistently observed for each individual spindle of every subject.

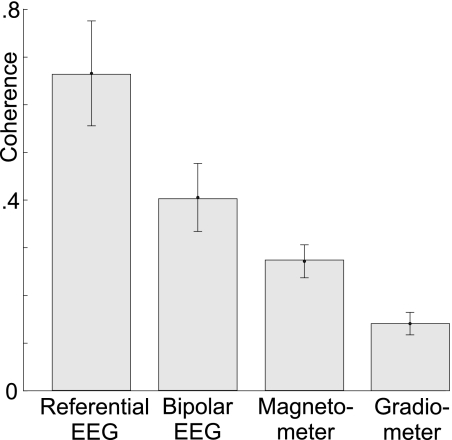
We quantified the more synchronous pattern of EEG versus MEG spindles by calculating all pairwise coherences across all spindles/subjects for a representative sample of sensors in each measurement modality. For each modality, a set of sensors was selected that were matched in number and distribution. Then, using the Welch method, the magnitude squared coherence between each pair of the selected modalities was calculated for each spindle, after band-pass filtering from 7 to 15 Hz. This was averaged across all spindles in each subject, and the mean and SD across subjects were determined. Referential EEG sensors had the highest pair-coherence (cross-subject mean and SD of 0.699 ± 0.083) of all measurement modalities and gradiometer sensors had the lowest coherence (0.306 ± 0.018). Bipolar EEG (0.504 ± 0.054) and magnetometers (0.403 ± 0.026) exhibited intermediate values. These numbers were evaluated by ANOVA with factors of measurement modality (with 2 levels of MEG and EEG) and measurement Δ (unipolar vs. bipolar). The main effects of measurement modality [F(1,24) = 159.98, P < 0.000001] and measurement Δ [F(1,24) = 56.37, P < 0.000001] were significant, as was the interaction between these factors [F(1,24) = 6.25, P < 0.0196]. In summary, across a large number of spindles, EEG is highly coherent (∼0.7 for referential and 0.5 for bipolar), whereas MEG is not (∼0.4 for magnetometers and 0.3 for gradiometers).

EEG and MEG have variable relationships during spindles

Spindles consist of oscillations that typically wax and wane in amplitude over the 4–20 cycles within a given spindle. Visual examination showed that the peaks of the envelopes of the EEG and MEG spindle oscillations occurred at different times (Fig. 1 and Supplementary Fig. S1). In addition, the peaks of each of the multiple MEG and EEG waves within a given spindle typically occur at different times, i.e., they exhibit a phase difference. The consistency of these phase differences across the time course of the spindle was examined by measuring the instantaneous phase difference between selected EEG and MEG channels calculated using the Hilbert transform (see methods section for details). As is shown in Fig. 2, C1 and C2, the phase lag between EEG and MEG channels varies substantially over the time course of a given spindle.

This variable relationship was confirmed by the low average coherences between sensors in different modalities. For example, the average coherence between the referential EEG channels and the magnetometer channels was 0.343 ± 0.024, lower than either referential EEG or magnetometers considered alone. Similarly, the average coherence between bipolar EEG and gradiometers was 0.368 ± 0.036—lower than bipolar EEG but higher than gradiometers considered alone (Fig. 3).

Fig. 3.

Within-modality coherence. Bars and error bars are cross-subjects means and SD of the average coherence between all pairs of sensors in each modality. EEG shows a higher within-modality coherence in comparison to MEG. In each modality, referential recordings show a higher degree of coherence than bipolar recordings (i.e., bipolar EEG is less coherent than referential EEG, and gradiometers are less coherent than magnetometers).

EEG and MEG spindles also differed in their frequency content. Spectral power was estimated in the lower (11–12 Hz) and higher (14–15 Hz) frequency bands during the middle 50% of each spindle (i.e., the segment of the spindle lying between 25 and 75% of spindle duration). Of the total EEG power in these bands, 38 ± 9.7% was in the lower band, whereas for MEG, the proportion was 51 ± 3.2%, a statistically significant difference (t = 3.38, P < 0.02).

Dimensionality of the spindle fields recorded by EEG and MEG

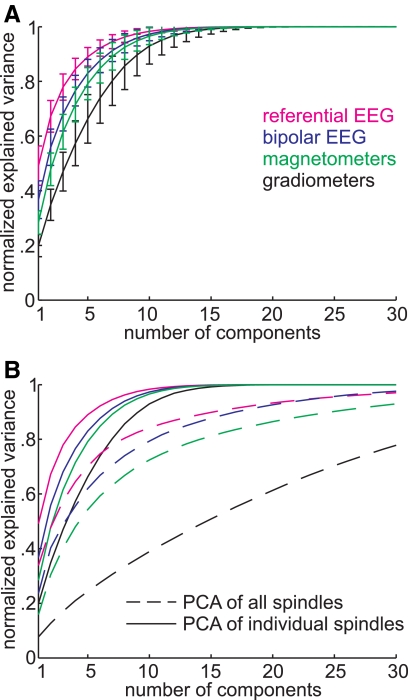
PCA extracts orthogonal components of the variance in a complex dataset. The first component is a linear combination of variables that accounts for the maximum amount of variance, the second component is chosen to account for the maximum amount of variance that remains, and so forth. Each component represents one spatial pattern, and thus the variance that is explained by successive components is a measure of the uniformity of the spindle's field pattern. Figure 4A shows the mean and SD of the cumulative variance explained by increasing numbers of PCA components for the different measurement modalities, calculated across 85 spindles in the seven subjects (the individual curves are shown in Supplementary Fig. S3). By this measure, referential EEG has the simplest pattern, with about one half of the variance explained by the first component. In contrast, only ∼20% of the variance in the gradiometer field pattern is explained by the first PCA component. Similarly, explaining 70% of the variance requires about two components for EEG and five for gradiometers. As usual, bipolar EEG and magnetometer fall between these two extremes, with bipolar EEG closer to referential EEG and magnetometers closer to gradiometers.

Fig. 4.

Spatiotemporal complexity in each modality evaluated with principal coaponent Analysis (PCA) of spindles. For each sensor modality, PCA was calculated and the variance of the data explained by increasing number of PCA components is plotted. A: cumulative sum of variance explained by PCA components calculated on 85 individual spindles in 7 subjects. PCA based on gradiometers (black lines) required the largest number of components to explain the data variance and referential EEG (magenta) the fewest. Bipolar EEG (navy blue) and magnetometer (green) gave intermediate values. Error bars indicate SD. B: comparison between PCA components that are calculated for individual spindles and applied to the same spindle (solid line, same procedure as in A) vs. PCA calculated on all spindles concatenated together and applied to each spindle separately (dashed line). Gradiometers are especially sensitive to the later process, which indicates that different spindles in a given subject have different spatiotemporal patterns.

ANOVA was performed on the proportion of variance explained by component 1, with factors of measurement modality (EEG, MEG) and measurement Δ (i.e., whether the device recorded in a referential vs. differential mode: referential vs. bipolar recordings for EEG, magnetometers vs. gradiometers for MEG). Significant main effects were found for Measurement modality [F(1,336) = 890.95, P < 0.000001], measurement Δ [F(1,336) = 276.07, P < 0.000001], and their interaction [F(1,336) = 10.1, P = 0.016]. Similarly, significant effects of measurement modality [F(1,336) = 521.89, P < 0.000001], measurement Δ [F(1,336) = 161.33, P < 0.000001], and their interaction [F(1,336) = 6.39, P = 0.0119] were found for the same ANOVA performed on the amount of variance explained by the fifth component.

Similarity of field patterns across spindles for EEG versus MEG

In the analysis described above, PCA was calculated on each individual spindle, and the variance explained by the PCA components on the same spindle was analyzed. In a second analysis, PCA was calculated on a group of spindles concatenated from a given subject. The PCA components were applied to the individual components, and the average amount of variance was analyzed. If the field patterns of individual spindles in a given subject were all identical, the two methods would yield identical results. In fact, less of the variance is explained by the second method by an amount that reflects the individuality of the different spindle spatiotemporal patterns. As is shown by a comparison of the solid and dashed lines in Fig. 4B, the decreased explanatory power of PCA components was true for all measurement modalities. This effect was most striking for the gradiometers, which required ∼15 components to account for 50% of the variance in the second method, whereas only ∼2 were required for the referential EEG. For quantification and statistical comparison, for each subject, these curves of cumulated variance explained versus number of PCA components were fitted with a two-term exponential equation with one single coefficient (see methods for details). These fits provided a single coefficient for each curve that were entered into ANOVA with factors of PCA calculation (individual or concatenated), measurement modality (EEG or MEG), or measurement Δ (unipolar or bipolar). Significant main effects were found for PCA calculation [F(1,48) = 499.09, P < 0.000001], measurement modality [F(1,48) = 299.47, P < 0.000001], and measurement Δ [F(1,48) = 129.38, P < 0.000001]. None of the interactions were significant (all F < 2, P > 0.05 for 95% CIs). These measures show that, across different spindles, the spatiotemporal EEG patterns are more similar to each other than are the spatiotemporal MEG patterns. Specifically, gradiometers show the highest degree of interspindle variability and thus seem to detect differences between spindles that are hidden from the EEG.

Distributed networks of MEG spindle generators

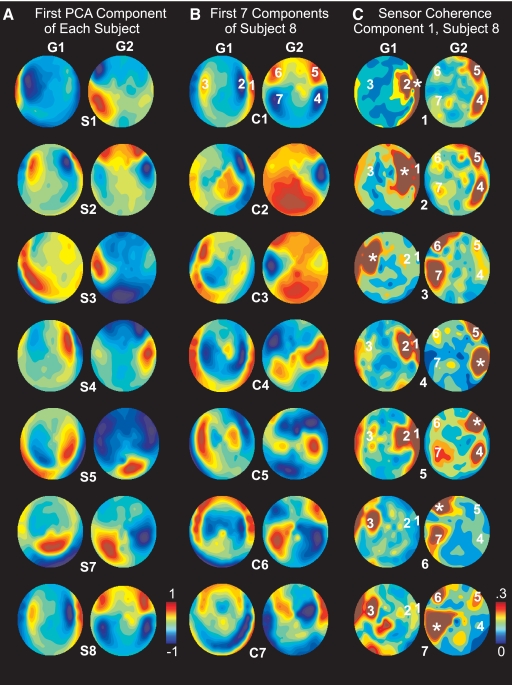
Figure 5 shows topographical plots of the loadings of each gradiometer sensor on various PCA components. These loadings represent the contributions of the sensor to that PCA component. Thus for example, if a PCA factor were caused entirely by spindle activity in the right frontal lobe, it would be reflected in these topographical plots as large loadings over the right frontal lobe. However, inspection of the topography of the PCA factor loadings showed that each factor involved multiple foci distributed across both hemispheres and multiple lobes rather than a single focus. A variety of spatial patterns are seen across the first factor of different subjects (Fig. 5A) and across successive PCA components within a given subject (Fig. 5B). For example, the first component in subject S8 showed strong factor loadings in gradiometers over the temporal, parietal, and frontal lobes of both hemispheres (Fig. 5B, top row). Note that, because the gradiometer signal to a generating neuronal dipole is maximal directly above that dipole, these maps provide an approximate indication of the probable location of the underlying generators. PCA factors were derived using recordings from both orthogonal planar gradiometers across all spindles in this subject simultaneously. The loadings on Grad1 and Grad2 sensors for a given PCA factor show little spatial correspondence, suggesting that the underlying generators do not have sufficient spatial extent to produce multiple equivalent dipole orientations.

Fig. 5.

Distributed coherent networks of MEG generators. A: topographical maps of the factor loadings for the first PCA factor for each subject (S1, S2 … S8). Factor loadings represent the contribution of each sensor to the PCA component. Separate maps are shown for the orthogonal planar gradiometers: grad1 (G1) and grad2 (G1). PCA factors were derived using grad1 and grad2 recordings after concatenating all spindles in a given subject (i.e., factors were chosen to account for the variance across all spindles simultaneously). Because gradiometer signals are maximal over their generating cortex, these maps may be interpreted as indicating the likely lobe and hemisphere of the variance underlying each indicated PCA factor. B: topographical maps of the factor loadings for the 1st 7 PCA factors (C1, C2 … C7) for subject 8. C: coherence maps in subject 8. The 7 sensors with the peak factor loadings in the 1st principle component were chosen as seeds (marked in the top row of B), and the coherence map was calculated to each seed as indicated by the * on each plot.

The relationship between the multiple locations with high factor loadings in a given PCA factor was explored by constructing maps of the coherence from each of these locations to all other sensors. As shown in Fig. 5C for an example component in a single subject, the coherence between these multiple sites is elevated. Although in many cases the locations of high coherence are adjacent to the seed point, this is by no means always the case. For example, seed 7 (indicated by an * in the bottom row of Fig. 5C) in the right occipitotemporal cortex has relatively strong coherence with prefrontal cortex sites in both the ipsilateral (locations 3 and 6) as well as contralateral (location 5) hemispheres.

These data indicate that the PCA factors are identifying networks of locations with higher mutual coherence during spindles. This was quantified by measuring the coherence between each pair of sensors with peak loadings in the first PCA factor in each subject, with the requirement that the sensors must be separated by ≥45°. In the seven subjects, three to seven (mean, 4.7) sensors were chosen. Their average coherence was 0.308 ± 0.055. Random sets of spindles (n = 1,000) were chosen in each subject with the same number of sensors, the same distribution between grad1 and grad2, and the same minimum (45°) and average (85°) angular separation. The average difference in angular separation between the PCA-based locations and the control sets was <1°. The average coherence of this control set across subjects was 0.177 ± 0.019, which was significantly lower than that of the PCA-identified peaks (paired 2-tailed t-test, P < 0.0001). In addition, the distribution of the random sets of spindles was used in each subject to create a probability distribution for the mean coherence under the null hypothesis. According to these resampling statistics, coherence was elevated in the network of PCA-identified locations in each subject considered independently at P < 0.001.

DISCUSSION

We found several respects in which EEG and MEG exhibit different characteristics during the same sleep spindle. First, pairs of EEG channels are highly coherent with each other across the scalp (average of ∼0.7), whereas MEG channels are not (average ∼0.3). The EEG results are consistent with earlier studies showing widespread synchrony during spindles (Achermann and Borbely 1998; Duckrow and Spencer 1992; Werth et al. 1997).

Second, the spatiotemporal pattern of EEG during the spindle is relatively constant within and between spindles, whereas that of MEG is not (only ∼2 PCA components were required to account for 50% of the variance of spindles recorded by referential EEG, whereas ∼15 were required for the gradiometer recordings). Although this comparison has not previously been made between MEG and EEG spindles, variable topography is implicit in the finding that several equivalent current dipoles are needed to account for the variance in multichannel MEG recordings (Lu et al. 1992; Shih et al. 2000; Urakami 2008).

Third, EEG during spindles has over twice as much power at 14–15 than at 11–12 Hz, whereas MEG during the same spindles has equal power at the two frequencies. Apparently this difference between EEG and MEG during spindles has not been reported previously. However, because EEG power during spindles in parietal leads is relatively greater at higher frequencies (Gibbs and Gibbs 1950), this might suggest a greater contribution of more posterior generators to EEG spindles. Urakami (2008) remarked that the frequency content of MEG and EEG spindles could be different but excluded such spindles from analysis. The remaining spindles were separated based on EEG into faster and slower spindles. Source analysis of the simultaneous MEG associated slower spindles with precentral dipoles and faster spindles with postcentral dipoles. Because we included all spindles in our analysis, our finding indicates a general difference between the MEG and EEG during spindles. Also, the number of PCA components required to account for the variance in our recordings implies that a model including only a slower frontal and faster parietal generator would be insufficient to explain the MEG data.

Overall, EEG spindles can be characterized as widespread and synchronous, whereas MEG spindles are composed of multiple asynchronous signals, necessarily implying multiple asynchronous generators. The ultimate sources of both EEG and MEG signals are active transmembrane currents, balanced by passive transmembrane return currents. Intracellular currents linking active and passive transmembrane currents generate MEG, and extracellular currents generate EEG. Because EEG and MEG are thus generated by different limbs of the same circuit, the striking differences in how they manifest during spindles must ultimately be related to biophysical differences in how they propagate from generators to sensors.

A major difference between EEG and MEG propagation is that each EEG sensor records from a larger cortical area than each MEG sensor, because EEG is smeared by the skull and cerebrospinal fluid (CSF) before reaching the scalp EEG sensors, whereas MEG is little affected by intervening tissue (Hamalainen and Ilmoniemi 1994). Furthermore, EEG is sensitive to dipoles that are either radial or tangential with respect to the skull, whereas MEG is mainly sensitive to tangential dipoles (Cohen and Cuffin 1983).

Because EEG records from larger leadfields than MEG, it tends to be dominated by distributed sources. For example, published data indicate that the ratio of EEG to MEG (measured as peak-to-peak amplitudes in μV and fT/cm) is ∼0.04 for the response to a single focal tangential dipole (e.g., electrical stimulation of the median nerve, at 20 ms; Huang et al. 2007; Komssi et al. 2004). In contrast, the EEG to MEG ratio was ∼2.0 during the current spindle recordings. Thus isolated focal sources could have produced MEG spindles of the observed amplitude without having produced at the same time detectable EEG spindles. Specifically, a focal source generating a MEG spindle of the observed size would produce an EEG spindle ∼50 times smaller than that actually observed. These observations are thus consistent with MEG spindles being generated by multiple scattered largely asynchronous sources, whereas the simultaneous EEG spindles are generated by a different source. Previous reports that some spindles are recorded by MEG but not EEG, and vice versa (Hughes et al. 1976; Manshanden et al. 2002; Nakasato et al. 1990; Yoshida et al. 1996), would also be consistent with the view that they are recording from different brain systems.

The nature of the generator of EEG spindles is suggested by the ratio of EEG spindle amplitude when recorded at the cortical surface versus at the scalp, ∼2:1 (Asano et al. 2007; Nakabayashi et al. 2001; Nakamura et al. 2003). Empirical and modeling studies suggests that this ratio is consistent with very widespread generation (Nunez and Silberstein 2000). Thus the observed differences between EEG and MEG spindles, as well as their relative amplitudes with respect to each other and to cortical recordings, are consistent with the possibility that MEG is recording from scattered focal asynchronous generators, whereas EEG is recording from a highly distributed and coherent generator.

Clearly, this view would explain the high level of synchrony between EEG sensors during spindles and the low level between MEG sensors. However, our results may also be consistent with the possibility that some EEG sensor synchrony reflects the superposition of multiple partially asynchronous sources, which are sampled more discretely by MEG. A single EEG sensor may receive significant contributions from all lobes in both hemispheres. Consequently, each cortical source may project to many different EEG sensors, resulting in high synchrony between sensors even when sources are independent (Srinivasan et al. 2007).

Another mechanism that could lead to high synchrony between EEG sensors is suggested by our finding that the sources detected with MEG seem to consist of multiple sets of generators, moderately coherent within each set, and incoherent outside the set. Each set is composed of discrete locations distributed across the lobes and hemispheres. Consequently, each EEG sensor may sample all of the sets, leading to the observed synchrony.

In summary, the variability of spindles across MEG sensors implies that they are recording from multiple partially independent cortical generators. Several of these generators may summate at each EEG sensor to produce synchronous signals. However, the relative amplitudes of MEG and EEG spindles suggest that the focal generators of MEG spindles may not be detectable by EEG. Rather, EEG may instead be dominated by a weak but widespread spindle generator. Modeling studies, exactly replicating the current recording regime, and incorporating results from intracranial recordings, are needed to determine which alternative is most consistent with the detailed characteristics of MEG and EEG during spindles.

Our finding that MEG spindles exhibit multiple incoherent foci is directly opposed to a cardinal feature of the most generally accepted account of mammalian sleep spindles. Extensive recordings in mammals led to the proposal that spindles during normal sleep are synchronous across the thalamus and cortex (Contreras et al. 1997). When desynchronization has been observed, it has been ascribed to the presence of lesions, in vitro recordings, or the influence of anesthesia (Contreras et al. 1997; Destexhe and Sejnowski 2003; McCormick and Bal 1997). Widespread synchrony of spindle generators was inferred in humans from the high correlation of spindles in scalp EEG (Contreras et al. 1997). Although our results directly confirm the human scalp EEG results of Contreras et al. (1997), with a larger number of channels (62 rather than 8), the simultaneous MEG recordings provide a radically different perspective. This difference between our conclusions in humans and those of Contreras et al. in cats may be a true species difference, arising in the 75 million years since our common ancestor. Alternatively, the largest distance between cortical electrodes (7 mm) studied by Contreras et al. may have been too small to show asynchronous generators in cats, let alone in humans, where the distance separating two locations on the cortical surface can be >400 mm. Indeed, the interelectrode cross-correlation reported by Contreras et al. (1997) had already fallen from 0.9 at 1 mm to 0.5 at 7 mm.

Studies in anesthetized cats showed that, in addition to cortical spindles that were widely synchronous, spindles could occasionally be restricted to small thalamo-cortical modules or manifest as complex spatial patterns of spindles oscillating in multiple areas, with largely independent durations, onsets, frequencies, and phase (Andersen and Andersson 1968). Ganes and Andersen (1975) showed that when spindles in distant cortical locations are coherent, that those locations are functionally related, such as the face areas of primary and secondary somatosensory cortices. This suggests that the multiple distant mutually coherent locations that we found to load on the same PCA factor for MEG spindles may be functionally related.

These classical studies showing both distributed and focal spindles were interpreted in terms of the recruiting and augmenting responses that characterize thalamo-cortical projections from the specific projection and nonspecific intralaminar nuclei, respectively (Spencer and Brookhart 1961). This distinction has evolved into a distinction between the core and matrix thalamo-cortical systems (Jones 2001). Core cells project highly focally, typically terminating with large boutons in layer 4, which transmit focal sensory information via ionotropic receptors (Zikopoulos and Barbas 2007). In contrast, matrix cells project very diffusely, often to multiple cortical areas, and terminate in a dense matrix of small boutons in layer 1, associated with slow modulatory N-methyl-d-aspartate (NMDA) and metabotropic transmission (Rubio-Garrido et al. 2009). The anatomy and physiology of the matrix projection is thus ideal to convey synchronous thalamically generated rhythms to large cortical areas. Matrix cells are present in all thalamic nuclei, but core cells predominate in the specific projection nuclei. Thus the classical studies of spindle discharges in cats showing both distributed and focal spindles seem to have reflected activation of the matrix and core thalamo-cortical systems, respectively.

Similarly, the differences between EEG versus MEG spindles may arise from their biophysically determined differential sensitivity to these different thalamocortical systems. EEG would be highly sensitive to activation by the matrix system of external cortex on the crowns of gyri, including that directly underlying the sensors. Because it is synchronous and EEG sensors have large leadfields, this matrix activation of the gyral crowns would tend to overwhelm the contribution from scattered focal asynchronous generators activated by the core system. In contrast, MEG would be insensitive to the matrix activation of external gyral crowns because these are generally radial dipoles. However, MEG would be highly sensitive to focal activation by the core system in an underlying sulcus. Neither MEG nor EEG would respond significantly to matrix activation within the sulci, where synchronous activation of the opposing banks would tend to cancel each other. Because the core and matrix systems are connected at both the thalamic and cortical levels, spindles in one system may be expected to often spread to the other, resulting in the loose linkage between MEG and EEG spindles observed in the current and other studies. If this hypothesis is correct, simultaneous recordings of spindles with MEG and EEG may offer a method to probe the two thalamocortical systems, and their interactions, noninvasively in humans.

GRANTS

This research was supported by National Institutes of Health Grants EB-009282, NS-18741, and NS-44623.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).