Generalization of Dynamics Learning Across Changes in Movement Amplitude

Abstract

Studies on generalization show the nature of how learning is encoded in the brain. Previous studies have shown rather limited generalization of dynamics learning across changes in movement direction, a finding that is consistent with the idea that learning is primarily local. In contrast, studies show a broader pattern of generalization across changes in movement amplitude, suggesting a more general form of learning. To understand this difference, we performed an experiment in which subjects held a robotic manipulandum and made movements to targets along the body midline. Subjects were trained in a velocity-dependent force field while moving to a 15 cm target. After training, subjects were tested for generalization using movements to a 30 cm target. We used force channels in conjunction with movements to the 30 cm target to assess the extent of generalization. Force channels restricted lateral movements and allowed us to measure force production during generalization. We compared actual lateral forces to the forces expected if dynamics learning generalized fully. We found that, during the test for generalization, subjects produced reliably less force than expected. Force production was appropriate for the portion of the transfer movement in which velocities corresponded to those experienced with the 15 cm target. Subjects failed to produce the expected forces when velocities exceeded those experienced in the training task. This suggests that dynamics learning generalizes little beyond the range of one's experience. Consistent with this result, subjects who trained on the 30 cm target showed full generalization to the 15 cm target. We performed two additional experiments that show that interleaved trials to the 30 cm target during training on the 15 cm target can resolve the difference between the current results and those reported previously.

INTRODUCTION

Generalization in motor control is the extent to which training affects movements in situations not encountered during learning. In this study, we examined generalization of dynamics learning using a well-known experimental task in which subjects learn to compensate for forces applied to the hand during reaching movements to targets (Lackner and Dizio 1994; Shadmehr and Mussa-Ivaldi 1994). Broadly speaking, there are two different ways that this kind of learning might be encoded in the brain (Atkeson 1989). One possibility is that the brain learns the structure of the relationship between movement states and the perturbing forces experienced during training. The other possibility is that adaptation does not involve any kind of general model of the new dynamics but instead involves changes in performance that are tied to the movements made during training. Patterns of generalization can distinguish between these possibilities. In the first case, dynamics learning would generalize to new movements that were not experienced during training, whereas in the second, there would be little or no effect of learning on movements other than those in the training task. Thus studies on generalization can be used to infer the underlying nature of dynamics learning.

Previous studies have shown that there is limited spatial generalization of dynamics learning (for an exception, see Hwang et al. 2003). For example, when subjects learn to compensate for forces while moving in one direction, the extent to which movements in other directions are affected by dynamics learning falls off as the separation between training and test directions increases (Donchin et al. 2003; Gandolfo et al. 1996; Huang and Shadmehr 2007; Mattar and Ostry 2007; Thoroughman and Shadmehr 2000; Thoroughman and Taylor 2005). This suggests that the learning is tightly coupled to the movements made during training. Studies have shown that dynamics learning can be tied to arbitrary cues (Krouchev and Kalaska 2003; Osu et al. 2004; but see Gandolfo et al. 1996) or to the context in which movements are made (Cothros et al. 2006, 2009; Kluzik et al. 2008). Moreover, dynamics learning acquired while producing one utterance does not generalize to a second utterance, even if the kinematics of the first utterance are embedded in the second (Tremblay et al. 2008). These findings support the idea that dynamics learning is tied to the situation in which it is acquired.

An important exception to the idea that dynamics learning does not generalize broadly comes from work examining generalization across changes in movement amplitude (Goodbody and Wolpert 1998). In that study, subjects learned a force field while moving to a target located 12.5 cm away. To evaluate generalization, subjects made movements to a target at 25 cm on trials interleaved throughout the training session. These movements were made in six different force fields, which were designed to test different possible patterns of generalization. The experimenters determined that, after training on the 12.5 cm target, subjects performed best on the 25 cm target when moving in the same force field. Thus having learned to compensate for the force field while moving to one target generalized, such that the forces were predicted and compensated for during movements to another target. This finding is consistent with the idea that dynamics learning generalizes to movement states (positions, velocities) beyond the range of states experienced during training. This suggests that the pattern of generalization for changes in movement amplitude is unlike the pattern seen for changes in movement direction. Here, dynamics learning was not tied to the situation in which it was acquired and instead appeared to generalize more broadly.

To understand this difference, we performed the following set of experiments. We examined generalization of dynamics learning across both increases and decreases in movement amplitude. We made use of the tendency for larger amplitude movements to be faster to examine the combined role of amplitude and velocity in dynamics learning and generalization. Unlike in previous studies in which training and transfer movements were interleaved, we fully separated training from tests of generalization. To assess the extent to which dynamics learning generalized, we analyzed the lateral forces that subjects applied to compensate for the force field. We also examined changes in movement kinematics after learning. Our results show an asymmetric pattern of generalization. When movement amplitude increases from 15 to 30 cm, both the kinematic and force measures show that subjects compensate for the force field only within the range of the longer movement that overlaps the shorter training movements. When movement amplitude decreases from 30 to 15 cm, generalization is complete. To address differences between our findings and those of others, we conducted two additional experiments in which we assessed the impact of interleaving trials to the 30 cm target during training to the 15 cm target, as was done previously (Goodbody and Wolpert 1998). We found that interleaved trials result in patterns of kinematic performance and lateral force production that suggest generalization of dynamics learning. Thus our results suggest that dynamics learning is local not only for changes in movement direction but also for changes in movement amplitude.

METHODS

Subjects and apparatus

Seventy-two right-handed subjects [33 males; overall mean age, 21.57 ± 3.61 (SD) yr] signed an institutionally approved consent form and agreed to participate in this study. All subjects were naïve. Thirty-six subjects participated in experiment 1. Experiments 2 and 3 had 12 and 24 subjects, respectively.

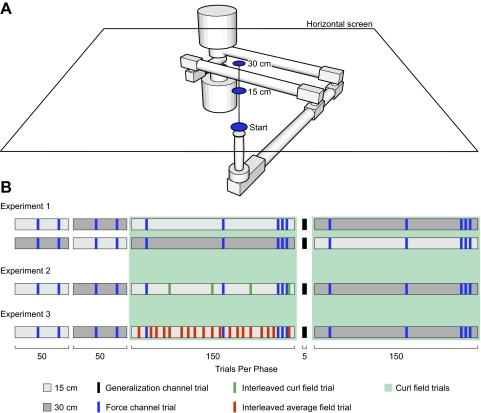
Subjects held the handle of a two-joint robotic device (InMotion2, Interactive Motion Technologies, Cambridge, MA) and made pointing movements to targets in the horizontal plane (Fig. 1A). Movement targets were presented on an LCD television (Sony, Tokyo, Japan) that was positioned ∼20 cm above the subject's hand. A semisilvered mirror suspended midway between the subject's hand and the television reflected the image from above and created the impression that targets were presented within the plane of movement. The screen was calibrated for each subject separately such that the position of reflected images on the screen was aligned with the subject's hand throughout the workspace. The calibration involved recording the actual position of the hand at each point within a two-dimensional array presented on the screen. We performed a regression to determine the mapping between the location of pixels on the screen and the hand's actual location. This allowed us to determine which pixels to illuminate such that, for the subject, the reflected image of the pixels would appear aligned with the hand's location. The robot's position was sensed at 400 Hz using 16-bit optical encoders (Gurley Precision Instruments, Troy, NY) and filtered using a third-order low-pass Butterworth filter at 30 Hz. Movement velocity was computed by numerically differentiating the filtered position signal. A force transducer measured forces applied to the robot handle (ATI Industrial Automation, Apex, NC). The force signal was filtered using a first-order low-pass Butterworth filter at 20 Hz. The robot could be programmed to apply forces to the subject's hand via torque motors connected to the robot's shoulder and elbow joints. The subject's arm was supported by an air-sled.

Fig. 1.

Apparatus and experimental protocol. A: subjects made movements to targets along the body midline while holding the handle of a 2-joint robotic manipulandum. Targets were located 15 and 30 cm from the start location. A horizontal screen, which consisted of a semisilvered mirror, reflected images presented on an LCD television that was suspended above the apparatus (not shown). This resulted in the visual illusion that the targets were located in the plane of reaching movements. B: the experiment comprised a sequence of 405 movements. Subjects began by making 50 baseline movements to both the 15 and the 30 cm target. On 2 movements during the baseline phase, the robot was programmed to apply a force channel. On all other movements, the robot applied no forces. Subjects made 150 movements during the training phase. Of these, 5 were force channels. In experiment 1, the remaining movements were made in a clockwise force field that pushed the hand predominantly to the right. In experiment 2, the training session included 4 movements to the 30 in the same force field. In experiment 3, 19 trials in the average force field were interleaved. Immediately after training, generalization across a change in amplitude was tested by having subjects make 5 movements in force channels. Subjects made 150 training movements to the generalization target in the same force field. Force channels during training tracked lateral force production.

Experimental task

Subjects made outward movements to targets along the body midline. The starting position was located ∼15 cm in front of the subject. Its position corresponded to shoulder and elbow angles of ∼50° relative to the frontal plane and ∼70° relative to the upper arm, respectively. The start position had a radius of 1 cm. Subjects began each trial by holding their hand within the start position for 1,000 ± 300 ms. A target of radius 1 cm appeared, either 15 or 30 cm from the start position. Subjects were required to move to the target and stay within its boundaries for 750 ms. Subjects received feedback on the movement's peak tangential velocity. Note that feedback was used only to encourage subjects to move as desired and was not used to exclude movements from analyses. The desired peak tangential velocities were 34.60 and 53.70 cm/s ±10%, for the 15 and 30 cm targets, respectively. Actual mean peak velocities were 33.11 ± 1.28 and 50.07 ± 3.36 (SD) cm/s, respectively. These desired peak tangential velocities were determined in an initial pilot study in which subjects were asked to make movements to each target at a pace that was “natural and comfortable” given the amplitude. We thus allowed movement velocity to vary between the 15 and 30 cm movements. At the end of each movement, the robot moved the subject's hand back to the start position.

Experiment 1

In experiment 1, subjects were assigned to one of two groups before beginning the experiment. The logic of the experimental design was to train subjects on one target and to test for generalization of dynamics learning during movements to the other target. For the first group (24 subjects), subjects trained on the 15 cm target and were tested for generalization on the 30 cm target. The second group (12 subjects) trained on the 30 cm target and were tested on the 15 cm target. The experimental protocol is shown in Fig. 1B. Rectangles show each phase of the experiment, and indicate movements to the 15 (light gray) and 30 cm (dark gray) targets. The experimental session was divided into five phases. Subjects completed 405 movements in total. In the first phase, subjects made 50 movements to the training target. In the second phase, subjects made 50 movements to the test target. In the first and second phase, on 48 of 50 movements, the robot applied no force to the subject's hand. These movements served as baseline measures of kinematic performance. On the remaining two movements, the robot was programmed to apply a force channel (Scheidt et al. 2000) to measure baseline lateral force production. In the third phase, subjects made 150 movements to the training target. One hundred forty-five of these movements served as training movements, during which the robot applied a clockwise force field to the subject's hand. On the remaining five movements, the robot applied a force channel to measure lateral force production during training. Immediately after completion of the third phase, subjects made five movements to the test target while the robot applied a force channel. These movements allowed us to measure how lateral force production on movements to the test target was affected by having learned to compensate for the force field on the training target. These trials are indicated by black rectangles in Fig. 1B. After the test for generalization, subjects were allowed a short break. They then completed 150 movements to the test target in the final phase of the experiment. Once again, 145 of these movements were made in the clockwise force field and the remaining 5 were made in force channels. Force channels throughout the experiment are indicated by vertical blue lines in Fig. 1B.

Experiments 2 and 3

The results we obtained in experiment 1 led us to conduct two additional experiments. In both of these experiments, we explored differences between our findings in experiment 1 and those of Goodbody and Wolpert (1998), who studied generalization of dynamics learning across changes in movement amplitude. An important methodological difference is that, in experiment 1, we separated training movements from the test for generalization. In Goodbody and Wolpert (1998), generalization was assessed on movements that were interleaved throughout training. On these interleaved movements, subjects moved to the farther target in one of six different force fields. The six different fields were modified versions of the force field subjects experienced during training. In experiments 2 and 3, our goal was to determine whether the pattern of generalization is affected by interleaving training and transfer movements.

In experiment 2, we interleaved four trials to the 30 cm target during training. We chose four interleaved movements based on Goodbody and Wolpert (1998). In that study, subjects made 50 outward movements in an initial block of trials, followed by a block of 192 movements during which generalization was tested on interleaved trials. Of the 192 outward movements made by subjects, 4 movements were made to the farther target in exactly the same force field in which subjects were trained when moving to the nearer target. As such, we replaced 4 of the 145 training movements with interleaved movements to the 30 cm target. These trials are indicated by vertical green lines in Fig. 1B.

In experiment 3, the logic was the same. In Goodbody and Wolpert (1998), on 24 of the 192 outward movements in the interleaved training sequence, subjects moved to the transfer target in one of the six different force fields designed to test for generalization. Here, we replaced 19 of the 145 training movements with interleaved movements to the 30 cm target. On these movements, subjects experienced a force field that was the average of the test fields explored in Goodbody and Wolpert (1998). We did this based on the assumption that subjects learned an average of the six fields that were used to assess generalization (Takahashi et al. 2001).

The design for experiments 2 and 3 is shown in Fig. 1B, plotted as it was for experiment 1. Subjects began by making baseline movements (48 movements plus 2 force channel trials) to the 15 cm followed by the 30 cm target. Subjects then made training movements. During the training block, we interleaved either 4 (experiment 2; vertical green lines in Fig. 1B) or 19 (experiment 3, vertical red lines) movements to the 30 cm target. The force field for interleaved movements differed for the two experiments; we used the clockwise force field in experiment 2 and the average force field in experiment 3. We also included five force channel trials to track production of lateral forces during training. The remaining trials (141 in experiment 2 and 126 in experiment 3) were made to the 15 cm target in the clockwise force field. Immediately after training, generalization was assessed by having subjects make five movements to the 30 cm target in force channels. After a short break, subjects made 145 movements to the 30 cm target in the clockwise force field. Training on the 30 cm target included five force channel trials.

Force channels

In all experiments, we used force channel trials to measure the lateral forces produced by subjects during outward movements (Scheidt et al. 2000). The use of force channels for measuring dynamics learning and generalization was introduced subsequent to previous work on generalization over changes in movement amplitude (Goodbody and Wolpert 1998). On channel trials, the robot was programmed to apply a stiff lateral boundary, such that lateral movements were prevented while movements toward the target were unconstrained. When subjects push into the channel wall, the robot applies an equal amount of force in the opposite direction to eliminate lateral movement. The forces recorded by the force transducer can thus provide an accurate record of subjects' lateral force production.

Force channels were positioned laterally such that they ran from the center of the start position through the center of the target. The channel was applied according to the equation

$$\begin{array}{l}{F}_{\text{x}}\text{=}\left(K{d}_{\text{x}}\right)+\left(D{V}_{\text{x}}\right)\hfill \\ F_{\text{y}}=0\hfill \end{array}$$ (1)

where F_x and F_y are forces in the lateral and sagittal directions (N), d_x is the lateral distance of the hand from the center of the channel (m), and V_x is the lateral velocity of the hand (m/s). D is a damping coefficient with a value of −60 Ns/m. K is a stiffness coefficient whose value depended on the lateral position of the hand with respect to the center of the channel. When the hand was >2.5 mm from the center of the channel, its value was held constant at −6,000 N/m. The coefficient was linearly ramped to zero from the 2.5 mm boundary to the center of the channel. In conjunction with the velocity damping, this reduced the harshness of the channel at the expense of permitting some lateral movement. Note that no forces were applied along the axis of movement. Our channel was defined in a manner similar to a previous report from another laboratory (Scheidt et al. 2000).

In experiment 1, one half of the subjects who trained on the 15 cm target and were tested for generalization on the 30 cm target were tested using force channels as described above. The remaining 12 subjects were tested in stiffer channels that more fully prevented lateral deviations of the hand. For these channels, we decreased the lateral range over which the stiffness coefficient was ramped. In this case, the stiffness coefficient changed linearly from 0 to −6,000 N/m as the hand's lateral deflection increased to 0.5 mm. The channel was otherwise defined as described above. Repeated-measures ANOVA on forces recorded during channel movements found no differences in performance related to the two channel types (F_(1,22) = 0.946, P > 0.30). As such we combined the two groups.

Clockwise force field

In all experiments, a clockwise force field was used during training. In experiment 2, the clockwise force field was also used on interleaved trials. This velocity dependent force field pushed the hand lateral to its instantaneous trajectory. The robot motors applied the force field according to the equation

$$\left[\frac{F_{\text{x}}}{F_{\text{y}}}\right]=\left[\frac{0D}{-D0}\right]\left[\frac{V_{\text{x}}}{V_{\text{y}}}\right]$$ (2)

where x and y are the lateral and sagittal directions, respectively, F_x and F_y are the forces applied to the hand by the robot (N), and V_x and V_y are the hand's velocity (m/s). D is a coefficient defining the strength of the clockwise force field and was set to 15 Ns/m.

Average force field

In experiment 3, we designed a force field based on the fields explored by Goodbody and Wolpert (1998). They tested for generalization of dynamics learning across changes in movement amplitude by having subjects make a series of movements to the test target in one of six different force fields (see Table 2 in Goodbody and Wolpert 1998). For four of these fields, the strength of the clockwise field (i.e., the slope of the force/velocity relationship) was varied relative to the field in which subjects made training movements. The test fields were 0.5, 1.0, 1.5, or 2.0 times as strong as the training field. The fifth test field was identical to the training field for the range of velocities experienced during training and was set to zero at velocities greater than those experienced during training (the cut-off field). The strength of the sixth test field was zero across all velocities. For experiment 3, we generated a force field that was the average of these six fields. Within the range of velocities experienced during training (i.e., for tangential velocities ≤34.60 cm/s), we set the strength of the force field (D in Eq. 2) to 15 Ns/m. The strength for faster velocities was 12.5 Ns/m.

Measures and statistics

Movement start and end were determined based on velocity profiles. Movement start was scored as the moment that tangential velocity exceeded 5% of its peak value. Movement end was scored as the moment that tangential velocity fell below 5% of its peak and remained below this threshold for 50 ms.

We quantified kinematic performance in the force field using a standard point-measure of movement curvature. We computed the maximum deviation of the hand perpendicular to a vector linking movement start and end. Changes in perpendicular error (PE) over the course of the experiment (i.e., dynamics learning) were quantified using repeated-measures ANOVAs. For both movement amplitudes, we normalized PE relative to mean performance in the baseline phase by subtracting mean baseline PE on a per subject basis. In experiment 1, we used ANOVA to compare how PE over the initial five and final five movements during training for both movement amplitudes differed depending on the order in which subjects moved to the two targets. We performed a second analysis, in which we grouped PE data from experiments 1, 2, and 3 and used ANOVA to determine how curvature on the initial five movements after the test for generalization depended on previous training. As in the previous analysis, PE data were normalized relative to baseline performance. Bonferroni-corrected post hoc tests were performed when appropriate.

We also performed analyses in which the time-varying performance during movement was left intact. Lateral forces applied to the walls of force channels were analyzed by comparing them to the forces that should have been applied had subjects fully learned the relationship between movement velocity and forces generated by the robot during training. We computed expected lateral forces (F_x) based on the measured movement velocity (V_y) on channel trials, multiplied by the strength of the force-velocity relationship experienced during training (15 Ns/m). Actual and expected lateral forces should be no different if subjects have fully learned to compensate for the force field during training. They should also be no different on tests of generalization if dynamics learning transfers across changes in movement amplitude. To assess for statistical differences between actual and expected forces, we performed functional ANOVAs (fANOVAs). This functional technique is an extension of the standard ANOVA approach, which requires data to be summarized as single values (Ramsay and Silverman 2005). Instead, we analyzed functional records of lateral force production. By not reducing force production to single values, we were able to examine the extent to which dynamics learning generalized throughout the movement trajectory. For each fANOVA, records of actual and expected lateral force production from movement start to movement end were normalized to a length of 100 samples. At each sample, an F-ratio was computed. This resulted in a time-varying function of F-ratios that allowed us to assess whether actual and expected lateral force production differed at each of the 100 samples. To correct for multiple comparisons and to maintain an fANOVA-wise α of 0.05, we adjusted our statistical threshold such that actual and expected forces were said to be different on any sample where the P value associated with the F-ratio was <0.0005 (i.e., α for each sample = 0.05/100).

In addition to fANOVA, we analyzed force data using a more standard repeated-measures ANOVA approach. The logic of this analysis was to test whether force production changed with changes in movement amplitude. For each subject, we computed a measure of total force production for channel movements at the end of training, during the test for generalization, and at the end of training on the test target. We normalized each movement to a length of 100 samples (as above) and computed the area under each profile of actual lateral force production. We used repeated-measures ANOVA to compare how this measure of performance changed over the course of the experiment. The ANOVA was followed by Bonferroni-corrected post hoc comparisons.

We also used measures of force production for between-group comparisons of performance. As described above, we computed total force production by calculating the area underneath the profiles of lateral force production. For each subject, we computed the ratio between force production during the test for generalization and force production at the end of training. This value describes the extent to which force production changed as movement amplitude changed. We used a one-way, between-subject ANOVA to determine whether there were differences in the pattern of force production that were related to the different experimental manipulations. We used this analysis to compare subjects who trained on the 15 cm target, subjects who trained on the 15 cm target with 4 interleaved trials to the 30 cm target, and subjects who trained on the 15 cm target with 19 interleaved trials to the 30 cm target. The ANOVA was followed by Bonferroni-corrected post hoc comparisons.

RESULTS

Generalization across an increase in movement amplitude

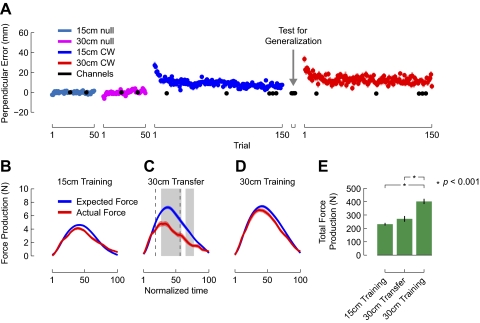
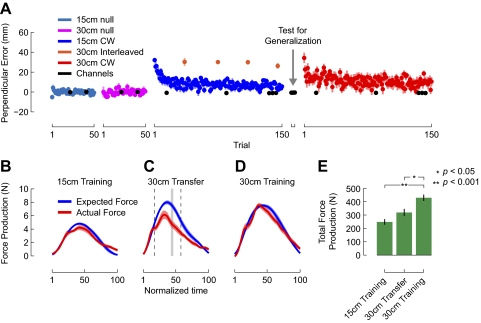
In experiment 1, our goal was to examine the extent to which dynamics learning generalizes across changes in movement amplitude. Figure 2A shows kinematic performance for subjects who made training movements to the 15 cm target and were tested for generalization to the 30 cm target. The figure shows mean PE measured on every trial throughout the experiment. On a per-subject basis, we computed mean baseline curvature and subtracted this value from each movement to normalize the data. We did this separately for both 15 and 30 cm movements. Throughout the experiment, we used channel trials to measure lateral force production that developed as subjects learned the force field. On these movements (shown in black), curvature was near zero. Subjects began by making baseline movements, first to the 15 cm target (cyan) and then to the 30 cm target (pink). Subjects experienced a clockwise force field while moving to the 15 cm target (blue). The force field resulted in initial curvature that was eliminated over the course of training. Generalization of dynamics learning to the 30 cm target was tested in force channels, as indicated by the arrow. After this test, subjects made movements to the 30 cm target in the clockwise force field (red). Initial movements to the 30 cm target showed lateral curvature, which was eliminated over the course of training.

Fig. 2.

Movement kinematics and force production for an increase in movement amplitude. A: on every trial we measured the maximum deviation from a straight line linking movement start and end [perpendicular error (PE)]. Datapoints give mean ± SE. On a per subject basis, data for each movement amplitude have been normalized relative to mean baseline performance for the 15 (cyan) and 30 cm (pink) targets. The force field resulted in curvature on initial 15 cm movements that was eliminated with training (blue). After the test for generalization to the 30 cm target, the force field resulted in some curvature, but less than shown by naïve subjects who had no previous experience with the force field (see Fig. 4A). This curvature was eliminated over the course of training (red). Curvature on channel trials was held at near-0 values (black). B: at the end of training on the 15 cm target, lateral forces that were actually produced (red) were no different from the forces that would have been required to compensate for the force field (blue). Each curve represents the mean ± SE time-normalized force record. C: during the test for generalization on the 30 cm target, actual force was less than expected. The gray band indicates where the curves are reliably different according to functional ANOVA (fANOVA). The range over which actual force was less than expected corresponds to the range of the movement where velocity was greater than velocities experienced during training. This range is given by the dashed vertical lines. D: at the end of training on the 30 cm target, subjects produced forces that fully compensated for the force field. This indicates that the failure to generalize shown in C is not caused by a general inability to produce the appropriate forces on the 30 cm target. E: a repeated-measures ANOVA shows that actual lateral force production at the end of training on the 15 cm target was no different from during the test for generalization. For each subject, we computed the area beneath the actual lateral force profiles. The bars give mean ± SE for the 3 channel movements.

Subjects who learned the force field on the 15 cm target show kinematic error on initial movements to the 30 cm target. However, they show less kinematic error than subjects who had no previous experience with the force field before moving to the 30 cm target (described in the next section, see Fig. 4A). This suggests that training on the 15 cm target led to a partial reduction in kinematic error on the 30 cm target. This reduction is consistent with the records of force production during the test for generalization, in which subjects show partial compensation for the force field.

Fig. 4.

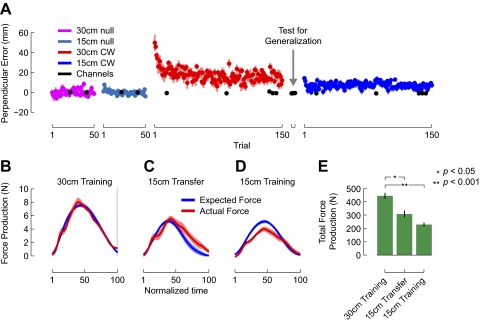
Movement kinematics and force production for a decrease in movement amplitude. Data are plotted as in Fig. 2. A: initial curvature on 30 cm movements was greater here than for subjects who had previous experience with the force field (Fig. 2A). Curvature was eliminated with training. After the test for generalization, curvature on 15 cm movements remained constant throughout training. B: at the end of training on the 30 cm target, subjects produced lateral forces that were no different from expected, except for the final 2 samples in the force record. C: during the test for generalization to the 15 cm target, subjects produced lateral force as expected. D: at the end of training on the 15 cm target, actual force was less than expected, but not reliably so. E: repeated-measures ANOVA showed that, after training on the 30 cm target, actual force production decreased during the test for generalization to a level that was no different from at the end of training on the 15 cm target.

Figure 2, B–D, shows lateral force production, measured at three points in the experiment. Figure 2B shows lateral force production on the final channel trial during force field training in the 15 cm condition. In blue are the forces that subjects should have produced to compensate for the force field. Expected forces were computed on a per-subject basis, based on the outward velocity of the channel movement and the strength of the force field. In red are shown the forces subjects actually produced. Figure 2B shows that immediately before the test for generalization, subjects produced lateral forces that compensated well for the clockwise force field. A functional ANOVA did not show any differences between actual and expected lateral force production.

Figure 2C shows lateral force production on the first channel movement to the 30 cm target. This trial was completed immediately after training on the 15 cm target, and it was designed to measure the extent to which dynamics learning generalizes across the change in movement amplitude. It can be seen that, at the start, and to a lesser extent at the end of the channel movement, the lateral forces produced by the subject were no different from the forces that should have been produced to compensate for the force field. In the middle of the movement, subjects produce less force than expected. A functional ANOVA on these data showed that the underproduction of lateral force was reliable in the middle of the movement (for each time point highlighted by the gray band, F_(1,22) > 16.63, P < 0.0005, which corrects for multiple comparisons; see methods).

The range of the channel movement over which subjects produced less force than expected aligns well with the moment that the channel movement velocity began to exceed velocities experienced during training. To determine this point, we computed for each subject the mean peak tangential velocity during training to the 15 cm target and the portion of the channel movement to the 30 cm target that exceeded this velocity. The vertical dashed lines give the average range. This suggests that, when moving to the 30 cm target, subjects produced the appropriate lateral force for familiar velocities but failed to do so for velocities beyond the range of their previous experience.

Figure 2D shows lateral force production on the final channel trial at the end of training on the 30 cm target. A functional ANOVA showed no differences between actual and expected lateral force. This indicates that the failure to produce the appropriate lateral forces during the test for generalization is a true failure to generalize force production from the 15 cm to the 30 cm target. It did not result because subjects are generally unable to produce the correct forces during 30 cm movements.

The statistical analyses of force production reported above used functional ANOVA. We also analyzed force production at the same three points in training as Fig. 2, B–D, using a more standard repeated-measures ANOVA approach. For each subject, at each phase of the experiment, we computed the area underneath the actual lateral force profile to gain an estimate of total force production. These values are shown in Fig. 2E. ANOVA showed differences in total force production across the three phases of the experiment (F_(2,46) = 45.541, P < 0.001). Force production at the end of training on the 15 cm target and during the test for generalization to the 30 cm target did not differ (P > 0.7). This suggests that subjects did not change their lateral force production as movement amplitude grew from 15 to 30 cm. At the end of training on the 30 cm target, subjects increased their lateral force production relative to the end of training on the 15 cm target (P < 0.001) and relative to the initial movement to the 30 cm target (P < 0.001). These results suggest that there was little transfer of learning from the 15 cm target to the 30 cm target, even though subjects were capable of compensating for the force field on the 30 cm target after direct training.

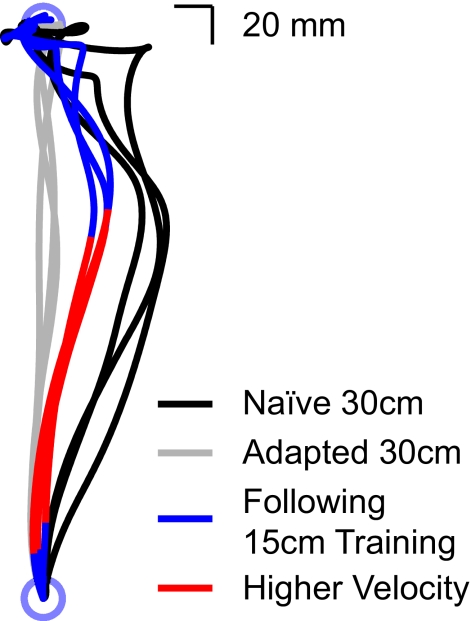
The kinematics of initial movements to the 30 cm target are consistent with the idea that subjects compensate for the force field within the range of velocities experienced during training. This can be seen in Fig. 3. In black are shown initial movements to the 30 cm target for three naïve subjects. In gray are shown three movements at the end of training. In red and blue are three initial movements made by subjects who previously learned the force field on the 15 cm target. It can be seen that overall curvature of these movements is less than curvature for naïve subjects, indicating partial generalization of dynamics learning. The blue portions of each trajectory show the range in which hand velocity was within the range of velocities experienced during movements to the 15 cm target. It can be seen that the initial trajectory of these movements is along the paths followed by adapted subjects. The red portions show the range in which movement velocity exceeds velocities experienced during training. It can be seen that it is within this range that kinematic error increases. This corresponds to the portion of the movement where subjects failed to produce forces that compensated for the force field.

Fig. 3.

Kinematic error emerges at higher velocities. Naïve movements to the 30 cm target show large rightward deflections (black). At the end of training, movement curvature has been eliminated (gray). For subjects who previously trained on the 15 cm target, movements are initially straight and they follow the trajectory of adapted movements (blue). Curvature emerges when movement velocity exceeds the range of velocities experienced during training (red portion of movements). This is the range of movements in which subjects produce less force than is necessary to compensate for the force field (Fig. 2C).

Generalization across a decrease in movement amplitude

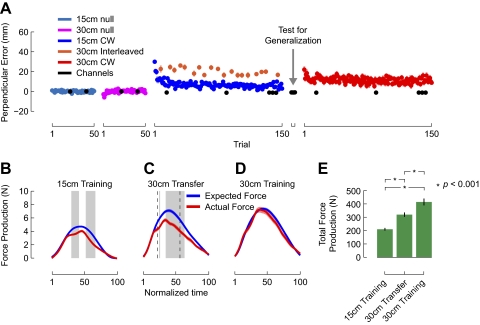
Figure 4A shows kinematic performance of subjects who were trained in the clockwise force field on the 30 cm target and were tested for generalization of dynamics learning on the 15 cm target. The data are plotted as they were in Fig. 2A. Subjects made baseline movements to the 30 cm target (pink) and then to the 15 cm target (cyan). They made movements to the 30 cm target in the force field (red). The initial lateral deflection was eliminated over the course of training. Immediately after these training movements, generalization was tested on the 15 cm target. Subjects moved to the 15 cm target in the force field (blue). Initial movements showed little curvature, and movements remained straight until the end of training. Channel trials were included throughout the experiment to measure lateral force production and generalization of learning (black).

Comparing the kinematic results shown in Figs. 2A and 4A shows an asymmetric pattern of generalization. Figure 4A shows that the force field results in large lateral deflections during initial movements to the 30 cm target. Figure 2A shows that the extent of these lateral deflections is reduced, but not eliminated, if subjects have previously learned to compensate for the force field while moving to the 15 cm target. In contrast, the initial deflections that are associated with 15 cm movements in the force field (Fig. 2A) are absent if subjects have previously learned the force field while making 30 cm movements (Fig. 4A). This suggests that there is rather limited generalization of dynamics learning across increases in movement amplitude and essentially full generalization across decreases in amplitude.

A statistical analysis of the kinematic data are consistent with this interpretation. For each subject, we computed average movement curvature on the initial five and the final five movements to both the 15 and 30 cm targets. We performed a repeated-measures ANOVA in which we compared subjects who trained first to the 15 cm target with subjects who trained first to the 30 cm target. We found that the pattern of kinematic error depended on the order of training (F_(3,102) = 18.639, P < 0.001). Post hoc comparisons showed that subjects who trained first on the 15 cm target showed curvature on initial movements that was eliminated with training (P < 0.001). They then made movements to the 30 cm target. Initial curvature was greater than at the end of training (P < 0.001) but less than the curvature on initial movements shown by subjects who trained first on the 30 cm target and had no previous experience with the force field (P < 0.01). This suggests that there was partial transfer of dynamics learning across the increase in movement amplitude. Subjects who trained first on the 30 cm target showed curvature that was initially large but decreased with training (P < 0.001). They then made movements to the 15 cm target. Curvature on initial movements was less than was shown by subjects who trained first to the 15 cm target and had no previous experience with the force field (P < 0.001). Moreover, curvature on initial movements to the 15 cm target was no different from on movements at the end of training (P > 0.90). This suggests that previous experience with the force field on the 30 cm target led to a complete elimination of kinematic error on the 15 cm target.

The profiles of lateral force production shown in Fig. 4, B–D, show the same asymmetric pattern of generalization. The profiles are plotted as in Fig. 2. Figure 4B shows expected and actual force production for the final channel trial during training on the 30 cm target. A functional ANOVA showed that subjects produced the expected lateral force on all but the final two samples of the force profile. Figure 4C shows that when tested for generalization of dynamics learning from the 30 to 15 cm target, subjects likewise produced forces that were no different from expected on the initial channel trial. This suggests that dynamics learning generalized across a decrease in movement amplitude. Figure 4D shows that at the end of training on the 15 cm target, force production on the final channel trial was slightly less but not reliably different from expected. This serves to verify that subjects were capable of producing the expected forces after direct training on the 15 cm target.

Figure 4E shows total force production for the movements shown in Fig. 4, B–D. A repeated-measures ANOVA found that force production changed across the three phases of the experiment (F_(2,22) = 24.898, P < 0.001). After training on the 30 cm target, lateral force production decreased as movement amplitude changed from 30 to 15 cm (P < 0.05). Force production on initial 15 cm movements was no different from force production at the end of training on the 15 cm target (P > 0.05). This suggests that subjects responded to a decrease in movement amplitude with an immediate reduction in force production to the levels appropriate for the shorter movement.

In summary, the results of experiment 1 show asymmetric generalization of dynamics learning across changes in movement amplitude. Movement kinematics show that having learned to compensate for forces while moving to the 15 cm target leads to a reduction but not an elimination of kinematic error when movement amplitude increases and subjects move to a 30 cm target. Measures of lateral force production show that subjects produce appropriate lateral forces on the 30 cm movement only within the range of velocities that are shared with movement to the 15 cm target. Subjects fail to generalize lateral force production beyond the range of their previous experience. In contrast, subjects who learn the force field while moving to the 30 cm target show complete generalization of dynamics learning when moving to the 15 cm target. Movement kinematics show that initial error is reduced to the level of error attained after 150 training movements. Analysis of lateral force production shows that subjects produce lateral forces as expected throughout the slower 15 cm movement.

Generalization after four interleaved trials: experiment 2

We performed two additional experiments to address differences between our findings in experiment 1 and the study of Goodbody and Wolpert (1998) on generalization of dynamics learning across changes in movement amplitude. That study found that “learning a novel dynamical environment, for a single movement, generalizes substantially to movements of the same orientation [of increased] amplitude” (Goodbody and Wolpert 1998, p. 1835). An important difference between our study and theirs was that, here, training movements at one movement amplitude were fully separated from tests of generalization at the other amplitude. In Goodbody and Wolpert (1998), training and test trials were interleaved together. Experiments 2 and 3 sought to determine whether the pattern of generalization that is observed is sensitive to interleaving training and test trials. We hypothesized that the interleaved trials provided subjects with experience in the conditions designed to test for generalization and that the improved performance during the test for generalization reflected this experience, rather than generalization per se.

In experiment 2, we interleaved four trials to the 30 cm target within training to the 15 cm target. As described in methods, we used this number of trials to match the frequency with which Goodbody and Wolpert (1998) interleaved test trials at the greater amplitude with smaller amplitude movements to the training target, using the same force field in both conditions. The kinematic results for experiment 2 are shown in Fig. 5A. The data are plotted as before. Subjects began by making baseline movements to the 15 cm (cyan) and then the 30 cm (pink) targets. They made training movements to the 15 cm target in the clockwise force field (blue). The force field led to deflections that were initially large but were eliminated by the end of training. Within the training session, subjects made four movements to the 30 cm target in the same clockwise force field (orange). Generalization of dynamics learning to the 30 cm target was tested in channel trials (black). After this test, subjects made training movements to the 30 cm target in the clockwise force field (red). Movement curvature that was present on initial movements diminished between initial and final movements.

Fig. 5.

Generalization across an increase in movement amplitude, with 4 interleaved trials. Data are plotted as in Fig. 2. A: movement kinematics show the same pattern as in Fig. 2A. Interleaved trials to the 30 cm target were made in the clockwise force field (orange). B: force production at the end of training was no different from expected. C: force production during the test for generalization was less than expected at velocities that exceeded velocities experienced during training (indicated by the dashed vertical lines). The difference was reliable (highlighted by the gray bar), but the extent of the difference was reduced compared with Fig. 2C. D: at the end of training on the 30 cm target, subjects produced the expected lateral forces. E: repeated-measures ANOVA revealed that actual force did not increase during the test for generalization.

Figure 5B shows lateral force production on the final channel movement at the end of training on the 15 cm target. It can be seen that actual force production did not differ from expected throughout the movement. A functional ANOVA found no reliable differences. Figure 5C shows force production on the initial channel movement during the test for generalization of dynamics learning. Actual force was less than expected, and functional ANOVA found reliable differences across a narrow range of the channel movement. As in experiment 1, the difference between actual and expected forces for the 30 cm movement is largest within the range where velocity exceeds velocities experienced during training on the 15 cm target (indicated by the dashed vertical lines). Compared with Fig. 2C, it seems there is a closer match between actual and expected forces. This suggests that generalization of dynamics learning across an increase in movement amplitude may be greater for subjects who experienced four interleaved trials to the 30 cm target during training. Figure 5D verifies that, on channel movements at the end of training on the 30 cm target, subjects were capable of producing lateral forces that compensated for the force field.

Figure 5E shows the results of a repeated-measures ANOVA on total force production for the channel movements shown in the panels to the left. The results here are consistent with the functional ANOVAs reported for Fig. 5, B–D. There were differences in lateral force production in different phases of the experiment (F_(2,22) = 12.678, P < 0.001). During the test for generalization, total force production was no different from force production at the end of training on the 15 cm target (P > 0.40). At the end of training on the 30 cm target, subjects produced more force than at the end of training on the 15 cm target (P < 0.001) and during initial movements to the 30 cm target (P < 0.05).

Thus these results suggest that the inclusion of four interleaved trials to the 30 cm target during training on the 15 cm target was not sufficient for producing performance indicative of complete generalization. In experiment 3, we studied the effect of many more interleaved trials. As described in methods, Goodbody and Wolpert (1998) used interleaved trials to test generalization on ∼12.5% of movements in total. On these interleaved movements, subjects experienced six different force fields. In experiment 3, we included 19 interleaved trials to the 30 cm target, in which subjects made movements in a force field that was the average of the six test fields used by Goodbody and Wolpert (1998).

Generalization after 19 interleaved trials:experiment 3

We tested 24 subjects in experiment 3. We found that the pattern of performance for these subjects was somewhat different from in experiments 1 and 2. The results are shown in Fig. 6. Movement kinematics are presented in Fig. 6A. After baseline movement to the 15 (cyan) and 30 cm (pink) targets, subjects moved to the 15 cm target in the clockwise force field (blue). Movements were initially curved but straightened with training. During the training session, subjects made 19 movements to the 30 cm target in the average force field (orange). These interleaved trials showed initial curvature that was reduced with training. Generalization of dynamics learning from the 15 cm to the 30 cm target was tested in force channels (black) after training. Subjects made training movements to the 30 cm target (red). Movements were initially straight and remained so throughout training.

Fig. 6.

Generalization across an increase in movement amplitude, with 19 interleaved trials. Data are plotted as in Fig. 2. A: movement kinematics show the same pattern as in Fig. 2A. Interleaved trials to the 30 cm target were made in the average force field. Curvature on these movements was reduced by the end of training (orange). B: actual force production at the end of training on the 15 cm target was less than expected. This complicates the interpretation of the underproduction of force shown in C. C: during the test for generalization, subjects again produced less force than expected after training with 19 interleaved trials. D: at the end of training on the 30 cm target, subjects produced the expected forces. E: repeated-measures ANOVA showed that subjects produced more force during the test for generalization to the 30 cm target than they did at the end of training on the 15 cm target. During the test for generalization, they produced less force than at the end of training on the 30 cm target.

Figure 6B shows that lateral forces produced on the final movement at the end of training on the 15 cm target did not match the expected forces. There was a tendency for subjects to produce less force than expected at the end of training. Likewise, actual and expected forces were not matched on the initial channel trial during the test for generalization of dynamics learning (Fig. 6C). At the end of training on the 30 cm target, actual and expected forces did not differ for the final channel trial (Fig. 6D). Functional ANOVA showed that the underproduction of force at the end of training and during the test of generalization was reliable. There were no differences at the end of training on the 30 cm target.

A repeated-measures ANOVA on total force production shows a pattern consistent with the fANOVA. Figure 6E shows that there were differences in total force production across the movements shown in the panels on the left (F_(2,46) = 56.474, P < 0.001). Force production at the end of training on the 15 cm target was reliably less than at the end of training on the 30 cm target (P < 0.001). Force production during the test for generalization lay in between these two extremes. It was reliably less than at the end of training on the 30 cm target (P < 0.001), but importantly, it was also greater than at the end of training on the 15 cm target (P < 0.001). This reliable increase in force production suggests generalization of learning after training on the 15 cm target with 19 interleaved trials to the 30 cm target. Note that the pattern of differences shown in Fig. 6E is different from the patterns shown in Figs. 2E and 5E, each of which characterizes a failure for learning to generalize across an increase in movement amplitude.

The difference in force production between initial and final channel movements to the 30 cm target would seem to indicate that there was less than complete generalization of learning. This interpretation is made difficult, however, by subjects' incomplete learning during training on the 15 cm target (Fig. 6B). That is, if for example subjects achieve only 80% adaptation at the end of training, full generalization of this incomplete learning would be characterized by the production of 80% of the expected force on movements to the 30 cm target. Under these circumstances, generalization could be said to have occurred even though force than at the end of training on the 30 cm target (at which point compensation for forces would likely be complete) would be greater than during the test for generalization. This general pattern is evident, both in the force profiles shown in Fig. 6, B–D, and in the ANOVA shown in Fig. 6E.

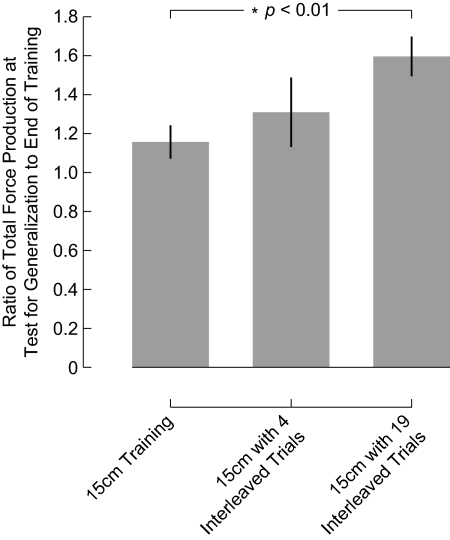
We thus performed a comparison to assess differences in the extent of generalization, for subjects who trained on the 15 cm target, for subjects who trained with 4 interleaved trials, and for subjects who trained with 19 interleaved trials. For this analysis, we computed on a per-subject basis the ratio of total force production during the test for generalization relative to total force production at the end of training on the 15 cm target. These values represent the change in force production that occurred as movement amplitude doubled from 15 to 30 cm. Expressing the data as a change in force production allows us to normalize for the reliable differences in the extent of adaptation at the end of training on the 15 cm target (F_(2,57) = 6.788, P < 0.01). The data are shown in Fig. 7. A one-way ANOVA found that there were differences in the extent to which force production changed during the test for generalization (F_(2,57) = 4.795, P < 0.05). For subjects who trained on the 15 cm target with no interleaved trials, there was no increase in the extent of force production; the ratio of force during the test for generalization to force at the end of training was no different from 1.0 (P > 0.10). In contrast, subjects who were trained with 19 interleaved trials showed a change in force production that was >1.0 (P < 0.001) and was greater than the change shown by subjects who trained with no interleaved trials (P < 0.01). For subjects trained with four interleaved trials, the change in force production lay intermediate to the change in force production for the other groups. The change was >1.0 (P < 0.05), but by post hoc tests was no different from training with no interleaved trials (P > 0.90) or with 19 interleaved trials (P > 0.30). Thus this analysis shows that force production consistent with generalization of dynamics learning depends on the inclusion of large numbers of interleaved trials.

Fig. 7.

Comparison across experiments of force production during the test for generalization relative to force production at the end of training. Values of 1.0 indicate no change in force production. After training on the 15 cm target, there was no change in force production on 30 cm movements in the absence of interleaved trials. After training that involved 4 interleaved trials to the 30 cm target, there was a slight increase in force production. After training with 19 interleaved trials, there was a reliable increase in force production that was greater than the change in performance shown by the other groups. The bars give mean ± SE.

Taken together, experiments 2 and 3 show that interleaved trials can have a substantial effect on the pattern of generalization that is observed. Relative to subjects for whom training and test movements were completely separated (experiment 1), the extent to which force production was consistent with generalization of dynamics learning increased following the inclusion of interleaved trials. Experiment 3 shows that interleaved trials can lead to the conclusion that there is robust generalization of dynamics learning when they occur at frequencies employed in previous studies.

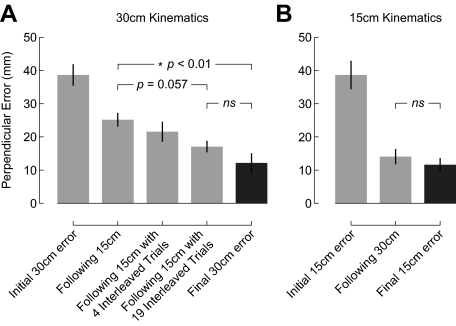
Figure 8 summarizes the effect of interleaved trials on movement kinematics and places these effects within the broader context of the entire experiment. Figure 8A shows curvature on the initial five movements to the 30 cm target after training on the 15 cm target. This represents a kinematic test for generalization of learning. At the left is movement curvature on the 30 cm target for naïve subjects who had no prior experience with the force field. At the right, in dark gray, is shown curvature on the final five movements to the 30 cm target made by naïve subjects. This value represents the extent to which movement curvature can be reduced. In between is curvature on the first five 30 cm movements after training on the 15 cm target without any interleaved trials, with 4 and 19 interleaved trials, respectively.

Fig. 8.

Comparison across experiments reveals an asymmetric pattern of generalization. Bars indicate mean ± SE perpendicular error for each of the indicated phases. A: the dark gray bar shows curvature at the end of training on the 30 cm target and represents fully adapted performance. Initial movements to the 30 cm target show large lateral deflections. The extent of curvature on 30 cm movements is reduced if subjects have previously learned the force field on the 15 cm target. If training included 4 interleaved trials to the 30 cm target, initial curvature is reduced further. If training included 19 interleaved trials to the 30 cm target, movement curvature is reduced to the level of fully adapted movements. B: the dark gray bar shows performance at the end of training on the 15 cm target and represents complete adaptation. Initial movements to the 15 cm target are deflected laterally. Initial movements to the 15 cm target show no lateral deflection if subjects had previously learned the force field on the 30 cm target.

An ANOVA on the data shown in Fig. 8A showed that there were reliable differences in initial curvature during movements to the 30 cm target that depended on previous training (F_(4,79) = 13.667, P < 0.001). Post hoc comparisons showed that for subjects who learned the force field while moving to the 15 cm target before being tested on the 30 cm target, there was a reliable reduction in movement curvature on initial movements (P < 0.01). This reduction is consistent with subjects applying force during the portions of the movement that overlap movement velocities experienced during training (experiment 1). However, generalization is incomplete, because movement curvature is reliably greater (P < 0.01) than curvature at the end of training on the 30 cm target (shown in red). Relative to subjects in experiment 1, curvature on initial movements to the 30 cm target was unchanged by the inclusion of four interleaved trials during training (experiment 2). Relative to subjects trained without interleaved trials, the inclusion of 19 interleaved trials led to a reduction in movement curvature on initial 30 cm movements that was nearly reliable (P = 0.057). For subjects trained with 19 interleaved trials, curvature on initial 30 cm movements was no different from fully adapted movements (P > 0.90, experiment 3). Thus this analysis suggests that generalization of dynamics learning across increases in movement amplitude is incomplete, and that performance on 30 cm movements is sensitive to the inclusion of interleaved trials during the initial training phase.

Figure 8B shows that generalization of dynamics learning is complete for decreases in movement amplitude. The data are plotted as in Fig. 8A. At the left is movement curvature on the 15 cm target, for naïve subjects who had no prior experience with the force field. At the right, in dark gray, is movement curvature for movements to the 15 cm target at the end of training. In the center is curvature on initial 15 cm movements after training on the 30 cm target. An ANOVA showed differences in movement curvature (F_(2,57) = 41.120, P < 0.001). Post hoc comparisons found that for subjects who learned the force field while moving to the 30 cm target, curvature on initial 15 cm movements was no different from on fully adapted movements (P > 0.90). This suggests complete generalization of dynamics learning across a decrease in movement amplitude.

In summary, our work here has shown an asymmetric pattern of generalization of dynamics learning across changes in movement amplitude. When movement amplitude increases from 15 to 30 cm, subjects produce lateral forces that compensate for the force field only within portions of the 30 cm movement that overlap velocities experienced during training (experiment 1). Likewise, movement kinematics show incomplete transfer of learning. The extent of generalization appears to increase when training involves interleaved movements in the test conditions (experiments 2 and 3). When a large number of trials are interleaved during training, dynamics learning seems to generalize fully (experiment 3). When movement amplitude decreases from 30 to 15 cm, we see a different pattern. Here, after training on the 30 cm target, subjects produce lateral forces that fully compensate for the force field throughout the 15 cm movement. This is consistent with the elimination of movement curvature on initial movements to the 15 cm target (experiment 1).

DISCUSSION

In this study, we showed that the extent to which dynamics learning generalizes across increases in movement amplitude is limited. In experiment 1, subjects learned to compensate for forces while moving to a 15 cm target. When tested for generalization on a 30 cm target, subjects produced the correct amount of force only within the range of velocities that overlapped their training movements. At velocities faster than were experienced during training, subjects did not produce forces that would have compensated for the force field. This suggests that at new velocities, subjects were unable to extrapolate the relationship between velocity and force. When subjects were tested on a 15 cm target after training on a 30 cm target, we observed complete generalization of dynamics learning. In this case, movement velocities during the test for generalization were a subset of the velocities experienced during training, and subjects were able to produce forces that fully compensated for the force field. Thus our results suggest that dynamics learning generalizes within, but not beyond the range of subjects' previous experience.

This result is in contrast to the findings of Goodbody and Wolpert (1998). In that study, subjects made training movements to a target at one amplitude and were tested for generalization of learning to a target farther away. Generalization was tested in different force fields on a series of trials that were interleaved throughout training. It was shown that, under those conditions, dynamics learning generalized across increases in movement amplitude (Goodbody and Wolpert 1998).

To determine the source of the difference between our results and theirs, we performed two experiments in which we interleaved trials to the 30 cm target during training on the 15 cm target. We found that performance on the test for generalization was sensitive to the inclusion of these interleaved trials. With 19 interleaved trials, subjects increased force production during the test for generalization relative to the end of training. On its own, this change in performance would be consistent with the idea that dynamics learning generalizes across an increase in movement amplitude. However, in experiment 1, we found that there was no generalization in the absence of experience on the 30 cm target. This suggests that the interleaved trials themselves were the source of the improved performance during the test for generalization. The interleaved trials provided subjects with experience in the force field while moving in the conditions used to test generalization. That is, the interleaved trials exposed subjects to the force field at velocities faster than those experienced during training, which overlapped with the velocities of the test movements. Thus these experiments suggest that in studies testing for generalization, interleaved force field trials may provide inadvertent training in the test conditions that can lead to the conclusion that dynamics learning generalizes.

We observed an asymmetric pattern of generalization across changes in movement amplitude. Dynamics learning generalized across decreases but not increases in movement amplitude. During the test for generalization across a decrease in movement amplitude, velocities on the 15 cm target were within the range of velocities experienced during training on the 30 cm target. In contrast, during the test for generalization across an increase in movement amplitude, velocities on the 30 cm target exceeded the range of velocities experienced during training. It was at these higher velocities that subjects did not produce lateral forces that would have compensated for the force field. These findings suggest that subjects were able to generalize dynamics learning within, but not beyond, their range of previous experience. Tests of generalization of dynamics learning across changes in movement direction show similar findings. When subjects are trained in only one direction, the extent to which learning generalizes falls off rapidly as subjects make movements in other directions (Donchin et al. 2003; Gandolfo et al. 1996; Huang and Shadmehr 2007; Mattar and Ostry 2007; Thoroughman and Shadmehr 2000; Thoroughman and Taylor 2005). The same has been shown for visuomotor learning, in which compensations for error between actual and perceived movement direction show a generalization gradient across changes in movement direction (Krakauer et al. 2000; Pine et al. 1996). In contrast, if subjects make training movements to two targets, dynamics learning generalizes fully to movements that lie between the training directions (Gandolfo et al. 1996; Mattar and Ostry 2007). This suggests that generalization is robust within, but not beyond, the range of one's previous experience.

In this experiment, the extent to which subjects were able to apply the expected lateral force during the test for generalization depended on the overlap between movement velocity and velocities experienced during training. This is consistent with the idea that dynamics learning is tied to the particular states experienced during training. Other studies have explored the link between generalization and the states experienced during training. It has been shown that dynamics learning acquired in the context of outward movements generalizes to circular movements that were selected to visit the same position and velocity states that were experienced during training (Conditt et al. 1997). Other studies have assessed generalization of dynamics learning from one area of the workspace to another by having subjects rotate the arm about the shoulder. These studies suggest that dynamics learning generalizes between movements that involve the same underlying changes in joint angle (Malfait et al. 2002). This study and others (Mah and Mussa-Ivaldi 2003; Shadmehr and Moussavi 2000; Shadmehr and Mussa-Ivaldi 1994) thus support the idea that dynamics learning is tied to the movements experienced during training.

Although our analyses focused on the link between lateral force production and movement velocity, it is likely that other information is relevant in determining the extent to which dynamics learning generalizes. In particular, the subject's intent can affect the extent of generalization. Dynamics learning acquired when subjects produce one utterance does not generalize to a second utterance that overlaps the kinematics of the first. That is, dynamics learning does not generalize when subjects say a second word, even if the kinematics of training movements are embedded within the second word (Tremblay et al. 2008). In reaching movements, dynamics learning generalizes weakly between movements in which the subject holds a robotic device and matched movements in which the subject is aware that the robot has been let go (Cothros et al. 2006; Kluzik et al. 2008). Moreover, dynamics learning does not generalize if the subject is fooled into thinking that the robot has been let go, when in actuality test movements are made while holding the robot (Cothros et al. 2009). In addition, there are reports that humans (Osu et al. 2004) and nonhuman primates (Krouchev and Kalaska 2003) are able to produce opposite patterns of lateral force for the same movements when cued visually (but see Gandolfo et al. 1996). In related work, it has been shown that healthy subjects who learn novel patterns of locomotion on a split-belt treadmill show limited generalization when they step off the treadmill and walk over normal ground (Reisman et al. 2009). Thus these studies all suggest that generalization does not depend only on overlapping velocities. Instead, they suggest that contextual information can also affect the extent to which dynamics learning generalizes.

Generalization of motor learning across changes in movement amplitude has also been studied in the context of visuomotor rotations. When subjects were trained on a target at one amplitude, it was found that the learning generalized to movements to two targets located closer and one target farther from the training target (Krakauer et al. 2000). This finding is not inconsistent with what we have observed here. The complete generalization to the two targets that were closer to the body than the training target is consistent with our finding that dynamics learning generalizes across decreases in movement amplitude. Presumably, movements to the closer two targets explored a subset of the states that were experienced during training. It is possible that generalization of visuomotor rotation learning to the farther target may have been caused by substantial overlap between movements. In that study, generalization was tested across a 33% increase in movement amplitude (from 7.2 to 9.6 cm). This suggests that the extent to which test movements involved states that were not experienced during training is much lower than in this study. Here, we used a 100% increase in movement amplitude to test for generalization, and this large change in movement amplitude allowed us to detect the failure to generalize.

In summary, we showed that dynamics learning generalizes asymmetrically across changes in movement amplitude. The extent to which dynamics learning generalizes depends on the overlap between training and test conditions. Our findings represent further evidence that dynamics learning is locally tuned to the situation in which it is acquired. In addition, our experiment has shown that interleaved trials provide subjects with inadvertent training in the test conditions, which can affect the conclusions that are drawn about the extent of generalization. This argues for experimental designs in which training and testing are fully separated.

GRANTS

This work was supported by National Institute of Child Health and Human Development Grant HD-48924, the Natural Sciences and Engineering Research Council of Canada, and Fonds Québécois de la Recherche sur la Nature et les Technologies.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).