Attractor-Map Versus Autoassociation Based Attractor Dynamics in the Hippocampal Network

Abstract

The autoassociative memory model of hippocampal field CA3 postulates that Hebbian associations among external input features produce attractor states embedded in a recurrent synaptic matrix. In contrast, the attractor-map model postulates that a two-dimensional continuum of attractor states is preconfigured in the network during development and that transitions among these states are governed primarily by self-motion information (“path-integration”), giving rise to the strong spatial characteristic of hippocampal activity. In this model, learned associations between “coordinates” on the attractor map and external cues can result in abrupt jumps between states, in the case of mismatches between the current input and previous associations between internal coordinates and external landmarks. Both models predict attractor dynamics, but for fundamentally different reasons; however, the two models are not a priori mutually exclusive. We contrasted these two models by comparing the dynamics of state transitions when two previously learned environmental shapes were morphed between their endpoints, in animals that had first experienced the environments either at the same location, or at two different locations, connected by a passageway through which they walked. As predicted from attractor-map theory, the latter animals expressed abrupt transitions between representations at the midpoint of the morph series. Contrary to the predictions of autoassociation theory, the former group expressed no evidence of attractor dynamics during the morph series; there was only a gradual transition between endpoints. The results of this critical test thus cast the autoassociator theory for CA3 into doubt and indicate the need for a new theory for this structure.

INTRODUCTION

The standard model of memory in neuroscience (Hebb 1949) postulates that external events are stored through bidirectional (symmetric) associative synaptic links, which are induced by coactivation of neurons that respond to a given input ensemble. This process is known as “auto-association” (Kohonen 1972). Depending on temporal patterning, Hebbian synaptic strengthening may lead either to stable activity states, which Hebb called “cell assemblies” and which are now commonly known as “attractors” (Amit 1994; Hopfield 1982), or to sequences of states representing temporally extended “episodes,” which Hebb called “phase sequences.” When a new input is sufficiently similar to a previously learned pattern, a network with attractor dynamics, in the absence of further synaptic change, will converge to the original pattern. This effect, which is a result of an abundance of symmetric connections among the active population, is sometimes referred to as “error correction” and/or “pattern completion” (Grossberg 1969, 1971; McClelland and Rumelhart 1985; McNaughton and Morris 1987). On the other hand, when a new input pattern is sufficiently dissimilar to previously stored ones, it presumably should be stored as a separate entity. Specific circuitry and dynamics possibly involving the dentate gyrus (McNaughton and Morris 1987; McNaughton and Nadel 1990) have been postulated to regulate the network's “decision” whether to form a new, uncorrelated representation by switching on synaptic plasticity or to leave plasticity off and retrieve a stored one (Hasselmo et al. 1995; McClelland and Goddard 1996; O'Reilly and McClelland 1994; Rolls and Treves 1998). Recent evidence (Leutgeb JK et al. 2007; CB Alme, RA Buzzetti, DF Marrone, JK Leutgeb, MK Chawla, MJ Schaner, JD Bohanick, T Khoboko, S Leutgeb, EI Moser, M-B Moser, BL McNaughton, and CA Barnes, unpublished data) has called this hypothesis into question.

An attractor state, once activated, will exhibit resistance to deactivation due to subsequent distortions of the input. If the input is distorted by making it increasingly similar to a different stored attractor, this hysteresis effect will result in an abrupt, nonlinear transition from one memory state to the other, at the point where the balance of similarity between the input and the two stored memories tips in favor of the other memory. Such an abrupt transition is a key signature of the presence of attractor dynamics.

The CA3 region has been assumed to be the primary attractor network of the hippocampus proper because it has abundant direct recurrent collaterals that are associatively modifiable, thus in theory enabling the formation of symmetric connections among coactive neurons (McNaughton and Morris 1987; Treves and Rolls 1992). Other candidates include the indirect association system of the dentate gyrus mediated by hilar mossy cells and possible recurrent connections within the entorhinal cortex. The CA1 region is notably lacking in abundant recurrent connections and is thus unlikely to support attractor dynamics, although it may exhibit abrupt transitions imposed by such dynamics in its inputs from CA3 or entorhinal cortex. Thus although abrupt transitions between states may be indicative of attractor dynamics somewhere in the brain, they do not necessarily indicate such dynamics within the population of recorded neurons.

Attractor dynamics are not limited to learned representations, however, nor are they limited to the representation of discrete, widely separated states. For example, a developmentally “preconfigured” network with Gaussian distributions of local excitatory connections (in one or more dimensions), combined with global feedback inhibition, can exhibit what is known as continuous attractor dynamics in which single, localized, quasi-stable “bumps” of activity can exist as one of a (quasi-) continuum of locally correlated attractor states (Amari 1977; Amit and Tsodyks 1991; Cugliandolo and Tsodyks 1994). Such dynamics have been suggested to underlie the establishment of spatial coordinate representations in the hippocampus and/or medial entorhinal cortex (McNaughton et al. 1996; Redish and Touretzky 1997; Samsonovich and McNaughton 1997; Tsodyks and Sejnowski 1995; Zhang 1996). In particular, network simulations show that, when different sensory inputs have become associated with different locations (“coordinates”) of the activity bump in the state space of a continuous attractor network, abrupt shifts of the bump location can be induced by applying excitation at the new location (Samsonovich and McNaughton 1997; see their Figs. 8 and 9A). Such an effect was shown experimentally by Gothard et al. (1996a, 2001).

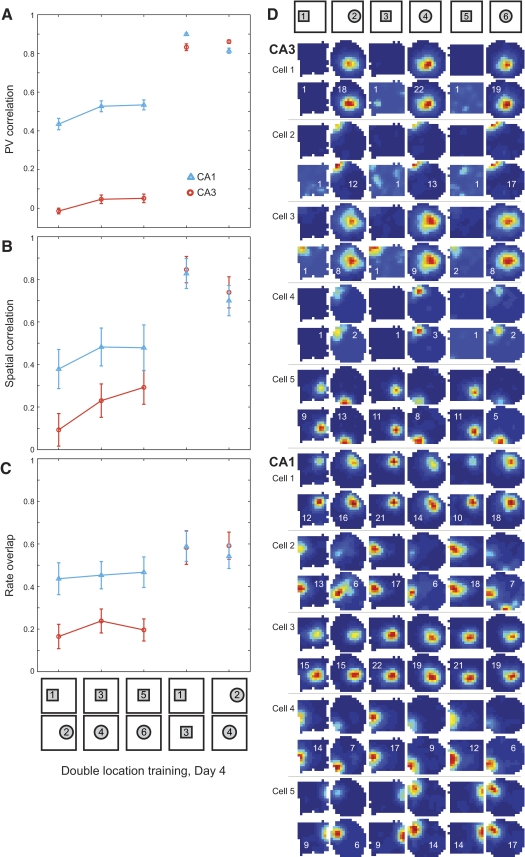
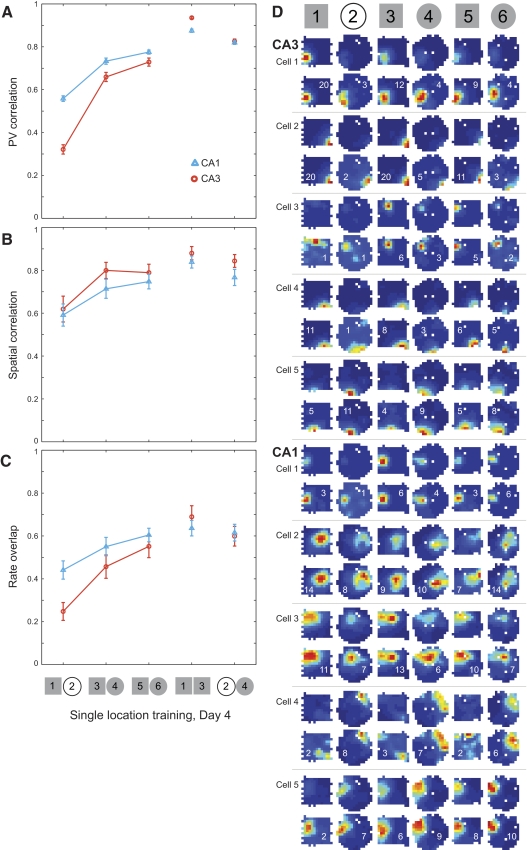
Fig. 8.

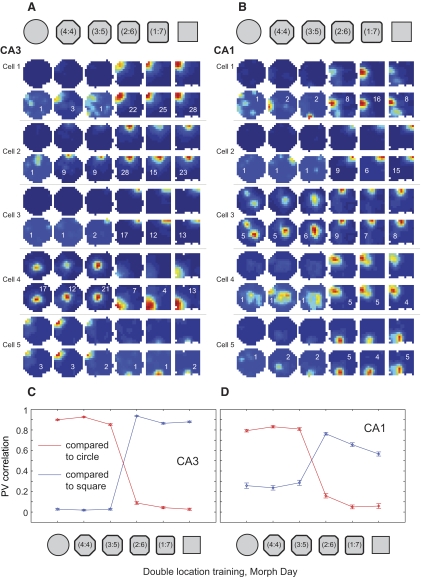
Changes in place cell firing properties on day 4 in the two location training group. PV correlations (A), spatial correlations (B), and rate overlap measures (C) are plotted (mean ± SE) for all place cells recorded in CA3 (orange circles, 46 cells from 4 rats) and CA1 (blue triangles, 29 cells from 3 rats). Low correlations were observed between the square and circle shapes presented in separate locations. When the shapes were moved to a common central location, the separation between square and circle representations was retained in both regions. D: color-coded rate maps (scaled as in Fig. 3) for representative place cells recorded in CA3 and CA1 in an example rat. The remainder of the cells recorded from this rat on this day are shown in Supplemental Fig. S6.

Fig. 9.

Color-coded PV cross-correlation matrices (color scale and axes as described for Fig. 4) between CA3 rate maps on day 4 in the two location training group for the sequence of shape pairs indicated above. No peaks in the cross-correlation matrices can be discerned for any of the opposite shape pairs, reflecting the formation of stable and independent representations for square and circle environments. Clear peaks in the center of the cross-correlation matrices are seen for identical shape pairs tested in different locations.

An abundance of evidence supports the view that self-motion signals provide the fundamental basis for the establishment of spatial firing rate distributions in cells of the hippocampal formation (place cells) and medial entorhinal cortex (grid cells). Whereas external sensory cues can modulate local firing rates and can correct for errors in the path-integration mechanism, path integration appears to determine which cells will be allocated to particular spatial coordinates (for a review of this evidence see McNaughton et al. 1996). In other words, path integration determines where cells fire initially, whereas external cues may affect how intensely they fire (Hetherington and Shapiro 1997; Leutgeb S et al. 2005b, 2006) and enable the same map to be retrieved over subsequent visits to the same place (Muller and Kubie 1987; Quirk et al. 1990). When synaptic plasticity is compromised, consistent map retrieval fails, although the new maps are nevertheless normal in appearance (Barnes et al. 1997; Kentros et al. 1998).

Two recent studies have addressed the presence of attractor dynamics in the hippocampal system by recording from hippocampal neurons during a continuous transformation (morphing) of a test environment between two previously experienced endpoints, one circular and one square. Wills et al. (2005) recorded from CA1 and observed, in some of their experimental animals, an abrupt shift in the spatial firing locations of neurons near the midpoint of the morph series. Some of their animals were rejected from the study, however, because their hippocampal CA1 representations of the two endpoints were not very different to begin with. Using a very similar experimental design, Leutgeb JK et al. (2005a) were unable to detect any abrupt shift. As with the animals that had been rejected from the study by Wills and colleagues, all of the animals in the study by JK Leutgeb and colleagues exhibited primarily differences in firing rates (“rate remapping”) rather than firing location (“global remapping”) between the endpoints. The hippocampal population representation (CA1 and CA3) exhibited progressive, rather than abrupt, changes in firing rates, with little or no changes in firing location, as the environment was gradually morphed between endpoints.

Based on the path-integrator concept, whether the hippocampus forms distinct or similar representations for two enclosures alternately located in the same place would depend strongly on state of the animal's path-integration system when the animal is first placed into the apparatus, which is when the initial associations between the external cues and the current path-integrator coordinates are presumed to be formed. Even for identical environments, significant differences in the hippocampal code can occur if the animal actively locomotes from one to the other (Fuhs et al. 2005; Skaggs and McNaughton 1998). At the behavioral level, animals subject to slow disorientation during transit to a room containing a radial arm maze are unable to learn the locations of food in relation to the distal sensory cues, a task that nondisoriented animals solve easily (Martin et al. 1997). Indeed, even while a rat is within an enclosure, a perturbation of the path integrator, such as an abrupt 180° rotation that places the head-direction system in conflict with the local cues, can result in immediate, global remapping (Knierim et al. 1998). Thus we conjectured that the reason for the differences between the two studies (Leutgeb JK et al. 2005a; Wills et al. 2005) was that, in the case of the Wills et al. animals that exhibited abrupt transitions between uncorrelated endpoints, these rats had failed to maintain consistent path-integrator coordinates during the initial transfers to the two different enclosures, whereas, for their rejected animals, as well as for the animals in the Leutgeb JK et al. study (2005a), these rats did maintain consistent path-integrator coordinates and thus generated representations of the two enclosures that differed primarily in how much the cells fired, not which cells fired.

The present experiment was thus designed as a critical test to distinguish between two different hypotheses on the origin of hippocampal attractor dynamics in the morph paradigm. 1) Hypothesis one is the standard autoassociator model of hippocampal subfield CA3, which assumes that CA3 neurons associate the coocurrence of input features in their recurrent collaterals, thus giving rise to attractor dynamics; 2) Hypothesis two is that the attractor dynamics reside in the path-integrator system. The path-integrator system is now widely believed to be centered on the circuitry of the medial entorhinal cortex (Burgess et al. 2007; Fuhs and Touretzky 2006; Hafting et al. 2005; McNaughton et al. 2006) and the expression of grid cell activity there; however, the exact location of this system is not essential to the present arguments so long as the system affects CA3. The difference between these two models lies in exactly how the external cues result in attractor dynamics, and these differences lead to different predictions in the morph experiment. In the autoassociator model, cues activate sets of neurons whose mutual synaptic interconnections are then modified according to Hebbian principles of coactivation (McNaughton and Morris 1987). In the attractor map model, the mutual interconnections have already been set up in early development, and it is the synapses conveying the external inputs to the map cells that are modified by coactivity (McNaughton et al. 1996; Samsonovich and McNaughton 1997). According to the former hypothesis, morphing the external features of the environment between two learned endpoints will always lead to nonlinear transitions between the endpoint representations, even if the endpoints are not completely uncorrelated. According to the latter hypothesis, sharp transitions will occur only if a rat is first able to establish different path-integrator coordinates for the two endpoints because there is no association formed among the input features per se, only between input features and path-integrator coordinates. We conjectured that the development of different path-integrator coordinates for the two endpoints would be strongly facilitated if the animal was able to locomote between them and that the resulting representations would be maintained during subsequent sessions in which the enclosures were actually placed in the identical spatial location. In other words, the associative binding of the external features of the environments would override the apparent error in the path-integrator coordinates resulting from placing the two enclosures in the same location. In this case, it was predicted that morphing the enclosure between the square and circular endpoints would result in the abrupt transition observed by Wills and colleagues (2005) in some of their animals, whereas, if no changes in path-integrator coordinates occurred, there would be only a smooth transition such as observed by JK Leutgeb and colleagues (2005a). Such an effect would suggest that the attractor dynamics are located in the path-integrator system and are the result of learned associations between environmental stimuli and path-integrator coordinates and not the result of learned associations among the spatial features of each environment per se.

The autoassociator and path-integrator models are not a priori mutually exclusive. External feature information affects the relative firing rates of CA3 cells (rate remapping), and thus it might have been the case that autoassociation of this external feature information would lead to attractor dynamics in CA3 during rate remapping. This possibility was already in doubt on the basis of the Leutgeb JK et al. (2005a) study; however, the present experiment provides a controlled test in groups of rats treated essentially the same except for the opportunity in one group to establish different path-integrator coordinates on the basis of locomoting between two test chambers during their initial experience.

METHODS

Overview of experimental design

We tested the prediction of the attractor map hypothesis that the firm establishment of different spatial coordinates for two test enclosures would later lead to the expression of attractor dynamics (abrupt global remapping) during the morphing procedure, whereas failure to establish different coordinates would lead only to progressive rate remapping. For this purpose, two different groups of rats were given initial training in a circular and a square arena that would later serve as the endpoints of a morphing procedure as reported previously (Leutgeb JK et al. 2005a; Wills et al. 2005). The principal difference between the two groups was that in the single location training group, the two apparati were placed alternately at the same spatial location during initial training, whereas in the double location training group, the two enclosures were placed at different locations and connected by a 22-cm passageway that permitted the animals to walk freely between them, thus allowing them ample opportunity to represent the enclosures as different locations. For the critical testing sessions, a single morphable enclosure was kept at a constant location and deformed in steps from one trial to the next.

Subjects

Eight male Long Evans rats (four each for single location training and double location training groups; ∼350–450 g) were used in this study. After surgery, the rats were housed individually in transparent Plexiglas cages (45 × 30 × 35 cm). Rats recovered from surgery for >1 wk before being put on a food-deprivation regimen that kept them at about 90% of free-feeding body weight. All rats were maintained on a 12-h light/12-h dark schedule. Testing occurred in the dark phase. Animal care and use were carried out in accordance with guidelines from the European Convention for the Protection of Vertebrate Animals Used for Experimental and Other Scientific Purposes and protocols approved by the Norwegian Animal Welfare Authority.

Surgery and electrode preparation

Rats were anesthetized with Equithesin (1 ml/250 g, administered intraperitoneally) and implanted with a “hyperdrive” (David Kopf Instruments, Tujunga, CA; Gothard et al. 1996b) with 12 independently movable tetrodes and two movable single-channel electrodes (prepared as reported previously; Leutgeb S et al. 2005b). Tetrodes were constructed from 17-μm polyimide-coated platinum–iridium (90–10%) wire. Electrode tips were plated with platinum to reduce electrode impedances to between 200 and 300 kΩ at 1 kHz. The drive was implanted above the right hippocampus (anteroposterior 3.8, mediolateral 3.0) and secured to the skull with jewelers' screws and dental cement. Two screws in the skull were connected to the hyperdrive ground. A single electrode was lowered to CA1 stratum lacunosum-moleculare and served as a monitor for hippocampal electroencephalography. Another single electrode was placed in or above the level of the corpus callosum and provided a reference signal for differential unit recording. Approximately half of the tetrodes were lowered to CA3 and the others were turned down to CA1.

Data collection

Tetrodes were gradually lowered to their target regions over 2–4 wk. Testing began when extracellular spikes emerged approximately at the proper depth for the region of interest, with amplitudes exceeding roughly fivefold the noise levels. Once behavioral testing and recording had begun, tetrodes were moved only after the day's recording had finished and, to enhance cell stability across recording sessions, were not moved ≳50 μm per day.

The hyperdrive was connected to a multichannel, impedance matching, unity gain headstage, the output of which was conducted via a lightweight, multiwire, tether cable and through an 82-channel, slip-ring commutator to a data acquisition system containing 64 digitally programmable analog amplifier/filter modules (Neuralynx, Bozeman, MT). Unit activity was amplified by a factor of 3,000–5,000 and band-pass filtered from 600 to 6,000 Hz. Spike waveforms above a threshold set by the experimenter (55–80 μV) were time-stamped and digitized at 32 kHz for 1 ms. Light-emitting diodes (LEDs) on the headstage were used to track the animal's movements at a 50-Hz sampling rate.

Testing procedures

In all testing protocols, behavioral sessions were conducted inside a black-curtained, circular testing arena, 2.5 m in diameter. Test boxes were placed on a table in the center of the arena. During behavioral sessions, the rat foraged for chocolate cereal crumbs randomly thrown into the enclosure. Testing environments were cleaned with water between behavioral sessions. All behavioral sessions were preceded and followed by 20-min rest sessions. During rest sessions, the rat remained in a towel-lined flower pot situated on a pedestal located outside of the curtained arena. Prior to each session, rats were carried from the pedestal to the arena along an identical trajectory and placed into the testing enclosure at the same entry site and orientation.

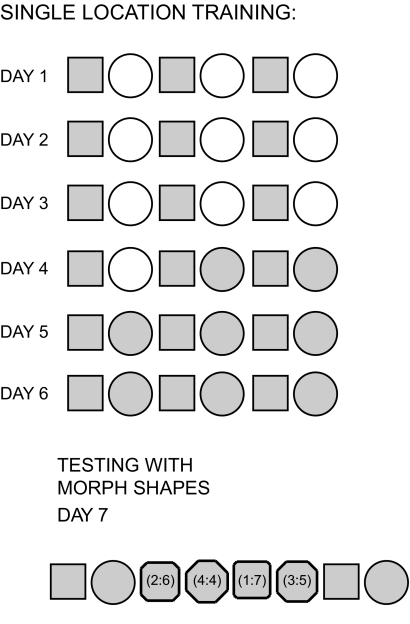
Single location training.

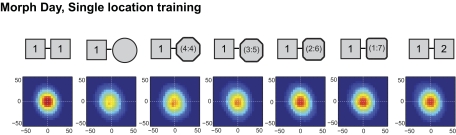
Rats in the single location group were trained according to a protocol reported by Wills et al. (2005). A white cue card (102 × 77 cm [width × height]) was taped to the curtains on one side of the arena and served as a constant external cue throughout all trials. Rats were tested for a total of 7 days (Fig. 1). There was no pretraining prior to these 7 days and rats had not undergone previous behavioral testing of any kind. Two testing enclosures were used: a “morph” enclosure and a white circle. The white circle was a white fiberglass-reinforced plastic mold, 79 × 50 cm (diameter × height). The morph enclosure was constructed from 32 rectangular pieces of lightweight aluminum (7.5 × 50 cm [width × height]) that were joined together with metal hinges and silver duct tape. The morph box could be configured into six different shapes: a 62-cm-sided square, a 79-cm-diameter circle, and a series of four polygonal shapes that were intermediate between square and circle (for additional details see Wills et al. 2005). Shapes were held in place using appropriately sized external aluminum frames for the square and four intermediate polygons and a plastic ring for the circle. The floor was of a vinyl material and was constant for all sessions. Behavioral sessions were 10 min in duration and the center of each shape was always placed in the same location.

Fig. 1.

Procedure for the single location training group. On the first 3 days of training, animals were tested in a morph square and a white cylinder across 6 behavioral sessions, consisting of the “morph square–white circle” sequence repeated 3 times. On the 4th day of training, the first 2 sessions were identical to earlier training days (i.e., morph square–white circle), but on the 4th session, the white cylinder was replaced with the morph circle (i.e., morph circle in sessions 4 and 6). On days 5 and 6, the 6 behavioral sessions consisted of the “morph square–morph circle” sequence repeated 3 times. On the 7th day, rats were tested first in the morph square and morph circle and then in a series of intermediate (“morph”) shapes presented in a fixed order (alternating between square-like shapes and circle-like shapes, as in Wills et al. 2005). The morph sequence was followed by repeated sessions in square and circle. The intermediate shapes were octagons with walls composed of different numbers of identical length segments. The numbers in parentheses indicate the numbers of identical length segments making up each wall of the octagon (i.e., 2:6 indicates 4 walls composed of 2 segments and 4 walls composed of 6 segments). Each session was 10 min in duration.

For the single location group, day 4 results were obtained for 55 CA3 cells and 70 CA1 cells from four rats and day 7 (morph day) results were obtained for 85 CA3 cells and 78 CA1 cells from four rats.

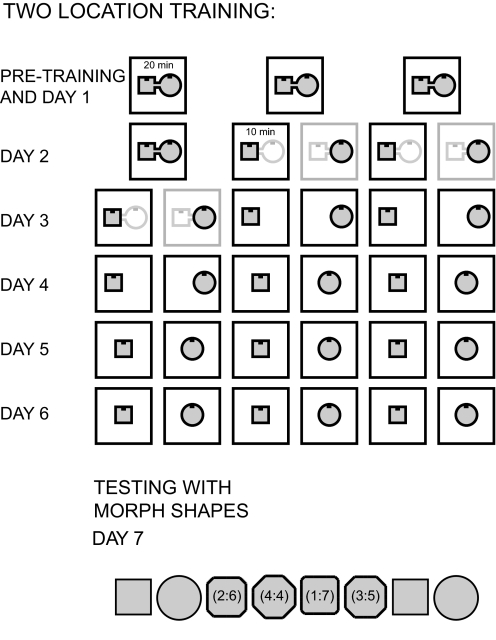
Double location training.

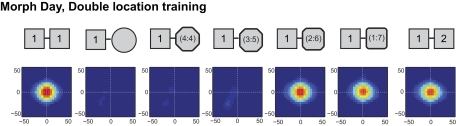
As in the single location group, double location group rats had no prior experience with behavioral testing (see Fig. 2). To minimize distal cues, no external cue card was used. Two side-by-side light bars containing four LEDs each (14 cm total length) served as an intrinsic cue that was placed at the same position, 3 cm below the top of the north wall, in all enclosures. Other lights were turned off during this experiment, so the light cues provided the only illumination within the arena. Two testing enclosures were used: the morph enclosure described earlier and another larger enclosure (“double morph”), consisting of a morph square connected to a morph circle via a corridor. The double morph enclosure had two intrinsic light cues, one in each shape. The double morph enclosure was constructed of the same materials as the single morph enclosure, except that only 30 rectangular pieces were used for each shape, with a 15-cm-wide gap left open on one side of each shape where the corridor was located. The corridor was constructed of six rectangular pieces, three on each side (i.e., 22.5 × 50 × 15 cm [length × height × width]), and positioned in the middle of the two shapes. The corridor had a door at each end that could be opened or closed by the experimenter. Each door was made of two rectangular pieces of the same material as that of the enclosures (50 × 15 cm [height × width]), such that no gaps remained in the walls when the doors were closed. With the corridor closed, the two portions of the double morph box appeared identical to the morph square and circle.

Fig. 2.

Procedure for the two location training group. Prior to day 1 of the experiment, animals received 3–7 days of pretraining in a double morph enclosure made up of a morph square and a morph circle connected by a corridor. Pretraining consisted of three 20-min sessions in the double morph box with the corridor open. Day 1 of the experiment was identical to the pretraining days. On day 2, the first session was another 20-min session in the double morph box with the corridor open. Sessions 2–5 consisted of 10-min sessions in the alternating square (sessions 2 and 4) and circle (sessions 3 and 5) portion of the double morph enclosure with the corridor doors closed. For the remaining days 3–7, behavioral sessions were always 10 min in duration. On day 3 of the experiment, the first 2 sessions were another sequence of square and circle sessions in the double morph box with the corridor closed. For the remaining 2 repetitions of the square–circle sequence, the double morph box was replaced with the single morph square and circle placed in the double morph box square and circle locations, respectively. On day 4, the first pair of sessions was identical to the last pair of sessions on the previous day. For the last 4 alternating square–circle sessions, the morph square and circle were placed in a common, central location. For the duration of the experiment, the center of all shapes was placed in this central location. Days 5 and 6 of the experiment were then identical to days 5 and 6 of the single location training experiment, with alternating morph square–morph circle sessions conducted in the same location. On day 7, the animals were tested in the series of intermediate morph shapes, identical to the procedure described for day 7 of the single location training group.

For the double location group, day 4 results were obtained for 46 CA3 cells from four rats and 29 CA1 cells from three rats and day 7 (morph day) results were obtained for 84 CA3 cells and 32 CA1 cells from four rats. Day 4 results for CA1 were obtained from only three of the four rats in the group because CA1 tetrodes in one of the animals had not yet reached their target location.

Data presentation and analyses

Presentation and reporting.

Data are reported as means ± SE. The results of most statistical tests are listed in Supplemental Tables S1–S4 and are referred to in the following text as appropriate.¹

Spike sorting and place fields.

Spike sorting was performed off-line using graphical cluster-cutting software (MClust; A. D. Redish, University of Minnesota, Minneapolis). Clustering was performed manually in two-dimensional projections of the multidimensional parameter space (consisting of waveform amplitudes and waveform energies), using autocorrelation and cross-correlation functions as additional separation tools and separation criteria. Putative pyramidal cells were distinguished from putative interneurons by spike width, average rate, and the occasional presence of bursts. Spatial firing rate distributions (“place fields”) for each well-isolated neuron were constructed in the standard manner, by summing the total number of spikes that occurred in a given location bin (5 × 5 cm), dividing by the amount of time that the animal spent in that location, and smoothing with a 5.16 cm SD Gaussian centered on each bin.

Rate overlap.

The “rate overlap” between the active cell populations in two shapes of a recording session was calculated by taking the ratio of the mean firing rate in each shape, with the smaller of the two means as the numerator. Cells with average firing rates of >0.25 Hz in at least one of the two shapes were considered active and the ratios for active cells were averaged for the cell population. These values were then compared with the values expected from two independent distributions, estimated by pairing the firing rate of a cell in shape A to the firing rate of every other cell in shape B (again, only active cells were included).

Spatial correlation.

Place fields across different trials were compared using the spatial correlation measure that was described previously by JK Leutgeb and colleagues (2005a). Each rate map was smoothed and spikes were sorted according to the location where they occurred using 12 × 12 bins of 5 × 5 pixels. The rates of firing across different trials in pixels corresponding to the same spatial location were correlated for each cell. Pixels visited <150 ms in either one of the trials and pixels not common to both maps were excluded. To estimate the expected values of spatial correlations between sessions, rate maps were correlated for random pairs of cells. The randomization procedure was repeated 1,000 times and the mean spatial correlation value for the sets of random cell pairings was taken as the expected spatial correlation value for each pair of sessions.

In-field rate analysis and curve fits.

In-field firing rates were estimated by first calculating an average rate map for all seven morph shapes and then finding the largest number of continuous pixels exceeding 20% of the maximum rate. The average firing within these pixels was calculated for each shape, and a cell was considered to have a field if its average in-field rate was >2 Hz in at least one of the morph shapes. Sigmoid functions were fit to the resulting firing rate data × session number data of these cells. Fits with values of P < 0.05 were considered significant.

Population vector correlations.

For the entire population of cells recorded in each condition, rate vectors were constructed by arranging all place fields for all animals within a session in an x–y–z stack, where x and y represent the two spatial dimensions (5 × 5 cm bins) and z represents the cell-identity index. The distribution of mean rates along the z-axis for a given x–y location represents the composite population vector for that location (i.e., a 25 cm² spatial bin). Cells from different regions (i.e., CA3 and CA1) were analyzed separately.

Population vector cross-correlations.

Cross-correlation coefficients between population vectors in CA3 were calculated for each pair of shapes by shifting the stack of rate maps for one shape in 5-cm increments along the x and y axes of the common area covered in both shapes until a separation of 50 cm was reached for each axis (Fyhn et al. 2007; Leutgeb JK et al. 2007). At each offset, the mean correlation coefficient of all overlapping population vectors was computed within the session. If the locations of the place fields in the two shapes remain the same, then the population vector cross-correlogram will show a peak at the origin. If the population exhibits spatial remapping such that the place field locations change substantially, then the peak in the cross-correlogram will disappear.

Histology

For verification of tetrode locations, brains were cut coronally at 30 μm and stained with cresyl violet. Each section through the relevant part of the hippocampus was collected for analysis. All probes of the 14-probe array were identified and the tip of each electrode was found by comparison with adjacent sections. The recordings from a tetrode were included in the data analysis if its deepest position was in the CA3 or CA1 pyramidal cell layer. The electrodes had not been moved after the recordings.

RESULTS

Single location training group

In the single location group (n = 4; Fig. 1), on day 4, the first pair of sessions was morph square followed by white circle as on earlier days. For the second and third presentations of square–circle session pairs, the white circle was replaced with a circle configured from the same gray box as the square (“morph box”).

Rate remapping was observed between the white circle and morph square (Fig. 3; Supplemental Fig. S1); however, as expected for rate remapping, the magnitude of the effect was significantly reduced when the environmental similarity was increased by replacing the white circle with the morph circle (Fig. 3, A–C). Rate and place field location changes across different shapes were first assessed by constructing location-specific population vectors (Fig. 3A; see methods; Leutgeb JK et al. 2005a). Population vector correlations between morph square and morph circle trials were significantly increased compared with correlations between white circle and morph square trials (Supplemental Table S1). To assess whether these effects involved changes in firing field locations, we calculated spatial correlations (see methods; Leutgeb JK et al. 2005a) between square and circle maps (Fig. 3B). Spatial correlations between the last pair of trials (morph square–morph circle) were increased significantly compared with spatial correlations between the first pair of trials (morph square–white circle; Supplemental Table S1). To determine whether firing rates also became more similar when the morph circle was introduced, we computed rate overlap scores (see methods; Leutgeb JK 2005a; Leutgeb S et al. 2004) and found that overlap between morph square and morph circle was significantly higher than the overlap between morph square and white circle (Fig. 3C and Supplemental Table S1).

Fig. 3.

Changes in place cell firing properties on day 4 of the single location training experiment. Mean (±SE) population vector (PV) correlations (A), spatial correlations (B), and rate overlap (C) measures are shown for the entire population of recorded place cells in CA3 (orange circles, 55 cells from 4 rats) and CA1 (blue triangles, 70 cells from 4 rats). Note that correlations and overlap increased when the white cylinder was replaced with the morph circle. D: color-coded firing rate maps are shown for 5 representative CA3 (A) and CA1 (C) place cells from an example rat. For each example cell, the maps are shown scaled to the maximum firing rate across all sessions (top) and to the cell's own maximum firing rate within a session (bottom). Red symbolizes the peak rate, blue represents no firing, and white pixels indicate areas that were not visited during the session. The firing rate maps for the remainder of cells recorded from this rat on this testing day are shown in Supplemental Fig. S1.

Population vector cross-correlations were computed in CA3 for each pair of shapes (see methods; Fyhn et al. 2007; Leutgeb JK et al. 2007). A peak was observed within the central area of the population vector cross-correlogram for each square–circle comparison (Fig. 4). The peak correlation between square and circle increased substantially after the white circle was replaced by the morph circle, which made the two enclosures more similar. Taken together, the results show that the animals in the single location training group did not develop orthogonal place codes for square and circle environments. The primary effect was variation of firing rate between shapes without change in place field location.

Fig. 4.

Color-coded PV cross-correlation matrices for CA3 for each pair of shapes indicated above on day 4 in the single location training group. Red represents the value of +1 and blue indicates correlation values ≤0. The x-axis and y-axis indicate distance (in cm) from the center of the cross-correlogram. The autocorrelation matrix for the 1st square session is shown on the left and a peak correlation of 1 occurs in the center, as expected. In the cross-correlation matrices for the square–circle pairings, central peaks can be seen that are lower than the peaks for identical shape pairs. The peak in the cross-correlation matrix for the morph square–white circle (i.e., 1st presentation of square and circle) maps is quite faint. The peak increased substantially in the morph square–morph circle (i.e., sessions 3 vs. 4 and 5 vs. 6) cross-correlograms.

Morphing after single location training

On day 7, the test for attractor dynamics was introduced by presenting four novel intermediate shapes configured from the morph box, interleaved with the familiar square and circle configurations (Figs. 1 and 5 and Supplemental Figs. S2 and S3). Population vector correlations were significantly lower between the square and circle than those between the square and all of the other shapes (Fig. 5, C and D and Supplemental Table S2). There was a significant linear trend in the correlations over the morph series in CA3 (P < 0.008), with no evidence of an abrupt transition. There were minor deviations from the linear trend (in both directions) that were mostly explained by order effects [i.e., the morph shapes were presented in scrambled order; significant interaction between presentation order and degree of similarity to end shape, F(1,286) = 18.3, P < 0.001].

Fig. 5.

Place cell firing properties across the morph sequence of shapes in the single location training group. A and B: color-coded firing rate maps (scaled as in Fig. 3) for example place cells from CA3 (A) and CA1 (B) in one of the rats. Note that place fields did not change location across shapes; only rate changes can be seen. The remainder of cells recorded on this day in this animal are shown in Supplemental Fig. S2. C and D: PV correlations are shown (mean ± SE) for all place cells recorded in CA3 (C, 85 cells from 4 rats) and CA1 (D, 78 cells from 4 rats). Increases in PV correlations as shapes became more similar and decreases in PV correlations as shapes became more different were seen in both regions, but changes were small and gradual. Rate overlap and spatial correlation measures for these sessions are shown in Supplemental Fig. S3.

No significant differences in spatial correlations were found for CA3 (Supplemental Table S2 and Fig. S3A), indicating that CA3 place field locations remained constant across increasingly dissimilar shapes. In CA1, however, small yet significant changes in spatial correlations were detected across progressively different shapes (Supplemental Table S2 and Fig. S3B), consistent with previous reports of slightly lower spatial correlations between different shapes in CA1 than those in CA3 (Leutgeb S et al. 2005b). The overall degree of spatial remapping in CA1 was low; spatial correlations between all session pairs were >0.6 (Supplemental Table S2). In both CA3 and CA1, a number of small yet significant changes in rate overlap occurred across the series of progressively different shapes (Supplemental Table S2 and Fig. S3, C and D).

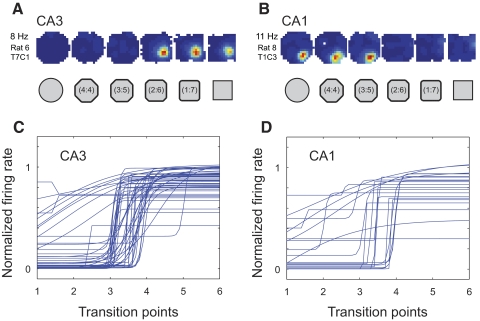
Next, the dynamics of individual neurons was examined to determine whether abrupt transitions between cell firing patterns may have been obscured in the averaging process. Examination of rate maps for individual neurons together with their sigmoid fits revealed that firing rate changes were subtle—not abrupt—and did not tend to occur at a central transition point (Fig. 6). To further substantiate this conclusion, abrupt shifts in firing rate distributions were defined by considering only place fields with rate changes that were significantly fit by the sigmoidal curve and then determining the transition points from high to low rates or vice versa (similar to procedures used in Leutgeb JK et al. 2005a and Wills et al. 2005; see methods and Supplemental Fig. S4). Only cells having in-field average firing rates of ≥2 Hz in at least one of the shapes were included in the analysis. For CA3, 28 fields from 85 cells exhibited rates that surpassed the threshold and 11/28 of these fields had rate values across progressively different shapes that could be significantly fit with a sigmoid function. For these cells, the most frequent transition point occurred in the middle of the sequence, but over half of the fields transitioned at other points in the sequence (Supplemental Fig. S4A). For CA1, 38 fields from 78 neurons were analyzed and 8 of these fields exhibited average firing rate changes across successively different shapes that were significantly fit by a sigmoid function. The transition points were distributed across all shapes in the sequence (Supplemental Fig. S4B).

Fig. 6.

Firing rates for individual place fields as a function of incremental changes in shape for the single location training experiment. A and B: example place cells from CA3 (A) and CA1 (B), with firing rate changes that were fit with a sigmoid. The color-coded rate maps for these cells are scaled to the maximum rate across all sessions (indicated on left). C and D: sigmoid fits for in-field firing rates for all place fields in CA3 (C) and CA1 (D) that surpassed the 2 Hz in-field mean firing rate threshold used for this analysis. Firing rates for individual fields were normalized by dividing by the maximum rate across sessions. The order of shapes was reversed for rates that decreased across the sequence so that all rate changes could be plotted in increasing order.

CA3 population vector cross-correlations between the square and subsequent shapes corroborated the foregoing conclusions. Cross-correlation values increased gradually as shapes became more similar (Fig. 7 and Supplemental Fig. S5), and the changes across shape transitions were small and subtle. For each pair of shapes, the peak of the cross-correlation matrix was located in the center, indicating that CA3 place field locations did not shift substantially across different shapes. Thus rate remapping was the predominant effect observed in the single location training group, and maps for increasingly different shapes typically changed gradually and inconsistently, not abruptly and coherently.

Fig. 7.

Color-coded PV cross-correlation matrices (color scale and axes as in Fig. 4) from CA3 cells in the single location training group for the sequence of morph shape pairs. The cross-correlation matrices between the initial square session and all other shapes are shown, indicating a clear central peak for all shape pairs. The lowest correlation was seen between the square and the circle. Correlations increased gradually as the shapes became more similar.

Double location training

In the double location training group (n = 4; Fig. 2), unlike in the single location group, sessions were conducted in the morph circle and morph square at all stages of training; however, the animals were initially trained with the morph square and morph circle placed in different locations in the curtained test arena and connected by a corridor. The purpose of the corridor was to facilitate the association of different path-integrator coordinates with the two different shapes (McNaughton et al. 1996; Samsonovich and McNaughton 1997). With this training procedure, distinct spatial firing patterns emerged for the two enclosures.

On the fourth day of the protocol, square and circle enclosures were placed in a common central location. Distinct square and circle representations were largely retained following the location shift (Fig. 8; Supplemental Fig. S6 and Table S3). In both CA3 and CA1, population vector correlations, spatial correlations, and rate overlap measures were significantly lower for opposite shapes in the central location than those for repeated square sessions in the central location. The location change was not without any effect because population vector correlations between square and circle were significantly higher in the common location than those in the different locations, as were spatial correlations (Supplemental Table S3); however, this effect was relatively small.

Population vector cross-correlations showed no peak for opposite shape pairs in different locations or in the same location, irrespective of the relative orientation of the stacks, supporting the foregoing conclusion that the distributions of firing among the active hippocampal neurons were highly independent for the different shapes, irrespective of whether the shapes were in different locations or a common central location (Fig. 9). Thus although there was a minor effect of the change in location, the cells continued to respond strongly to differences in shape, exhibiting changes in both firing rates and place field locations.

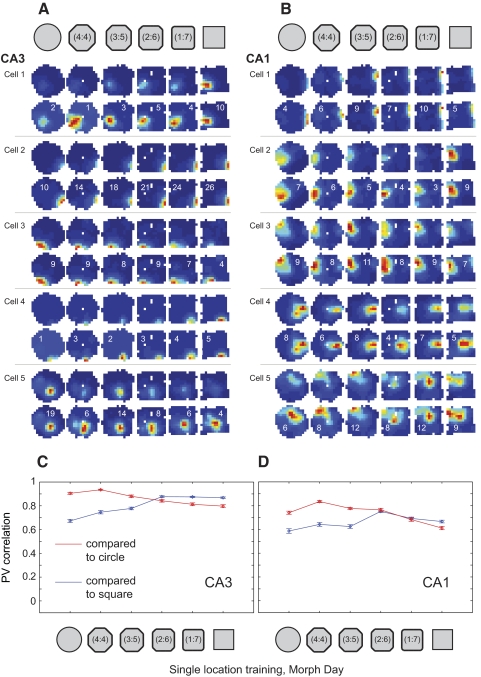
Morphing after double location training

The strong separation of square and circle representations was maintained on day 7 (i.e., the morph day; Fig. 10; Supplemental Fig. S7 and Table S4). In CA3, population vector correlations between the square and the three circular sessions were not significantly higher than zero (0.03 ± 0.11 for square vs. circle, 0.02 ± 0.09 for square vs. 4:4 shape, 0.03 ± 0.11 for square vs. 3:5 shape; binomial test, P > 0.1). In both CA3 and CA1, population vector correlations between the square and the three circular-shaped sessions were significantly lower than population vector correlations between the square and subsequent sessions in the square and square-like intermediate shapes. At the midway point in the morph sequence, where shapes transitioned from circle-like to square-like, population vector correlations switched abruptly from low to high values. Similar patterns of results were obtained for spatial correlation and rate overlap measures (Supplemental Fig. S8 and Table S4), indicating that separation of square and circle representations involved significant changes in both place field locations and firing rates. Taken together, the results indicate that CA3 and CA1 place cell firing patterns were consistent within the categories of square-like and circle-like shapes and largely independent between categories.

Fig. 10.

Place cell firing properties in the two location training group across the morph series of shapes. A and B: color-coded firing rate maps (scaled as in Fig. 3) for example place cells from CA3 (A) and CA1 (B) in one of the rats. Note the abrupt place field changes, involving both firing rate and field location, occurring coherently midway through the series of intermediate shapes. The remainder of cells recorded on this day in this animal are shown in Supplemental Fig. S7. C and D: PV correlations are shown (mean ± SE) for all place cells recorded in CA3 (C, 84 cells from 4 rats) and CA1 (D, 32 cells from 4 rats). In both regions, an abrupt change in correlations can clearly be seen at the middle transition point.

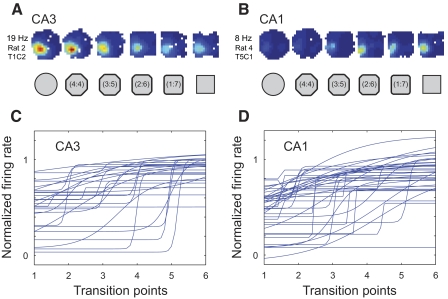
Nonlinear changes across the morph series were also seen in the firing properties of individual cells after double location training. Fitting sigmoid curves to the in-field firing rates revealed that most firing rate changes were abrupt and the abrupt transitions most often occurred at the middle transition point in the morph sequence (Fig. 11). For CA3, 51 fields from 84 cells had in-field firing rates that surpassed the 2-Hz criterion for inclusion in this analysis. Thirty-four of these fields had rates that were significantly fit by a sigmoid curve. This proportion was significantly higher than that for CA3 fields in the single location training group (comparison of two binomial distributions, Z = −2.35, P < 0.01 with one-tailed test and <0.02 with two-tailed test). The slopes of the significant sigmoid fits in the double location training group (35.2 ± 12.4 for CA3; 26.7 ± 14.5 for CA1) were about fivefold higher than those in the single location training group (7.4 ± 2.2 for CA3 and 4.4 ± 2.2 for CA1; one-tailed Mann–Whitney U test, P < 0.01 for CA3 and P < 0.03 for CA1). Also, in contrast to the single location training group, almost all (30/34) of the transitions in CA3 occurred at the same point, midway between the intermediate shapes (Supplemental Fig. S9A). The other four fields had transitions at the point adjacent to the middle of the sequence. In CA1, of 21 suprathreshold-rate fields from 32 cells, 9 were significantly fit by a sigmoid function. The proportion of sigmoid fits in CA1 in this group was also higher than that in the single location training group (Z = 1.77, P < 0.05 with one-tailed test and N.S. with two-tailed test) and, similar to the pattern of results obtained in CA3, 7/9 of the CA1 fields in the two location training group shared the same transition point, exactly at the midpoint in the sequence of intermediate shapes (Supplemental Fig. S9B).

Fig. 11.

A and B: example place cells with sigmoidal firing rate functions in CA3 (A) and CA1 (B). The color-coded rate maps for each example cell are scaled to the maximum rate across all sessions (indicated on left). C and D: sigmoid fits for in-field firing rates for all place fields in CA3 (C) and CA1 (D) that surpassed the 2 Hz in-field mean firing rate threshold. Firing rate sigmoid fits are shown normalized and ordered as described in Fig. 6, C and D.

When CA3 population vectors were cross-correlated for the square and the three most similar shapes (i.e., repeated square session and the two square-like shapes), a clear peak of similar magnitude was visible in the center of the cross-correlogram for all three shape pairs (Fig. 12; see Supplemental Fig. S10 for cross-correlograms between the circle and the intermediate shapes). On the other hand, when population vectors for the square and the three circular shapes (i.e., the circle and the two circle-like shapes) were cross-correlated, there was no detectable correlation peak across any of the shape pairs (Fig. 12). These results are very different from the results seen under identical morph day testing conditions in the single location training group (compare with Fig. 7). Thus when the parent representations were strongly spatially differentiated as a result of two location training, hippocampal networks switched sharply from one representation to the other, without any intermediate representations, when the balance of similarity tipped in favor of one endpoint versus the other.

Fig. 12.

Color-coded PV cross-correlation matrices (color code and axes as described in Fig. 4) for CA3 rate maps on the morph day in the two location training group for the sequence of shape pairs shown above. Clear peaks in the center of the matrix of nearly equal magnitude (close to 1) can be seen for the square–square cross-correlation as well as for the cross-correlation between the square and the 2 most square-like intermediate shapes. No peaks are seen in the cross-correlation matrices for the square–circle pair and for the square paired with the 2 most circular shapes.

DISCUSSION

A number of previous studies have demonstrated, in hippocampal ensemble recordings, the abrupt transition between states that is one hallmark of attractor dynamics. Gothard et al. (1996a, 2001) showed that, when there is a mismatch between the actual location of an animal relative to an initial reference point and the external cues that should normally appear at that location, an abrupt transition occurs that results in the expression of a pattern of activity consistent with the actual current location. Subsequently, using the morphing protocol described herein, Wills et al. (2005) showed that, in some animals, an abrupt transition occurred in CA1 activity when two previously experienced, differently shaped environments were morphed between the endpoints. In that study, in the included animals, the abrupt transition occurred at the midpoint between endpoints of the morph series. A later study demonstrated that CA3 cell ensembles that formed different representations of a testing enclosure in light and darkness and could abruptly switch between the two representations when the lights were switched on and off (Fyhn et al. 2007). These studies leave little room for doubt that the hippocampal formation either contains circuitry commensurate with attractor dynamics or is connected to and strongly driven by such a network. The question posed by the present study is thus not whether the signature of attractor dynamics can be observed in the hippocampus, but why it is seen in only some cases and not in others. The study was designed to contrast between two main hypotheses. 1) The autoassociator hypothesis is that external input features drive cells with modifiable recurrent connections (widely believed to be located in CA3) that therefore form attractors representing the stimulus features (McNaughton and Morris 1987; Treves and Rolls 1992). 2) The alternative, attractor-map hypothesis (Samsonovich and McNaughton 1997) is that the attractor dynamics exists as a consequence of associations between external inputs and a preexisting, continuous attractor network at the core of the path-integration system, which is currently widely believed to be located in medial entorhinal cortex (Fuhs and Touretzky 2006; Hafting et al. 2005; McNaughton et al. 2006). In this case, the external features alone are insufficient to create attractor dynamics.

An abundance of evidence supports the conclusion that the hippocampal formation as a whole is a network that is highly preconfigured to enable patterns of activity to be allocated to particular regions of space on the basis of the animal's movements between places—i.e., path integration. Hippocampal neurons do not “represent” external inputs in the sense that they exhibit invariant responses to certain constellations of external inputs. Rather, external inputs are secondarily associated with groups of neurons active at a given location and serve to set the origin of the path integrator when entering a familiar environment and to correct for cumulative error (McNaughton et al. 1996). These facts were already well established on the basis of studies up until 1996 that were reviewed at that time (McNaughton et al. 1996), and most of the available data were accounted for in simulations using the attractor-map model (Samsonovich and McNaughton 1997). Data supporting this theoretical perspective include: persistence of fields in darkness after cue removal (Markus et al. 1994; O'Keefe and Speakman 1987; Quirk et al. 1990); persistence of fields first expressed in darkness when the cues are subsequently illuminated (Quirk et al. 1990); symmetry breaking by hippocampal place fields in an environment with twofold radial symmetry (Sharp et al. 1990); omnidirectionality of place fields in open fields (Muller et al. 1994); instability of map representations in aged-long-term potentiation (LTP)–deficient animals or in animals with induced LTP impairment (Barnes et al. 1997); rapid realignment of fields (Gothard et al. 1996a); instantaneous global remapping of fields following mismatch between vestibular and visual cues (Knierim et al. 1998); global remapping of fields in two identical environments with 180° opposite orientations (Fuhs et al. 2005); distortions of fields with distortions of familiar but not novel environments (O'Keefe and Burgess 1996; Samsonovich and McNaughton 1997); general insensitivity of field size or local density to the local “information density” of external cues (Battaglia et al. 2004); and global remapping in identical environments located in different rooms (Leutgeb S et al. 2005b).

Changes in the hippocampal output at a given location in space have generally been referred to as “remapping” (Muller et al. 1991). Recently, a distinction has been shown between two types of remapping (Colgin et al. 2008; Leutgeb S et al. 2005b): “rate remapping” implies a change in the firing rate of individual neurons under the influence of different sensory inputs, without a change in the location of firing, whereas “global remapping” implies a change in the active set of cells at a given location, possibly even when the sensory inputs are the same. Global remapping is typically associated with an actual location change, although there are experimental circumstances in which it is not. In most of these cases, however, a change in path-integrator coordinates can reasonably be inferred. Indeed, the entire concept of hippocampal remapping (i.e., forming orthogonal representations at the same location when the cues are altered radically) was based originally on studies by Muller and Kubie (1987), using a circular and a square enclosure located at the same place. However, in that study the animals had actually initially been trained in the two enclosures in different locations (see Colgin et al. 2008). In addition, simply changing the relationship between the directional component of the path integrator and external cues can be sufficient to induce global remapping (Fuhs et al. 2005; Knierim et al. 1998).

Global remapping can also occur when there is no apparent reason to assume a change in path-integrator coordinates. One can imagine two possible mechanisms for this. In the simplest case, it is reasonable to assume that, on their first entry to the circular and square enclosures, some animals may not maintain consistent path-integrator coordinates from their point of origin. Arriving in the enclosures with two different sets of coordinates would be followed by associative linking of the external features to these different coordinates and thus a persistent global remapping in hippocampus. The included rats in the Wills et al. (2005) study may reflect this mechanism. A second mechanism might be related to mismatch detection: the hippocampal system may contain a mechanism for resetting the path integrator to some arbitrary coordinate when confronted with a large mismatch between the expected and actual cues experienced at a given coordinate. Something like this was observed by Knierim et al. (1998) following abrupt, 180° rotations of the recording chamber with the rat inside. In another study, global remapping occurred across sessions in a box placed in a single location when the floor and wall color used during a relatively extensive training period was changed during testing (Jeffery et al. 2003). More recently, Fyhn et al. (2007) trained rats in two very different enclosures at the same location and explicitly attempted to avoid disorienting the rats during transport from the holding platform to the enclosure. Realignment of the entorhinal grid cell system (the presumed basis of the path-integrator coordinates) was invariably accompanied global remapping in CA3, whereas rate remapping in CA3, induced by more modest environmental changes, was accompanied by grid coordinate stability.

In the present study, we explicitly attempted to associate the two different enclosure shapes with two different spatial coordinates in one group of rats and with the same spatial coordinates in a second group. When the rats' internal representations were probed using the morph procedure, the results were clear: animals with two location training exhibited relatively uncorrelated codes for the circle and square and a sharp, coherent transition between representations at the middle of the morph series, whereas animals with single location training exhibited more highly correlated codes for the endpoints and no evidence of a discontinuous shift during the morph sequence. In the latter case, the experimental error was sufficiently small, relative to the overall shift, that a discontinuity could have been detected if it had been present. Thus, associations among the represented features of the two boxes were not sufficient to produce attractor dynamics in the hippocampus, whereas associations between the features and an internal representation of relative location produced strong attractor dynamics. Our data are consistent with those of Leutgeb S et al. (2005b) in indicating that, although external features and events may affect the relative firing rates of the set of hippocampal neurons belonging to a particular coordinate representation, they typically scarcely affect the membership of the set. In contrast, changes in spatial location (except in some exceptional cases) produce changes in the active set if the distances are sufficiently large.

We conclude that the available evidence does not favor the theory that CA3 is a standard autoassociative network whose purpose is to encode associations among the sensory features of the environment. This conclusion is parsimonious with recent evidence that casts doubt on the other component of the autoassociator theory: that of an orthogonalizing network in the dentate gyrus (Leutgeb JK et al. 2007; Alme et al., unpublished data). If the autoassociator theory is incorrect, then what might be the function of CA3? Based on the evidence for sequence encoding and retrieval in the hippocampus (August and Levy 1999; Jensen and Lisman 1996; Mehta et al. 1997; Skaggs et al. 1996) and, as suggested by Knierim et al. (2006) and others (e.g., August and Levy 1999), it appears that at least one primary purpose of the CA3 recurrent collateral network is to create “phase sequences” of place codes that can, for example, encode the coordinates of a route as a vector field amenable to flexible route selection (Blum and Abbott 1996) and could also be used as index-code sequences to assist recall of memory episodes whose actual data are stored in distributed form in the neocortex.

GRANTS

This work was supported by a Centre of Excellence grant from the Norwegian Research Council, a grant from The Kavli Foundation to M.-B. and E. Moser, an Alberta Heritage Foundation for Medical Research Polaris Award, and a joint U.S. Public Health Service/National Institute of Neurological Disorders and Stroke Grant NS-020331 to B. L. McNaughton.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).