Taste-Specific Cell Assemblies in a Biologically Informed Model of the Nucleus of the Solitary Tract

Abstract

Although the cellular organization of many primary sensory nuclei has been well characterized, questions remain about the functional architecture of the first central relay for gustation, the rostral nucleus of the solitary tract (NTS). Here we used electrophysiological data recorded from single cells in the NTS to inform a network model of taste processing. Previous studies showed that electrical stimulation of the chorda tympani (CT) nerve initiates two types of inhibitory influences with different time courses in separate groups of NTS cells. Each type of inhibition targeted cells with distinct taste response properties. Further analyses of these data identified three NTS cell types differentiated by their latency of evoked response, time course of CT evoked inhibition, and degree of selectivity across taste qualities. Based on these results, we designed a model of the NTS consisting of discrete, reciprocally connected, stimulus-specific “cell” assemblies. Input to the network of integrate-and-fire model neurons was based on electrophysiological recordings from the CT nerve. Following successful simulation of paired-pulse CT stimulation, the network was tested for its ability to discriminate between two “taste” stimuli. Network dynamics of the model produced biologically plausible responses from each unit type and enhanced discrimination between taste qualities. We propose that an interactive network of taste quality specific cell assemblies, similar to our model, may account for the coherence in across-neuron patterns of NTS responses between similar tastants.

INTRODUCTION

In the study of neural systems, it is generally accepted that functional capacity is in part a manifestation of structural organization. The structural organization of the olfactory bulb for example, mirrors the chemical complexity of odorants, encompassing both modular organization and significant intranuclear projections (Friedrich and Laurent 2001; Kay and Stopfer 2006). In the relay nuclei of the visual (Hamos et al. 1985; Lindstrom 1982) and auditory systems (Huang et al. 1999), a specific pattern of connectivity between dedicated neural elements contributes to the functional capacity of the region. While the cellular organization of many sensory relay nuclei has been well characterized, the architecture of the central relays for gustation remains unclear.

The afferent and efferent connectivity of the first central gustatory relay, the rostral nucleus of the solitary tract (NTS), has been well characterized; however, the organization of the internal circuitry of this region remains an area of active investigation. The NTS, located in the caudal medulla, receives input from the oropharyngeal cavity through branches of the facial, glossopharyngeal, trigeminal and vagus nerves (Bradley et al. 1985; Contreras et al. 1982; Felizardo et al. 2009; Hamilton and Norgren 1984; May et al. 2007) that project topographically from rostral to caudal, respectively (Hamilton and Norgren 1984; May and Hill 2006). The rostral, taste-responsive portion of the NTS consists of four major anatomical subdivisions, each with distinct neuroanatomical and functional characteristics (Halsell et al. 1996; Whitehead 1988). Taste-responsive cells derived from CT input are most numerous in the rostral central subdivision (McPheeters et al. 1990). It is from cells in this area that most of the projections to the parabrachial nucleus of the pons (PbN) originate (Norgren and Leonard 1973). Many taste-responsive neurons in the NTS have intranuclear projections, extending both mediolaterally and rostrocauadally (Whitehead 1988) and many of these are GABAergic (Lasiter and Kachele 1988).

Although neurochemical studies have shown that the peripheral taste nerves make excitatory, glutamatergic contacts with second order cells of the NTS (Li and Smith 1997; Smith et al. 1998), GABAergic inhibition is known to affect nearly 2/3 of the cells in this structure (King 2003; Liu et al. 1993; Smith and Li 1998; Wang and Bradley 1993). Inhibition in the NTS mediates breadth of tuning, spontaneous activity (Lemon and Di Lorenzo 2002; Rosen and Di Lorenzo 2009; Smith and Li 1998), temporal and spatial encoding of taste stimuli (Lemon and Di Lorenzo 2002), and synaptic plasticity (Bradley and Grabauskas 1998; Grabauskas and Bradley 1998, 1999, 2003).

Chemical and electrical stimulation of the chorda tympani nerve (CT; a branch of the facial nerve innervating the anterior 2/3 of the tongue) initiates a recurrent inhibitory influence that attenuates subsequent taste responsivity in many NTS cells (Lemon and Di Lorenzo 2002; Rosen and Di Lorenzo 2009). Cells of the geniculate ganglion, which convey fibers of the CT nerve, synapse with a variety of NTS circuits including those that ascend to the PbN, descend to the reticular formation, and project locally within the NTS (Zaidi et al. 2008). Furthermore, it was recently shown that electrical CT stimulation initiates two types of inhibitory influences in separate groups of NTS cells (Rosen and Di Lorenzo 2009). The two forms of inhibition had distinct time courses and were observed in cells with different taste response properties. Cells that exhibited inhibition with an early peak (10 ms) and a rapid decay (∼100 ms) were narrowly tuned to taste, responding selectively across the basic taste qualities (sweet, sour, bitter, and salty). Cells that exhibited a prolonged inhibitory time course (∼500 ms) with a delayed peak (50 ms) were more broadly tuned to taste, responding with similar magnitudes across taste qualities. Further analysis of these data showed that in addition to the narrowly tuned group of cells, the broadly tuned cells could be divided into two subgroups based on their time course of inhibition, yielding three distinct types of taste-responsive cells (see methods section below).

In the current investigation, we constructed a computational network model of the gustatory NTS informed by the findings of previous electrophysiological and neurochemical investigations (Grabauskas and Bradley 2003; Smith and Li 1998; Rosen and Di Lorenzo 2009). Our goal was to study how the pattern of connectivity between previously characterized gustatory cell types, defined by their taste selectivity and time course of CT stimulation-evoked inhibition (Rosen and Di Lorenzo 2009) might contribute to taste-specific spatial and temporal patterns of activation.

We began with the prediction that the cell types observed by Rosen and Di Lorenzo (2009) were organized into discrete cell assemblies each dedicated to the processing of a particular taste quality. This type of organization is an attractive framework for the organization of NTS cells because it allows for the emergence of taste specificity even though most taste-responsive neurons in the NTS are multisensitive. That is, as we show here, interactions among cooperative groups of taste-specific and more broadly tuned cells have the capability of sharpening signal-to-noise ratios associated with the input generated by a particular taste quality by subduing activity in other assemblies tuned to other taste qualities. This would be akin to lateral inhibition, a common feature of other sensory systems.

The concept of a cell assembly was first described by Hebb (1949). Hebb proposed that the connections between functionally related neurons were strengthened through repeated co-activation. The enhanced connectivity produces groups or assemblies of cells that process information cooperatively, acting as a “block” devoted to the same purpose. Importantly, cell assembly organization has been described as a feature of the circuitry of the caudal extension of the NTS, an area that is largely dedicated to respiratory, cardiovascular, and digestive function. Specifically, studies have shown that baroresponsive neurons in the caudal NTS transiently organize into cell assemblies that function in respiratory processing (Chang et al. 2000; Kawai and Senba 1996). It may be that the same functional organization extends rostrally to aid in processing of gustatory information. In fact, higher-order structures within the central gustatory neuraxis such as the gustatory cortex and basolateral amygdala also process taste information with this mechanism (Grossman et al. 2008; Katz et al. 2002; Stapleton et al. 2007).

The idea that NTS cells are organized into functional cell assemblies is further supported by several observations that are consistent with the criteria of cell assembly organization put forward by Harris (2005). The first of these is that stimulus-evoked spike trains must show temporal structure that is not determined solely by the temporal structure of the input. In the case of the NTS, for example, flow rate might represent the temporal structure of a taste stimulus. Although early reports suggested that the magnitude (firing rate) in the early, phasic portion of taste responses was a reflection of flow rate, a more recent report suggested that many cells use spike timing rather than spike count to convey information about flow rate and that many cells do not encode any information about flow rate (Di Lorenzo and Victor 2007). The second criterion for the presence of cell assemblies is that responses to repeated trials of the same stimulus show variable responses. This feature of taste responses in the NTS has been documented several times (Di Lorenzo and Victor 2003, 2007; Di Lorenzo et al. 2009; Roussin et al. 2008). The third criterion is evidence of coordinated activity of spike trains that is not strictly tied to stimulus input. Observations of cross-correlated spike timing of simultaneously recorded NTS cells by Adachi et al. (1989) relates to this requirement. The fourth criterion for cell assemblies is the coordination of population activity with ongoing internal processes, e.g., attention, novelty, etc., and is the most difficult to satisfy. However, NTS taste responses are known to reflect many features of the internal and external environment. For example, homeostatic properties such as thirst and salt-deprivation (Jacobs et al. 1988; Morton et al. 2006) and associative learning in the form of conditioned taste aversions (Chang and Scott 1984; McCaughey et al. 1997) are all factors that alter the way that NTS cells respond to taste stimuli. These collective observations support our hypothesis that cell assemblies are actually a feature of taste processing in the NTS.

Here we utilized a novel computational paradigm in which spiking neural networks were used in conjunction with “evolutionary computation” (see methods) to successfully simulate response properties of the gustatory NTS. In our model network, taste quality-specific cell assemblies were reciprocally interconnected via lateral inhibition. Connectivity within each assembly involved feedforward, recurrent, and lateral inhibitory projections. The dynamics of the system were shown to enhance the contrast between “taste” responses produced by quality-specific assemblies. The NTS network model replicated cell-type specific inhibitory time courses and biologically plausible discrimination between different taste qualities. The pattern of connectivity predicted in the network model affords empirically testable hypotheses of the cellular organization and mechanisms of encoding within the gustatory NTS.

METHODS

Gustatory cell types in the NTS

In a previous investigation (Rosen and Di Lorenzo 2009) on which the current model is based, the activity of single cells in the gustatory NTS was recorded during presentation of tastants (0.1 M NaCl, 0.01 M HCl, 0.01 M quinine, and 0.5 M sucrose) and following paired-pulse electrical stimulation of the CT. The breadth of tuning of taste-responsive cells was calculated in part with the selectivity measure that was designed to capture both breadth of tuning and magnitude of response. Selectivity was defined as the difference in response magnitude in spikes per second (sps) between the sum of the two strongest responses and the sum of the two weakest responses. Analysis of paired-pulse stimulation data revealed the nature (suppression, facilitation, or no effect), duration, and peak time of the paired-pulse effect. Paired-pulse suppression was defined as a significant decrease in the number of spikes following the test (2nd) pulse as compared with the conditioning (1st) pulse. The peak time of the paired-pulse effect was defined as the interpulse interval (IPI) at which the greatest difference in spikes between pulses was observed. The duration of the paired-pulse effect was quantified with a decay time constant (see Rosen and Di Lorenzo 2009).

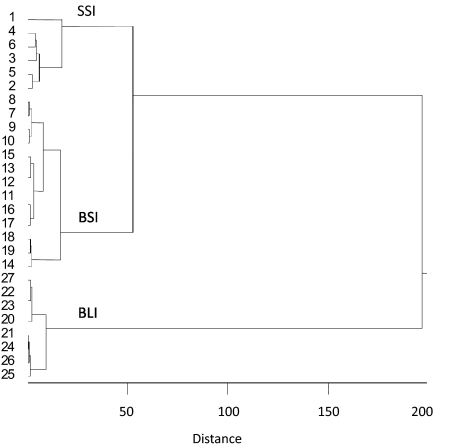
To define cell types based on data from Rosen and Di Lorenzo (2009), we applied hierarchical cluster analyses to the sample of 27 cells characterized by their latency of response to electrical CT stimulation, the time course of inhibition (based on results of paired-pulse stimulation experiments), and their selectivity to taste stimuli. In this analysis, cells are grouped sequentially beginning with the two most similar cells based on the Pearson product-moment correlation across relevant variables. As the analysis progresses, cells are added to existing groups or new groups are formed guided by similarity. The Ward method was used to form clusters.

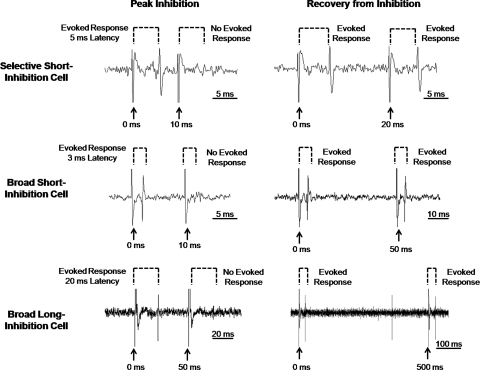
Results, presented in Fig. 1, suggested that there were three distinct cell types rather than two as originally reported. Two groups of cells with short latencies of evoked response to CT stimulation were identified. “Selective short-inhibition” (n = 6) cells showed short latencies of evoked response [mean = 4.5 ± 1.0 (SE) ms] and high selectivity to taste (mean = 22.1 ± 2.1 sps). Selective short-inhibition cells also exhibited the shortest time course of inhibition (mean decay time constant = 12.5 ± 6.5 ms). “Broad short-inhibition” (n = 13) cells showed a short latency of evoked response (mean = 4.2 ± 0.4 ms); however, they exhibited low selectivity to taste (mean = 6.4 ± 0.8 sps) and a slightly longer time course of inhibition (mean decay time constant = 33.5 ± 8.3 ms). “Broad long-inhibition” (n = 8) cells comprised the final group and showed a long latency of evoked response to CT stimulation (mean latency = 18.2 ± 1.1 ms). Broad long-inhibition cells showed a very long time course of inhibition (mean decay time constant = 356.3 ± 67.8 ms) and low selectivity to taste (mean = 3.0 ± 0.5 sps). Figure 2 shows examples of recordings from each cell type illustrating the responses to paired-pulse stimulation.

Fig. 1.

Results of a hierarchical cluster analysis of nucleus of the solitary tract (NTS) cells recorded in a previous investigation (Rosen and Di Lorenzo 2009). Latency of response to chorda tympani (CT) stimulation, time course of inhibition following paired-pulse stimulation of the CT nerve, and taste selectivity were used as variables. Similarity across cells was measured by the Pearson product-moment correlation. The Ward method of cluster formation was used. Cell numbers are indicated on the left. Three groups of cells were suggested by the analysis. See text for details. SSI, selective short-inhibition; BSI, broad short-inhibition; BLI, broad long-inhibition.

Fig. 2.

Examples of electrophysiological responses to paired-pulse stimulation of the CT nerve in each cell type suggested by the hierarchical cluster analysis. Left: records show failure of the evoked responses when the test pulse occurs during the interpulse interval that produces the most reliable inhibition of the evoked response. Right: records show a recovery from inhibition when the interpulse interval is longer than the period of inhibitory influence. Note the differences in scale for each record.

The statistical reliability of the neuronal grouping was further evaluated using an ANOVA. Significant main effects of selectivity, inhibitory decay time and latency of evoked response to CT stimulation on group were found [F(2,26) = 67.24, P < 0.01], [F(2,26) = 26.98, P < 0.01], and [F(2,26) = 104.65, P < 0.01], respectively. Post hoc analysis with Tukey's HSD test showed that the selectivity of the selective short-inhibition cells was significantly higher than that of the broad short and long-inhibition cells (α = 0.01). Post hoc analyses also showed that the latency of evoked response and inhibitory decay time constant of the broad long-inhibition cells were significantly longer than those of the selective and broad short-inhibition cells (α = 0.01).

General modeling strategy

Our overall strategy for constructing and testing our computational model consisted of two stages. The goal of the first stage was to find an arrangement of units (simulating cell types) that emulated the effects of electrical stimulation of the CT nerve in the NTS. For each iteration of the model, we determined the arrangement and type of connection (excitatory or inhibitory). A “genetic” computational algorithm (see following text for details) was then used to optimize free parameters. If/when the model failed, we modified the topology based on what aspects of the responses to the simulated inputs did not match what we see in the biological system. So, for example, if a unit's response was not inhibited at the right time and/or showed an anomalous time course of excitation or inhibition, we rearranged the connections between unit types to correct the error. In the second stage, we asked whether the model could discriminate between two simulated “taste” stimuli. The only modification to the model at this time was the addition of activity dependent plasticity before testing for taste stimulus discrimination. This modification was based on reports in the literature that this type of mechanism is characteristic of the gustatory portion of the NTS (Grabauskas and Bradley 2003). Successful discrimination was defined primarily by the responses, or lack thereof, of the selective short-inhibition units because they would be expected to be narrowly tuned, i.e., respond to one stimulus but not the other. However, success of the model was further gauged by a comparison of the temporal patterns of responses of all three units with that of their biological counterparts. That is, taste responses were required to show phasic and tonic portions as is common in the NTS.

Construction of the network model

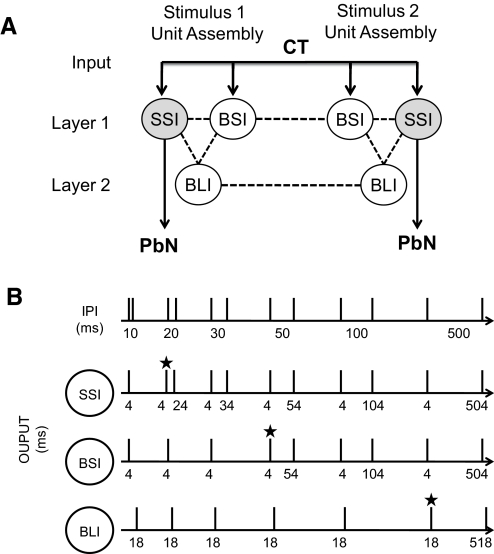
We began by interconnecting three representative “units,” each based on a physiologically identified cell type described in the preceding text, into a stimulus-specific assembly. Several features of the assembly organization were established a priori and founded on the observations of past studies. For example, because the input to NTS cells from peripheral nerves is known to be excitatory (Bradley and Grabauskas 1998), we arranged for the simulated “CT” input to directly activate the selective short-inhibition and broad short-inhibition units. Selective short-inhibition and broad short-inhibition cells in the biological system showed short latency responses to CT stimulation, suggesting a monosynaptic connection. Because of a recent report from Suwabe and Bradley (2009) showing that “strong” synapses join the CT nerve and PbN projection neurons of the NTS, our simulated CT activation was directly coupled to the selective and broad short-inhibition units. We modeled the selective short-inhibition cell as an NTS-PbN relay unit based on reports suggesting that, collectively, more NTS-PbN relay than nonrelay cells convey information as labeled lines, i.e., they are more selective (Di Lorenzo and Monroe 1997). The broad long-inhibition cells showed long and variable latencies of evoked response and were therefore indirectly connected to the model input via an excitatory connection with the selective short-inhibition units. This provided a place to start, and we labeled this model A. Two subsequent versions, each with reasoned improvements, were labeled models B and C.

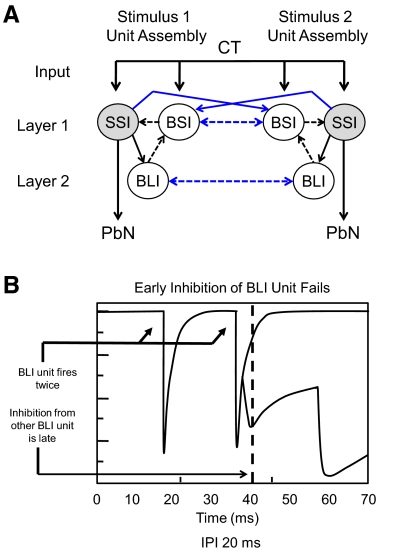
The model network had two layers: layer one contained units directly connected to the CT while the units of layer two received excitatory input from layer one (see Fig. 3). Lateral projections connected units within either layer one or two while feedforward projections traveled from layer one to two and recurrent projection from layer two to one. Both intra- and interassembly projections were included. Reciprocal connectivity was defined as two cells that both projected to and received projections from one another.

Fig. 3.

A: diagram of general model architecture. —, excitatory input and output; - - -, inter-unit connections. Layer 1 units receive direct excitatory input from the CT nerve while layer 2 units receive input from the selective short-inhibition units. The selective short-inhibition units are predicted to be relay units that project to the PbN while the broad short-inhibition and broad long-inhibition units are predicted to local interneurons. B: diagram of simulated paired-pulse input and optimal output of the network model. Top: the simulated paired-pulse stimulation at various interpulse intervals (IPIs). Numbers under the simulated “trace” indicate the particular IPI. The target output for each cell type was recovery from inhibition at a particular IPI. Rows 2–4: the simulated target responses of the model network in the SSI, BSI, and BLI units, respectively. Numbers under each simulated trace indicate the latency of “response” to the simulated stimulation shown in the 1st row. The SSI and BSI units showed a 4 ms response latency; the BLI unit showed an 18 ms response latency. ★, the IPI at which each pulse evokes a response, i.e., recovery from “inhibition.” Target output for the SSI, BSI, and BLI units was recovery from inhibition at IPIs 20, 50, and 500 ms, respectively.

The cell assemblies were named for the stimulus sensitivity of their relay unit (i.e., stimulus one assembly; stimulus two assembly). The interconnections between and within assemblies were systematically modified along with the synaptic weights (ω), delays (D), and membrane time constants (τ_m). See Table 1 for a list of fixed and modified parameter values. The parameter values were static during the paired-pulse simulation when the network architecture and values evolved; however, the decay time constant (τ_m) was made dynamic during the taste response simulation to allow for such short term plasticity described by Grabauskas and Bradley (1998, 1999, 2003). See appendix a for the mathematical formulation of activity dependent plasticity applied during the taste discrimination simulation.

Table 1.

Parameter values for each synapse

Parameter	Value
A. Modifiable
Weight	0–100
Delay	0–32
Membrane Time Constant	0–100 ms
B. Fixed
Synaptic Time Constant	1 ms
Absolute Refractory Period	2 ms
Relative Refractory Period	3 ms

Computational methods

We utilized a spiking neural network simulator that employs Gerstner's spike response model (SRM) for leaky integrate and fire neurons (Gerstner and Kistler 2002) along with dynamic synapses (Maass and Markram 2002; Markram et al. 1998) for spike timing dependent short term plasticity. The SRM is well suited to simulate neuronal communication at the abstract level. It reproduces electrical activity of the neuronal unit using kernels allowing for quick access mathematical modification of the shape of neuronal output behavior. The SRM model expresses the membrane potential at time t as an integral over past activation (Gerstner and Kistler 2002). The active neural dynamics of the system are influenced by the dynamics of the recent past. The SRM does not consider the spatial structure of the neurons nor the mechanisms that rule dynamics at the ionic level (Gerstner and Kistler 2002). See appendix a for the mathematical formulation of the SRM.

The network simulator was used in conjunction with “evolutionary computation” to systematically modify the network parameters to assess whether a given cellular organization could account for the input/output relationships observed in the biological data. Evolutionary computation refers to a category of computational techniques that utilize processes inspired by biology such as inheritance, mutation, selection, and recombination to solve complex problems. A popular type of evolutionary computation is genetic algorithms, a form of global search heuristic, for search and optimization problems. The genetic algorithm utilized in the current experiment was cross-generational-elitist selection, heterogeneous recombination, cataclysmic mutation, or “CHC” (Eshelman 1991). CHC is a genetic algorithm variant that uses survival competition between parent and offspring and vigorous crossover but only when two individuals are sufficiently distant (incest prevention). Incest prevention is among the criteria for soft restarts, where one individual survives and is used as a template chromosome for the rest of the population and mutated (biased toward the best solution). Using a soft restart helps avoid local maxima.

The network architecture (number of neurons and their synaptic connections) was specified manually, informed by the properties described in the preceding text. The genetic algorithm then selected parameter values for the neuron and synapse constructs based on initialization and choice of fitness function. The similarity between simulated spike outputs and cell type-specific target data was evaluated using a fitness function that measured distance between actual and target spikes. The genetic algorithm would search for viable synapse parameters (weights, delays, and membrane time constants) within experimenter-defined ranges to determine whether a given network architecture could produce cell type-specific target output. By employing evolutionary computation to tune our models, that is to cope with the combinatorially explosive nature of tuning the many free parameters, we sought some confidence that a failure to generalize may be interpreted as a failure of the topology to truly capture that of the NTS and not simply our failure to tune it properly. While there can be no guarantee that the tuning is optimal (Wolpert and Macready 1997), evolutionary computation in general and CHC in particular have been found to be quite robust for such large parameter optimization tasks (Eshelman 1991).

Evaluation and modification of the network model

Computational simulation was executed in two consecutive experimental phases: paired-pulse simulation and taste discrimination simulation. During the paired-pulse simulation, three network models were serially constructed and evaluated. The network architecture and synapse parameters were systematically modified. Modification enabled biologically accurate latencies of evoked response and time courses of inhibition for each unit type. We show results from two unsuccessful models to illustrate the ways in which alternative network architectures failed to simulate the characteristics of biological cell types in a paired-pulse stimulation and “taste” discrimination paradigm. Each network model was then further evaluated during the taste discrimination simulation. The network architecture and synapse values were unchanged; however, we allowed for activity dependent plasticity of the membrane time constants. Results showed that the network architecture of the final model could effectively emulate the results of paired-pulse stimulation experiments as well as effectively discriminate between “taste” stimuli.

Paired-pulse simulation

The objective of the paired-pulse simulation was to identify a network architecture and parameters that could produce cell types with biologically accurate: latencies of evoked response and time courses of inhibition. The time course of inhibition of each cell type was determined by its network connectivity and the associated synapse values. Three network architectures were created, each modified in succession in an attempt to reproduce the cell type-specific time courses of inhibition. The success or failure of the model was assessed by comparing the simulated network output with the “target” biological data. To be successful, a model was required to match the latency of evoked response and time course of inhibition of the biological cell types.

The input was pairs of “pulses” separated by an IPI that ranged from 10 to 500 ms. The target output (see Fig. 3) was recovery from inhibition at a particular IPI. Target output for the selective short-inhibition, broad short-inhibition, and broad long-inhibition units was recovery from inhibition at IPIs 20, 50, and 500 ms, respectively. Recovery from inhibition was observed as spiking following both of the paired-pulses. The target output for the paired-pulse simulation was informed by the mean latency and decay time constant observed for each cell type (see Table 2).

Table 2.

Latency of evoked response and decay time constant for biologically defined cell types and target recovery IPI for the model

Cell Type	Latency, ms	Decay Time Constant, ms	Target Recovery IPI, ms
Selective short-inhibition	4.5 ± 1	12.5 ± 6.5	20
Broad short-inhibition	4.2 ± 0.4	33.5 ± 8.3	50
Broad long-inhibition	18.2 ± 1.1	356.3 ± 67.8	500

Values are means ± SE. Target recovery was defined as the interpulse interval (IPI) at which spiking following both paired-pulses was observed.

Taste discrimination simulation

The taste discrimination simulation assessed each network's ability to respond differentially to trains of “tastant specific” stimulation. Taste-evoked responses in single CT nerve fibers range from 1 to 60 Hz in magnitude (Ganchrow and Erickson 1970; Ogawa et al. 1968) and are generally highest during the initial 1 s of the response (Ogawa et al. 1974). Input to the network therefore consisted of 1 s trains of evenly spaced pulses, at frequencies of 10, 25, 50, 75, and 100 Hz. This input was designed only as a first approximation of the average firing rate of CT fibers and ignored the temporal variations in the firing rates of responses, some aspects of which have been shown to convey information about taste quality (Nagai and Ueda 1981). Input was delivered through one of two “input sets,” each with synaptic weights that favored one taste assembly and representative of a discrete taste quality (see appendix b). The input was simultaneously delivered to the selective short-inhibition and broad short-inhibition units of both assemblies because biologically, these two cell types showed short latency CT-evoked responses. The network parameters in the taste discrimination simulation were the same as in the paired-pulse simulation; however, we allowed for activity dependent plasticity of the decay time constants. In other words, the time course of the synaptic potentials could persist ≤400 ms with sufficient activation. This form of plasticity has been observed using a slice preparation of the NTS where tetanic stimulation of the solitary tract induced frequency dependent increases in the time course of inhibitory currents (Grabauskas and Bradley 2003).

RESULTS

Three network models were serially constructed and evaluated with simulated paired-pulse stimulation. The network architecture of each successive model was modified to correct the limitations of earlier versions. While the first two models failed, the final network produced cell type-specific latencies of evoked response and time courses of inhibition that emulated the biological data (Rosen and Di Lorenzo 2009). We include a description of each prior model, its limitations, and the steps necessary to improve the model to justify the configuration of the final network. Each network model was then evaluated for performance in a taste discrimination task simulation. Results of this simulation showed that the final network could discriminate between two “tastants” of different qualities and produce biologically realistic and cell type-specific taste responses. Moreover, the taste discrimination simulation showed how the spike timing of each cell type was instrumental in the orchestration of taste discrimination. The membrane time constants, delays and weights for each synapse in models A–C are listed in appendix b.

Model A: recurrent inhibitory network with feedforward interassembly inhibition

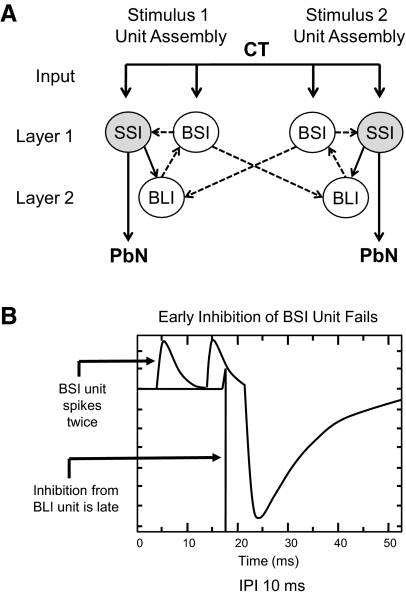
The initial network architecture (Fig. 4) consisted of two stimulus-specific cell assemblies, interconnected via feedforward inhibitory projections from the broad short-inhibition units to the broad long-inhibition units of the opposite assembly. The intraassembly lateral inhibitory projections from broad short-inhibition units successfully produced the early (10 ms) inhibition of selective short-inhibition units. Model A was found to be deficient because the onset of inhibition of the broad short-inhibition units occurred later (22 ms) than biologically observed (10 ms; see Fig. 4). As a result, the broad short-inhibition units spiked after each of the paired-pulses at an IPI of 10 ms and therefore failed to match the target biological data. The inhibition of broad short-inhibition units in model A was derived entirely from the recurrent intraassembly inhibitory projections from broad long-inhibition units that were not active until 18 ms after the onset of stimulation. The broad long-inhibition units were therefore not active in time to account for the early (10 ms) inhibition of broad short-inhibition units. For this reason, it was hypothesized that the early inhibition of the broad short-inhibition units may result from the inhibitory projections of other broad short-inhibition units. These were the only inhibitory units active at 4 ms, a feature necessary to produce the observed inhibition at 10 ms. As such, the subsequent model included reciprocal interassembly lateral inhibitory connectivity.

Fig. 4.

A: model A: recurrent inhibitory network with feedforward inhibition. SSI and BSI units received input from the CT directly. BLI units received input through an excitatory projection from SSI units. In this initial configuration, the 2 assemblies were interconnected via feedforward inhibitory projections from BSI units to BLI units. —, excitatory connections; - - -, inhibitory connections. B: simulated output from a BSI (top) and a BLI (bottom) unit in model A following simulated paired-pulse stimulation at an interpulse interval of 10 ms. The BSI unit shows 2 spikes in response to the pair of input pulses indicating the lack of short term inhibition. At this IPI, the BSI unit should have spiked only once. This can be accounted for by the late arrival of inhibition from the BLI unit.

Model B: recurrent inhibitory network with reciprocal interassembly lateral inhibition

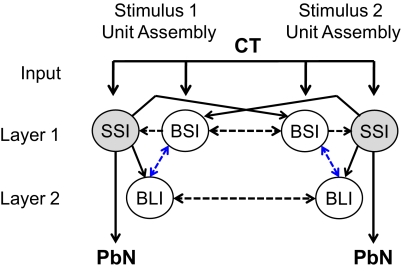
In model B (Fig. 5), the two cell assemblies were interconnected with reciprocal, lateral inhibitory connections to correct for the delayed inhibition of the broad short-inhibition units observed in the previous model. The broad short-inhibition units and the broad long-inhibition units of opposite assemblies were reciprocally interconnected with lateral inhibitory projections. In addition, lateral excitatory projections from selective short-inhibition units to broad short-inhibition units of the opposite assembly were included to drive the lateral inhibition between assemblies. The new connections were meant to decorrelate taste responses via lateral inhibition of competing assemblies and simultaneous self-disinhibition. The new lateral inhibitory connections between broad short-inhibition units allowed for their early (10 ms) inhibition that was not present in the previous model. The recurrent intraassembly projections from broad long-inhibition units achieved the late (30 ms) inhibition of broad short-inhibition units. Although the modifications inherent to model B allowed for the complete time course of inhibition in broad short-inhibition units (10–30 ms), the model could not simulate the complete time course of inhibition observed in the broad long-inhibition units (20–500 ms). The lateral connections between broad long-inhibition units produced delayed inhibition (42 ms) but could not account for the earlier (20 ms) inhibition biologically observed in these cells (see Fig. 5). To correct for this, a feedforward intraassembly inhibitory projection from broad short- to broad long-inhibition units was included in the subsequent model. A feedforward inhibitory projection from broad short- to broad long-inhibition units would include one less synapse in the inhibitory pathway and was therefore hypothesized to allow for the early (20 ms) inhibition of broad long-inhibition units.

Fig. 5.

A: model B: recurrent inhibitory network with reciprocal lateral inhibition. The 2 assemblies were interconnected via reciprocal inhibitory lateral projections between BSI units and between BLI units, and lateral excitatory connections between the SSI units and the broad short-inhibition units of the opposite assembly. —, excitatory connections; - - -, inhibitory connections. Blue lines indicate connections that were different from those in model A. The lateral inhibitory connections between BSI units enabled the early inhibition (10 ms) of these cells. B: output from a BLI unit in model B following simulated paired-pulse stimulation at an IPI of 20 ms. At this IPI of stimulation, the BLI unit should have fired only once. However, the lateral inhibitory influence from the broad long-inhibition unit of the opposite assembly was delayed allowing the BLI unit to fire twice.

Model C: recurrent inhibitory network with reciprocal interassembly lateral inhibition and feedforward intraassembly inhibition

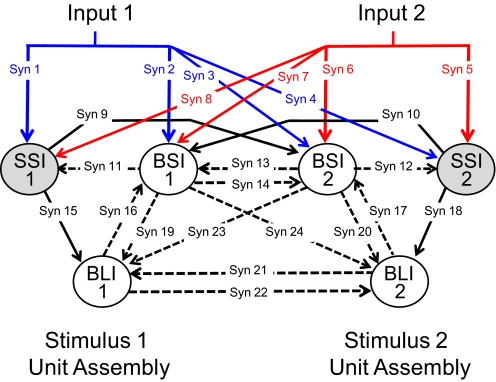
In the final network configuration (Fig. 6), a feedforward inhibitory connection from broad short- to broad long-inhibition units of the same assembly was included to allow for the early component (20 ms) of the inhibition observed in the broad long-inhibition units. This projection had fewer synapses than the lateral inhibitory projection that was the sole source of inhibition to the broad long-inhibition units in the previous model. With this new projection, the early inhibition (20–30 ms) observed in these units was successfully produced through the feedforward projection from broad short-inhibition units while the later inhibitory component (50–500 ms) resulted from the lateral projections between broad long-inhibition units. With this final network configuration, all of the simulated cell type-specific time courses of inhibition and latencies of evoked response matched those observed in the three biological cell types.

Fig. 6.

Model C: recurrent inhibitory network with lateral and feedforward inhibitory projections. The feedforward projections from broad short-inhibition units to broad long-inhibition units enabled the early inhibition (20 ms) of the broad long-inhibition units. —, excitatory connections; - - -, inhibitory connections. Blue lines indicate connections that were different from those in model B.

Results of the paired-pulse simulation predicted dedicated functional roles for the broad short-inhibition neurons which likely receive direct input from the CT, and the broad long-inhibition neurons with predicted polysynaptic connectivity with the CT. The early component of inhibition in each of the three cell types was produced by the broad short-inhibition units while the late component of inhibition was produced by the broad long-inhibition units.

Taste discrimination simulation

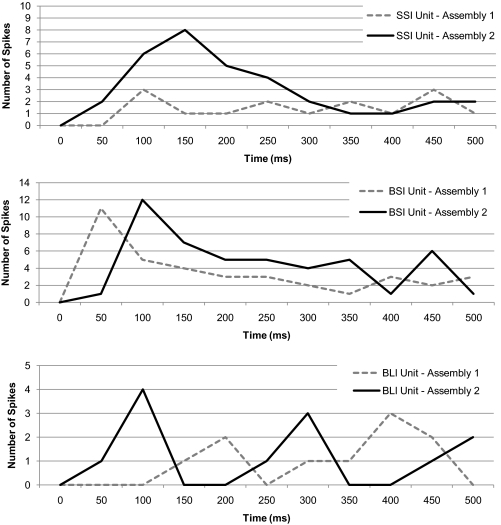
The taste discrimination simulation revealed cooperative dynamics between cell types and the instrumental role of spike timing in taste discrimination. We observed the functional specificity of each cell type as well as the manner in which they influenced one another. The three units of the stimulus 2 assembly are shown responding when stimulus 1 input and then stimulus 2 input was presented to the model C (Fig. 7).

Fig. 7.

A: simulated taste responses of unit assembly 2 to presentation of stimulus 1 followed by stimulus 2 (both at 25 Hz). Stimulus 2 evoked a phasic-tonic pattern of response in the SSI unit that was not observed with presentation of stimulus 1. Both broadly tuned units responded nearly equally well to both stimuli 1 and 2. B: electrophysiological responses to a 5 s presentation of 2 different taste stimuli recorded from NTS neurons of each cell type. Similar to the network model, a phasic-tonic response pattern was apparent in the SSI neuron's response to its “best” stimulus (stimulus 2) and was absent with presentation of stimulus 1. Both broadly tuned units responded nearly equally well to both stimuli 1 and 2.

Presentation of stimulus 1 resulted in weak activation of the stimulus 2 selective short-inhibition (relay) unit. As a consequence there was delayed activation of the broad long-inhibition unit to which it projects. The delayed responsivity of the broad long-inhibition unit resulted in early disinhibition and thus robust phasic activation of the broad short-inhibition unit. The early phasic responding of the broad short-inhibition unit served to “gate” the response of the stimulus 2 relay unit via its lateral inhibitory influence.

Presentation of stimulus 2 resulted in strong activation of the stimulus 2 relay unit and immediate firing in the broad long-inhibition unit. The early firing of the broad long-inhibition unit produced transient inhibition of the broad short-inhibition unit, precluding its lateral inhibitory influence over the relay unit. Without the lateral inhibitory influence of the broad short-inhibition unit, the stimulus 2 relay unit responded with a phasic burst of activation when presented with stimulus 2.

Similar cell type-specific temporal dynamics can be observed in the responses of biological NTS cells as illustrated in Fig. 7. This figure shows three cells representative of each cell type responding to two different stimuli. The selective short-inhibition cell responds to its best stimulus with a phasic burst and sustained spiking. The broad short-inhibition cell responds with sporadic bursts and lower selectivity between stimuli. The broad long-inhibition cell shows weak responses to both stimuli with periods of sustained quiescence.

Figure 8 compares the output of the assembly one and assembly two units of model C when stimulus 2 was presented. Analogous cell types belonging to opposite assemblies were compared to reveal the interassembly dynamics and “temporal gating” of network output. The output of the relay (selective short-inhibition) units was differentiated by their magnitude of response or spike count as is common for narrowly tuned cells in the NTS (Di Lorenzo and Victor 2003; Di Lorenzo et al. 2009; Roussin et al. 2008). The output of the model interneurons (broad short- and long-inhibition units) was differentiated by the time course of their responses as is observed in many broadly tuned NTS cells (Di Lorenzo and Victor 2003; Di Lorenzo et al. 2009; Roussin et al. 2008). The reciprocal inhibitory relationship between and within assemblies was evident in the offset in peak firing observed in the interneuron subtypes. The timing of interneuron inhibition ultimately determined the response magnitude of the selective short-inhibition units.

Fig. 8.

Time course of simulated responses in analogous cell types belonging to unit assemblies 1 and 2 responding to stimulus 2 (at 25 Hz). The responses of the SSI units to each stimulus were differentiated by spike count. The responses of the BSI and BLI units to each stimulus were differentiated by the timing of the peak firing rate. Note the differences in scale across graphs.

In Fig. 9 and Table 3, earlier versions of the network model were compared with the final network model in the taste discrimination simulation. Both models A and B did not produce biologically plausible responses to paired-pulse simulation and failed to emulate biological responses to taste simulation (see responses in Fig. 7B compared with those in Fig. 9). In Table 3, all models were tested with input frequencies between 10 and 100 Hz with and without inhibitory connections. Spike counts from all three unit types of unit assembly 2, tuned to stimulus 2, are shown.

Fig. 9.

Simulated responses to stimuli 1 and 2 (both at 25 Hz) in each unit type from unit assembly 2 in models A–C. Data from model C are repeated from Fig. 7 for comparison with output from earlier models. See text for details.

Table 3.

Effects of removal of inhibition on model output

	Inhibition						No Inhibition
	SSI 2		BSI 2		BLI 2		SSI 2		BSI 2		BLI 2
Input Frequency, Hz	S1	S2	S1	S2	S1	S2	S1	S2	S1	S2	S1	S2
A. Model A
10	52	42	27	20	9	4	73	57	38	37	34	29
25	72	35	18	32	7	4	92	50	29	40	32	24
50	81	29	20	20	7	2	101	40	32	35	31	29
75	84	39	28	35	12	4	104	48	42	44	30	24
100	88	36	20	32	11	4	101	55	29	43	32	27
B. Model B
10	26	29	15	31	15	16	46	50	53	77	41	31
25	23	26	7	44	15	9	55	40	45	86	40	28
50	39	27	7	23	16	21	60	37	36	79	39	29
75	32	21	14	47	13	9	61	45	44	77	40	39
100	37	21	2	44	29	13	61	54	53	70	39	29
C. Model C
10	0	36	43	13	0	26	0	58	64	35	0	64
25	14	33	40	47	15	12	24	49	63	76	52	42
50	21	30	39	45	11	10	25	40	62	73	53	36
75	21	38	34	45	13	10	34	47	51	80	55	44
100	4	40	49	26	5	33	33	55	58	73	55	52

Responses over 500 ms to stimulus 2 in models A–C when the input frequency was varied between 10 and 100 Hz. Responses from models with inhibitory connections disabled are shown on the right.

In general, increasing the input frequency did not result in consistent increases in the output frequencies of any of the cells; instead, changes in stimulus intensity changed the selectivity of various unit types depending on the model. In model A, the selective short-inhibition unit favored stimulus 1 and became less selective at low input frequencies. The broad long-inhibition unit also fired selectively to stimulus 1. These characteristics are the opposite of what one would expect of taste-responsive neurons because stimulus 1 was associated with a lower synaptic weight than stimulus 2 in the stimulus 1 assembly. In model B, the selective short-inhibition unit was broadly tuned and the two broadly tuned units were selective, in direct contradiction of observations of actual NTS cells. In model C, the selective short-inhibition unit was selective at all input frequencies and the broadly tuned units were broadly tuned with inputs at 25, 50, and 75 Hz. At very low (10 Hz) and very high (100 Hz) input frequencies, both broadly tuned units became more selective. These results predict that NTS cells may respond with greater selectivity at low- and high-input frequencies, presumably corresponding to stimuli of low and high concentration, respectively.

Not surprisingly, disabling the inhibitory connections increased spike counts across the board and changed selectivity. In model A, for example, the broad long-inhibition unit became more broadly tuned without inhibition. The selective short-inhibition unit, however, remained selective to stimulus 1, a biologically improbable result. In model B, all units became broadly tuned with amplified spike counts following the deletion of inhibitory interactions. In model C, the selective short-inhibition unit became less selective at 75 and 100 Hz but remained selective at lower input frequencies without inhibition. The two broadly tuned units remained selective at the lowest input frequency (10 Hz) but became broadly tuned at the highest input frequency (100 Hz) compared with their output when inhibition in the network was functional. Interestingly, the temporal features such as sustained periods of quiescence in the broad long-inhibition cells were absent when the inhibition was disabled but were successfully emulated with inhibition intact (not shown). Inhibition was therefore a necessary feature for the simulation of biologically plausible “taste” responses.

DISCUSSION

Using a biologically constrained computational model, we explored the idea that cells in the NTS could function as taste-specific assemblies to discriminate among taste stimuli. We first defined three discrete NTS cell types differentiated by their latency of evoked response to electrical stimulation of the CT nerve, time course of CT stimulation-evoked inhibition, and selectivity of responsiveness across taste qualities. We then used evolutionary computation along with a spiking neural network simulator to construct a model that included one exemplar of each cell type. Targeted modifications were made through three iterations until the final model could reproduce the time course of inhibition and stimulus selectivity of the biological counterparts of each component unit of the model. Further, this model successfully simulated taste discrimination when tested with different inputs. The results generate several empirically testable hypotheses about the functional roles of the identified NTS cell types, the pattern of connectivity between these cells and the processing mechanisms intrinsic to the proposed organization.

Temporal gating of spatial encoding channels

Temporal gating is a mechanism in which the spike timing of neural elements is instrumental in the selective propagation of information. The distinct time courses of inhibition in both the model and the biological cell types likely underlie such a mechanism to aid in taste coding. For example, it was suggested in a previous study (Rosen and Di Lorenzo 2009) that the short inhibitory influence observed in the selective short-inhibition cells, along with their narrow tuning and short, stable latencies, could allow for the transfer of robust, stimulus specific signals from the NTS to the PbN, site of the next synapse in the rodent central taste pathway. Network simulation suggests that the slightly longer time course of inhibition observed in broad short-inhibition units appears to parse or gate the output of the selective short-inhibition units through a lateral inhibitory influence. In addition broad long-inhibition units, with their prolonged time course of inhibition, modulated the output of the broad short-inhibition units. The long time course of inhibition observed in the broad long-inhibition cells may produce a transient record of recent taste activation that can alter responses to taste stimuli processed shortly thereafter. The long time course may therefore be active in the activity-dependent modulation of taste responsivity observed in the NTS (Di Lorenzo et al. 2003). In addition, it has been suggested that the long time course of inhibition may serve to mediate the temporal dynamics of taste responses and to regulate the background activity or noise against which stimulus selective cells carry their message forward (Rosen and Di Lorenzo 2009). The current investigation expands on this hypothesis by suggesting mechanisms through which broadly responsive inhibitory interneurons may gate or release the flow of neural information though stimulus-dedicated channels.

Temporal gating is observed in a variety of neural systems (Arevian et al. 2008; Salinas and Sejnowski 2001; Schiff et al. 1999; Venugopal et al. 2007). In the transfer of information between the primary and secondary olfactory relays, for example, the timing and thus the synchrony of spiking is critical to the selective transfer of olfactory signals (Laurent et al. 2001; Salinas and Sejnowski 2001; Wehr and Laurent 1996). Temporal gating enables the decorrelation of odor responses in the primary olfactory relay and plays a key role in the decoding of responses in the next olfactory relay. The results of our network simulation suggest that temporal gating may also be active in taste response decorrelation and the selective propagation of neural signals in the NTS. Specifically, in our network model, the spike timing of locally projecting inhibitory units modulated the output of stimulus specific relay units. In other words, the stimulus-specific relay units constituted spatial encoding channels that were “gated” by the temporal dynamics of a network of broadly tuned, interconnected inhibitory interneurons. The temporal dynamics of interneuron firing either allowed or prohibited the associated relay unit to carry its stimulus-specific signal forward.

Inhibitory neural networks

The cellular organization proposed in the current investigation was informed by the intracellular investigations and resulting NTS circuitry hypothesized by Bradley (2007). One common configuration is intranuclear feedback inhibition that targets excitatory projection neurons. Feedback inhibition is supported by the observed latencies of excitatory (4.8 ms) and inhibitory (8.8 ms) postsynaptic potentials recorded from NTS cells in vitro with stimulation of the solitary tract (Bradley 2007; Grabauskas and Bradley 1996). The observed time courses suggest monosynaptic activation of excitatory NTS elements and a delayed recurrent inhibitory influence that involves multiple synapses (Bradley 2007), both of which are present in the current network model. In addition, Bradley and Sweazey (1992) identified distinct groups of NTS cells, distinguished by the pattern of their evoked responses in a hyperpolarization/depolarization paradigm. One group of cells showed delayed responsivity to depolarizing current after hyperpolarization while the other group was unaffected by the early inhibition. In an additional group, hyperpolarization resulted in an irregular spiking pattern following depolarization while these cells fired regularly in the absence of inhibition (Bradley and Sweazey 1992). Inhibition therefore plays an essential role in discriminating the spike output patterns of different cell types.

Inhibitory time course has been shown to be a crucial determinant of output selection in a variety of neural systems. For example, within the reticular formation, to which the NTS sends direct projections, there is the central pattern generator for several key oromotor behaviors. It has been suggested that the time course of inhibition between premotor interneurons in the reticular formation is critical to the selection of appropriate motor programs (Venugopal et al. 2007). In our network model, cell type-specific time courses of inhibition were integral to the selective propagation of taste-specific neural information.

A critical feature of the NTS model was reciprocal lateral inhibitory connectivity between cells assemblies that produced competitive dynamics between them. That is, disinhibition of the assembly with the greatest input and simultaneous inhibition of the competing assembly evoked self-perpetuating excitation. Recurrent and lateral inhibitory networks, similar to the one described in the current study, have been observed in a variety of sensory and motor systems (Coultrip et al. 1992; Friedrich and Laurent 2001; Kay and Stopfer 2006; Mink 1996). The temporal characteristics of the inhibition within these neural networks have been shown to influence the selective propagation of sensory and motor signals. Reciprocal inhibition often produces a condition where excitation of one assembly contributes to the inhibition of competing assemblies. This type of inhibitory process has generally been shown to sharpen neural output patterns, enhancing discrimination between competing stimuli (Mao and Massaquoi 2007).

Our model suggests that such dynamics in the NTS may allow for the exponential and selective amplification of small differences in afferent information. In other words, contrast enhancement and response decorrelation inherent to the inhibitory network dynamics may improve detection of subtle differences in gustatory stimuli. Competitive dynamics observed in our NTS network model are typical of recurrent and lateral inhibitory networks observed in various sensory relay nuclei, e.g., in the olfactory system (Friedrich and Laurent 2001; Kay and Stopfer 2006), in motor structures such as the basal ganglia (Mink 1996) and even within the hippocampus (Coultrip et al. 1992).

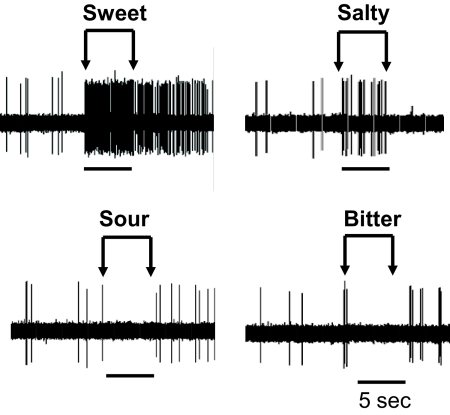
Studies of taste processing in the brain stem show evidence of reciprocal inhibition between taste-specific neural elements. For example, Smith et al. (1994) have shown reciprocal inhibition between parallel neural pathways dedicated to appetitive and aversive taste stimuli. Reciprocal inhibition between competing assemblies may also account for inhibitory responses to taste stimulation observed in some NTS cells. This phenomenon can be seen in the electrophysiological responses to taste stimuli recorded from the NTS cell shown in Fig. 10. The cell in this figure shows excitation in response to sweet and salty tastants and inhibition in response to sour and bitter tastants. The presence of both excitation and inhibition suggests interdependence between neural elements dedicated to different taste qualities. Certain stimuli may excite one neuron while simultaneously inhibiting the activity of another as was the case in the network model. This could serve to enhance contrast between stimuli, improve signal resolution and ultimately facilitate the selection of taste-specific behavior.

Fig. 10.

Electrophysiological responses to taste stimuli recorded in a single NTS cell. Excitatory responses were observed with presentation of sweet (0.5 M sucrose) and salty (0.1 M NaCl) solutions while presentation of sour (0.01 M HCl) and bitter (0.01 M quinine HCl) solutions suppressed responsivity.

Limitations and predictions of the network model

As with any computational model of a biological system, our model of the NTS is necessarily incomplete. This is partly by design in that we aimed to include only the most essential properties of taste-responsive NTS cells and to explore the limits of performance of such a network. In doing so, we inevitably neglected some properties of NTS cells that, had they been included, might have improved or changed the network function. That said, it is notable that the network functioned as well as it did with so few of the known characteristics of NTS cells.

There were several omissions that may have impacted our findings. For example, because the model is based on cells that respond to electrical stimulation of the CT nerve, it ignores input from the glossopharyngeal, trigeminal and vagus nerves (Bradley et al. 1985; Contreras et al. 1982; Felizardo et al. 2009; Hamilton and Norgren 1984; May et al. 2007). In addition, the model did not include descending input from higher-order structures that would be expected to affect taste processing (Cho et al. 2002, 2003; Di Lorenzo and Monroe 1995). On the other hand, it is important to note that the “input” to the model was “generic” and could be reasonably conceptualized as arising from any or all of those sources and even to convey thermal and mechanical information (Ogawa et al. 1968, 1984) as well. That is, the input was simply a train of simulated pulses at a steady frequency; it varied only in the strength of the impact it had on each of the units in the model. So even though it was meant to simulate CT taste-related input, one could argue that two inputs, originating from some source, generated differential outputs due to the particular network architecture and synaptic weights. Still, it is possible that a more realistic simulation of the various inputs to the model NTS cells might have produced different results. The contribution of the present model is that it is capable of generating testable hypotheses about the anatomy and physiology of the circuitry of the NTS because much of it was constrained by biological data.

Four notable predictions could be advanced by the model results. First, results from model C predict that changes in stimulus concentration will produce changes in selectivity. Specifically, at very high and very low concentrations, the model suggests that all cells will become more selective. This is the natural result of different slopes of the intensity-response functions for each stimulus. That is, when the slope of the intensity-response function for one stimulus is steeper than that for another, the cell might show comparable responses to midrange concentrations of both stimuli but preferentially respond to one or the other stimulus at either extreme of the intensity-response function. This prediction is verifiable experimentally. The second prediction is that without inhibition, cells will become more broadly tuned. Evidence for this prediction already exists. Specifically, application of biculluline, a GABA_A receptor blocker, has been shown to broaden the tuning of NTS cells in hamster (Smith and Li 1998). The third prediction is that there are two sources of inhibition, one early and the other late, that influence cells in the NTS. The early and late inhibitory influences may be related to the two types of inhibitory postsynaptic currents observed by Grabauskas and Bradley (2003). In that study, electrical stimulation of the solitary tract produced inhibitory postsynaptic currents with either one decay time constant of 59 ms or two time constants of 38 and 181 ms (Grabauskas and Bradley 2003). The fourth prediction is that the three NTS cell types described here will process taste cooperatively as an ensemble. By defining an architecture that optimizes stimulus discrimination, the model specifies the types of interactions among these cell types that should occur.

Conclusions

A major contribution of the model is the proposed stimulus-specific cell assembly organization. This organization suggests a solution to a long-standing controversy surrounding the mechanism of taste coding in the NTS. That is, the modular organization of the proposed network satisfies both the “labeled line” and “across neuron pattern” theories of taste coding (for a review, see Smith and St John 1999). The stimulus selectivity of the model assemblies is consistent with a labeled line account while the reciprocal connectivity between assemblies and resulting distribution of activity is consistent with the across neuron pattern theory. Finally, the model also suggests that the temporal dynamics of spike patterns within and across cell assemblies may be instrumental in the selective propagation of taste specific information. In particular, interactions among cells types may sculpt the time course and spike timing of taste responses, two characteristics that are known to convey information about taste stimuli (Di Lorenzo and Victor 2003; Di Lorenzo et al. 2009; Roussin et al. 2008).

GRANTS

This work was supported by National Institute of Deafness and Other Communication Disorders Grant DC-006914 to P. M. Di Lorenzo.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX A

Mathematical formulation of the spike response model

$$u_j\left[t\right]={\displaystyle \sum _{t_j^{(f)}\epsilon Fj}\eta \left[t-t_j^{(f)}\right]+{\displaystyle \sum _{i\epsilon \text{Γ}j}{\displaystyle \sum _{l_i^{(g)}\epsilon Fi}{w}_{ij}}}}\times \epsilon \left[t-t_i^{(g)}-d_{ji}\right]$$

The preceding equation is the mathematical formulation of the spike response model, where the total membrane potential of neuron j, u_j (t), is the sum of all the postsynaptic potentials (PSPs) caused by the presynaptic spiking of neurons i and the refractory effect of a negative reset potential. Once neuron j generates a spike at time t_j the membrane potential is reset by the spike afterpotential, described by η[t − t_{(f )j} ]. Hence, the total membrane potential of neuron j is composed of the η-function modeling its own refractoriness and the ε-function describing the effect of the presynaptic spikes of neurons i with weights w_j i and delays d_ji. Let Γ_j be the set of all neurons that make synaptic contact with the dendritic tree of neuron j. Then, F_i represents the spike train from presynaptic neurons i and F_j the spike train from the current neuron j that affect the potential of neuron j. The ε-function and η-function are not fixed in the spike response model. but there are certain limitations outlined by Gerstner (Maass and Bishop 2001; Gerstner and Kistler 2002). In fact, the ε-function must have a short rise time followed by a longer decay. Moreover, the η-function requires that η(t) = 0 for t ≤ 0.

Equations for activity dependent plasticity

$$\text{frac}\left(t\right)=\text{frac}\left(t-1\right)\times [1-\text{util}\left(t-1\right)]\times \exp \frac{-\left(\Delta t\right)}{D}+\left(1-\exp \frac{-\left(\Delta t\right)}{D}\right)$$

$$\text{util}\left(t\right)=\text{util}\left(t-1\right)\times \exp \frac{-\left(\Delta t\right)}{F}+\text{U}\times \left[\text{1}-\text{util}\left(t-1\right)\times \text{exp}\frac{-\left(\Delta t\right)}{D}\right]$$

$$\text{contr(}t)=A\times \text{frac}\left(t\right)\times \text{util}\left(t\right)$$

In the preceding equations, frac(t) refers to the proportion of transmitter remaining in the synapse at time t. The value for frac(t) was initialized to 1 providing full functional capacity to the synapse. The parameter util(t) corresponds to the utilization or degree of use of the synapse represented as a percentile. The initial value of util(t) is the constant U in the range of [0,1]. The parameter contr(t) refers to the contribution of a given network parameter at time t, when the network is active. The magnitude of this contribution is calculated by multiplying constant A by frac(t) and util(t). The constant A refers to the initial value for the parameter of the dynamic synapse (e.g., membrane time constant). The initial parameter value can change depending on spike timing or frequency. Constants D and F control the magnitude of depression and facilitation, respectively.

APPENDIX B

Synapse parameter values for models A–C are listed. The patterns of network connectivity were specified manually (Table 4). Evolutionary computation via a genetic algorithm was used to search for synapse parameter values that could allow the network to produce cell type-specific target output. Modification of network connectivity from model to model was performed manually and was designed to correct for the limitations of earlier versions (Fig. 11).

Table 4.

Synapse parameter values for models A–C

Synapse	Membrane Time Constant, ms			Delay, ms			Weight
	Model A	Model B	Model C	Model A	Model B	Model C	Model A	Model B	Model C
1 & 5	2	2	2	4	4	4	10	10	10
2 & 6	2	2	2	4	4	4	4	4	4
3 & 7	2	2	2	4	4	4	1	1	1
4 & 8	2	2	2	4	4	4	1	1	1
9 & 10	NA	2.2	1.5	NA	6	1	NA	5	50
11 & 12	4.1	3.7	8.5	10	9	6	−92.2	−101.6	−27.9
13 & 14	NA	7.4	38.9	NA	6	1	NA	−21.8	−68
15 & 18	44.3	2.3	4.9	13	13	14	2	3.5	9.9
16 & 17	10.8	7.2	4.3	4	6	15	−8.6	−57.2	−69.8
19 & 20	NA	NA	8.5	NA	NA	20	NA	NA	−75.9
21 & 22	NA	68.4	64.8	NA	13	22	NA	−91	−46.7
23 & 24	83.2	NA	NA	16	NA	NA	−76.9	NA	NA

Fig. 11.

Diagram of the network model indicating the synapses that were modeled. Units are labeled according to type (SSI, BSI, or BLI) and unit assembly (1 or 2). —, excitatory connections; - - -, inhibitory connections. In each model, not all synapses were present.