Assessing the Incremental Role of Novel and Emerging Risk Factors

Abstract

Many novel and emerging risk factors exhibit a significant association with cardiovascular disease, but have not been found to improve risk prediction. Statistical criteria used to evaluate such models and markers have largely relied on the receiver operating characteristic curve, which is an insensitive measure of improvement. Recently, new methods have been developed based on risk reclassification, or changes in risk strata following use of a new marker or model. Associated measures based on both calibration and discrimination have been proposed. This review describes previous methods used to evaluate models as well as the newly developed methods to evaluate clinical utility.

Introduction

During the past two or three years, new methods have been proposed for the evaluation of risk prediction models and the assessment of novel risk factors. Previously, while many novel markers were found to be associated with cardiovascular disease events, and to have a biologic impact, these were found not to add to risk prediction [1]. Despite much recent progress in understanding the various biologic pathways leading to atherosclerosis and the development of a cardiovascular event, standard risk factors identified in the Framingham Heart Study over 30 years ago remain the primary basis of cardiovascular risk prediction [2, 3].

Methods of comparing models and evaluating markers used to arrive at this conclusion have relied almost exclusively on the receiver operating characteristic (ROC) curve [4], a statistical measure that assesses discrimination. New methods for comparing models have recently been introduced, and are gaining popularity in the cardiovascular literature [5–8]. For example, in evaluating the Reynolds Risk Score, investigators used risk reclassification to determine how using the score may affect clinical practice [9, 10]. This review will first describe the components of model accuracy, the origin and limitations of the ROC curve, then new methods for the evaluation of predictive models and novel and emerging risk factors.

Components of model accuracy

Two components of model accuracy for disease outcomes have been described, calibration and discrimination [11]. Calibration is the ability of a predictive model to accurately assign risk estimates. It compares the risk predicted from a model to that actually observed from a model-free perspective. In linear regression the outcome is a continuous variable such as blood pressure or cholesterol level, and it is relatively straightforward to compare the predicted level with that observed by plotting the observed vs. predicted values of blood pressure, for example. For binary outcomes such as disease this is more problematic since the outcome only takes on only two values, such as 0 or 1, rendering such a plot less useful. Smoothed estimates of the observed yes-no outcome can be used, but these are more complex and depend on the bandwidth or other smoothing parameters [12].

More easily interpretable and more commonly used to assess calibration is a comparison based on categories of risk. The familiar Hosmer-Lemeshow test [13] places individuals within deciles of estimated risk, although other categorizations could be used. The average predicted probability of disease within each category is compared with the observed proportion with disease. A chi-square test compares these observed and predicted probabilities in a goodness-of-fit test, which is usually interpreted as a test of calibration. The test, however, is not sensitive in detecting variables omitted from a model. For example, when traditional risk factors are left out of a predictive model for cardiovascular disease, none of the tests for calibration indicate a deviation between the observed and expected values [14•].

Discrimination, on the other hand, is the ability of a marker or model to separate cases and controls, or those in various disease states. It is a function of the relative ranks only; the actual predicted probabilities or score from a marker or model are not important. Ideally we would like all the ranks for the cases to be higher than all those for the controls, such that they are perfectly separated and display perfect discrimination. The most commonly used measure of discrimination is the area under the ROC curve, described in detail below.

Discrimination is most useful for diagnosis of disease among those with symptoms or for case-control studies, where separation into classes is of primary interest. For example, among those who present to the emergency room with chest pain, we would like to separate those who are truly having a myocardial infarction from those with angina or indigestion. When estimation of future risk is the goal, full separation is usually not achievable. This is because, except perhaps for rare genetic disorders, the future is not completely determined, and there is an element of chance involved [15].

The ROC curve in historical context

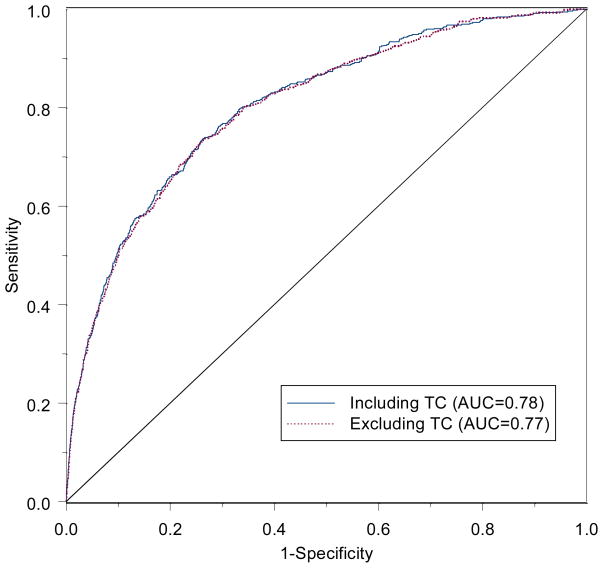
The ROC curve has emerged as the most popular means of evaluating model accuracy. It has its roots in signal detection theory, used in discriminating between signal and noise [16]. It was first used for the detection of enemy objects using radar signals during World War II. In medical testing it is used to discriminate between those with and without disease. The curve is a function of sensitivity and specificity, where sensitivity is the probability of a positive test among persons with disease, and specificity is the probability of a negative test among persons without disease. For binary tests with either a positive or negative result, only one value for sensitivity and specificity can be computed, providing one point on a hypothetical curve. For tests based on a continuous measure, such as cholesterol or blood pressure, a ‘positive test’ could be defined at any cutoff point along the continuum, such as 200, 220, or 240 mg/dl for total cholesterol. The ROC curve is constructed by plotting sensitivity versus 1-specificity for each cutoff value. An example is shown in the figure. An ideal test or cutoff value would correspond to a point in the upper left corner of the plot.

Figure.

Receiver operating characteristic (ROC) curves for models including traditional risk factors for cardiovascular disease in the Women’s Health Study but with and without total cholesterol (TC) [24].

Hanley and McNeil [17] described the meaning of the area under the curve (AUC), with application to radiologic testing. Given one person with disease and one without, the AUC, also called the c-statistic, is equal to the probability of correctly ranking these using the measure or model. It is the probability that the person with disease has a higher assigned risk. The area has a value of 0.5 for a useless test, which randomly assigns scores to individuals. The value of 0.5 corresponds to the area below the line of chance, or the diagonal line in the figure. The AUC has a maximum of one, for perfect discrimination or separation of diseased and non-diseased. It corresponds to a test with sensitivity and specificity both equal to one. Hanley and McNeil [17] showed that the AUC was equivalent to a Wilcoxon statistic, leading to a readily available computational method. Complementary nonparametric methods are available for testing differences in the AUCs [18, 19].

In 1982 Harrell et al [20] introduced a similar measure, called the concordance index or c-index, specifically for survival or time-to-event data. It has a similar interpretation to the AUC; for pairs for whom the survival time can be ordered, it is the fraction such that the patient with the higher score has the longer survival time. It has a similar range and properties as the AUC. A confidence interval for this measure is also available [21], although bootstrap methods are often used to compare correlated curves [22].

The AUC has been widely used to evaluate predictive models, which assign a probability to the risk of having or developing disease. It has been viewed as an overall summary of diagnostic accuracy [4, 23]. Comparisons between models, and the evaluation of new or emerging biomarkers, have typically used differences in the AUCs to determine whether a new marker has ‘clinical utility’. This definition of clinical utility, however, has been disputed [24••, 25]. Sensitivity is the probability of having a positive test among patients who already have disease. More important for patients and their treating physicians is the probability of having disease given a positive test result, or the positive predictive value [26]. This is even more important in prognostic models that predict risk in the future, since case status is not known at the time of the test [15]. Moreover, since it is based solely on ranks, the AUC is an insensitive measure of model improvement. Large changes in predicted risk and true improvement in clinical utility may lead to little change in the AUC.

While the ROC curve has been used to evaluate new biomarkers, to put these results in context it is worthwhile to consider the impact of traditional risk factors on the curve. In data from the Women’s Health Study [27], the traditional and well-known Framingham risk factors had little individual effect on the AUC. In a model containing age, systolic blood pressure, smoking, and total and low-density lipoprotein cholesterol, the AUC was 0.78 for predicting cardiovascular disease over a 10-year period [24••]. The impact of any individual predictor was a change in the AUC of 0.02 for systolic blood pressure and smoking, and of only 0.01 for the cholesterol measures. The ROC curves for the full model and that without total cholesterol are shown in the figure and virtually overlap. Only age had a sizeable effect on the area, with an AUC of 0.73. If these strong, well-known and proven risk factors cannot change the AUC, there is little hope that novel and emerging risk factors, even those that may have a strong biologic effect, would pass this stringent test.

A marker with a large association, and a large accompanying relative risk, may thus have little effect on the ROC curve. Pepe et al showed that a predictor or set of predictors needs an odds ratio as high as 16 per two standard deviations to lead to reasonably accurate decisions [28]. When added a new marker to an existing score, an odds ratio of 2, higher than that for traditional risk factors, leads to little change in the ROC curve [15]. Despite this, a large relative risk is an indication that the predictive value or probability of disease could change substantially given the result of the test or value of the marker [24••]. A relative risk of 3 indicates that the probability of disease could triple given a particular test result. Since guidelines are sometimes based on estimates of absolute risk [3], treatment decisions could change depending on the value of a marker, even if it does not change the ROC curve. For example, a tripling of risk from 8% to 24% would cross the Adult Treatment Panel III treatment boundaries [3], even though such a marker may not have a sizeable impact on the ROC curve.

Novel Methods Based on Risk Reclassification

New methods based on risk strata have been proposed to address the problem of the insensitivity of the ROC analyses and resulting AUC measure. The concept of risk reclassification, which was introduced in 2006 [29] and further described in 2007 [24••], directly compares pretest and posttest probabilities within clinically important risk strata. A risk reclassification table is a cross-tabulation of risk strata based on two models. While these are often models with and without a particular biomarker or risk factor of interest, they could actually compare any two predictive models. An example is shown in Table 1, again comparing models with and without total cholesterol based on the Reynolds Risk Score in the Women’s Health Study data [14]. For each model, women were classified into one of four risk strata. While the majority of women in this cohort were of low risk, and were classified as having less than 5% 10-year risk under both models, over 20% of those in the intermediate risk categories were reclassified into higher or lower risk strata.

Table 1.

Comparison of 10-year risk strata for the Reynolds Risk Score for cardiovascular disease with and without total cholesterol in the Women’s Health Study

Without TC		With TC				Total
		0% to < 5%	5% to < 10%	10% to < 20%	20%+
0% to < 5%	Patients, n	20,666	419	0	0	21,085
	% Reclassified	98.0	2.0	0.0	0.0	2.0
	Observed risk, %	1.4	5.7	-	-
	Predicted w/o TC, %	1.6	4.4	-	-
	Predicted with TC, %	1.5	5.7	-	-
5% to < 10%	Patients, n	345	1789	186	0	2320
	% Reclassified	14.9	77.1	8.0	0.0	22.9
	Observed risk, %	2.9	8.0	12.2	-
	Predicted w/o TC, %	5.6	6.9	8.7	-
	Predicted with TC, %	4.3	6.9	11.2	-
10% to < 20%	Patients, n	0	134	667	43	844
	% Reclassified	0.0	15.9	79.0	5.1	21.0
	Observed risk, %	-	7.7	15.0	21.5
	Predicted w/o TC, %	-	11.2	13.5	17.6
	Predicted with TC, %	-	8.8	13.6	22.9
20%+	Patients, n	0	1	50	258	309
	% Reclassified	0.0	0.3	16.2	83.5	16.5
	Observed risk, %	-	0.0	19.9	32.0
	Predicted w/o TC, %	-	21.2	22.0	31.7
	Predicted with TC, %	-	7.9	17.5	32.0
Total	Patients, n	21,011	2343	903	301	24,558

TC—total cholesterol; w/o—without.

(Data from Cook and Ridker [14•].)

While the percentage reclassified may be of interest in considering the ramifications of a new risk factor or model, it is not sufficient to judge a model’s superiority or a risk factor’s importance. Whether the reclassification is more accurate is of prime interest. One way of evaluating this is to compare the observed risk in the reclassified categories to see if it is close to that predicted. In Table 1, the observed risk represents the crude proportion of women who experienced an event. Comparing these to the defined risk strata indicates that those who are reclassified are put into more accurate strata. For example, among those who are initially in the 5-<10% stratum in the model without total cholesterol, the 345 women reclassified downward to the 0-<5% stratum had a 2.9% risk, which falls within the new 0-<5% range. The 186 women who are reclassified from the 5-<10% to the 10-<20% stratum have an observed risk of 12.2%, which falls within the new 10-<20% range. In each of the reclassified cells, the observed risk falls within the new risk stratum, indicating that the risk estimate from the model including total cholesterol is more accurate.

To more formally evaluate this accuracy, a test comparing the calibration in the reclassified categories has been proposed [14•]. This test is analogous to the Hosmer-Lemeshow goodness-of-fit test, and directly compares the predicted probabilities to the observed proportion with disease within cells of the table containing at least 20 individuals. It is computed as

$${\text{X}}_{RC}^2=\sum _{i=1}^K\frac{{(O_k-n_k{\overline{p}}_k)}^2}{n_k{\overline{p}}_k(1-{\overline{p}}_k)}\sim {\text{X}}_{K-2}^2$$

where n_k is the number of individuals in the kth cell of the table, O_k is the number of events in that cell, and p̄_k is the average predicted risk from the model for these individuals. The numerator explicitly compares the number of observed events to the number predicted from the model in each cell of the table. Under the null hypothesis of no difference in prediction, the statistic follows an approximate chi-square distribution with K-2 degrees of freedom, where K is the number of cells with at least 20 observations in the table. A significant result indicates a lack of fit. This test can be readily adapted to survival data by substituting Kaplan-Meier estimates, which take censoring into account, for the observed proportions.

For the cholesterol example in Table 1, the average predicted risks from models both with and without total cholesterol are shown for each cell. On visual inspection, the observed probabilities appear closer to those predicted from the model that includes total cholesterol. For example, for the 345 women moving from down from the 5-<10% to the 0-<5% stratum the observed proportion with disease of 2.9% is closer to the 4.3% predicted using total cholesterol than to the 5.6% predicted without cholesterol. For the 186 women moving up from the 5-<10% to the 10-<20% stratum the observed proportion with disease of 12.2% is closer to the 11.2% predicted using total cholesterol than to the 8.7% predicted without cholesterol. For the model without cholesterol, the value of the chi-square statistic is 16.1 (p=0.04), indicating that there is a deviation from fit, or lack of calibration, using this model [14]. For the full model including total cholesterol, the chi-square value is 7.3 (p=0.51), indicating closer agreement between the observed and predicted probabilities.

In 2008, Pencina et al [30••] proposed a different way of examining the reclassification table by conditioning on case or control status. They proposed displaying separate reclassification tables for cases and controls as seen in Table 2 for the same two models. With an improved model, we would expect that the cases would move up in risk strata while controls would move down. They thus examined the net movement in cases vs. controls, calling it the net reclassification improvement (NRI). The NRI is the percent of cases moving up vs. down plus the percent of controls moving down vs. up. It is defined explicitly as

Table 2.

Reclassification by case-control status comparing 10-year risk strata for the Reynolds Risk Score for cardiovascular disease with and without total cholesterol in the Women’s Health Study

Without TC	With TC				Total	%
	0% to < 5%	5% to < 10%	10% to < 20%	20%+
Cases as of 8 y, n
0% to < 5%	232	19	0	0	251	44.8
5% to < 10%	8	114	18	0	140	25.0
10% to < 20%	0	8	80	0	95	17.0
20%+	0	0	8	66	74	13.2
Total	240	141	106	73	560
%	42.9	25.2	18.9	13.0
Non-cases as of 8 y, n
0% to < 5%	20,204	387	0	0	20,591	87.2
5% to <10%	322	1619	158	0	2099	8.9
10% < 20%	0	116	560	30	706	3.0
20%+	0	1	40	174	215	0.9
Total	20,526	2123	758	204	23,611
%	86.9	9.0	3.2	0.9

TC—total cholesterol.

(Data from Cook and Ridker [14•].)

$$\mathit{NRI}=[Pr(up\mid \mathit{case})-Pr(\mathit{down}\mid \mathit{case})]+[Pr(\mathit{down}\mid \mathit{control})-Pr(up\mid \mathit{control})].$$

In Table 2, 44 cases move up a category and 24 move down a category, resulting in an improvement of 20/560 = 3.6% among cases. Among controls, 479 moved in the correct downward direction, but 575 moved up, resulting in a 96/23,611 = 0.4% worsening of the classification. The NRI combines these two and equals 3.6% − 0.4% = 3.2% [14]. This means that a net 3.2% of cases are classified higher using the model with total cholesterol. This statistic has an approximately normal distribution, with a standard error provided by Pencina et al [30••]. The improvement with total cholesterol is statistically significant, with p=0.032.

Note that the number of cases plus controls (24,160) does not add up to the total number of women in Table 1 (24,558). This is because 398 women were censored by dying of other causes. Because it conditions on case-control status, the NRI does not take censoring into account, although a modification has been proposed [31]. In addition, while the NRI is a simple measure to understand, its value is not inherent to the biomarker under consideration. The value depends on what other variables are in the model, what variables are in the comparison model, and what categories are used. For example, if only three risk strata are formed by collapsing the middle two strata, the NRI is only 1.8% (p=0.18), suggesting that total cholesterol is not helpful in reclassifying individuals [14•]. The reclassification calibration test, however, remains significant (p=0.033), suggesting that there is an improvement in calibration.

Pencina et al also presented a version of the NRI that is free of categories, called the integrated discrimination improvement (IDI). This is based on reclassification using only two categories, but integrates sensitivity and specificity over all possible cutoffs. It can more easily be defined based on the difference in predicted probabilities between cases and controls. The IDI is the difference in these differences between models, defined as

$$\mathit{IDI}={({\overline{p}}_{\mathit{cases}}-{\overline{p}}_{\mathit{controls}})}_{\text{new}\text{model}}-{({\overline{p}}_{\mathit{case}s}-{\overline{p}}_{\mathit{controls}})}_{\text{old}\text{model}}$$

where p̄ is again the predicted probability, averaged over all cases or controls. Since we would like the estimated risk in cases to be high and that among controls to be low, the difference in estimated risk should be large. This difference is also known as the Yates or discrimination slope, and the IDI is the difference in such slopes. Pepe et al [32•] showed that the IDI is equivalent to a difference in R-squared measure applied to a binary model. As for the NRI, censored observations are not taken into account.

In the cholesterol example, the average predicted probability in the model without total cholesterol was 7.8% in cases and 2.2% in controls, yielding a slope of 5.6%. In the model including total cholesterol, the average predicted probability was 7.9% in cases and 2.2% in controls, yielding a slope of 5.7%. The difference between these, or the IDI, is 0.1% (p=0.16) [14]. This means that the difference in average predicted probabilities between cases and controls increased by 0.001 when total cholesterol was added to the model. While this measure exhibits some desirable statistical properties, its typically small values provide some limitation to its interpretability.

A description of sources of programming code for the various statistical measures is provided in the appendix.

Conclusions

Since their initial presentation, reclassification and the measures associated with it have become widely used to compare models and to assess the clinical utility of biomarkers. Reclassification has been used to evaluate the utility of several novel or emerging risk factors for cardiovascular disease, including lipoproteins [7, 33], ankle brachial index [5], and brachial flow-mediated dilation [34], and for other cardiovascular conditions such as atrial fibrillation [35], heart failure [6], and stroke [36]. While many of these analyses suggest that new markers may improve risk stratification, that is not always the case [8, 37]. Even if a marker has statistically significant association with disease, it may still not have clinical utility in terms of reclassifying risk strata.

How to analyze risk stratification remains under discussion. Just as in the overall model assessment, there are two components to consider. The NRI is a measure of discrimination, or separation of the cases and controls into strata. It does not depend on the predicted probabilities themselves, but could easily be generalized to examine movement across other types of categories, such as quartiles of a score or biomarker [38]. Both the NRI and IDI condition on case-control status, and adaptations to survival data are needed. The reclassification calibration statistic, on the other hand, is a test of calibration, or agreement of predicted and observed probabilities, and can be readily extended to survival data. It specifically addresses the questions of whether the predicted risk estimates are more accurate under the new model. It is theoretically possible for the NRI to be very high, but for the new model to be uncalibrated. While useful for discrimination, further work would be needed to accurately predict risk for new patients.

In assessing the incremental role of a novel or emerging risk factor in risk prediction, several steps should be taken in the statistical analysis [24••]. First, the factor should be statistically significant to show that it is at least associated with the disease in question. Statistical tests and estimates of relative risks, etc., cannot determine clinical utility by themselves, but are a necessary first step. In addition, the usual measures of model fit should not be abandoned. Both the AUC and the Hosmer-Lemeshow goodness-of-fit test offer useful information. If there is a substantial change in the AUC, then this is a strong indication that the marker can aid in discrimination. A lack of calibration indicates that the model does not fit well, and is particularly important when applying it to an external population [39]. Risk reclassification, however, can go further and determine whether a marker or model can aid in prediction within clinically useful risk strata. Both the NRI and the reclassification calibration statistic offer useful and complementary information regarding the improvement in fit and the clinical utility of a new marker. Finally, since all measures of association, model fit, and clinical utility can be over-estimated in data from which they are initially derived, both internal and external validation of such measures should be conducted [11].

The utility evaluated through reclassification has more meaning if the categories used correspond to levels of risk of interest to the clinician, particularly those corresponding to treatment decisions. The right individuals should be assigned to the right risk groups, and treated accordingly. Changes in such categories can then be explored more thoroughly using cost-effectiveness analysis to determine whether a new test or biomarker should be included in routine practice [40]. In many situations it may be that screening within intermediate risk groups, identified through risk stratification, can ultimately prove more cost-effective. Reclassification methods can assist in determining how much impact this may have on clinical practice.

In a scientific statement from the American Heart association, Hlatky et al [41••] outlined recommendations for the reporting of novel risk markers and included both the traditional and novel measures described above. They also suggested phases of evaluation of a novel risk marker. The marker must fulfill the statistical criteria described above, including assessments of its association with disease with prospective validation, of whether it adds incremental value to standard risk markers as assessed by discrimination, calibration, or reclassification, and of its clinical utility, or whether it changes individual risk enough to change recommended therapy. A final definitive phase consists of evaluating whether the use of a risk marker improves clinical outcomes, especially as assessed in randomized trials. Cost-effectiveness can then be considered for the inclusion of novel markers in clinical guidelines. Such considerations, while stringent, open the door to improved assessment of individual risk, and to the incorporation of novel markers on top of traditional measures.

Appendix

Coding for the statistical procedures described above is available as follows:

Area under the ROC curve – Several software packages compute the AUC for binary outcomes. For example, it is printed in the default output from PROC LOGISTIC of SAS (SAS Institute, Cary, North Carolina). The complementary statistic for survival data, often called the c-index, is available using the validate function from the Design library of SPlus (Insightful Corp., Seattle, Washington) or R (The R Foundation for Statistical Computing).

Reclassification statistics – SAS macros for computing the reclassification calibration statistics for either binary or survival data, as well as the NRI and IDI for binary outcomes, are contained in an appendix to reference 14, which can be accessed at www.annals.org.