Insights on protein-DNA recognition by coarse grain modelling

Abstract

Coarse grain modelling of macromolecules is a new approach potentially well adapted to answer numerous issues, ranging from physics to biology. We propose here an original DNA coarse grain model specifically dedicated to protein–DNA docking, a crucial, but still largely unresolved, question in molecular biology. Using a representative set of protein–DNA complexes, we first show that our model is able to predict the interaction surface between the macromolecular partners taken in their bound form. In a second part, the impact of the DNA sequence and electrostatics, together with the DNA and protein conformations on docking is investigated. Our results strongly suggest that the overall DNA structure mainly contributes in discriminating the interaction site on cognate proteins. Direct electrostatic interactions between phosphate groups and amino acids side chains strengthen the binding. Overall, this work demonstrates that coarse grain modelling can reveal itself a precious auxiliary for a general and complete description and understanding of protein–DNA association mechanisms.

Introduction

In the cell, numerous proteins interact almost continuously with DNA to ensure standard or unusual biological functions such as transcription control, integration of exogenic DNA, genetic code maintenance or storage. Most of the time, these DNA-binding proteins can also associate with other proteins to form very large macromolecular assemblies. The knowledge of the overall structure of these assemblies as well as the details of the interactions are essential to understand the underlying biological processes or to develop new therapeutic strategies. In spite of spectacular progresses, the determination of the tridimensional structure of such large complexes at the atomic resolution by means of X-ray crystallography or nuclear magnetic resonance remains a difficult task. As a consequence, most experimentally determined structural informations only concern a limited part of the assembly, in other terms, two partners interacting together. However, even in the case of binary complexes, the number of available structures only represents a minor fraction of the existing assemblies.

Given the deficit of structural information on these assemblies, theoretical approaches appear as promising tools. Docking methods are more and more reliable and efficient for assembling macromolecular complexes, especially when the partners do not present any large internal deformation. Numerous studies were dedicated to protein–protein interactions [1] and the world wild challenge ”Critical Assessment of PR-edicted Interactions” (CAPRI) [2, 3] reveals the interest of the scientific community for this domain. The prediction of protein–DNA complexes is also a subject of interest for different groups that use several methods such as discretization on grid and Fourier transform [4] or ambiguous interaction restraints in the HADDOCK program developed by Bonvin and collaborators [5].

Both protein–protein and protein–DNA complexes are large size systems. From the in silico point of view, the prediction of macromolecular complexes from a systematic sampling of the energy landscape is computationally expensive because of the large number of atoms involved and the multiple calculations of the interaction energy. This has prompted the emergence of simplified macromolecule representations, which reduce the dimensionality of the problem by using a reduced number of particles, or pseudo-atoms. This type of approach, called ”coarse grain”, aims at rendering specific characteristics of the molecules, like the steric and electrostatic properties of the complex. In the molecular biology framework, a coarse grain approach based on the reproduction of steric and electrostatic characteristics has been used by Marrink and coworkers [6] for lipid and surfactant systems. It has then been extended to proteins by Bond and Sansom for the purpose of the insertion of proteins into membranes [7]. For the protein–protein docking purpose, Zacharias and collaborators [8, 9] have shown that low resolution approach is valuable to predict with a good confidence the geometry of protein–protein complexes. Particularly, the combination of the docking procedure ATTRACT [8] with this reduced model performed very well at rounds 3 and 5 of the CAPRI contest [10].

To our knowledge, there is so far no DNA coarse grain model dedicated to the docking problem. However, some coarse grain models of DNA have been developed recently for other purposes, with resolution ranging from 1 to 16 beads (or pseudo-atoms) per structural block, the latter being the complementary nucleotides considered as the relevant units for DNA. The model of Mergell et al. [11] is composed of one rigid ellipsoid per base pair with an internal energy derived from the Gay-Berne potential. This resolution allows the study of phase transition from B- to S-DNA upon stretching. Other models rely on a more common bead and spring representation of the internal energy. Tepper and Voth [12] built for instance a spring network model with 16 beads per structural block and 2 different types of bead for the backbone/sugar and base elements. Starting from a straight ladder conformation, this model reproduces the helicity of DNA. More recently, Knotts and coworkers [13] proposed a topological model with 3 beads per nucleotide (phosphate, sugar and base). This model successfully reproduces several physical and mechanical properties of DNA, including salt-dependent melting.

In this article, we propose a DNA coarse grain model specifically designed for modelling protein–DNA complexes, that is very efficient in term of prediction for a low computational cost. In a first part, we introduce the reduced DNA model we have developed with 11 beads per complementary nucleotides. We show its compatibility with the Zacharias protein model and also the good stability of protein–DNA complexes represented at low resolution using the two combined models. In the second part, we show on a large range of protein–DNA complexes that our model is able to predict protein–DNA assemblies, using the rigid body docking procedure ATTRACT [8]. We then assess the relative contribution of the electrostatics and van der Waals terms in the energy function, thus exploring the energetic components that participate to the recognition process.

Materials and Methods

Protein representation

With the protein–protein docking issue in mind, Zacharias proposed a reduced protein model with up to three pseudo-atoms per residue [8], which makes about 4 heavy atoms per bead. In this model, each amino acid is represented by one pseudo-atom located at the position of the C_α atom and up to two pseudo-atoms for each side chain, depending on its length.

This model assumes no internal energy evaluation since it has been developed for systematic rigid body docking. Actually, only the interaction energy is needed to evaluate the geometry of a complex. The effective interaction between two partners I and J is the sum of a soft Lennard-Jones potential and an electrostatic potential,

$$E=\sum _{i\in I}\sum _{j\in J}\left(\frac{B_{ij}}{r_{ij}^8}-\frac{C_{ij}}{r_{ij}^6}\right)+\sum _{i\in I}\sum _{j\in J}\left(\frac{q_i{q}_j}{\epsilon r_{ij}}\right),$$ (1)

with B_ij = A_iA_j(R_i + R_j)⁸ and C_ij = A_iA_j(R_i + R_j)⁶. In the previous formula, r_ij is the distance between bead i of partner I and bead j of partner J. A_i, A_j, R_i and R_j are the Lennard-Jones parameters, q_i and q_j are the charges of bead i and j respectively, and finally, ε is a distance-dependant dielectric function defined as ε = 15 × r_ij.

The protein model is described by 29 types of beads with three parameters each, namely A_i, R_i and q_i. Charges are only set on charged amino acids, as full charges (+1 or −1) on the last bead of the residues.

DNA representation

Our central assumption is that the design of a DNA model for the study of protein–DNA complexes requires a good reproduction of the volume occupied by the DNA. This volume is characterized by a contrast between the minor and major grooves and the sharp phosphodiester backbones. Both the level of resolution and the parameters have been determined to be coherent with the protein model of Zacharias [8]. The bead partition is also related to a model developed by Khalid and Sansom [14] for the insertion of a DNA into a membrane. Hence, our model is defined by 5 to 6 beads per nucleotide: one bead per phosphate backbone, two beads per sugar and 2 to 3 beads per base (2 for cytosine and thymine, and 3 for adenine and guanine). Between three and four heavy atoms are grouped within each bead. Only one bead of thymine contains five heavy atoms in order to represent the methyl group. The topology of our DNA model is depicted in figure 1. The center of a given bead is the geometric center of the heavy atoms included in this bead. Each bead is defined by 3 parameters, which are consistent with the reduced protein model (table 1). The parameters have been derived from the chemical composition of each bead. The Lennard-Jones parameters A_i are 0.6 RT^0.5 for all beads, reflecting their identical polarities. The van der Waals radii (Table 1) were directly calculated from the radius of the atomic components of the beads. For a given bead that reduces N atoms i, the van der Waals radius R is

Figure 1.

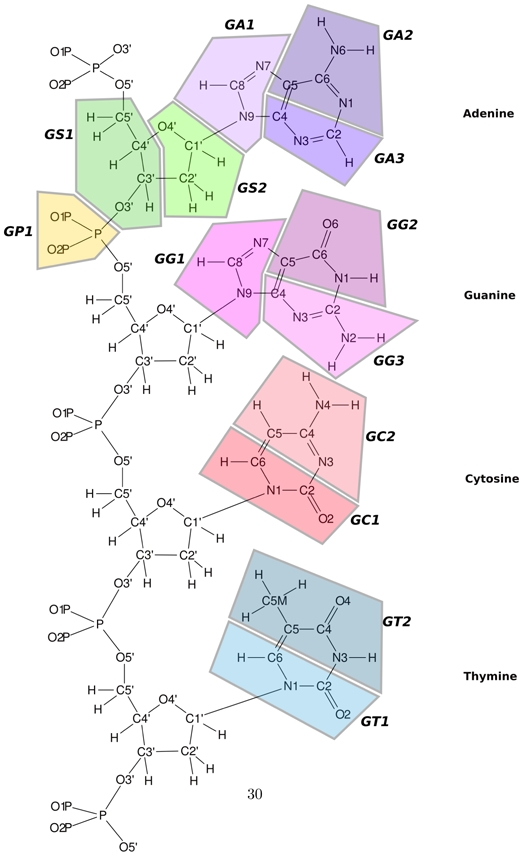
Coarse grain partition of the DNA model. Each colored domain represents a different bead.

Table 1.

Energy parameters of the coarse grain DNA model.

ID	bead		parameters
	name	group	Ri [Å]	Ai [(RT)0.5]	qi
1	GP1	phosphate	2.640	0.600	−0.700
2	GS1	sugar	2.900	0.600	0.000
3	GS2	sugar	2.650	0.600	0.000
4	GA1	adenine	2.530	0.600	0.000
5	GA2	adenine	2.650	0.600	0.000
6	GA3	adenine	2.590	0.600	0.000
7	GG1	guanine	2.530	0.600	0.000
8	GG2	guanine	2.650	0.600	0.000
9	GG3	guanine	2.830	0.600	0.000
10	GC1	cytosine	2.840	0.600	0.000
11	GC2	cytosine	2.650	0.600	0.000
12	GT1	thymine	2.840	0.600	0.000
13	GT2	thymine	2.940	0.600	0.000

$$R=\frac{1}{N}\sum _{i=1}^N{d}_i+\frac{1}{N}\sum _{i=1}^N{R}_{\mathit{vdw},i}$$ (2)

where d_i is the distance between the center of the grain and the center of atom i, and R_vdw,i is the van der Waals radius of atom i. Finally, charges are set only on phosphate beads using a 30% screening, that gives a charge of −0.7 when starting with a full negative charge. The whole DNA molecule is described by 13 different beads.

ATTRACT protocol

Docking simulations were performed with the ATTRACT protocol developed by Zacharias [8]. ATTRACT performs systematic docking without using any experimental data concerning the native complex. This algorithm relies on a minimization of the interaction energy, the DNA center being placed at regular positions around the protein surface at a distance slightly larger than its biggest dimension. For each starting position, around 230 initial DNA orientations are generated. For each starting geometry, energy minimization (quasi-Newton minimizer) is performed using translational and rotational degrees of freedom of the DNA. During this minimization, no cut-off is used to compute the interaction energy. The full sampling of the ≈ 60,000 positions and orientations of the DNA around the protein required 14 hours on a 3 GHz monoprocessor in the case of compound 1A74 (see below). Since the minimizations are independent, the sampling can easily be distributed on many processors. For instance, when distributed on 14 processors, the full calculation on 1A74 takes about one hour.

Protein–DNA complexes

We have tested our coarse grain DNA model on six systems that represent a large range of protein–DNA interactions. These systems are namely:

• the transcription factor ETS-1 with DNA [15] (2.4 Å resolution, PDB code 1K79).

• the Arc repressor-operator complex [16] (2.6 Å resolution, PDB code 1PAR).

• the complex between the E2 transcription factor of the bovine papillomavirus and DNA [17] (1.7 Å resolution, PDB code 2BOP).

• the intron-encoded homing endonuclease I-PpoI dimer complexed with DNA [18], (2.2 Å resolution, PDB code 1A74).

• the yeast TATA-box binding protein (TBP) interacting with a DNA TATA box sequence [19] (1.8 Å resolution, PDB code 1YTB)

• the NMR complex between the core DNA-binding domain of human transcription factor NFATC1 and DNA [20] (PDB code 1A66). As usual for NMR determined structures, several models are proposed within the PDB. Out of the 18 available, we have performed docking tests on several models. The results being equivalent, we present here those obtained with the first model.

Atomic coordinates of these test cases were obtained from the Protein Data Bank [21]. The DNA curvature has been characterized with CURVES [22], while B-DNA structures were generated by JUMNA [23]. Hydrogen bonds between DNA phosphate and charged residues were determined by HBPLUS [24].

Quality and quantity assessment of the simulated complexes

The quality of our simulations is evaluated by the Root Mean Square Deviation (RMSD) calculated on all beads of the DNA between the reference and the simulated complexes. However, this measure may be insufficient to precisely characterize the position of DNA with respect to its proteic partner [4]. We thus used an additional parameter, namely the geometric center distance (GCD). This distance is calculated between the geometric center of the DNA in the reference complex and the geometric center of the DNA in the simulated complex, after superposition of the protein partners of both complexes.

Exploring the effect of the DNA sequence and shape on recognition does not easily allow a comparison in terms of RMSD. In these cases, we analyzed the fraction of the protein interface residues in the native structure which are recovered in the prediction, f_pib. A protein residue is defined to belong to the interface when one of its beads is within 7Å from any DNA bead [9]. In the same way, f_dib is the fraction of native DNA interface nucleotides which are recovered in the predictions. In this article, f_pib and f_dib are expressed as percentages.

Final geometries are clustered within 0.1 RT units in energy and 0.1 Å in RMSD.

Results

To assess the robustness of our model, the studied complexes were chosen to encompass a large range of protein–DNA interactions. In this purpose, we used the taxonomy of Luscombe and collaborators [25, 26] to select six representative complexes suitable for the rigid body docking: 1K79 [15], 1PAR [16], 2BOP [17], 1A74 [18], 1YTB [19] and 1A66 [20]. In these complexes, most proteins are transcription factors except 1A74 which is a hydrolase.

The five first complexes are crystallographic structures with DNA Binding Domain (DBD) identified [25] as respectively helix-turn-helix, β-hairpin/ribbon, other α helix, enzyme and β sheet structural groups (see table 2). The last complex 1A66 is issued from NMR measurements and has been selected for its interface made of loops.

Table 2.

For each complex, the protein DNA Binding Domain (DBD) and the DNA interface are provided, as well as the length of the DNA part implied in the interface, the number of specific interaction sites (DNA bases involved in intermolecular hydrogen bonds) and the curvature intensity. This table also presents the ratio between the number of contacted phosphates (P) and the number of contacted bases, the ratio between the number of contacted phosphates and the total number of phosphates, the CG percentage and if the DNA sequence is palindromic (+) or not (−).

complex	1K79	1PAR	2BOP	1A74	1YTB	1A66
DNA Binding Domain	helix-turn-helix	β sheets	α helices	β sheets/α helices	β sheets	loops
DNA interface type	MG	MG	MG	MG/mg	mg	MG
DNA interface length [bp]	10	17	16	18	8	10
specific interaction sites	1	2	2	1	1	1
curvature intensity [°]	23	28	35	55	69	14*
cont. P/cont. bases	2.0	0.6	1.8	0.3	1.0	1.3
cont. P/total P	0.30	0.16	0.33	0.11	0.28	0.2
% GC	50	41	75	44	0	40
palindromic sequence	−	+/−	+	+	−	−

MG stands for major groove whereas mg means minor groove.

^*For 1A66, the curvature range on all conformations is 6–22°.

The DNA interfaces are characterized in table 2, as well as some structural features of the DNA. The contacts are mainly made in the major groove apart from 1YTB. The continuous DNA stretches implied in the interface with the cognate protein range from 8 to 18 base pairs (bp). For 1PAR and 2BOP, there are two identical half sites separated by 5 and 4 base pairs, respectively. The curvature intensity is variable, ranging from 14° in 1A66 to 69° in 1YTB. The ratio between the number of contacted phosphates and bases displays high variability, as well as the ratio between the number of contacted phosphates and the total number of phosphates (table 2). The sequence varies between GC rich sequences (2BOP) and AT rich sequences (1YTB). Finally, two sequences (2BOP and 1A74) are palindromic and one (1PAR) is quasi-palindromic. Although not comprehensive, our selection aimed to cover a large variety of protein DBD as well as DNA structures.

The coarse grain representations of the complexes introduced above are shown in figure 2. The reduced models reproduce correctly the overall shape of both the DNA and the protein. The change in resolution, from atomic to coarse grain, induces a reduction of 70 to 80 % of the total number of particles that allows systematic docking simulations within a reasonable simulation time.

Figure 2.

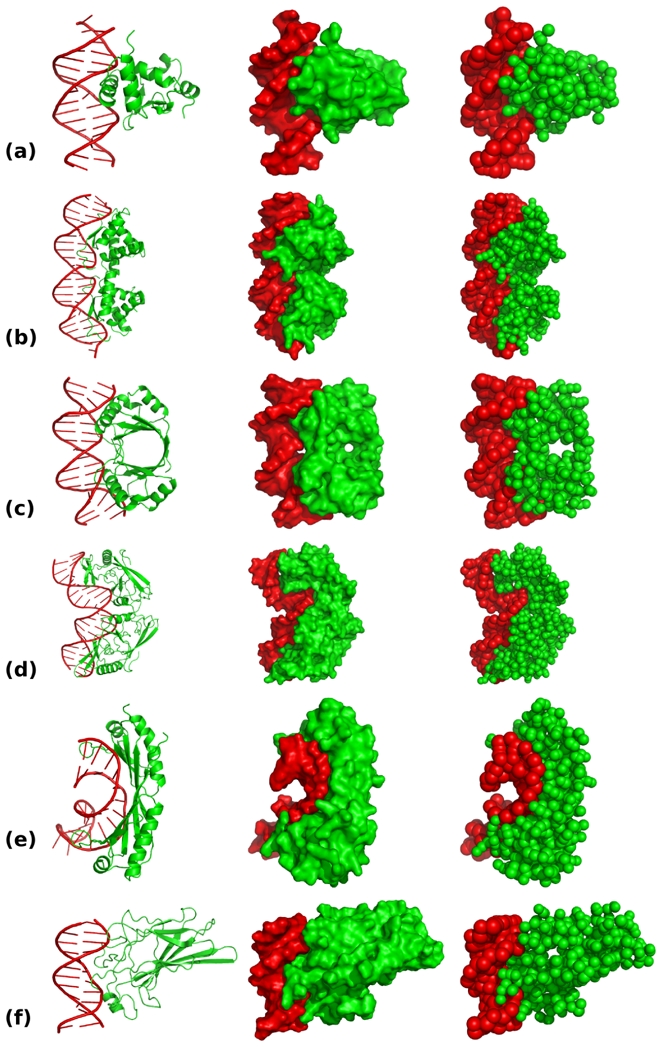
All-atom cartoon, all-atom surface and coarse grain representation for (a) 1K79, (b) 1PAR, (c) 2BOP, (d) 1A74, (e) 1YTB and (f) 1A66 complexes. The protein and the DNA are in green and red respectively. Pictures were obtained with Pymol [29].

Coarse grain minimization

The diminution of resolution increases the particle radii up to 2.94 Å (table 1). In order to remove possible steric clashes introduced by the coarse grain representation, we relaxed the complex structures taken from the PDB with both partners in their reduced representation. We performed an ATTRACT minimization that allows the DNA to move in translation and rotation around the fixed protein. This procedure is called ”coarse grain optimization” in what follows. The interaction energy and both the RMSD and the GCD between the native and the minimized DNA structures are reported in table 3. The average values of RMSD and GCD are 0.7 and 0.5 Å respectively, ensuring that the reduced models introduce a negligible shift compared to the native all-atom complexes. In this article, the non-minimized PDB structures will be taken as references.

Table 3.

Interaction energy and RMSD relative to the native complex obtained after coarse grain minimization.

complex	interaction energy [RT]	RMSD [Å]/native	GCD [Å]/native
1K79	−38.6	1.3	0.7
1PAR	−74.6	0.6	0.5
2BOP	−55.4	0.2	0.1
1A74	−68.7	0.7	0.4
1YTB	−55.7	0.4	0.3
1A66	−35.6	1.2	1.0

Rigid body protein–DNA systematic docking

For each complex, we then performed systematic docking simulations to determine if the combination of the DNA and protein coarse grain models with the ATTRACT systematic docking procedure could generate and select the reference complexes. For these simulations, the conformations of both protein and DNA are exactly those found in the experimental complexes. All final geometries generated by the docking algorithm were sorted out according to their interaction energy. In parallel, the RMSD and GCD relative to the native structure were calculated on all DNA beads. The plot of the interaction energy versus RMSD is represented in figure 3 for each complex.

Figure 3.

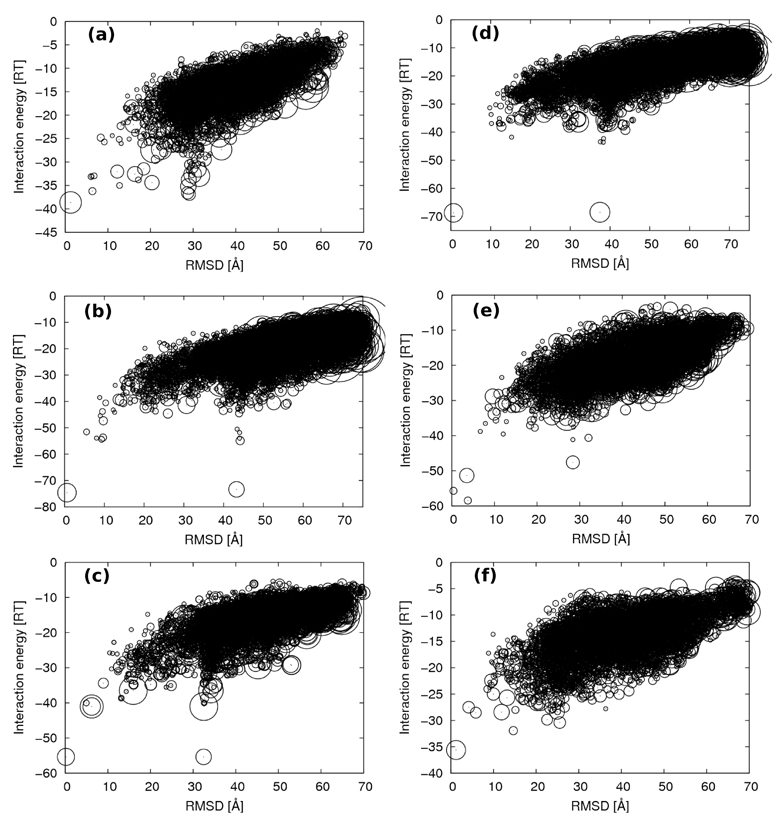
Plots of the interaction energy versus the RMSD for (a) 1K79, (b) 1PAR, (c) 2BOP, (d) 1A74, (e) 1YTB and (f) 1A66. Circle radii are proportional to the square root of the cluster populations.

For the six studied systems, the energy rank, the interaction energy, the RMSD, the GCD and the cluster population are given in table 4 for the four most stable geometries. In five cases out of six (1K79, 1PAR, 2BOP, 1A74 and 1A66), the lowest energy conformation corresponds to the lowest RMSD and GCD, demonstrating that the interaction energy works efficiently as a scoring function for the docking purpose. The most stable geometries are identical to the structures obtained upon coarse grain minimization, showing the efficiency of the conformational space sampling by ATTRACT. Furthermore, these favorable geometries are generally highly populated, indicating the good convergence of the simulation. However, some low energy conformations are also characterized by high RMSDs (roughly 30 Å) and low GCDs. Most of them are head-to-tail geometries, corresponding to a half-turn rotation of the DNA around the normal of the protein interaction surface starting from its position in the native complex (as described by Aloy and coworkers [4]). These ”reverse” conformations occur with palindromic or quasi-palindromic DNA (1PAR, 2BOP and 1A74), with energy difference lower than 2 RT with respect to the most stable prediction. For the DNA sequence found in 2BOP, which is both palindromic and structurally symmetric, the energy gap vanishes and the cluster with the head-to-tail DNA (cluster rank 2) is perfectly equivalent to the near native geometry (cluster rank 1), both in terms of energy and structure. In the case of 1A74, the DNA is not exactly structurally symmetric, with a RMSD between the reference and the head-to-tail DNA conformations of 0.6 Å. This explains the slight energy penalty of 0.2 RT units found between the clusters of ranks 1 and 3.

Table 4.

Energy ranks, interaction energies, RMSD relative to the native structure, RMSD relative to the coarse grain optimized structures, GCD relative to the native structure and cluster population for the four lowest energy geometries obtained by systematic docking simulations.

complex	energy rank	interaction energy [RT]	RMSD [Å]/native	RMSD [Å]/CG opt.	GCD [Å]/native	cluster population
1K79	1	−38.6	1.3	0.0	0.7	27
	2‡	−36.9	29.1	29.1	5.8	9
	3‡	−36.6	28.7	28.7	2.6	9
	4	−36.2	6.4	6.2	3.9	3
1PAR	1	−74.6	0.6	0.0	0.5	20
	2†	−73.4	43.2	43.2	0.8	14
	3	−54.9	44.2	44.2	9.0	4
	4	−54.4	9.3	9.2	8.8	2
2BOP*	1	−55.4	0.2	0.0	0.1	17
	2†	−55.4	32.5	32.5	0.1	14
	3	−41.0	6.2	6.1	3.4	31
	4	−41.0	32.5	32.5	3.4	45
1A74*	1	−68.7	0.7	0.0	0.4	20
	2†	−68.5	37.5	37.5	0.5	23
	3	−43.6	38.3	38.4	9.6	1
	4	−43.5	37.6	37.6	5.0	1
1YTB	1	−58.5	3.8	3.7	0.4	3
	2	−55.7	0.4	0.0	0.3	3
	3	−51.4	3.5	3.6	2.7	12
	4	−47.6	28.4	28.4	12.9	10
1A66	1	−35.6	1.2	0.0	1.0	21
	2	−31.9	14.7	14.1	10.4	4
	3‡	−30.4	25.5	25.3	6.8	8
	4	−29.9	22.6	22.7	8.4	7

^*The symbol pinpoints complexes with palindromic DNA.

^†The symbol shows head-to-tail configurations and

^‡indicates a screwing along the DNA helical axis.

In the case of 1YTB, the second most stable structure (energy difference of 2.8 RT units with respect to the most stable conformation) is exactly the structure obtained after coarse grain optimization. The fact that this structure, which is the prediction closest to the native complex, is not the lowest energy one is probably linked to the structural particularity of the DNA within this complex. Indeed, the severe DNA curvature (69°) induced by the TBP renders the minor groove convex instead of, as usual, concave. As a consequence, the geometric contrast between grooves and backbones almost disappear, rendering the surface of interaction of the DNA less distinctive than in the other complexes.

Among other geometries located very close to the native interface, we find predictions with screwing displacements of the DNA along the helical axis by 2 or 3 bp with respect to the native or head-to-tail conformations. These structures are separated from the most stable geometries by an energy difference between 2 and 5 RT units (see cluster 3 for 1A66 and clusters 2 and 3 for 1K79 in table 4), reflecting that a good proportion of the correct interaction is found.

Finally, the energies of the most stable predictions are generally clearly separated out from the energy bulk of other conformations (figure 3). In most cases, and if one excludes the head-to-tail and screwed geometries, the energy gap is at least 10 to 12 RT. Except for the very deformed TBP complex (1YTB), our model does exactly retrieve the important features of atomic resolution protein–DNA interactions in easily discriminating the correct candidate among the multiple combinations of the partner geometries.

Balance of terms in the interaction energy

DNA is a highly charged macromolecule and it can be expected that its electrostatic nature plays a significant role in protein–DNA interactions. Nadassy and collaborators [27] showed from the analysis of crystallographic data that the protein–DNA interfaces often present a protein side scattered with positively charged amino acids (lysine and arginine), responding to the DNA trace dominated by the negative phosphate groups. It is therefore interesting to explore which role electrostatics plays in the interaction energy, and what is its contribution to our scoring function.

To study the influence of electrostatics, we performed additional docking simulations with DNA phosphate bead charges all set to −1 or to 0, removing in the later case the electrostatic part of the interaction energy. Setting phosphate charge to −1 did not improve the prediction. The results with uncharged phosphate beads are represented in table 5. Comparing to the results obtained with charges set to −0.7 (table 4), the weight of the electrostatic component in the total energy is between 20 and 30%. For all complexes but one, the predictions closest to the reference structures are found at first rank, even for 1K79 and 2BOP for which the ratio between the contacted phosphates and bases are very high (table 2). Only for one case, i.e. 1YTB, no geometry is found at less than 3.6 Å from the reference complex, showing that electrostatics is essential for the quality of the prediction of this particular complex.

Table 5.

Energy rank, interaction energy, RMSD relative to the native structure and cluster population for the four lowest energy geometries of the six studied complexes after systematic docking without charge. The rank of the closest cluster in the simulation with charges is also reported.

complex	energy rank	interaction energy [RT]	RMSD [Å]/native	cluster population	simulation with charge rank (RMSD/pop)
1K79	1	−27.0	1.2	6	1 (0.1/27)
	2‡	−25.8	29.1	5	2 (0.1/9)
	3‡	−25.3	28.7	1	3 (0.1/9)
	4	−24.3	13.1	2	-
1PAR	1	−54.2	0.7	4	1 (0.0/20)
	2†	−53.2	43.2	3	2 (0.1/14)
	3	−32.4	43.4	1	10 (0.1/1)
	4	−29.5	26.0	1	13 (0.1/5)
2BOP*	1	−37.6	0.2	1	1 (0.1/17)
	2†	−37.6	32.5	2	2 (0.1/14)
	3	−26.4	35.0	6	-
	4	−26.4	24.1	11	-
1A74*	1†	−56.9	37.5	3	3 (0.1/23)
	2	−30.7	45.8	2	-
	3	−30.4	26.6	2	-
	4	−30.4	28.7	2	67 (0.2/1)
1YTB	1	−46.8	3.8	3	1 (0.1/3)
	2	−40.5	3.7	7	3 (0.2/12)
	3	−37.0	28.4	8	4 (0.1/10)
	4	−32.0	32.1	4	6 (0.1/3)
1A66	1	−24.7	1.2	3	1 (0.1/21)
	2	−24.0	37.2	3	47 (0.2/3)
	3	−23.0	44.3	3	-
	4	−21.8	41.0	1	-

The RMSD with respect to the uncharged corresponding cluster and the population are also indicated in parentheses. A dash indicates that no cluster was found with a RMSD less than 0.5 Å.

Considering the relative population of the targeted complexes, the inclusion of the electrostatic term clearly increases the number of best predicted geometries in all cases (see columns 5 and 6 of table 5). The Coulomb interaction acts as an electrostatic guide towards the native complex.

Sensitivity to DNA sequence

The DNA sequence can be discriminated on the basis of direct contacts between nucleic base functional groups and amino acid side chains in the minor and major grooves (direct recognition), but also via the energy level necessary to deform DNA in such a way that it optimally fits the protein structure (indirect recognition). Due to the absence of hydrogen-bonding potential in our reduced representation of DNA and protein, the coarse grained model presented here does not pretend to correctly reproduce the direct contacts between amino acid side chains and DNA functional groups. We have nevertheless evaluated the sequence sensitivity in the light of the steric differences that arise in our model from the differential van der Waals radii of GA3, GG3, GC2 and GT2 pseudo-atoms of A, G, C and T, respectively (see table 1).

Among our complexes, we considered two contrasted cases, 2BOP for which the consensus DNA contains 75% of GC and 1PAR where the consensus DNA counts 41% of GC (table 2).

We use as references the docking simulations of 2BOP and 1PAR with the consensus DNA sequences described in table 4. We also generated d(AT) and d(CG) repeated sequences threaded on the structure of the reference DNAs. Since the RMSD is meaningless here, we compared the fractions of protein interface beads in the native structure which are recovered in the prediction, f_pib (see Materials and Methods). Concerning 2BOP, most stable structures have energies of −49.7, −50.1 and −52.7 RT units, for respectively the consensus, d(AT) and d(CG) repeated sequences, while f_pib are 100, 95 and 100% respectively. The high values of f_pib obtained here indicate that the predictions are very close to the reference complex. Besides, the very low energy and large f_pib obtained with d(CG) repeated sequence may be interpreted by the fact that 80% of the intermolecular hydrogen bonds involve bases G and C of the native DNA sequence.

In the case of 1PAR, the lowest energies are respectively of −73.0, −67.9 and −59.0 RT units for the consensus, d(AT) and d(CG) repeated sequences. The values of f_pib are 95% for the consensus while 92% and 91% for the AT and CG repeats. In this case, the lowest energy complex obtained with the consensus DNA has also the highest f_pib. Indeed, hydrogen bonds are equally distributed between A, T, C or G bases in the native complex.

Although our model has not been designed to be sequence attuned, we found here a good sensitivity to sequence, confirming the pertinence of our coarse grain representation.

Sensitivity to deformation

Designed with a shape recognition in mind, we expect our model to be sensitive to DNA and protein deformations but we also hope it will accept some structural fluctuations. This tolerance was evaluated by docking a non-native form of either DNA or protein on the native conformation of their partner.

Keeping the original base composition, we began to dock the proteins belonging to our set of complexes with consensus DNA presenting structures that deviate more or less from the experimental structures. In these calculations, the quality of the predicted complexes will be assessed by the fractions of conserved interface residues in protein (f_pib) and DNA (f_dib) rather than the RMSD, which results both from the differences between native and non-native DNA conformations and from the deviations in the positioning.

We first used DNA average structures extracted from a 15 ns molecular dynamics (MD) simulation of 2BOP [28]. In this trajectory, the E2 protein was rather rigid and remained very close to its X-ray counterpart. In contrast, the DNA was significantly flexible, so that the structures could be gathered in four clusters. The cross-RMSD between the four corresponding average structures were around 1.0 Å, and they all differed by at least 1.0Å from the crystallographic conformation. Using these structures allows us to test the effect of moderate distortions on the docking efficiency. Indeed, we found that, whatever the MD average DNA structure, the best complex in terms of energy is very close to the reference one (at worst, a difference of 1.3 RT). Also, the average f_pib and f_dib are similar to the values obtained with the corresponding crystallographic DNA, i.e. cleaned from non pairing bases that do not exist in the MD oligomer (see first line of table 6). These results mean that our docking simulations well tolerate some fluctuations around the native conformation. Nevertheless, in this case, the global structural DNA features are preserved, in particular the curvature. A more severe test is to consider the recognition between proteins and straight canonical B-DNA. The results of these docking simulations are summarized in table 6 for the best predictions in term of energy for the 1A66, 1K79, 2BOP and 1A74 complexes. In these complexes, the reference structures of the bound DNA exhibit different curvature intensities (table 6), from 14 (1A66) to 55° (1A74). The RMSD calculated between experimental and B oligomers reflect these distortions, with values lying between 1.0 Å (1A66) and 7.6 Å (1A74) (table 6). A large proportion of the reference interface is predicted with 1A66 protein and B-DNA, which is very close to the reference DNA (RMSD of 1.0 Å). We found f_pib ~ 70% and f_dib ~ 45% for the first ranked complex structure, 81% and 83% for the second ranked prediction that is within 0.1 RT units in energy of the first. For 1K79, the results are even better (f_pib ~ 85%, f_dib ~ 80%) while the B-DNA is significantly different from the bound DNA reference structure (RMSD = 3.2 Å). However, in the case of 2BOP, where the DNA also differs by 3.2 Å from the B-DNA but with a marked curvature, we find a relatively low value of f_pib (50%) and f_dib (20%). Indeed, one DNA half-site is well located while the second does not contact its cognate protein part. Finally, our procedure fails to retrieve the right protein–DNA interface in 1A74, the complex that contains the most distorted DNA. Nevertheless, even in this case, the B-DNA is located near the protein region where the native interaction occurs, so that, 22% of the protein residues implicated in the native interface are retrieved in the best predictions. For an illustration purpose, the output geometries for 2BOP, clusterized within 0.1 RT in energy and 0.1% in f_pib, are reported in figure 4. It can be noted that in spite of a 35° curvature deformation of the DNA, the best ranked geometries in terms of energy recover more than 50% of the interface residues of the protein.

Table 6.

Docking simulation results on systems where the DNA conformations differ from their native structures. Columns 2 to 4 figure the curvature, lowest energy, f_pib and f_dib for the best prediction with both docking partners in their native conformation (see table 4). Columns 6 to 9 present results obtained with a modelled DNA: RMSD between the reference and the non-native DNA, lowest predicted energy and the corresponding f_pib and f_dib. For 2BOP_a, the native DNA has been cleaned from its terminal non-pairing bases. Non-native DNAs were extracted from a 15 ns molecular dynamics simulation of the complex (see text) and the corresponding RMSD, interaction energy, f_pib and f_dib are averaged over these MD structures. For the four other complexes, the non-native DNA structure was a straight canonical B-form.

complex	reference DNA				non-native DNA
	DNA curvature [°]	interaction energy [RT]	fpib (%)	fdib (%)	RMSD [Å]/reference	interaction energy [RT]	fpib (%)	fdib (%)
2BOPa	35	−49.6	100	100	1.0	−49.7	95	95
1A66	14	−35.6	94	89	1.0	−29.6	68	44
1K79	23	−38.6	94	90	3.2	−35.3	85	79
2BOP	35	−55.4	100	100	3.2	−38.2	50	20
1A74	55	−68.7	93	100	7.6	−37.5	22	29

Figure 4.

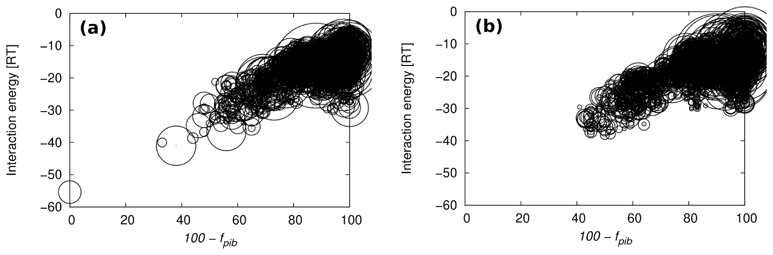
Fraction of the protein interface residues in the native structure of 2BOP, which are recovered in the prediction (f_pib), against the interaction energy for the docking simulations of the E2 protein with (a) the native DNA structure and (b) the canonical B-DNA conformation. Output geometries are clustered within 0.1 RT units in energy and 0.1% in f_pib. Circle radii are proportional to the square root of the cluster populations.

To complete this study, we have explored the sensitivity of the protein–DNA model to protein conformational variation, by carrying out similar tests with structures of proteins that are not complexed with any DNA, keeping intact the conformation of the bound DNA. Among our data set, X-ray structures of DNA-free (unbound) proteins are available for 1PAR, 2BOP and 1K79. The global structures of bound and unbound proteins are very similar, as shown by the rather low values of RMSD (table 7). However, some noticeable differences are observed in protein interfaces. Focusing on amino acids of the DNA/protein interfaces highlights that between 27 and 41% of them differ from 1.6 to 4.5Å in RMSD (table 7), reflecting that side chain conformations are submitted to dramatic changes upon DNA binding. In addition, 30 and 25% of the amino acids belonging to the DNA binding domains are lacking in 1BAZ [30] and 1JJH [31], the unbound counterparts of 1PAR and 2BOP proteins. The results of the docking simulations are summarized in table 7 for the first ranked predictions. Note that the interaction energies reported here for 1BAZ and 1JJH cannot be compared to those of native protein–native DNA docking (table 3), because of differences in protein interface compositions. The use of IJJH and 1BAZ leads to very good docking predictions. The best complex simulated with 1GVJ [32], related to 1K79, shows a very large RMSD associated to low GCD and high f_pib and f_dib values, a feature that corresponds to a head-to-tail conformation, as described above. Reminding that, in these complexes, the proteins contact the major groove of their targets, these results mean that DNA major grooves in coarse grain representation remain large enough for supporting amino acids side chain conformations significantly altered comparing to their native form. Also, deletions of several amino acids in protein DNA binding domains can occur without damaging the prediction.

Table 7.

Docking simulation results on proteins in their unbound forms (PDB codes are in the column 2). Columns 3 and 4 indicate the level of structural differences between the bound and the unbound protein. The RMSD in column 3 is a global measure, taken on the heavy atoms. F_aac is the percentage of amino acids implicated in the protein–DNA interface for which the RMSD calculated between their bound and unbound forms is more than 1.6 Å. We consider that a residue belongs to the interface if it is located at less than 5 Å from any DNA atom. Columns 5 to 9 present the results of the docking simulations using the unbound protein for the best ranked prediciction: interaction energy, RMSD and GCD compared to the native position of the DNA, f_pib and f_dib.

complex	unbound protein	RMSD [Å]/bound	Faac (%)	interaction energy [RT]	RMSD [Å]/native	GCD [Å]/native	fpib (%)	fdib (%)
1PAR	1BAZ	1.8	27	−44.1	7.5	5.8	72	100
2BOP	IJJH (chain A)	1.4	33	−50.5	1.2	0.0	90	91
2BOP	IJJH (chain B)	1.2	33	−54.0	1.3	0.3	89	91
1K79	1GVJ	1.5	41	−36.6	28.7	1.8	85	80

In sum, these results show that our procedure is sensitive to DNA and protein distortions. However, the major part of the beads composing the interaction surface can be predicted without prerequisite about deformations, providing that they are not too much important. Actually, our model seems to support differences in DNA curvature up to 30° and variations in a third of the interacting amino acids conformers.

Discussion

In this work, we propose an original DNA coarse grain model dedicated to protein–DNA docking. Our representation is derived from Zacharias reduced model of proteins, with 13 bead types for electrostatics and Van der Waals interaction. Such model is devoted to reproduce the volume occupied by the DNA, and thus the shape of its interaction surface. A special attention was directed to the groove dimensions and the curvature in order to render at best the global DNA conformation. Actually, because DNA is often deformed within protein–DNA complexes, it is reasonable to expect that DNA protein recognition mainly depends on the form of the two partners. A second element is the charge-charge attractions between the negative DNA phosphate groups and the positively charged amino acid side chains. This is taken into account in our DNA model through negative charged beads representing the phosphate groups.

Despite its simplicity, our model has shown remarkable performances when used to assemble a representative set of protein–DNA complexes, differing by both the DNA binding domain in proteins and the deformations in bound DNAs, in particular their curvatures. The correct geometry of association could be predicted unambiguously in all cases, except for the TBP complex in which the DNA structure, markedly distorted, loses the typical contrast between hollow grooves and sharp backbones. However, even in this case, the first ranked prediction was very close to the correct geometry and the second was the correct one. So, the loss of atomic details did not appear to be an obstacle to the docking prediction of DNAs on their cognate proteins.

When dealing with coarse grained models, it is important to delineate their scope, i.e. the molecular properties that can be reproduced, comprising the features that do not benefit from explicit treatment. First, we examined the sensitivity of our methodology to the DNA sequence. The base composition appears as a fundamental element of protein–DNA complexes, via the hydrogen bonds occurring between the DNA bases and the amino acid side chains. At the low resolution used to represent proteins and DNA in our model (nucleic acid beads often group together both acceptor and donor groups), this type of direct interactions is not explicitly treated. This may obliterate the capacity of the model to confidently retrieve the sequence the most appropriate for a given protein. For this investigation, we drastically muted the DNA sequence without modifying its conformation. In all cases, the base composition of the sequence energetically favored well correlated to that of the consensus sequence. Thus, even in absence of any explicit energetic formulation of the hydrogen bonds between the DNA bases and the amino acids, the differences between A, G, C and T in terms of van der Waals parameters are sufficient for detecting DNA sequence preferences. Besides, this result illustrates the role of the steric hindrance of the functional groups within the DNA grooves in the protein–DNA interactions.

Second, we investigated the tolerance of the coarse grain model to DNA and protein structures. For this purpose, we docked the proteins with conserved DNA sequences but with structures altered with respect to their native forms. Conversely, we also tested native DNA with free-DNA protein conformations. Slight alterations in terms of curvature of the DNA target, with RMSD up to 1 Å, were fairly tolerated and did not at all modify the docking results. A more stringent test consisted to use a canonical straight B-DNA. Deviations in DNA curvature up to 28° did not notably modify the predicted protein interface. For more intensive DNA bending, the interaction surfaces were either partially predicted (curvature of 35°) or only indicative of the protein region where the DNA interacts (curvatures > 55°). Comparable results were obtained when using deformed protein structures and native DNA forms. So, differences in more than 40% of the side chain conformations belonging to the interface did not prevent the complex to occur in the right place. Since no aberrant positioning was generated, these results are encouraging in the view of further docking applications, suggesting that a rough exploration of DNA and protein deformations should be sufficient to succeed a realistic docking. However, at the same time, they highlight the importance for the DNA to be pre-deformed or flexible to correctly realize their interaction with a protein.

Finally, the electrostatics was completely eliminated on the phosphate groups of the DNA model, in order to estimate its role in the docking prediction. Unexpectedly, we found that electrostatics was not really essential for achieving reliable interaction between the two species. The steric complementarity was sufficient in most cases to unambiguously predict the correct geometry of the complex, underlining again the role of the structural complementarity of the partners. It must be noted however that alternative interfaces could also be found among the firstly ranked candidate geometries, but they were easily discriminated upon reintroduction of electrostatics. So, inclusion of electrostatics on DNA was found to strengthen the interaction and broaden the attraction energy well, in addition to eliminating non electrostatic-matching interfaces.

This coarse grain model is an exciting working model, one of the most attractive aspects being its simplicity which makes it a promising tool in large system treatment, due to the consequent gain in computer time. The present calculations already indicate that this new type of method, specifically developed to treat protein–DNA associations, is instrumental in obtaining an overall structure of a representative set of complexes. Furthermore, it allows to infer valuable informations about the elements that guide such macromolecular constructs. We anticipate that our approach could be used for successfully predict the interface between numerous protein–DNA systems, on condition that the partners are not strongly distorted in the complex. Many complexes involving transcription factors respond to this requirement. Their DBD domains are often highly structured and are not submitted to dramatic changes upon binding. Similarly, the curvatures of DNA engaged in such complexes rarely exceed 30°. Nevertheless, it is clear that a general and complete comprehensive view of macromolecular docking should include flexibility of both partners, protein and DNA. We have already shown that it is possible to account for protein fragment flexibility in the course of docking simulations ([9], [33]). Our next task will thus be to couple a stochastic exploration of DNA deformations with the present coarse grain systematic docking procedure.