Statistical analysis of large-scale neuronal recording data

Abstract

Relating stimulus properties to the response properties of individual neurons and neuronal networks is a major goal of sensory research. Many investigators implant electrode arrays in multiple brain areas and record from chronically implanted electrodes over time to answer a variety of questions. Technical challenges related to analyzing large-scale neuronal recording data are not trivial. Several analysis methods traditionally used by neurophysiologists do not account for dependencies in the data that are inherent in multi-electrode recordings. In addition, when neurophysiological data are not best modeled by the normal distribution and when the variables of interest may not be linearly related, extensions of the linear modeling techniques are recommended. A variety of methods exist to analyze correlated data, even when data are not normally distributed and the relationships are nonlinear. Here we review expansions of the Generalized Linear Model designed to address these data properties. Such methods are used in other research fields, and the application to large-scale neuronal recording data will enable investigators to determine the variable properties that convincingly contribute to the variances in the observed neuronal measures. Standard measures of neuron properties such as response magnitudes can be analyzed using these methods, and measures of neuronal network activity such as spike timing correlations can be analyzed as well. We have done just that in recordings from 100-electrode arrays implanted in the primary somatosensory cortex of owl monkeys. Here we illustrate how one example method, Generalized Estimating Equations analysis, is a useful method to apply to large-scale neuronal recordings.

1. Introduction

1.1 Motivation

Recording large-scale neuronal data in vivo is an expanding field; however, methods that can best describe and quantify the results of these recordings are essential to utilizing these data. Our laboratory with our colleagues have implanted multi-electrode arrays into somatosensory and motor regions of the cortex in non-human primates (e.g., Nicolelis et al., 1998; Jain et al., 2001; Reed et al., 2008), and we recognize the challenges that performing such experiments and analyzing these data present. Data can be analyzed in traditional ways, treating simultaneous neuron recording as an efficient means of increasing the sample size of neurons recorded from each monkey. However, these traditional analyses rely on the assumption that the data collected from each neuron is independent, which may not be a valid assumption. Thus, we intend to introduce alternative analysis methods that may not be widely considered or used in current neurophysiological research. From in vivo recordings, computational neuroscientists often make neural network models that can include complex properties of real neurons, such as the dependence of the observed firing rate on the spiking history (e.g., Lewi, Butera, & Paninski, 2009). Such models have been used to understand the properties of individual neurons considered in isolation from the recorded population (e.g., Pei et al., 2009) as well as to understand network properties (e.g., Deadwyler & Hampson, 1997, review). Here, we review selected methods for analyzing the variance of in vivo recording measures of large-scale neuronal populations, while we intend for neural network modeling to be addressed by others.

In particular, we focused on two extensions of the Generalized Linear Model (McCullagh & Nelder, 1989), the Generalized Estimating Equations (Liang & Zeger, 1986; Zeger & Liang, 1986) and the Generalized Linear Mixed Models (e.g., Laird & Ware, 1982; Searle, Casella, & McCulloch, 1992), as practical methods of estimating the contributions of selected factors to the variance in the dependent measures of interest due to the existence of correlations inherent in large-scale recording experiments. Forms of the Generalized Linear Models are already commonly used to model individual neuron properties, with recent examples from Lewi, Butera, & Paninski (2009) and Song et al. (2009); however, we did not find examples of analysis of neuron populations using Generalized Linear Models in our recent search (Pubmed, September 1, 2009). We hope that a review of analysis methods and practical considerations for their use will aid researchers in making decisions about how to analyze the complex data sets obtained from large-scale neuronal recordings.

1.2 Use of generalized linear model analysis in other research fields

Reviews have been written for other fields to encourage the use of the Generalized Estimating Equations, Generalized Linear Mixed Models, and other extensions of the Generalized Linear Models. Edwards (2000) described both Generalized Estimating Equations and Generalized Linear Mixed Models analyses for biomedical longitudinal studies. Other examples include behavioral research (Lee et al., 2007); ecology (Bolker et al., 2008); epidemiology (Hanley et al., 2003); psychology and social sciences (Tuerlinckx et al., 2006); and even political science (Zorn, 2001) and organizational research (Ballinger, 2004). Within most of these reviews, the term “subjects” is applied to people (patients, participants in research, etc.) for the purpose of statistical analysis of “between-subjects” or “within-subjects” effects on the variance of the dependent variable of interest. The term “subjects” is a general one, and for longitudinal data or other studies with clustered observations, it refers to the variable for which observations may be correlated (with respect to standard errors). In many neurophysiological studies, “subjects” are individual neurons. These neurons are nested within individuals, monkeys, in our case. This situation is analogous to studies in which human participants are nested within communities, for example. Most neurophysiological studies, especially those on non-human primates, provide the number of animals used in the experiment, but pool all of the neurons across animals so that the number of subjects for analysis of variance is large (number of neurons) instead of small (number of animals). By incorporating the nested effects of neurons within animals, neurophysiologists can continue to investigate neurons as subjects without violating important statistical assumptions (e.g., Kenny & Judd, 1986) as long as appropriate measures are used to try to account for the likely correlations within subjects. Section 2 of this review describes this issue and how extensions of the Generalized Linear Model can be used to address multielectrode recording data. Now that these methods are becoming more widely used in other fields and many options for these analyses are included in commercially available statistical software packages, re-introducing Generalized Estimating Equations and Generalized Linear Mixed Models analysis for applicability to parallel neural recordings appears to be overdue. However, as we will describe, we do not have ideal answers for all of the questions that arise when analyzing complex neuronal data.

2. Complexities of parallel neuronal recording data and how to address them

2.1 Complexities of parallel neuronal recordings and experimental designs

The use of multi-electrode array to simultaneously record from small populations of neurons allows neuroscientists to study how neural ensembles may work (e.g., Buzsáki, 2004, review) and has played a role in the study of brain-machine-interfaces for neuroprosthetics (e.g., Chapin, 2004, review). There are diverse questions that can be addressed using large-scale neuronal recordings. Here, we consider issues that typically apply to such studies. While individual experiments have specific design considerations, many designs are aimed at recording the responses of large numbers of individual neurons in order to relate changes in activity to specific sensory or behavioral conditions. Some sensory experiments can be more easily performed in anesthetized animals than in awake animals, while behavioral experiments require animals to behave in the awake state. All of our experiments have been performed in lightly anesthetized animals.

Experiments can also be divided into “chronic” and “acute” recording categories. We have implanted microwire multi-electrode arrays chronically for long-term studies in primary somatosensory and primary motor cortex of squirrel monkeys (Jain et al., 2001), and we have implanted the 100-electrode silicon “Utah” array in primary somatosensory cortex of owl monkeys (Reed et al., 2008) for acute studies (in which the electrodes are not fixed permanently as for animal recovery experiments). New World monkeys (such as squirrel monkeys and owl monkeys) are often used for multielectrode recording studies because many cortical areas of interest are available on the cortical surface rather than buried in a sulcus. We chose owl monkeys because the area of interest in our case, area 3b, is not buried in the central sulcus, and the somatosensory cortex has been well studied (e.g., Cusick et al., 1989; Garraghty et al., 1989; Merzenich et al., 1978; Nicolelis et al., 2003). The acute recording experiment is a relatively simple design that still requires special consideration. In such experiments, recordings are made from the multiple electrodes implanted in one subject during a single experiment, and data are collected from multiple subjects to obtain the sample population of neuronal recordings. A common, but more complicated experiment is the chronic or longitudinal recording experiment. In such experiments, electrodes are chronically implanted so that the position of the electrodes is the same over time, and the recordings are made periodically over an extended time, which sometimes encompasses a period in which changes are expected to occur (e.g., Jain et al., 2001). For example, long-term recordings could be made in behaving animals before learning a task and after learning a task or before and after injury or treatment. Even in acute experiments, signals from the same neurons can be recorded under different conditions within the recording session, but unlike chronic recording studies, these neurons are not tracked over months of time. As the ability to track neuronal signals over days to months becomes more reliable (such as through the recent single neuron stability assessments introduced by Dickey et al., 2009), analysis methods concerned with the complexities of longitudinal recordings will increase in importance.

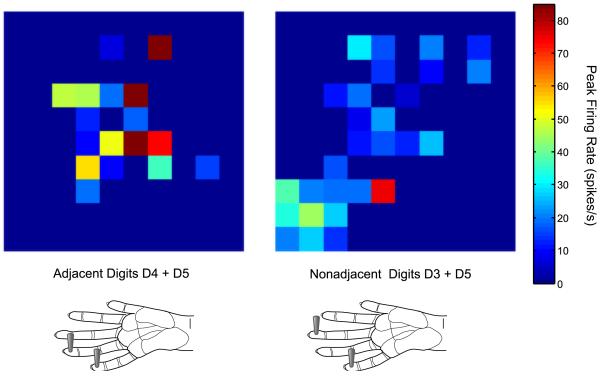
From a practical standpoint, these data require advanced techniques to process the signals to isolate single neuron signals from multi-neuron clusters (called “spike sorting”), careful organization and data management, and high-level analysis techniques. These data can be analyzed in traditional ways by looking at neurons individually for their response properties or looking at correlations across neurons. Often “snapshots” of neuronal activity distributed across the electrode arrays are generated from these data (e.g., Rousche et al., 1999 [rat whisker representation]; Ghazanfar & Nicolelis, 1999 [rat whisker representation]; Reed et al., 2008 [monkey hand representation]); however, how such snapshots can be analyzed rather than described has not been clear. A snapshot of peak firing rates across the 100-electrode array in the primary somatosensory cortex hand representation of one owl monkey under two different conditions is shown in Fig. 1 as an example to illustrate changes that can be visualized.

Fig 1. Snapshots of activity recorded from a 100-electrode array under two different stimulation conditions.

Activity snapshots were plotted in color maps of the peak firing rate measured across the 10 × 10 electrode array in monkey 3. Each square represents an electrode in the array and the color indicates the peak firing rate value during the 50 ms response window. Electrodes from which no significant responses (firing rate increases over baseline) were obtained during the stimulations shown are indicated in dark blue (no squares). The lower schematics indicate the locations of the stimulus probes on the owl monkey hand. Left panel shows the activity when adjacent digit locations on digit 4 (D4) and digit 5 (D5) were stimulated simultaneously (0 ms temporal onset asynchrony). Right panel shows the activity when nonadjacent digit locations on digit 3 (D3) and D5 were stimulated simultaneously. Differences between the patterns of activity during the two stimulation conditions are obvious and can easily be described visually, but quantitative measures are desired.

In somatosensory research, we are interested in contributions to the responses from stimulation across different parts of the skin to different parts of the brain. How neurons may integrate information from within and outside of their receptive fields is one question we ask to determine how the cortex processes tactile stimuli. Our research seeks to address how stimuli presented with varying spatial and temporal relationships affect neuron response properties in primary somatosensory cortex to reveal widespread stimulus integration. Here the term “widespread interaction” applies to when the effects of stimuli on the neurons occur when the stimuli are presented widely separated in space or time. We therefore categorize our stimulus parameters to use as predictor variables for analysis of variance (ANOVA) when we analyze these data to quantify spatiotemporal stimulus interactions. Data from both acute and chronic recording studies have properties that differ from those assumed by typical ANOVA procedures based on linear model theory. In the following sections, we illustrate properties of parallel neuronal recordings that could be better analyzed by extensions of the Generalized Linear Model. We have selected a particular route for analyzing the data, which we justify and illustrate in the following sections.

2.2 Correlated instead of independent observations in multi-neuron recordings

The data from large-scale neuronal recordings are likely to be correlated, but the types of correlations may vary depending on the experiment. Generally, the neuronal signals recorded during even acute experiments without repeated measures designs are best considered to be correlated rather than independent observations. Specifically, the errors in the predictions of the neuronal measures may be correlated. This violates the assumption of linear model theory that the error is distributed independently with a zero mean and constant variance (Gill, 2001, p. 2). Biologically, correlations could take the form of the neurons in a particular brain area behaving similarly under the given experimental conditions since they are likely to be interconnected; thus, within each experimental human or animal subject, the neuron measures are correlated rather than independent. In a chronic recording experiment, measures of an individual neuron recorded at one time would also be expected to correlate with measures of the same neuron recorded at a later time. Many traditional analyses disregard the likely correlations and assume that each neuron measure is an independent observation. Most analyses also tend to assume that individual subjects do not vary enough to prevent pooling of the neuronal data between subjects without regard to subject identity. This may prove to be a reasonable assumption, but it seems worth considering.

An important article on the topic of assuming that neuron responses are independent observations in analysis of variance was published by Kenny and Judd in 1986. The review focused on identifying “nonindependent” observations and examining the consequences of violating the independence assumption of analysis of variance (ANOVA). When neurons are used as subjects and observations made from these neurons under different stimulus conditions are assumed to be independent in order to meet the assumptions of linear model theory, possible bias in the analysis can arise. Here we briefly recall the main points from Kenny and Judd (1986). Three main types of nonindependence were identified for typical neurophysiological recordings: “nonindependence due to groups”, “nonindependence due to sequence”, and “nonindependence due to space”. Nonindependence due to groups refers to correlations between members of a functional group; perhaps all of the neural responses collected from one subject will be grouped and slightly different from all of the responses collected from a second subject. Or perhaps neurons within an individual subject are linked in functional groups and these neurons will have similar responses and differ from other neurons outside the functional group. Nonindependence due to sequence will occur when observations are taken from the same neuron unit over time, as it is likely that observations taken close together in time will be more similar than observations that are separated by more time. Finally, nonindependence due to space occurs when neighbors in space are more similar than neurons farther away spatially; which is a reasonable assumption for most brain areas.

Kenny and Judd (1986) and others have demonstrated the general consequences of violating the assumption of independence; therefore, we do not repeat the derivations, but summarize the key points. When these effects of nonindependence are ignored, bias in the mean square for the independent variable and in the mean square for error can affect the F ratios in ANOVA and alter the type I errors in either direction (Kenny & Judd, 1986). Treating neurons collected from individual animals as independent greatly increases the sample size, and when between-subjects differences are the measures of interest, the type I errors (false positives) can be increased (e.g., Snijders & Bosker, 1999, p. 15). When within-subject differences are of interest, the type I errors can be too low (e.g., Snijders & Bosker, 1999, p. 16). For instance, if the data are correlated but analyzed as though they are independent, the estimate of the variance may be larger than the estimate that would be obtained when the correlation is included in the analysis; and this affects the hypothesis testing (e.g., Fitzmaurice, Laird, and Ware, 2004, p. 44). When nonindependence due to groups (e.g., nesting of neurons within monkeys) is ignored, the bias introduced depends on the real correlation and the true effect of the independent variables on the dependent variables, as demonstrated in detail by Kenny and Judd (1986). Thus, parallel neuronal recording experiments with or without repeated measures within neurons should be analyzed using methods that take into account the potential for neuron measures to be correlated in the ways outlined by Kenny and Judd (1986).

2.3 Distribution assumption may be violated by neural recording data

The distribution assumption of linear model theory may be violated by parallel recordings of neuronal activity (i.e., it is not universally true that neuronal recording data are non-normally distributed). When the data do not fit the normal (Gaussian) distribution, the generalized linear model extends the linear model theory to accommodate measures which were drawn from non-normal distributions (Gill, 2001, p. 2) to select a variety of distributions from the exponential family of distributions (Hardin & Hilbe, 2003, p. 7-8). To be clear, the term “exponential family” does not imply restrictive relationship to the exponential probability density function. Instead, this refers to a method in which the terms in the probability functions are moved to the exponent to transform the functions to a common notation that is mathematically useful (Gill, 2001, p. 9-10). A “link function” is added to Generalized Linear Models to define the relationship between the linear predictor and the expected value from the mean of the dependent variable (e.g., Zeger & Liang, 1986; Gill, 2001, p. 30; Hardin & Hilbe, 2003, p. 7-8). Thus, the generalized linear model should be used when the distribution of the dependent variable is believed to be non-normal or even discontinuous, as in the binomial distribution; and when the relationship between the dependent variable and the predictor variables may not be linear (e.g., McCullagh & Nelder, 1989, review).

Models of the data will fit better when the appropriate probability distribution and link functions are selected, and the best fitting parameters can be tested within the model analysis. One can perform Kolmogorov-Smirnov tests and create Probability-Probability plots to assess whether the experimental distribution differs from the normal distribution (or other distributions). Inappropriate distribution and link function choices may result in under- or over-estimating the predicted values. One can use the Generalized Linear Models analyses since these methods generalize to data distributions beyond the normal distribution.

2.4 How to analyze neural recording data to avoid violating assumptions

Given some examples in this Section of the ways in which large-scale neuronal recording data can differ from the assumptions of standard linear model theory, the alternative methods should be able to account for these violations or be robust in the face of violations. We review two extensions of generalized linear models that are well-suited options for analyzing the sources variance associated with measures of interest from parallel neuronal recordings. Generalized Estimating Equations analysis was developed for longitudinal studies to account for the presence of clustered or correlated data (e.g., Liang & Zeger, 1986; Zeger & Liang, 1986; Hardin & Hilbe, 2003). Similarly, Generalized Linear Mixed Models can be used for clustered data and unbalanced longitudinal studies, particularly when effects within subjects are of experimental interest (review, Breslow & Clayton, 1993; tutorial, Cnaan, Laird, & Slasor, 1997). Such methods should be considered for large-scale neuronal recordings, specifically due to the presence of correlated data as outlined by Kenny and Judd (1986) and for cases in which the data are not normally distributed (e.g., count data).

For the remainder of this article, we explain why the Generalized Estimating Equations and Generalized Linear Mixed Models analyses could be employed to analyze parallel recording data and highlight the differences between the two approaches (Section 3). We then illustrate the use of one approach, Generalized Estimating Equations analysis, with neurophysiological data from our experiments in Section 4. There are multiple alternative analysis methods depending on the research question, some of which are discussed in Section 5; however, we focus on Generalized Estimating Equations and Generalized Linear Mixed Models as two practical methods.

3. Generalized Estimating Equations and Generalized Linear Mixed Models analysis for neuronal recordings

3.1 Comparisons of Generalized Estimating Equations and Generalized Linear Mixed Models

Both Generalized Estimating Equations and Generalized Linear Mixed Models use the correlation or covariance between observations when modeling longitudinal data. Longitudinal studies can be generally divided into two categories which affect their analysis. In the first category, the experimental focus is on how predictor variables influence the dependent variable, and the number of subjects must be larger than the number of observations per subject. In the second category, the experimental focus is on the correlation or within-subjects effects, and the number of experimental subjects may be small. (Diggle et al., 2002, p. 20) Generalized Estimating Equations are well-suited to address the first category of experiments and Generalized Linear Mixed Models are well-suited to address the second category.

Generalized Estimating Equations analysis is categorized as a marginal method which allows interpretation of population-average effects. Mixed models are random effects models which allow both the population effects and subject specific effects to be interpreted. (e.g., Edwards, 2000) Regarding the issue of correlated error in the data observations within subjects, dependence can be considered an interesting focus to be investigated or a nuisance that must be taken into account to properly investigate between subjects (Snijders & Bosker, 1999, p. 6-8). How non-independence is regarded by the investigator depends on the research questions. Generalized Estimating Equations regards dependence as a nuisance; thus, Generalized Estimating Equations may be the analysis method of choice when population-average effects between subjects are of interest. Mixed models include random effects for the within-subject variables and dependence within these effects is regarded as a characteristic of interest. Mixed models are preferred when within- subject effects are important to answer the research questions. When the data are normally distributed and related to the prediction with the (linear) identity link, then the difference between the solutions from the two methods is slight. But when the data are non-normal and nonlinear, there can be differences in the results derived from the two methods.

Generalized Estimating Equations analysis requires large sample sizes, and Generalized Linear Mixed Models are preferred for small samples. Generalized Estimating Equations may underestimate the variance in the samples and have inflated type I errors (false positives) when the number of subjects with repeated observations is less than 40 (e.g., Kauermann & Carroll, 2001; Mancl & DeRouen, 2001; Lu et al., 2007). However, Lu et al. (2007) compared two correction methods (Kauermann & Carroll, 2001; Mancl & DeRouen, 2001) for small samples using Generalized Estimating Equations analysis and proposed corrections that may perform well when the number of samples (with repeated observations) is 10 or greater. The repeated measures taken within these samples should be balanced (taken at specific time points across subjects) and as complete as possible (few missing observations) when using the Generalized Estimating Equations approach. Neurophysiological experiments may comply with these guidelines better than some studies requiring observations from human subjects at strict time points.

It is not uncommon to have missing observations in any experiment, and Generalized Estimating Equations analysis and Generalized Linear Mixed Models have slight differences in their tolerances for missing data. Generalized Estimating Equations can account for missing values; however, the missing values are assumed to occur completely at random (MCAR) and without intervention by the investigator, the routine will proceed with an analysis of only complete observations (e.g., Hardin & Hilbe, 2003, p. 122). This method is still likely to be appropriate when the data are missing due to a dropout process (like losing the neuronal signal for the last observations in a series) if the process is not related to the parameters of interest (Hardin & Hilbe, 2003, p. 127). Generalized Linear Mixed Models is mathematically valid for data missing at random (MAR) and MCAR data. MAR is the term applied when the mechanism that causes the missing observations does not depend on the unobserved data. MCAR refers to the case when the probability of an observation being missing does not depend on the observed or the unobserved data (e.g, Hardin & Hilbe, 2003, p. 122-123). The problem when the missing data are “nonignorable” or are missing in a non-random pattern (MNAR) is briefly discussed in section 5.2 on “Limitations”. Here we focus on analyses that can be performed using the methods commonly available in statistical software for more widespread applicability, but readers are encouraged to investigate alternatives and extensions appropriate for the data.

3.2 Note on practicality of use

An incomplete list of software packages that contain commands for the Generalized Estimating Equations routine include SAS (SAS Institute Inc.), SPSS (SPSS Inc.), and Stata (Stata Corp). For a review of software for performing Generalized Estimating Equations analysis, see Horton and Lipsitz (1999). Note that their 1999 review excluded SPSS, which currently includes the Generalized Estimating Equations analysis. See Bolker et al. (2008) for a list of software packages for Generalized Linear Mixed Models analysis. Each software package has different directions and implementations, and the current review does not specify the steps to perform the analysis for each package. However, the ability for researchers and students to employ the Generalized Estimating Equations and Generalized Linear Mixed Models through the use of standard statistical software makes these methods relatively practical for widespread use to analyze large-scale neuronal recordings, particularly with the help of statisticians as needed.

4. Illustration of use of Generalized Estimating Equations for neuronal recording data

For our research question, we selected Generalized Estimating Equations instead of Generalized Linear Mixed Models for a few reasons. Our research question was specific to population average effects and we did not intend to determine neuron-specific predictions for our effects. We measured neuron responses to several stimulation conditions over short periods of time and our simultaneously recorded neuronal data were likely to be correlated, we selected the Generalized Estimating Equations analysis to investigate the sources of the variance related to these neuron responses while accounting for the aspect of correlation that was most important in our experiment: the correlation within individual neurons measured over short periods of time. Of a practical consideration, our data were highly complex and large numbers of neurons were sampled from a small number of monkeys, and this proved computationally challenging. In addition, one feature of the Generalized Estimating Equations that we have highlighted is the ability consistently estimate the parameters even when the correlation structure is mis-specified, as we illustrate in this section. For other research situations, including those related to subject-specific effects, Generalized Linear Mixed Models analysis is recommended.

4.1 Methods to obtain example data

Here we assume that data has been collected and measures of relevance have been determined. We obtained our measures from recordings using a 100-electrode array implanted in anterior parietal cortex of three adult owl monkeys (Aotus nancymaae) following the guidelines established by the National Institutes of Health and the Vanderbilt University Animal Care and Use Committee, and using methods described previously (Reed et al., 2008, Reed et al., in press). Computer-controlled pulse stimuli were delivered by two motor systems (Teflon contact surface, 1 mm diameter) that indented the skin 0.5 mm for 0.5 s, followed by 2.0 s off of the skin were presented for at least 100 trials (~ 4 min). These stimuli were selected for experimental purposes beyond the scope of this review, but in general were used to investigate how spatiotemporal stimulus relationships affected neuron response properties.

4.2 Pre-processing methods for the sample data set and hypothesis

For simplicity in this example, we focused on only one neuronal response property: response magnitude in the form of peak firing rate (spikes/s). Peak firing rate measures were calculated using Matlab (The Mathworks, Natick, MA). Data were compiled in Excel (Microsoft) and imported into SPSS 17.0 for summary statistical analysis. Generalized Estimating Equations routines were performed to determine the convincing contributions to the variance in the peak firing rate measures. We related categorical factors (or predictor variables) to the variance observed in the measure of interest, peak firing rate. Data were classified based on the stimulus conditions and the relationship of individual neurons to the stimulus conditions. These stimulus conditions were the categorical predictors we expected would be associated with the variance in the neuronal measures. With the two tactile stimulus probes, we stimulated paired locations on the hand which could include adjacent digits or nonadjacent digits. The two tactile stimuli were presented at varying temporal onset asynchronies including 0 ms (simultaneous) and 30, 50, and 100 ms. The measurement intervals were consistent for the neurons recorded throughout the experiment. We selected data to include in the analysis such that the preferred stimulus for a given neuron was presented second and the non-preferred stimulus was presented first, for the purposes of addressing our experimental hypothesis.

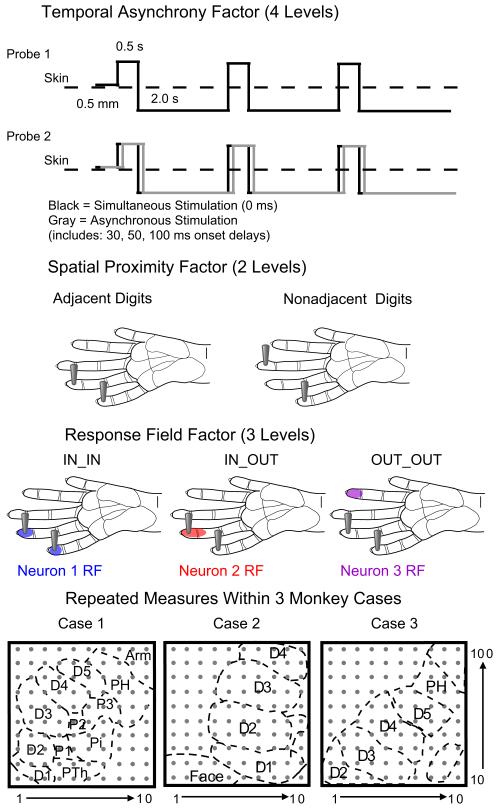
In addition to calculating response properties of the neurons, we determined the relationship of the tactile stimulus probes to the neuron’s receptive field. To do this, we examined the firing rates of the neurons across all of the given set of stimulus locations on the hand. Since we used a classification measure based on the firing rate in response to indentation stimulation, we used the term “Response Field” to refer to the classification since the full receptive field properties of the neuron were not characterized. When the peak firing rate (after the average baseline firing rate was subtracted) was greater than or equal to 3 times the standard deviation of the average firing rate for the population of neurons recorded on the electrode array, then that stimulus site was classified as “Inside” the neuron’s Response Field. Otherwise, the stimulus site was classified as “Outside” the neuron’s Response Field. Since the stimulus sites were paired, the combination of the Response Field categories for each single stimulus site was used to classify the Response Field relationship of the neuron to the two (paired) stimuli. Thus, the final categories for Response Field were: 1) both probes Outside of the Response Field (OUT_OUT); 2) one probe Inside the Response Field and one probe Outside (IN_OUT); and 3) both probes Inside the Response Field (IN_IN). This classification was important to our hypothesis that the location of the stimulation relative to the Response Field of the neurons would impact the changes in their firing rates. See Fig. 2 for a schematic representation of the predictor variables used in this example data set.

Fig 2. Schematic of factors evaluated in the example data set.

The categorical factors related to the stimulus parameters and the experimental subjects are shown with schematics to represent the levels over which the categories vary. The temporal stimulation asynchrony factor involves the relationship between the onset of stimulation by two tactile probes. The gray line represents how the onset of the second stimulation can be delayed in time relative to the onset of the stimulus provided by probe 1. The spatial proximity factor relates to the location of the two tactile probes on the hand. The Response Field factor categorizes the relationship of the stimulus probes to the Response Fields of each neuron. The final factor categorizes the data from which monkey case the signals were recorded. Schematic representations of the location of the 100-electrode array relative to the hand representation in primary somatosensory cortex (area 3b) are shown to designate each monkey case. (D = digit; P = palm pad; Th = thenar; H = hypothenar; i = insular.)

Our experiments involved presentations of paired stimuli that varied in spatial and temporal characteristics in relation to each other and to the Response Fields of the neurons, and we formulated several hypotheses as follows. 1) We expected that when two stimuli were presented to locations on the hand with different temporal onset asynchronies, the presence of the first, non-preferred stimulus would suppress the response (decrease the peak firing rate) to the second, preferred stimulus. 2) The location of the paired stimulus probes may affect the peak firing rate of neurons, since stimuli close in proximity could have a suppressive or additive effect on the peak firing rate. 3) Since neuron firing rates are related to the location of stimuli within their receptive fields, we predicted that when both stimulus probes were outside the Response Field, the peak firing rate would be low. When one stimulus probe was inside the Response Field and the other probe was outside the Response Field, we predicted that the peak firing rate would be higher, and the highest peak firing rates would occur when both stimulus probes were inside the Response Field. 4) Finally, since all three of these effects act in concert, we expected possible interactions between these factors. For example, the spatial proximity could affect which level of the temporal onset asynchrony condition caused the greatest suppression, and the relationship of the stimulus probes to the Response Fields could affect these firing rate decreases.

4.3 General use of Generalized Estimating Equations

The Generalized Estimating Equations uses quasi-likelihood estimation for longitudinal data analysis of clustered or correlated data. Estimating equations are derived by specification of the quasi-likelihood for the marginal distributions of the observed (dependent) variable and the working correlation matrix, which refers to the time dependence for the repeated observations from each subject (e.g., Liang & Zeger, 1986; Zeger & Liang, 1986). There are a few aspects of the Generalized Estimating Equations procedure that require basic knowledge of the data in order to specify the model, as described below.

4.3.1 Distribution and link function

The researcher must select the type of data distribution from which the dependent variable comes, and the Generalized Estimating Equations analysis allows one to select a variety of distributions from the exponential family of distributions along with a general link function that relates the linear predictor to the expected value (e.g., Zeger & Liang, 1986; Hardin & Hilbe, 2003, p. 7-8). (Distributions include the normal distribution, gamma, Poisson, binomial, Tweedie, etc. Link functions include, but are not limited to the identity link, log, logit, and reciprocal.)

4.3.2 Variable assignment, model effects to test

The dependent variable of interest must be selected. The subjects and the within-subjects measures specifying the repeated measurement condition must be specified in the model. First, the full factorial model can be selected, or main effects and interactions specific to a research hypothesis can be tested. In addition, the factors included in (or excluded from) the model can be varied to determine the best fit to achieve a final model of the data.

4.3.3 Working correlation matrix structure

The first model specification we describe is the working correlation matrix. The working correlation matrix structure can be selected based on the researcher’s best estimate of the time dependence in the data, and this parameter can be varied to determine if alternative correlation structures better fit the data. Brief descriptions of a subset of the options are as follows (from Hardin & Hilbe, 2003, p. 59-73), and selected example working correlation matrices are shown from our experimental data. The “independent correlation” derived by Liang and Zeger (1986) assumes that repeated observations within a subject are independent (uncorrelated). All off-diagonal elements of the matrix are zero (compare with the exchangeable working correlation matrix example in Table 1). In the case of repeated observations on the same subjects, the variance of the repeated measurements is usually not constant over time. The dependence among the repeated measurements is accounted for by allowing the off-diagonal elements of the correlation matrices to be non-zero (Fitzmaurice, Laird, & Ware, 2004, p. 30). The “exchangeable correlation” (or “compound symmetry”) is appropriate when the measurements have no time dependence and any permutation of the repeated measurements is valid. This type of structure may not be the most appropriate for repeated measures gathered across long periods of time, since the exchangeable structure does not account for the likelihood that measures obtained closely together in time are expected to have stronger correlations than measures obtained further apart in time. In our experiments, the first measure in the repeated measures series was taken less than 40 minutes before the last repeated measure in the series; therefore, we tested the exchangeable correlation structure (Table 1), along with other structures. The “autoregressive correlation” is used when time dependence between the repeated measurements should be assumed, such as in a long-term recovery of function or other treatment study. An example of the first-order autoregressive correlation matrix tested from our data is found in Table 2. The “unstructured correlation” is the most general correlation matrix, as it imposes no structure. While this unstructured option may seem the best for all situations, efficiency increases and better model fits will be obtained when the closest approximation to the actual correlation structure of the data is found (Zeger & Liang, 1986). This depends also on the number of time points relative to the number of subjects. An example of the unstructured correlation matrix tested using our data is found in Table 3. Each of these example structures shows the matrices when only the repeated measures within neurons are considered. When we consider that the repeated measures on neurons may show dependencies within monkeys, the working correlation matrix structure increases in complexity. The unstructured working correlation matrix was highly complex when we tested the effects of repeated measures dependent within neurons, and in turn dependent within monkeys, and given our large number of neurons, this working correlation matrix was too large to illustrate.

Table 1.

Exchangeable working correlation matrix from example data with simple repeated measures

Working Correlation Matrix
	Measurement
Measurement	0 ms	30 ms	50 ms	100 ms
0 ms	1.000	.593	.593	.593
30 ms	.593	1.000	.593	.593
50 ms	.593	.593	1.000	.593
100 ms	.593	.593	.593	1.000

Table 2.

First-order autoregressive working correlation matrix from example data with simple repeated measures

Working Correlation Matrix
	Measurement
Measurement	0 ms	30 ms	50 ms	100 ms
0 ms	1.000	.705	.498	.351
30 ms	.705	1.000	.705	.498
50 ms	.498	.705	1.000	.705
100 ms	.351	.498	.705	1.000

Table 3.

Unstructured working correlation matrix from example data with simple repeated measures

Working Correlation Matrix
	Measurement
Measurement	0 ms	30 ms	50 ms	100 ms
0 ms	1.000	.488	.443	.505
30 ms	.488	1.000	.982	.836
50 ms	.443	.982	1.000	.764
100 ms	.505	.836	.764	1.000

4.3.4 Estimating equations and testing

In addition to the correlation matrix structure, the variance-covariance estimator must be selected. This variance estimator can be a “robust estimator” or a “model-based estimator”. The mean and variance of the response must be correctly specified for the model based estimator. The robust estimator is consistent even when the working correlation matrix is mis-specified, so the robust estimator is usually recommended (e.g., Hardin & Hilbe, 2003, p 30). Using statistical software packages, the Generalized Estimating Equations routine runs for a selected number of iterations to reach the specified model convergence. The results of the analysis include estimated regression coefficients for the main effects and interactions in the model and estimated marginal means, along with estimates of significance. When the effects have multiple levels, the researcher selects the adjustment for multiple comparisons (e.g., the Bonferroni correction).

4.4 Performing summary data analysis using Generalized Estimating Equations

An important aspect of the analysis is choosing the best final model of the data. A guide for model selection is the goodness-of-fit statistic: either the quasi likelihood under independence model criterion (QIC) or the corrected quasi likelihood under independence model criterion (QICC) are often used, as they resemble Akaike’s information criterion (AIC), which is a well-established goodness-of-fit statistic (Hardin & Hilbe, 2003, p. 139). The smallest value is best using the QIC and QICC. Note that the goodness-of-fit statistic should not be used as the sole criterion for selecting the best working correlation structure for the data—if there are experimental reasons to specify a particular correlation structure, follow this reasoning. Similarly, the QIC is particularly useful when choosing between models including various main effects and interactions between factors, but the effects of interest for the model may be determined by the research hypothesis rather than the goodness-of-fit statistics. (Hardin & Hilbe, 2003, p. 142).

The procedure for determining the best model for the data using Generalized Estimating Equations involves changing the model parameters to select the best fit based on goodness-of-fit statistics. We compared models which assumed the data were normally distributed with models that assumed the data followed a gamma distribution. In addition to the distribution, several other characteristics of the data must be selected by the researcher, as described in Section 4.3, and some of these can be varied to test the best model fit. Here we describe the different selections specific to the models that we tested using the gamma and normal distribution functions.

In our models, we selected various correlation matrix structures in order to determine the best fit. For the normal distribution (linear relationship), the link function is typically the “identity” link function (Hardin & Hilbe, p. 8), and this is what we used for our models using testing the linear relationship of our variables. We used the typical link function for the gamma distribution, the “log link” function, in our models using the gamma distribution. The reciprocal link function is canonical for the gamma distribution; however, this link function does not preserve the positivity of the data distribution, so the log link function is commonly used (e.g., Lindsey, 2004, p. 30). For additional distributions and link functions, see Hardin and Hilbe (2003, p. 8). We always selected the robust estimator of the variance-covariance matrix since this selection is robust in the general case (e.g., Hardin & Hilbe, 2003, p 30).

The subject identification variables and the within-subjects measures indicating the repeated measurement condition must be specified in the model. In our case, the subjects were the individual neuron units from which the repeated measures were taken. We performed the analysis two ways. In the first, the within-subjects repeated measurements were the varying levels of the stimulation conditions (without regard to the individual monkeys). In the second, the varying levels of the stimulation conditions measured for the neurons were regarded as dependent within the individual monkeys. These two methods affected the working correlation matrix structure used to determine the Generalized Estimating Equations solutions.

The Generalized Estimating Equations analysis was performed with peak firing rate as the dependent variable. We selected several categorical predictor variables for the model: temporal stimulation asynchrony; spatial stimulation proximity; and Response Field relationship. For our example data, we used a final model with all three main effects and one three-way interaction effect. The tests of model effects for our best fit models using the gamma and normal distributions are shown in Tables 5 and 6, respectively.

Table 5.

Tests of Generalized Estimating Equations model effects on peak firing rate using the normal probability distribution with the identity link function

Tests of Model Effects
	Type III
Source	Wald Chi- Square	df	Sig.
(Intercept)	105.024	1	<.0005
Temporal Asynchrony	36.591	3	<.0005
Spatial Proximity	7.225	1	.007
Response Field (RF)	12.960	2	.002
Temporal * Spatial * RF	40.580	17	.001

Dependent variable: peak firing rate (spikes/s). Model parameters: normal distribution, identity link, first-order autoregressive correlation matrix. Subject effects for 126 neurons, with four levels of within-subject repeated-measures stimulation (total N = 499, 5 missing).

Table 6.

Regression parameter estimates from the Generalized Estimating Equations routine for peak firing rate using the gamma probability distribution with the log link function (only main effects shown)

Parameter Estimates
			95% Wald Confidence Interval		Hypothesis Test
Parameter	B	Std. Error	Lower	Upper	Wald Chi- Square	df	Sig.
(Intercept)	3.893	.2811	3.342	4.444	191.778	1	<.0005
Temporal 0 ms	−.053	.1967	−.438	.333	.072	1	.788
Temporal 30 ms	−1.603	.5124	−2.608	−.599	9.792	1	.002
Temporal 50 ms	−1.121	.4357	−1.975	−.267	6.623	1	.010
Temporal 100 ms	0a
Spatial Adjacent	−.562	.4190	−1.383	.260	1.797	1	.180
Spatial Nonadjacent	0a
RF OUT_OUT	−1.309	.5187	−2.326	−.293	6.372	1	.012
RF IN_OUT	−.804	.3150	−1.421	−.186	6.511	1	.011
RF IN_IN	0a
(Scale)	1.653

Redundant parameters set to 0 indicated by ^a. RF = Response Field. See text for other abbreviations.

4.5 Results of data analysis using Generalized Estimating Equations

While neuronal signals were recorded from all 100 electrodes of the array, only the signals that were likely to come from single neurons (rather than multi-neuron clusters) were included in this analysis. During the selected stimulus conditions, only a subset of the electrodes implanted in each monkey recorded neural activity from which we were able to isolate single neurons. From monkey 1, results from 19 single neurons were collected and 4 repeated measures were collected from each neuron (except for 2 missing observations), for a total of 74 observations. From monkey 2, results from 46 single neurons were collected with 4 repeated measures each, for a total of 184 observations. From monkey 3, 61 single neurons were collected with 4 repeated measures (except for 3 missing observations), for 241 observations. Thus, the total number of observations was N = 499, while 5 values were excluded due to missing observations from the repeated measures series. The mean response magnitude for the data set was 18.05 spikes/s, with a standard deviation of 23.81.

The results for model fitting using both the gamma and normal distributions are described here for illustration purposes. We investigated working correlation matrices of: first-order autoregressive, exchangeable, and unstructured for the normal distribution with the identity link function and for the gamma distribution with the log link function. For all working correlation matrices specified, the goodness-of-fit statistic QIC was substantially better using the gamma distribution compared to the normal distribution (e.g., 1480.789 and 239,348.869, respectively, under the same model parameters, described to follow). In addition, we tested correlation structures that incorporated only the repeated measures taken from individual neurons and those that included repeated measures within monkeys (which we term “complex model”). We again examined the QIC goodness-of-fit statistic to help determine the best correlation structure for the analysis. After reducing the effects included in the model from the full factorial model, we selected possible correlation matrices, and checked the QICC goodness-of-fit statistic to determine the best model parameters to fit the data. The QICC did not differ between models that included all main effects and the 3-way interaction and those that included the main effects, 3-way interaction, and 2-way interactions. Because the 2-way interactions were never significant sources of variance in the models, we selected the model that only included the significant effects (3 main effects and the 3-way interaction).

Under the model including 3 main effects and the 3-way interaction, the QIC values were very similar (sometimes identical) when the repeated measures were considered to be dependent within monkeys. The final model we selected used the gamma distribution with the log link function and the first-order autoregressive correlation matrix structure, and had a goodness-of-fit QIC = 1480.789 (Model Effects shown in Table 4). The equivalent model using the normal distribution and identity link function resulted in a QIC value of 239,348.869 (Model Effects shown in Table 5). Although this model using the normal distribution reported significant effects similar to those reported using the gamma distribution, there are some differences in the effects that reach significance, different regression parameter estimates, and clearly a large difference in model fit. Thus, we rejected the Generalized Estimating Equations model using the normal distribution in favor of the Generalized Estimating Equations model using the gamma distribution, and for these data we reject other analysis methods that rely on the assumption of independent observations from the normal distribution.

Table 4.

Tests of Generalized Estimating Equations model effects on peak firing rate using the gamma probability distribution with log link function

Tests of Model Effects
	Type III
Source	Wald Chi- Square	df	Sig.
(Intercept)	552.354	1	<.0005
Temporal Asynchrony	28.564	3	<.0005
Spatial Proximity	9.037	1	.003
Response Field (RF)	11.380	2	.003
Temporal * Spatial * RF	35.417	17	.005

Dependent variable: peak firing rate (spikes/s). Model parameters: gamma distribution, log link, first-order autoregressive correlation matrix. Subject effects for 126 neurons, with four levels of within-subject repeated-measures stimulation (total N = 499, 5 missing).

From the Generalized Estimating Equations analysis, we obtained a model that included the factors that relate to the variance in the observed measurements (Table 4); the estimated regression parameters that describe the relationships of the factors to the dependent variable the estimated marginal means of these factors (see one example Fig. 3); and pairwise comparisons for significance between the levels of each factor. We used the estimated marginal means and the significance calculations to determine how the spatiotemporal stimulus relationships affected the peak firing rates of the neurons we recorded within the three monkeys. Selected regression parameter estimates for the best model are shown in Table 6. We can interpret the parameter estimates to describe the relationships between the factors in the data. In general, linear regression coefficients are interpreted such that the coefficient represents the amount of change to the response variable for a one-unit change in the variable associated with the coefficient, with the other predictors held constant (e.g., Hardin & Hilbe, 2007, p. 133). Examining our data for example, as expected for the somatosensory system, the relationship of the location of the paired stimuli to the Response Field of the neuron influenced the peak firing rate. The parameter estimate for the case when the paired stimulus probes were both outside of the Response Field (OUT_OUT) was −1.309, which was less than the estimate for the case when one of the stimulus probes was inside the Response Field and the other probe was outside of the Response Field (IN_OUT) of the given neuron (−0.804), and these values refer to the comparison when both stimulus probes were inside the Response Field (IN_IN).

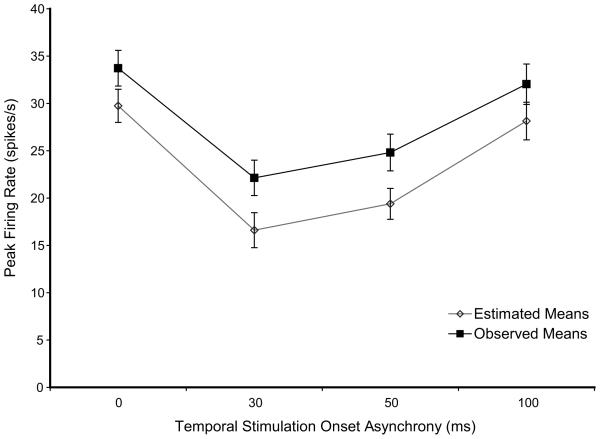
Fig. 3. Observed means and estimated means for the temporal asynchrony factor from the best model.

The categories from one factor, temporal asynchrony is plotted on the x-axis and the dependent variable, response magnitude (spikes/s) is plotted on the y-axis. Observed mean response magnitudes are shown by category with filled squares. Estimated marginal means from the best fitting Generalized Estimating Equations routine is shown by category with open diamonds. Although the values of the estimates are not equal to the observed values, the patterns of the effects of the predictor variable categories on the response magnitude are the same.

These Generalized Estimating Equations results provide population average effects of the categorical predictor factors on the dependent variable of interest, while accounting for individual-level correlations. To focus on the individual data subjects, a subject-specific Generalized Estimating Equations model would need to be created (programmatically) that resemble within-subjects effects analysis, or alternative methods such as Generalized Linear Mixed Models could be performed. Our experimental questions referred to population averages rather than within-subjects effects; thus, we were able to find support for our hypotheses and determine quantitative estimates of the ways spatiotemporal stimulus properties affect neuron firing rates in primary somatosensory cortex of owl monkeys.

5. Limitations and alternatives

The example in Section 4 was intended to illustrate how specific types of data can be modeled using the Generalized Estimating Equations analysis. The Generalized Estimating Equations analysis is particularly useful for large samples of longitudinal or repeated measures data that are expected to be correlated or clustered and that may not have linear relationships or fit the normal distribution. Another advantage of the Generalized Estimating Equations approach is that it provides consistent estimates for the regression parameters of the model even if the working correlation selected by the researcher is not the most appropriate (Tuerlinckx et al., 2006). There are limitations to this analysis, which may not be ideal for all designs, and there are alternative analysis methods that may be generally applicable to large-scale neuronal recording data to consider.

5.1 Limitations of the Generalized Estimating Equations analysis

A possible limitation of the Generalized Estimating Equations analysis for some designs is that interpretation of cluster-specific effects (within-subjects effects) is usually not included in the analysis within standard software packages, even though the analysis does take into account the correlated structure of the data for the between-subjects effects. The Generalized Estimating Equations method itself does include two main classifications that address between-subjects and within-subjects effects, respectively, the population-averaged model and the subject-specific model (Hardin & Hilbe, 2003, p. 49). Those who are concerned with the within-subjects variance and require methods built into a commercial statistical package would be best served by an alternative analysis method, such as Generalized Linear Mixed Models, as described in Section 3.1.

Another limitation of Generalized Estimating Equations analysis is one that is shared by most other methods, and this involves the biases possible when accounting for nonignorable missing data values (also called informatively missing data or nonrandom missing data). By nonignorable, we refer to missing data that are caused by a nonrandom process related to the condition under study. There are a few occasions that come to mind in which missing data are unlikely to occur at random in neurophysiological experiments. For instance, in an experiment when one measures response latency, there will be missing values when the neuron fails to respond to specific stimulus conditions (no response = no response latency). This situation is not simply random since the failure of the neuron to respond is related to the stimulus condition. Nonignorable missing data is a recognized problem in several types of clinical longitudinal studies, and methods accounting for such data have been described for use in Generalized Linear Mixed Models analysis (e.g., Ibrahim, Chen, & Lipsitz, 2001); and Hardin and Hilbe (2003, p 122-128) describe techniques to deal with missing data for Generalized Estimating Equations analysis. First, the data can be divided into complete and incomplete series, and then typically missing values are replaced with values imputed from the data. Investigators should carefully consider when to use data imputation methods. Alternative methods include modeling the complete data and the missing data separately. Currently, there appear to be no standard ways to account for nonignorable missing data, such as occurs for latency observations. While the problem of nonignorable missing data does not plague all neurophysiological measurements, it is a concern that is not directly addressed without data imputation or other procedures, and certainly methods are not built into commercial statistics packages to specifically analyze data sets including nonignorable missing data.

Finally, as mentioned previously, the Generalized Estimating Equations analysis as implemented in software packages allows for one dependent variable (but multiple covariates) to be analyzed. Multivariate research questions may be better analyzed with an alternative method. In addition, complex clustering is not easily incorporated into the Generalized Estimating Equations. In our example using SPSS, we were able to include clustering of the repeated measures on neurons within our individual monkey subjects. However, as the complexity of the working correlation structure increased, the Generalized Estimating Equations routine was not able to come to convergence on a solution. Random effects models, such as Generalized Linear Mixed Models, can typically handle complicated nesting structures due to differences in the calculation of random effects compared to marginal models of residuals. In our case, recall that the model fits were equivalent when the complex dependence was used for the working correlation matrix and when the simple dependence (without accounting for dependencies of neuron observations within monkeys) was used, except when the unstructured matrix was chosen rather than a structured (autoregressive or exchangeable) matrix. Thus, methods of choice depend on the measure of interest and computational considerations. Since the correlation matrix structure of the Generalized Estimating Equations analysis could not incorporate nested effects, we were not able to account for potential correlations in measures between neurons (which might be expected due to spatial proximity, for example). Dependency between neurons is not precisely known, and here we considered that neurons were independent; however, adaptations of Generalized Linear Mixed Models or other analysis methods may be able to model the possible dependencies better.

5.2 Some alternatives to the Generalized Estimating Equations analysis for large-scale neuronal recordings

Here we briefly describe selected alternatives to Generalized Estimating Equations analysis that may have useful applications to large-scale neuronal recording data. We assume that data from parallel microelectrode recordings are likely to have correlated or non-constant variability due to recording from clusters of neurons over time. We also suggest that good alternative analysis methods will allow for the dependent measure of interest to possibly come from non-normal distributions to account for the different types of data that may be obtained through such neuronal recordings.

As previously introduced, Generalized Linear Mixed Models are similar to Generalized Estimating Equations, in that both are extensions of Generalized Linear Models and may be used to analyze correlated or clustered data from non-normal distributions (e.g., Tuerlinckx et al., 2006, review). Generalized Linear Mixed Models may be advantageous over Generalized Estimating Equations when the dependence or correlations within subjects is of interest (rather than a nuisance; e.g., Snijders & Bosker, 1999, p. 6-7) so that subject-specific predictions can be made and when the number of clustered observations is low (e.g., < 40), since Generalized Estimating Equations tend to underestimate the true variance in small samples (Lu et al., 2007).

An addition to some statistical packages (e.g., Amos, SAS) is structural equation modeling, which can link the dependent variables with independent observed variables and latent variables (e.g., Tuerlinckx, 2006). A benefit of structural equation modeling is that researchers may build models to express unobserved latent variables that are expected to contribute to the observed measures by expressing latent variables in terms of the observed variables, which could be of interest in some neuronal recording experiments. The use of structural equation modeling to examine latent variables is similar to the use of Principal Components Analysis and Independent Component Analysis to identify underlying sources of variance related to the observed measures.

Principal Component Analysis (PCA) has already been applied to neuronal recording data (e.g. Chapin & Nicolelis, 1999; Devilbiss & Waterhouse, 2002), as a method to describe the linear relationship between variables (i.e., how stimulus information relates to neuron spike trains). Proportions of the variance are explained by each Principal Component, with the first PC accounting for the most variance in the data. The interpretation of PCA may not be intuitive in all experimental designs, and this analysis assumes linear relationships between variables and that the sources of the variance have a normal distribution. But given the right circumstances, PCA provides an interesting way to assess changes distributed among recorded neurons (e.g., Devilbiss & Waterhouse, 2002) and to estimate relationships within neuronal ensembles (e.g., Chapin & Nicolelis, 1999).

Similar to PCA, Independent Components Analysis (ICA) has also been used to examine data from parallel neuronal recordings, and has been shown to identify groupings of neurons with correlated firing distributed over the recorded neuronal ensembles (Laubach, Shuler, & Nicolelis, 1999). ICA was found to perform better than PCA at identifying groups of neurons with correlated firing when those neurons shared common input (Laubach, Shuler, & Nicolelis, 1999). Unlike PCA, ICA should be used when the sources of variance do not have a normal distribution (Makeig et al., 1999). However, ICA has limitations, one of which is that a given IC can represent a linear combination of sources of variance, rather than an “independent” source (Makeig et al, 1999), and similarly, ICA cannot identify the actual number of source signals. Thus the reliability, accuracy, and interpretation of results of ICA can be difficult to determine in general.

Pereda et al. (2005) reviewed nonlinear multivariate methods for analyzing parallel neurophysiological recordings to determine the synchronization across the signals. These methods are not limited to describing the linear features of neuronal signals, and neuronal signals may be intrinsically nonlinear. Such multivariate measures can assess the interdependence between simultaneously recorded neuronal signals or data types, and this assessment is a feature not possessed by standard Generalized Estimating Equations analysis methods. Nonlinear multivariate methods of “generalized synchronization” and “phase synchronization” have a wide range of applications to neurophysiology. These methods range from nonlinear correlation coefficients to information-theory-based methods. Many of these methods examine pairwise interactions (e.g., cross-correlations) between neuronal signals (e.g., spike trains), but a subset can be used to analyze high-order interactions. (Pereda, Quiroga, & Bhattacharya, 2005) Most of these applications are not part of commercial statistical software, but sometimes the implementation of these analysis methods are made available by authors or can be found in neurophysiological analysis software.

Many neurophysiological studies, including the example provided in this review, rely on multiple trials to average the responses (or other measurements) of individual neurons. This technique is rooted in the study of single neurons with single electrodes, in which the average over multiple trials resembles the information received by a postsynaptic neuron that receives input from several other neurons performing in a similar way to the recorded neuron. When the experimental system and research questions are appropriate, analyses of multiple-neuron recordings to extract information from neuronal populations within one or a few trials may provide a more realistic depiction of how the brain works. In their recent review, Quiroga and Panzeri (2009) described two main (and complementary) approaches to obtaining information from neuronal population recordings for the purpose of application to single-trial analysis: decoding and information theory. Decoding algorithms predict the likely stimulus (or behavior) related to the observed neuronal response. Using the information theory approach, one can quantify the average amount of information gained with each stimulus presentation or behavioral event. (Quiroga & Panzeri, 2009) Typically, decoding neuronal responses and applying information theory requires carefully planned experiments, careful interpretation and knowledge of programming since such algorithms are not often found in commercial statistical packages. However, as knowledgeable users continue to employ these methods, their use will likely extend and become more widespread as experiments utilizing large-scale neuronal recordings increase.

6. Conclusions

Current statistics packages and incarnations of the Generalized Estimating Equations and Generalized Linear Mixed Models analyses can accomplish many of the data analysis goals required by the increasingly complex large-scale neuronal recordings. Specifically, these analyses address concerns that have been largely overlooked when analyzing parallel neuronal recording data collected over time: that these data are likely to be correlated or clustered and that the normal distribution may not be the appropriate distribution to test. We illustrated our use of Generalized Estimating Equations to address questions regarding stimulus-response relationships in simultaneously recorded neurons in monkey somatosensory cortex. The Generalized Estimating Equations analysis has limitations, and alternative methods may provide more appropriate answers to some research questions.

In our data example, the goal was to determine how the responses of populations of neurons may be influenced by specific stimulus parameters recorded over relatively short periods of time; however, the technological advancements in chronic recording techniques and algorithms to determine when electrophysiological signals are stable over time and likely to originate from the same neuron will surely aid the progress of such longitudinal studies. Although we used the response magnitude example for simplicity, measures of correlated activity that can only be made by simultaneous neuronal recordings (such as those reviewed by Pereda, Quiroga, & Bhattacharya, 2005) can be used as the dependent measure when the goal is to determine how independent variables may affect the variance in these measures recorded longitudinally. The options are nearly unlimited. The analysis of long-term, large-scale neuronal recordings promises to increase our understanding of complex brain activity, and meeting the challenge to produce and employ efficient and appropriate analysis methods is important to reach this goal.