Analysis of Kinetic Intermediates in Single-Particle Dwell-Time Distributions

Abstract

Many biological and chemical processes proceed through one or more intermediate steps. Statistical analysis of dwell-time distributions from single molecule trajectories enables the study of intermediate steps that are not directly observable. Here, we discuss the application of the randomness parameter and model fitting in determining the number of steps in a stochastic process. Through simulated examples, we show some of the limitations of these techniques. We discuss how shot noise and heterogeneity among the transition rates of individual steps affect how accurately the number of steps can be determined. Finally, we explore dynamic disorder in multistep reactions and show that the phenomenon can obscure the presence of rate-limiting intermediate steps.

Introduction

Biochemical and biophysical processes generally pass through one or more intermediate steps. Enzymatic reactions, for instance, typically follow a pathway that involves substrate binding followed by catalysis and substrate release (1). Conventional ensemble-averaging techniques necessarily blur individual steps in an enzymatic reaction. For example, steady-state measurements are often used to gain access to simplified kinetic parameters such as k_cat, the turnover rate at saturating substrate concentration, and K_m, a measure of the binding affinity of the substrate. Stopped-flow kinetics can overcome these limitations (2), but time resolution and coherence of the reaction can still be limiting. Kinetic measurements of single molecules or particles are inherently free of these experimental limitations. Moreover, development of sensitive imaging and manipulation methods have greatly enhanced our ability to analyze a number of biochemical and biophysical processes (3–5). For example, optical trapping and fluorescence imaging have been used to track individual motor proteins and have led to new insights about the mechanism by which they move along protein filament tracks (6–9), and basic mechanistic questions about DNA replication have been addressed by observing the activity of single replication proteins and complexes (10–13).

Although kinetic measurements of large ensembles of biomolecules provide access to average reaction times, single-molecule trajectories show the fluctuations in those times and reflect the underlying stochastic nature of biochemical reactions. Rather than being regarded as noise, these random fluctuations encode mechanistic information that can be extracted by statistical modeling. For instance, in a previous study we analyzed the distribution of lag times of membrane fusion by influenza virus particles to identify a multistep process corresponding to the number of fusion proteins that participate in a fusion reaction (14). Similar analysis of the dwell times of motor proteins provided clues about the underlying kinetic intermediates that precede a power stroke (15,16).

In this study, we describe how experimental single-molecule kinetic data can be used to study multistep processes. We will discuss some of the limits of what can be learned from experimental data and use simulations of stochastic processes to inform an appropriate interpretation of experimental results. In particular, we discuss how the statistical quality of the data influences the accuracy in determining the number of steps and intermediate transition rates of multistep processes. We also characterize how heterogeneity in the rate constants for each of the individual steps impact the ability to accurately determine the number of rate-limiting steps. Finally, we explore the effects of dynamic disorder in multistep reactions and show that the phenomenon can obscure the presence of rate-limiting intermediate steps.

Theory background

At the single-molecule level, chemical and physical processes are stochastic, meaning that a reaction takes a variable time, τ, to complete a cycle. The distribution of waiting times, p(τ), contains information about the mechanism of the process. If completion of a cycle, such as a transition from state A to state B, occurs in a single step, the distribution of τ follows a single exponential decay, k × exp[−kτ], where k is equal to 1/〈τ〉. The brackets denote the expectation value of τ. If the A to B transition proceeds through formation of an intermediate X:

$$A\stackrel{k_1}{\to }X\stackrel{k_2}{\to }B,$$ (1)

p(τ) becomes the joint probability density of two sequential stochastic processes. If B is formed within a time τ, then formation of the intermediate must have occurred at time t < τ, and B was formed from the intermediate in the remaining time τ − t. The probability of an A → B event occurring at time τ is equivalent to the joint probability of an A → X turnover at time t and a X → B turnover occurring at time τ − t. The probability distribution of A → B is obtained by integrating over all possible times t < τ:

$$p_{A\to B}\left(\tau \right)={\int }_0^{\tau }{P}_{A\to X}\left(t\right)P_{X\to B}\left(\tau -t\right)dt\text{.}$$ (2)

Equation 2 shows that the joint probability of two sequential processes is the convolution of each individual process (17). If the probability distributions for the individual transitions are described by single-exponential decays, we obtain p_A→B(τ) by convolving k₁ × exp[−k₁ τ] and k₂ × exp[−k₂ τ]:

$$p_{A\to B}\left(\tau \right)=\{\begin{array}{l}\frac{k_1{k}_2}{k_1-K_2}\left(e^{-k_2\tau }-e^{-k_1\tau }\right),k_1\mathrm{\ne }{k}_2\\ k^2\tau e^{-k\tau },k_1=k_2\end{array}\text{.}$$ (3)

Instead of a single exponential decay, p_A→B(τ) represents a distribution characterized by a rise and decay (Fig. 1, red trace). Even if only the final state can be observed in an experiment, information about the hidden intermediate is encoded in the shape of the waiting-time distribution. Many biochemical processes consist of more than two steps (14,18), so we extend the above argument to multiple intermediate steps:

$$A\stackrel{k}{\to }{X}_1\stackrel{k}{\to }{X}_2\to \stackrel{k}{\to }{X}_{N-1}\stackrel{k}{\to }B\text{.}$$ (4)

Figure 1.

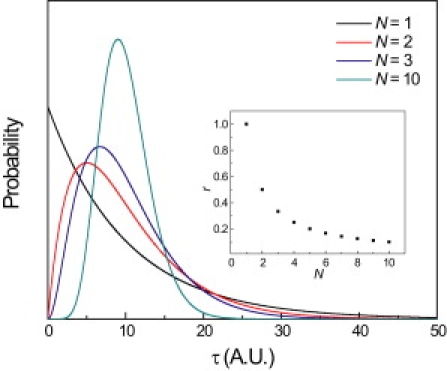
The presence of multiple rate limiting steps is encoded in the shape of p(τ). A single step process results in a dwell time distribution characterized by a single exponential decay. Two or more steps give a rise and decay shaped distribution that can be modeled with a gamma distribution. Shown are gamma distributions where N = 1, 2, 3, and 10. The randomness parameter, r, is a measure of the width p(τ) relative to its mean and is equal to 1/N if p(τ) is gamma distributed (inset).

This scheme describes the simplest case for a process consisting of N steps in which the transition between each step is described with a single rate constant k. The assignment of a single rate constant is a reasonable simplification because only the slowest steps in a reaction will contribute significantly to p_A→B(τ) (see below). As in Eq. 1, we can derive p_A→B(τ) for this process by convolution. This calculation is cumbersome for large N, so instead we work with Laplace transforms because convolution in the time domain is equivalent to multiplication in the frequency domain (19). In Laplace space, ${\tilde{P}}_{A\to B}\left(s\right)$ is the product of transformed density function of each intermediate transition, p(τ). As before, we assume step is exponentially distributed

$$\tilde{P}\left(s\right)={\left({\int }_0^{\mathrm{\infty }}p\left(\tau \right)e^{-s\tau }d\tau \right)}^N={\left(\frac{k}{s+k}\right)}^N\text{.}$$ (5)

To obtain p_A→B(τ) we take the inverse transform:

$$p_{A\to B}\left(\tau \right)=\frac{1}{2\pi i}{\int }_0^{i\mathrm{\infty }}{\tilde{P}}_{A\to B}\left(s\right)e^{s\tau }ds=\frac{k^N{\tau }^{N-1}}{\Gamma \left(N\right)}{e}^{-k\tau }\text{.}$$ (6)

Equation 6 is a gamma distribution where Γ(N) is the gamma function, equivalent to (N − 1)! for integral N.

Fig. 1 shows gamma distributions of various N plotted as a function of τ. Note that N is qualitatively encoded in the shape of the curve: increasing N causes the distribution to become narrower and more symmetric about its peak. Fitting experimental experimentally measured waiting-time distributions to a gamma distribution allows determination of the turnover rates and number of steps, assuming that the rate constants of each step are comparable (2,20,21).

Determining p(τ) requires observations of many events spread over a large dynamic range of timescales. This can be challenging in cases where events are lost to instrumental noise, or other experimental limitations prevent measurement of very short or long event times. Schnitzer and Block proposed using the randomness parameter (r) to characterize p(τ) using realistically noisy and incomplete experimental data (15). The randomness parameter is essentially a measure of the spread in event waiting times compared to the typical time:

$$r=\frac{\langle {\tau }^2\rangle -{\langle \tau \rangle }^2}{{\langle \tau \rangle }^2}\text{.}$$ (7)

A regular clock-like process will have a low r value approaching zero, and more random or irregular processes have higher r values. For single-step processes, where p(τ) is a single exponential decay, the standard deviation equals the mean and r = 1. For a multistep process with identical rate constants, p(τ) is a gamma distribution (Eq. 7) with 〈τ〉 = N/k and 〈τ²〉 − 〈τ〉² = N/k², and r = 1/N (Fig. 1, inset). Therefore the randomness parameter is also a measure of the number of rate limiting steps.

Methods

Multistep stochastic processes were generated with software written in MATLAB (The MathWorks, Natick, MA). Waiting times for N step sequential processes were generated from the sum of N exponentially distributed random numbers with a decay constant, k, set to a specified value. To simulate disorder, the rate constant for the disordered step was generated from the logarithm of a normally distributed random number. A total of 10⁴ events were simulated for each experimental condition.

Results and Discussion

The effect of shot noise on the determination of N

The accuracy with which we can determine the parameters of a multistep process depends on both the number of experimental observations (n) and the number of steps in the process. Poisson or shot noise is inherent to any waiting-time distribution with a finite n; its magnitude is proportional to $\sqrt{n}$. The actual number of steps also affects how accurately we can estimate N for a given n because the distinction between gamma distributions with N and N + 1 steps diminishes as N becomes large.

To characterize the effect of Poisson noise on the accuracy of N obtained from fitting dwell-time distributions with a gamma distribution, we simulated dwell-time distributions from processes consisting of N = 1, 3, 6, or 10 steps. Fig. 2, A–D, illustrate the χ² fitting error when comparing the simulated dwell-time distributions to p(τ) as a function of k and N. The contour plots clearly point to the difficulty of fitting distributions with large N. Contour maps of the χ² fitting error of p(τ) show that the best solutions lie on a diagonal with a slope N/k equal to 〈τ〉. If p(τ) is a single-exponential decay (N = 1), the global minimum is distinct, and the error rises sharply as one moves away from the correct solution (Fig. 2 A). As N increases, however, the error topology along the diagonal becomes increasingly flat, and the accuracy of the fitted parameters becomes increasingly limited by the shot noise and experimental error of the data.

Figure 2.

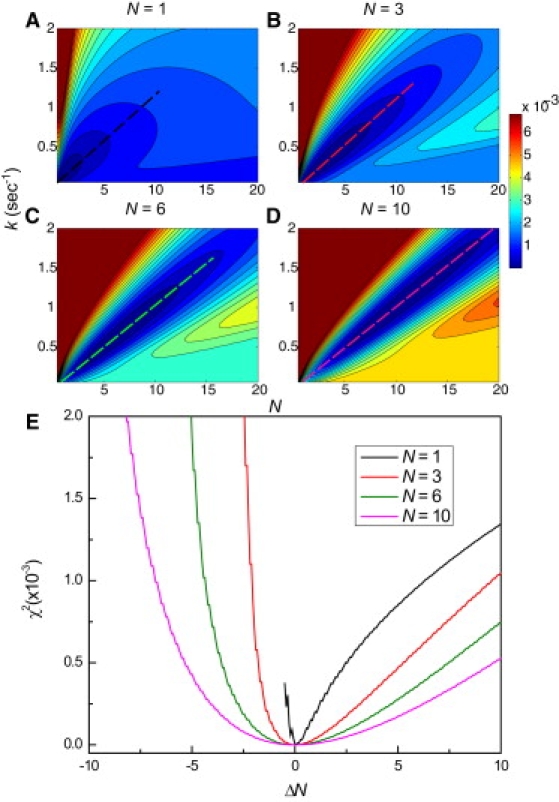
Accurately determining the number of steps in a process becomes more difficult with increasing N. (A–D) Contour plots show the mean-square deviation (χ² error) of gamma distributions of varying k and N with a gamma distributed process consisting of 1, 3, 6, or 10 steps and 〈τ〉 = 10 s. (E) Error profiles along the diagonal (slope = k/N) of A–D.

To determine how many observations are required to estimate N with a known uncertainty, it is useful to consider the standard deviation of the randomness parameter (Eq. 7). The standard errors of the mean and variance of τ are, respectively, $\sigma /\sqrt{n}$ and ${\sigma }^2\sqrt{2}/\sqrt{n}$, where n is the number of observations, and σ and σ² are the standard deviation and variance of τ, respectively. Propagating these errors through Eq. 7 gives the standard deviation of the randomness parameter, or equivalently, the estimated N:

$${\sigma }_N=\frac{2\sqrt{N}+N\sqrt{2}}{\sqrt{n}}N\text{.}$$ (8)

The minimum number of observations, n, required to determine N with a given uncertainty σ_N is therefore

$$n_{\min }=\frac{{\left(2\sqrt{N}+N\sqrt{2}\right)}^2}{{\sigma }_N^2}\text{.}$$ (9)

Equation 9 is plotted in Fig. 3 (solid lines) and indicates the minimum number of observations needed to estimate the number of steps in a process with an error of 1, 2, or 3 steps. For instance, ∼50 events are sufficient to distinguish 2 steps from 3, but ∼300 observations would be required to resolve a 9-step process from one of 10 steps.

Figure 3.

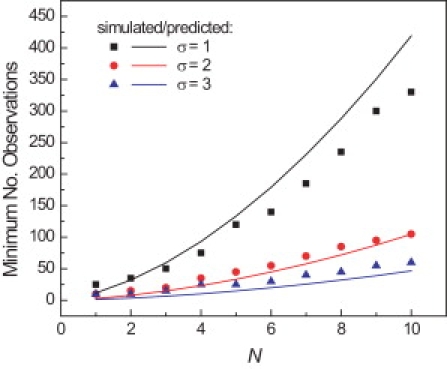
Estimating N with a given uncertainty requires more observations as the number of steps increases. Multiple simulated waiting time distributions were generated and fit to gamma distributions. The standard deviation of the fitted N from the actual number of steps was calculated and used to determine the number of observations necessary to estimate N with an error of 1 (squares), 2 (circles), or 3 (triangles) steps. The solid lines are plots of Eq. 9 where σ_N = 1 (black), 2 (red), or 3 (blue) steps. (Color version available online).

Simulated waiting-time distributions show the same trend when fit with gamma distributions. Multistep processes with N ranging from 1 to 10 steps were simulated, and waiting time distributions were compiled with a varying number of observations. To estimate the error in the fitted parameters, the simulations were repeated to produce 500 waiting-time distributions for each condition. The distributions were fitted to produce a distribution of fitted N for a given number of observations. The root mean-square deviation of the fitted N from the actual number of steps gives the fitting error. The number of observations required to estimate N with an error of 1, 2, or 3 steps is consistent with Eq. 9 (Fig. 3, squares, circles, and triangles, respectively).

Multistep processes with unequal rate constants

The above constraints on shot noise for determining N assume that the turnover rates for each step are identical. To determine the effect of unequal rate constants, we considered a multistep process in which one of the transitions occurs at a different rate than the other steps:

$$A\stackrel{k}{\to }{X}_1\stackrel{k}{\to }{X}_2\to \stackrel{k}{\to }{X}_{N-1}\stackrel{k_N}{\to }B\text{.}$$ (10)

Only the slowest transitions in such a process are considered rate-limiting, as can be seen by inspecting the Laplace transform of the probability density function for this process:

$$\tilde{P}\left(s\right)={\left(\frac{k}{s+k}\right)}^{N-1}\left(\frac{k_N}{s+k_N}\right)\text{.}$$ (11)

Equation 11 collapses into the transform of a single-exponential decay when k_N is small and a gamma distribution of N − 1 steps when k_N is large. In between these two extremes, where k_N is comparable but not equal to k, all N steps are rate limiting and can still be recovered by gamma-distribution analysis. To get a quantitative understanding for what constitutes comparable rate constants, we carried out Monte Carlo simulations of a multistep stochastic process described in Eq. 10, in which k_N is varied in relation to the other identical constants, k. For each experiment, 10,000 events were simulated from a 3- or 8-step sequential process. The event times were binned and fitted to gamma distributions to estimate the number of steps and rate constant. Gamma distribution fitting and the randomness parameter accurately determine the number of steps when k_N is equal to k (Fig. 4 A). When k_N is smaller than k, the apparent number of steps decreases sharply and is reduced to half the actual number when k_N is 10 times slower than k. The apparent N ultimately converges to a single step and is indistinguishable from a single-step process when k_N is much slower than k. In the opposite situation, when k_N more than an order of magnitude >k, the lifetimes of the slower N − 1 steps dominate p(τ), and the apparent number of steps approaches N − 1. In these cases, N must be interpreted as the number of rate-limiting steps or generally as a lower bound of the total number of steps.

Figure 4.

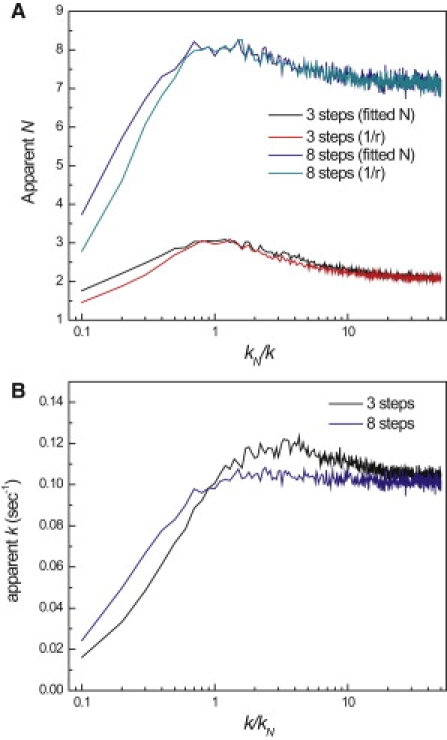
Only rate-limiting steps can be recovered from p(τ). Three- and 8-step processes were simulated in which the rate constant of the final step, k_N, was varied whereas the rate constants of the previous steps, k, were held constant at 0.1 s⁻¹. The resulting waiting time distributions were fit to gamma distributions to obtain the apparent number of (A) steps and (B) rate constant as a function of k/k_N. The inverse of the randomness parameter was also calculated as a separate measure of N (A, green and red traces). (Color version available online).

Disorder

Up to this point, we have assumed that multistep processes are defined by a set of distinct rate constants. However, a number of single molecule studies of enzyme kinetics have shown that catalytic rates of individual enzyme molecules can fluctuate by more than an order of magnitude (22–25).

Enzyme kinetics are generally described according to a two-step Michaelis-Menten model in which an enzyme reversibly binds to a substrate to form a complex ES. The product P is formed from this complex and released to regenerate the enzyme for the next cycle.

$$E+S\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}ES\stackrel{k_2}{\to }E+P\text{.}$$ (12)

Time-dependent fluctuations in the catalytic rate (k₂) of multiple enzymes have been observed and is attributed to slow interconversions between different conformational states of the enzyme molecule. In one notable example, English et al. (23) used confocal microscopy to observe the catalytic activity of single β-galactosidase molecules. Under saturating substrate conditions, the catalytic step is rate limiting, but the distribution of waiting times between enzymatic cycles did not follow a single-exponential decay. Instead, a multiexponential decay distribution was observed, showing that the catalytic rate fluctuated during the course of the experiment. The results were consistent with a kinetic model in which the enzyme slowly samples a large number of conformers, giving rise to a continuous distribution of catalytic rates (23,26).

Dispersive kinetics can potentially reveal information about the conformational dynamics of enzymes, but it can also mask the presence of multiple rate-limiting steps by increasing the spread in waiting times. To explore this effect of dynamic disorder, we carried out simulations of a two-step enzymatic reaction (Eq. 12) in which the rate constant of the catalytic steps, k₂, was allowed to randomly fluctuate according to a distribution, w(k₂). We made explicit the connection between conformational dynamics and the catalytic rate by modulating k₂ with a normally distributed transition state activation energy w(E_a) according to the Arrhenius equation.

$$w\left(k_2\right)=k_0\exp \left[-w\left(E_a\right)/k_{B}T\right]\text{.}$$ (13)

The prefactor k₀ represents the rate in the absence of a barrier; k_B and T are the Boltzmann constant and temperature in Kelvin, respectively. The association step k₁ was given a discrete value equal to the median of w(k₂) and was assumed to be irreversible (k₁ >> k₋₁).

For each simulation, values of E_a were generated from w(E_a) with a predetermined variance, and w(k₂) was calculated from Eq. 13. The effect of increasing the disorder in k₂ can be seen in waiting time distributions in Fig. 5, A–C. As the width of w(k₂) increases, the width of p(τ) also increases and gradually resembles an exponential decay. A plot of the apparent number of steps as a function the mean-square normalized variance of w(k₂) confirms this trend (Fig. 5 D). Both k₁ and k₂ are rate limiting in the sense that the median values are equal. However, the apparent number of steps tends to decrease as the dispersion in k₂ increases. Both 1/r and N begin to drop sharply when the mean square normalized variance of w(k) (σ_k2²) > 1, which is the same magnitude of disorder observed in β-galactosidase and cholesterol oxidase (23,25). The effect of disorder on the apparent number of steps is even more pronounced if both k₁ and k₂ are dispersed: 1/r and N drop rapidly for σ_k² > 0.1 (Fig. 5, E and F, red traces). Processes containing more than two steps also show the same trend (Fig. 5, E and F, green and blue traces).

Figure 5.

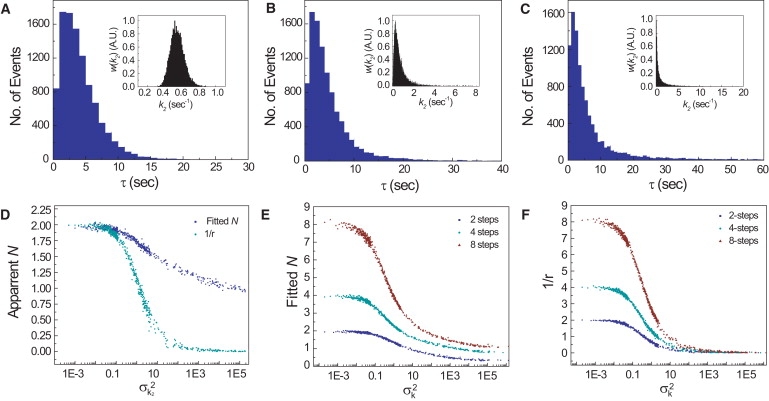
Dynamic disorder masks the presence of rate-limiting intermediate states. (A–D) Results of simulations based on a two-step enzymatic reaction (Eq. 12). The association rate, k₁, was set to 0.5 s⁻¹, and the catalytic rate constant, k₂, was allowed to fluctuate within w(k₂) distributed around 0.5 s⁻¹. The width of w(k₂) was varied to determine the effect on p(τ). (A–C) Waiting time distributions and w(k₂) (inset) in which the variance in k₂ was 0.01, 1, and 100. (D) Apparent number of steps as a function of the mean-squared variance of w(k₂) (σ_k2²). N was determined by fitting to gamma distributions (blue squares) or the inverse of the randomness parameter (green circles). (E and F) Apparent number of steps of 2-, 4-, or 8-step processes (Eq. 4) as a function of the variance of k. The rate constant, k, for each step was identically distributed with a median of 0.5 s⁻¹. (Color version available online).

In these simulations, dynamic disorder is apparent from the anomalously large r values (recall that the randomness parameter can only take values between 0 and 1 in a simple multistep mechanism). Moreover, the quality of the fits gamma distributions deteriorates as the width of p(τ) becomes large. We note that the range and number of observations of τ that can be measured in an actual experiment are typically limited. Realistic experimental limitations could mask the presence of dynamic disorder and lead to an underestimation of the number of steps.

If dynamic disorder were a general phenomenon in biochemical processes, multistep processes would be experimentally indistinguishable from processes with fewer intermediates or even reactions with a single step. The fact that multiple rate-limiting steps have been observed in several biochemical processes (14,16,18,27) suggests dynamic and static disorder of the magnitude observed may not be typical. Conversely, we may conclude that there is little kinetic dispersion in systems in which multistep kinetics are observed.

Many organisms depend on precisely timed biochemical reactions for their survival. A number of biological processes ranging from gene expression to sleep cycles in animals are regulated by circadian clocks that precisely oscillate with a 24-h period (28,29). Propagation of action potentials through and between neurons and circulation of blood via rhythmic contraction also require precise timing and coordination (30). These biological oscillators, which consist of sequences of stochastic biochemical reactions, can achieve clock-like precision as a consequence of the Central Limit Theorem. Increasing the number of exponentially distributed intermediate steps in a multistep process causes the spread in waiting times to narrow. As N becomes large, p(τ) approximates a Gaussian distribution with an increasingly small r. However, the randomness in multistep processes reappears if there is too much disorder in the intermediate transition rates. The need for precise control over the timing of these and other biological processes suggests that dynamic disorder is limited or nonexistent in many biochemical systems. Additional measurements of larger variety of systems are needed to gauge the prevalence of kinetic dispersion.

It is clear that one must be cautious in the interpretation of experimental waiting time distributions. Shot noise resulting from a finite number of observations introduces uncertainty in the determination of the number of steps in a multistep reaction. Heterogeneity in the rate constants governing individual steps requires one to interpret N as the number of rate-limiting steps. Even rate-limiting steps can be overlooked if there is significant fluctuation in transition rates for individual steps. Other analytical methods have been developed to detect intermediate steps, in which the early dwell times of p(τ) exhibits a power-law dependence on N (31). A related technique uses stabilized integral transformations to reconstruct the underlying kinetic parameters (20). However, these methods are also subject to limitations imposed by shot noise and kinetic dispersion.

We have shown that the presence of significant disorder can obscure the presence of intermediates in multistep processes. Until now, dynamic disorder has been measured in just a few biological systems. Studies of other enzymes and biochemical systems are necessary to determine whether dynamic disorder of the magnitude observed previously is a common phenomenon.