A Three-State Multi-Ion Kinetic Model for Conduction Properties of ClC-0 Chloride Channel

Abstract

A three-state, multiion kinetic model was proposed to enable the conduction properties of the mammalian channel ClC-0 to be well characterized. Using this rate-theory based model, the current-voltage and conductance-concentration relations were obtained. The five parameters needed were determined by fitting the data of conduction experiments of the wild-type ClC-0 and its K519C mutant. The model was then tested against available calculation and simulation data, and the energy differences between distinct chloride-occupancy states computed agreed with an independent calculation on the binding free energies solved by using the Poisson-Boltzmann equation. The average ion number of conduction and the ion passing duration calculated closely resembled the values obtained from Brownian dynamics simulations. According to the model, the decrease of conductance caused by mutating residue K519 to C519 can be attributed to the effect of K519C mutation on translocation rate constants. Our study sets up a theoretical model for ion permeation and conductance in ClC-0. It provides a starting point for experimentalists to test the three-state model, and would help in understanding the conduction mechanism of ClC-0.

Introduction

ClC proteins are found in both prokaryotic and eukaryotic cells. These proteins complete many important functional tasks, including the maintenance of membrane potential, the regulation of transepithelial chloride transport, and control of intravesicular pH (1). The physiological importance of these proteins can best be illustrated by the existence of hereditary diseases caused by defective ClC proteins (2).

Dutzler et al. (3) solved the three-dimensional structure of ClC proteins by resolving bacterial ClC homologs. The structure shows that the bacterial ClC protein is a homodimer and each subunit contains a pore. This double-barreled structure was already predicted based on the physiological experiments of ClC-0 (4). Three anion-binding sites surround the pore: one internal site, S_int, near the intracellular entrance to the pore; a central site, S_cen, at which chloride is coordinated by the side-chain hydroxyl of S107 and Y445; and an external site, S_ext, which is occupied by Cl⁻ when the gating residue E148 is mutated and flips out to the extracellular solution (5). Theoretical and experimental studies suggest that all three ion-binding sites can be occupied simultaneously during the open state (6,7).

The solved x-ray structure enables theoretical methods to be used to investigate the details of gating and permeation mechanisms, thus improving the study of ClC proteins at the atomic level. The most accurate method, all-atom molecular dynamics (MD), was successfully used on the study of fast gating and ion conduction (8–13). However, MD requires an expensive time commitment. The following methods have also been used: the Monte Carlo simulation to study the ion permeation pathway and fast gating mechanism (14–17), Brownian dynamics (BD) for ion conduction on a microsecond timescale (18), the continuous electrostatic calculation method to determine ion stability and analyze fast gating (7,19), and the discrete-state model to study gating (19).

Soon after Dutzler et al. (3) solved the x-ray structure, others showed that the bacterial ClC homolog is not an ion channel but rather a Cl⁻/H⁺ exchange transporter with stoichiometry 2:1 (20). Subsequently, two mammalian ClC proteins (ClC-4 and ClC-5) were suggested to be transporters (21,22). Over the years, Miller and co-workers (23–28) performed many experimental studies on the coupling property of H⁺ and Cl⁻ on the transporter EcClC. Very recently, Lisal and Maduke (29) and Mindell (30) proposed the investigations on the proton transport in ClC-0.

Although the ClC family includes two mechanistic subclasses—i.e., channels and exchange transporters—evidence indicates that the subclasses share many common features (1,31). There are many conserved residues for all ClC proteins and they play similar functional roles. For example, the gating residue E148 of EcClC is conserved for all ClC proteins excluding the ClC-K channel. In addition, the neutral S107 and Y445 residues, as well as other important charged residues in the pore, are also conserved. Therefore, the basic architecture of the bacterial ClC transporter structure can be used to investigate the function of the ClC channels (31).

Many experiments have indicated the effect of important residues on conduction in the ClC channel. For example, the charged residue K165, located at the external end of the ClC-0 pore, is important for channel conductance (32), and the mutation of the neutral residue S123T, situated at the center of the permeation pathway, reduces single-channel conductance (33). Chen and Chen (34) conducted a series of experiments to investigate the effect of the residue on the conduction of ClC-0 chloride channels. They found that the conductance of the channel decreased as the charge at position 519 became more negative, and the charge effect on the channel conductance diminished in the presence of a high intracellular Cl⁻ concentration. The charge effect is not consistent with a simple surface charge mechanism but with the electrostatic force from the residue K519, which could affect Cl⁻ interaction with the binding sites.

Despite extensive experimental data, the conduction process remains unclear. The conduction model and the qualitative theoretical description of the current-voltage and conductance-concentration relations are lacking. In addition, a theoretical understanding of how the mutation of a residue affects the conduction of the ClC channel is not yet fully developed. This article presents a simple three-state multiion kinetic model with the purpose of investigating the process of ion permeation and conduction for ClC-0 chloride channels. The results obtained from this model agree with experimental conclusions (34) and Brownian dynamics simulation data (18). This model was also tested by an independent calculation on the binding free energy by solving the Poisson-Boltzmann equation.

Computational Methods

Three-state multiion model

Both experiments and theory (6,7) suggest that ion transport in ClC is a multiion process and that all the three binding sites can be occupied simultaneously. There are four possible multiion states for ClC: state 1 (yyn, namely the sites S_int and S_cen are occupied and S_ext is empty), state 2 (nyy, S_cen and S_ext are occupied and S_int is empty), state 3 (yyy, all three sites are occupied), and state 4 (yny, S_int and S_ext are occupied and S_cen is empty). Gervasio et al. (12) investigated the chloride translocation by metadynamics and confirmed the multiion mechanism in which an ion-push-ion effect lowers the main barriers to chloride ion translocation in ClC chloride channels. They also showed that the minimum free energy path corresponds to a coordinated movement of the two ions with one ion going from S_int to S_cen and pushing the other ion from S_cen to S_ext. Therefore, state 4 is unlikely in chloride translocation. Based on these observations, we neglected state 4 and proposed a three-state multiion model for chloride ion translocation in ClC chloride channels (see Fig. 1). The translocation between state i and state j is related by the translocation rate k_ij. Fig. 2 plots the ion-permeation pore, chlorides at the binding sites, and important residues around the ion-permeation pore for the three states.

Figure 1.

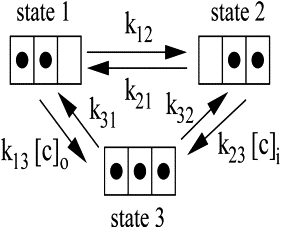
Three-state multiion model. There exist three chloride-occupied states. Each state has three chloride binding sites S_ext, S_cen, and S_int. In state 1, S_int and S_cen are occupied and S_ext is empty; in state 2, S_cen and S_ext are occupied and S_int is empty; and in state 3, all three sites are occupied.

Figure 2.

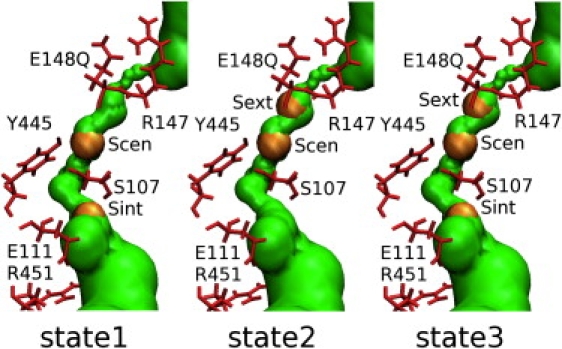
(Color online) The chloride binding sites S_ext, S_cen, and S_int in the EcClC-E148Q channel. Chlorides are represented by van der Waals balls in orange color and ion-permeation pores calculated by HOLE (51) are plotted by green pores. Several important residues around the ion-permeation pore residues are drawn by bonds in red color. In state 1, S_int and S_cen are occupied and S_ext is empty. In state 2, S_cen and S_ext are occupied and S_int is empty. In state 3, all three sites are occupied.

Expression of the ion current

We used rate theory to describe the translocation from one state to another in the three-state multiion model. Rate theory has been discussed comprehensively (35,36), and has been used to investigate conductance and selectivity of K⁺ channel (37–39). According to this theory, the kinetic equations can be determined from the state diagram as

$$\begin{array}{l}{\dot{S}}_1=k_{21}{S}_2+k_{31}{S}_3-\left(k_{12}+k_{13}{\left[C\right]}_{\text{o}}\right)S_1,\\ {\dot{S}}_2=k_{32}{S}_3+k_{12}{S}_1-\left(k_{21}+k_{23}{\left[C\right]}_{\text{i}}\right)S_2,\\ {\dot{S}}_3=k_{13}{\left[C\right]}_{\text{o}}{S}_1+k_{23}{\left[C\right]}_{\text{i}}{S}_2-\left(k_{32}+k_{31}\right)S_3,\end{array}$$ (1)

where S_i represents the occupancy probability of the i^th state (i = 1,2,3), $\stackrel{.}{S_i}=d{S}_i/dt$, [C]_i and [C]_o are intracellular and extracellular chloride concentration, respectively, and k_ij represents the translocation rate constant from state i to state j. At equilibrium or in the steady-state occupancies, the occupancy probability S_i can be determined by solving the matrix equation MS=0, where S represents the vector of occupancies and M represents the rate constant matrix obtained from Eq. 1. To satisfy the condition of single-state occupancy, we adopt the normalized occupancy probability S_i by taking S₁ + S₂ + S₃ = 1,

$$\begin{array}{l}{S}_1=\frac{k_{21}{k}_{32}+k_{31}{k}_{21}+k_{31}{k}_{23}{\left[C\right]}_{\text{i}}}{\alpha },\\ S_2=\frac{k_{12}{k}_{31}+k_{12}{k}_{32}+k_{32}{k}_{13}{\left[C\right]}_{\text{o}}}{\alpha },\\ S_3=\frac{k_{21}{k}_{13}{\left[C\right]}_{\text{o}}+(k_{12}{k}_{23}+k_{13}{k}_{23}{\left[C\right]}_{\text{o}}){\left[C\right]}_{\text{i}}}{\alpha },\end{array}$$ (2)

where α is defined as

$$\alpha =\left(k_{21}+k_{12}\right)\left(k_{31}+k_{32}\right)+\left(k_{32}+k_{21}\right)k_{13}{\left[C\right]}_{\text{o}}+\left(k_{31}+k_{12}+k_{13}{\left[C\right]}_{\text{o}}\right)k_{23}{\left[C\right]}_{\text{i}}.$$

The properties of the channel can be determined by the unidirectional translocation rate constants k_ij, among which paired rate constants are connected with each other through the relevant energy difference E_ij = E_i − E_j, where E_i represents the energy of the system at state i. With a solved forward rate constant, the backward rate can be determined; for instance (39)

$$k_{12}=k_{21}{e}^{E_1-E_2},k_{23}=k_{32}{e}^{E_2-E_3},\text{and}{k}_{31}=k_{13}{e}^{E_3-E_1}.$$

The membrane potential biases the energies of ions in the channel. Faraldo-Gómez and Roux (7) distributed the membrane potential to several segments of the channel and obtained the fraction for each segment in the ClC chloride channel. The fraction of the membrane potential δ₁ = 0.1 for the segment between the intracellular side of the channel protein and the binding site S_int; δ₂ = 0.25 for that between S_int and S_cen; δ₃ = 0.15 for that between S_cen and S_ext; and δ₄ = 0.5 for that between the site S_ext and the extracellular side of the channel protein. Assuming that the energy barrier is located at the halfway point of each segment, the rates with the transmembrane voltage v are

$$\begin{array}{l}{k}_{12}\left(v\right)=k_{12}{e}^{\frac{1}{2}\left({\delta }_2+{\delta }_3\right)\Psi },\\ k_{21}\left(v\right)=k_{21}{e}^{-\frac{1}{2}\left({\delta }_2+{\delta }_3\right)\Psi },\\ k_{23}\left(v\right)=k_{23}{e}^{\frac{1}{2}{\delta }_1\Psi },\\ k_{32}\left(v\right)=k_{32}{e}^{-\frac{1}{2}{\delta }_1\Psi },\\ k_{31}\left(v\right)=k_{31}{e}^{\frac{1}{2}{\delta }_4\Psi },\\ k_{13}\left(v\right)=k_{13}{e}^{-\frac{1}{2}{\delta }_4\Psi },\end{array}$$ (3)

where Ψ = ev/k_BT, v represents the membrane voltage, k_B the Boltzmann constant, and T the absolute temperature.

The ionic current i can be determined by considering the ion flow between adjacent states which corresponds to the transition from state 2 to state 3 or from state 3 to state 1. Thus, the ionic current is

$$i=P\left(k_{23}{\left[C\right]}_{\text{i}}{S}_2-k_{32}{S}_3\right)=P\left(k_{31}{S}_3-k_{13}{\left[C\right]}_{\text{o}}{S}_1\right),$$ (4)

where P = 1.6 × 10⁻⁷ is the conversion factor from ions/sec to picoAmps. Inserting the voltage-dependent rate constant k_ij(v) into Eq. 4, the ionic current under the transmembrane voltage v can be calculated by

$$\begin{array}{l}i\left(v\right)=P\frac{A_1-\frac{A_2}{{\left[C\right]}_{\text{i}}}}{1+\frac{A_3}{{\left[C\right]}_{\text{i}}}},\\ A_1=\frac{k_{12}\left(v\right)k_{31}\left(v\right)}{k_{12}\left(v\right)+k_{31}\left(v\right)+k_{13}\left(v\right){\left[C\right]}_{\text{o}}},\\ A_2=\frac{k_{21}\left(v\right)k_{13}\left(v\right){\left[C\right]}_{\text{o}}{k}_{32}\left(v\right)}{k_{23}\left(v\right)\left(k_{12}\left(v\right)+k_{31}\left(v\right)+k_{13}\left(v\right){\left[C\right]}_{\text{o}}\right)},\\ A_3=\frac{\left(k_{21}\left(v\right)+k_{12}\left(v\right)\right)\left(k_{31}\left(v\right)+k_{32}\left(v\right)\right)+\left(k_{32}\left(v\right)+k_{21}\left(v\right)\right)k_{13}\left(v\right){\left[C\right]}_{\text{o}}}{k_{23}\left(v\right)(k_{12}\left(v\right)+k_{31}\left(v\right)+k_{13}\left(v\right){\left[C\right]}_{\text{o}})}.\end{array}$$ (5)

Method to build EcClC-E148Q and EcClC-E148Q-R451C channel-membrane-water systems

To calculate the electrostatic binding energy, an atomic model of the chloride channel must be built. Unfortunately, the atomic structure of ClC-0 is not available. Based on the sequence similarity, EcClC's crystal structures are currently the only possible models to be cautiously used for modeling and understanding the molecular mechanisms of ClC-0 functions (7,8,11,17–19), despite the fundamental differences between ClC-0 and EcClC (28). Building the model was achieved by two steps, i.e., setting up the initial channel-membrane-water system and then achieving system equilibrium. Upon considering that no distinct binding site S_ext exists in wild-type EcClC, the open state structure of the chloride channel, EcClC-E148Q was chosen as the substitute for wild-type ClC-0 (31). Furthermore, R451 of EcClC appears to be located at a strategic position similar to K519 of ClC-0 (34), so EcClC-E148Q-R451C was used as a substitute for ClC-0-K519C. To make the model resemble the real situation, the channel should be placed in the cell membrane, and the membrane should be immersed in the aqueous solution. For convenience we first built the initial EcClC channel-membrane-water system, and then built the EcClC-E148Q and EcClC-E148Q-R451C channel-membrane-water systems.

The initial EcClC protein structure was taken from the Protein DataBank (entry code: 1OTS) (5,40). The missing hydrogen atoms were added using PSFGEN of VMD (41). Moreover, Faraldo-Gómez and Roux (7) pointed out that in the EcClC channel residues E113, H175, H281, and H284 of both chains A and B, and R417 of chain A, are protonated, so we protonated these residues using VMD. The N-terminal of each monomer was capped with a neutral acetyl group (ACE), and the C-terminal was capped with N-methyl group (CT3), leaving a charge of +13e for the dimer. In this structure, chloride ions occupied the S_cen and S_int sites in each chain.

The above EcClC channel structure was then embedded in an explicit membrane palmitoyloleoylphosphatidylethanolamine (POPE). The POPE membrane was constructed by VMD with dimensions 12 nm × 12 nm. The membrane consisted of 280 POPE molecules and each POPE molecule has 125 atoms including hydrogens. The z axis of the membrane was considered to be parallel with the twofold symmetry axis of the protein dimer. The POPE molecules that overlapped with the protein dimer were removed from the membrane. A layer of water with the thickness of 15 Å was added on both top and bottom of the membrane using VMD. Meanwhile, 18 Cl⁻ and 5 Na⁺ ions were mingled with water in order for the concentration of solution to reach 100 mM and the total charge of the system to become zero. There are four Cl⁻ ions in the dimeric protein. The whole system consisted of 142,744 atoms, among which 13,607 atoms belonged to the EcClC channel, 35,000 to the membrane, 94,110 to TIP3P water molecules, and 27 were ions. The atomic charges were obtained from the CHARMM27 force-field parameters (42).

To equilibrate the constructed EcClC channel-membrane-water system, energy minimization and molecular dynamics simulation were used. For energy minimization, the method of steepest descent was adopted to make the structure compact, by using nanoscale molecular dynamics (NAMD) (43) for 5000 steps. Then the refined system was equilibrated by MD simulation under constant NPT condition using NAMD. These simulations were carried on at the computer cluster (DAWNING TC4000). In each simulation, NAMD was run for 1 ns while restraining the positions of all protein atoms and Cl⁻ ions at the binding sites, then NAMD was run for 16 ns while allowing all atoms to be free. The force-field parameters for lipid, protein, ions, and waters were taken from the CHARMM27 force field. The periodic boundary condition was applied in all the dimensions. Long-range electrostatics was handled by using the PME algorithm. The temperature was maintained at 300 K by employing the Langevin dynamics method. The pressure was maintained at 1 atm by applying the Nosé-Hoover piston pressure control with a barostat oscillation time constant of 200 fs. The time step was 1 fs and configurations from the trajectories were saved for analysis every 1 ps.

To model the EcClC-E148Q mutant channel, the initial EcClC-E148Q channel-membrane-water system was built based on the equilibrated EcClC channel-membrane-water system. Specifically, the atomic coordinates of the mutated residue Q148 were generated by employing PSFGEN of VMD (41) and substituting Q148 for E148 in equilibrated EcClC channel-membrane-water system. It should be noted that, 1), the EcClC channel has two chains, so the E148 residue was replaced by Q148 for each chain; and 2), the E148 residue was electronegative but the mutated residue Q148 was neutral, so two Na⁺ ions were removed from the bulk electrolyte to preserve the electroneutrality of the system. Because there is also an external binding site in EcClC-E148Q, two Cl⁻ ions were moved from the electrolyte to the S_ext site of each chain. The initially built structure was then optimized to reach equilibration by using the following procedures. First, the mutant channel-membrane-water system was compacted by energy minimization for 5000 steps. Then, the compacted system was equilibrated by MD simulation. To save computational time on MD simulation, the system was divided into two regions: the affected region and the unaffected region by E148Q mutation. The affected region was defined as the region within 10 Å of E148Q, which consisted of 871 atoms. It was found that after substitution of Q148 for E148 the atomic number in the affected region was rather small. As a result, the process of equilibration was easy. We kept the atoms in the unaffected region fixed and put the atoms in the affected region of the compacted initial mutated system in equilibrium by MD simulation for 4 ns. After that, put the whole system, including the equilibrated affected region and original unaffected region, in equilibrium by MD simulation for 4 ns.

The double mutant channel, EcClC-E148Q-R451C, was built based on the above EcClC-E148Q model. Specifically, we generated the atomic coordinates of the mutated residue C451 by employing PSFGEN of VMD (41) and substituting C451 for R451 in the equilibrated EcClC-E148Q channel-membrane-water system. When the residue R451 was mutated to cysteine, the charge of the residue changed from +1 to 0. In addition, R451 was replaced with cysteine in both chains. Therefore, two Cl⁻ ions were removed from the electrolyte to preserve the electroneutrality of the system. The constructed EcClC-E148Q-R451C channel-membrane-water system was equilibrated using the same procedure as described for the initial EcClC-E148Q channel-membrane-water system.

Calculation of the electrostatic binding energy from the Poisson-Boltzmann equation

The Poisson-Boltzmann equation (44,45) is a differential equation which describes electrostatic interactions between molecules in ionic solutions. The fundamental equation in the Debye-Hückel theory (46) is a three-dimensional second-order nonlinear partial differential equation that describes the electrostatic potential Φ(r) at a field position r. This equation can be written as

$$-\nabla ·\left(\varepsilon \left(r\right)\nabla \Phi \left(r\right)\right)+{\overline{\kappa }}^2\left(\frac{k_{\text{B}}T}{e_C}\right)\sinh \left(\frac{e_c\Phi \left(r\right)}{k_{\text{B}}T}\right)=4\pi \sum _{i=1}^N{q}_i\delta \left(r-r_i\right),$$ (6)

where ɛ(r) takes appropriate values of the dielectric constants in the different regions of the model, e.g., ɛ_m in the molecular region and ɛ_w in the solution region. The modified Debye-Hückel parameter $\overline{\kappa }=\sqrt{{\varepsilon }_w}\kappa$ is proportional to the ionic strength of the solution, where κ is the usual Debye-Hückel parameter, and the modification makes $\overline{\kappa }$ dielectric-independent. The molecule consists of N atoms and the i^th atom is characterized by point charge q_i at position r_i, in the form of the δ-function. The constants e_c, k_B, and T represent the charge of an electron, Boltzmann's constant, and the absolute temperature, respectively.

Equation 6 is referred to as the nonlinear Poisson-Boltzmann equation (47), and is usually approximated by the linear Poisson-Boltzmann (PB) equation (45)

$$-\nabla ·\left(\varepsilon \left(r\right)\nabla \Phi \left(r\right)\right)+{\overline{\kappa }}^2\left(r\right)\Phi \left(r\right)=4\pi \sum _{i=1}^N{q}_i\delta \left(r-r_i\right).$$ (7)

By solving Eq. 7, the electrostatic potential Φ(r) can be obtained and the electrostatic energy can be calculated. The electrostatic energy ΔG_elec is the work required to assemble the charges q_i of the solute in the solvent, which can be expressed as

$$\Delta G_{\text{elec}}=\frac{1}{2}\sum _i^N{q}_i\Phi \left(r\right),$$ (8)

where Φ(r) refers to the electrostatic potential in the solvent environment. The electrostatic binding free energy ΔG_b,elec of ion (i) bound to a system (s) can be expressed as

$$\Delta G_{b,\text{elec}}=\Delta G_{\text{elec}}^{is}-\left(\Delta G_{\text{elec}}^s+\Delta G_{\text{elec}}^i\right),$$ (9)

where $\Delta G_{\text{elec}}^{is}$, $\Delta G_{\text{elec}}^s$, and $\Delta G_{\text{elec}}^i$ represent the electrostatic energies of the ion-occupied system, isolated ion-unoccupied system, and isolated ion, respectively, in the solvent environment. Illustration of Eq. 9 is given in Fig. 3.

Figure 3.

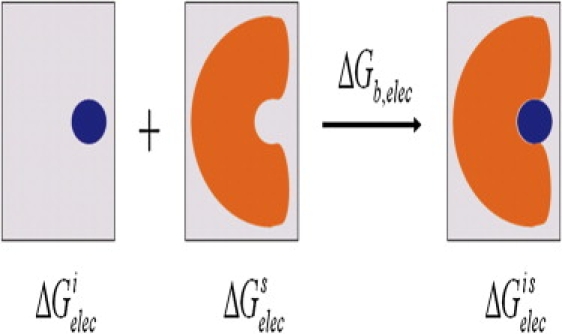
Illustration of calculating variation in the electrostatic binding free energy. When an isolated ion (plotted in blue) is embedded in an ion-unoccupied system (in orange), an ion-occupied system forms and the difference in the electrostatic component of the total free energy is $\Delta G_{b,elec}$, the electrostatic binding free energy. These three systems are in a solvent dielectric medium (in gray).

Method to solve the Poisson-Boltzmann equation

To obtain the numerical solutions of the linear Poisson-Boltzmann equation, we employed software APBS 0.5.0 (48), in which a finite element method with a multigrid (49) was used. Specifically, the automatically configured sequential method was applied. The APBS parameters were set as follows. The number of grid points was 161 × 161 × 129. The size of the coarse grid region was 130 × 130 × 110 Å. The size of the focusing fine grid region was 40 × 40 × 40 Å. A dielectric constant of 4 was assigned to the interior of the region, which represented the all-atom structure and was defined by molecular surface and harmonic average smoothing. The molecular surface was constructed by using a water probe radius of 1.4 Å. For the solvent, a dielectric constant of 78 was employed. The temperature of the system was set to 300 K (room temperature). The single Debye-Hückel boundary condition was used. As a usual method for assigning charge distributions on a grid, the atomic charges were mapped onto the nearest-neighbor grid points.

Results and Discussions

Determination of the parameters of the model

The parameters of the three-state multiion kinetic model were determined by fitting Eq. 5 into the experimental data of the current-voltage relations for the wild-type ClC-0 and its K519C mutant. The rate constants obtained by fitting are listed in Table 1. There are only five fitting parameters k₂₁, k₂₃, k₃₁, k₃₂, and k₁₃, based upon which the dependent parameters are obtained. For example: the sixth rate constant k₁₂ = 0.60 (for ClC-0-WT) and 0.70 (for ClC-0-K519C), which are the energy differences between two states of E₁₂ = −1.19 and 0.11; E₃₂ = −1.55 and 1.00; and E₃₁ = −0.35 and 0.8 kcal/mol for ClC-0-WT and ClC-0-K519C, respectively. The fitting and experimental (34) current-voltage curves are plotted in Fig. 4. In this figure the solid lines represent the result of this model and the symbols denote experimental data. In addition, the current-voltage relations of simulating by BD (18) and fitting by this model are shown in the inset of Fig. 4 a with the experiments (4). It follows from this inset that the conductance is 11.3 pS (from the BD simulation (18)), 10.1 pS (from our model), and 9.4 pS (from the experiment (4)), which are consistent.

Table 1.

The translocation rate constants of the three-state multi-ion kinetic model

	k13	k21	k23	k31	k32
ClC-0-WT	15.8	4.5	19.4	8.7	1.4
ClC-0-K519C	3.1	0.58	2.0	13.9	10.8

The translocation rate constants of the three-state multiion kinetic model determined by fitting Eq. 5 into the experimental conductance for the wild-type ClC-0 channel and its K519C mutant (34). The unit of the rate constant is 10⁷ s⁻¹ (for k₂₁, k₃₁, and k₃₂) and 10⁷ s⁻¹ M⁻¹ (for k₁₃ and k₂₃).

Figure 4.

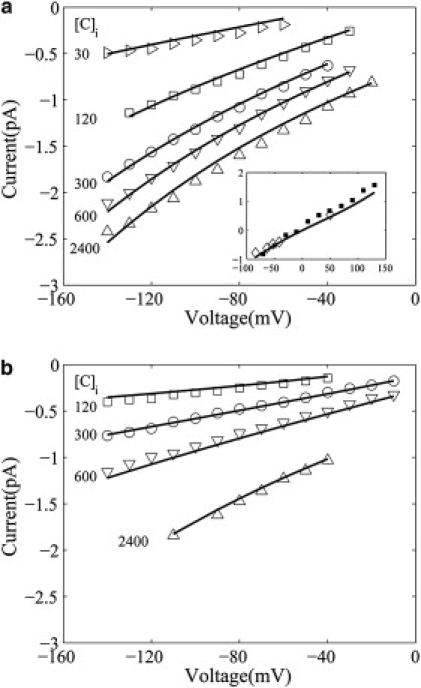
Current-voltage curves of wild-type ClC-0 channel (a) and its K519C mutant (b) for a series of the intracellular chloride concentration [C]_i at the extracellular chloride concentration [C]_o = 120 mM. (Solid lines) Plots of Eq. 5, and (symbols) experimental data by Chen and Chen (34). (Inset) Current-voltage relation of the wild-type ClC-0 channel at [C]_i = [C]_o= 150 mM. (Solid squares) Brownian dynamics simulation (18); (open diamonds) Miller's experimental data (4).

By fitting data between −50 and −110 mV in the I-V plots in Fig. 4 to straight lines, the conductance of wild-type ClC-0 and its K519C mutant can be estimated. Fig. 5 shows the conductance-concentration relation for the wild-type ClC-0 and its K519C mutant. The experimental data and the conductance values calculated from Eq. 5 are in nice agreement.

Figure 5.

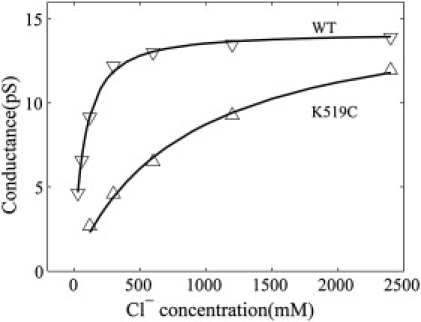
Conductance-concentration relation of wild-type ClC-0 channel and its K519C mutant. The extracellular chloride concentration [C]_o = 120 mM. (Solid lines) Plots of Eq. 5 and (symbols) experimental data by Chen and Chen (34).

It can be seen from fitting parameters listed in Table 1 that, as the K519C mutation takes place in the ClC-0 channel protein, the translocation rate constants k₂₁, k₂₃, and k₁₃ decrease, while k₃₂ and k₃₁ increase. This behavior can be understood as follows. As K519C mutation takes place, the electropositive residue K519, which resides near S_int, mutates to the neutral residue C519. Before mutation, the electropositive residue K519 exhibits an attraction for Cl⁻ and hinders the translocation of Cl⁻ from S_int to the intracellular side, from S_int to S_cen, and from S_cen to S_ext, as well as from S_ext to the extracellular side. After mutation, the neutral C519 residue does not attract Cl⁻. As a consequence, K519C mutation makes the translocation of Cl⁻ from S_int to the intracellular side (indicated by k₃₂) and from S_ext to the extracellular side (indicated by k₃₁) easier, so that k₃₂ and k₃₁ increase. In the meantime, K519C mutation makes the translocation of Cl⁻ from the intracellular side to S_int (indicated by k₂₃), from the extracellular side to S_ext (indicated by k₁₃), and the combined translocation from S_int to S_cen and from S_cen to S_ext (indicated by k₂₁) more difficult; thus, k₂₃, k₁₃, and k₂₁ decrease.

As stated above, the three-state multiion kinetic model can accurately describe the conductance of the ClC-0 channel. In the following subsections, we will show that this model can also accurately describe other conduction properties.

Test for the model: average ion number and ion passing duration

To test this, the average ion number and ion passing duration were calculated using our present model and compared to those obtained by BD simulation. This model contains three occupancy states. For states 1, 2, and 3, the ion occupancy numbers are 2, 2, and 3 and the normalizing occupancy rates are S₁, S₂, and S₃, respectively. Therefore, the average ion number is

$$\overline{n}=2S_1+2S_2+3S_3.$$ (10)

On the other hand, the average ion number can be directly obtained by BD simulation. Formerly, Corry et al. (18) made BD simulations of conduction of chloride in the ClC-0 channel based on the x-ray structure data of EcClC channel and putting two ends of the channel in saline solution with intracellular and extracellular concentrations of 150 mM. They obtained the current-voltage relations, the average number, and the average entering and expelling time of ions. In the BD simulation, the ClC-0 channel contained, on average, 2.3 ions in the conducting state with a voltage of −80 mV and intracellular and extracellular chloride concentrations of 150 mM (18). In the case with v = −80 mV and [C]_i = [C]_o = 150 mM, the calculated state probability by Eq. 2 are S₁ = 0.77, S₂ = 0.16 and S₃ = 0.07, so our model gives the average ion number $\overline{n}=2S_1+2S_2+3S_3$ = 2.07 in a ClC-0 pore.

Compared with experimental measurements, the effect of 150 mM of Cl⁻ is roughly equivalent to that of 60 mM of Br^- (36). According to Fig. 3 C of Lobet and Dutzler (6), the estimated average ion number is ∼(0.7 + 0.8 + 0.9) ∼2.4. Thus, the calculated ion number obtained by using our model closely resembles the number estimated from the experimental measurements.

In our model, Eq. 4 represents the ionic current i. The ion passing duration, defined as the time for the ion to cross the channel, is then calculated by

$$\tau =\frac{P}{i}=\frac{1}{k_{23}{\left[C\right]}_{\text{i}}{S}_2-k_{32}{S}_3}=\frac{1}{k_{31}{S}_3-k_{13}{\left[C\right]}_{\text{o}}{S}_1}.$$ (11)

The ion-throughput rate is r = 1/τ. In the case of v = −70 mV and [C]_i = [C]_o = 150 mM for ClC-0 channel, τ was 212 ns calculated by Eq. 11, and therefore r = 4.72 × 10⁶ s⁻¹. The predicted value of the ion-throughput rate for ClC-0 awaits experimental verification.

Test for the model: changes of binding energies caused by mutation

In addition to the test by BD simulation, a comparison with an independent approach in solving the PB equation was made. Without a doubt, the change in the binding energy of chloride caused by mutation of a certain residue is an important quantity to evaluate the effect of this residue on the function of the channel. The change of the binding free energy can be obtained via our model. According to this model, the transition from state 3 to state 1 corresponds to the chloride moving from binding site S_ext to the extracellular solution (see Fig. 1). Therefore, the change of energy from state 1 to state 3 (E₃₁) corresponds to the binding free energy of chloride at the binding site S_ext of the channel. Analogously, E₃₂ corresponds to the binding free energy of chloride at S_int (i.e., E_b,ext = E₃₁ and E_b,int = E₃₂). When the residue K519 mutates to K519C in ClC-0, the energy of the system will vary whether for state 1, 2, or 3. According to our model and denoting the values for mutants by prime, the change of binding energy caused by the mutation of K519 can be obtained as

$$\Delta E_{b,\text{ext}}=E_{31}-E_{31}^{\prime }=-1.24\text{kcal}/\text{mol},{\text{at}S}_{\text{ext}},$$

$$\Delta E_{b,\text{int}}=E_{32}-E_{32}^{\prime }=-2.55\text{kcal}/\text{mol},{\text{at}S}_{\text{int}}\text{.}$$ (12)

On the other hand, the binding free energy of chloride can also be calculated by solving the PB equation. The binding free energy includes polar (electrostatic) and nonpolar contributions, so the binding free energy can be described as

$$\Delta G_b=\Delta G_{b,\text{elec}}+\Delta G_{b,\text{np}},$$ (13)

where $\Delta G_{b,\text{np}}$ is the change in the free energy of the nonpolar term and $\Delta G_{b,\text{elec}}$ is the electrostatic term. The change of the nonpolar term is caused by mutation and corresponds to the cavity formation. Compared to the wild-type structure, the mutated structure experiences a very small change in volume, so we assume that the change of nonpolar contribution caused by mutation can be ignored. Then the change of binding free energy by mutation can be described as

$$\Delta \Delta G_b=\Delta G_{b,\text{elec}}-\Delta G_{b,\text{elec}}^{\prime },$$ (14)

where prime denotes the quantity belonging to the mutant. The electrostatic binding free energy $\Delta G_{b,\text{elec}}$ and $\Delta {G^{\prime }}_{b,\text{elec}}$ can be calculated by Eq. 9.

Usually the function of ClC-0 is investigated at an atomic level through the structure of bacterial homolog, but only x-ray structure data exists for the bacterial ClC channel homolog at high resolution (31). It is likely that residue K519 of ClC-0 corresponds to the residue R451 of EcClC because both positively charged residues are located at the intracellular end of the ion-transport pathway (34). Therefore, others have used the change of electrostatic binding free energy caused by the mutation of the residue R451 in EcClC instead of the change caused by the mutation of K519 in ClC-0. As there is no distinct binding site S_ext in wild-type EcClC, we chose the open state structure of chloride channel, EcClC-E148Q, as the substitute. By using the all-atom electrostatic calculation and solving the Poisson-Boltzmann equation, we obtained the electrostatic binding energies $\Delta G_{b,\text{elec}}$ and $\Delta {G^{\prime }}_{b,\text{elec}}$ = −16.03 and −14.55 (at S_ext), −10.62 and −8.20 (at S_int) kcal/mol, respectively. As a result, the changes of the binding energy caused by the mutation of the residue R451 in EcClC-E148Q channel is

$$\begin{array}{l}\Delta \Delta G_b=-1.48\text{kcal}/\text{mol}\text{at}{S}_{\text{ext}},\\ \Delta \Delta G_b=-2.42\text{kcal}/\text{mol}\text{at}{S}_{\text{int}}.\end{array}$$ (15)

Comparing Eq. 15 with Eq. 12, it can be seen that the changes of the binding energy calculated by solving the PB equation closely match those projected by our model.

Table 2 sums up the average computed ion number, ion passing period, and change of the binding free energies caused by K519C mutation of ClC-0 by using our model and other methods. It shows that the results of our model resemble the available data of other methods.

Table 2.

Comparisons of the results from our three-state multi-ion kinetic model with the results from other methods

	n(ion)	ΔEb,ext	ΔEb,int
Model in this article	2.07	−1.24	−2.55
Other methods	2.4exp	−1.48PB	−2.42PB

Comparisons of the results from our three-state multiion kinetic model with the results from other methods: average ion number achieved in Brownian dynamics (BD) simulation (18), experimental ion-throughput rate (36), and our all-atom calculation of the change in binding energy at S_ext and S_int by solving the linear Poisson-Boltzmann (PB) equation. The change of the binding energy is caused by mutation K519C of ClC-0. The unit of energy is kcal/mol.

Recently, Picollo et al. (50) reported thermodynamic parameters for Cl-binding to EcClC measured with isothermal titration calorimetry. The apparent affinities obtained from the isothermal titration calorimetry measurements were assumed to be close to the binding affinities by neglecting possible conformational changes of EcClC upon Cl⁻ binding. They found that E148A mutation surprisingly increases the Cl⁻ apparent binding affinity for the protein and suggested that increasing the occupancy of the pore increases Cl⁻ affinity. It is worthwhile to investigate the effect of different mutations on Cl⁻ binding energies and occupancy of the pore in future theoretical studies.

Conclusions

A three-state multiion kinetic model has been developed to describe the conduction properties of the ClC-0 chloride channel, with very few parameters. Despite the simplicity of the model, it can accurately describe the conduction properties of the ClC-0 chloride channel. The results predicted by this model are consistent with the experimental data, BD simulation, and our all-atom calculation of the change in electrostatic binding energy by solving the Poisson-Boltzmann equation. This model also reveals why the residue K519C mutation reduces conduction. In the ClC-0 channel, the positively charged residue K519 resides near the internal binding site S_int and imposes an attraction for Cl⁻. After the mutation, the neutral residue cysteine substitutes for the lysine. The neutral residue does not attract Cl⁻ and therefore the K519C mutation makes the translocation of Cl⁻ toward residue 519 more difficult and the translocation away from 519 easier. In summary, our model can be used to investigate conduction properties and the effect of residue mutations on the function of the ClC-0 channel.