Mechanical Properties of a Complete Microtubule Revealed through Molecular Dynamics Simulation

Abstract

Microtubules (MTs) are the largest type of cellular filament, essential in processes ranging from mitosis and meiosis to flagellar motility. Many of the processes depend critically on the mechanical properties of the MT, but the elastic moduli, notably the Young's modulus, are not directly revealed in experiment, which instead measures either flexural rigidity or response to radial deformation. Molecular dynamics (MD) is a method that allows the mechanical properties of single biomolecules to be investigated through computation. Typically, MD requires an atomic resolution structure of the molecule, which is unavailable for many systems, including MTs. By combining structural information from cryo-electron microscopy and electron crystallography, we have constructed an all-atom model of a complete MT and used MD to determine its mechanical properties. The simulations revealed nonlinear axial stress-strain behavior featuring a pronounced softening under extension, a possible plastic deformation transition under radial compression, and a distinct asymmetry in response to the two senses of twist. This work demonstrates the possibility of combining different levels of structural information to produce all-atom models suitable for quantitative MD simulations, which extends the range of systems amenable to the MD method and should enable exciting advances in our microscopic knowledge of biology.

Introduction

Microtubules (MTs) are ubiquitous biological filaments found in all eukaryotic cells. The largest type of cytoskeletal filament, MTs are critical to many cellular functions, including positioning of the centriole, providing a track for biological motors to enable organelle motility, forming the mitotic spindle during M-phase of eukaryotic cell division, and providing the mechanical core of eukaryotic flagella, cilia, and the axons of neuronal cells (1). Because of their essential role in cellular function, especially during cell division, MTs are the target of many cancer treatments. By disrupting the MT structure, drugs such as taxol and vinblastine dramatically alter the dynamics of MT assembly and disassembly, either stabilizing (in the case of taxol) or destabilizing (vinblastine) the structure and leading to cell death (2). Several applications of MTs in bionanotechnology have been suggested as well (3,4).

The basic building block of an MT is the αβ-tubulin dimer, shown in Fig. 1 A. The dimers associate end-to-end, forming so-called protofilaments (PFs). Because of the heterogeneous nature of the αβ-tubulin dimer, PFs have a polarity. An MT, then, consists of a number of parallel PFs, and is itself polar, with a plus- and a minus-end, as shown in Fig. 1 B. In vivo, MTs are most often composed of 13 PFs, in which case the PFs are parallel to the MT axis. In vitro MTs, on the other hand, may comprise anywhere from 11 to 17 PFs (5).

Figure 1.

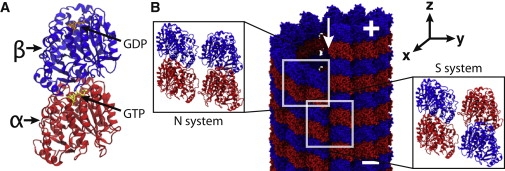
Microscopic model of a tubulin dimer and a microtubule (MT). (A) The αβ-tubulin dimer. The α-tubulin (bottom) and β-tubulin (top) are shown in cartoon representation, and GTP and GDP are shown in licorice representation. (B) All-atom model of an MT. The protofilaments (PFs) form α-β lateral contacts at the seam of the MT (indicated by the arrow) and α-α and β-β lateral contacts in the rest of the MT. These two types of the PF contacts are studied using two systems: N (normal) and S (seam), shown in the insets.

The all-atom structure of αβ-tubulin was solved some time ago (6), and later refined (7), showing α- and β-tubulin to be structurally very similar to one another, and revealing the binding site of taxol, which was used to stabilize the structure during crystallization. The tubulin in these studies was crystallized in antiparallel sheets, rather than parallel tubes as in an MT. Thus, while the longitudinal bonds within the PFs presumably represent those found in MTs, the same cannot be said for the lateral bonds between PFs. These lateral bonds are thought to play a vital role in MT structure and dynamics, as highlighted by the position of taxol very near the lateral interface (7). More recently, the structure of a complete MT was solved at 8 Å resolution using cryo-electron microscopy (cryo-EM) techniques (8). Although it is not of atomic resolution, this map is detailed enough to show the arrangement of the secondary structural elements of tubulin in MT form.

Due to their structural importance, the mechanical properties of MTs have been extensively studied (9–14). However, because of the small size of MTs and their high rigidity, the experimental studies have mainly relied either on measurement of flexural rigidity using MT bending or buckling (9–11), or on some variation of radial indentation of the MT wall (12–14). In both cases, the Young's modulus is only arrived at indirectly, and depends on the choice of elastic model used during analysis. Indeed, estimates of the Young's modulus have varied wildly, spanning almost four orders of magnitude (12,15). More-sophisticated anisotropic elastic models have helped reconcile discrepancies in the reported moduli (15), but precise investigation of MT elasticity remains a daunting experimental challenge.

The molecular dynamics (MD) method allows the elastic properties of a biopolymer to be determined computationally (16,17). Successful examples include systems such as titin (16), ankyrin (17), cadherin (17), actin (18), spectrin (19), collagen (20), and DNA (21). Although elastic (15,22), molecular-mechanics (23), and finite-element (15) models can be used to interpret the results of experiments, relating the atomic structure of an MT to its mechanical properties requires an all-atom approach. There have already been a number of all-atom studies that investigated the energetics of inter-PF interactions (24,25), the effect of GTP hydrolysis on intrinsic dimer bending (26), the effect of the drug taxol on tubulin flexibility (27), and the elastic moduli of individual tubulins (28). Nevertheless, modeling the entire MT has not been (until now) accomplished because of the sheer size of the system and the lack of an atomic resolution structure.

In this study, using a variation of a recently reported technique (29), we built an all-atom model of a complete MT by fitting the atomic model of αβ-tubulin into the cryo-EM map of a complete MT. We used the obtained structure to study the mechanical properties of a complete MT subject to longitudinal extension and compression, radial indentation, and twist deformations. The calculated elastic moduli were found to be in agreement with available experimental data. This study is one of the first to utilize cryo-EM-fitted structures for all-atom molecular dynamics, demonstrating the usefulness of the technique and expanding the range of systems amenable to simulation using MD.

Materials and Methods

MD methods

All simulations were performed using the software package NAMD (30), 1–2–4-fs multiple timestepping, CHARMM27 parameters (31) with CMAP corrections (32), a 10–12 Å cutoff for van der Waals and short-range electrostatic forces, and the particle-mesh Ewald method for long-range electrostatics computed over a 1.0 Å-spaced grid. The temperature was maintained at 310 K using the Langevin thermostat with a damping constant of 1.0 ps⁻¹. For NpT simulations, the Langevin piston method was used, with a period of 200 fs and a decay of 100 fs. Parameters for GDP and GTP were adapted from those for ADP and ATP, respectively. Flexible fitting was performed using the Grid-Steered Molecular Dynamics feature of NAMD (33). A custom anisotropic pressure protocol was implemented in NAMD to independently control the diagonal components of the pressure tensor (21). Visualization and analysis were performed using VMD (34).

Initial structural data

Coordinates for αβ-tubulin were taken from the Protein Data Bank, code 1JFF. The αβ-tubulin was crystallized in antiparallel sheets and originally resolved to 3.7 Å resolution (6) and later refined to 3.5 Å resolution (7). The structure includes αβ-tubulin, GDP, GTP, and an Mg²⁺ ion in the GTP binding pocket. Taxol, used to stabilize the structure, was removed.

A cryo-EM map of a 13-PF MT at 8 Å resolution (8) was provided by the lab of Kenneth H. Downing. At this resolution, α- and β-tubulin are indistinguishable, and therefore 13-fold helical symmetry was utilized in making the map.

The 1JFF structure is missing coordinates for residues 35–60 of α-tubulin. Therefore, we used an alternative tubulin structure, PDB code 1SA1 (35), for residues 35–39 and 45–60. Coordinates for residues 40–44 were missing from the alternative structure as well; however, the remaining gap was near the stretched length of five amino acids, and the coordinates were therefore reconstructed using the Molefacture plugin in VMD (34). This region is located on the inner microtubule surface and, by using the NCBI's Conserved Domain Database (36), is seen to be poorly conserved across species. Residue 1 of α- and β-tubulin were both missing as well; their coordinates were taken from the structure PDB code 1TUB (6).

Construction of the N and S systems

The N and S systems were built to contain two PFs each in a simulation cell (Fig. 1 B). Each PF was made of one αβ-tubulin dimer. Through periodic boundary conditions (PBC), the PFs were effectively infinite.

Coordinates for one PF were obtained by rigid-fitting the tubulin dimer to a subset of the cryo-EM map using the CoLoRes program (37) with a 2° step and Laplacian correlation. The original map was a 200 × 200 × 96 grid (∼1.7 Å/gridpoint), which was trimmed to the range [54, 148] in x, [14, 59] in y, and [0, 74] in z, for a 95 × 46 × 75 grid. The grid size corresponds, approximately, to the cross section of three PFs, and a height of three monomers. The best fit from CoLoRes was used. Coordinates for a second PF were obtained from the first by geometric transforms consistent with the MT helical lattice, i.e., a rotation of 360°/13 about the map center, and an axial displacement of (3/2) × 81.2 Å/13. This became the N system. The S system was then obtained from the N system by the exchange of α- and β-tubulin, and their associated nucleotides, in the second PF. Due to PBC, this is the equivalent of an axial shift of 40.6 Å or one monomer.

To place water and ions, we constructed two additional systems that had an extra monomer on the minus-end of each PF (see Fig. S1 in the Supporting Material). Coordinates for the extra monomers (two β-tubulins for the N system, one α-tubulin and one β-tubulin for the S system) were obtained by shifting the coordinates of the monomers and nucleotides by 81.2 Å in the –z direction. The water placement procedure and the protonation states of the histidines are detailed in the Supporting Material. The SOLVATE program (38) was used to place ions in isotonic Debye-Hückel concentration. Next, the extra monomers and nucleotides were removed; water and ion atoms were trimmed to conform to the 81.2 Å dimension of the system in the z direction. The resulting assembly was embedded in a rectangular volume of preequilibrated water using the Solvate plugin in VMD. The final systems contained 80 K⁺ and 10 Cl⁻ ions each (corresponding to an ∼190 and ∼24 mM concentration of K⁺ and Cl⁻ ions, respectively), measured 134 × 94 × 81.2 ų, were electrically neutral, and were comprised of ∼98,000 atoms.

After minimization and 1-ns equilibration in the NVT ensemble, the cryo-EM map of a complete MT was used as an external potential to refine the conformation of the PFs. The original 200 × 200 × 96 gridpoint map was trimmed to the range [54, 118] in x, [14, 59] in y, and [0,47] in z, producing a 65 × 46 × 48 grid. The grid values were then inverted, shifted, and rescaled to the range [0, 0.1]:

$$V_{ijk}^{\text{rescaled}}=0.1\text{kcal}/\left(\text{mol}·\text{amu}\right)·\left[2-\left(V_{ijk}-V_{\min }\right)/\left(V_{\max }-V_{\min }\right)\right]\text{.}$$ (1)

The forces derived from the potential were multiplied by the mass of the protein's or the nucleotide's atoms. The typical scale of the features in the resulting potential was ∼k_BT. Both systems were simulated for 5 ns, subject to the potential. Harmonic restraints of 200 kcal/mol·rad were imposed on the dihedral angles of all α-helical and β-sheet fragments of the protein to maintain the secondary structure and avoid overfitting (29). Subsequent equilibration is described in Results and Discussion.

Construction of the infinite MT system

The initial model of a complete MT was built by assembling 12 copies of the α₁-β₁ PF from the N system and one copy of the α₁-β₁ PF from the S system along with the solvent into 2π/13 radial sectors of the MT. The atomic coordinates of the PFs were taken from the states attained at the end of equilibration-III (Fig. 2; and see Results and Discussion). Additional water and ions were added, producing a 300 × 300 × 81.2 ų system of ∼750,000 atoms. The MT was effectively infinite due to PBC.

Figure 2.

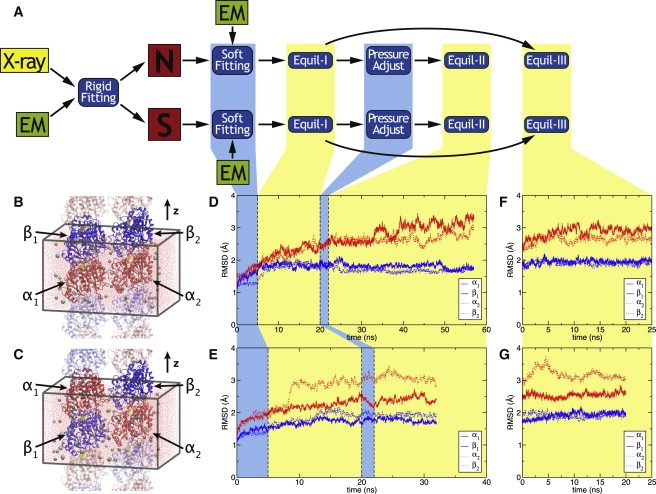
Construction of the 2-PF systems. (A) Outline of the procedure. (B and C) N (B) and S (C) all-atom systems. Through periodic boundary conditions, the PFs are effectively infinite. Periodic images of the protein are shown translucently. The α-tubulin and β-tubulin are shown in cartoon representation, GTP and GDP in licorice representation, and ions as spheres. Boxes indicate the periodic cell. (D and E) Backbone RMSD of N (D) and S (E) system from the initial structures. Traces are shown for α₁, β₁, α₂, and β₂ as labeled. (Vertical dashed lines) Different simulation phases (from left to right): flexible fitting, equilibration with L_z fixed to the crystal value (equilibration-I), P_zz adjustment, and equilibration with L_z free to change (equilibration-II). (F and G) Backbone RMSD of N (F) and S (G) system during extension of equilibration with L_z fixed (equilibration-III.) The color scheme is the same as in D and E.

The interface between the PFs was adjusted using the coordinates of the α-α, β-β, and α-β interfaces in the equilibrated N and S systems as a template. To produce the target coordinates for the interfaces, the N and S systems after equilibration-III were again simulated with Grid-Steered Molecular Dynamics for 5 ns, using the same parameters as during the flexible fitting stage, ensuring that the angle and axial alignment between the two PFs matched that required for a 13-PF MT. Coordinates of atoms corresponding to a 2π/13 radian sector centered on the center-of-mass of the two PFs were then taken from each system. The target structure was constructed from 12 copies of the N system interface coordinates and one copy of the S system interface coordinates, shown in Fig. 4 B. The interface fitting was performed using the following harmonic restraint potential applied to all heavy atoms of the PFs:

$$U=-\sum _{i}k{\beta }_i{\left({\mathbf{r}}_i-{\mathbf{r}}_{i,0}\right)}^2/2.$$ (2)

where r_i and r_i,0 are the current and reference positions of the ith atom, respectively.

Figure 4.

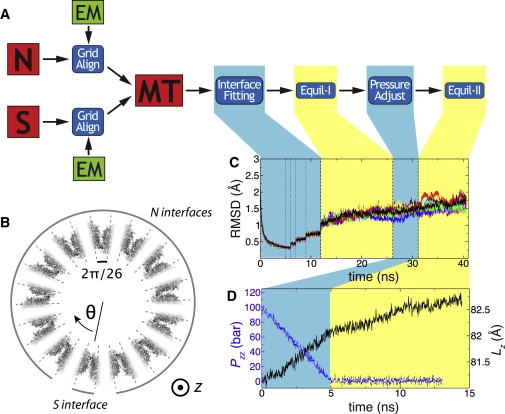
Construction of the MT system. (A) Outline of the procedure. (B) A view of the MT system from the +z direction. The MT structure is shaded according to the proximity of its atoms to the PFs' interface: the darker the shading, the closer the atom is to the interface. During the interface fitting procedure, atoms shown in black were subject to maximum restraints, while atoms shown in white were unrestrained (see Materials and Methods). (C) RMSD of the interface's backbone atoms from their target coordinates during interface fitting, equilibration with L_z fixed, pressure adjustment, and free equilibration simulations, excluding residues 35–60 of α-tubulin. Each trace shows the RMSD value of a single interface (13 traces total are shown), defined as a 2π/26-radian sector in panel B. The vertical dotted lines in the interface fitting part indicate simulations carried out using different restraint scaling factors (see Materials and Methods). (D) L_z (solid line) and P_zz (dashed line) of the MT system during pressure adjustment and equilibration simulations. The scales for L_z and P_zz are shown on the right and left vertical axes, respectively.

The scaling factor β_i = [1 + cos(13θ_i)]/2, where θ_i is the radial angle of atom i with respect to the MT seam (visualized in Fig. 4 B), was introduced to accentuate the restraint potential at the interface atoms. Note that in the initial model of the MT, half of all interface atoms already had the target coordinates. The restraints were applied linearly increasing the spring constant from k = 0 to 1 kcal/mol·Å over 5 ns. A value of k = 1.0 kcal/mol·Å was then maintained for 1 ns, after which simulations with k = 0.3, 0.1, and 0.03 kcal/mol·Å were carried out sequentially over 1, 2, and 2.88 ns, respectively. In total, the interface adjustment simulations lasted 11.88 ns and were performed with L_z of the periodic cell fixed at the value suggested by the crystal structure of tubulin.

Construction of the finite MT system

The structure used for the twist simulations was constructed by combining three copies of the unit cell of the infinite MT system with a fourth copy that contained only the solvent, using the set of coordinates obtained at the end of equilibration-II (see Fig. 4). To minimize the extent of the system along the z axis, some monomers were shifted by 3 L_z in the –z direction, as shown in Fig. 6 A. That system was solvated and ionized, producing an electrically neutral system of ∼2.83 million atoms.

Figure 6.

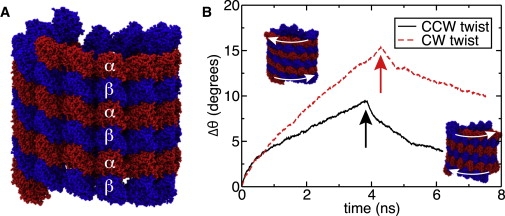
Twist simulations. (A) Finite-length MT system, at the beginning of the twist simulations. (B) Total angular displacement of the microtubule's terminal monomers in the simulations of the counterclockwise (solid line) and clockwise (dashed line) twist deformations, as seen from +z direction. The arrows indicate the moment when the twisting forces were set to zero and the structures were allowed to relax.

Stress calculation

Under the anisotropic pressure condition P_xx = P_yy ≠ P_zz, the difference ΔP ≡ P_zz – P_xx must be borne by the PFs (21). The total force on the PFs is then ΔP multiplied by the cross-sectional area of the system:

$$f\left(t\right)=\left[P_{\mathit{zz}}\left(t\right)-1\text{bar}\right]·L_x\left(t\right)L_y\left(t\right).$$ (3)

The stress on the PFs is the negative of this divided by the cross-sectional area of the PFs,

$$\sigma \left(t\right)=-f\left(t\right)/N_{\text{PF}}{A}_{\text{PF}}=-\left[P_{zz}\left(t\right)-1\text{bar}\right]\times L_x\left(t\right)L_y\left(t\right)/N_{\text{PF}}{A}_{\text{PF}},$$ (4)

where N_PF is the number of PFs, either 2 for the N and S systems or 13 for the MT system, and A_PF is the cross-sectional area of a PF, taken as 50 × 50 Å². Strain was computed as ε(t) = [L_z(t) – L_z,₀]/L_z,₀, where L_z,₀ is the equilibrium length of the periodic cell along the PFs, taken as 83.92 Å for the N and S systems and 83.08 Å for the MT system (see Results and Discussion).

Radial compression

To model the radial compression experiments, we defined the compression force acting on atom i as a moving step function directed toward a plane passing through the MT axis:

$${\mathbf{f}}_{\mathit{i}}\mathbf{=}-{\mathit{f}}_{\mathbf{0}}\mathbf{n}\left({\mathbf{r}}_{\mathit{i}}·\mathbf{n}\right)/\left|{\mathbf{r}}_{\mathit{i}}·\mathbf{n}\right|$$

when |r_i·n| ≤ d₀ − vt, and

$${\mathbf{f}}_{\mathit{i}}=0$$

otherwise.

Here |r_i·n| is the distance of atom i from the plane (the MT axis passes through the origin of our coordinate system); f₀ = 100 pN; d₀ = 140 Å; v = 12.5 Å/ns; and n is the unit vector normal to the plane. The force was applied to all heavy atoms of tubulin using the TclBC feature of NAMD (39).

Twist

The twist deformation was produced by forcing the tubulin monomers located at the ends of the finite MT system to rotate in opposite directions. The force on atom i was computed as

$${\mathbf{f}}_{\mathit{i}}=C\gamma \left({\mathbf{r}}_{\mathit{i}}\right)\left(\mathbf{k}\times {\mathbf{r}}_{\mathit{i}}\right)m_i/M,$$ (5)

where C = ±1 kcal/mol·Å², γ (r_i) = ±1 for the atoms located at the plus (+) and minus (–) ends of the MT, k was the unit vector directed along the MT axis, m_i was the i^th atom mass, and M was the total mass of all forced atoms. To maintain the integrity of the tubulin monomers subject to the external force and whose ends were exposed to solvent, some backbone dihedral angles were harmonically restrained with a spring constant of 400 kcal/mol·rad, using the “extrabonds” feature of NAMD. Specifically, the dihedral restraints were applied to the atoms of the terminal monomers located closer to the MT ends than the center-of-mass of the respective monomers.

Results and Discussion

To build the atomic resolution model of a complete MT, we constructed two 2-PF systems, referred to as N (for normal) and S (for seam), that represented the two types of inter-PF interactions found in a complete MT (Fig. 1 B). Specifically, the N system features lateral bonds between like-monomers, i.e., α-α and β-β bonds, whereas the S system features lateral bonds between unlike monomers, i.e., α-β and β-α bonds.

Construction and equilibration of the N and S systems

The procedure for construction of the N and S systems is outlined in Fig. 2 A. The crystal structure for αβ-tubulin was first rigidly fit to the cryo-EM density map to produce the initial structures. Flexible fitting was then performed to conform the atomic coordinates of the PFs to the cryo-EM density map of the complete MT. These steps are detailed in Materials and Methods.

After flexible fitting, the N and S systems were equilibrated at constant pressure, with axial periodic dimension L_z fixed at the value suggested by the crystal structure and no external forces applied, for 15 ns (equilibration-I). We found the P_zz component of the stress tensor in both the N and S systems to be ∼100 bar, much higher than other diagonal components (P_xx ≈ P_yy ≈ 1 bar), indicating that the filaments were under compression. Therefore, we performed 2-ns axial stress adjustment simulations of the N and S systems, during which P_zz^target, the Langevin piston target for the P_zz component, was linearly decreased from 100 to 1 bar in 1-bar increments. This was followed by 35-ns (N) and 20-ns (S) equilibration in the NpT ensemble (equilibration-II). The pressure and extension of the systems during the pressure adjustment simulation and the subsequent equilibration are shown in Fig. S2. During the equilibration, L_z was observed to attain an equilibrium value of ∼84 Å in both systems. Equilibration-III, a continuation of equilibration-I, was performed for 25 and 20 ns for the N and S systems, respectively. The structures obtained at the end of equilibration-III were used to build the complete MT system.

Structural changes and stability of the N and S systems

Average root mean-square deviation (RMSD) of backbone coordinates from the starting structure (crystal structure plus reconstructed loop) of the N and S systems during flexible fitting, equilibration-I, pressure adjustment, and equilibration-II are shown in Fig. 2, D and E, while data for equilibration-III is shown in Fig. 2, F and G. Alpha-tubulin is seen to have a higher overall RMSD than β-tubulin, which is quite stable with a backbone RMSD of ∼2 Å. The difference between α- and β-tubulin can be attributed to the rebuilt residues 35–60 in α-tubulin (see Materials and Methods), as the RMSD plots become virtually identical when these residues are excluded from the calculation. Backbone RMSD values from equilibration-III are similar to those observed during the pressure adjustment and equilibration-II simulations.

The RMSD of individual residues at various stages of the simulation are shown in Fig. S3. After flexible fitting, the N system showed only small changes other than in residues 35–60 of α-tubulin, while the S system displayed changes in the M-loop (residues 272–288) at the PFs' interface. After flexible fitting, the M-loop displayed significant change (RMSD ≳ 5 Å), maintained in all subsequent simulations. Other regions of significant change were the H6-H7 loop (residues 216–224) at the longitudinal interface, the S9-S10 loop (residues 357–372) in the N system, and helix H4 in α-tubulin. PDBs of the N and S systems after equilibration-II are provided in the Supporting Material.

To determine whether the fitting procedure created a stable structure, we computed the root mean-square fluctuation (RMSF) of the interface residues, shown in Fig. S4, A and B. The interfaces of both systems began with RMSF values of ≳1.0 Å, and attained lower values (≲0.9 Å) by the end of equilibration-II and equilibration-III. The low RMSF values imply a reasonably equilibrated, stable structure of the PF interface. The number of inter-PF contacts (shown in Fig. S4, C–J), in general, was seen to increase through the course of the simulations. The contacts present within the first 1 ns of equilibration-I were approximately maintained, while new contacts formed in both the N and S systems.

Axial extension and compression of the N and S systems

To determine the mechanical response of the N and S systems to axial extension and compression, we carried out a set of simulations in which P_zz^target was changed gradually during the course of the simulation, producing continuous stress-strain curves, shown in Fig. S5, A and B. The obtained stress-strain curves were found to exhibit some dependence on the rate at which P_zz^target was changed, especially for positive strains (extension). Therefore, we carried out multiple simulations of both systems at different fixed P_zz^target values, monitoring the change of the PF's extension L_z, and Fig. S5 C and E.

In Fig. 3, A and B, we plot the stress and strain in the N and S systems during steady-state fragments of the simulations performed at constant P_zz^target values. The curves exhibit interesting nonlinearities, notably a marked softening for positive strains. For the N system, we also performed simulations with L_z fixed, thus controlling strain, to verify the stress-controlled results, see Fig. S5 D. The starting configurations for the latter simulations were taken from the dynamically controlled stress simulations. The results of the strain-controlled simulations are shown as solid squares in Fig. 3 A, and agree well with the stress-controlled data.

Figure 3.

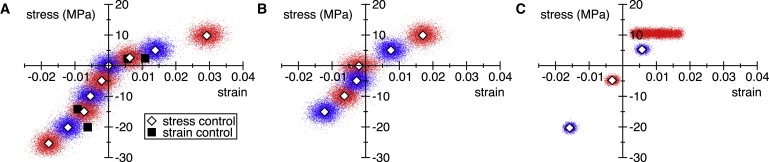
Axial stretching and compression simulations. (A) Stress-strain data for the N system. Stress and strain were calculated every 5 ps. Each dot indicates the stress value calculated from the 5-ps average of P_zz and the strain value calculated from the instantaneous value of L_z. Data were taken from the last 5 ns of the simulation performed at constant P_zz^target value. The points are colored alternating shades to distinguish datasets corresponding to different P_zz^target values. The mean stress-strain value of each 5-ns data set is shown as an open diamond. The solid squares indicate the mean stress observed in the constant strain simulations. (B) Stress-strain data for the S system. The symbols have the same meaning as in panel A. (C) Stress-strain data for the complete MT. The symbols have the same meaning as in panel A, but the stress-strain values were taken from the last 2 ns of the simulations at each P_zz^target value. The simulation at P_zz^target ≈ 10 MPa did not reach an equilibrium strain within the simulation time of 12 ns.

The stress-strain data for the N system in Fig. 3 A appears to fall into two or perhaps three distinct domains, each with a different Young's modulus. For positive strain, or stretching, a linear fit yields a Young's modulus of 0.3 GPa. For negative strain, or compression, the system is significantly stiffer. When fitting the –0.01 < ε ≤ 0 and ε < –0.01 domains separately, we find Young's moduli of 1.9 and 1.0 GPa, respectively, while a fit to the whole ε < 0 domain yields a value of 1.4 GPa. These values are in broad agreement with experimental estimates (22), as well as MD simulations of the elastic properties of tubulin (28). A fit to the entire range of strains, meanwhile, yields a Young's modulus of 0.7 GPa, in very good agreement with the estimate of 0.6 GPa based on fitting to atomic force microscopy radial indentation data (14). Data for the S system is displayed in Fig. 3 B and shows behavior similar to that of the N system, with calculated negative- and positive-strain Young's moduli of 1.3 and 0.5 GPa, respectively.

To disentangle monomer deformation and monomer separation in the stretching and compression simulations, we examined the strains of the individual monomers, shown in Fig. S6. The monomer strain analysis showed that negative strains involve more deformation of the monomers compared to positive strains. This should be expected because the monomers are already in close contact at zero strain. There is a noticeable asymmetry between α- and β-tubulin: α-tubulin tends to deform more than β-tubulin, especially for positive strains. These results are consistent with previous findings showing β-tubulin to be axially stiffer than α-tubulin (28).

Construction and equilibration of the MT system

The procedure for constructing the atomic scale model of a complete MT is outlined schematically in Fig. 4 A. Using the equilibrated conformations of the PFs from the N and S systems, the initial model of the MT system was produced by placing the PFs according to the MT's geometry. Using harmonic restraints, the interface between the PFs in the MT model was adjusted to reproduce the PFs' contacts observed in the equilibrated N and S systems. These steps are described in detail in Materials and Methods.

Using the interface fitting procedure, the system was equilibrated for 14.24 ns in the NpT ensemble with L_z fixed to the crystal value (equilibration-I). As in the case of the 2-PF systems, the P_zz component of the stress tensor in the simulation of the MT system was ∼100 bar. Using anisotropic pressure control, P_zz^target of the Langevin piston was changed from 100 to 1 bar over 5 ns in 1-bar increments, followed by 8.0-ns equilibration with P_zz^target set to 1 bar (equilibration-II). Fig. 4 D shows P_zz and L_z during the pressure adjustment and equilibration simulations.

To examine the structural changes during and after the interface fitting procedure, the RMSD of the interface atoms in the MT structure were computed relative to the corresponding coordinates in the equilibrated N and S systems (see Fig. 4 C). For these RMSD plots, atoms within a 2π/26-radian sector centered between PFs were defined as interface atoms (see Fig. 4 B). The graph shows that the interfaces maintain RMSDs in a tight range below their starting value, indicating that the interface fitting procedure succeeded in producing a stable MT structure. The examined atoms exclude residues 35–60, as inspection of the trajectory showed that a portion of one of the reconstructed loop in α-tubulin shifted at t ∼19 ns. A PDB of the system after equilibration-II is provided in the Supporting Material.

Axial extension and compression of the MT system

Using the anisotropic pressure controls method, we examined the mechanical response of a complete MT to axial compression and extension. Simulations were carried out at four P_zz^target values corresponding to axial stress of ∼10, 5, –5, and –15 MPa.

The stress-strain curve for the complete MT is shown in Fig. 3 C. The plot shows stress-strain data calculated every 5 ps, as well as averages for each, with the exception of the 10-MPa simulation which had a rising strain value that did not reach a steady state; Fig. S5 F shows the values of L_z for each simulation. The shape of the stress-strain curve is similar to that seen for the N and S systems, notably the softening seen for positive strains. A linear fit to the averages yields a Young's modulus of 1.2 GPa, in good agreement with that found for the N and S systems above. It should be mentioned, however, that the system demonstrated very slow relaxation in L_z during equilibration, as seen in Fig. 4 D, raising the possibility that the stress-controlled simulations did not reach genuine steady states.

Stretching of the MT was found to reduce its radius, as intuition may suggest. For the case of –20 MPa stress, we found the average MT radius (measured to the PF centers-of-mass) to be 111.57 ± 0.07 Å, compared to 110.23 ± 0.07 Å for the +5 MPa stress simulation. At zero stress, the MT radius was found to be 110.45 ± 0.06 Å.

Radial compression of the MT system

To probe the mechanical behavior of a complete MT under radial compression, two forcing surfaces were moved toward one another and the center of the MT at a constant velocity (see Materials and Methods). Because of the asymmetry of the MT, two compression simulations were performed differing in the directions of the compression force: parallel and perpendicular to the radial position vector of the seam. These simulations are referred to as S^‖ and S^⊥, respectively.

The strain introduced by the compression force was calculated by fitting an ellipse to the xy coordinates of the PFs' centers-of-mass for each trajectory frame. The fit was performed under the following constraints: the ellipse's center had the same coordinates as at the beginning of the compression simulation; and the major axis of the ellipse was always directed parallel to the forcing surfaces. The initial length of the minor axis (L_minor) was taken as a zero strain reference (ε = 0), while the strain in the rest of the trajectory was calculated as ε = (L_minor,0 – L_minor)/L_minor,0. Note that this is the negative of the standard definition.

In Fig. 5 A, the average compression force is shown as a function of the strain for both S^⊥ and S^‖ systems. The inset images show the S^⊥ and S^‖ systems from the +z direction at a strain of 0.13. The slabs represent the forcing surfaces. The simulated MT systems were effectively infinite along the z direction.

Figure 5.

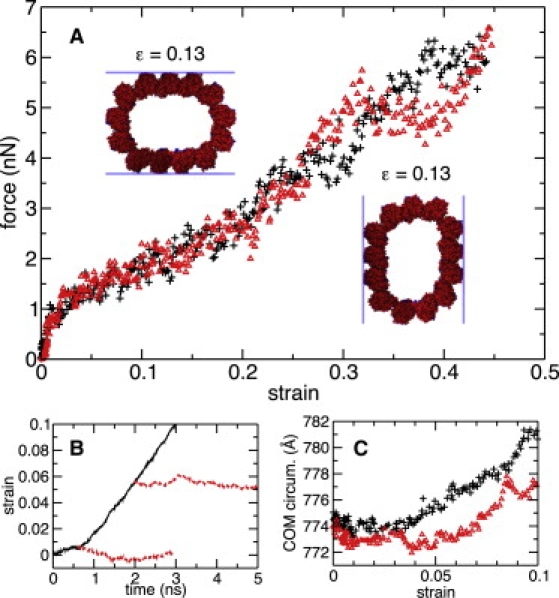
Radial compression of a complete, infinite MT. (A) Compression force versus MT strain for the S^⊥ (pluses) and S^‖ (triangles) systems. The average force from the two surfaces is shown. Each point represents a 25-ps-window average. Inset images show the systems from the +z direction at ɛ = 0.13. The seam is at the bottom of the images. (B) Relaxation simulations of the S^‖ system. The solid trace shows a fragment of the compression simulation, whereas the dashed traces show two equilibration simulations started from different points along the compression trajectory: after 0.6 and 2.0 ns. (C) Center-of-mass circumference of the MT versus strain. This circumference is defined as the sum of the lengths of the line segments connecting the PF centers-of-mass in the xy plane. Symbols are the same as those used in A.

The simulated force-versus-strain dependences have similar shape for both S^⊥ and S^‖ systems. Both systems exhibited an initial high resistance to deformation, to strains of ∼0.01, followed by a softer response. The regime past ε ∼ 0.2 ceases to increase monotonically, displaying steps in the response curve for both systems. We hypothesized that the change in resistance to deformation at ε ∼ 0.01 represents a transition from elastic to plastic deformation. To investigate this possibility, we performed two equilibrium simulations, starting from ε ≈ 0.005 and 0.055, i.e., before and after the transition, of the S^‖ system. Results of these simulations are shown in the inset of Fig. 5, which shows strain as a function of time. The first simulation is seen to return to ε ≈ 0. The second simulation, on the other hand, displays only a slight return toward zero strain, remaining above 0.05, supporting the idea of plastic deformation.

In experiment, the radial indentation of an MT using AFM demonstrated reversible deformation up to 15% deformation (14). Calculating the effective spring constant of our MT for the strains 0.05 < ε < 0.15, we find k ∼ 0.3 N/m, somewhat higher than the value of ∼0.07 N/m found in Schaap et al. (14). However, the deformation mode from a finite AFM tip differs from the compression applied in our simulations, which effectively indents the MT along its entire length. Given this difference, and the factor of ∼10⁷ higher loading rate in simulation versus experiment, the approximate agreement in k is satisfying.

We also investigated the deformation mode during compression. Backbone RMSD of the individual PFs was very low throughout the entire process, remaining below 1.7 Å. Therefore, the deformation is primarily composed of hingelike motion between PFs, and relative motion of PFs. Analysis of the deformation revealed a constant MT circumference, defined as the sum of straight-line segments between PF centers-of-mass in the xy plane, to strains of ∼0.05, after which it began to rise. This is shown in Fig. 5 C. This may imply a larger elastic regime more consistent with experiment.

Twist deformation of the MT system

To examine the mechanical response of an MT to twist deformation, we constructed a finite-length model of the MT (see Materials and Methods) that contained three repeats of the αβ-tubulin dimer per protofilament (shown in Fig. 6 A). Forces were applied to the terminal monomers of the MT, to produce displacement of the MT's plus- and minus-ends in opposite circumferential directions (see Materials and Methods).

Fig. 6 B plots the total displacement angle versus simulation time for counterclockwise (CCW) and clockwise (CW) twist deformation. The total torque imparted in both cases was ∼89 nN nm, increasing slightly (< 3%) during the course of the simulations due to increased MT radius (see Fig. S7 A). For deformations <4°, both directions of the torque produced twists of comparable value. Thereafter, twisting the MT clockwise produced a greater twist strain than counterclockwise. After ∼4 ns of torque application, the forces were switched off, allowing the system to relax. The twist strain was observed to decrease toward zero, although complete recovery of the initial structure was not observed within the timescale of our simulations. The length of the MT fragment under the twist deformation displayed similar behavior in both CCW and CW simulations: the length remained nearly constant, shrinking by 0.5% at high strains in the CW simulation (Fig. S7 C).

If modeled as an isotropically elastic tube with outer and inner radii of r_o = 125 Å and r_i = 75 Å, respectively, a torque of τ = 89 nN nm is expected to produce an angular strain of Δθ ≲ 8°, using Δθ = τL/JG, where L is the length, $J=\pi /2\left(r_o^4-r_i^4\right)$ is the torsion constant, and G = E/2(1 + ν) is the shear modulus. We have taken the Young's modulus E = 1.2 GPa, and the Poisson ratio ν = 0.5 to set an upper bound on the predicted strain. This prediction is clearly exceeded in Fig. 6 B, demonstrating the inadequacy of an isotropic treatment of MT elasticity using a thick cylindrical tube model. An MT is softer than was predicted by the isotropic tube model, and displays an asymmetry between the two directions of twist deformation.

Conclusions

In this study, we combined structural data at multiple resolutions to construct an all-atom model of a complete MT. This model should not be considered a substitute for a crystallographic model, and most likely contains small errors, but nevertheless performed very well. Using this model, we were able to determine a detailed stress-strain dependence clearly showing different behavior under extension and compression. Furthermore, the computed Young's moduli were in very good agreement with published data and estimates. We studied the properties of an MT under radial compression and identified a possible elastic-to-plastic transition. Finally, we applied twisting force and showed a dramatic asymmetry in the MT reaction to the two senses of twist. The twist simulations in particular demonstrate the range of possibilities afforded by the MD method, which allows for the computation of quantities well beyond the current reach of experiment. The excellent agreement of the axial strain simulations with available experimental data gives confidence in the other quantities for which experimental data are not available.

This work is one of the first, to our knowledge, to combine cryo-EM and crystal structures for subsequent all-atom MD simulation. The successful performance of such a model opens the door to the simulation of many other systems whose constituent units are known in atomic detail but whose complete structure is known only at lower resolution. Such simulations allow more biologically relevant length scales to be probed, promising to expand our knowledge of the microscopic mechanisms of life.

Supporting Material

Seven figures and PDBs of the N, S, and complete MT systems after equilibration-II are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00536-9.