Scrutinizing Molecular Mechanics Force Fields on the Submicrosecond Timescale with NMR Data

Abstract

Protein dynamics on the atomic level and on the microsecond timescale has recently become accessible from both computation and experiment. To validate molecular dynamics (MD) at the submicrosecond timescale against experiment we present microsecond MD simulations in 10 different force-field configurations for two globular proteins, ubiquitin and the gb3 domain of protein G, for which extensive NMR data is available. We find that the reproduction of the measured NMR data strongly depends on the chosen force field and electrostatics treatment. Generally, particle-mesh Ewald outperforms cut-off and reaction-field approaches. A comparison to measured J-couplings across hydrogen bonds suggests that there is room for improvement in the force-field description of hydrogen bonds in most modern force fields. Our results show that with current force fields, simulations beyond hundreds of nanoseconds run an increased risk of undergoing transitions to nonnative conformational states or will persist within states of high free energy for too long, thus skewing the obtained population frequencies. Only for the AMBER99sb force field have such transitions not been observed. Thus, our results have significance for the interpretation of data obtained with long MD simulations, for the selection of force fields for MD studies and for force-field development. We hope that this comprehensive benchmark based on NMR data applied to many popular MD force fields will serve as a useful resource to the MD community. Finally, we find that for gb3, the force-field AMBER99sb reaches comparable accuracy in back-calculated residual dipolar couplings and J-couplings across hydrogen bonds to ensembles obtained by refinement against NMR data.

Introduction

Conformational dynamics underlies the multitude of functions that proteins carry out. Motility, signal transduction, allosteric regulation, and molecular recognition are all examples where, on the molecular level, protein dynamics are at the heart of biological function. Molecular dynamics (MD) simulation is a well-established method that shows promise to provide quantitative and detailed models of protein dynamics. However, in contrast to the wealth of structural data (>55,000 structures in the Protein DataBank), accurate data on protein dynamics is much more sparse, rendering development and validation of MD protocols and force fields challenging. NMR spectroscopy can quantify protein motions on a wide range of timescales with atomic resolution (1) and, thus, can complement structural (crystallographic) data and quantum mechanical calculations for force-field development (2–5).

Traditionally, NMR relaxation experiments (6) and MD simulations (7) have been used to study protein dynamics in solution, but both have been limited mostly to the nanosecond regime. NMR relaxation studies are limited by the overall rotational tumbling, and the computational cost involved with MD simulations, in order to render supra-nanosecond simulations, is highly impractical. Not affected by the rotational tumbling, residual dipolar couplings (RDCs) provide a sensitive probe of protein structure and dynamics up to the microsecond timescale (8–10). In parallel, due to developments in computer architecture and algorithms, MD simulations of small proteins start to reach the microsecond timescale on a routine basis (11,12). Thus, with the microsecond timescale reachable in experiment and computation it becomes possible to directly test the compatibility of simulated dynamics to experiment, as probed by RDCs (13).

To scrutinize force fields on the microsecond timescale we test the agreement between measured RDCs and RDCs computed from simulated ensembles for the proteins ubiquitin and protein G, two small globular α/β folds for which extensive NMR data are available. Microsecond MD simulations were carried out in six popular atomistic force fields (OPLS/AA, CHARMM22, GROMOS96-43a1, GROMOS96-53a6, AMBER99sb, and AMBER03) using two different schemes for calculating electrostatic interactions (cut-off/reaction field and particle-mesh Ewald, or PME).

AMBER99sb, in particular, has shown promise in yielding accurate predictions of RDCs (13) and has recently been shown to be more accurate than semiempirical methods (14). In addition to RDCs, J-coupling and nuclear Overhauser enhancement (NOE) data were used to assess the agreement between simulation and experiment. The agreement was assessed on the data level and then translated to the structure level to enable an assessment of the agreement to NMR data in terms of structural features and conformational sampling. The results show that, in general, multiple short (50 ns) simulations yield a better agreement to the NMR data than a single simulation of 1 μs. In addition, PME improves the agreement between simulation and NMR data, also for force fields originally developed employing a cut-off or reaction-field scheme. Finally, deviations from experiment in J-couplings across hydrogen bonds suggest that there is room for improvement in the description of hydrogen bonds in most of the tested force fields.

On a structural level, we found considerable consensus between the different force fields. Using principal component analysis (PCA), we investigated whether this consensus is due to a common model of the native conformational state of the respective protein. To address this question, we select structures from MD simulations of different force fields that fall within a common region in conformational space and test the agreement between measured NMR data and data back-calculated from the thus-constructed consensus ensemble.

In the following, we compare RDCs, J-couplings across hydrogen bonds, and NOEs, respectively, to NMR data. In addition, we analyze PCA modes, backbone dihedrals, and the area of the molecular surface, respectively, to show how the differences in the fit to the experimental data are reflected structurally in the different MD ensembles. Finally, we investigate the structural consensus between different force-field trajectories.

Methods

Molecular dynamics simulations

All molecular dynamics (MD) simulations were carried out using the GROMACS simulation package (15,16) in explicit solvent and periodic boundary conditions. The following all-atom force fields were used: OPLS/AA-l (17); AMBER99sb (4) and AMBER03 (18,19); CHARMM-22 (20); and GROMOS96-43a1 and GROMOS96-53a6 (21). Details are given in the Supporting Material.

Computation of residual dipolar couplings

Residual dipolar couplings (RDCs) were computed from the least-squares fitted MD ensembles with snapshots every 1 ns, obtained as described above. Details are given in the Supporting Material.

Scalar couplings across hydrogen bonds

Scalar couplings across hydrogen bonds ^h3J_NC′ are time averages on timescales similar to the ones probed by RDCs (22). Because of their strong dependence on H-bond geometries, they are used to cross-validate structural data (23,24). We have computed ^h3J_NC′ for several structural ensembles using Eq. 6 in Barfield et al. (25), which has been parameterized against results obtained with density functional theory. The ^h3J_NC′ couplings for protein gb3 (26) and ubiquitin (27) have been measured previously.

Nuclear Overhauser enhancements

Nuclear Overhauser enhancement (NOE) is a sensitive probe of the mean protein structure. Available interproton NOEs were used to assess a complementary analysis of the agreement in terms of structure between simulation and experiment. As the measured NOEs represent time and ensemble averages, the back-calculated, time-averaged NOE distances from the simulations were calculated from 5 ns trajectory fragments as averages in the form

$$\overline{r_{effkl}^{-3}}=\frac{1}{N}{\sum }_{j=1}^N{r}_{kl,j}^{-3},$$

which were subsequently ensemble-averaged as

$$\overline{r_{kl}^{-6}}=\frac{1}{N}{\sum }_{j=1}^N{r}_{effkl,j}^{-6}.$$

Five nanoseconds correspond approximately to the rotational tumbling time of ubiquitin and protein G. This corresponds to an interpretation of multiple independent simulation windows of 5 ns, and allows a direct comparison to ensemble-refined (and ensemble-averaged) structure ensembles. Deviations between simulation and experiment were evaluated as violations of the experimental NOE distance bounds, and were summed over all measured interproton NOEs.

Principal component analysis

Principal component analysis (PCA) was carried out on backbone atoms of residues 1–70 and 6–61 of protein ubiquitin and gb3, respectively. The covariance matrix was averaged over all structures of a selected ensemble and all structures of the reference ensemble and subsequently diagonalized.

Construction of consensus ensembles

To construct consensus ensembles, all frames were selected for which at least N_select = 6 other ensembles contain M_match = 1 conformations within a sphere of 0.1 nm. The flexible tails were excluded from the fit and from the root mean-square deviation (RMSD) calculation.

Results and Discussion

Back-calculated residual dipolar couplings

For the two proteins, gb3 and ubiquitin, MD simulations with a length of 1 μs were carried out applying the different force fields and electrostatic treatments as mentioned in Methods, yielding a total of 20 μs of simulation time in 20 independent trajectories. In this section, we analyze the agreement between the resulting ensembles and the measured RDC data for these proteins. For both proteins, RDCs have been measured in a sufficiently large number of different alignment media such that the R_RDC value

$$R={\left({\Sigma }_k^n{\left(d_{k,calc}-d_{k,exp}\right)}^2/\left(2{\sum }_k^n{d}_{k,exp}^2\right)\right)}^{1/2}$$

is sensitive to differences in the ensembles that go beyond differences of the average structure (8).

For both proteins, R_RDC varies widely. Interestingly, simulations with cut-off electrostatics show higher R_RDC values for all force fields including those originally parameterized with cutoff electrostatics. But also within the group of simulations carried out with full electrostatic treatment (i.e., PME), a large variation of the R_RDC is observed for both proteins. Strikingly, for both proteins AMBER99sb shows the smallest R_RDC. See Fig. 1.

Figure 1.

Comparison of R_RDC computed from MD ensembles generated with various force fields and two different electrostatic treatments (see Methods). No error bars are given in this figure, as only a single trajectory of 1 μs was available; refer to Fig. 3 to judge the variation in the respective R_RDC.

An interesting question to ask is what length of trajectory yields the best R-values, and how this optimal length varies with force field. An ideal force field should yield optimal results if multiples of the ∼1-μs timescale are reached upon which the RDC experiment averages. At the time of this writing, we cannot yet reach multiple microseconds of simulation time. Nevertheless, one would expect an increased accuracy for longer simulation times. We tested this hypothesis by computing the fit to the RDC data for windows of different length t ≪ 1000 ns. Indeed, as shown in Fig. 2, a–c, ensembles created during only t = 1 ns have systematically higher $R_{RDC}^t$ than ensembles based on longer simulation times. However, for most force fields no significant improvement of the $R_{RDC}^t$ is reached for t > 25 ns (Fig. 2 d). Slightly longer averaging times can be seen for AMBER99sb (simulation index 2 and 12), for which $R_{RDC}^t$ improves until t = 100 ns and t = 50 ns for gb3 and ubiquitin, respectively, and for AMBER03, which improves the $R_{RDC}^t$ for ubiquitin until t = 100 ns.

Figure 2.

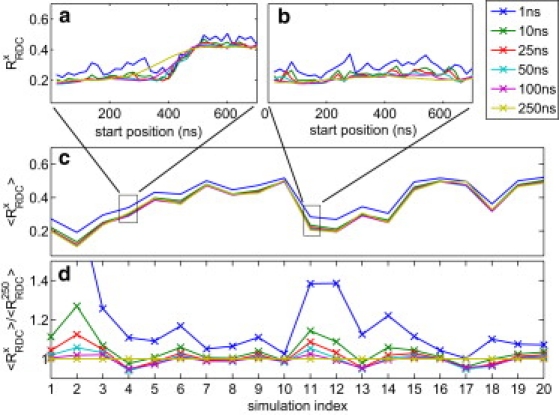
Fit of RDC data (R_RDC^x) computed from different-sized windows between x = 1 ns and x = 250 ns. (a and b) R_RDC^x resolved by starting position within the 1000 ns trajectories gb3_CHARMM22_PME and UBI_AMBER03, respectively. (c) For each trajectory (for numbering on x axis, use key given in legends of Fig. 3), R_RDC^x has been averaged over all possible windows. (d) For each trajectory (for index, see Fig. 3), the ratio R_RDC^x/R_RDC²⁵⁰ has been averaged over all possible windows. For most simulations, the ratio is close to 1 with x = 50 ns and x = 100 ns. This demonstrates that no significant improvement in R_RDC is gained by going to the longer averaging window of x = 250 ns.

For some trajectories, longer averaging can even yield, on average, worse $R_{RDC}^t$ (Fig. 2 d, simulations 4, 13, 17, and 18). Thus, increasing simulation time beyond t = 50–100 ns does not significantly improve the fit to the RDC data. The reason could be that for both proteins all motions are sampled within the nanosecond timescale. Alternatively, one might want to conclude that beyond 100 ns simulation time, the improved sampling does not outweigh the increasing accumulation of force-field inaccuracies (28). In support of the latter explanation, we find four cases where $R_{RDC}^t$ deteriorates with longer sampling time t. In line with our finding, Showalter and Bruschweiler (13) reported, for simulations of ubiquitin with AMBER99sb, that a 50 ns simulation yields a better fit to a subset of the RDC data than does a 20 ns.

As shown above, an averaging time of t = 50 ns is close to optimal for all force fields, such that we restrict the following analysis to $R_{RDC}^{50}$. As Fig. 3 shows, $R_{RDC}^{50}$ changes significantly during the time course of the simulations. The trajectories show three distinct behaviors:

• Case 1.

  A rapid (<5 ns) increase of $R_{RDC}^{50}$.

• Case 2.

  A prolonged phase of relatively low $R_{RDC}^{50}$, followed by a sharp increase.

• Case 3.

  A stable and low $R_{RDC}^{50}$ throughout the full length of the 1-μs simulation.

Figure 3.

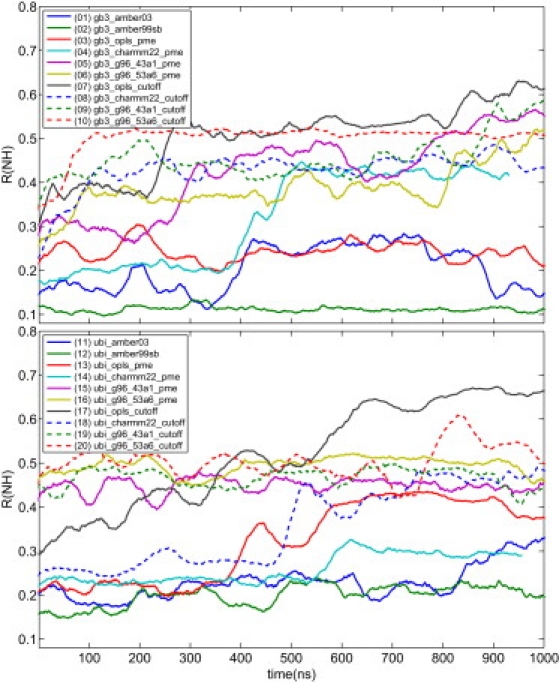
Time-resolved R_RDC for MD simulations with various force fields. The residual dipolar couplings were computed from the respective MD trajectory in overlapping windows of 50 ns length. The figure key shows the simulation index used on the x axis of Fig. 2d in parentheses. The results shown here are computed for NH RDCs. Results for CH and NC RDCs are shown in the Supporting Material.

Case 3 has only been observed for simulations in AMBER99sb, in accordance with the low overall $R_{RDC}^{1000}$ of this force field in the analysis shown above (compare to Fig. 1). Force fields showing behavior in Case 2 are AMBER03, OPLS/AA, and CHARMM22 when PME electrostatics is applied. For these, low $R_{RDC}^{50}$ values comparable to the AMBER99sb trajectory are observed for several hundreds of nanoseconds. The g96 family of force fields and generally cut-off (OPLS/AA and CHARMM22) or reaction-field (g96xxx) simulations fall under Case 3 (with the exception of the g96_43a1_PME for gb3 and CHARMM22_cutoff for ubiquitin, which are more similar to Case 2).

In summary, with PME electrostatics the native state ensemble is well described by most force fields and stable in simulation for several hundred nanoseconds. Transitions to states of high $R_{RDC}^{50}$ are irreversible at the studied timescales. Most cut-off simulations, in contrast, show a high $R_{RDC}^{50}$ from the start; a systematic bias appears to drive the simulated systems quickly away from the native basin. The discussion here is based on NH RDCs for which most data is available. As shown in Fig. S19 and Fig. S20 in the Supporting Material, the conclusions are also supported by RDCs computed for CH or NC couplings.

To gain more statistics on the distinct low $R_{RDC}^{50}$ regions sampled by the force fields, we computed structural ensembles for which we carried out 20 × 50 ns simulations for the OPLS/AA, AMBER03, and AMBER99sb force fields starting from the crystal structure (see Methods). To account for possible equilibration, we only analyze the second-half of the trajectories. Indeed, the likelihood of an infrequent transition to a high $R_{RDC}^{50}$ conformational state is low during 50 ns simulation time, and none of the 60 trajectories have such high R-values as observed during transient phases in the respective continuous simulations (see Fig. S2).

Back-calculated J-couplings across hydrogen bonds

J-couplings measured across hydrogen bonds yield an experimental observable that is notoriously difficult to reproduce by unbiased computational ensembles (30). Table 1 shows an overall $R_{H-bond}^{1000}$ for J-couplings computed from the same trajectories discussed above in terms of RDCs. Also, for $R_{H-bond}^{1000}$, significant variations between different force fields and electrostatic treatments are observed. In general, the cut-off simulations yield higher $R_{H-bond}^{1000}$ than trajectories computed with full electrostatic treatment (PME). Within the subset of PME simulations, the relative performances measured by $R_{H-bond}^{1000}$ are similar to those reported above for $R_{RDC}^{1000}$.

Table 1.

Quality measurement of R-free and correlation coefficient r for ^3hJ couplings across hydrogen bonds predicted with various force fields with PME electrostatics

	RH–bond(gb3)	rH–bond(gb3)	RH–bond(ubi)	rH–bond(ubi)
AMBER03	0.29	0.58	0.26	0.55
AMBER99sb	0.16	0.85	0.19	0.80
OPLS/AA	0.28	0.67	0.29	0.64
CHARMM22	0.26	0.68	0.23	0.70
g96_43a1	0.30	0.45	0.29	0.36
g96_53a6	0.31	0.2	0.28	0.39
2k39			0.19	0.81
2igd	0.20	0.85
1igd	0.30	0.81
AMBER03_50ns	0.25	0.69	0.24	0.58
AMBER99sb_50ns	0.16	0.85	0.18	0.81
OPLSAA_50ns	0.26	0.69	0.26	0.76

The last three rows refer to predictions based on 20 × 50 ns MD simulations rather than a single 1000 ns simulation. A graphical version of this table is shown in Fig. S3 and includes values for cut-off and reaction-field simulations.

Fig. 4, a–f, shows a detailed comparison of ^3hJ couplings back-calculated from the MD simulations with their respective experimental values. The Supporting Material contains numerical values for ^3hJ couplings in Table S1 and additional figure panels in Fig. S4 for those simulations omitted in Fig. 4, a–f.

Figure 4.

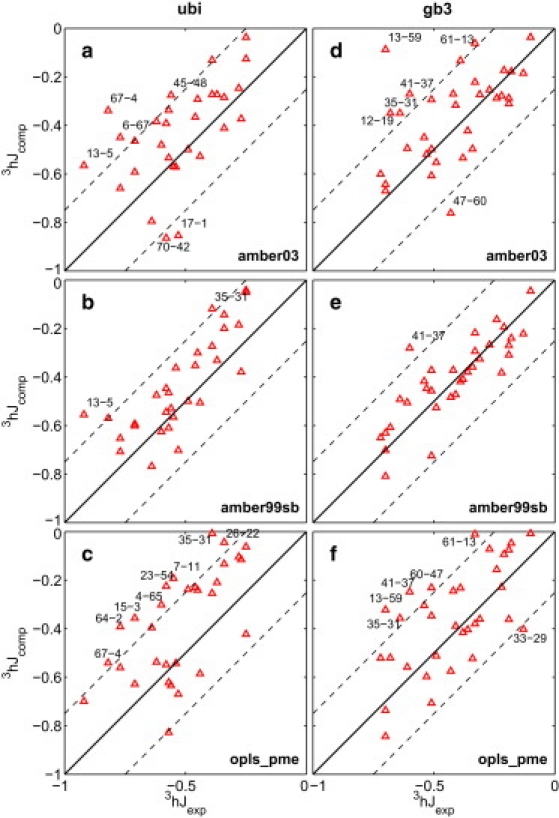
Comparison of ^3hJ_exp couplings across hydrogen bonds for proteins ubiquitin (left) and gb3 (right) with couplings back-calculated from MD simulations carried out with force-fields AMBER03 (a and d), AMBER99sb (b and e), and OPLS/AA (c and f). The second panel compares ^3hJ back-calculated from MD simulations that were restarted from the crystal structure every 50 ns. (Dashed lines) Mean ± 0.25 Hz.

In general, the analysis is in line with previous findings that ^3hJ couplings are challenging to reproduce by free MD simulation (31–33). Moreover, the differences between the various force fields is less pronounced than for the prediction of RDCs (see Table 1), and in particular the g96 force fields yield comparatively low $R_{H-bond}^{1000}$ in contrast to their high $R_{RDC}^{1000}$. A promising exception is the AMBER99sb force field, which yields remarkably low $R_{H-bond}^{1000}$ for both proteins, gb3 and ubiquitin. The good performance of AMBER99sb corroborates the empirical formulas derived from DFT calculations for back-calculation from structures (25) and largely rules out measurement errors as cause for the bad performance of most force fields. In general, hydrogen-bond couplings are too-weakly predicted by MD simulations (see Fig. S6).

However, there are couplings that are not well described by any force field including AMBER99sb. For ubiquitin, for instance, the J-couplings across the hydrogen bonds from HN 13 to CO 5 and HN 35 to CO 31, and for gb3, from HN 41 to CO 37, are too weak in all simulations. In principle, the possibility of a measurement error or misinterpretation of the raw NMR data cannot be excluded for these few notorious outliers, but the deviation of the prediction toward weaker values is in-line with the general tendency of too-weakly-predicted couplings.

Interestingly, resetting the MD simulations every 50 ns as discussed above, yields only little improvement in the prediction of hydrogen bonds (see Fig. S5 and Fig. S7). In particular, most of the poorly described hydrogen bonds in each respective force field remain poorly predicted in the resetted simulations, suggesting that the poor descriptions of the hydrogen bonds are inherent to the particular force field's description of the most consistently sampled nativelike conformational states rather than due to transitions to conformational states with high R_RDC. However, the PCA shown below implicates hydrogen bonds with inaccurate ^3hJ couplings to play a role in structural transitions to nonnative conformational states.

Comparison of AMBER99sb ensemble to previously published ensembles of gb3

The AMBER99sb force field shows a remarkably low $R_{H-bond}^{1000}$ for gb3. To our knowledge, this is the first time for this protein that a significantly lower $R_{H-bond}^{1000}$ than that computed from the high-resolution crystal structure (30) has been reported. Taken together with the extremely low $R_{RDC}^{1000}$, this suggests that AMBER99sb describes the solution dynamics of gb3 on the pico- to microsecond timescale reasonably well. Because none of the data has been used for refinement, both $R_{H-bond}^{1000}$ and $R_{RDC}^{1000}$ are comparable to free R-factors in fully cross-validated ensemble refinement and are thus remarkably low. Note that previously determined ensembles (34,35) use a cross-validation scheme based on omittance of RDCs in one medium, from a set of RDCs in multiple alignment media. In such a scheme, however, redundancy of RDCs between the free and work sets is likely to persist, as different media do not usually yield fully orthogonal alignment tensors (36). Thus, even the free R_RDC computed from these previously determined ensembles might be lowered due to overfitting, and cannot be directly compared with the here-reported $R_{RDC}^{1000}$.

It would be interesting to compare the AMBER99sb ensemble of gb3 presented here with the ensemble obtained in Markwick et al. (37) with accelerated molecular dynamics (AMD). The AMD ensemble has not been refined against RDC data, and thus, R_RDC could be compared to our results. Unfortunately, R_RDC values are not reported in Markwick et al. (37) and we were not able to obtain the structures from the authors to compute the values ourselves. The AMD method has also been applied to ubiquitin (38); that study showed a remarkably low free R_RDC for an unbiased simulation after the boost factor was adjusted to minimize the overall R_RDC.

Consistency of computational ensembles with NOE distance constraints

Fig. S16 shows the time evolution of the NOE violations in ubiquitin and protein G in the different simulations. In general, similar trends are observed as for the RDCs. The simulations using PME show fewer violations than the simulations employing a cut-off or reaction-field scheme. Both the AMBER99sb and AMBER03 force fields show particularly low NOE violations for both proteins, indicative of a stable mean structure that is compatible with the experimental observations. OPLS/AA, with cut-off electrostatics, shows a rapid increase of violations for both proteins, but, if PME electrostatics is employed, shows few NOE violations for the full-length of the gb3 trajectory and for the first 300 ns of the ubiquitin trajectory, respectively. Also, the g96_43a1 force field, in combination with PME, yields trajectories with a low number of violations (for the whole simulation length for ubiquitin and for the first 700 ns for gb3); this is remarkable, because these extended phases of little NOE violation coincide with phases of relatively high $R_{RDC}^{50}$. As observed above for RDCs and J-couplings, transitions that lead to substantial NOE violations are found to be mostly irreversible at the simulated timescale.

Conformational analysis

PCA is a powerful method to analyze conformational ensembles (39). Systematic conformational changes between different conformational states tend to be well resolved by projections onto the principal components. To find out whether systematic conformational changes correlate with the occurrence of high R_RDC values and how to characterize such changes structurally, we carried out PCA on all MD ensembles discussed so far. As it is the nature of this analysis, the exact direction of the eigenvectors identified by PCA changes for each ensemble. To aid the understanding of the mutual relations of these projections, we also show in each plot a common reference ensemble projected onto the respective PCA subspace. For ubiquitin, we chose as reference an ensemble that has been obtained by ensemble refinement against available RDC and NOE data and was shown to be highly similar to an ensemble of >40 x-ray structures (40) (PDB code: 2k39). For gb3, we chose the AMBER99sb ensemble as reference for all gb3 ensembles, because this ensemble yields values for both R_RDC and R_H-bond that are similar to those found for the 2k39 ensemble for ubiquitin.

Fig. 5 and Fig. S17 show the projections onto the first two principal components of selected MD ensembles and of the reference ensemble for ubiquitin and gb3, respectively. (For the g96_53a6_cutoff ensembles, omitted here due to space constraints, see Fig. S8 and Fig. S9.) For both proteins, low R_RDC values (blue colors) are usually found in conformational regions consistent with the reference ensemble (black triangles). In contrast, a sharp transition toward high R_RDC values is found upon the reference ensemble leaving this conformational region. This behavior is pronounced for force fields AMBER03, AMBER99sb, OPLS/AA_PME, and CHARMM22, whereas it is not observed for the g96_53a6 or g96_43a1 force field, respectively. In fact, the g96 MD ensembles do not show low R_RDC values, even if they sample regions close to the reference ensemble. This suggests differences between the reference ensemble (and other low R_RDC MD ensembles) and the g96 ensembles that are not of the systematic structural nature highlighted by the PCA analysis.

Figure 5.

PCA of ubiquitin ensembles. For each panel, PCA is carried out over the combined set of structures taken from 2k39 and the respective force-field ensemble. The projection to principal components 1 and 2 (pc #1 and pc #2) are plotted on x and y axis, respectively. The coloring depicts the 50 ns window average of R_RDC for a given snapshot (compare to Fig. 3); all panels use the same color-scale with blue for the lowest R_RDC values and red for the highest R_RDC values. The first principal component (pc #1, x axis) contributes >30% to the overall motion for all trajectories.

Under full electrostatic treatment (PME) and with force fields AMBER03, AMBER99sb, OPLS/AA, CHARMM22, and g96_43a1, the MD ensembles show high populations in a mutually consistent conformational region. For ubiquitin, an ensemble directly refined against solution NMR data exists (40), and it turns out to be highly similar to this mutually consistent region; for gb3, this mutually consistent region shows extremely low R_RDC and R_H-bond. This suggests that a consensus exists between the various force fields and that it describes the native conformational ensemble well. Indeed, consensus ensembles constructed using an RMSD-based selection (see Methods) achieve a high accuracy in the predicted RDC data (R_RDC of 13.9% and 10.8% for ubiquitin and gb3, respectively) that for ubiquitin even surpasses that of the best individual force-field trajectory (R_RDC of 18.6% and 10.4%). Similar low R_RDC ensembles are accessible by selecting frames within 0.9 RMSD of the x-ray structures (R_RDC of 14.4% and 11.8%). Thus, for the relatively rigid proteins ubiquitin and gb3, the selection of consensus frames acts similarly to a selection around the x-ray structure. It will be interesting to see whether such consensus ensembles also improve accuracy for more flexible proteins. This will be addressed in further studies.

A complementary view of the relative flexibilities sampled in different force fields is provided by an analysis of the backbone RMSD. The RMSD curves shown in Fig. S10 confirm the observation that excursions from the conformational region around the crystal structure frequently lead to relatively high R_RDC values. NH order parameters are frequently used to assess backbone flexibility in reference to NMR data. Fig. S21 shows NH order parameters for selected force-field variants compared for ubiquitin to the EROS RDC-refined ensemble (40), an AMD-derived ensemble (38), and a structure-free GAF model (41). With the exception of the simulation carried out using the OPLS force field, all curves show a surprisingly similar behavior; this indicates a consistent picture of the microsecond backbone dynamics of ubiquitin, in line with the consensus approach discussed above.

The various force fields differ in the frequency of excursions and the relative population of conformational states that are not consistent with the consensus conformational state. Usually, excursions from this consensus conformational state are also correlated with transient high R_RDC values. In general, cut-off electrostatics gives rise to a higher frequency and population of such off-consensus conformational states.

Fig. 6 shows selected snapshots for MD ensembles OPLSAA-PME and AMBER03, respectively. The snapshots were selected from regions of high R_RDC conformations that yield distinct clusters in the projection to the first principal components (compare to Fig. 5). It can be seen that hydrogen bonds whose respective back-calculated ^3hJ couplings are far from the experimental values (labeled in Fig. 4), are found in regions where the PCA analysis highlights systematic movement away from the reference ensemble.

Figure 6.

Snapshots from ubiquitin ensembles (green) and x-ray structure (1ubi, gray). Arrows are shown between residue pairs whose hydrogen bond is an outlier in Fig. 4. (a) Ubiquitin structure taken from the high R_RDC region of the OPLS/AA-PME ensemble. The projection of the selected structure to the PCA coordinates shown in Fig. 5 is (1.03; 0.45); see red/orange cluster in upper-right corner in that figure. (b) Ubiquitin structure taken from the high R_RDC region of the AMBER03 ensemble. The two selected frames project into the green cluster in Fig. 5, with (0.38; 1.24) and (1.23; 0.23), for the dark-green and light-green structures, respectively.

Peptide backbone dihedral angles

Recent efforts in force-field development have focused upon the parameterization of peptide backbone dihedral angles (4,18,19,42). One relevant metric in the current context therefore is the sampled backbone ϕ-ψ space compared to statistics obtained from high-resolution protein structures. To this end, we analyzed the backbone torsion angles of the various MD ensembles in terms of the ROSETTA Ramachandran (Rama) energy term (43). This term assigns low energies to ϕ-ψ combinations compatible with statistics derived from the Protein DataBank of high-resolution protein structures. Fig. S13 shows running averages (50 ns) computed for structures of the different MD ensembles. Similar to the analysis shown above, significant differences between the various force fields are observed. The structures in the AMBER99sb ensemble have the highest compatibility with the respective Ramachandran plots.

The Rama score correlates with $R_{RDC}^{50}$: For both proteins and across all force fields we find that high Rama scores (>12) are simultaneously present with high $R_{RDC}^{50}$, whereas low Rama scores (<12) coincide with a relatively low $R_{RDC}^{50}$ (see Fig. S14). Thus, improvements of torsion potentials will likely improve the reproduction of native state dynamics, as quantified by R_RDC. However, an analogous correlation to $R_{RDC}^{50}$ is observed for the reproduction of hydrogen bonds (see Fig. S15). Hence, it is not clear whether both problems can be improved independently. Structures with relatively high Rama-scores might be sampled here, exactly because the hydrogen bonds are described too weakly.

Structures within the conformational region of the reference ensemble have lower Rama scores than other conformations (for selected examples, see Fig. S18). However, in some instances, e.g., UBI_CHARMM22_PME and GB3_OPLS_PME, the variation of the Rama score within an ensemble is significantly smaller than the variation between different ensembles.

It should be noted that our CHARMM22 simulations were carried out without the CMAP extension for backbone torsion angles (42). It will be interesting to see how the inclusion of CMAP alters the back-calculated NMR statistics presented here.

Conclusions

Recent experimental and computational advances opened the possibility to assess conformational protein dynamics on the microsecond timescale. A comparison of measured and computed RDCs provides a sensitive probe to validate dynamics predicted by MD simulations, as current force fields were developed without fitting to reproduce RDC data. We found marked differences among six state-of-the-art, molecular-mechanics force fields, highlighting the need for continued force-field development.

For an ideal force field, the best match between experiment and simulations would be expected if the timescales of both were similar. However, it turns out that the best fit to the RDC data that probe protein dynamics on the microsecond timescale is reached by multiple multinanosecond MD simulations rather than a microsecond trajectory for the majority of current force fields: To accurately predict RDCs, the optimal length of MD simulations lies at ∼50 ns with current force-field technology. Longer trajectories are necessary to probe processes with long correlation times, but these also entail an accumulated probability of sampling conformational states that are nonnative, in the sense that they are only weakly populated in the physical system but are hard to escape from in the timescales available during current computer simulations.

Based on currently available knowledge, it cannot be decided whether the force fields are at fault and need to be corrected to destabilize such conformational states, or whether much longer simulation times are required to allow the relative weight of these nonnative states to converge in the final accumulated ensemble to values as low as suggested by the experimental data. It might well be that a combination of both is needed, and clearly, interesting times for force-field development lie ahead, inasmuch as the microsecond timescale became recently available both computationally and experimentally.

Each force field has been tested with two techniques for the treatment of the long-range electrostatics, PME, and a cut-off (in combination with a reaction field in the case of the g96 force fields). We generally found a significantly better fit to all observables (RDCs, ^3hJ, Ramachandran statistics, and NOE violations) with PME electrostatics, also for those force fields that have been developed using cut-offs (CHARMM22, OPLS/AA) or reaction fields (g96_xxx). This finding corroborates a number of previous observations (16,44–46). It has been shown recently that simulation of a small protein in AMBER99-GS with reaction-field electrostatics yields the same protein-folding kinetics as with PME electrostatics (47). Here we have compared reaction-field electrostatics and PME only for the g96 force fields; for this family, we find considerable improvement in reproduction of the experimental data if PME is used. On a structural level, we found considerable consensus among AMBER03, AMBER99sb, OPLS/AA, and CHARMM22 force fields, when applying PME for long-range electrostatic calculations, with, on average, >35% of the ensemble within the consensus conformational region (see Table S4).

Hydrogen bonds are generally not well described by the various force fields with the exception of AMBER99sb. Interestingly, the newly adjusted torsion potentials in AMBER99sb have also improved the description of the hydrogen bonds. For all force fields (including AMBER99sb), the hydrogen bonds are, on average, weaker than suggested by the experimental data. For a couple of hydrogen bonds, the back-calculated ^3hJ_NC were strong outliers (>0.25 Hz) for almost all force fields. These challenging hydrogen bonds lie in regions that showed considerable displacement during conformational transitions that lead away from the low $R_{RDC}^{50}$ conformational state. This suggests that a better description of hydrogen bonds would decrease the likelihood to sample the nonconsensus regions with high $R_{RDC}^{50}$ and thus greatly improve the overall fit to residual dipolar couplings. Probably, adjustments of torsion potentials as in AMBER99sb, and direct improvements of hydrogen bonds by manipulation of partial charges as in Schmid and Meuwly (33), will be necessary. Interestingly, a dedicated hydrogen-bond potential was found to be useful in the field of structure prediction (48), whereas the 10–12 hydrogen-bond potentials have recently been removed from CHARMM.

In practical terms, for small and relatively rigid single domain proteins starting from an x-ray structure, a simulation protocol involving multiple short (∼50 ns) simulations, as opposed to a single long simulation, can be expected to improve the prediction of native-state conformational ensembles.

The presented 1-μs ensemble of the gb3 domain of Protein G reaches an accuracy in back-calculated RDC data and J-couplings across hydrogen bonds (30) which is comparable to that obtained with ensembles refined against RDC data (34,35).

Supporting Material

Twenty-one figures and four tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00560-6.