Abstract
The translocation of catalytic protein kinase A (cPKA) in response to cyclic-adenosine mono-phosphate (cAMP) depends on the pattern of stimulus applied to the cell. Experiments with IBMX have shown that 1), sustained cAMP elevation is more effective than oscillations of cAMP at getting cPKA into the nucleus; and 2), cPKA enters the nucleus by diffusion. We constructed mathematical models of cAMP activation of cPKA and their diffusion in order to study nuclear translocation of cPKA, and conclude that hindered diffusion of cPKA through the nuclear membrane by a rapid-binding process, but not globally reduced diffusion, can explain the experimental data. Perturbation analysis suggests that normal physiological oscillations of glucose would not result in nuclear translocation, but chronically high glucose that produces extended calcium plateaus and/or chronic glucagonlike peptide-1 stimulation could result in elevated levels of nuclear cPKA.
Introduction
Consuming a meal activates multiple signaling events from neural satiation signals to chemical preparation signals, which are greater than those in response to the same amount of glucose supplied intravenously. The enhanced stimulus to insulin secretion accompanying glucose delivered through a meal is called the incretin effect (1,2).
A key signal of the incretin pathway is secretion by intestinal L-cells of glucagonlike peptide-1 (GLP-1), which acts on pancreatic β-cells on both short and long timescales to potentiate glucose-stimulated insulin secretion. GLP-1 stimulates adenylyl cyclase (AC) to produce cyclic-adenosine monophosphate (cAMP), which activates cAMP's downstream targets, exchange protein activated by cAMP (EPAC) and protein kinase A (PKA) (3). Both EPAC and the catalytic subunit of PKA (cPKA) increase the efficiency of insulin granule exocytosis acutely by sensitizing the release machinery in the cell periphery (subplasma membrane) to calcium (4). On a longer timescale, cPKA additionally enters the nucleus, where it activates transcription of genes important for preservation and amplification of β-cell mass (5,6). The rapid effects are appropriate for responding to transient increases in plasma glucose with increased insulin secretion, whereas the slow effects are appropriate for responding to chronic increases in glucose, which tax the β-cell and may call for expansion of cell mass or number.
These beneficial effects of GLP-1 on insulin secretion, along with effects on other tissues such as the liver, pancreatic α-cells, and the brain, have led to a new generation of drugs that stimulate this pathway. This pathway is stimulated either by long-lasting (degradation-resistant) agonists of the receptor or by inhibition of the enzyme, DPP-IV, which degrades native GLP-1.
The main goal of this study is to understand how β-cells distinguish between brief and maintained cAMP rises and thus how they decide whether to engage the long- or short-term responses. This may provide insights into the mechanisms of action of GLP-1-based therapies and lead to further improvements in that area.
We approach this question by modeling data obtained in β-cells by Dyachok et al. (7), who showed that pulsatile cAMP stimulus by isobutylmethylxanthine (IBMX) was effective at raising peripheral cPKA but resulted in only low levels of nuclear cPKA, whereas a sustained stimulus raised nuclear cPKA. The translocation of cPKA to the nucleus is thought to be rate-limiting for subsequent nuclear phosphorylation events (8). DiPilato et al. (9) similarly showed in other cell lines that cPKA kinetics in the nucleus are much slower than at the plasma membrane (20–30 min versus 2–3 min), despite the fact that cAMP penetrates the nucleus rapidly. Harootunian et al. (10) argued that cPKA entry into the nucleus is diffusive, rather than a result of active transport or release from nuclear PKA holoenzyme—based in part on the insensitivity of the kinetics to temperature.
We hypothesize that the order-of-magnitude delay in nuclear cPKA elevation results from reduced effective diffusion through the nuclear envelope owing to binding of cPKA to molecules at the nuclear envelope. We hypothesize further that this binding is very rapid, analogous to the slowed diffusion of calcium in the cytosol and endoplasmic reticulum by rapid buffers (11), which accounts for the insensitivity of the kinetics to temperature. To address this hypothesis we develop a model of cAMP/PKA signaling in a spatially heterogeneous β-cell with subplasma membrane (submembrane), cytosolic, and nuclear regions.
In the next section, we discuss the components in the signaling cascade from GLP-1 to nuclear cPKA and the experimental techniques of Dyachok et al. (7) for visualizing cPKA. In Modeling Methods we construct a three-compartment ordinary differential equation model of the β-cell, which is convenient for comparison with experimental data and for analysis.
In Results, we show the main finding, i.e., that low effective diffusion across the nuclear membrane can account for reduced nuclear translocation of cPKA under pulsatile-versus-sustained cAMP stimulus protocols. Perturbation analysis reveals the inverse relationship between effective diffusion across the nuclear membrane and the period of the cAMP stimulus protocol.
Experimental Background
The ability of cAMP to carry a diversity of signals is attributed to both differentiated degradation by a variety of phosphodiesterases (PDEs) (12) and spatial localization of targets using scaffolding proteins such as A-kinase-anchoring proteins (AKAPs) (13), sometimes in conjunction with PDEs (14). However, the nuclear membrane serves as an additional, and critical, signal diversifier through the main cAMP effector, cPKA, which can be active independent of constraints by either PDE or scaffolding.
The pathway from GLP-1 interaction with the β-cell to catalytic PKA activation is illustrated in Fig. 1. GLP-1 binds to the GLP-1 receptor, which is coupled to the G protein, Gs. Gs activation then causes cAMP production by adenylyl cyclase (AC). cAMP is degraded by PDE bound within the AKAP structure attached to AC, as well as by free PDE and PDE bound to other structures. cAMP also binds protein kinase A, a tetramer made up of two homodimers—i.e., a pair of regulator proteins (rPKA) and a pair of catalytic monomers (cPKA). Free cPKA has multiple targets at the plasma membrane as well as nuclear targets. Nuclear target activation requires cPKA entry through the nuclear membrane.
Figure 1.
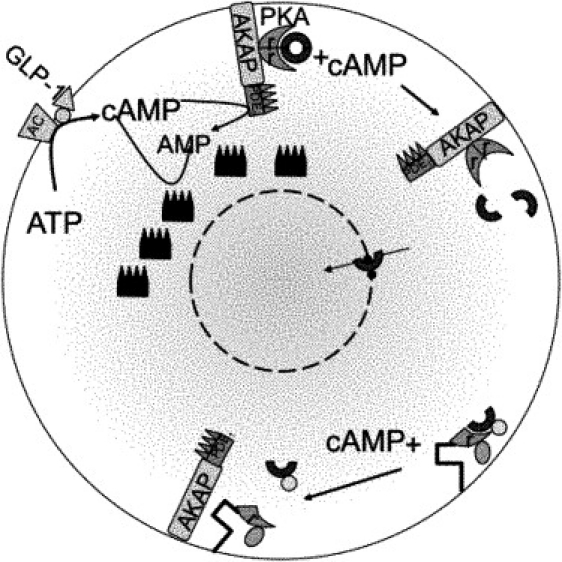
Cartoon of cAMP-dependent PKA nuclear translocation. GLP-1 activation of the GLP-1 receptor, a G-protein coupled receptor, triggers adenylyl cyclase (AC)-mediated production of cAMP from ATP. cAMP is degraded by various phosphodiesterase (PDE) isoforms. Binding to protein kinase A (PKA) anchored to the membrane through A-kinase-anchoring protein (AKAP) releases the catalytic subunits (cPKA) from the regulatory subunits (rPKA). cPKA can then enter the nucleus through nuclear pores. Dyachok et al. (7) labeled rPKA with cyan fluorescent protein (CFP) and cPKA with yellow fluorescent protein (YFP) and independently anchored labeled rPKA. Measuring with TIRF within 100 nm of the plasma membrane detects cPKA separation as a reduction in the YFP signal. YFP-tagged cPKA cannot enter the nucleus, so epifluorescence was used to measure cPKA penetration of the nuclear membrane when cAMP was raised. We hypothesize a rapidly buffering protein (small, dark blue dots) that delays cPKA entry into the nucleus.
Dyachok et al. (7) used total internal reflection fluorescence (TIRF) and epifluorescence techniques to examine the effect of cAMP oscillations on submembrane cPKA. In the TIRF experiments, yellow-fluorescent protein (YFP)-labeled cPKA separated from cyan fluorescent protein (CFP)-labeled rPKA and diffused beyond the TIRF range from its submembrane location. Brief pulses of IBMX, a PDE blocker, produced rapid submembrane release of cPKA-YFP and reduction of the YFP signal, which recovered rapidly upon removal of IBMX. Because YFP-labeled cPKA cannot enter the nucleus, a second set of experiments was performed in which cPKA tagged with the fluorescent biarsenical dye FlAsH was measured for nuclear translocation. Brief pulses of IBMX showed much less nuclear translocation than equivalent constant total IBMX, remaining at basal levels.
Modeling Methods
In this section we develop a three-compartment model, including the components in Fig. 1. We also construct a relationship between labeled molecular concentrations and experimental measures for comparison with data and use steady-state data from Dyachok et al. (7) to constrain the dynamic models. Because we have fluorescence data only at the plasma membrane (TIRF zone) and spatially averaged data from the epifluorescence experiments, it is appropriate to construct a simplified model with a small number of compartments to fit parameters. We also find that, with those parameter values, the solutions to the full partial differential equation system rapidly equilibrate spatially within each compartment (see Section S3 in the Supporting Material).
Previous modeling has focused largely on short timescale activities related to cAMP potentiation of exocytosis (15,16), and coupling of cAMP and Ca2+ (17) in β-cells, as well as on short-term behavior of cAMP in other cell types, such as HEK cells (18–21) and cardiac cells (22). These studies have shown how the potent second-messenger cAMP can localize its impact through compartmentalization.
Here we concentrate on the regulation of the nuclear signaling of cAMP through slowing the entry of cPKA into the nucleus, even when cAMP rapidly equilibrates throughout the cell. We model the β-cell as three concentric shell compartments. ACs are located at the plasma membrane embedded in the scaffolding AKAPs. AKAPs also bind G-protein coupled receptors such as glucagonlike peptide-1 receptor, GLP-1R, which activate AC upon stimulation by GLP-1. Production of cAMP activated in this manner is thus initially localized to the submembrane region. Rapid degradation of cAMP by phosphodiesterases, in part attached to AKAPs, limits cAMP diffusion out of the submembrane space. Nearby membrane-bound PKA holoenzymes bind cAMP, releasing cPKA subunits. Active cPKA diffuses to phosphorylation targets in the cytosol and the nucleus.
There are three natural spatial domains of interest:
-
1.
The boundary, which is where cAMP is produced and degraded, and where PKA is primarily activated and TIRF measurements are made;
-
2.
The cytosol, which is where cAMP and cPKA diffuse and react; and
-
3.
The nucleus, which is where cPKA actively controls gene regulation (although we only model the transport, not the signaling).
cAMP generation from adenylyl cyclase
We model cAMP (a) formation as a constant production rate, AC, varied as a parameter to represent the activation level of AC.
cAMP degradation by PDE
Pyne and Furman (12) report a PDE distribution in the β-cell of 60–70% PDE3B, 20–30% PDE4, and 14–30% PDE1, accounting for ∼90% of the PDE activity. A general expression for cAMP degradation due to PDE, including inhibition by IBMX, is given in Rich et al. (21):
As cAMP concentration is comparable to or smaller than Km, typically > 1 μM (23), we make the linear approximation
and let the rate of anchored PDE be given by
| (1) |
This ignores the feedback from kinases on the PDE activity (24), but captures the apparent effective release of cPKA seen in experiments.
Dyachok et al. (7) applied pulsatile IBMX (100 μM IBMX, 1 min on, 3 min off, repeated) and continuous IBMX (25 μM) stimulation, resulting in equal average concentration. We assume that 25 μM IBMX is maximally stimulating in that higher IBMX concentrations do not increase cAMP release.
PDE4 is bound to AKAP (14), and as these cAMP and PDE reactions occur at the membrane, we define a region within ∼100 nm of the plasma membrane, which corresponds to the measurement domain of the TIRF experiments where these reactions take place. As hypothesized in Pyne and Furman (12), we assume that IBMX-insensitive, soluble PDE8 with a cAMP dissociation constant of Km = 0.7 μM is found throughout the cytosol and degrades cAMP at the linearized rate .
We label the boundary, cytosol, and nucleus as regions 3, 2, and 1, respectively, and let V3, V2, and V1 correspond to the volumes of the boundary, cytosol, and nuclear shells, respectively. Neglecting buffering of cAMP by PKA during activation (but see (21)), and modeling cAMP flux out of the submembrane region and across the nuclear membrane yields the following equations for cAMP,
| (2) |
| (3) |
| (4) |
where and , and r1, r2, r3 are the shell thicknesses, and Sj is the outer surface area of the jth shell. Both AC and are nonzero only within the submembrane shell. The soluble PDE is assumed to be active everywhere except in the nucleus.
Activation of PKA by cAMP
Protein kinase-A (PKA) is a holoenzyme consisting of two regulatory subunits in a homodimer (rPKA) that bind cAMP and release two catalytic subunits (cPKA) (25,26). We first write down the equations for native PKA species and then for the labeled species used in the experiments. Lindskog et al. (27) account for PKA activation with two reaction steps, using two cAMP molecules binding at each step. We assume a simplified form of PKA activation
where kb is the dissociation rate constant, which depends upon cAMP, kb(a). In Section S4 in the Supporting Material we carry out a quasi-steady-state reduction of the model of Lindskog et al. (27) for cAMP binding to PKA and releasing cPKA to yield the following dissociation rate constant dependence on cAMP:
| (5) |
Movement of cAMP and PKA
Movement of cAMP in the cytosol is taken to be unbuffered, so the only impediment to cAMP movement is molecular degradation by PDE. PKA is not subject to degradation in the model, and cPKA, once unbound from rPKA, can move throughout the cell, including into the nucleus (10). In most of the simulations, cPKA only moves by diffusion, but Section S2 in the Supporting Material considers the modulating effect of protein kinase inhibitor, which exports cPKA from the nucleus.
The model for the native PKA components then is
| (6) |
| (7) |
| (8) |
| (9) |
where is the total concentration of unbound rPKA homodimer (Rj) and PKA holoenzyme (Pj) in the volume Vj, j ∈ {2, 3} (there is no rPKA in the nucleus, j = 1) and Cj is the free cPKA in volume Vj, j ∈ {1, 2, 3}. If we let CT be the total concentration of cPKA within the entire volume V, conservation requires
which can be solved to eliminate C2. Conservation of rPKA is given by
This leaves seven ordinary differential equations including the equations for cAMP (Eqs. 2–4). Cyclic-AMP at the boundary and in the cytosol exerts its effect through the dissociation reaction rate kb(a) (Eq. 5).
We expect significant numbers of regulatory subunits at the boundary because of either their affinity to plasma membrane bound AKAPs or the experimentally enhanced plasma membrane binding sequence CAAX (7). Although rPKA may also exist in soluble form, we neglect rPKA diffusion. The regulatory subunits are excluded from the nucleus.
The exchange of cPKA between the submembrane and cytosolic compartments is proportional the diffusion coefficient, Dc. Diffusive flux across the nuclear envelope is proportional to the local effective diffusion coefficient, DN, which is smaller than Dc to account for the fraction of the nuclear membrane occupied by pores.
As this does not produce sufficiently slow kinetics, we postulate in addition rapid binding and unbinding of cPKA at the nuclear membrane by some molecule, as yet unknown. If the binding is fast compared to the other timescales in the system, we can apply the rapid buffering approximation (11) to obtain
where k– and k+ are the backward and forward binding rates of cPKA to the nuclear portal proteins; bT is the buffer concentration; and σ = 0.073 is the proportion of the nuclear membrane that is occupied by the pores (28). To make the rise of cPKA sufficiently slow, DN must be in the range 0.01–0.001 μm2/s. Because we assume that Dc ≈ 30 μm2/s (for 41 kDa cPKA), the buffering factor θ must be in the range 200–2000. Although we do not have a candidate for the buffering molecule, the expression for θ suggests some constraints on its properties. The most favorable condition for achieving a large value of θ is for the dissociation constant k–/k+ to be comparable to or larger than the concentration of cPKA at the nuclear membrane, C2. Even in this case, bT would need to be much greater than k–/k+. The larger C2 is, the larger bT would have to be.
This degree of buffering is strong but plausible. If we assume nuclear envelope thickness Δr = 0.1 μm and nuclear radius r = 1 μm, the volume of the shell would be
and
would correspond to ∼105 molecules (or binding sites, if the molecule has multiple binding sites), ∼50 per pore. Alternatively, if the binding molecules were tiled over the surface of the nuclear envelope with a spacing of 10 nm, 105 molecules could be accommodated.
Comparison with experimental measurements
To compare the model with the experiments of Dyachok et al. (7), we need to add equations for the labeled species (see Table 1). For the TIRF experiments we need a measure of rPKA bound to cyan fluorescent protein (CFP) and of cPKA bound to yellow fluorescent protein (YFP) at the boundary. These are determined by
and
where PKAxc3 is the labeled rPKA bounded to unlabeled cPKA in the submembrane region, so the TIRF ratio = CFP/YFP is given by
| (10) |
Table 1.
Reactions with labeled species
| TIRF | Epifluorescence | |
|---|---|---|
| Species | x ≡ rPKA-CFP (monomer) | z ≡ cPKA-FlaSH |
| y ≡ cPKA-YFP | c ≡ cPKA | |
| Reactions | rPKA + 2zPKAr2z | |
| x + yPKAxy | rPKA + c + zPKArcz | |
| x + cPKAPKAxc | rPKA + z + cPKArzc | |
| rPKA + 2cPKAr2c |
Species and reactions included to mirror the experimental conditions of Dyachok et al. (7). Subscripts on PKA refer to rPKA native (r) or labeled (x) and one or two bound cPKA native (c) or labeled (y). See Section S5 in the Supporting Material for the full equations.
In the epifluorescence experiments, fluorescence is obtained along the line of light that emanates from below the cell. There is then a combination of nuclear, cytoplasmic, and boundary fluorescence in the nuclear measure, Nuc, and cytoplasmic and boundary fluorescence in the cytosolic measure, Cyto. In the experimental figures the cells appear relatively flat, so we assume the Nuc and Cyto measurements have the same total fractional length (i.e., γ + ε + r3 – r2), where γ and ɛ are the fractions of nucleus and cytosol, respectively, captured from the vertical fluorescence emission. Based on the appearance of the cells we assume that the radius of the nucleus is γ = r1 and ε = 1. See Fig. S1 in the Supporting Material for a graphic of the geometry.
Nuc and Cyto then are given by
and
where PKArczj = PKArzcj for each j ∈ {2, 3}. The subscripts on PKA refer to rPKA (r) bound to two labeled cPKA(2z), one each of labeled and unlabeled cPKA (cz or zc), or two labeled cPKA (2c) in the shell j. The EPI ratio = Nuc/Cyto. The parameter values are determined by fitting to the steady-state experimental data (as described in the Supporting Material, and listed in Table 2). The values in the table correspond to basal AC production of 1 μM/s, chosen to achieve steady-state level in the epifluorescence model experiment within the 25 min dictated by the actual experiments.
Table 2.
Parameters for both compartmental and spatial models
| EPI | TIRF | ||
|---|---|---|---|
| Dc = 100 μm2 s−1∗ | ka = 1 μM−2 s−1∗ | CT = 0.017 μM† | CT = 0.11 μM† |
| DN = 0.01 μm2 s−1† | s−1∗ | = 1.3 μM† | = 1 μM† |
| Da = 100 μm2 s−1∗ | khi = 100 s−1∗ | RT = 2.5 μM† | RT = 0.8 μM† |
| r1 = 1.0 μm† | klow = 1 s−1† | zT = 0.15 μM† | yT = 1.9 μM† |
| r2 = 5.9 μm† | AC = 1 μM s−1† | = 4.4 μM† | |
| r3 = 0.1 μm† | ga = 6.0 s−1† | xT = 1.5 μM† | |
| Kd = 0.13 μM† |
Estimated from the literature.
Fitted to the data.
Results
Steady-state results
It is convenient to set the model to steady state to investigate the dependence of the levels of cAMP and cPKA on parameters. Inspection of Eqs. 6–8 shows that C is constant across the compartments. Thus, we can calculate the steady state of cAMP ai and feed that forward into the steady distribution for R2 and R3 in terms of a steady, constant C = C∗. Taking Eqs. 2–4 to steady state yields
where
Note that if there is no decay of cAMP in the cytosol and nucleus (i.e., ), then cAMP is uniform across the three compartments,
Feeding forward into the rPKA Eqs. 8 and 9, we have
where kd(a) = kb(a)/ka and, using the conservation of cPKA, we get that C∗ solves the equation
| (11) |
or C∗ is the solution to VCT = f(C), where f(C) is the right-hand side of Eq. 11. Because f(C) is monotonic, a unique steady state is guaranteed. In Fig. 2, we plot VCT and f(C) to represent, graphically, the parameter variation and its effect on the steady state. The black square marks the intersection of f(C) with VCT, which is the steady-state level of free cPKA, C∗. Increasing total cPKA (CT) would raise the black square and increase C∗. For other parameters, it helps to look at their effects on the individual terms of Eq. 11, represented by the colored lines. Increasing total cytosolic rPKA (R2T) would increase the second term of Eq. 11 (raise the red curve), which would raise the black curve and shift the square to the left (reduce C∗), and similarly for R3T. If R2T or R3T were decreased toward 0, C∗ would increase, ultimately approaching CT (i.e., all cPKA would be free). Increasing kd(a3), which corresponds to increasing cAMP in the submembrane shell (Eq. 5), would shift the red curve to the right, lowering the black curve, and moving the black square to the right. Thus, C∗ would increase, as it should, and similarly for kd(a2).
Figure 2.
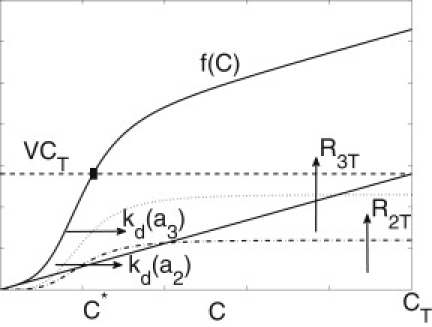
Steady-state cPKA dependence on cAMP and rPKA. The dashed line and solid curve (extending above the dashed line at C∗) are the left- and right-hand sides of Wagner and Keizer (11), respectively. Below the dashed line, the diagonal line and the dotted and dot-dashed curves are the first, second, and third terms on the right-hand side of Wagner and Keizer (11), respectively, and their sum makes up the solid curve.
Simulation of the TIRF and EPI experiments
The experiments of DiPilato et al. (9) showed that while the submembrane and cytosol cAMP and cPKA concentrations equilibrate to near steady-state levels within tens of seconds, nuclear levels of cPKA evolve slowly. Dyachok et al. (7) found that constant elevated IBMX yields high nuclear cPKA, whereas pulsatile IBMX yields low nuclear cPKA measured by epifluorescence. Fig. 3 A shows the basal EPI ratio and the response to oscillating and maintained IBMX in correspondence with the experiments of Dyachok et al. (7) using the three-compartment model. (Note that the epifluorescence experiments provided only the final values, not a full time-course.) Fig. 3 B shows a simulation of the TIRF measurements at the submembrane, which agree well with the experiments. These measurements are unaffected by the nuclear transport rates, but the EPI ratio is. The nuclear concentrations of cPKA for varying nuclear membrane permeabilities (DN = 0.0005 μm2/s, 0.001 μm2/s, and 0.01 μm2/s) and pulsatile IBMX stimulus are shown in Fig. 4. As DN increases, nuclear cPKA (C1) oscillates with increased amplitude and higher mean level. A value of DN > 0.005μm/s and sustained stimulus will produce an EPI ratio of ∼0.95 after 1500 s in agreement with Dyachok et al. (7). Because the EPI ratio data for IBMX pulsatile stimulus protocol consist of a single value taken after 1500 s, it is difficult to compare over the range of oscillations produced by the model. However, even the minimum of the model oscillation in EPI ratio is ∼15% over the baseline. The model predicts that the nuclear levels of cPKA measured as a function of time, though near basal, would be slightly elevated and oscillatory. Fig. S2 shows that those oscillations are largely suppressed if protein kinase inhibitor is added to the model. (Fig. S3 shows that the full spatial model gives very similar results to the three-compartment model, validating our approximation of spatial homogeneity.)
Figure 3.
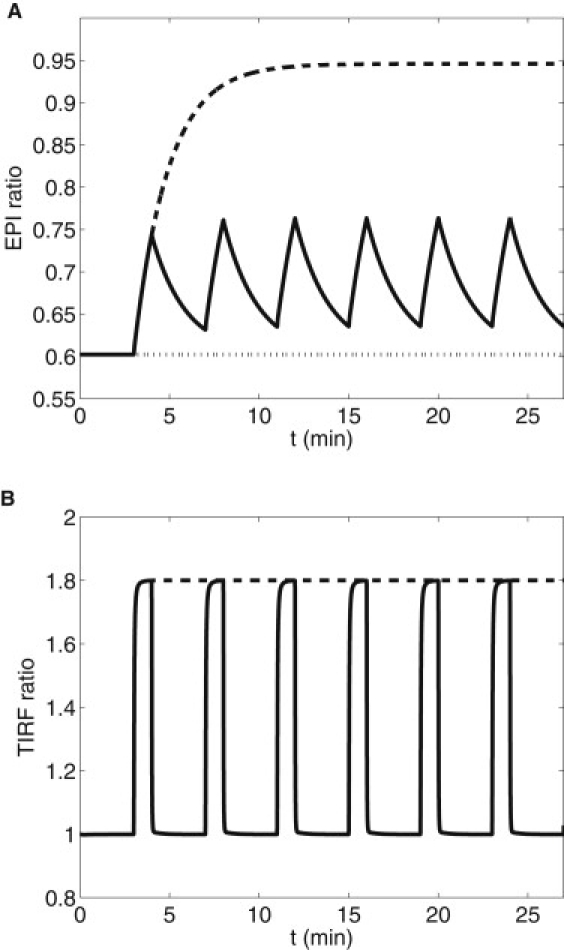
Simulation of epifluorescence (A) and TIRF (B) experiments of Dyachok et al. (7) in response to oscillating and maintained IBMX. Diffusion through the nuclear membrane DN = 0.01. (A) basal (dotted), pulsatile IBMX (on for 1 min every 4 min, beginning at 3 min; solid), and step of IBMX (on at 3 min; dashed). (B) TIRF response to pulsatile and stepped IBMX.
Figure 4.
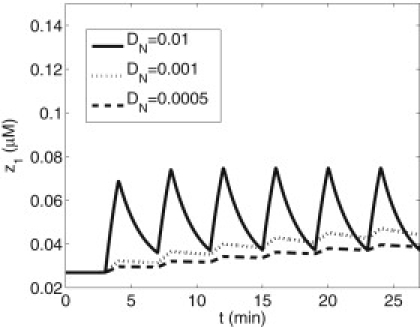
Effects of nuclear envelope diffusion rate for cPKA, DN, on the labeled cPKA, z1. DN = 0.0005 μm/s, 0.001 μm/s, and 0.01 μm/s for the lower, middle, and upper curves, respectively.
Timescale analysis
We now discuss a timescale analysis (see Section S6 in the Supporting Material for details), which shows that the nuclear cPKA is the slowest variable and how it depends on the frequency of the IBMX stimulus. There are three timescales inherent in this system:
-
1.
Fast: Diffusion of cAMP and cPKA.
-
2.
Intermediate: The period of IBMX stimulation.
-
3.
Slow: The passage of cPKA through the nuclear envelope.
We let
define the rate of flux across the nuclear membrane and ω be the frequency of IBMX forcing so we can rescale time in units of stimulus period, τ = ωt. The lowest-order approximation for C1 (from Eq. S15) is then
| (12) |
where ε = δ/ω.
Because δ is proportional to the restricted diffusion coefficient, DN, at the nuclear envelope, Fig. 5 shows formally that decreasing DN reduces the variation in nuclear cPKA, as already seen for selected simulations in Fig. 4. The inset in the figure shows the time course of χ(τ), illustrating that from the point of view of the nucleus, the cPKA signal in the cytosol is a square wave. Note that one unit of τ is one stimulus period. The figure also shows that the amplitude of the nuclear cPKA approaches the amplitude of the cytosolic signal as ɛ increases. If z2 were superimposed in the dimensional three-compartment model simulation in Fig. 4, it would also be a square wave, and z1 would be seen to track z2 more faithfully as DN was increased.
Figure 5.
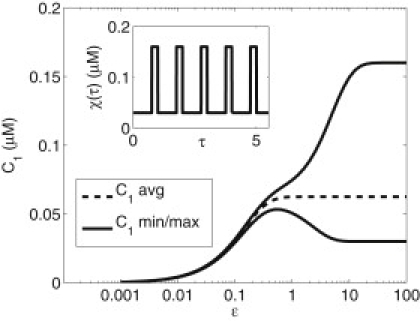
Separation of average and oscillatory components in nuclear cPKA. First-order behavior of C1 from 0 initial state and average behavior (dashed). The maximum and minimum amplitude of oscillations at later times in the stimulus protocol (solid). The three trajectories in Fig. 4 for DN = 0.0005 μm2/s, 0.001 μm2/s, and 0.01 μm2/s correspond to ɛ = 0.1, 0.2, and 2.
Decreasing the period of stimulation with IBMX (increasing ω) would decrease ɛ equivalently to decreasing DN in the nondimensional formulation and would thus reduce the amplitude of nuclear cPKA oscillations. The stimulus period, moreover, is experimentally accessible, so this prediction could be tested by measuring nuclear cPKA amplitude or perhaps the efficacy of cPKA regulation. In Dyachok et al. (7), the stimulation by IBMX had a period of 4 min, which corresponds to ɛ = 1.8.
Alternatives to hindered diffusion at the nucleus
The preceding sections have shown that hindered diffusion at the nuclear membrane could account for the delayed rise in cPKA in the nucleus and is also compatible with the rapid kinetics observed in Dyachok et al. (7) in the subplasma membrane (TIRF) region. In this section we consider alternative models.
One alternative is that cAMP diffusion away from the subplasma membrane region is slow. This might be expected to limit the rise of cPKA in the cytosol, and hence, entry into the nucleus, because free cPKA subunits diffusing in from the periphery could be rebound to excess free rPKA. Restricted diffusion of cAMP would not be compatible with the data of DiPilato et al. (9) in HEK293cells showing that the rise in nuclear cAMP is as rapid in the nucleus as at the plasma membrane. However, in the interest of completeness, we used the three-compartment model to assess the effect of a 100-fold reduction in the diffusion coefficient Da of cAMP in the cytosol (Fig. 6). In the compartmental model this just amounts to a reduced flux from the boundary region to the cytosol, but similar results would be seen with the partial differential equation model. The TIRF ratio under this assumption shows a sharp overshoot, resulting from a similar overshoot in cAMP in the boundary region because cAMP builds up faster than it can diffuse out and liberates cPKA at a very high rate. Such an overshoot was not seen in the experiments of Dyachok et al. (7), and because the time resolution in those experiments was sufficiently fine to have detected it, we conclude that in INS-1 cells, cAMP is not compartmentalized to the point of restricting its flux out of the submembrane region. We do not know whether this conclusion extends to primary β-cells.
Figure 6.

Functional compartmentalization of cAMP. Reducing Da to 1 μm2/s between the submembrane and cytosol compartments from the default value of 100 μm2/s results in an overshoot of cPKA at the submembrane as measured by TIRF and, ironically, an increase of the peak EPI ratio due to restricted reuptake at the submembrane.
In contrast, Rich et al. (18) used a diffusion model to propose that cAMP must be compartmentalized to explain their observations of cAMP-activated ion channels (CNG channels) in HEK293 cells. Specifically, their model showed that cAMP would not rise high enough in the submembrane space to activate the channels unless its diffusion was restricted.
Another possible way to slow down access of cPKA to the nucleus would be to have a small diffusion coefficient for cPKA throughout the cytosol, not just at the nuclear membrane. Simulations with the partial differential equation model (not shown) in which the cytosolic diffusion coefficient is reduced confirm that this would result in a slow rise in the nucleus, but would also produce an overshoot of cPKA in the submembrane region because of the hindered release of cPKA to the cytosol. This would manifest as an overshoot in the TIRF signal similar to that in Fig. 6, and would again not be consistent with the data in Dyachok et al. (7). We find that we are left with no viable alternative to hindered diffusion of cPKA at the nuclear envelope.
Discussion
In response to agonists that raise cAMP in pancreatic β cells, the concentration of the catalytic subunit of Protein Kinase A (cPKA) rises in both the cell periphery, where it potentiates exocytosis of insulin granules, and in the nucleus, where it acts as a regulator of gene transcription through binding to CREB. Where cPKA appears depends on the nature of the stimulus. We have developed here a mathematical model to account for the experiments of Dyachok et al. (7), in which a rapid rise was seen in cPKA at the plasma membrane in response to both oscillatory and maintained IBMX stimuli, although only maintained IBMX could achieve nuclear translocation of cPKA. We confirmed that a three-compartment, ordinary differential equation model was adequate by showing with a full spatial (partial differential equation) model that all species rapidly achieved spatial homogeneity within the cytoplasm using the most plausible set of parameters (Fig. S3).
With the three-compartment model, we were able to reproduce the TIRF and epifluorescence experiments in Dyachok et al. (7) by assuming reduced diffusion of cPKA through the nuclear membrane (Fig. 3). This reduction, we propose, results from the low-pore/nuclear-surface-area ratio but also binding of cPKA to some unspecified molecule as it passes through the nuclear membrane. Harootunian et al. (10) concluded that the translocation of cPKA was not the result of an active binding process but purely diffusive, based in part on the insensitivity of the rate to temperature. Our hypothesis does not contradict this conclusion, provided that the binding is so rapid that, like the buffering of calcium, it can be regarded as instantaneously achieving steady state. In this case, the result of the binding is a reduced effective diffusion constant (11) that would not be affected by variation in the binding rate, such as by changing temperature. Temperature would then also not affect the kinetics of cPKA. We were driven to this hypothesis because an alternative mechanism, a globally reduced diffusion constant for cPKA, results in an overshoot of cPKA at the plasma membrane that was not observed in the experiments. A similar overshoot was found in the model if we assumed reduced cAMP diffusion in the cytosol, which might also help to localize cPKA (Fig. 6). Slow diffusion of cAMP is moreover not compatible with the observations of DiPilato et al. (9). Another way to localize cAMP, and hence cPKA, to the cell periphery, is via degradation by phosphodiesterase (PDE), as shown experimentally by (22,29,29), and in the models of Rich et al. (18,21). However, rates of degradation that are compatible with the likely low rates of cAMP production in β-cells and other small cells are too low to produce a significant gradient in cAMP (see Fig. S3). Nonetheless, in larger cells such gradients may play a bigger role (22). Conditions under which a gradient of cAMP would be predicted are shown in Fig. S5 and discussed further in Section S3 in the Supporting Material.
The multiple timescales in the system lend themselves to perturbation analysis (two-timing). From this analysis we predict that the amplitude of nuclear cPKA depends strongly not only on the submembrane level of cPKA generated, but also the frequency of stimulation (Fig. 5). The perturbation analysis further predicts that nuclear cPKA would be entrained by the oscillatory stimulus with an amplitude that would increase with the period of the stimulation. The model predictions are robust to variations in the fast processes, such as cAMP production and cPKA release, or errors in how the model represents them, as their only role is to conspire to produce a rise in cAMP at the nuclear envelope that is rapid relative to the timescale of nuclear entry. As a corollary, a critical test of the model is that the predictions should hold for isolated nuclei as well as intact cells.
The period of IBMX stimulation in Dyachok et al. (7) was chosen to mimic typical calcium oscillations in β-cells because calcium activates the predominant adenylyl cyclase isoform in β-cells, ACVIII. This period (∼4 min) is too small to result in much nuclear translocation of cPKA. In contrast, maintained high calcium, such as would result from continuous electrical spiking activity or maintained stimulation of the glucagonlike peptide (GLP-1) receptor, would result in significant translocation.
This would be functionally appropriate as it could be considered a stress condition for the β-cell that would require the activation of a nuclear response program, perhaps enhanced cell protective mechanisms or cell proliferation. From this point of view, one could summarize the roles of rapidly oscillating versus maintained stimuli as follows: Episodic challenges, such as normal meals, are met by increasing β-cell function (increased release of insulin per cell) through a combination of increased calcium and increased cAMP in the periphery, which enhances the efficiency of calcium-mediated exocytosis. Chronic challenges, such as persistent overnutrition leading to hyperglycemia or elevated fatty acids, are met through both increased function and increased β-cell mass (larger, more robust cells or production of new cells) triggered in part by nuclear entry of cPKA.
We have not addressed here the stimulation of cAMP production by calcium, but this model should dovetail with a model of shorter term dynamics that does address the calcium activation of both ACVIII and effectors such as calmodulin and PDE4 (27). Fridlyand et al. (17) have another model using mechanisms from Yu et al. (30) that can account for both in-phase and anti-phase oscillations of cAMP and calcium. Combining our model with such elements may shed further light on the functional consequences of the various oscillatory patterns on a wide range of timescales exhibited by β-cells. Finally, we suggest that, although the details of cAMP and PKA regulation likely differ widely among cell types, the simple mechanism described here for distinguishing acute and chronic signals and choosing the appropriate response may have broad application.
Supporting Material
Five figures, three tables, and 40 equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00541-2.
Supporting Material
Acknowledgments
We thank Anmar Khadra for a careful reading of the manuscript.
A.S. was supported and B.P. supported (in part) by the Intramural Research Program of the National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases.
References
- 1.Holst J.J., Deacon C., Bjerre-Knudsen L. On the treatment of diabetes mellitus with glucagon-like peptide-1. Ann. N. Y. Acad. Sci. 1998;865:336–343. doi: 10.1111/j.1749-6632.1998.tb11193.x. [DOI] [PubMed] [Google Scholar]
- 2.Kim W., Egan J.M. The role of incretins in glucose homeostasis and diabetes treatment. Pharmacol. Rev. 2008;60:470–512. doi: 10.1124/pr.108.000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Holz G.G., Kang G., Chepurny O.G. Cell physiology of cAMP sensor EPAC. J. Physiol. 2006;577:5–15. doi: 10.1113/jphysiol.2006.119644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hatakeyama H., Takahashi N., Kasai H. Two cAMP-dependent pathways differentially regulate exocytosis of large dense-core and small vesicles in mouse β-cells. J. Physiol. 2007;582:1087–1098. doi: 10.1113/jphysiol.2007.135228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Doyle M.E., Egan J.M. Mechanisms of action of glucagon-like peptide 1 in the pancreas. Pharmacol. Ther. 2007;113:546–593. doi: 10.1016/j.pharmthera.2006.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.White M.F. Insulin signaling in health and disease. Science. 2003;302:1710–1711. doi: 10.1126/science.1092952. [DOI] [PubMed] [Google Scholar]
- 7.Dyachok O., Isakov Y., Tengholm A. Oscillations of cyclic AMP in hormone-stimulated insulin-secreting β-cells. Nature. 2006;439:349–352. doi: 10.1038/nature04410. [DOI] [PubMed] [Google Scholar]
- 8.Daniel P.B., Walker W.H., Habener J.F. Cyclic AMP signaling and gene regulation. Annu. Rev. Nutr. 1998;18:353–383. doi: 10.1146/annurev.nutr.18.1.353. [DOI] [PubMed] [Google Scholar]
- 9.DiPilato L.M., Cheng X., Zhang J. Fluorescent indicators of cAMP and EPAC activation reveal differential dynamics of cAMP signaling within discrete subcellular compartments. Proc. Natl. Acad. Sci. USA. 2004;101:16513–16518. doi: 10.1073/pnas.0405973101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Harootunian A.T., Adams S.R., Tsien R.Y. Movement of the free catalytic subunit of cAMP-dependent protein kinase into and out of the nucleus can be explained by diffusion. Mol. Biol. Cell. 1993;4:993–1002. doi: 10.1091/mbc.4.10.993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wagner J., Keizer J. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 1994;67:447–456. doi: 10.1016/S0006-3495(94)80500-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pyne N.J., Furman B.L. Cyclic nucleotide phosphodiesterases in pancreatic islets. Diabetologia. 2003;46:1179–1189. doi: 10.1007/s00125-003-1176-7. [DOI] [PubMed] [Google Scholar]
- 13.Langeberg L.K., Scott J.D. A-kinase-anchoring proteins. J. Cell Sci. 2005;118:3217–3220. doi: 10.1242/jcs.02416. [DOI] [PubMed] [Google Scholar]
- 14.Willoughby D., Cooper D.M. Ca2+ stimulation of adenylyl cyclase generates dynamic oscillations in cyclic AMP. J. Cell Sci. 2006;119:828–836. doi: 10.1242/jcs.02812. [DOI] [PubMed] [Google Scholar]
- 15.Chen Y.D., Wang S., Sherman A. Identifying the targets of the amplifying pathway for insulin secretion in pancreatic β-cells by kinetic modeling of granule exocytosis. Biophys. J. 2008;95:2226–2241. doi: 10.1529/biophysj.107.124990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pedersen, M. 2007. A Calcium-Based Model of Fast Exocytosis in Insulin-Secreting β-Cells. Poster at: Mathematical Biosciences Institute Workshop on Diabetes.
- 17.Fridlyand L.E., Harbeck M.C., Philipson L.H. Regulation of cAMP dynamics by Ca2+ and G protein-coupled receptors in the pancreatic β-cell: a computational approach. Am. J. Physiol. Cell Physiol. 2007;293:C1924–C1933. doi: 10.1152/ajpcell.00555.2006. [DOI] [PubMed] [Google Scholar]
- 18.Rich T.C., Fagan K.A., Karpen J.W. Cyclic nucleotide-gated channels colocalize with adenylyl cyclase in regions of restricted cAMP diffusion. J. Gen. Physiol. 2000;116:147–161. doi: 10.1085/jgp.116.2.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rich T.C., Fagan K.A., Karpen J.W. A uniform extracellular stimulus triggers distinct cAMP signals in different compartments of a simple cell. Proc. Natl. Acad. Sci. USA. 2001;98:13049–13054. doi: 10.1073/pnas.221381398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rich T.C., Karpen J.W. Review article: cyclic AMP sensors in living cells: what signals can they actually measure? Ann. Biomed. Eng. 2002;30:1088–1099. doi: 10.1114/1.1511242. [DOI] [PubMed] [Google Scholar]
- 21.Rich T.C., Xin W., Conti M. Cellular mechanisms underlying prostaglandin-induced transient cAMP signals near the plasma membrane of HEK-293 cells. Am. J. Physiol. Cell Physiol. 2007;292:C319–C331. doi: 10.1152/ajpcell.00121.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Saucerman J.J., Zhang J., McCulloch A.D. Systems analysis of PKA-mediated phosphorylation gradients in live cardiac myocytes. Proc. Natl. Acad. Sci. USA. 2006;103:12923–12928. doi: 10.1073/pnas.0600137103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Beavo J.A. Cyclic nucleotide phosphodiesterases: functional implications of multiple isoforms. Physiol. Rev. 1995;75:725–748. doi: 10.1152/physrev.1995.75.4.725. [DOI] [PubMed] [Google Scholar]
- 24.Conti M., Beavo J. Biochemistry and physiology of cyclic nucleotide phosphodiesterases: essential components in cyclic nucleotide signaling. Annu. Rev. Biochem. 2007;76:481–511. doi: 10.1146/annurev.biochem.76.060305.150444. [DOI] [PubMed] [Google Scholar]
- 25.Hofmann F., Bechtel P., Krebs E. Concentrations of cyclic AMP-dependent protein kinase subunits in various tissues. J. Biol. Chem. 1977;253:1441–1447. [PubMed] [Google Scholar]
- 26.Beavo J.A., Bechtel P.J., Krebs E.G. Activation of protein kinase by physiological concentrations of cyclic AMP. Proc. Natl. Acad. Sci. USA. 1974;71:3580–3583. doi: 10.1073/pnas.71.9.3580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lindskog M., Kim M., Kotaleski J.H. Transient calcium and dopamine increase PKA activity and DARPP-32 phosphorylation. PLOS Comput. Biol. 2006;2:e199. doi: 10.1371/journal.pcbi.0020119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kirschner R.H., Rusli M., Martin T.E. Characterization of the nuclear envelope, pore complexes, and dense lamina of mouse liver nuclei by high resolution scanning electron microscopy. J. Cell Biol. 1977;72:118–132. doi: 10.1083/jcb.72.1.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zaccolo M., Magalhães P., Pozzan T. Compartmentalization of cAMP and Ca2+ signals. Curr. Opin. Cell Biol. 2002;14:160–166. doi: 10.1016/s0955-0674(02)00316-2. [DOI] [PubMed] [Google Scholar]
- 30.Yu X., Byrne J.H., Baxter D.A. Modeling interactions between electrical activity and second-messenger cascades in Aplysia neuron R15. J. Neurophysiol. 2004;91:2297–2311. doi: 10.1152/jn.00787.2003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


