Dendritic Signals Command Firing Dynamics in a Mathematical Model of Cerebellar Purkinje Cells

Abstract

Dendrites of cerebellar Purkinje cells (PCs) respond to brief excitations from parallel fibers with lasting plateau depolarizations. It is unknown whether these plateaus are local events that boost the synaptic signals or they propagate to the soma and directly take part in setting the cell firing dynamics. To address this issue, we analyzed a likely mechanism underlying plateaus in three representations of a reconstructed PC with increasing complexity. Analysis in an infinite cable suggests that Ca plateaus triggered by direct excitatory inputs from parallel fibers and their mirror signals, valleys (putatively triggered by the local feed forward inhibitory network), cannot propagate. However, simulations of the model in electrotonic equivalent cables prove that Ca plateaus (resp. valleys) are conducted over the entire cell with velocities typical of passive events once they are triggered by threshold synaptic inputs that turn the membrane current inward (resp. outward) over the whole cell surface. Bifurcation analysis of the model in equivalent cables, and simulations in a fully reconstructed PC both indicate that dendritic Ca plateaus and valleys, respectively, command epochs of firing and silencing of PCs.

Introduction

The cerebellum has only two inputs: climbing fibers (CFs) and mossy fibers (MFs). MFs contact excitatory granule cells (GCs) whose axons (parallel fibers (PFs)) activate the Purkinje cells (PCs) and stellate cells (SCs) that inhibit PCs via a feedforward network. The CFs, PFs, and SCs thus converge onto the PCs, whose simple spike (SS) discharge is the sole output of the cerebellar cortex. The SS patterns are crucial for controlling posture and balance, achieving fine coordination of complex movements and adaptation of ocular responses, and learning conditioned reflexes (1). Therefore, it is essential to understand the mechanisms behind these patterns to elucidate the cerebellum's contribution to the motor system.

PCs process synaptic inputs via a complex set of nonlinear membrane properties. Both soma and dendrites produce large-amplitude spikes and smaller-amplitude plateaus (2,3). Plateaus are depolarizations that survive the end of their triggering stimulus and last from tens of milliseconds to seconds. This dual electroresponsiveness relies on distinct ion current distributions in the soma and dendrites. In the soma, voltage-dependent Na channels sustain both the SS and underlying subthreshold plateaus on which they systematically ride (2,4). In dendrites, spikes and plateaus are sustained by high-threshold, voltage-dependent P/Q Ca channels (5). Unlike somatic signals, spikes have a higher threshold than plateaus in dendrites. They are observed in vivo only upon CF activation, which triggers so-called complex spikes (CSs) (4,6). The interaction between intrinsic somatic and dendritic signals and its role in setting PC firing patterns remains incompletely understood.

PCs display two stable states in vitro: a quiescent down state and an SS firing up state (2,7). In vivo, PCs also exhibit two states: epochs of SS firing and pauses of variable duration (8,9). Transitions between these states can be triggered by CF inputs, but they can also occur spontaneously (7,8). An underlying bistable mechanism cannot account for such spontaneous transitions in the absence of synaptic noise. Moreover, the limited synaptic fluctuations observed in vitro or in vivo in anesthetized animals are unlikely to account for spontaneous transitions (8,10). By contrast, a mechanism displaying states of finite duration would directly account for the spontaneous transitions observed both in vitro and in vivo. Plateau potentials are an attractive putative mechanism to explain spontaneous transitions, especially given their duration range (11), which encompasses that of SS firing epochs/pauses observed in vivo (6,8).

Llinás and Sugimori (4) were the first to propose that dendritic plateaus could be responsible for the triggering and maintenance of SS firing in the soma. Experimental amputation of the dendrite demonstrated that dendrites provide a capacitive load that raises the SS threshold in the absence of synaptic excitation, but also an inward current to the soma during synaptic excitation (12). Moreover, it was shown that bias currents, mimicking background synaptic inputs, modulate the propagation of CF responses down to the PC axon (13). Unfortunately, Llinas and Sugimori's hypothesis cannot be tested pharmacologically because channel blockers eliminate both plateaus and spikes. It also has proved elusive to most biophysical models, which cannot explain how a single-channel type can underlie both fast spikes and lasting plateaus (14,15). However, our group theoretically demonstrated that an interplay between P/Q Ca channels and two high-threshold, noninactivating K channels explains the cardinal features of dendritic Ca spikes and plateaus (11). Moreover, this model (hereafter referred to as the Genet and Delord (G&D) model) predicts that transient SC inputs can elicit outlasting hyperpolarizations (valleys) in PC dendrites. The pauses in SS firing with variable duration that have been observed in PCs after inhibitory input volleys (16) could evidence dendritic valleys. Thus, in accord with the hypothesis proposed by Llinás and Sugimori (4), dendritic valleys could account for the spontaneously resetting pauses in SS firing observed in vivo (6,8).

In this study, we investigated the generalized hypothesis that active dendritic electric signals command patterns of SS firing in PC. Specifically, we addressed the following questions: 1), can dendritic plateaus and valleys propagate to the PC soma; and 2), do dendritic signals determine steps and pauses in SS firing? We tackled these issues by performing a dynamical system analysis of the G&D model in equivalent cable representations of a reconstructed PC. We also simulated the model in the fully reconstructed PC with the NEURON software to cross-validate our results. The model quantitatively reproduces the cardinal features of PC, including Na-Ca bursts (4), SS frequencies (7,17), and the recently identified hysteresis in the frequency-current relation (18).

Methods

Scope and strategy

PCs display a repertoire of transient and lasting signals respectively referred to as spikes and plateau potentials in the literature. The mathematical model investigated here focuses on the dendritic propagation of Ca-dependent, large-amplitude spikes and self-sustained plateaus as previously reported (2,3), and their impact on fast (∼1.5 ms), large-amplitude (∼60-80 mV) somatic firing. Our model extends the isopotential G&D model to a whole PC by 1), distributing it over dendrites of a reconstructed PC (19); and 2), endowing the soma with a new biophysically grounded model of its electroresponsiveness. Below, we derive a set of partial differential equations (PDEs) that govern the dynamics of this model. The solutions of these equations were searched in three increasingly complex representations of Shelton's PC architecture (19): 1), an infinite cable to identify which signals can be propagated by dendrites; 2), electrotonic equivalent cables to account for impedance mismatches at branch points and termination of dendrites at various distances from the soma; and 3), a detailed representation of the cell to cross-validate previous results.

Model equations

The dynamics of the membrane potential V (mV) are described by the cable equation:

$$C\frac{\partial V}{\partial t}=\frac{R_d}{2R_i}\frac{{\partial }^{2}V}{\partial x^2}-\left(I_{CaP}+I_{Kdr}+I_{Ksub}+I_L\right)+I_s,$$ (1)

where x denotes the space coordinate along the principal dendritic axis, C (μF/cm²) is the specific membrane capacitance, R_i (kΩcm) is the cytoplasm resistivity, R_d (cm) is the local dendritic radius, and I_s (nA/cm²) is the density of the synaptic currents. The MF system can carry tonic and phasic inputs to dendrites, and we accordingly write I_s = I_dc + I_ϕ . The model retains the basic set of membrane currents used by Genet and Delord (11): those of P-type Ca (I_CaP), delayed rectifier (I_Kdr), subthreshold (I_Ksub) K channels, and a leakage current (I_L) (see Section II of the Supporting Material). We ascertained that the model keeps its overall properties when other active currents found in PCs are added to its basic formulation (Supporting Material Section II). The internal calcium concentration ([Ca]_i, μM) PDE was derived by adding a longitudinal Ca²⁺ diffusion term to the balance equation of Ca²⁺ ions (Eq. 12 of Genet and Delord (11); see Section I). However, simulations using realistic values for the Ca²⁺ diffusion coefficient (20) failed to show significant differences in Ca dynamics between the full model and a version without Ca diffusion. Therefore, all of the results illustrated below were obtained with the following simplified PDE:

$$\frac{\partial {\left[Ca\right]}_i}{\partial t}=-{\left[1+\frac{{\left[B\right]}_T/K_d}{{\left(1+{\left[Ca\right]}_i/K_d\right)}^2}\right]}^{-1}\left[\frac{{10}^{-9}{I}_{Ca}{R}_d}{F\delta \left(2R_d-\delta \right)}+\frac{2k\left({\left[Ca\right]}_i-{\left[Ca\right]}_b\right)\left(R_d-\delta \right)}{\delta \left(2R_d-\delta \right)}\right],$$ (2)

where [B]_T and K_d (μM) are respectively the concentration and dissociation constant of a buffer modeling Ca-sequestering proteins in PCs, and [Ca]_b is the basal Ca²⁺ concentration. Eqs. 1 and 2 are completed with a PDE describing the local dynamics of a gating variable, n (activation of I_Kdr):

$$\frac{\partial n}{\partial t}=\left(n_{\mathrm{\infty }}-n\right)/{\tau }_n,$$ (3)

where n_∞ and τ_n are respectively the (V-dependent) equilibrium value and time constant of n (Section I).

Results and Discussion

Unifying mechanism for the dual electroresponsiveness of the soma and dendrites

Equations 1–3 reduce to the G&D model after the spatial derivative in Eq. 1 is zeroed. We first recall the properties of the G&D model because they are the backbone of the model presented here. I_CaP underlies the depolarization of both plateaus and spikes, in agreement with experiments (4). I_Ksub balances moderate levels of I_CaP (obtained, e.g., upon PF activation), resulting in lasting plateaus (Fig. 1 A). Higher levels of I_CaP (obtained, e.g., by CF activation) cannot be balanced by I_Ksub and result in large-amplitude Ca spikes repolarized by I_Kdr (Fig. 1 B). The model bifurcation diagram with I_dc as the bifurcation parameter summarizes these properties (Fig. 1 C). This diagram exhibits an S-shaped region, Ω, with two branches formed by resting (R) and plateau stable (P) states connected by a middle branch (M) of saddle points. The M states act as thresholds between the R and P states, so that the model is bistable within Ω: a depolarizing I_ϕ can switch it from the R state to the P state, whereas a hyperpolarizing I_ϕ can induce the opposite transition (Fig. 1, A and D). Low V time derivative values resulting from distortions of the model's vector field at the left of Ω (Fig. 7 B of Genet and Delord (11)) explain the finite-duration plateaus elicited from the R state (Fig. 1 A). Symmetrical distortions at the right of Ω allow long hyperpolarizations from the P state, termed valleys, to outlast their stimulus (Fig. 1 D). For larger I_dc, the P state eventually destabilizes and leads to firing of Ca spikes (Fig. 1, B and C). According to the model, the background MF activity, mimicked by I_dc, strongly affects the PCs' dendrite response to phasic inputs. From negative values, increasing I_dc lengthens the plateaus until their duration diverges at the left boundary of Ω, Inf (Ω). Beyond the right boundary of Ω, Sup (Ω), further increases in I_dc decrease the valley's duration. The model displays bistability within Ω over the entire range of dendritic radii found in PCs, i.e., 0.5–6.0 μm (19) (not shown). The G&D model thus reproduces both infinite and spontaneously terminating transitions between the R and P states. As demonstrated below, the spatially extended model is able to travel CS-like waves made of an initial Ca spike followed by plateaus/valleys. To avoid confusion, we restrict the use of the term “plateaus/valleys” to those that spontaneously reset dendritic responses lacking an initial Ca spike.

Figure 1.

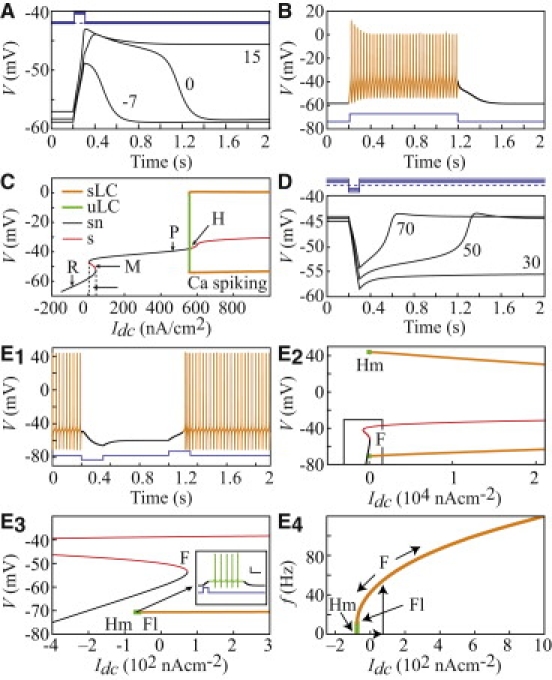
Local models of dendritic and somatic dual electroresponsiveness (see text). (A) Plateaus triggered by a depolarizing current pulse (100 ms, 130 nA/cm², blue traces) with different I_dc values (nA/cm²). (B) Ca spiking (I_ϕ = 10³ nA/cm². (C) Bifurcation diagram of the dendritic model. R: resting state; M: middle branch; P: plateau; Ω: bistability zone; H: Hopf bifurcation; (u)sLC: (un)stable limit cycles; sn: stable node; s: saddle. (D) Valleys triggered by a hyperpolarizing current pulse (100 ms, −130 nA/cm²) with different I_dc values. (E) Bifurcation analysis of the isolated soma model. (E₁) Soma bistability (I_ϕ = −150 nA/cm² and 150 nA/cm²). (E₂) Bifurcation diagram. F, Fl, Hm: fold, flip and homoclinic bifurcations. Inset: Spontaneously resetting Na plateau with I_dc lying between Hm and Fl; scale bars: 20 mV/ 200 ms. (E₃) Magnification of the rectangle shown in E₂. (E₄) f-I relation.

To address the impact of dendritic signals on SS firing, we investigated the soma's intrinsic electroresponsiveness with an original isopotential model including I_Ksub and a realistic description of the peculiar Na current of PC (Section I). With no I_dc, this model spontaneously fires SS but can be silenced by a hyperpolarizing I_ϕ, indicating bistability between a down (D) and an up (U) state (Fig. 1 E₁). In upstroke mode (i.e., increasing I_dc), SS firing arises from D at a fold (F) bifurcation (Fig. 1 E₂). In downstroke mode, the firing frequency can be decreased below its rheobase value (hysteresis) and firing eventually vanishes at a saddle homoclinic bifurcation (Hm) (situated below F; Fig. 1 E_3–4) as predicted by a recent model (19). However, in opposition to that model (19), SS firing in our model destabilizes at a flip bifurcation (Fl) between Hm and F. This feature is crucial because, for I_dc ∈ [Hm, F1], it endows depolarizing I_ϕ with the capacity to trigger the spontaneously resetting Na plateaus (Fig. 1 E₃, inset) observed experimentally (2). This analysis suggests that both the soma and dendrites of PCs are bistable: dendrites can be switched between two stable states (R and P), whereas the soma can be switched between a silent mode and an SS-firing one (D and U). In both cases, a transient balance between I_Ksub and an inward current (I_CaP in dendrites or the resurgent component of I_Na in the soma) accounts for finite-duration plateaus (Section I). This finding provides additional support for the notion that I_Ksub plays a key role in PC electrogenesis.

Dendritic processing of Ca-dependent spikes and plateaus/valleys

The ability of PC dendrites to propagate the above Ca-dependent electric signals involves two factors. The ratio of the membrane currents generated by plateaus/valleys and spikes to the axial current loss along dendrites is the first determinant. The peculiar morphology of PC dendrites adds geometric factors: impedance mismatches at the tree branch points impede propagation of active signals, whereas reflection of axial currents at the dendrite tips boosts propagation (21).

Infinite cable case

To investigate the propagation of Ca-dependent spikes and plateaus/valleys in a formal way, we idealized the complicated PC dendrites as an infinite straight cable. Indeed, the constant speed of the expected solutions allows the model equations to be rewritten as ODEs in a co-moving frame accompanying these waves (Section III), and the solutions correspond to intrinsically propagated signals in PC dendrites.

Dendritic bistability

The traveling system has resting points with V, Ca, and n values identical to those of the original model (Eqs. 1–3) and its spatially uniform version (11), with the additional coordinate V_ξ = 0 (i.e., no V change). Therefore, each stationary state in the R, M, and P branches of the bifurcation diagram of the uniform system translates into a spatially uniform solution of the PDE system. All resting states in the traveling system are unstable according to classic algebraic criteria (22). However, the stability of the resting states of a continuously distributed dynamical system rewritten in a co-moving frame is unrelated to the stability of the corresponding uniform states of the original system (22). Simulations of the dynamics of small V perturbations from these states in long cables approximating the infinite dendrite show that the R and P uniform states are stable, whereas the M ones are unstable. In theory, the bistability found in the G&D model could thus extend to the entire dendritic tree. To test this hypothesis, we searched homoclinic orbits connecting the manifolds of each R and P state to themselves in the traveling system, as evidence for traveling spikes and plateaus/valleys. We also searched heteroclinic orbits connecting one state to the other as evidence for traveling fronts switching the entire cable between its P and R uniform states. Synaptic inputs that are able to trigger these waves are investigated in the next section.

Ca spikes propagate

To identify traveling Ca spikes, we searched large-amplitude homoclinic and heteroclinic solutions of the traveling system. Fig. 2 A₁ displays the speed of the different solutions identified as a function of I_dc. Starting from the left, one first encounters S₁, a branch of homoclinic solutions on the R state. When I_dc is increased, S₁ gives birth to five other branches in an S-shaped curve (solid box). The solid diamond indicates the propagating solutions' subthreshold to full Ca spikes, which we analyze in the next section. Fig. 2 A₂ is a magnification of the solid box with representative wave solutions in the time domain. Branch S₁ corresponds to a traveling Ca spike starting from and ending on R after a plateau. The plateau duration increases with I_dc and becomes infinite at 26.52 nA/cm² (Fig. 2 A₃). At this bifurcation point, S₁ is replaced by S₂, a branch of heteroclinics extending up to Sup(Ω), where the Ca spike switches the system from R to P. S₅ is symmetric to S₂, with the Ca spike switching the system from P to R. In S₆ (I_dc > Sup(Ω)), the spike starts from and ends on P after a valley. When I_dc is increased, the valley duration decreases down to zero at a bifurcation point (I_dc = 561.2 nA/cm²; solid circle in Fig. 2 A₁) where S₆ is replaced by a branch of traveling trains of Ca spikes (not illustrated). Simulations of the model in long dendrites proved that the traveling solutions on branches S_1-2, and S_5-6 are stable. Two additional branches of heteroclinics were found in Ω: S₄ was identified for I_dc ∈ ]Inf(Ω), 37.5[ and consists of orbits connecting M to R, whereas S₃ corresponds to orbits connecting M to P and was found for I_dc ∈ ]37.5, Sup(Ω)[. S₃ and S₄ have no physiological meaning because they start from an unstable state that cannot be actually achieved, due to natural V fluctuations (resulting from spontaneous synaptic potentials and ion channel flickering). Similar results were obtained for any radius in the range of Shelton's PC dendrites (not shown). The predicted range of Ca spikes' propagation speeds (10–20 cm/s) matches the range of observed speeds (23).

Figure 2.

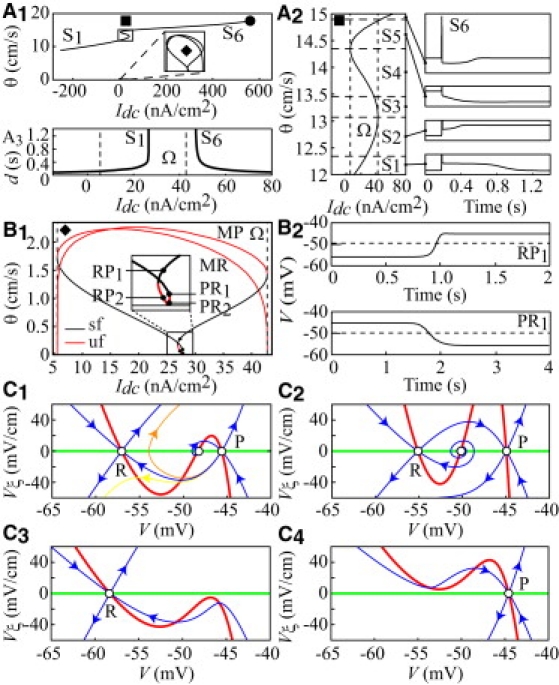
Infinitely long dendrite. (A) Ca spikes propagate. (A₁) Bifurcation diagram of traveling Ca-spike solutions. Propagating fronts between R and P subthreshold to Ca spikes are found in Ω (♦); (•), emergence of traveling Ca spikes trains. (A₂) (Left) Enlarged view of the “▪” box. (Right) Samples of unitary traveling Ca spikes from branches S_1-2 and S_5-6 (branches S_3-4 are unstable). (A₃) Plateau and valley duration (d) in S₁ and S₆ versus I_dc. (B) R ↔ P fronts propagate. (B₁) Enlarged view of the “♦” box; uf: unstable fronts, sf: stable fronts. (B₂) Examples of RP₁ and PR₁ fronts. Dashed lines indicate the M state voltage. (C) Plateaus and valleys cannot propagate. V (green) and V_ξ (red) nullclines and stable and unstable manifolds (blue) of steady states of the 2D simplified model rewritten in the ξ reference frame, for different I_dc values (nA/cm²): 15 (C₁) and 33 (C₂) inside Ω, and 0 (C₃) and 45 (C₄) outside Ω. In C₁, orange and yellow unstable manifolds are for θ = 0.45 and 0.55 cm/s, and the blue one is for 0.497 cm/s. θ = 0.23 in C₂ and 1.00 in C_3-4.

Dendrites propagate R↔P fronts

We also found heteroclinic solutions, indicating traveling fronts between the R and P dendritic with I_dc ∈ Ω (solid diamond in Fig. 2 A₁, enlarged in Fig. 2 B₁). We found traveling fronts connecting R to P (RP), P to R (PR), M to R (MR), and M to P (MP) states. Starting from Inf(Ω), one first encounters the MP branch. Such fronts cannot be observed experimentally due the practical impossibility of achieving the unstable M state. The MP branch terminates at Sup(Ω) and is replaced by branch RP₁. The RP₁ branch ends at I_dc = 26.88 nA/cm². It is replaced by a branch of similar fronts (RP₂) that show smaller propagation speeds and smoother voltage changes compared to the RP₁ fronts (not shown). RP₂ ends at I_dc = 27.64 nA/cm², where the front propagation speed vanishes. On the right of the bifurcation diagram in Fig. 2 B₁, the MR branch emerges with a zero propagation speed. Because of the instability of M states, we do not discuss this branch further. The MR branch terminates at Inf(Ω) and is replaced by PR₁. PR₁ ends at I_dc = 27.8 nA/cm² and gives birth to branch PR₂, whose fronts have smaller propagation speeds than the PR₁ fronts. Simulations of PDE in long cables yielded only front solutions with speeds consistent with those of the PR₁ and RP₁ solutions, demonstrating that these fronts are stable whereas the PR₂ and RP₂ ones are unstable. Fig. 2 B₂ shows examples of P→R and R→P fronts in the time domain.

Plateaus and valleys fail to propagate

Propagating plateaus/valleys were expected as small-radius homoclinic solutions of the traveling system. We failed to identify such solutions, which suggests that plateaus/valleys cannot propagate. However, these solutions could have escaped our tracking in the four-dimensional (4D) phase space of the traveling system. We derived a definitive conclusion using a simplified version of the model that captures its essential dynamics and assumes instantaneous activation of I_Kdr as well as equilibrium values for [Ca]_i at each time point (Section III). This 2D model has the same resting points as the full model, and has the advantage that homo-heteroclinics can easily be visualized. Fig. 2 C₁ illustrates the phase portrait of the 2D model for I_dc < Inf(Ω), i.e., where the full model can produce a PR traveling front (branch PR₁, Fig. 2 B₁). At θ = 0.497 cm/s, the P unstable manifold merges with the R stable manifold. This heteroclinic connection corresponds to a PR traveling front, and its speed is of the same order as that in the full model (0.86 cm/s). The symmetrical topology of the vector field for I_dc > Sup(Ω) accounts for RP fronts in the full model (Fig. 2 C₂). Similarly to the PR fronts, the propagation speed of the RP fronts is smaller in the 2D model than in the full model (0.23 vs. 0.60 cm/s). These differences arise from the simplifications we made in the 2D model. Instantaneous I_Kdr activation decreases the inward membrane current during depolarization, which decreases the RP propagation speed. In contrast, the smaller propagation speed of the PR fronts results from the instantaneous [Ca]_i equilibrium, which reduces the current provided by cable regions in the R state to switch the remaining regions from P to R. These results hold for any dendritic radius for which Ω exists (not shown).

Now, in Fig. 2 C₃ we sketch the phase-plane of the 2D model for I_dc = 0 nA/cm², a value at which the uniform model produces plateaus in response to depolarizing stimuli (Fig. 1 A). Whatever θ, the V_ξ nullcline of the 2D model is located below the V nullcline for all V > V_R, so that a trajectory leaving R along the right branch of its unstable manifold remains inside the lower half-plane. Moreover, upon time reversal, trajectories leaving R along its stable manifold cross the middle branch of the V_ξ nullcline twice, so that the trajectory remains inside the lower half-plane. Therefore, the stable and unstable manifolds cannot merge in these conditions, which implies that no small-radius homoclinic is connecting R to itself, and thus no propagating plateaus can occur. This finding holds for any I_dc < Inf(Ω) and for P points, which cannot form homoclinic loops with I_dc > Sup(Ω) (Fig. 2 C₄). Thus, according to our model, neither finite-duration plateaus nor valleys can propagate in PC dendrites.

Electrotonic equivalent cable models of a PC

Unifying explanation for the CS variability. The existence of traveling CS waveforms suggests that dendrites actively propagate these signals using the classical spike mechanism. Although this hypothesis is supported by several experimental reports showing CS propagation over the whole dendrite (24), it is challenged by experimental evidence of occasional failures (25). Moreover, we are still lacking a comprehensive explanation for the fact that CS responses exhibit a spectrum of different shapes. To tackle both of these issues, we simulated the G&D model in an equivalent somatofugal cable representation of Shelton's PC (Section III). We explored the effects of I_dc on the shape of the responses triggered by a CF input. Let us denote the responses starting from R and ending on R after Ca spikes and a plateau as RspR (R→spikes→plateau→R) responses. Fig. 3 A₁ displays examples of RspR responses for five different I_dc values. Increasing I_dc smoothly lengthens the late plateau component in these responses. This reproduces the plateaus with variable duration-ending CSs observed in vivo (26), which are lengthened by membrane depolarizations (27). The plateau duration becomes infinite at I_dc = −24.9 nA/cm², and between this value and Sup(Ω), CF activation triggers a burst of Ca spikes followed by a switch to P (RsP responses; Fig. 3 A₁). Now, starting with the P state and depolarizing I_dc, the CF triggers a burst of Ca spikes, followed by a plateau ending on R (I_dc ∈ [Inf(Ω), −12.75]; Fig. 3 A₂). The plateau duration of these PspR responses increases with I_dc and diverges at −12.75 nA/cm², where it triggers PsP responses. The shape of the PsP responses is hardly sensitive to an I_dc increase up to 28.54 nA/cm². There, a marked shape change occurs: the burst is terminated by a larger-amplitude Ca spike that switches the entire cable to R (Fig. 3 A₃). These PsR responses persist up to 29.65 nA/cm². With larger I_dc, responses to the CF consist of a burst of Ca spikes ended by valley potentials whose duration smoothly decreases with increasing I_dc (PsvP responses; Fig. 3 A_3–4). The transition between PsR and PsvP responses at I_dc = 29.65 nA/cm² coincides with divergence of the valley duration. All waveforms of Fig. 3 A propagate to the tip of the somatofugal cable. This supports the premise that the occasional propagation failures of Ca spikes are due to the activation of inhibitory synapses at dendritic branch points (25). Moreover, simulations in equivalent somatopetal cables showed that Ca spikes do not propagate in the centripetal direction (not shown), in agreement with experimental results (28). Taken together, these results provide the first comprehensive explanation for the whole range of observed dendritic responses to the CF input (1).

Figure 3.

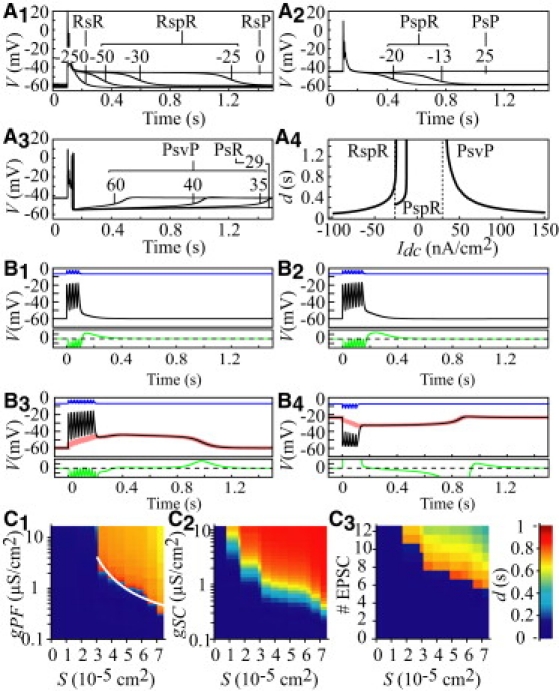
Electroctonic equivalent cables. (A) Responses of the somatofugal cable to CF inputs. Starting from either R or P, the CF (g_CF = 1.2 μS uniformly distributed over smooth dendrites) triggers a burst of Ca spikes (s), followed by a plateau (p) or a valley (v) and convergence to R or P. Samples of RsR, RspR, RsP (A₁), PspR and PsP (A₂), and PsvP and PsR (A₃) responses are shown with the corresponding I_dc value (nA/cm²). (A₄) Duration (d) of plateaus and valleys versus I_dc. (B) Responses of somatopetal reduced cables to distal inputs. Membrane potential of the farthest dendritic point from the soma (black) stimulated by EPSC/IPSC trains, and the soma (red). Green: Membrane current at the stimulation site. Blue: Synaptic currents. Five (B₁), eight (B₂), and 10 (B₃) EPSCs with g_PF = 0.1 μS/cm²; I_dc = −25 nA/cm². Six IPSCs (B₄) with g_SC = 0.5 μS/cm² and I_dc = 45 nA/cm². (C) Duration of plateaus (C₁: six EPSCs; C₃: g_PF = 0.5 μS/cm²; I_dc = −25 nA/cm²) and valleys (C₂: 6 IPSC; I_dc = 45 nA/cm²) as a function of synaptic parameters. S (absicca): Stimulated membrane surface.

Dendritic plateaus/valleys are threshold signals spreading over the entire cell. The above results suggest that Ca plateaus and valleys are intrinsically unable to propagate. Yet, previous in vitro works have established that PF inputs in distal spiny PC dendrites can trigger Ca plateaus (4,24) that correlate with low internal Ca elevations spreading over the entire cell. This suggests that dendrites can actually propagate Ca plateaus in the somatopetal direction. To resolve this issue, we simulated the model in equivalent cables, capturing the PCs' electrotonic characteristics in the somatopetal direction (Section III). The results illustrated in Fig. 3 were obtained by stimulating spiny branchlet 68 (20) which is the farthest from the soma in electrotonic units, and hence the best choice for investigating the somatopetal conduction of plateaus/valleys. The branchlet was stimulated with trains of PF excitatory postsynaptic currents (EPSCs) to compare the model's response with in vivo recordings of dendritic plateaus (29). The voltage responses of the most distal segment in branch 68 to an increasing number of EPSPs are illustrated in Fig. 3 B_1–3. After five EPSPs (Fig. 3 B₁), V relaxes exponentially toward its resting value. A shouldering appears after the last EPSP with eight shocks (Fig. 3 B₂), but it is only after 10 EPSPs that the model produces a long-duration plateau potential (Fig. 3 B₃). These responses closely mimic the threshold properties of plateaus in the dendritic recordings of Campbell et al. (29) (see their Fig. 4). These authors could only speculate about the propagation of these signals in the dendritic tree from their point recordings. However, superimposed voltage traces in the soma and dendrites of the equivalent cable on Fig. 3 B₃ show that the plateau potential triggered in the spiny branch invades the entire tree and the soma without any attenuation, whereas the dendritic capacitance heavily filters the EPSPs. Fig. 3 B₄ illustrates the responses to six SC inhibitory postsynaptic currents (IPSCs) delivered to spiny branch 68, with the equivalent cable previously turned to its plateau state by a depolarizing tonic current, and shows that valleys can also invade the entire PC.

Figure 4.

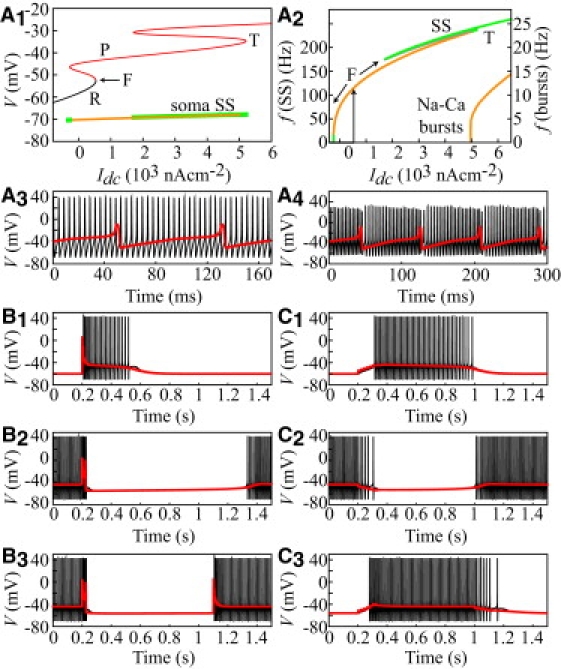
Dendritic control of SS firing. (A₁) Bifurcation analysis of the somatofugal equivalent cable with I_dc (injected into the active soma). Thick line: Lower bound of the somatic limit cycle corresponding to SS firing (orange: stable, green: unstable). Thin lines: Dendritic voltage at electrotonic distance L = 0.15 from the soma (the spike amplitude is ∼0 at this distance). SS firing arises, as in the isolated soma, from a fold (F) bifurcation and is substituted for by Na-Ca bursting at a torus (T) bifurcation. (A₂) F-I_dc curves of SS and Na-Ca bursts (see text). (A₃) Na-Ca bursting (I_dc= 6×10³ nAcm⁻²; black: soma voltage; red: dendritic voltage). (A₄) The same as A₃, with g_c raised to 15 μS. (B) Dendritic control of SS firing by CF (see text). (B₁) I_dc = −25 nA/cm². (B₂) I_dc = 45 nA/cm². (B₃) I_dc = 25 nA/cm². (C) Dendritic control of SS firing by PF EPSCs and SC IPSCs (see text). (C₁) Volley of six EPSCs (50 Hz), g_PF = 0.5 μS/cm², I_dc = −25 nA/cm². (C₂) Volley of six IPSCs (50 Hz), g_SC = 0.5 μS/cm², I_dc = 45 nA/cm². (C₃) Same PF volley as in C₁ followed by the same SC volley as in C₂ with I_dc = 25 nA/cm².

These findings agree with experimental reports that dendrites actually propagate Ca plateaus in the somatopetal direction, but contradict the results obtained above with the infinite cable, which establish that Ca plateaus/valleys cannot propagate. We resolved this discrepancy as follows: First, we examined the membrane current (I_m) along somatopetal equivalent cables during plateaus and valleys. The bottom traces in Fig. 3 B display the I_m time course in the compartment that is most distal from the stimulation site. When the response from the cable is passive (short EPSC trains), I_m remains outward after the stimulus offset (B_1-2). By contrast, I_m is inward at the stimulus break when the EPSC number is large enough to trigger a rectangular plateau (B₃). The instant t_I at which I_m changes sign in the compartment farthest from the excitation locus precisely corresponds to the instant at which V crosses the middle branch of the V-nullcline in that compartment (not illustrated). Recall that this branch locates the voltage threshold of rectangular plateaus in the isopotential model (see Fig. 4 C in Genet and Delord (11)). Since the passive properties imply that the amplitude of the membrane depolarization elicited by a focal I_ϕ decays with distance from the stimulation site, V must have crossed as well the V-nullcline at every intermediate locus along the cable before t_I. Hence, the synaptic inputs that drive V across the voltage threshold at all points of the cable trigger a rectangular plateau. Symmetrically, before we can observe a valley potential, the membrane current must become transiently outward on all cable points at the stimulus break (Fig. 3 B₄). This explains why, according to simulations of the model in equivalent cables, the whole cell generates a plateau/valley altogether. However, all points along the cell do not cross the plateau/valley threshold at the same time. The rising phase of plateaus/valleys travels with low speeds, on the order of the conduction speed of the electrotonus (a few centimeters per second; Section VII). By contrast, the decaying phase of plateaus/valleys travels at speeds three orders of magnitude larger due to the slow dynamics of these signals. These properties are at odds with the definition of a traveling wave (i.e., all points travel with a unique speed), which prevents us from classifying the plateaus/valleys as propagating spikes. Two specific features of plateaus/valleys also preclude their classification as a passive electrotonus: 1), they have uniform amplitude over the cell surface, whereas an electrotonus exhibits attenuation with distance from the stimulation locus; and 2), they exhibit a voltage threshold, which is a characteristic property of active electric signals. These original properties suggest that Ca plateaus/valleys may represent a hybrid mechanism of electric signaling in PC dendrites, mixing properties of the electrotonus and spikes. We further characterized this mechanism by investigating the dependence of the plateau/valley threshold on synaptic inputs. Fig. 3 C₁ displays the plateau duration in the somatopetal cable as a function of g_PF and of the surface, A, of the spiny branch over which this excitatory conductance was distributed. The total magnitude of the stimulating conductance therefore is G_PF = Ag_PF. Fig. 3 C₁ first shows that the g_PF values that can trigger plateaus diverge as the conductance is delivered to smaller portions of the spiny branch. The figure then shows a nonmo notonous behavior: with increasing g_PF values, the plateau length first increases and then decays (for constant stimulated surface). Indeed, strong stimuli increase [Ca²⁺] in the dendrites, which shifts the balance of membrane currents during plateaus toward hyperpolarizing currents and shortens the plateau. We found that the g_PF level necessary to trigger a plateau with a given duration scales as 1/A (the white curve in Fig. 3 C₁ illustrates this relationship for 1 s plateaus). This implies that a total synaptic conductance G_PF is required to trigger plateaus with a given duration, regardless of the spatial distribution of this conductance. As illustrated in Fig. 3 C₂, the same conclusions hold for the symmetrical valley case. Finally, Fig. 3 C₃ shows that the number, n_syn, of EPSCs in branch 68 required to trigger a plateau diminishes when A increases (valleys share the same characteristics; not illustrated). Thus, the magnitude of the plateaus/valleys' threshold synaptic conductance does not depend on the conductance time course, but on its time integral. We quantitatively evaluated this conclusion by computing the total amount of electric charges supplied by synaptic currents, $Q_{syn}=\underset{0}{\overset{\mathrm{\infty }}{\int }}{G}_{syn}\left(t\right)\left(V\left(t\right)-E_{syn}\right)dt$ (with $syn\in \left\{PF,SC\right\}$), and the amount of charges required to make voltage trajectories at all points along the cable crossing the plateau threshold, $Q_m=C\sum _{i=1}^{n_c}{\int }_{V_R}^{V_{Th}}{A}_{i}d{V}_i=C{A}_T\left(V_{Th}-V_R\right)$, where n_c is the number of compartments of the cable, and A_is are the respective compartment areas. Consistent with our conclusion, we found that Q_syn ∼1.5 Q_m. It has been estimated that coactivation of ∼50 PF is required to depolarize a PC by 10 mV from rest (Ref. 77 in the Supporting Material). Given that V_Th – V_R is ∼13 mV in our model, we estimate that the simultaneous activation of ∼100 PF should suffice to trigger a dendritic plateau, involving a tiny fraction (∼0.1%) of PF inputs to PC. Similar results were obtained with valley potentials or when the inputs are delivered to other spiny branches of the tree, showing that plateaus and valleys can be triggered from any dendritic location once the synaptic inputs exceed an electric charge threshold. Once this threshold is crossed, the plateaus/valleys spread over the entire neuron, including its soma.

Dendritic control of PC firing dynamics

Evidence from simulated somatic recordings

To determine how active dendritic signals impact the SS dynamics, we performed a bifurcation analysis of the somatofugal model endowed with the excitable soma studied above. Fig. 4 A₁ shows the superimposed bifurcation diagram of the dendrites and the lower bound of the limit cycle corresponding to SS firing in the soma. The current injected into the soma is the bifurcation parameter. The SS limit cycle of the soma, once the latter is included in the whole cell, retains some of the characteristics found in the isolated soma (Fig. 1 G). However, it also exhibits striking differences that reveal the role of dendrites in SS dynamics. With negative I_dc, the soma is in its D silent state, and the dendrites are in their R state. When I_dc is increased, SS firing emerges in the entire cell at a fold bifurcation, as in the isolated soma (Fig. 4 A_1–2). However, the rheobase current is larger in the whole cell (534.1 nA/cm²) owing to the large capacitive load imposed by the dendrites to the soma. One could expect this passive load to decrease the SS frequency in the whole cell, but it is actually twofold higher (115 vs. 54 Hz) at the rheobase. Although it is counterintuitive, this result is consistent with observations that the minimum SS frequency attainable from the D state increases from ∼20 Hz to ∼100 Hz in adult neurons, paralleling the growth of their dendrites (17). According to our dynamical analysis, this effect stems from the fact that dendrites jump onto their P state at the fold bifurcation (Fig. 4 A₁). Once in the P state, the dendrites' influence on the soma becomes a boosting, depolarizing current during interspike intervals, which explains the higher SS frequencies found in the entire cell. Direct evidence for this mechanism is provided in Section IV of the Supporting Material.

SS firing also retains hysteresis in the whole cell: when one starts from dendrites in the P state and a firing soma, decreasing I_dc below the F point results in stable SS firing with lower frequencies than at the rheobase. The SS firing loses stability below 16 Hz and eventually vanishes at a homoclinic bifurcation, as in the isolated soma. This bifurcation occurs at the lower bound of the P branch (Fig. 4 A₁), confirming that the large current sink constituted by dendrites in their R state prevents tonic SS firing in the soma. In support of these conclusions, our model also reproduces two cardinal features of the f-I_dc relationship: from the rheobase, the SS frequency increases in a close to linear fashion with I_dc up to a maximum value of 233.5 Hz (I_dc = 5011 nA/cm²), where the limit cycle destabilizes. Linearity of the SS frequency-current relationship is well documented in PCs (2,18), and previous studies have shown that mature PCs can fire SS at frequencies > 200 Hz (2,17,30). With further I_dc increases, the model undergoes a supercritical Neimark-Sacker bifurcation (at I_dc = 5011 nA/cm²) at which a stable torus arises from the SS limit cycle (Fig. 4 A_1–2). This bifurcation marks the emergence of a branch of limit cycles corresponding to repetitive bursts of SS terminated by a dendritic Ca spike (Na-Ca bursts). Fig. 4 A₃ illustrates a sample of Na-Ca burst in the model, which qualitatively reproduces this typical firing mode of PC in response to large driving currents (2). Experimentally, Na-Ca bursts have been shown to exhibit a progressive decrease of the SS amplitude and period during the rising foot of Ca spikes (2). We were able to reproduce these features in our model by increasing the dendrosomatic coupling conductance, g_c (Fig. 4 A₄). This proves that the dendritic control of SS firing predicted by the model does not represent an artifact resulting from overestimation of the dendrosomatic coupling. We also used the somatofugal cable endowed with the excitable soma to address the impact of CF-triggered plateaus and valleys on SS firing. Fig. 4 B_1–2 illustrate the time course of the dendritic and somatic voltages after a single CF input for two I_dc values. When $I_{dc}<Inf(\Omega )$, the dendrites are in the R state and the soma is silent. The CF input triggers a Ca spike followed by a dendritic plateau. This plateau triggers SS firing, which terminates at the plateau reset. When $I_{dc}>Sup(\Omega )$, the dendrites are in the P state and the soma fires SS. The CF-triggered Ca spike is followed by a dendritic valley during which SS firing is interrupted (Fig. 4 B₂). Finally, with I_dc ∈ Ω, two consecutive CF inputs trigger bidirectional transitions between the R and P dendritic states, inducing corresponding transitions between the D and U somatic states (Fig. 4 B₃). This result reproduces the toggle-switch capabilities of the CF input (8).

Synaptically triggered dendritic plateaus/valleys command firing/pauses

The above results were derived from a somatofugal representation of PC dendrites. Because dendrites exhibit different electrotonic properties in the centripetal direction, we simulated the model in equivalent somatopetal cables (Section III) to determine whether PF/SC-triggered dendritic plateaus/valleys can also trigger/interrupt SS firing. From rest, a volley of six EPSCs delivered to the dendritic branchlet farthest from the soma triggers a dendritic plateau of ∼750 ms duration (Fig. 4 C₁). This plateau invades the entire neuron, including its soma, in which it elicits an SS firing epoch whose duration precisely matches that of the dendritic plateau. The soma continuously fires SS when the dendrites are turned to their P state by a depolarizing I_dc (Fig. 4 C₂). A train of six IPSCs triggers a dendritic valley during which SS firing is interrupted and firing resumes at the valley break. Identical results were obtained for plateaus/valleys with different durations obtained by varying I_dc. In addition, the same successive PF and SC inputs can respectively trigger R→P and P→R dendritic transitions (D→U and U→D in the soma) when I_dc lies within Ω (Fig. 4 C₃). Thus, dendritic plateaus/valleys triggered by distal inputs can also elicit/break SS firing. All of these results were reproduced in the fully reconstructed Shelton's PC (Section V). This proves that the equivalent cables built in this study reliably capture the PC's electrotonic properties, and supports the soundness of the bifurcation analysis in these cables (which is unfeasible in the fully detailed neuron) and the conclusion that dendrites control SS dynamics.

Comparison with experimental data

Converging evidence suggests that dendrites are a major determinant of PC firing dynamics (12,17), which is unsurprising considering that dendrites account for ∼99% of the PC surface (19,31) and are endowed with active properties. However, the precise role of dendrites remains unclear. On the basis of the results presented here, we propose a hypothesis that unifies the experimental data. First, our simulations show that under weak net synaptic excitation, dendrites impose a large current sink to the soma that accounts for the lower threshold and increased firing frequency of SSs observed after dendrotomy (12). Our study suggests that under a strong synaptic drive, the depolarizing current fed by dendrites (12) evokes dendritic bistability. Under these conditions, dendrites are likely switched to their P state, in agreement with dual patch-clamp recordings from PC soma and dendrites showing that dendrites remain depolarized during interspike intervals (32). In fact, this hypothesis is strongly supported by early dendritic recordings showing that SSs ride on underlying Ca plateaus (4). Our conclusion that dendrites control PC firing is also consistent with studies indicating that the SS threshold lies between the mean voltages of dendritic plateaus and valleys (17,33). Moreover, it has been observed that brief SC inputs trigger dendritic hyperpolarizations and SS firing pauses lasting up to several hundreds of milliseconds (16,34). In addition, dendritic valleys reproduce the as-yet-unexplained nonlinear relation between the duration of the pauses and the number of inhibitory inputs (Section VI). The experimental demonstration that depolarizing currents can shorten these pauses confirms this conclusion. Altogether, our findings quantitatively support the early hypothesis of Llinás and Sugimori (4) that phasic PF inputs must elicit dendritic plateaus to trigger somatic SS firing. We extend this hypothesis by proposing that the spontaneous resetting of both dendritic plateaus and valleys determines the pauses in SS firing. The dependence of plateau/valley duration on the background synaptic current, coupled with the variability of the background currents, would account for the variability of the firing pattern after CF activation. In the model, the complete range of PC responses to phasic inputs requires bias currents ranging from a hyperpolarizing limit (∼−150 nA/cm²) to a depolarizing one (∼150 nA/cm²). The range of background synaptic currents in PCs cannot be estimated directly, as the relationship between PF frequency and the net output of the feedforward inhibition network remains unknown. However, the peculiar electrotonic architecture of PCs allows us to address this question indirectly. PCs are electrotonically very compact in response to steady currents, leading to close to uniform V changes across the neuron (21,31). It has been shown that synaptic currents injected into the PC soma in vitro (via the dynamic-clamp technique) mimic natural in vivo background inputs distributed over the dendrites (35). Hence, the range of injected currents used by Jaeger and Bower (35) may be used as a crude estimate of the range of background inputs experienced by PCs in vivo. Our [−150, 150] nA/cm² range given above, once multiplied by the cell surface, yields a range of currents of ∼[−0.65,1] (nA). The upper current bound triggers an SS frequency of >200 Hz, matching experimental currents required to trigger PC firing with similar high frequencies (2,17). On the other hand, previous studies have demonstrated that uncorrelated inputs into the MF system provide a baseline hyperpolarizing current to PCs whose mean amplitude (∼−0.45 nA (35,36)) is consistent with the lower bound we predict.

Our analysis suggests that PCs may actually have larger computing capabilities than would be expected from their current representation as bistable neurons. Hence, the dendritic control of the PC output by plateaus/valleys allows synchronized PF/SC inputs, putatively signaling salient sensory-motor events, to elicit spontaneously resetting epochs of SS firing and pauses, thus controlling the duration of these traces. In addition, it was recently shown that irregular PC firing in vivo may in fact reflect periods of regular firing with little frequency variability but with interruptions by pauses (37). Such properties are predicted by our model, in which firing frequency is constant during spontaneously terminating plateaus of variable duration. Moreover, the dependence of trace duration on the background synaptic input suggests a novel role for synaptic plasticity in the MF pathway. Rather than setting the gain of the PC I/O relationship, synaptic plasticity could determine the duration of SS firing epochs and pauses, which are essential for motor control.

Supporting Material

Additional explanation, seven figures, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00554-0.