Designing a sensitive and quantifiable nanocolloid assay with dielectrophoretic crossover frequencies

Abstract

Dielectrophoretic nanocolloid assay is a promising technique for sensitive molecular detection and identification, as target molecule hybridization onto the probe-functionalized nanocolloids can change their surface conductance and consequently their dielectrophoretic crossover frequencies. Thus, instead of relying on surface charge density increase after hybridization, as in many capacitive and field effect transistor impedance sensing techniques, the current assay utilizes the much larger surface conductance (and dielectrophoresis crossover frequency) changes to effect sensitive detection. Herein, we present a Poisson–Boltzmann theory for surfaces with finite-size molecular probes that include the surface probe conformation, their contribution to surface charge with a proper delineation of the slip and Stern planes. The theory shows that the most sensitive nanocolloid molecular sensor corresponds to a minimum in the dielectrophoretic crossover frequency with respect to the bulk concentration of the molecular probes (oligonucleotides in our case) during nanocolloid functionalization. This minimum yields the lowest number of functionalized probes that are also fully stretched because of surface probe-probe interaction. Our theory provides the surface-bulk oligonucleotide concentration isotherm and a folding number for the surface oligonucleotide conformation from the crossover frequency, the zeta potential, and the hydrodynamic radius data.

INTRODUCTION

For decades, laboratory based microarray detection for DNA hybridization has been the most reliable technique in the scientific community.¹ However, the use of fluorescence detection limits its usage to lab-based applications only because of its considerable equipment and fluorophore-labeling needs. The same disadvantages also apply for real-time polymerase chain reaction (PCR)—despite claims to the contrary, a viable portable real-time PCR kit has yet to appear. Functionalized nanoparticle and microparticle based assays, with two orders of reduced mass transport times through their large surface volume ratio and high concentration of particles, are proving to be a promising rapid assay platform.² This new assay platform has been used to carry out genetic detection of viruses, bacteria, and other pathogens.^{3, 4, 5, 6, 7, 8, 9, 10} Although fluorescence detection is still done in conjunction with the nanocolloid assay,⁴ the nanocolloid platform also allows label-free and nonfluorescence detection based on electrochemical sensing,⁵ electrophoresis,⁸ and dielectrophoresis (DEP).^{7, 9, 10} DEP relies on the fact that molecular hybridization on the nanocolloid can significantly change its crossover frequency—the frequency at which the induced dipole of the nanocolloid vanishes exactly and changes direction. Since the nanocolloids will swarm toward either the high-field region or the low-field region on a microelectrode, the crossover frequency can be detected by simple visual observation⁷ or impedance sensing.⁶

Our DEP technique is related to impedance sensing assays. DNA hybridization can change the electron transfer rate to a metal electrode and hence effect a significant reduction in impedance, sometimes in the form a constant-phase Warburg spectrum if the reaction is diffusion limited.⁵ If the sample buffer does not allow such Faradic impedance detection, which includes cyclic voltammetry, then, capacitive and field-effect transistor sensing is often used with oligonucleotides functionalized on inert electrodes or semiconductors.¹¹ However, such nonreactive sensing assays rely on the increase in surface charge density after hybridization. As the hybridized DNAs also attract counterions which screen their charges, the sensitivity of such surface-charge density assays is often low. The screening counterions do increase the local ionic strength and conductivity of the electrolyte near the surface. Hence, a far more sensitive hybridization assay would be to detect the change in double-layer conductance after hybridization. Such a non-Faradic conductance assay is most conveniently manifested with dielectric nanocolloid sensors, whose overall conductance is very sensitive to changes in double-layer conductance. The dielectrophoretic crossover frequencies of these nanocolloids are, in turn, very sensitive to their overall conductance. We hence propose a dielectrophoretic nanocolloid sensing assay for DNA hybridization.

Silica and latex nanocolloids are often employed in detection protocols because of their well-known surface chemistry and as their dielectrophoretic crossover frequencies are well documented in literature.^{6, 12, 13, 14, 15, 16} The DEP crossover frequency changes upon hybridization due to differences in electronic, chemical, or physical properties in post- and pretreated nanocolloids with biomolecules.⁷ We shall examine with a detailed quantitative mathematical theory, without fitting parameters, how target molecule hybridization and molecular functionalization alter the charge density, molecular size∕conformation, and double layer conductivity to affect the crossover-frequency shift. In fact, we shall employ DEP to develop the most optimal molecular probe density and conformation for hybridization assays. To do so, we need to reexamine the issue of nanocolloid surface conductance and how functionalized or hybridized molecules affect this property.

THEORY

The classical formulation for DEP states that in the presence of an applied ac electric field (where E is the rms value), and frequency ω (which is the angular frequency∕2π), in a solvent with characteristic permittivity and conductivity, ε_M and σ_M, respectively, the dielectrophoretic force on a particle is given by¹⁷

$$F=2\pi a^3{\epsilon }_M\text{\hspace{0.17em}Re}\left(f_{\text{CM}}\right)\nabla {\left|E\right|}^2,$$ (1)

where a is the radius of the particle. The Claussius–Mossotti factor f_CM for a lossy dielectric homogenous spheroid is¹⁷

$$f_{\text{CM}}=\left(\frac{{\epsilon }_P^{\ast }-{\epsilon }_M^{\ast }}{{\epsilon }_P^{\ast }+2{\epsilon }_M^{\ast }}\right),$$ (2)

where ε^*=ε−2πjσ∕ω is the complex permittivity of the medium (M) and particle (P). The frequency at which the induced dipole exactly vanishes is known as the crossover frequency ω_CO,¹⁷

$${\omega }_{\text{CO}}=\frac{1}{2\pi }\sqrt{\left(\frac{\left({\sigma }_P-{\sigma }_M\right)\left({\sigma }_P+2{\sigma }_M\right)}{\left({\epsilon }_M-{\epsilon }_P\right)\left({\epsilon }_P+2{\epsilon }_M\right)}\right)}.$$ (3)

The crossover frequency for nanocolloids∕biomolecules having higher conductivity and lower permittivity than the solvent can be obtained from Eq. 3 using approximations¹⁸ as it requires the “effective” conductivity and permittivity of the particle—which are almost always very different from the known bulk values, because of the polarizability of the electrical double layer, as discussed in details in this paper. However, for latex and silica particles, which have a lower conductivity than most of the solvents including de-ionized (DI) water, the crossover should not exist at all according to Eq. 3. Researchers have attributed this inconsistency mainly to the existence of a Stern layer^{12, 13, 14, 15, 16, 17, 19} with a small diffuse layer contribution. This Stern layer is assumed to be a nanometer-thick conducting ionic layer around the particle, where the ions are strongly bound to the surface to allow tangential electric flux.¹⁹ The conducting Stern layer increases the nanocolloid conductivity to produce positive DEP of latex and silica nanoparticles in low-conductivity buffer solutions.

Several theories have been put forward to account for the conductance of a dielectric particle with a Stern layer.^{12, 13, 14, 15, 16, 17, 19} The effective particle conductivity σ_P is often stipulated to be the volume average of the intrinsic particle conductivity, the Stern layer conductivity, and diffuse layer conductivity. As such, it is proportional to the Stern layer surface conductance K_S, the diffuse layer conductance K_D, and also the particle size a. For latex and silica particles with negligible intrinsic particle conductivity and no diffuse layer contribution this effective conductivity becomes¹⁹

$${\sigma }_P=\frac{2K_S}{a}+\frac{2K_D}{a}=\frac{2\mu {\sigma }_s}{a}\left(\frac{2K_D}{a}⪡\frac{2K_S}{a}\right).$$ (4)

Although the surface charge density σ_S can be estimated from the zeta potential, the mobility of the counterions μ in the Stern layer is unknown. As such, the Stern layer conductivity has always been estimated empirically.^{12, 13, 14, 15, 16, 17, 19} Moreover, when this Stern layer appears, how it affects the measured zeta potential has not been delineated with a fundamental theory. Earlier theories which sum the conductance of both the Stern layer and the diffuse layer 4 to obtain the particle conductance use the implicit assumption that the currents in both layers are parallel to each other, viz., tangential to the particle surface. Further, these theories model the conduction (electromigration) flux in the diffuse layer but not the diffusive flux that can oppose the electromigration flux. Both the assumptions (parallel Stern layer and diffuse layer conductive fluxes and omission of diffuse layer diffusion flux) break down when the Debye screening length is comparable or more than the particle size and the normal field within it is comparable to the tangential field, as shown in our previous paper.¹²

In our previous paper, we showed that the tangential migration of ions in a double layer gives rise to size-dependent crossover frequency driven by Stern layer conduction and absorption.¹² This earlier theory invokes the linearized Debye–Huckel theory for the double layer and assumes the existence of a surface Stern layer without providing an estimate for its dimension and conductance (the mobility)—both values were estimated empirically as in earlier theories. In this paper, we develop an explicit theory for the Stern layer at low medium conductivity. We show that for large zeta potential (⪢RT∕F), the double layer develops a concentrated polarized layer near the surface that is essentially the Stern layer. This concentrated layer with a large potential drop is bounded by a long diffuse tail with a far smaller potential drop that cannot be described by the Debye–Huckel linear theory. Within the concentrated polarized layer, which we define as a collapsed diffuse layer of thickness λ_s=(2RT∕FE_s), the ion diffusivity retains the bulk value but its ionic strength is sensitive to the conformation and concentration of molecular probes functionalized to the colloid surface. This theory quantitatively accounts for the conductance of the colloid and the measured DEP crossover frequency without any fitting parameter. The collapsed diffuse layer is essentially the speculated Stern layer in earlier theories.

The collapsed diffuse layer region of the double layer is small and of the order of a few nanometers. For medium and strong electrolytes whose zeta potential is much smaller than (RT∕F), the zeta potential can be estimated from the Debye–Huckel linearization as E_Sλ_D, where E_S and λ_D are the surface electric field and the Debye screening length, respectively. For weak electrolytes, however, analysis of the full nonlinear zeta potential from the Boltzmann distribution gives us the nonlinear scaling of the zeta potential with respect to the surface field, 2(RT∕F)ln(E_sλ_DF∕RT), which is much larger than (RT∕F), and the ion distribution cannot be described by the Debye–Huckel theory.²⁰ A thin collapsed layer of dimension λ_s=(2RT∕FE_s) exists near the surface. This thin collapsed layer and the large overall zeta potential value thus suggest that most of the electric field lines are focused into this layer to produce significant electromigration. Thus, we can shift the dielectric jump from the colloid interface to the collapsed diffuse layer∕diffuse tail plane. We can relate the perturbation in potential for the dielectric colloid with a conducting layer (collapsed diffuse layer) to that of a conducting particle.²¹ This allows us to obtain a Stern-layer-like surface conductance term K_λS dependent on the surface charge of the colloidal particle but with bulk diffusivity,²²

$$K_{\lambda S}=\frac{D{\sigma }_s}{2RT∕F}=\frac{\epsilon D}{{\lambda }_S}.$$ (5)

For ε_M⪢ε_P and σ_P⪢σ_M, the crossover frequency from Eqs. 3, 5 is

$${\omega }_{\text{CO}}=\frac{1}{2\sqrt{2}\pi }\left(\frac{2K_{\lambda S}}{a{\epsilon }_M}\right).$$ (6)

The collapsed layer thickness λ_s=(2RT∕FE_s) and the surface charge density σ_S can hence be estimated from the crossover frequency.

To determine the surface charge density in Eq. 5 from the zeta potential requires the solution of the full nonlinear Boltzmann equation,²³

$${\nabla }^2\varphi =\frac{RT}{F{\lambda }_D^2}\text{sinh}\left(\frac{\varphi F}{RT}\right).$$ (7)

Using the boundary conditions that both the electric field and the potential vanish at infinity and the potential at the surface is the zeta potential, Eq. 7 is integrated once to obtain the relation between the surface field and the zeta potential ζ,

$$\zeta =2\left(\frac{RT}{F}\right){\text{sinh}}^{-1}\left(\frac{F{\lambda }_D{E}_S}{2RT}\right).$$ (8)

Since zeta potentials are typically measured from the electrophoretic velocity, they correspond to the potential at the hydrodynamic radius (the slip plane). However, with hydrodynamic screening by large functionalized molecules, the slip plane is typically above the true surface and beyond the Stern layer. Hence, one cannot use the above formula to estimate the surface charge density from the measured zeta potential. Further resolution of the ion and potential distribution outside the collapsed layer is necessary.

Integrating Eq. 7 twice with the above boundary conditions gives the potential distribution as^{22, 23}

$$\varphi =-2\left(\frac{RT}{F}\right)Ln\left(\frac{A\text{\hspace{0.17em}exp}\left(x∕{\lambda }_D\right)-1}{1+A\text{\hspace{0.17em}exp}\left(x∕{\lambda }_D\right)}\right),$$ (9)

where x is measured from the colloid surface and A is related to the zeta potential by

$$A=\frac{1+\text{exp}\left(-\zeta ∕2\left(RT∕F\right)\right)}{1-\text{exp}\left(-\zeta ∕2\left(RT∕F\right)\right)}.$$ (10)

The scrutiny of the detailed ion distribution is important, as the slip plane determined from the hydrodynamic radius is often not located at the surface. We shall use these formulas to estimate the surface field and the surface charge density from the usual relationship²⁴

$$E_S={\sigma }_S∕{\epsilon }_M.$$ (11)

A universal (surface charge independent) asymptotic tail exists for Eq. 9 at large x when ζ is larger than (RT∕F),²²

$$\varphi \sim 4\left(RT∕F\right)\text{exp}\left(-x∕{\lambda }_D\right).$$ (12)

This is the Gouy–Chapman high-zeta potential distribution in the diffuse tail and it resembles a Debye–Huckel-like exponential decay with a universal effective zeta potential. Hence, when the slip plane protrudes into this diffuse plane, we expect the potential distribution (and osmotic pressure) to be independent of the surface charge (field), even though the true zeta potential ζ is still a function of the surface charge. This universal potential distribution will be shown to be responsible for the zeta potential reaching certain saturated values when charge molecules are functionalized onto the surface.

This system of equations can be used to quantify and qualify the data on probe-functionalized nanocolloids by Gagnon et al.^{7, 9} They measure the zeta potential using a commercial zeta potentiometer, the hydrodynamic diameter using light scattering, and also the DEP crossover frequency for 100 nm silica particles functionalized with different oligonucleotide concentrations of 9 nm in length (27 nucleotide bases) in DI water. The hydrodynamic diameter from the zeta potentiometer is indeed about 20 nm larger than that of the bare colloid at high bulk oligonucleotide concentrations (Fig. 2). However, it is significantly lower than that at lower bulk concentrations, suggesting that the oligonucleotides have collapsed onto the silica surface. It is not a complete condensation, however, as the slip plane remains significantly higher than the true surface. Instead, the surface molecules adopt coil-like conformations. This conformation is not surprising as the persistent length of ssDNA is about 1.5 nm or about five bases long. Both the silica nanocolloid and the oligonucleotides are negatively charged, and hence the charge density, zeta potential, and crossover frequency are all expected to increase with the extent of functionalization. This expected trend is, however, not observed in the data shown in Fig. 1, which exhibits curious extrema in the crossover frequency and zeta potential. Only certain fractions of the surface oligonucleotides contribute to the surface charge while others contribute to the mobile ion density in the collapsed diffuse layer.

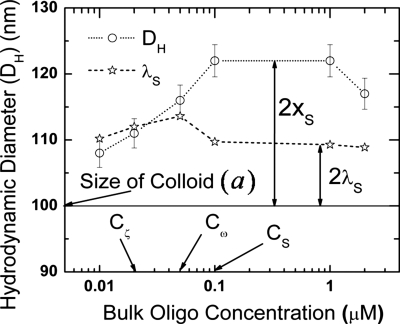
Figure 2.

Variation in hydrodynamic diameter D_H and shift in shear slip plane x_S with change in bulk oligonucleotide concentration. The position of the collapsed layer λ_S, estimated from the crossover frequency, is also indicated for all the bulk concentrations. The important critical bulk oligonucleotide concentrations C_ζ, C_ω, and C_S (as defined in Fig. 1) are also shown.

Figure 1.

Variation in measured zeta potential ζ_M at the slip plane and crossover frequency ω_CO with change in bulk oligonucleotide concentrations. The important critical bulk oligonucleotide concentrations C_ζ, C_ω, and C_S for maximum zeta potential (absolute), minimum crossover frequency, and saturation, respectively, are also shown.

The experimentally measured zeta potential is obtained at the hydrodynamic radius r_H, which is the size of the particle, as seen by the zeta potentiometer. This corresponds to a slip plane location of x_S measured from the surface at x=0. From Eqs. 9, 10, knowing that the measured zeta potential is actually the value at x_S, we can easily obtain the actual zeta potential on the surface of the nanocolloid. The zeta potential can then be converted to an equivalent surface field using Eq. 8. The surface field using Eq. 11 then gives us the surface charge density. The surface charge density can be also derived from the crossover frequency using Eqs. 5, 6. The surface charges calculated through both the methods should always be the same—however, it is not true in our case. The surface charge calculated using crossover frequency is one order of magnitude higher than that from zeta potential measurements.

The inconsistencies are because in our theory thus far, Eq. 11 specifically assumes that the charges are all on the surface without any volumetric distribution. However, as the oligonucleotides with charged backbone stick out of the surface, the charges remain dispersed across the collapsed layer and are not confined to the surface of the nanocolloid. Oligocharges close to the surface contribute to both the surface charge density and the collapsed diffuse layer conductivity while those away from the surface contribute only to the conductivity of the collapsed diffuse layer. To correct for this overcounting of surface charge, we replace ε_M by ε_Mf in Eq. 11, where f is a dielectric correction factor to be determined. Equating the surface charge distribution from crossover frequency to the surface field from zeta potential using modified Eq. 11, E_S=(σ_S∕fε_M) gives σ. Hence, the dielectric correction factor represents the ratio of the “total” surface charge density σ, which includes contributions from the functionalized oligonucleotides in the collapsed layer to the surface charge σ_S that includes only charges on the surface—those of the bare silica charge and those from collapsed oligonucleotides. Knowing the dielectric correction factor, the collapsed layer thickness, and relevant properties of the colloids such as the hydrodynamic radius and the size, we can estimate the number of oligonucleotides attached on the silica surface and the folding number (conformation) of the oligonucleotides. We will also examine the conditions for different configurations of the oligonucleotides at different bulk oligonucleotide concentrations by this theory.

RESULTS AND DISCUSSION

Figure 1 depicts the variation in measured zeta potential at the slip plane and crossover frequency with increasing bulk oligonucleotide concentrations for silica nanocolloid measured in DI water using zeta potentiometer and a quadrupole electrode, respectively.^{7, 9} The zeta potential initially increases (in the negative direction) with increasing bulk oligonucleotide concentration until it reaches a maximum value of ζ_max=22 mV at an oligonucleotide concentration of C_ζ=0.02 μM and then decreases gradually to reach an asymptotic value ζ_S of 16 mV at higher bulk oligonucleotide concentrations beyond C_S=0.1 μM. The crossover frequency decreases initially to reach a minimum at C_ω=0.05 μM while at higher bulk oligonucleotide concentrations it increases until it reaches an asymptotic value. The asymptotic values in zeta potential and crossover frequency are reached at the same bulk oligonucleotide concentration of C_S=0.1 μM. From our result in Eq. 12, the asymptotic value of the zeta potential at large bulk oligoconcentration must correspond to a highly elevated slip plane, which will indeed be confirmed in Fig. 2. It is, however, important to note that the maximum in (absolute) zeta potential is attained at a lower bulk oligonucleotide concentration than the crossover frequency. We will show subsequently that this has an important bearing on the surface configuration of the oligonucleotides on the silica surface.

Figure 2 presents the estimated slip plane location x_S=(D_H−a)∕2 from the hydrodynamic diameter D_H from light scattering experiments and the true diameter of the particles a=100 nm.^{7, 9} The slip plane location is seen to increase with functionalization until it reaches an asymptotic value of about 10 nm from the surface. The estimated collapsed diffuse layer position from the crossover frequency 5 is also shown in Fig. 2. The slip plane lies within the collapsed diffuse layer until C_ζ=0.02 μM, where the zeta potential exhibits the maximum absolute value in Fig. 1. Beyond this intersection, the slip plane is beyond the collapsed diffuse layer and continues to move away from the nanocolloid surface with increasing bulk oligonucleotide concentration until it reaches an asymptotic value of 10 nm at the same concentration C_S, where both the crossover frequency and zeta potential saturate in Fig. 1.

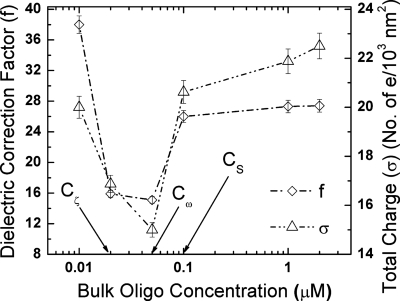
To explain the different extrema and critical bulk oligonucleotide concentrations observed in Figs. 12, we plot the total surface charge density (σ) from the crossover frequency and the dielectric correction factor (f) at different bulk oligonucleotide concentration in Fig. 3. From Fig. 3, we see that f and σ show a remarkable similarity across most bulk oligonucleotide concentrations with a minimum at C_ω=0.05 μM. A physical interpretation of the dependence of both on bulk oligonucleotide concentration offers information about the conformation of the attached oligonucleotides, as we will subsequently show. The total surface charge data σ from Fig. 3 will be used to determine the number of oligonucleotides attached to the silica nanocolloid surface.

Figure 3.

Variation in the dielectric correction factor f and the total surface charge density σ from crossover frequency with change in bulk oligonucleotide concentration. The important critical bulk oligonucleotide concentrations C_ζ, C_ω, and C_S (as defined in Fig. 1) are also shown.

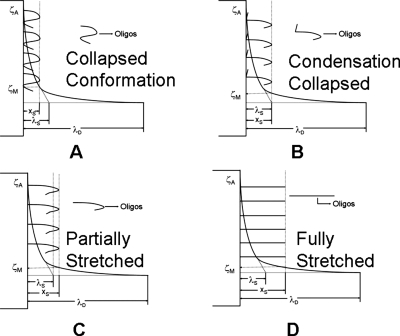
The DNA nanocolloid assay can now easily be quantified and the different observed experimental trends explained. The measured zeta potential at the slip plane and the crossover frequency has two distinct regions depending on whether the slip plane is closer to the surface [Figs. 4a, 4b] or away from the surface [Figs. 4c, 4d] than the collapsed diffuse layer∕diffuse tail plane. The measured zeta potential (absolute) for the first two data points, whose slip plane lies within the collapsed diffuse layer (Fig. 2), shows an increasing trend with bulk oligoconcentration (Fig. 1). We can see from the trends in f, σ, and ω_CO that they all decrease [Figs. 13] in this region. A decrease in σ or ω_CO indicates a decrease in the concentration of free counterions in the collapsed diffuse layer, even though the opposite is expected since the free oligos are expected to bring more mobile counterions into the collapsed layer. This trend can only be explained if the extra osmotic pressure due to increased bulk oligonucleotide concentration drives the collapse of the functionalized oligonucleotides onto the surface [Figs. 4a, 4b]. This collapse reduces the density of the functionalized oligonucleotides in the collapsed layer and also the number of mobile counterions there. As a result, the collapsed layer conductivity diminishes and ω_CO decreases toward the minimum shown in Fig. 1. As more oligonucleotides collapse onto the surface, it should however lead to an increase in the surface charge, which is indeed reflected by an increase in measured zeta potential, as seen in Fig. 1. This concomitant increase in surface charge density (zeta potential) and decrease in screening mobile ion concentration (crossover frequency) are also consistent with a significant decrease in f, as seen in Fig. 3.

Figure 4.

Schematic representation of four possible different conformations of oligonucleotide attachment on the surface of the silica nanocolloid. The relative positions of the diffuse collapsed layer λ_S and slip plane location x_S are shown. Actual ζ_A and measured zeta potential ζ_M values are indicated. (a)–(d) represent four types of conformational states of oligonucleotide linkage: (a) collapsed, (b) condensation collapsed, (c) partially stretched, and (d) fully stretched.

The maximum zeta potential occurs when the hydrodynamic radius is equal to the collapsed diffuse layer [Fig. 4b]. Beyond this point the slip plane lies in the diffuse tail of the double layer. As shown in Eq. 12, the potential drop across the diffuse tail of the double layer is independent of surface charge. However, the measured zeta potential is the difference between the potential at the slip plane relative to the bulk. Thus, it continues to decrease monotonically as the slip plane is further elevated from the surface until both reach asymptotic values corresponding to a slip plane produced by fully extended oligonucleotides. The crossover frequency, on the other hand, depends not only on the surface charge but also on the conformation of the oligonucleotide attached to the nanocolloid surface as seen above. The oligonucleotides now stretch beyond the collapsed diffuse layer post the zeta potential maximum. As they stretch, they move from a condensed collapsed configuration [Fig. 4b] to a partially stretched configuration [Fig. 4c]. This reduces both the total charge and the surface charge contribution from the surface bound oligonucleotides. Hence, f is a measure of total versus surface charge plateaus out, while σ (total charge) decreases, as seen in Fig. 3. This leads to a further decrease in crossover frequency. This phenomenon continues until the minimum in crossover is reached when all the oligonucleotides are fully erected [Fig. 4d]. This corresponds to the maximum separation between each oligonucleotide and is thermodynamically most favorable toward hybridization. Beyond this point, the crossover frequency increases as more and more oligonucleotides are added to the surface. No more addition of oligonucleotides to the silica surface occurs once the slip plane location saturates at 10 nm, roughly corresponding to the 9 nm length of the oligonucleotide. From the saturation point, zeta potential and crossover frequency attain asymptotic values of ζ_S=16 mV and ω_S=2.2 MHz, respectively, with x_S constant at 10 nm.

Thus the minimum crossover frequency shown by functionalized silica nanocolloids is the point of ideal concentration of oligonucleotides on silica surface to study DNA assay at maximum efficacy. It offers the twin advantages of the maximum difference in crossover between hybridized state and unhybridized state with the least conformational resistance to hybridization. These observations are tabulated in Table 1 which represents the necessary conditions for functionalized silica nanocolloids to satisfy the appearance of each conformational mode governed by its interrelation among zeta potential, crossover frequency, and hydrodynamic radius.

Table 1.

Necessary conditions for each conformational state with expressions to calculate the number of oligonucleotides and the number of folds: (a) ζ_max=maximum value of zeta potential, (b) ω_min=minimum value of crossover frequency, (c) l_e=contour length of an oligonucleotide, and (d) C_ζ,C_ω=constant asymptotic value in zeta potential and crossover frequency, respectively.

Surface conformation	Slip plane xS	Slip plane zeta potential ζM	Crossover frequency ωCO	No. of oligonucleotides N0	Folding No.F0
Collapsed	xS<λS	ζM<ζmax	ωCO>ωmin	$N_O=\frac{\pi {\sigma }_O{a}^2}{e_l{l}_e}$	$\left(\frac{l_e}{x_S}\right)$
Condensation collapsed	xS=λS	ζM=ζmax	ωCO>ωmin	$N_O=\frac{\pi {\sigma }_O{a}^2}{e_l{l}_e}$	$\left(\frac{l_e}{x_S}\right)$
Partially stretched	xS>λS	ζM<ζmax	ωCO>ωmin	$N_O=\left(\frac{\pi {\sigma }_O{a}^2}{e_l{\lambda }_S}\right)\left(\frac{x_S}{l_e}\right)$	$\left(\frac{l_e}{x_S}\right)$
Fully stretched	xS>λS	ζM<ζmax	ωCO=ωmin	$N_O=\frac{\pi {\sigma }_O{a}^2}{e_l{\lambda }_S}$	1
Saturated conformation	xS=le	ζM=Cζ	ωCO=Cω	$N_O=\frac{\pi {\sigma }_O{a}^2}{e_l{\lambda }_S}$	1

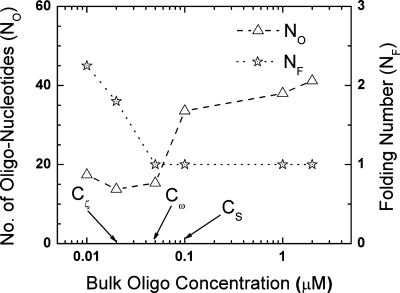
Each conformational state demonstrates the presence of certain number of oligonucleotides and the number of folds (the folding number). Using bare surface measurements,⁷ the surface charge density of the carboxylated silica nanocolloid is σ_B=5e∕10³ nm². Knowing the total surface charge density σ from Fig. 3, the number of surface charges (σ_O) that the oligonucleotides contribute can be estimated by subtracting σ_B from σ. Further, the charge per unit length of each individual oligonucleotide can be approximated as e_l=3 e∕nm.²⁵ The total number of electrons for a particle with size a and surface charge σ_O is (πσ_Oa²). The charge contribution from the oligonucleotides is only from those oligonucleotides which lie in the collapsed layer. Thus the number of oligonucleotides can then be estimated as N_O=πσ_Oa²∕(e_ll), where l is the length of the oligonucleotide in the collapsed layer. If the collapsed layer is less than the slip plane (x_S≤λ_S), then the whole oligonucleotide lies in the collapsed layer and l=l_e, where l_e is the contour length of the oligonucleotide (9 nm here), which leads to N_O=πσ_Oa²∕(e_ll_e). However, when (x_S>λ_S), the oligonucleotides can stretch beyond λ_S, yet fold onto itself inside the collapsed layer [Fig. 4c]. As such we need to define a folding number N_F, which relates to how many folds the oligonucleotides make. The folding number is N_F=(l_e∕x_S), where (N_F=1) is the zero folding state which refers to the state of completely stretched conformation at the minimum crossover. Hence, in the semicollapsed configuration [Fig. 4c], the number of oligonucleotides can be inferred by introducing the correction factor (x_S∕l_e) to give N_O=((πσ_Oa²)∕(e_lλ_S))(x_S∕l_e). The folding number expression N_F=(l_e∕x_S) can also be extended to calculate the number of folds when (x_S≤λ_S). From the minimum crossover all the oligonucleotides stand up and stretch beyond the collapsed diffuse layer. The folding number N_F goes to 1. Hence for all points from the minimum crossover frequency and beyond the length of the oligonucleotide in the collapsed layer is λ_S and the number of oligos is thus N_O=πσ_Oa²∕(e_lλ_S). The folding number and number of surface oligonucleotides with increasing bulk oligonucleotide concentration are shown in Fig. 5, and the different equations to explicitly calculate the same are tabulated in Table 1.

Figure 5.

The number of folds that an oligonucleotide makes (folding number N_F) along with the number of oligonucleotide linkages to the silica nanocolloid surface (N_O) is plotted with change in bulk oligonucleotide concentration. The important critical bulk oligonucleotide concentrations C_ζ, C_ω, and C_S (as defined in Fig. 1) are also shown.

Theoretical calculation of the number of oligonucleotides on the 100 nm silica nanocolloid surface is in good agreement with literature data.²⁶ What is offered in Fig. 5, however, is a full isotherm for a range of bulk concentrations. The fold number of less more than 3 is also consistent with the fact that the 26 base oligo is no more than 5 persistent lengths long. A monotonic decrease in the folding number with increasing bulk oligonucleotide concentration is observed until saturation at C_ω as expected (Fig. 5). The number of oligonucleotides has asymptotic behaviors at low and high bulk oligonucleotide concentrations, as it is difficult to increase the number of oligonucleotide linkages to the surface of the nanocolloid. This is because of steric hindrance due to the collapsed configuration of the oligonucleotides at low concentrations. At high concentrations there is steric hindrance again because of the polymeric brushlike structure of the oligonucleotides on the surface of the nanocolloid. This further reillustrates the fact that the optimal separation in oligonucleotides for maximum hybridization efficacy corresponds to a minimum DEP crossover frequency.

CONCLUSION

To conclude, we have presented a quantification methodology for DNA nanocolloid assay based on an observation of the solution to the Poisson–Boltzmann equation at large zeta potential, with proper correction to the slip plane location, the identification of the Stern layer, and the conductivity within the assay. The collapsed diffuse layer imparts a high zeta potential to the dielectric colloid and the actual zeta potential measured at the slip plane gives an estimate of the oligonucleotide coverage and conformation by comparing the actual intrinsic surface charge with the experimental value obtained at the hydrodynamic radius. This is achieved by introducing a dielectric correction factor to account for the assumption that all the charges are confined to the surface of the nanocolloid. The variation in the zeta potential, hydrodynamic radius, along with crossover, gives necessary conditions to determine the conformation of the oligonucleotide on the surface of the colloid. The optimum surface oligonucleotide coverage for DNA assay is at the dielectrophoretic crossover minima. Such an understanding of surface oligonucleotide coverage helps to quantify and optimize DNA silica nanocolloid assay.