Performance of the score systems Acute Physiology and Chronic Health Evaluation II and III at an interdisciplinary intensive care unit, after customization

Abstract

Background:

Mortality predictions calculated using scoring scales are often not accurate in populations other than those in which the scales were developed because of differences in case-mix. The present study investigates the effect of first-level customization, using a logistic regression technique, on discrimination and calibration of the Acute Physiology and Chronic Health Evaluation (APACHE) II and III scales.

Method:

Probabilities of hospital death for patients were estimated by applying APACHE II and III and comparing these with observed outcomes. Using the split sample technique, a customized model to predict outcome was developed by logistic regression. The overall goodness-of-fit of the original and the customized models was assessed.

Results:

Of 3383 consecutive intensive care unit (ICU) admissions over 3 years, 2795 patients could be analyzed, and were split randomly into development and validation samples. The discriminative powers of APACHE II and III were unchanged by customization (areas under the receiver operating characteristic [ROC] curve 0.82 and 0.85, respectively). Hosmer-Lemeshow goodness-of-fit tests showed good calibration for APACHE II, but insufficient calibration for APACHE III. Customization improved calibration for both models, with a good fit for APACHE III as well. However, fit was different for various subgroups.

Conclusions:

The overall goodness-of-fit of APACHE III mortality prediction was improved significantly by customization, but uniformity of fit in different subgroups was not achieved. Therefore, application of the customized model provides no advantage, because differences in case-mix still limit comparisons of quality of care.

Introduction

Scoring systems are used in intensive care to control for various case-mix factors in order to compare patient populations. Score-based predictions of mortality in ICU patients may be used for quality assurance and comparison of quality of care [1,2,3]. If a scoring system is intended to be used in a patient population that is different from the original population used in the development of the system (development sample), then it should be validated in this new population [4,5,6,7].

Calibration measures how closely mortality prognosis fits the observed mortality. Poor calibration in a patient sample does not necessarily mean that the quality of care in that particular ICU is better or worse than in the development sample.

Several clinical case-mix as well as nonclinical factors are not accounted for by such scoring systems [8]. The overall fit of a score in a particular patient sample can be improved by customization using logistic regression. This is possible for the whole population in question [9], but can also be done independently for specific subgroups [10,11]. In the latter case, the customized score can only be used in this subset of patients. If a customized model derived from the whole population is used, then uniformity of fit for the relevant subgroups should still be tested. Knowledge of the influence of subgroups is important, because future changes in case-mix may compromise the improvement achieved by customization.

The aim of the present study was to test the performance of APACHE II and III, after customization of these scales for use in future assessment of quality of care in our unit.

Patients and methods

Patients

Over a 3-year period (October 1991-October 1994), 3382 patients were consecutively admitted to the 12-bed interdiciplinary ICU of a 571-bed, university-affiliated community hospital. For the APACHE II analysis, 274 patients who were readmitted to the ICU, 208 patients who were in the ICU for less than 4 h, 16 patients who were admitted for dialysis only, two patients who were younger than 16 years and 87 patients with missing data were excluded. Thus, 2795 patients were included in the analysis. For APACHE III, 79 patients who were admitted to rule out myocardial infarction and 55 cardiosurgical patients were excluded, leaving 2661 for analysis.

Data collection

Data collection was done according to the criteria and definitions described by the developers of APACHE II and III [12,13]. The data were collected by ward doctors after 4 weeks training in how to use the APACHE system. They had access to a detailed manual, including definitions and procedures. Constant supervision by a documentation assistant included regular comparison of the original with the collected data, and review of completeness. In order to assess reliability of data collection, data from a random sample of 50 patients were recorded by two data collectors independently. Interobserver reliability was analyzed by Kendall's coefficient of concordance and κ statistics. In addition, data collection software, which was provided by APACHE Medical Systems Inc (Washington, DC), automatically checked that the data were plausible. The whole data set was tested using a box-plot technique in order to analyze extreme values seperately. Vital status at hospital discharge was recorded.

Statistical analysis

The sample was split randomly into a development (n = 1863 for APACHE II and n = 1772 for APACHE III) and a validation sample (n = 932 for APACHE II and n =889 for APACHE III). Development of the original model by logistic regression [14] led to the following equation:

logit(or) = β₀ + Σβ_i × x_i     (1)

where β₀ is a constant, β_i are coefficients, and x_i encompasses the various patient factors that are included in the model. The probability of hospital death is calculated as follows:

P(or) = e^logit(or)/1 + e^logit(or)     (2)

In the present study the APACHE II equation was used as indicated by the developers [12]. The APACHE III equation was provided by APACHE Medical Systems Inc, and it has not been published for commercial reasons. In customizing the scales, the original logit was used as the independent variable and hospital death was used as the dependent variable. The new probability of hospital death was calculated as follows:

P(cust) = e^logit(cust)/1 + e^logit(cust)     (3)

and logit(cust) is calculated as follows:

logit(cust) = β^c₀ + [β^c₁ × logit(or)]     (4)

where β^c₀ is the constant and β^c₁ the coefficient derived by logistic regression. The customized coefficients were calculated to be those shown in Table 1.

Table 1.

Customized coefficients used in the calculation of probability of hospital death

	Coefficient
Model	βc0	βc0
APACHE II	0.1926	1.0686
APACHE III	0.4022	1.0177

Discrimination and calibration were analyzed for the original and customized models. Discriminative power was tested by calculating the areas under the ROC curves [15], and calibration was calculated using standardized mortality ratio (SMR; observed deaths/expected deaths), with 95% confidence intervals [16], and using the Hosmer-Lemeshow goodness-of-fit H and C tests [17]. Comparison of the development and validation samples was done by Χ² test and Mann-Whitney U test, because values were not normally distributed.

Statistical analysis was performed using the SPSS 6.1 software package (SPSS, Chicago, IL, USA). P < 0.05 was considered statistically significant.

Results

Completeness of data was good; excluding just one variable (24-h urine), 94.6% of all necessary data were collected on average for each patient; 24-h urine was available in only 78.1% of patients. Reliability analysis revealed Kendall's coefficients for clinical and laboratory data above 0.9 except for blood gas values (0.878) and 24-h urine (0.870). κ values were low only for diagnosis of renal failure (0.49) and Glasgow Coma Scale score (0.54). Despite that, differences in calculated scores were very low, with Kendall's coefficients above 0.92. Thus, overall reliability of data collection was good.

Demographic and clinical characteristics were very similar for the development and validation samples (Table 2), and no significant differences were detected. Both models showed good discrimination, which was unchanged by customization.

Table 2.

Demographic and clinical data for APACHE II sample

Patient characteristic	Development	Validation
Cases (n)	1863	932
Age (mean ± SD)	62.5 ± 16.1	61.8 ± 16.3
Medical (%)	65.5	66.0
Surgical (%)	34.5	34.0
Direct admission (%)	69.9	68.1
Referral (%)	30.1	31.9
< 65 years (%)	49.1	52.0
≥ 65 years (%)	50.9	48.0
Cardiovascular (%)	38.9	38.6
Gastrointestinal (%)	32.9	31.8
DOS ICU (mean ± SD)	3.95 ± 7.0	3.48 ± 5.4
DOS hospital (mean ± SD)	25.35 ± 22.4	25.26 ± 22.5
Hospital mortality (%)	18.5	17.2
APACHE II prediction (%)	17.3	16.6
APACHE III prediction (%)	14.7	14.7

There were no differences for the APACHE III sample (1772/889 cases). Direct admission is defined as admission from emergency room, operating theatre, or recovery room; and transferral is defined as admission from other hospital, other ICU, or floor. DOS, duration of stay.

The original APACHE II prediction calibrated adequately in the patients studied, with minor improvements after customization. APACHE III originally showed inadequate calibration, which was considerably improved by customization, and was adequate afterwards (Table 3). The calibration curves (Fig. 1) reveal that calibration after customization was good for APACHE II up to the 70-80% mortality risk decile, but was still far from ideal for APACHE III. When interpreting the greater deviations from the ideal line in the 80-90% and 90-100% deciles, the small numbers of cases in these groups have to be borne in mind.

Table 3.

Discrimination and calibration of APACHE II and III before and after customization

Prediction	Sample	n	ROC area	H	C	SMR (95% CI)
APACHE II original	Development	1863	0.817	10.46	9.38	1.07 (0.98-1.16)
	Validation	932	0.826	8.02	10.68	1.04 (0.91-1.16)
APACHE II customized	Development	1863	0.817	9.37	5.53	1.00 (0.92-1.08)
	Validation	932	0.826	6.23	8.59	0.97 (0.85-1.09)
APACHE III original	Development	1772	0.849	34.30†	34.96†	1.25 (1.15-1.34)
	Validation	889	0.863	20.13*	20.19*	1.18 (1.05-1.31)
APACHE III customized	Development	1772	0.849	7.29	6.14	1.00 (0.92-1.08)
	Validation	889	0.863	15.10	11.72	0.94 (0.83-1.06)

^*P = 0.01, ^†P < 0.001. C, Hosmer-Lemeshow goodness-of-fit C test; H, Hosmer-Lemeshow goodness-of-fit H test; CI, confidence interval.

Figure 1.

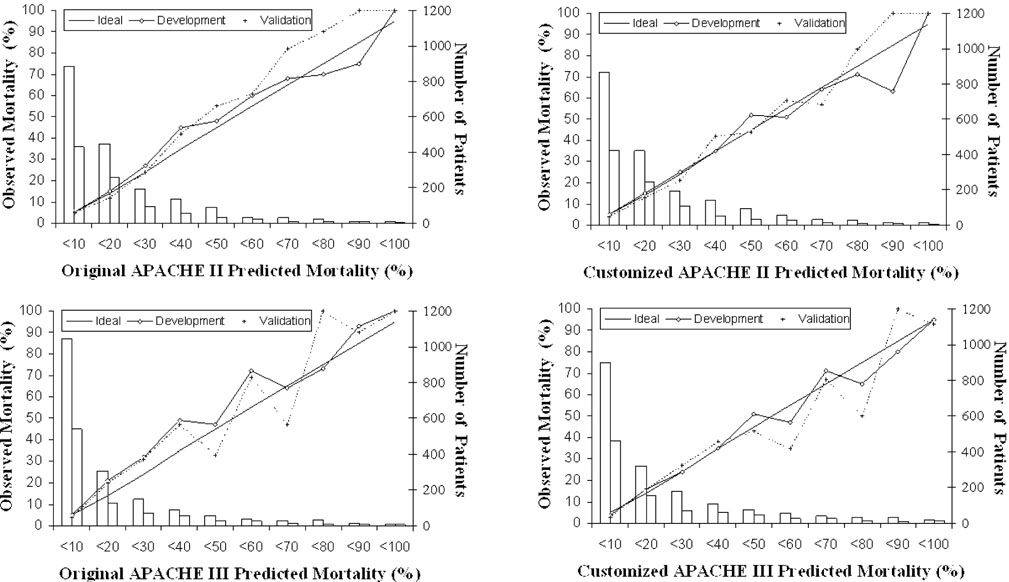
Calibration curves for APACHE II and APACHE III before and after customization for development and validation samples. The diagonal line is the line of ideal correspondence between observed and expected mortality. The solid line represents the development sample and the dotted line the validation sample. Case numbers for the development sample are represented by white bars, and those of the validation sample by grey bars.

Subgroup analysis of the validation sample is shown in Table 4 for APACHE II and in Table 5 for APACHE III. Fit was not uniform for APACHE II, with varying SMRs. Goodness-of-fit was insufficient for patients younger than 65 years and for those directly admitted. Although goodness-of-fit improved for most subgroups after customization, it was still not uniform. These findings were similar for APACHE III. Goodness-of-fit was insufficient for medical, younger, directly admitted and cardiovascular patients. Fit was improved for all but younger and transferred patients. However, it was still not uniform after customization.

Table 4.

Discrimination and calibration of APACHE II before and after customization for various subgroups of the validation sample

Subgroup	Prediction	n	ROC area	H	C	SMR (95% CI)
Medical	Original	615	0.842	5.89	12.08	1.08 (0.94-1.23)
	Customized		0.842	7.90	9.65	1.01 (0.88-1.15)
Surgical	Original	317	0.758	5.48	7.15	0.91 (0.65-1.18)
	Customized		0.758	6.87	7.53	0.86 (0.60-1.11)
< 65 years	Original	485	0.859	14.31	20.13†	0.91 (0.70-1.13)
	Customized		0.859	8.82	19.90*	0.86 (0.66-1.07)
≥ 65 years	Original	447	0.774	8.09	8.31	1.11 (0.96-1.27)
	Customized		0.774	7.16	7.27	1.04 (0.89-1.19)
Direct admission	Original	635	0.816	12.12	16.01*	0.99 (0.82-1.10)
	Customized		0.816	7.98	15.57*	0.93 (0.77-1.10)
Transferral	Original	297	0.814	3.05	3.90	1.10 (0.87-1.23)
	Customized		0.814	7.06	2.74	1.03 (0.85-1.20)
Cardiovascular	Original	360	0.879	9.21	11.13	1.05 (0.86-1.24)
	Customized		0.879	10.44	8.83	0.99 (0.80-1.17)
Gastrointestinal	Original	296	0.855	11.12	12.82	0.76 (0.53-0.98)
	Customized		0.855	12.31	13.73	0.71 (0.49-0.92)

Direct admission is defined as admission from emergency room, operating theatre, or recovery room; and transferral is defined as admission from other hospital, other ICU, or floor. C, Hosmer-Lemeshow goodness-of-fit C test; H, Hosmer-Lemeshow goodness-of-fit H test; CI, confidence interval. ^*P < 0.05, ^†P = 0.01.

Table 5.

Discrimination and calibration of APACHE III before and after customization for various subgroups of the validation sample

Subgroup	Prediction	n	ROC area	H	C	SMR (95% CI)
Medical	Original	590	0.861	22.01†	24.90†	1.15 (1.01-1.29)
	Customized		0.861	15.83*	18.27*	0.93 (0.81-1.06)
Surgical	Original	299	0.842	8.51	13.18	1.28 (0.96-1.60)
	Customized		0.842	4.75	7.62	0.98 (0.71-1.25)
< 65 years	Original	464	0.894	16.62*	15.59*	1.19 (0.95-1.42)
	Customized		0.894	21.24†	10.19	0.94 (0.74-1.14)
≥ 65 years	Original	425	0.812	13.63	15.74*	1.17 (1.02-1.33)
	Customized		0.812	12.93	9.42	0.95 (0.81-1.08)
Direct admission	Original	614	0.874	19.41*	23.46†	1.29 (1.10-1.48)
	Customized		0.874	9.07	11.67	1.02 (0.86-1.18)
Transferral	Original	275	0.817	9.54	12.18	1.05 (0.87-1.23)
	Customized		0.817	15.80*	15.18*	0.86 (0.70-1.01)
Cardiovascular	Original	317	0.890	16.72*	19.21*	1.11 (0.92-1.35)
	Customized		0.890	18.47*	15.61*	0.90 (0.74-1.07)
Gastrointestinal	Original	296	0.887	8.17	5.56	1.08 (0.81-1.34)
	Customized		0.887	7.80	5.26	0.85 (0.62-1.08)

Direct admission is defined as admission from emergency room, operating theatre, or recovery room; and transferral is defined as admission from other hospital, other ICU, or floor. C, Hosmer-Lemeshow goodness-of-fit C test; H, Hosmer-Lemeshow goodness-of-fit H test; CI, confidence interval. ^*P < 0.05, ^†P = 0.01.

Discussion

Customization of APACHE II and III in a large patient population from a single unit led to an improvement in the overall goodness-of-fit of APACHE III, which showed poor calibration in its original version. Despite a similar improvement of fit in several subgroups that were large enough to be tested, good uniformity of fit was not achieved.

These results are comparable with those of a large multi-center study [9] that analyzed customization of the Mortality Prediction Model. In that study, a second-level customization, in which new coefficients were developed for all single patient factors included in the original model, improved calibration even further. Second-level customization was not attempted in the present patient sample because there were not enough patients for that purpose. Time to collect data in a sufficiently large patient sample in a single unit would probably be so great that real changes in case-mix or ICU treatment might occur during the study, which would confound the results. First-level customization will probably be a more practical method for single units to improve the overall fit of score systems that are to be used for quality assessment.

At present, however, we would not recommend customization routinely. This is because a major problem is still unresolved; although good calibration can be achieved for the whole patient sample, uniformity of fit remains unsatisfactory. This is the case even for APACHE III, which accounts for more case-mix factors, such as diagnostic categories and lead time, than do the other models. Nevertheless, achievement of uniformity is important, because change in case-mix over time will otherwise lead to a loss of accuracy of a customized model. It would be difficult to interpret whether a change in the mortality ratio over time would be due to a change in quality of care or in case-mix.

If a customized model still has a poor fit for a certain subgroup at a specific unit, then customization for this sample can be attempted separately [10,11]. This could be attempted in medical and cardiovascular patients at our unit for APACHE III, because these groups are sufficiently large and because general customization did not lead to a good fit. However, the practicality of such an approach is questionable.

We conclude that the customized models of APACHE II and III did not provide an advantage over the original versions. First-level customization did not solve the problem of differences in case-mix, leading to different score results, which do not necessarily reflect differences in quality of care [18]. Data collection is ongoing to test variation in the original and customized scores over time in a second large sample from our unit.