Contrasting Two Frameworks for ROC Analysis of Ordinal Ratings

Abstract

Background

Statistical evaluation of medical imaging tests used for diagnostic and prognostic purposes often employ receiver operating characteristic (ROC) curves. Two methods for ROC analysis are popular. The ordinal regression method is the standard approach used when evaluating tests with ordinal values. The direct ROC modeling method is a more recently developed approach that has been motivated by applications to tests with continuous values, such as biomarkers.

Objective

In this paper, we compare the methods in terms of model formulations, interpretations of estimated parameters, the ranges of scientific questions that can be addressed with them, their computational algorithms and the efficiencies with which they use data.

Results

We show that a strong relationship exists between the methods by demonstrating that they fit the same models when only a single test is evaluated. The ordinal regression models are typically alternative parameterizations of the direct ROC models and vice-versa. The direct method has two major advantages over the ordinal regression method: (i) estimated parameters relate directly to ROC curves. This facilitates interpretations of covariate effects on ROC performance; and (ii) comparisons between tests can be done directly in this framework. Comparisons can be made while accommodating covariate effects and comparisons can be made even between tests that have values on different scales, such as between a continuous biomarker test and an ordinal valued imaging test. The ordinal regression method provides slightly more precise parameter estimates from data in our simulated data models.

Conclusion

While the ordinal regression method is slightly more efficient, the direct ROC modeling method has important advantages in regards to interpretation and it offers a framework to address a broader range of scientific questions including the facility to compare tests.

1. INTRODUCTION

Receiver operating characteristic (ROC) curves have long been used to characterize the inherent accuracy of medical tests for diagnosis and prognosis.¹ They have been particularly popular in evaluating imaging modalities where images are rated on an ordinal scale according to the reader’s certainty of a positive diagnosis.² In this context a large body of statistical methodology has developed for ROC analysis of ordinal rating data. These methods have drawn primarily on ordinal regression modeling methods.³ For example, the classic Dorfman and Alf algorithm⁴ for estimating binormal ROC curves employs ordinal regression methods, as does the Tosteson and Begg⁵ methodology for evaluating factors influencing test accuracy. This approach continues to be refined for addressing ever more complex statistical questions.⁶

In parallel a second body of literature has developed for ROC analysis over the past decade motivated by applications where test results are on a continuous scale. We call this approach the direct ROC modeling approach and describe it in detail below. For example, biomarkers used for diagnosis and prognosis are typically measured on a continuous scale.⁷ It has been noted that the direct ROC modeling methodology can also be applied to ordinal valued tests.^8,9 The purpose of this paper is first to make explicit the close connections that exist between the ordinal regression (OR) and direct ROC modeling (DM) methods for statistical evaluation of ROC curves. Second, we contrast the approaches in terms of their conceptual frameworks, the range of questions addressed by them and the statistical efficiency with which they utilize data.

We illustrate with two applications. The first example concerns interpretation of initial screening mammograms by radiologists using the BI-RADS scale.¹⁰ We compare 1000 women who were found to have breast cancer within one year of the mammogram to 1000 women with no diagnosis of breast cancer. Both groups are randomly sampled from larger populations from the Breast Cancer Surveillance Consortium (http://breastscreening.cancer.gov/). The BI-RADS scale is ordered in terms of increasing likelihood of breast cancer as follows: (1) Negative; (2) Benign finding; (3) Probably benign finding; (0) Need additional imaging; (4) Suspicious abnormality; and (5) Highly suggestive of malignancy. Due to the small number of women without cancer who had readings in category 5, we collapsed categories 4 and 5 together for this example. It has been shown that this ordering corresponds to increasing cancer rates.¹¹ The zero category is intended as a placeholder until additional imaging resolves uncertainty, but in practice the zero is often not replaced. For each subject, in addition to the image rating and case or control status, the dataset includes data on breast density measured on the BI-RADS coding system: (1) almost entirely fat; (2) scattered fibroglandular densities; (3) heterogeneously dense; and (4) extremely dense. Very few women had breasts classified as almost entirely fat in this sample so categories (1) and (2) were combined and labeled as ‘not dense’. We seek to estimate the ROC curves associated with mammography for women with each level of breast density and to describe the effect if any that breast density has on the accuracy of mammographic readings.

The second dataset is similarly set in the context of breast cancer diagnosis, but now a continuous valued biomarker is measured for each woman in addition to her mammographic reading. For women diagnosed with cancer, the stage of her disease is noted in the dataset. Some scientific questions of interest are: (i) to compare ROC curves for the biomarker and mammogram tests; (ii) to evaluate the accuracies of the tests for detecting late stage cancer compared with their capacities for detecting early stage cancer; and (iii) to determine if the relative performance of the tests varies with breast cancer stage.

2. TWO CONCEPTUAL FRAMEWORKS

The key distinction between the OR and DM approaches to ROC analysis is in the entities that are modeled statistically. The OR method formulates a statistical model for the probability distribution of the test results given case or control status and covariates. That is, we model Prob[Y=r|D, X] where Y is the image rating result (which takes values r=1,2,…,R, where R is the number of possible ratings), D is case or control status (D=1 for a case and D=0 for a control) and X denotes covariates. From this one can calculate the corresponding ROC curves for the test in populations with specified covariate values X=x. In contrast, the DM method directly formulates a statistical model for the ROC curves as an explicit function of X. In other words, OR models probability frequencies of ratings while DM models the relationship between those probability frequencies for cases and controls, which is the trade-off between true and false positive rates.

2.1 Simple Binormal ROC Curves

To see the correspondence between OR and DM model formulations, consider the classic binormal ROC curve without covariates that is discussed in depth in Pepe (2003, sections 4.4–4.5). The binormal ROC curve assumes that the tradeoff between false positive rates (f_r = Prob[Y ≥ r | D = 0]) and true positive rates (ROC(f_r)= Prob[Y ≥ r | D = 1]) associated with different decision cut points, r = 2,…, R , for classifying an image as positive is given by:

$$\text{ROC}(f_r)=\mathrm{\Phi }({\gamma }_I+{\gamma }_S{\mathrm{\Phi }}^{-1}(f_r))$$ (1)

with Φ denoting the standard normal cumulative distribution function. The parameters γ_I and γ_S are called the binormal ROC intercept and slope parameters, respectively, with corresponding indices I and S. The DM formulation specifies the ROC curve as having the form in equation (1).

The OR formulation instead specifies a model for the probability frequencies of ratings conditional on case or control status, D =1 or 0, respectively:

$$\text{Prob}[Y<r|D]=\mathrm{\Phi }(\{{\theta }_r-{\alpha }_{1}D\}/\text{exp}\{\beta D\})$$ (2)

The θ_r are called intercepts or ‘cut points’ associated with the rating thresholds r. By setting D=0 for controls, the model writes the R −1 false positive rates as Prob[Y>=r|D=0]=1−Φ(θ_r). We see that θ_r is a reparameterization of f_r. In particular, f_r=1−Φ(θ_r) and conversely, θ_r = −Φ⁻¹(f_r). The parameters α₁ and β are called the mean and scale parameters for the ordinal regression model.

To calculate the ROC curve that corresponds to the OR model, recall that the ROC curve is defined as the true positive rate, Prob[Y ≥ r | D =1], written as a function of the false positive rate, f_r = Prob[Y ≥ r | D = 0] . Starting with the OR formulation, we write the true positive rate corresponding to f_r as:

$$\begin{array}{cc}\text{ROC}(f_r)=\text{Prob}[Y\ge r|D=1]\hfill & =1-\mathrm{\Phi }(\{{\theta }_r-{\alpha }_1\}/\text{exp}\{\beta \})\hfill \\ \hfill & =\mathrm{\Phi }(\{-{\theta }_r+{\alpha }_1\}/\text{exp}\{\beta \})\hfill \\ \hfill & =\mathrm{\Phi }(\{{\mathrm{\Phi }}^{-1}(f_r)+{\alpha }_1\}/\text{exp}\{\beta \})\hfill \end{array}$$

the last equality following from the OR stipulation that f_r = Φ(−θ_r). Therefore the OR formulation gives rise to the binormal ROC curve that is modeled directly with the DM approach with correspondences between parameters being :

$$f_r=1-\mathrm{\Phi }({\theta }_r),{\gamma }_S=1/\text{exp}\{\beta \},{\gamma }_I={\alpha }_1/\text{exp}\{\beta \}$$ (3)

Conversely, one can start with the binormal ROC curve and show that one minus the true positive rate and one minus the false positive rate derived from it follow the OR formulation using the same correspondences between parameters, now written as:

$${\theta }_r=-{\mathrm{\Phi }}^{-1}(f_r),\beta =\text{log}\{1/{\gamma }_S\},{\alpha }_1={\gamma }_I/{\gamma }_S$$

That is, when considering a single test and no covariates, the two models are equivalent, being simple reparameterizations of each other.

Popular formulations for OR and DM models that include covariates are:

$$\text{OR}:\text{Prob}[Y<r|D,X]=\mathrm{\Phi }(\{{\theta }_{\mathit{\text{rX}}}-{\alpha }_{1}D-{\alpha }_3\mathit{\text{DX}}\}/\text{exp}\{\beta D\})$$ (4)

$$\text{DM}:{\text{ROC}}_X(f)=\mathrm{\Phi }({\gamma }_I+{\gamma }_{\mathit{\text{IX}}}X+{\gamma }_S{\mathrm{\Phi }}^{-1}(f))$$ (5)

where f ∈ {f_2X, f_3X, …,f_RX} are the false positive rates within the population with covariate value X. Again it is easy to see that the two formulations are equivalent:

$${\gamma }_S=1/\text{exp}\{\beta \},{\gamma }_I={\alpha }_1/\text{exp}\{\beta \},{\gamma }_{\mathit{\text{IX}}}={\alpha }_3/\text{exp}\{\beta \},f_{\mathit{rX}}=1-\mathrm{\Phi }({\theta }_{\mathit{\text{rX}}})$$ (6)

The DM approach parameterizes the covariate specific ROC curve directly (i.e. the ROC curve for the population with covariate value X, ROC_X) as a binormal curve with intercept γ_I+γ_IXX and slope γ_S while the OR approach parameterizes the distributions of the test result as an ordinal regression model with probit link function, mean 0 and scale 1 in controls, mean α₁+α₃X and scale exp{βD} in cases, with category cut points {θ_rX , r=2,…, R}in the population with covariate value X. In the DM approach, one estimates (γ_I, γ_IX, γ_S) directly while in the OR approach one estimates (α₁,α₃,β) from which (γ_I,γ_IX,γ_S) are calculated using the above formulas.

2.2 Extensions and Special Cases

Observe that no particular structure is assumed for θ_rX, or equivalently for f_rX, in the formulations discussed above. In practice we need to choose if and how to model them. When X is comprised of a few categories, one may take an entirely nonparametric approach, empirically estimating the false positive rates, f_rX (or equivalently θ_rX) separately for each value of X. However, one can also choose to model them with an ordinal regression model, f_rX = Prob[Y ≥ r | D = 0, X] = Φ(−θ_r + α₂X). This will be necessary in fact when X is continuous. We then write the two equivalent model formulations as

$$\text{OR}:\text{Prob}[Y<r|D,X]=\mathrm{\Phi }(\{{\theta }_r-{\alpha }_{1}D-{\alpha }_{2}X-{\alpha }_3\text{DX}\}/\text{exp}\{\beta D\})$$ (7)

$$\begin{array}{cc}\text{DM}:{\text{ROC}}_X(f)\hfill & =\mathrm{\Phi }({\gamma }_I+{\gamma }_{\mathit{\text{IX}}}X+{\gamma }_S{\mathrm{\Phi }}^{-1}(f))\hfill \\ \hfill & f_{\mathit{\text{rX}}}=\mathrm{\Phi }(-{\theta }_r+{\alpha }_{2}X)\hfill \end{array}$$ (8)

Here in the OR approach, the ‘cut point’ θ_rX is parameterized as θ_r−α₂X. The DM approach achieves the same model by stipulating a parametric ordinal regression model for covariate effects on test results in controls in addition to its modeling of the ROC curve as shown in the pair of equations (8). If the model assumption is true, the formulation as two equations (8) is identical to the formulation as one equation (7), where f_rX = Φ(−θ_r + α₂X) is the part of the model (7) pertaining only to controls.

In the general DM framework as laid out by Pepe (2003, chapter 6), one formulates a regression model for covariate effects on test results in controls, f_rX, and a separate regression model for covariate effects on the ROC curve, denoted by ROC_X(f). The covariates entering these two models and the model forms themselves may be completely different. For example, a covariate such as X=study site in a multicenter study may be associated with the degree of conservatism exercised by readers in rating images. This would affect the site specific false positive values, f_rX, in the sense that images from controls would be rated differently across sites. However the ROC curves in different sites would be the same if the inherent accuracy of the test was the same across study sites. Under this scenario the covariate X=study site would be a component of the model for f_rX, but would not be a component of the model for ROC_X(f). We would have α₂≠0 in the model for f_rX but γ_IX=0 in the model for ROC_X(f). This would typically be described as movement along the same ROC curve due to a criterion shift induced by the covariate. In the OR formulation (7) this same phenomenon would manifest as a main effect of X in α₂ but no interaction with case-control status, i.e. α₃=0. One cannot (easily) allow the corresponding model forms for f_rX and ROC_X (f) to differ when using the OR approach since both are formulated within a single model for the probability distributions (7) with a single link function. This contrasts with the DM approach that allows completely independent specifications of models for f_rX and ROC_X (f).

Another possibility is that covariates affect the ROC curve but not the image ratings in controls. A special example concerns disease specific covariates such as stage of breast cancer. The ROC comparing late stage cancer to controls is likely to be higher than that comparing early stage cancer to controls, so X=stage should enter the ROC model, perhaps as a term of the form γ_IXX . This covariate would not enter the f_rX model, since disease stage is not defined for controls. Disease specific covariates are naturally accommodated in the DM framework. In contrast disease specific covariates have, to our knowledge, never been suggested for inclusion in OR models, perhaps because covariates that are defined only for cases and not for controls are not naturally accommodated in a single model that includes case and control data simultaneously. Nevertheless, we note that they can be incorporated into OR models by including them as having interaction terms with D, α₃DX, but not main effect terms α₂X.

The seminal paper by Tosteson and Begg⁵ on using OR for ROC analysis allowed covariates to enter the scale component as well as the location component:

$$\text{Prob}[Y<r|D,X]=\mathrm{\Phi }\left(\frac{\{{\theta }_r-{\alpha }_{1}D-{\alpha }_{2}X-{\alpha }_3\mathit{\text{DX}}\}}{\text{exp}\{{\beta }_{1}D+{\beta }_{2}X+{\beta }_3\mathit{\text{DX}}\}}\right)$$ (9)

This is equivalent to the DM formulation

$$\begin{array}{cc}{\text{ROC}}_X(f)\hfill & =\mathrm{\Phi }\left(\frac{{\alpha }_1+{\alpha }_{3}X+\text{exp}({\beta }_{2}X){\mathrm{\Phi }}^{-1}(f)}{\text{exp}\{{\beta }_1+({\beta }_2+{\beta }_3)X\}}\right)\hfill \\ \hfill & f_{\mathit{\text{rX}}}=\mathrm{\Phi }(\{-{\theta }_r+{\alpha }_{2}X\}/\text{exp}\{{\beta }_{2}X\})\hfill \end{array}$$

This formulation is unappealing because the effect of X on the ROC curve is complicated. It enters the ROC model in a non-linear fashion and does not give rise to simple summaries of the effect of X on test accuracy. An alternative DM formulation for an ROC model is written as

$${\text{ROC}}_X(f)=\mathrm{\Phi }({\gamma }_I+{\gamma }_{\mathit{\text{IX}}}X+({\gamma }_S+{\gamma }_{\mathit{\text{SX}}}X){\mathrm{\Phi }}^{-1}(f))$$ (10)

An advantage of this model is that the effects of X on ROC intercept and slope are summarized succinctly in the parameters γ_IX and γ_SX, respectively. It does not, however, in general correspond to the general Tosteson and Begg OR model in equation (9) because Φ⁻¹(ROC_X (f)) is a linear function of X in (10) while it is a nonlinear function of X in the DM formulation unless β₂ = β₃ = 0 . In practice, most applications of the Tosteson and Begg model allow the scale to depend only on disease status as in equation (7), so that covariates affect only ROC intercept and not slope, as in equation (8). The DM model in (10) allows the covariate to affect the ROC slope as well and in a simple way.

The Tosteson and Begg model is rooted in a latent decision variable conceptual framework. In this framework, one considers that underlying the observed ordinal test result is categorization of an unobservable latent decision variable L with a normal distribution in cases and in controls and that (θ_rX , θ_(r+1)X) is the interval for L that defines the r^th ordinal category, Y=r. In the latent decision variable framework one interprets (α₂X, exp{β₂X}) as the (mean, standard deviation) of L in the control population with covariate value X and (α₁+α₂X+α_3X, exp{β₁+β₂X+β₃X}) is interpreted as the (mean, standard deviation) of L in cases with covariate value X. Therefore α₃ and β₃ are interpreted as differences between cases and controls in regards to effects of X on the mean and scale of L. Although the concept of latent variables is popular, we note that it is unnecessary. Instead one can think of the parameters as relating simply to the probability frequency distributions of the observed ratings and avoid the additional assumptions concerning existence and behaviors of unobservable latent decision variables. This is the straightforward approach of DM which simply specifies that the relationship between the R−1 true and false positive rates in the population with covariate value X follows a parametric mathematical function, ROC_X(f).

Since (9) and (10) are not equivalent models, one must choose between them when ROC slope appears to depend on covariates other than disease status. The choice between the two presumably depends on which model better fits the data and the goal of the analysis –– to summarize effects of X on the ROC curve in a simple fashion or to summarize effects of X on test result distributions.

2.3 Illustration

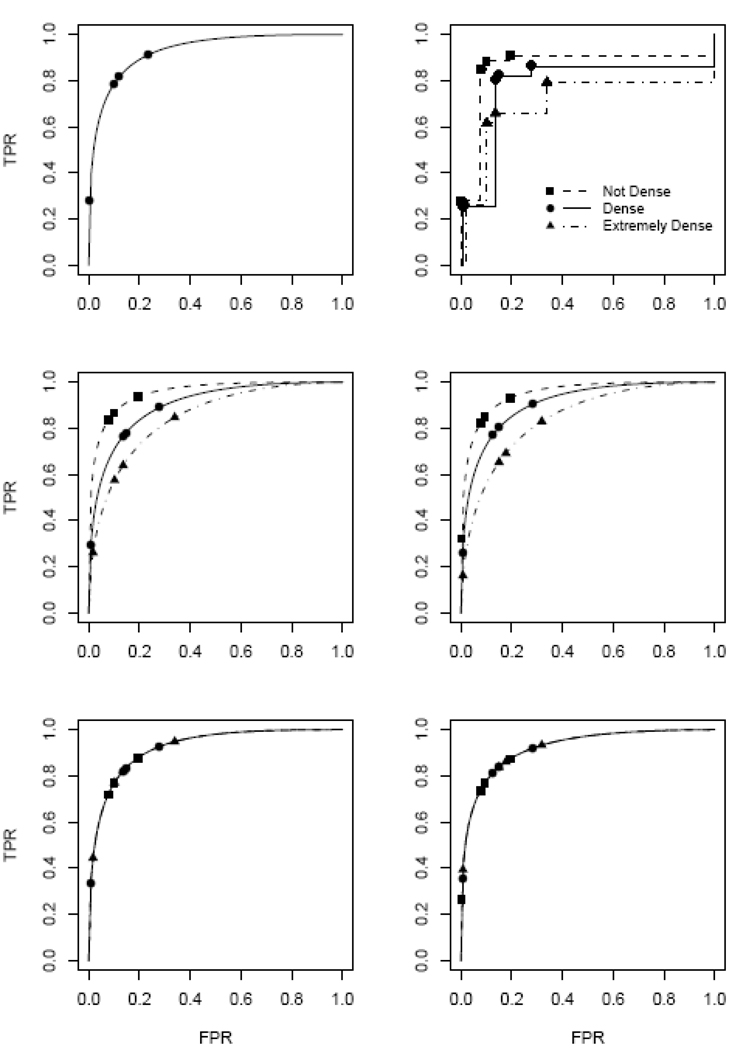
To illustrate a variety of ROC analyses, in Figure 1 we show ROC curves calculated with the Breast Cancer Surveillance Consortium data described earlier. The raw data are displayed in the top right panel of Figure 1 as empirical ROC curves for women in each of the 3 breast density categories. In the top left panel a fitted binormal ROC model is shown that ignores the covariate, breast density. This corresponds to the model displayed as equation (1). The observed false positive rates {f̂₂,…,f̂₅} are also displayed. The middle panels show ROC curves associated with the three breast density categories modeled using equation (5) with the covariate X comprised of two binary variables X=(X₁, X₂) where X₁ and X₂ are dummy variables for “dense” and “extremely dense” breast density. That is, the ROC intercepts were allowed to vary with breast density but the slopes were assumed to be the same in all three categories. In the left panel no assumptions were made about the effect of density on false positive rates f_rX or equivalently on ‘cut points,’ while in the right panel we assumed that they followed an ordinal regression model as in equations (7) and (8). The bottom panels show the ‘averaged’ ROC curve, which allows the ‘cut points’ (θ_rX or f_rX) to vary with breast density but instead of modeling covariate specific ROC curves, it models the vertical average of breast density specific ROC curves. That is, in equation (8) we set γ_IX=0. This is called the covariate adjusted ROC curve and can be interpreted as the vertical average of breast density specific ROC curves.^12,13

Figure 1.

Binormal ROC models for mammography including breast density as a covariate. Models can be formulated either within OR or DM frameworks. Top left panel: no covariate model, equations (1) and (2); Middle panels: ROC intercept depending on breast density category, equations (4) and (5); Bottom panels: average ROC curve across breast density categories. In the left panels no modeling assumptions are made about the false positive rates while in the right panels they are assumed to follow an ordinal regression model with X=(X₁, X₂) where X₁ = {1 for dense, 0 otherwise} and X₂ = {1 for extremely dense, 0 otherwise}. Models shown are those estimated by applying the DM fitting algorithms to the Breast Cancer Surveillance Consortium data. Symbols show (FPR, ROC(FPR)) points that correspond to the 5 categories of the test. Also shown in the top right panel are the empirical ROC curves within each breast density category.

3. FITTING MODELS TO DATA

In the previous section we showed that DM and OR models are different representations of the same models. We now consider how to fit models to data. Different algorithms have traditionally been used by analysts depending on how they formulate the model, as DM or as OR.

3.1 Algorithms

The OR formulation naturally gives rise to maximum likelihood algorithms for estimating parameters. However, standard software for ordinal regression maximum likelihood only accommodates location parameters and does not allow scale parameters. Therefore, even the simplest binormal model (equation (2)) cannot be fit using standard ordinal regression algorithms because the model includes the scale component exp(βD). For this simple model without covariates, several statistical software packages provide the Dorfman and Alf maximum likelihood estimation algorithm. More generally, methods for nonlinear models can be adapted. We wrote our own code in the R environment¹⁴ for maximum likelihood estimation of parameters. Methods for fitting these models in SAS with the NLMIXED procedure have been described.¹⁵ These apply when the scale component only depends on D and not on X.

Algorithms for fitting ROC models have been proposed within the general DM framework.^8,16,17 Implementation in the Stata software package¹⁸ is well developed and has been documented in detail.^9,19 We also implemented this in the R package to perform simulation studies. The key steps in the algorithms are to (i) estimate the covariate specific rating distributions in controls, i.e. the false positive rates, {f̂_rX, r=2, …,R}, either empirically or by fitting a standard ordinal regression model to rating data on controls; (ii) for each case test result, Y_i, create R−1 binary variables U_ir = I[Y_i ≥ r] for r=2,…,R; (iii) Noting that E(U_r) = Prob[Y ≥ r | D=1,X] = ROC_X (f_rX), use a standard binary regression package to estimate the parameters in the ROC regression model. In the case of the general model given in (10), we include all observations with dependent variable U_ir and corresponding predictor vector [1,X_i, Φ⁻¹(f̂_rXi), X_iΦ⁻¹(f̂_rXi)], the total number of such observations being R−1 times the number of cases and specify a probit link function for the binary regression in order to estimate the ROC parameters (γ_I, γ_IX, γ_S, γ_SX). For models with fewer terms than (10) corresponding predictors would be dropped; (iv) use bootstrap resampling to estimate standard errors.

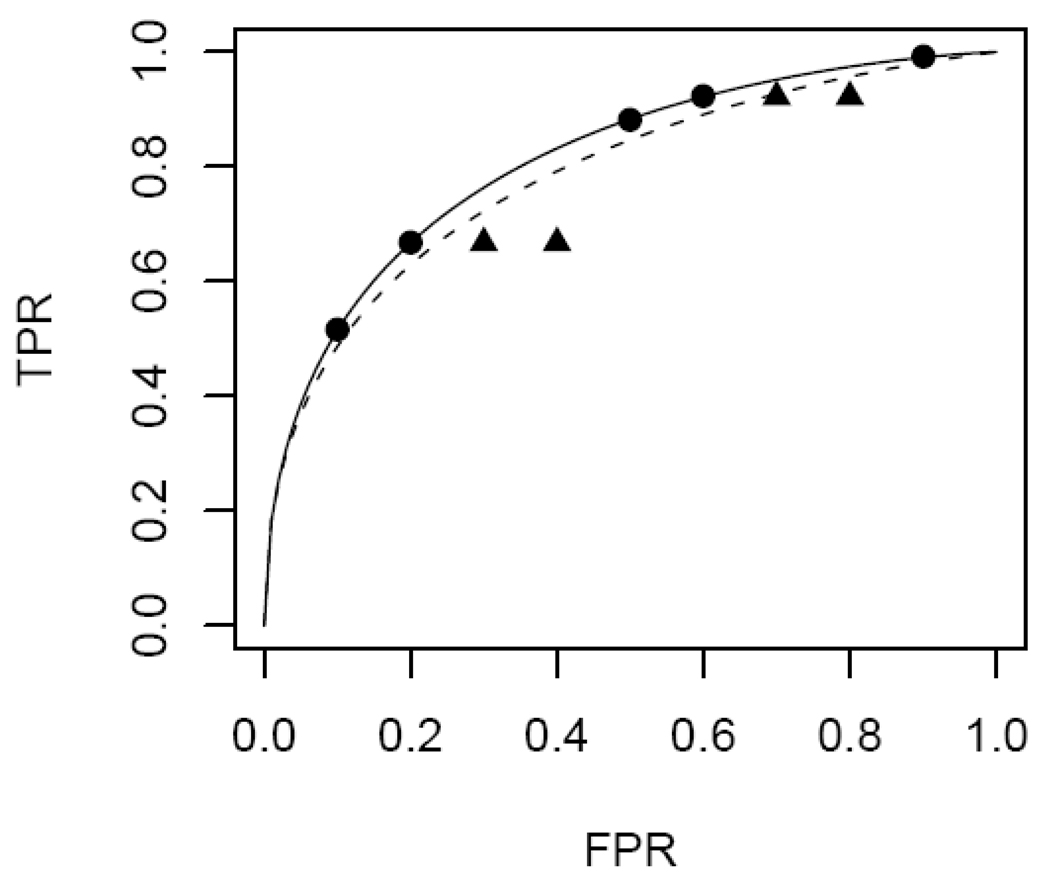
The DM algorithms were originally developed for continuous test results where binary variables U_if are defined based on a set of f values that are user specified, usually equally spaced in (0,1) or in some subinterval of (0,1). However, equally spaced f’s can result in biased ROC curves for ordinal data. This is demonstrated in Figure 2 for the setting where no covariates are involved. The true ROC points associated with the 6 rating categories are shown on the top (solid) curve. Employing 9 equally spaced f values in the DM algorithm essentially creates some additional intermediate ROC points that have larger FPR but equal TPR values. The fitted binormal ROC curve is attenuated by these points (dashed curve) relative to the original curve on which the observed ROC points lie. Therefore for fitting DM ROC models to tests with ordinal values, the modified selection of f ∈ {f̂_2Xi,…,f̂_RXi} and the corresponding change to the predictor vector [1,X_i, Φ⁻¹(f̂_rXi), X_iΦ⁻¹(f̂_rXi)] are recommended in applying the DM algorithm.

Figure 2.

Biased ROC estimation when unobserved FPR values are employed with the DM fitting algorithm. The five observable ROC points are indicated by circles on the solid curve. The curve fitted by choosing equally spaced f values (circles and triangles) is indicated with a dashed curve.

The DM algorithm estimates parameters in the false positive rate model first and then estimates parameters in the ROC model. In contrast with the OR algorithm, it is not symmetric in its treatment of case and control data. If one switched the labeling of cases and controls, different estimates would result. Moreover, the DM algorithms are not maximum likelihood methods. In particular parameters in the false positive rate model are estimated only with data from controls. In contrast, the OR algorithm estimates all parameters in both models at the same time by maximizing the likelihood of all the data. As a consequence data from cases can impact estimated values of the false positive rate parameters. This may lead to better efficiency for the OR fitting algorithm. The two-step DM approach allows for the forms of the model to be different thereby providing flexibility. However, as noted earlier, if one constrains the forms to be the same (for example, both probit) one can fit the false positive rate and ROC models simultaneously using the same maximum likelihood algorithm that the OR approach uses by reparameterizing the models as a single OR model.

3.2 Comparing Statistical Efficiency of DM and OR fitting algorithms

When the DM and OR algorithms are used to fit the same model, it is of interest to know which one is most efficient in the sense of producing the most precise estimates. It is known from established statistical theory that estimates calculated by maximizing the likelihood function are asymptotically optimal in terms of being consistent and having the least sampling variability.²⁰ This general result implies that parameter estimates and ROC values derived from the OR fitting algorithm, which are maximum likelihood, have the smallest standard deviations at least as sample sizes become large. The optimality of the maximum likelihood algorithm usually manifests in small samples too. Since the DM fitting algorithm is not maximum likelihood we use simulation studies to investigate the extent to which they are suboptimal.

For our simulations data were generated under a variety of scenarios that gave rise to different true binormal regression models. In all scenarios simulated, subjects were first assigned their case or control status and then their ordinal marker Y was derived by categorizing a continuous marker L generated from a normal distribution that had standard deviation 1 and mean shown in Table 1. In particular the cut points {Φ⁻¹ (.1), Φ⁻¹ (.3), Φ⁻¹ (.5), Φ⁻¹ (.7), Φ⁻¹ (.9)}={−1.28, −0.52, 0.00, 0.52, 1.28} gave rise to Y. In all, 5 scenarios were studied, one in which no covariate was involved, two in which a categorical covariate was defined and two in which a continuous covariate was defined. The covariate was generated from the same distribution in cases and controls, namely from 4 categories with equal frequencies for the categorical covariate and from a uniform distribution on (−1, 1) for the continuous covariate. We generated datasets with equal numbers of cases and controls (n=100, 200, 500) and fit the appropriate models using DM and OR algorithms.

Table 1.

Simulation scenarios used to evaluate the relative efficiency of ordinal regression (OR) versus direct ROC modeling (DM) fitting algorithms. After assigning a subject his case-control status and covariate value, a normally distributed variable with mean indicated in the table and standard deviation equal to 1 was generated and categorized as described in the text. The categorical covariate with 4 levels is represented as 3 dummy variables (X₂, X₃, X₄) = (0, 0, 0) for level 1, (1, 0, 0) for level 2, (0, 1, 0) for level 3, (0, 0, 1) for level 4. The continuous covariate is denoted by X.

Covariate	Covariate Effects on FPR	Covariate Effects on ROC	Mean in controls	Mean in Cases
none	no	no	0	1.19
categorical	yes	no	−0.2 +0.1X2+0.3X3+0.4X4	1.19−0.2+0.1X2+0.3X3+0.4X4
continuous	yes	no	X	1.19+X
categorical	yes	yes	−0.2 +0.1X2+0.3X3+0.4X4	1.19−0.2+0.15X2+0.5X3+0.65X4
continuous	yes	yes	0.5X	1.19+X

FPR: false positive rate

ROC: receiver operating characteristic

Table 2 shows results of analyses when no covariates were involved. Recall that the OR maximum likelihood algorithm is the classic Dorfman-Alf method for estimating the binormal curve. It is compared with the DM method in Table 2. Interestingly the mean and standard deviations for estimates calculated with the DM method are almost identical to those from the Dorfman-Alf algorithm indicating that in this setting the DM fitting algorithm provides estimates that are very near the theoretically optimal maximum likelihood estimates.

Table 2.

Estimated ROC points calculated from simulated data when no covariates are involved. The setting corresponds to “no covariates” in Table 1. The FPR estimate is the estimate of Prob[Y≥r|D=0] for r=2,3,4,5 and 6. The ROC (FPR) estimate is the ROC point corresponding to a fixed FPR value f, ROC(f)=Φ(γ_I+γ_S Φ⁻¹(f)). Average estimates over 500 simulation studies are displayed with standard deviations in parentheses.

		FPR estimate		ROC(FPR) estimate
(FPR,ROC(FPR))	n	DM	OR	DM	OR
(0.900,0.993)	100	0.897 (0.032)	0.898 (0.028)	0.992 (0.007)	0.992 (0.007)
	200	0.899 (0.021)	0.900 (0.021)	0.992 (0.004)	0.993 (0.004)
	500	0.899 (0.021)	0.900 (0.021)	0.992 (0.004)	0.993 (0.004)
(0.700,0.957)	100	0.697 (0.047)	0.699 (0.042)	0.956 (0.021)	0.957 (0.021)
	200	0.698 (0.031)	0.702 (0.030)	0.956 (0.014)	0.957 (0.014)
	500	0.698 (0.031)	0.702 (0.030)	0.956 (0.014)	0.957 (0.014)
(0.500,0.883)	100	0.499 (0.048)	0.502 (0.047)	0.883 (0.034)	0.884 (0.035)
	200	0.498 (0.035)	0.504 (0.034)	0.883 (0.024)	0.884 (0.024)
	500	0.498 (0.035)	0.504 (0.034)	0.883 (0.024)	0.884 (0.024)
(0.300,0.747)	100	0.303 (0.046)	0.304 (0.047)	0.748 (0.051)	0.748 (0.051)
	200	0.299 (0.031)	0.302 (0.030)	0.749 (0.037)	0.749 (0.037)
	500	0.299 (0.031)	0.302 (0.030)	0.749 (0.037)	0.749 (0.037)
(0.100,0.464)	100	0.100 (0.030)	0.102 (0.031)	0.464 (0.082)	0.460 (0.083)
	200	0.099 (0.022)	0.101 (0.021)	0.467 (0.058)	0.465 (0.058)
	500	0.099 (0.022)	0.101 (0.021)	0.467 (0.058)	0.465 (0.058)

FPR: false positive rate

ROC(FPR): true positive rate corresponding to FPR

DM: direct ROC modeling algorithm

OR: ordinal regression algorithm

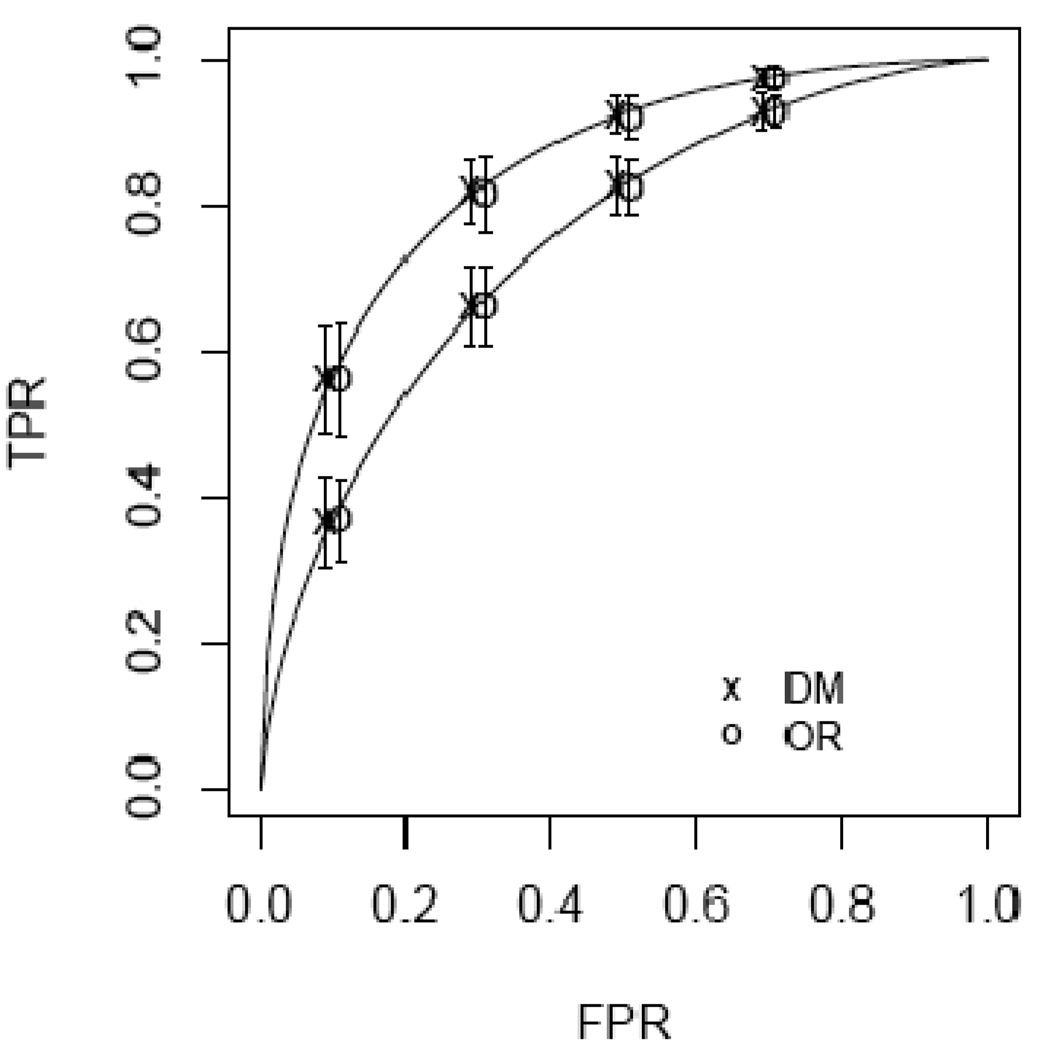
A subset of our results, pertaining to models generated and fit when covariates affect both the false positive rates and the ROC curve are shown in Table 3 and in Figure 3. Conclusions were similar for scenarios not reported. As expected the OR algorithms are somewhat more efficient but the differences appear to be small. Interestingly ROC values seem to be estimated with essentially the same precision using DM and OR fitting algorithms. The FPR values associated with each category of Y appear to be estimated a little more precisely with the OR than with the DM method. An intuitive explanation is that the DM method uses only data from controls to estimate the FPR values, while the OR method incorporates data from cases as well by utilizing all the modeling assumptions in the likelihood that is maximized.

Table 3.

Accuracy estimates based on simulated data when a categorical covariate affects both false positive rates and ROC curves. The sample size is n=200 cases and 200 controls. Means and standard deviations (in parentheses) displayed are calculated from 500 simulation studies. Direct ROC modeling (DM) and ordinal regression (OR) fitting algorithms use covariate stratified non-parametric FPR estimates, i.e. no modeling assumptions were made about FPR values.

False Positive Rate
X category	1			2			3			4
	True	DM	OR	True	DM	OR	True	DM	OR	True	DM	OR
r
2	0.860	0.860 (0.051)	0.861 (0.048)	0.881	0.878 (0.048)	0.879 (0.045)	0.916	0.916 (0.038)	0.917 (0.036)	0.931	0.930 (0.038)	0.930 (0.036)
3	0.627	0.623 (0.069)	0.622 (0.067)	0.664	0.663 (0.066)	0.663 (0.064)	0.734	0.732 (0.059)	0.733 (0.058)	0.766	0.765 (0.062)	0.766 (0.059)
4	0.421	0.415 (0.072)	0.414 (0.071)	0.460	0.459 (0.071)	0.457 (0.067)	0.540	0.539 (0.070)	0.538 (0.068)	0.579	0.578 (0.071)	0.576 (0.068)
5	0.234	0.230 (0.062)	0.228 (0.054)	0.266	0.265 (0.060)	0.264 (0.057)	0.336	0.337 (0.068)	0.335 (0.063)	0.373	0.373 (0.066)	0.371 (0.065)
6	0.069	0.068 (0.037)	0.070 (0.030)	0.084	0.085 (0.041)	0.087 (0.035)	0.119	0.119 (0.046)	0.119 (0.040)	0.140	0.140 (0.049)	0.141 (0.044)
ROC(f)
X category	1			2			3			4
f	True	DM	OR	True	DM	OR	True	DM	OR	True	DM	OR
0.860	0.993	0.991 (0.007)	0.993 (0.006)	0.994	0.992 (0.007)	0.993 (0.006)	0.996	0.995 (0.005)	0.996 (0.004)	0.997	0.996 (0.004)	0.996 (0.003)
0.627	0.957	0.953 (0.024)	0.957 (0.024)	0.961	0.957 (0.023)	0.96 (0.023)	0.972	0.969 (0.018)	0.971 (0.017)	0.975	0.973 (0.015)	0.975 (0.015)
0.421	0.883	0.881 (0.045)	0.886 (0.046)	0.893	0.89 (0.044)	0.893 (0.045)	0.918	0.915 (0.037)	0.918 (0.037)	0.925	0.923 (0.034)	0.925 (0.033)
0.234	0.747	0.752 (0.070)	0.753 (0.072)	0.763	0.765 (0.070)	0.765 (0.071)	0.807	0.809 (0.062)	0.808 (0.064)	0.820	0.822 (0.062)	0.821 (0.063)
0.069	0.464	0.482 (0.095)	0.472 (0.099)	0.484	0.499 (0.097)	0.487 (0.098)	0.543	0.559 (0.095)	0.546 (0.099)	0.563	0.579 (0.103)	0.566 (0.105)

FPR: false positive rate, DM: direct ROC modeling algorithm, OR: ordinal regression algorithm

f: false positive rate value, r: rating threshold defining a positive classification, True: true value of entity estimated.

Figure 3.

Accuracy estimates based on simulated data when a continuous covariate X affects both false positive rates and ROC curves. ROC values associated with covariate values X=−.5 and X=.5 are displayed. The sample size is n=200 cases and controls. Shown are average estimates of ROC_X(f_r) for r= 3,4,5,6 where f_r is the theoretical FPR associated with the r^th category. Mean estimates are displayed with symbols offset by +/− .01 for visual clarity. Error bars display ±1 SD across the 500 simulations.

3.3 Application to Breast Cancer Surveillance Consortium Data

Results of fitting the binormal models described in relation to Figure 1 using the OR and DM fitting algorithms are displayed in Table 4 and Table 5. The estimated ROC values at false positive rates equal to (0.1,0.3,0.5) are shown in Table 4. The estimates agree reasonably well. The confidence intervals are for DM and OR fitting algorithms agree closely when covariates effects on false positive rates are assumed not to exist, or when they are assumed to follow an ordinal regression model. However, they appear to be substantially smaller for the maximum likelihood OR algorithm for these data when the false positive rates are calculated separately within each breast density category.

Table 4.

ROC values estimated with the direct ROC modeling (DM) and ordinal regression (OR) algorithms applied to the Breast Cancer Surveillance Consortium mammography data. Shown are point estimates and confidence intervals in parentheses. Confidence intervals were calculated using 500 bootstrapped samples. Covariate effects are denoted by ‘ignored’ when X = breast density is not included in the model, by ‘stratified nonparametric’ when FPR estimates pertaining to each category of breast density are calculated without modeling assumptions, and as ‘ordinal model’ when an ordinal regression model is assumed for effects of the covariate on FPRs or equivalently on θ_rX . The binormal ROC model allows X to affect intercept but not the slope (equation (5)). Results for the DM estimation algorithm correspond to curves shown in Figure 1.

Covariate Effects Modeled
ROC	False Positive Rates	Breast Density Category	Estimation Method	AUC	ROC(0.1)	ROC(0.3)	ROC(0.5)
ignored	ignored	---	DM	0.929 (0.914,0.940)	0.786 (0.751,0.823)	0.939 (0.911,0.958)	0.981 (0.961,0.990)
		---	OR	0.921 (0.907,0.934)	0.787 (0.751,0.824)	0.917 (0.893,0.939)	0.963 (0.942,0.978)
Binormal	stratified	Not dense	DM	0.955 (0.939,0.966)	0.867 (0.826,0.903)	0.968 (0.940,0.982)	0.991 (0.973,0.996)
Model	nonparametric	Not dense	OR	0.950 (0.933,0.962)	0.865 (0.829,0.897)	0.951 (0.927,0.968)	0.979 (0.960,0.989)
Binormal	stratified	Medium	DM	0.903 (0.879,0.925)	0.714 (0.652,0.788)	0.905 (0.863,0.939)	0.966 (0.933,0.984)
Model	nonparametric	Medium	OR	0.895 (0.868,0.920)	0.731 (0.670,0.795)	0.879 (0.841,0.914)	0.939 (0.909,0.964)
Binormal	stratified	Extreme	DM	0.848 (0.765,0.913)	0.571 (0.419,0.747)	0.822 (0.696,0.917)	0.925 (0.830,0.976)
Model	nonparametric	Extreme	OR	0.820 (0.742,0.893)	0.578 (0.457,0.733)	0.773 (0.665,0.876)	0.871 (0.783,0.940)
Binormal	ordinal model	Not dense	DM	0.951 (0.936,0.962)	0.857 (0.820,0.891)	0.965 (0.937,0.979)	0.990 (0.974,0.996)
Model		Not dense	OR	0.943 (0.927,0.954)	0.842 (0.809,0.874)	0.944 (0.919,0.962)	0.977 (0.958,0.988)
Binormal	ordinal model	Medium	DM	0.908 (0.886,0.928)	0.727 (0.666,0.794)	0.912 (0.873,0.943)	0.970 (0.942,0.984)
Model		Medium	OR	0.902 (0.879,0.924)	0.741 (0.684,0.799)	0.891 (0.856,0.922)	0.949 (0.922,0.970)
Binormal	ordinal model	Extreme	DM	0.844 (0.771,0.906)	0.559 (0.414,0.734)	0.816 (0.703,0.908)	0.923 (0.844,0.969)
Model		Extreme	OR	0.848 (0.778,0.908)	0.622 (0.479,0.766)	0.814 (0.713,0.897)	0.903 (0.831,0.953)

ROC: receiver operating characteristic, FPR: false positive rate, AUC: area under the ROC curve.

DM: direct ROC modeling algorithm, OR: ordinal regression algorithm,

Table 5.

Model parameters estimated with the direct ROC modeling (DM) and ordinal regression (OR) algorithms applied to the Breast Cancer Surveillance Consortium mammography data. Shown are point estimates and confidence intervals in parentheses. Confidence intervals were calculated using 500 bootstrapped samples. The parameters γ_I(a,b) and α_I(a,b)correspond to ROC parameters, γ_IX , and FPR parameters, α₂ , in equation (8), when X₁=a and X₂=b and recall that the covariate X is comprised of two dummy variables X=(X₁, X₂) to indicate the 3 categories of breast density: X₁ = {1 for dense, 0 otherwise} and X₂ = {1 for extremely dense, 0 otherwise}. Covariate effects are denoted by ‘ignored’ when X is not included in the model, by ‘stratified nonparametric’ when FPR estimates pertaining to each category of breast density are calculated without modeling assumptions, and as ‘ordinal model’ when an ordinal regression model is assumed for effects of the covariate on FPRs or equivalently on θ_rX . The binormal ROC model allows X to affect the intercept but not the slope (equation (5)). Results for the DM estimation algorithm correspond to curves shown in Figure 1.

Covariate Effects Modeled
ROC	FPR	Estimation Method	γI	γS	αI(0,1)	αI(1,0)	γI(0,1)	γI(1,0)
ignored	ignored	DM	2.074 (1.760,2.344)	0.999 (0.761,1.187)	-	-	-	-
		OR	1.790 (1.568,2.021)	0.775 (0.562,0.953)	-	-	-	-
Binormal model	stratified nonparametric	DM	2.371 (1.925,2.696)	0.982 (0.596,1.192)	-	-	−0.548 (−0.809,−0.253)	−0.933 (−1.362,−0.409)
		OR	2.037 (1.749,2.307)	0.729 (0.520,0.905)	-	-	−0.487 (−0.728,−0.236)	−0.905 (−1.250,−0.425)
Binormal model	ordinal model	DM	2.339 (1.949,2.640)	0.993 (0.754,1.177)	0.288 (0.120,0.450)	0.394 (0.022,0.701)	−0.462 (−0.688, −0.219)	−0.916 (−1.329, −0.427)
		OR	1.991 (1.727,2.253)	0.771 (0.563,0.951)	0.227 (0.087,0.372)	0.309 (0.018,0.579)	−0.357 (−0.557,−0.153)	−0.693 (−1.075,−0.266)

ROC: receiver operating characteristic, FPR: false positive rate,

DM: direct ROC modeling algorithm, OR: ordinal regression algorithm

4. Extending the Range of Research Questions to Comparing Tests

The DM approach can be applied to continuous tests essentially as we have described it here. The analogue of the OR approach for application to continuous tests is to model the continuous test result distributions for cases and for controls. Covariates can be incorporated into the models if appropriate. These two approaches to evaluating continuous diagnostic tests, DM and modeling test results, have been compared qualitatively.^8,21 We refer the reader to previous publications since similar conclusions apply in the context we consider here, namely ordinal valued tests. Perhaps the most important advantage identified for the DM framework over the OR framework is that DM allows one to succinctly compare the ROC accuracies of tests. Moreover, it has been shown how such comparisons can be made while accommodating covariate effects on test results at the same time. We now explore this methodology when ordinal valued tests are involved.

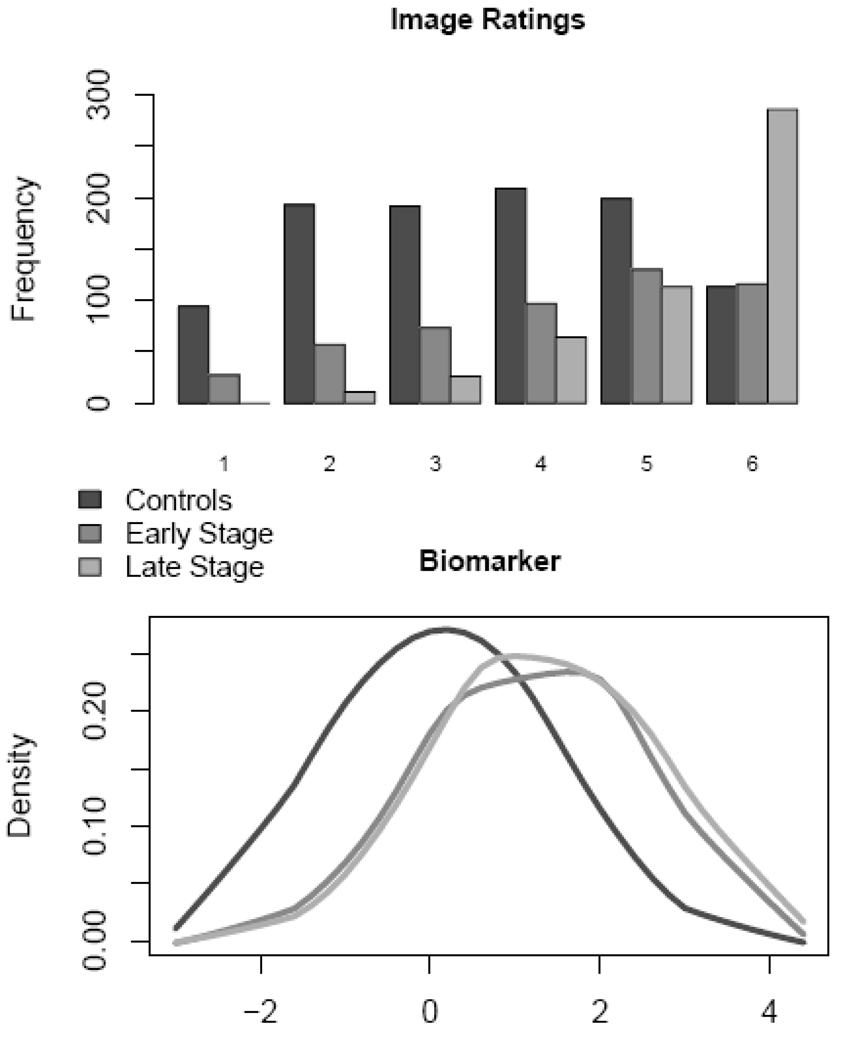
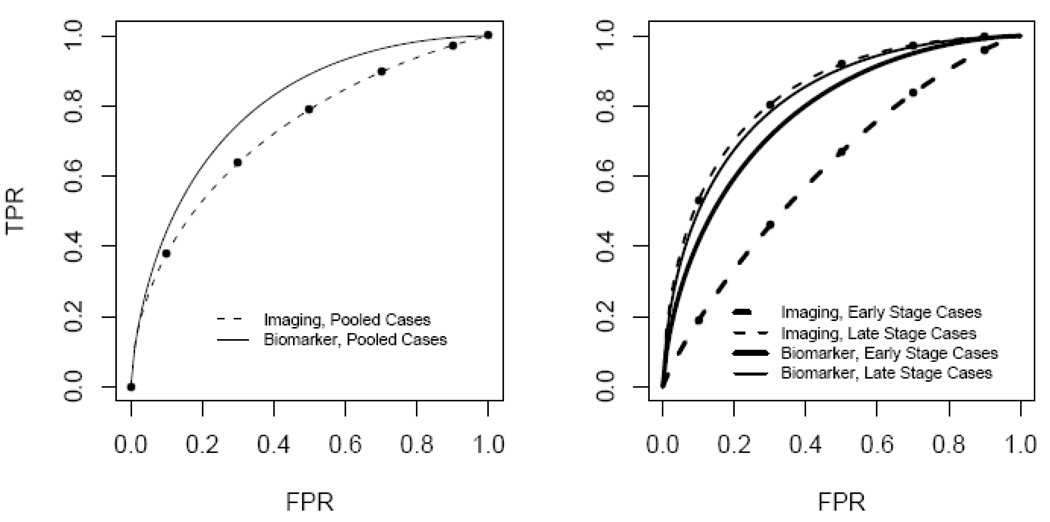
Comparisons are possible in the DM framework even when tests themselves are on different scales. As an example, consider the data displayed in Figure 4 where a continuous biomarker test and an ordinal valued imaging test are available for 1000 cases and 1000 controls data (These data were simulated and are available online at http://labs.fhcrc.org/pepe/dabs/datasets.html). Binormal ROC curves fit to the data for all cases combined and for controls are displayed in the left panel of Figure 5. Define a covariate, X_test, that specifies the test, X_test=0 for the ordinal imaging test and X_test=1 for the continuous biomarker test. The following is a comprehensive ROC model that includes both tests:

$${\text{ROC}}_{X_{\text{test}}}(f)=\mathrm{\Phi }({\gamma }_I+{\gamma }_{{\mathit{\text{IX}}}_{\text{test}}}{X}_{\text{test}}+({\gamma }_S+{\gamma }_{{\mathit{\text{SX}}}_{\text{test}}}{X}_{\text{test}}){\mathrm{\Phi }}^{-1}(f))$$

When X_test=0, the ROC curve relates to the ordinal test and has intercept γ_I and slope γ_S . When X_test=1, the ROC curve relates to the continuous test and has intercept γ_I + γ_IX and slope γ_S + γ_SX . The DM methodology allows one to assess if γ_IX = 0 and if γ_SX = 0, i.e., to assess if the binormal ROC curves are equal. We found γ̂_IX = 0.421 with a 95% confidence interval (0.275,0.842). We found γ̂_SX = 0.198 with a 95% confidence interval (0.07,0.356). A joint Wald test of these two parameters was statistically significant (p-value < .001) and we conclude that the ROC curves for the two tests are not equal.

Figure 4.

Data distributions for imaging and biomarker tests for breast cancer in controls, in cases with early stage cancer (darker shading) and in cases with late stage cancer (lighter shading).

Figure 5.

ROC curves comparing imaging versus biomarker tests for breast cancer. Left panel groups all diseased subjects together for comparison with controls. Right panel separately compares late stage cases and early stage cases with controls. Points displayed on ROC curves for the imaging test correspond to estimated ROC points associated with the image rating categories.

An additional covariate in this dataset concerns stage of disease, defined only for cases. The curves in the lower right panel of Figure 4 incorporate this covariate into the comparison of the two tests. We see that the accuracy of the biomarker test appears to be superior to the imaging test in detecting early stage disease but that they have similar performance for distinguishing between late stage disease and controls. The DM framework allows us to make rigorous statistical inference about these comparisons. Define X_sev=1 for late stage and X_sev=0 for early stage. We fit the following model to our data

$${\text{ROC}}_X=\mathrm{\Phi }({\gamma }_I+{\gamma }_{{\mathit{\text{IX}}}_{\text{test}}}{X}_{\text{test}}+{\gamma }_{{\mathit{\text{IX}}}_{\text{sev}}}{X}_{\text{sev}}+{\gamma }_{{\mathit{\text{IX}}}_{\text{int}}}{X}_{\text{test}}{X}_{\text{sev}}+{\gamma }_S{\mathrm{\Phi }}^{-1}(f))$$

after determining that the slope parameter was unaffected by either X_test or X_sev. The ROC curve for the baseline covariate values X_sev=0 and X_test=0 (early stage disease versus controls using the imaging test) is determined by estimates of its intercept γ̂_I = 0.438 (95% CI= 0.322,0.557) and its slope γ̂_S = 1.031 (95% CI= 0.96,1.1). The parameter γ̂_IXtest concerns the comparison between imaging and biomarker tests for distinguishing between subjects with early stage disease and controls. We found = γ̂_IXtest = 0.668 with a 95% confidence interval (0.506,0.842) that does not include 0 and conclude that the biomarker test is superior in this setting. The interaction term is statistically significant, = γ̂_IXint = −0.746, 95% CI=(−0.962, −0.537), indicating that the relative performance of the two modalities is different for detecting late stage disease. For late stage disease, the difference in the ROC intercepts for the two tests is γ̂_IXtest + γ̂_IXint = −0.078, 95% CI=(−0.269,0.088). Since this is close to 0 and not statistically significant we conclude that the tests have similar performance for detecting late stage disease.

Methods to implement analyses for comparing tests using the DM framework have been described previously.⁸ Briefly, the data are arranged as one data record per test result. Thus in our setting each subject has 2 data records, one for the imaging test and one for the biomarker test. Each record contains the variables (Y, D, X_test, X_sev). Since the variable X_sev is only relevant for cases with disease, it is coded as missing for controls. The f̂_rXtest values are calculated empirically for the imaging test. That is, the observed proportions of controls with imaging test ratings at or exceeding r give rise to values f̂_rXtest when X_test=0. We use the same values of f̂_rXtestfor the continuous biomarker test. This means that the same values on the horizontal axis of the ROC plot are used for fitting the test specific ROC curves. The DM algorithm proceeds by calculating U_r,i values for r=2, …, R for each case observation (Y_i, X_{test i}) and fitting the binary probit regression model to (U_ir , X_test,i , X_sev,i , X_test,i X_sev,i , Φ⁻¹ (f̂_rX)).

DISCUSSION

The main purpose of this article is to contrast the direct ROC modeling method that is popular for continuous tests with the ordinal regression method that is widely popular for image rating tests. Table 6 summarizes our findings. We show that when a single test is under consideration, the models are usually equivalent in the sense that they make the same modeling assumptions. One is typically a reparameterization of the other. We hope that this recognition will help unify these apparently discrepant approaches to ROC analysis.

Table 6.

Comparison & contrast of Direct ROC modeling and Ordinal Regression.

	Direct ROC modeling	Ordinal Regression
Entity modeled	ROC curve and probability frequencies of ratings for controls	Probability frequencies of ratings for cases and for controls
Disease specific covariates	Naturally included in the ROC regression model	Indirectly incorporated.
Multiple tests	Can be evaluated and compared within a single ROC model	Not allowed. Suitable for single test evaluation.
Type of test result data	Can be continuous or ordinal	Ordinal only
Computational algorithms	Requires two steps to fit FPR and ROC models in sequence.	One step.
	Asymmetric treatment of cases and controls	Symmetric treatment of cases and controls
Statistical efficiency	Less efficient	Theoretically optimal. Fully efficient with standard maximum likelihood fitting procedures.
Random effect models e.g. for large numbers of raters	Not yet accommodated	Are easily accommodated.

Yet there are major advantages for using the DM framework. In particular, when several tests are under consideration, it can be used to address scientific questions concerning comparisons between diagnostic tests. We showed through an example that additional covariates can be incorporated as well. Further examples of this general approach are provided in Pepe 2003 (section 6.4)⁸ where applications to continuous tests are illustrated. Here we applied the methodology to compare a continuous test with an ordinal test. This sort of comparison cannot be done within the OR framework to ROC analysis.

One advantage of the OR framework is that statistically optimal maximum likelihood methods are naturally employed for estimation with data. A variety of algorithms have been proposed for model fitting in the DM framework. We investigated the efficiency of one algorithm relative to maximum likelihood using simulation studies. We found that when the binormal model holds for the ROC curves this algorithm has performance almost equal to maximum likelihood. However, when the data deviate from modeling assumptions, the DM and OR methods may produce different results.

An issue that arises frequently in evaluations of imaging tests is that readers rate multiple images giving rise to observations that are clustered by reader. When many readers participate in a study, such as in the Breast Cancer Surveillance Consortium data, and one wants to make inference pertaining to the population of readers, random effect models are often entertained in the OR framework.^6,22 Random effects for readers may pertain to the thresholding criteria or to the ROC curves, or to both. The DM framework does not yet accommodate random effects in ROC models. Extensions to the DM approach to accommodate random effects warrants further research.