Implementation of Discrete Element Analysis for Subject-Specific, Population-Wide Investigations of Habitual Contact Stress Exposure

Abstract

There exist no large-series human data linking contact stress exposure to an articular joint’s propensity for developing osteoarthritis because contact stress analysis for large numbers of subjects remains impractical. The speed and simplicity of discrete element analysis (DEA) for estimating contact stresses makes its application to this problem highly attractive, but to date DEA has been used to study only a small numbers of cases. This is because substantial issues regarding its use in population-wide studies have not been addressed. Chief among them are developing fast and robust methods for model derivation and the selection of boundary conditions, establishing accuracy of computed contact stresses, and including capabilities for modeling in-series structural elements (e.g., a meniscus). This article describes an implementation of DEA that makes it feasible to perform subject-specific modeling in articular joints in large population-based studies.

The development of expeditious methods suitable for determining in vivo articular contact stress distributions is critical to understanding normal articular function and the mechano-pathology of osteoarthritis (OA). Excessive functional loads habitually applied to at-risk joints (shoulder, wrist, hip, knee, ankle) can negatively impact the health of articular cartilage, eventually leading to degeneration (Buckwalter & Brown, 2004). Many computational models have been developed to determine contact stresses in a variety of joints, mostly using finite element analysis (FEA) (Li et al., 2008). For the most part, however, these studies have involved lengthy and concerted efforts in well-controlled research settings, and have yielded articular contact stresses for only small numbers of cases. The high logistical cost of performing 3-D contact FEA on a subject- or patient-specific basis makes FEA of limited attraction for stress analysis in large epidemiologic studies (Englund et al., 2007; Felson & Nevitt, 2004; Lester, 2008). Advancement of expeditious methods for determining in vivo articular contact stress distributions will enhance the understanding of normal articular function, and of the mechano-pathology of OA.

Chao and colleagues popularized the use of rigid body spring modeling (now commonly known as discrete element analysis, or DEA) in biomechanics, as a simple numerical framework to model articular contact (An et al., 1990; Genda et al., 2001; Iwasaki et al., 1998; Li et al., 1994; Volokh et al., 2007). The DEA formulation involves treating bones as rigid bodies, and the cartilage at a given joint as an array of compressive-only springs distributed over the articulating bone surfaces. This modeling approach has been used to study contact mechanics in various diarthrodial joints, most recently progressing to fully 3D subject-specific geometry (Elias & Cosgarea, 2007; Elias et al., 2004; Iwasaki et al., 1998). However, it has rarely been used to study large numbers of cases. To our knowledge, the largest 3-D study reported has been that by Iwasaki et al., in which 10 cadaver wrist models were solved (Iwasaki et al., 1998). Although not designated as DEA, similarly conceived elastic foundation contact models have recently been integrated into commercial multibody dynamics software (Bei & Fregly, 2004; Fregly et al., 2003), but again, with analysis of only very limited numbers of cases. Similarly conceived proximity-based analyses have been performed based upon kinematic data for contacting bones obtained using biplanar fluoroscopic (Bingham et al., 2008; DeFrate et al., 2004; Wan et al., 2008), radiographic (Anderst & Tashman, 2003), or MRI-based (Pillai et al., 2007) data captures. In none of these studies, however, have there been more than a handful of subjects analyzed.

Whereas the speed and simplicity of DEA is attractive for subject-specific modeling, substantial issues regarding its implementation in population-wide studies remain to be addressed. Chief among these issues has been developing fast and robust methods for model derivation and implementation of boundary conditions, establishing the accuracy of computed contact stresses, and including capabilities to model in-series structural elements such as menisci. This technical note describes and applies methods to address these issues.

Methods

Model Generation, Derivation of Boundary Conditions, and DEA Solution

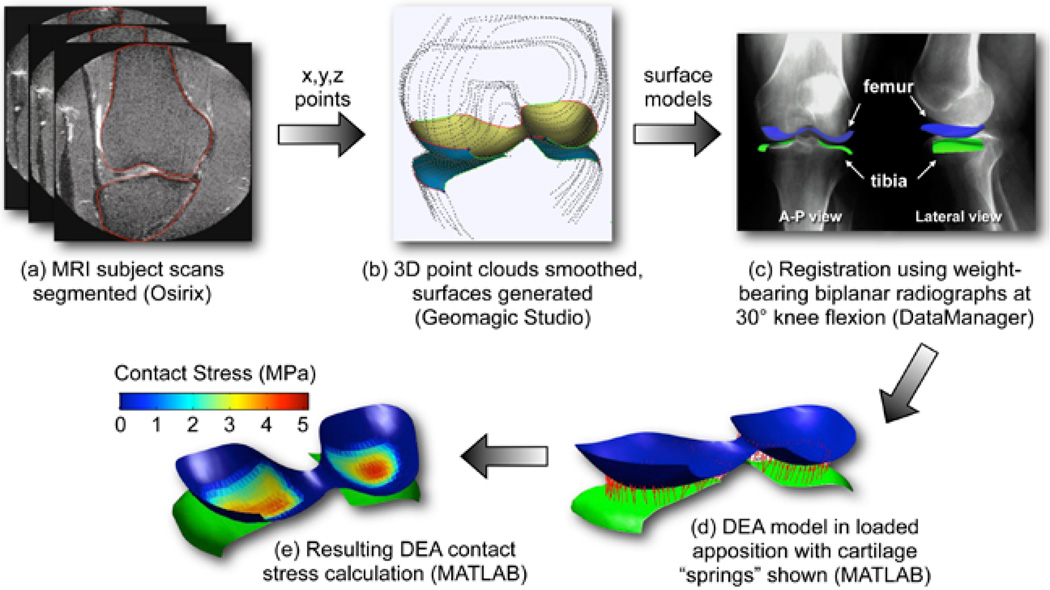
A DEA implementation framework suitable for population- wide investigations is shown schematically in Figure 1. Medical image data (CT or MRI) provide the requisite geometric information. In the case of CT, since cartilage is not visible (unless with arthrography), assumptions are necessary regarding cartilage thickness distribution. For contemporary MR imaging, the cartilage can be clearly visualized. The segmentation of source image data to obtain bone (and cartilage, from MRI) surfaces involves either manual tracing (Figure 1a) or the use of automated methods. The limit of practicality for manual segmentations (in 3D) is in the range of dozens of cases, reasonable for moderate-sized series. Continuing developments in automated segmentation (Yin et al., 2009) hold promise for studying hundreds or even thousands of subjects. Manual segmentations generate point clouds (x, y, z points) for the articulating bone surfaces, and in the case of MRI, for their overlying cartilage regions, and triangulated surfaces are fit to these point cloud data (Figure 1b). With automated segmentation methods, surfaces are generally output directly.

Figure 1.

Schematic of DEA implementation for population-wide investigations. The process involves (a) segmentation (either manual or automated), (b) surface generation (performed here using Geomagic Studio software (Geomagic, Inc, Research Triangle Park, North Carolina), (c) registration to a loaded apposition (here accomplished using DataManager 3D visualization environment (Biocomputing Competence Center, Italy), (d) DEA model generation, and (e) final DEA solution for contact stress distributions. Steps (d) and (e) are implemented in custom-written MATLAB code.

Specification of boundary conditions for DEA requires load and/or displacement data. As a practical matter, contemporary population-based cohorts of human subjects have usually not been designed for rigorous biomechanical analyses, so ideally subject-specific load or displacement data have generally not been available. Extrapolation of normative gait data for this purpose assumes that study subjects exhibit reasonably normal gait. Alternatively, functional weight-bearing plain radiographs provide a snapshot of a loaded joint apposition.

To use this snapshot, CT or MRI-derived surface models must be registered to the loaded apposition (Figure 1c), using approaches such as those presented by Moro-oka et al. (Moro-oka et al., 2007). Biplanar radiographs (or fluoroscopic images) are placed in a virtual environment, and the bone surfaces registered to the radiographs, such that the outlines of the bones to be modeled match the visually apparent surface boundaries. Fregley et al. (2008) found that contact stress estimates could be highly sensitive to variation in input displacements with this approach. Presumably this sensitivity would vary inversely with the characteristic magnitude of deformation, which was quite small in the metal-polyethylene joint replacement scenario they studied, compared with what is typically seen in loaded articular cartilage. For this reason, utilizing combinations of applied nominal loads and measured displacements would be prudent.

Finally, with preprocessing steps complete, construction of the DEA model, application of boundary conditions, and solution of the resulting equations (Figures 1d and 1e) can proceed. Model construction is from the bone surfaces, primarily, with cartilage surfaces providing the distribution of cartilage thickness to be used in modeling, when available. In cases where loads are applied, the DEA methods directly follow those previously published (An et al., 1990; Genda et al., 2001; Iwasaki et al., 1998).

When displacements are instead applied to the model, modifications to the DEA methods are required (Bei & Fregly, 2004). First, the bone surfaces are placed in the loaded pose, and closest-point pairings are made between the articulating regions. Then, surface element pairings with proximities less than that of the combined cartilage layer thicknesses are identified. All further calculations, beginning with the assignment of springs over the surface, are restricted to these in-contact elements. From the corresponding point pairings, individual spring deformations are then computed as the difference between their proximity and the unloaded cartilage thickness. To calculate contact stress (σ) from this deformation, the spring stiffness (k) is multiplied times the spring deformation (δ – normalized to initial cartilage thickness, and resolved along surface normals), with spring stiffness a function of linear elastic cartilage material properties (E = 12 MPa, ν = 0.42; Barker & Seedhom, 2001; Jin & Lewis, 2004) and the combined cartilage thickness (h).

$$k=\frac{E(1-\nu )}{(1+\nu )(1-2\nu )h}\sigma =k\delta$$

Finally, the engendered joint contact forces may be calculated, using the aggregate stiffness matrix incorporating all springs, and accounting for individual areas over which each acts (please see Genda et al., 2001, for further details).

Validation of Methods

A previously described procedure for physical validation of an FE model of the ankle joint (Anderson et al., 2007), provided an opportunity to directly validate the DEA implementation. As part of that prior work, contact stress distributions had been measured (using a Tekscan pressure sensor; Brown et al., 2004) in two cadaveric ankles in a loaded apposition. CT scans in that apposition provided bony geometries (automated segmentation, with subsequent manual surface editing), while biplanar radiographs obtained with stainless steel K-wires crossing the ankle joint and piercing the pressure sensors enabled spatial registration of contact stress data to the joint surface.

For the FE models, an articular cartilage region was extruded along subchondral bone surface normals to a uniform thickness of 1.7 mm. The FE analysis was performed using ABAQUS software, with displacement and load boundary conditions derived from the physical experiments. For the DEA models, a uniform tibio-talar separation of 3.4 mm was therefore set as the corresponding undeformed length for the system of springs representing cartilage. The displacements obtained from the load-driven FE simulations were input to the DEA model, and comparisons with the experimentally applied force magnitude, contact areas, and stress distributions were then made. The FE-computed displacements were used in this context as a surrogate for displacements obtained in the proposed framework by aligning 3-D reconstructed models with images from weight-bearing films.

Feasibility of DEA Implementation Established in Epidemiologic Study Cohort

The feasibility of the DEA implementation was established using data from the NIH/NIA-funded Multicenter Osteoarthritis (MOST) study (Englund et al., 2007). The MOST study used a population-based sampling frame to recruit 3026 community-dwelling men and women, age 50–79 years, with frequent knee symptoms (progression cohort) or at risk for developing symptomatic knee OA, based on a history of knee injury, surgery, or being overweight/obese (incidence cohort). The reader is referred to Englund et al. (2007) for a more precise definition of the study cohorts.

Weight-bearing, biplanar, fixed-flexion knee radiographs had been obtained for all subjects, and subjects had also been surveyed for knee symptoms, at baseline and at 15-month follow-up. In addition, standardized knee MRI scans had been obtained upon study entry using a 1.0-tesla dedicated MR system (OrthOne, ONI Inc., Wilmington, MA) with a circumferential extremity coil. A coronal short T1 inversion recovery (STIR) pulse sequence had been used in acquiring the images, following a protocol described previously (Roemer et al., 2005; TR 6,650 ms, TE 15 ms, TI 100 ms, 3-mm slice thickness, 0-mm interslice gap, 28 slices, 256 × 192 matrix, two NEX, 140 mm × 140 mm field of view, echo train length 8, 4 min 6 s scanning time). To investigate the relationship between habitual contact stress exposure and the development of incident symptomatic knee OA, 30 MOST subjects were randomly selected from those who had developed frequent knee pain by their 15-month follow-up visit (i.e., incident symptomatic knee OA), and these cases were matched with 30 control subjects who had not, in a nested case-control study design (Segal et al., 2009). None of the knees analyzed by DEA had frequent knee pain at the start of the study. The bones of the 60 MOST study knees were manually segmented, with surface generation and registration to the weight-bearing apposition done concurrently by a second analyst. Subject-specific DEA models were generated and solved in MATLAB, assuming a uniform 6-mm combined tibiofemoral cartilage layer. (The cartilage boundaries could not be reliably discriminated in the relatively low MR field strength images.)

Implementation of Additional In-Line Structural Elements

Discrete element analysis models, as conventionally implemented, have not incorporated intervening tissues between contacting cartilage surfaces. One important example of such intervening tissues in the knee is the meniscus, which plays an important role in juxta-articular stress transfer. In principle, menisci can to a first-order approximation reasonably be treated as another deformable in-series structure, using basic DEA concepts. This of course requires meniscal geometry (available from contemporary MR images) and appropriate modification to the underlying formulation of DEA equations being solved.

The basic DEA implementation constructs a system of linear compressive elements at closest-point vertex pairings between the tibia and the femur, with the spring constants reflecting local effective stiffness, based upon the elastic modulus, Poisson’s ratio, and thickness of the cartilage. When menisci are included, the local effective stiffness can instead be taken as a series composite of the local meniscus and local cartilage stiffnesses, with deformations distributed between the two tissues according to their respective individual stiffness values.

$$\begin{array}{c}\hfill k_{\text{meniscus}}=\frac{E_{\text{meniscus}}(1-{\nu }_{\text{meniscus}})}{(1+{\nu }_{\text{meniscus}})(1-2{\nu }_{\text{meniscus}})h_{\text{meniscus}}}\hfill \\ \hfill (1/k_{\text{composite}})=(1/k_{\text{cartilage}})+(1/k_{\text{meniscus}})\hfill \end{array}$$

The meniscal thickness distribution is computed first, using a closest point algorithm between superior and inferior meniscal surfaces. Those tibia-femur vertex pairings having an intervening meniscus segment are next identified. The meniscus is assumed to not move with respect to the tibia during a simple quasi-static loading at a fixed knee flexion angle. The meniscal thickness to be associated with a given tibiofemoral vertex pairing is obtained by indexing the closest point on the inferior surface of the meniscus with the tibia. A combined stiffness matrix is then constructed using the paired meniscal and cartilage thicknesses, and the correspondingly modified DEA equations are solved to calculate contact stress.

To assess the feasibility of meniscus inclusion in a knee DEA model, the menisci were subsequently segmented for 24 of the MOST study knees for which the menisci could be reasonably discriminated. Linear elastic compressive material properties (E_meniscus = 80 MPa, ν_meniscus = 0.3; Donahue et al., 2002) were assigned for the meniscus. The meniscal DEA formulation was then applied, with the same displacements applied as for the models without menisci, yielding alternative contact stress values for comparison.

Results

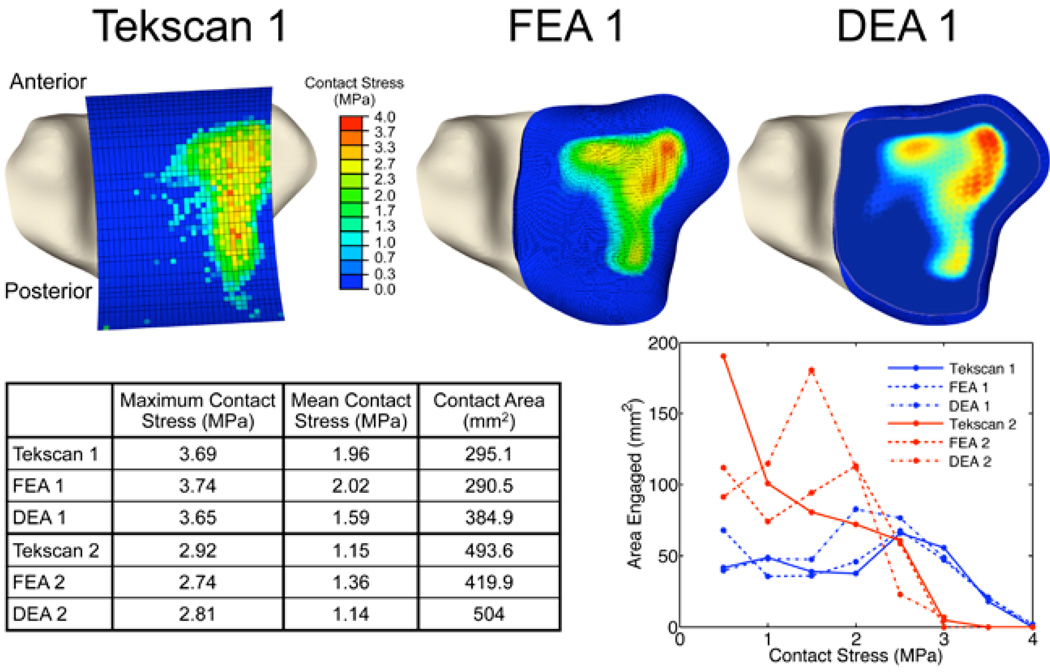
The ankle DEA model showed good agreement with measured contact stress values (Figure 2a). The level of agreement was roughly comparable to that obtained previously using FEA. Maximum DEA contact stress values were within 4% of those physically measured (1.1% for ankle 1, 3.8% for ankle 2), whereas less accurate contact area estimations (30.4% in excess for ankle 1, 2.1% for ankle 2) were obtained (Figure 2b). Area engagement histograms showed that DEA tended to overestimate areas at intermediate levels of contact stress, while much more accurately approximating area engagement at higher (presumably more deleterious) contact stress values.

Figure 2.

Validation of DEA methods by comparison with physical measurements and with the results of FEA in two cadaveric ankles. In addition to acceptable visual agreement, there was likewise good quantitative agreement, as shown both in tabular and histogram form

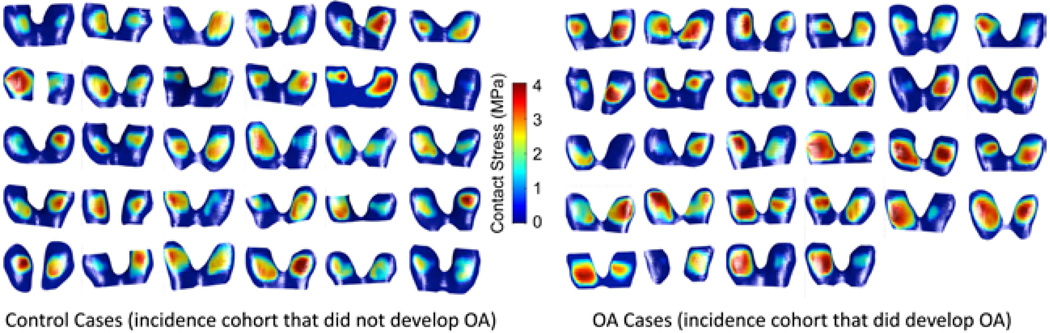
The calculations of contact stress for all of the 60 MOST study subjects’ knees took approximately 5.5 min to complete, including the generation of contact stress distribution plots (Figure 3) and area engagement histograms. The knees of subjects that developed symptomatic knee OA had higher maximum contact stresses (3.92 ± 0.55 MPa) compared with controls (3.38 ± 0.58 MPa; p < .001).

Figure 3.

Demonstration of DEA contact stresses computed for individual MOST study subjects.

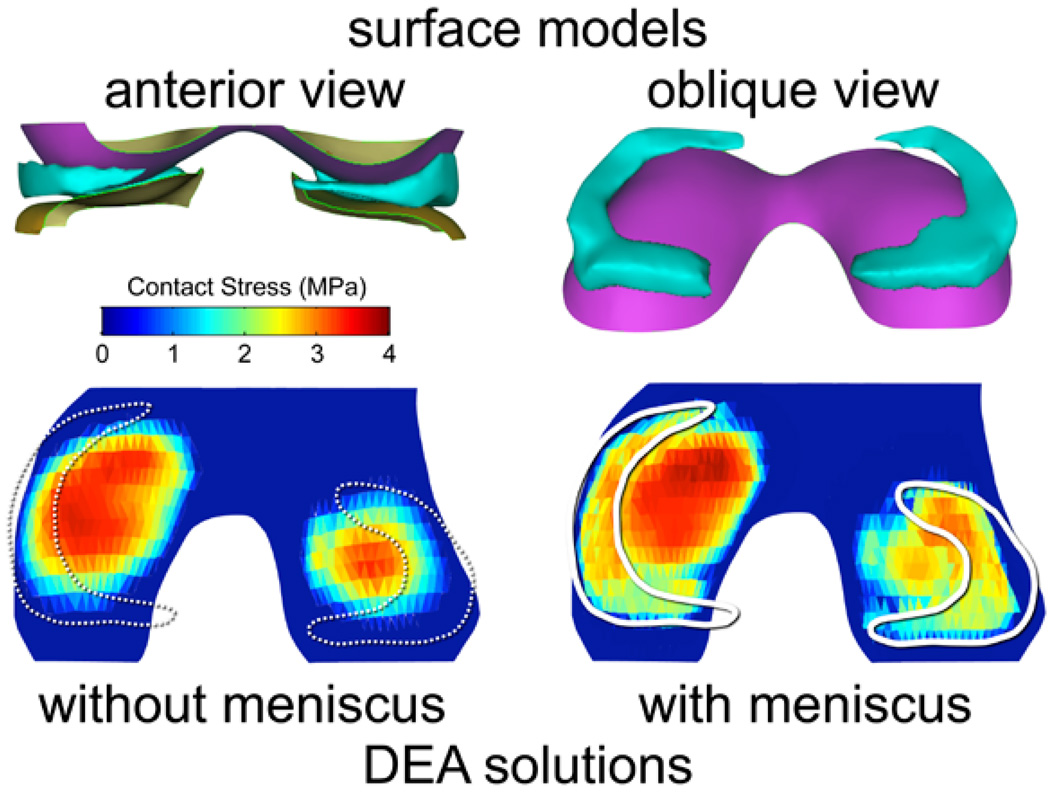
When the knee DEA formulation was modified to include a meniscus, the computed contact stress distributions extended over a larger contact area, as expected (Figure 4). The inclusion of menisci resulted in model run times similar to those without menisci. There were only minor changes in the computed maximum contact stress values, which still occurred centrally on the joint surfaces.

Figure 4.

An illustrative case, showing that inclusion of a meniscus in the knee DEA model (n = 24 knees) resulted in a broader distribution of contact stress over the articular surface. The maximum contact stress still occurred centrally.

Discussion

The DEA implementation for population-wide investigations presented here constitutes an advance in the use of noninvasive subject-specific modeling to help understand contact mechanics in the loaded articular joint. Validation of the methods in cadaver ankles showed excellent agreement with previous physical measurements of contact stress. The exploration of feasibility used DEA to study 60 knees from a larger subject population. It relied upon manual segmentation of the source images, manual registration of the bones from an unloaded to a loaded apposition, and it assumed that the menisci do not move relative to the tibia when loaded. These limitations, and the future refinements contemplated to address them, warrant further discussion.

Discrete element analysis does not explicitly model the cartilage as a continuum, but rather as an effective local stiffness distribution. Variations in cartilage thickness are implicitly modeled in the distribution of stiffness values and in the proximity assessments. In the present feasibility study, the distribution of cartilage thickness was assumed to be uniform, but in future work where the appropriate thickness variation data are available, they should be integrated into the modeling. Automated MRI cartilage segmentation methods are beginning to appear, and they hold substantial promise for providing these thickness data in a more reliable and (especially) expeditious manner. While not yet included in this DEA implementation, other investigators have successfully automated the process of registering 3-D models into a loaded apposition, as provided either by 2-D biplanar or 3-D volumetric data captures. Finally, although the primary implementation in this feasibility study used input displacements, the DEA methods are equally amenable to either displacement or load inputs. In fact, given a suitable iterative solution approach, a mixture of kinematic and kinetic inputs can be supported.

Based upon pilot work aimed at identifying local mechanical risk for incident symptomatic knee OA, the presented subject-specific implementation of DEA has shown itself as a feasible method for exploring the associated articular joint mechano-pathology. These methods therefore open the way for more widespread use of subject-specific determination of risk for OA attributable to habitual contact stress exposure.