Towards real time 2D to 3D registration for ultrasound-guided endoscopic and laparoscopic procedures

Abstract

Purpose

A method to register endoscopic and laparoscopic ultrasound (US) images in real time with pre-operative computed tomography (CT) data sets has been developed with the goal of improving diagnosis, biopsy guidance, and surgical interventions in the abdomen.

Methods

The technique, which has the potential to operate in real time, is based on a new phase correlation technique: LEPART, which specifies the location of a plane in the CT data which best corresponds to the US image. Validation of the method was carried out using an US phantom with cyst regions and with retrospective analysis of data sets from animal model experiments.

Results

The phantom validation study shows that local translation displacements can be recovered for each US frame with a root mean squared error of 1.56 ± 0.78 mm in less than 5 sec, using non-optimized algorithm implementations.

Conclusion

A new method for multimodality (preoperative CT and intraoperative US endoscopic images) registration to guide endoscopic interventions was developed and found to be efficient using clinically realistic datasets. The algorithm is inherently capable of being implemented in a parallel computing system so that full real time operation appears likely.

Introduction

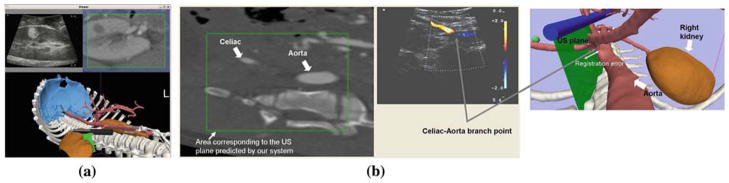
Minimally invasive procedures, such as endoscopic or laparoscopic interventions, have increased in volume, partially due to the availability of real time local imaging techniques that increase the operator’s confidence. Ultrasound is often used since it offers a flexible, easy to integrate, and real time imaging source that penetrates into tissue, thereby complementing standard optical (video) imaging. Further benefits may accrue from incorporating pre-procedure data; the gap between novices and expert operators can be reduced when using such “Image Registered” systems [15]. These systems are based on the use of preoperative volumetric CT (or MRI) images, loosely registered with the real time ultrasound image (Fig. 1). The operator can navigate more effectively and better understand the content of the real time ultrasound image by comparing it to a synthetic CT image formed in the plane of the preoperative volume corresponding to the US plane. Using a calibrated electromagnetic tracker, the registration error of this reference image is less than 5mm [2], which is adequate to guide many surgical procedures.

Fig. 1.

Image Registered system. The system uses an initial rigid body registration to find the global transformation between the preoperative CT scans and the OR coordinate system. a Laparoscopic examination of a kidney tumor. The tumor is shown both in the US image and the reformatted preoperative CT. b Scan of the branch point between the celiac and the aorta. The image shows the out-of-plane misalignment incurred by the system

A more ambitious goal is to improve the registration by doing a continuous real-time local correction based on incremental shifts between the ultrasound image and a subvolume of the CT data reformatted in the coordinate frame of the ultrasound. This approach neglects the possibilities of non-uniform warping or movement of tissue, but merely accommodates local displacements between the data from the two modalities. However, the image matching is restricted to a local region, so improvement is likely.

For practical utility we require that the registration occurs quickly: ideally with no lag, but within a few seconds at worst. Also, if the registration correction is rapid, organ shifts due to breathing (and other motions) may easily be accommodated. We note that our registration problem involves fitting a 2D slice to a 3D volume. Although other groups are successfully studying the registration of 3D ultrasound to 3D preoperative volumes [7–9], clinical laparoscopic and endoscopic procedures are carried out with 2D US probes; this is not likely to change in the near future. Other authors have successfully applied different registration strategies using a collection of tracked 2D transabdominal ultrasounds and CT [18,20]. Still, these works require a set of US images before the registration can be accomplished and the techniques are very demanding computationally.

We present here a method that is designed to register US images as they become available during the course of the intervention. We propose a new registration method based on phase correlation (PC). The direct application of PC to our problem is complicated by the different signal characteristics between the preoperative CT (or MRI) source, and the US source. Also, a successful approach must accommodate missing information in the intra-operative US images due to shadowing and phantom reflections caused by non-orthogonal incident angles between the US wave and the imaged object surface.

Background

The increasing use and quality of radiologic techniques (CT, MRI, SPECT, PET) for screening and diagnosis will stimulate the demand for minimally invasive biopsy and intervention. While these procedures might optimally be conducted inside the imaging device itself, practical considerations, including convenience and cost, will continue to limit “in-scanner“ approaches. Thus endoscopic and (to some extent) laparoscopic imaging are likely to be more broadly applied to the follow-up diagnosis of disease and the staging of care. Also, optical biopsy techniques, which can use smaller probes, may be increasingly utilized.

One approach to improving the guidance of instruments in real time is the use of intra-procedure ultrasound. While ultrasonic laparoscopic and endoscopic devices are widely available, they have not been maximally adopted by gastroenterologists and surgeons due to the long learning curve and lack of confidence in ultrasound interpretation, which manifests as difficulty in navigation and targeting for the probe to reach the radiologically determined target. We have therefore developed Image Registration techniques [2,15] which show the position and orientation of the ultrasound probe in anatomic context and display of re-formatted CT (or MR) reference images to improve the accuracy and confidence of physician operators (see Fig. 1b). The Image Registration approach is based on two assumptions:

1. The operator may function most effectively when presented with a simplified representation of the anatomy showing only key structures to guide probe positioning, and

2. Real time display of the position and orientation in this anatomic context may be more efficient than the use of more complex 3D plane displays of the radiologic information.

That is, Image Registration techniques may have added value because the instrument position and orientation is displayed accessibly and understood easily and intuitively.

Experimental studies in porcine models have shown that both laparoscopic ultrasound (LUS) and endoscopic ultrasound (EUS) users are significantly more effective at identifying multiple anatomic targets in a timed trial using the Image Registration system [16]. Kinematics measurements, which record and analyze position, orientation, and motion of instruments, have been shown to correlate well with the expertise of the user [14]. Experiments comparing LUS and EUS user performance with and without Image Registration (IR) show that the IR system permits novice users to perform like experts in some tasks, and even appears to improve the performance of experts in limited tests [15]. Users overwhelmingly preferred the Image Registration approach for both endoscopy and laparoscopy.

Functionally, our system requires four capabilities:

1. construction of a useful model from the pre-procedure 3D data (Segmentation),

2. alignment and fitting of the model to the real time anatomy (Registration),

3. determining the position of the instruments (Tracking), and

4. presenting the information to guide the procedure (Display).

A typical screen-shot of the display of our system is shown in Fig. 1a. Table 1 shows key attributes for these sub-system functions to make a successful Image Registration system.

Table 1.

Main attributes for a imaged registered system for laparoscopic and endoscopic interventions

Subsystem	Key attributes
Segmentation	Semi-automatic, rapid
Registration	Rapid set up, accurate, complaint with patient and organ motion
EM tracking	Noise-free, unobtrusive, easily implemented under sterile conditions
Display	Intuitively understood, high quality, real-time (lag free)

The method presented in this paper addresses the improvement of registration for small shifts from the initial registration. The most relevant of these motions is the out-of-plane mis-registration between the US image and the reformatted CT image. While in-plane shifts can more easily be recovered by the operator without a huge mental burden, out-of-plane misalignments may be critical for clinical interpretation. The integration of such a registration technique has to be done in the main tracking loop, so continuous updates can be made available as new US images provide more information about the mis-registration that the system is incurring.

Traditional phase correlation

Phase correlation is a well-known image registration method that exploits the Fourier shift theorem. Even though PC is limited to estimating translational shifts between two images, this approach is robust to frequency-dependent noise and limited image overlap areas. Furthermore, it can be calculated rapidly by means of the fast Fourier transform (FFT). This method can also achieve sub-pixel accuracy by using spectral techniques [12] or by means of least squares fitting of a Dirichlet function [3].

Let f_CT (x) and f_US (x) be two n-D images defined in ℝⁿ, where n = 2 or 3. In our case, f_CT and f_US will be the CT and US image respectively. For now we will also assume that both images have the same dimensionality. Let f̂_CT (u) = {f_CT} = |f̂_CT|e^jΦ_CT and f̂_US (u) = {f_US} = f̂_US = |f̂|e^jΦ_US be the corresponding Fourier transform of the images, where u is the spatial frequency coordinate. Let us assume that the CT image is shifted in the spatial domain f_CT(x − x₀) where x₀ is a translation. The normalized cross power spectrum, i.e the PC function, is defined as

$$\begin{array}{l}{\mathrm{\Psi }}_{f_{\text{CT}}{f}_{\text{US}}}(\mathbf{u})=\frac{{\widehat{f}}_{\text{CT}}(\mathbf{u}){\widehat{f}}_{\text{US}}{(\mathbf{u})}^{\ast }}{\mid {\widehat{f}}_{\text{CT}}(\mathbf{u}){\widehat{f}}_{\text{US}}{(\mathbf{u})}^{\ast }\mid }\\ =e^{-j{\mathbf{u}}^T{\mathbf{x}}_0}{e}^{j{\mathrm{\Phi }}_{\text{CT}}(\mathbf{u})-{\mathrm{\Phi }}_{\text{US}}(\mathbf{u})},\end{array}$$ (1)

where * denotes the complex conjugate and u^T x is the inner product between u and x₀. As we can see, the PC, Ψ, between the US image and the translated CT image is given by a complex exponential of a linear term incorporating the translation. However the phase discrepancy between the images, Φ_d (u) = Φ_CT(u) − Φ_US(u), appears in the PC function as a nuisance term. Therefore, the PC function in the spatial domain, Ψ(x), is not merely a Dirac delta centered at x₀ but additional terms appear complicating the estimation process.

The phase discrepancy term, Φ_d (u), arises from several sources: (1) Noise in both images. (2) Deformations between the images that cannot be accounted by a simple translation. (3) Differences between the phase signatures of the images, which are particularly evident when the images come from different imaging modalities. Since noise is not correlated with the signal, it is therefore easier to manage [12]. However, phase discrepancy due to high order deformations and multimodality imaging exhibits structured components that may yield a concentration of the phase spectrum energy in a harmonic different from that which corresponds to the desired translation.

Since we seek to register images from different modalities, phase discrepancy makes PC, as defined in Eq. (1), impractical. To illustrate this, we simulated an US image of a cyst phantom using the simulator field II [4] (hereon we will use this example to illustrate our method). The simulation is based on a scattering map (Fig. 2b). This represents the power of the scattering sites distributed in the medium and is thus a realization of the underlying tissue density (and therefore closer to the CT image properties). Let us assume that the scattering map is translated x₀ = [15, 10] in pixel units with respect to the ultrasound image. Figure 3 shows the PC function in the spatial domain when traditional PC is applied to the translated scattering map and the simulated ultrasound image. Instead of a Dirac delta function at x₀, the PC function exhibits multiple local maxima and the global maximum is not located at the corresponding displacement location as desired.

Fig. 2.

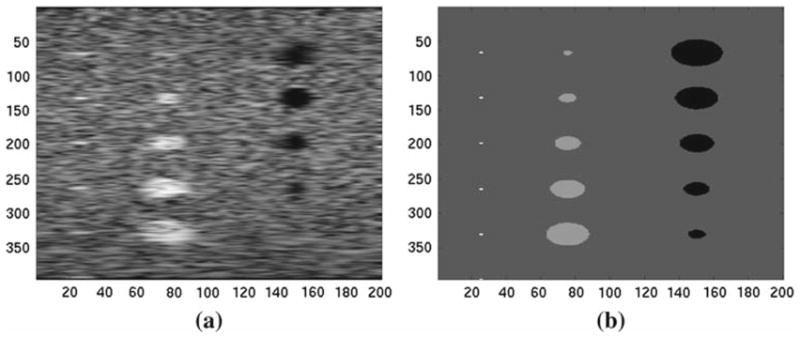
Simulated ultrasound image (a) and the corresponding scattering map (b). These images are used to illustrate the phase discrepancy associated to the use of different modalities. The scattering map is a density map of the scatters element that forms the US signal. In our example, the scattering map can be associated with a CT image, or at least it has phase properties that are closer to a CT image of the same phantom

Fig. 3.

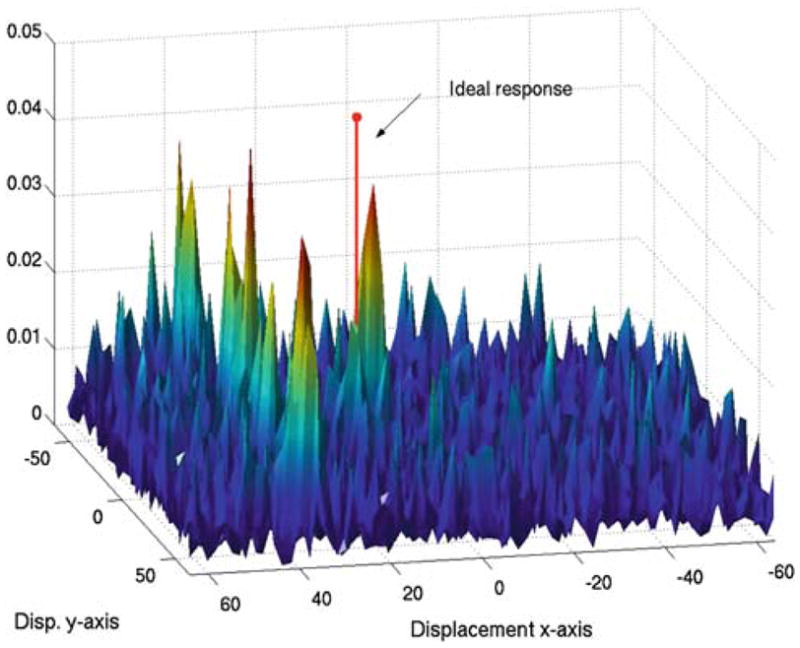
Traditional phase correlation, Ψ_fCTfUS, between images a and b in Fig. 2 when a displacement x₀ = [15, 10] is applied

In summary, traditional PC methods cannot be directly applied to multimodality 2D-to-3D registration due to:

• Different phase spectra content in the signals to registered: CT or MRI and US

• Different signal dimensionality: we have to perform a 2D to 3D registration where the US data is given in a 2D plane with a given known orientation and the CT data is given in a 3D grid that has an initial positioning with respect to the 2D plane based on a initial registration process when the patient is place in the OR table.

Method

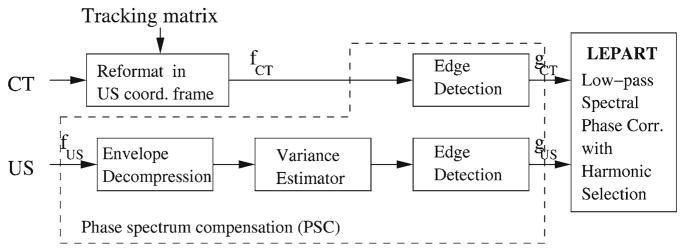
Here we present a new PC-based method which offers a robust approach to multimodality registration, specially for the registration of US to CT. Figure 4 outlines our approach, which we now discuss in detail:

Fig. 4.

Approach to multimodality registration based on phase correlation

Phase spectrum compensation

The first step of our method is to produce phase compensation between the CT and the US signal by preprocessing the signals from both modalities. This step is aimed at suppressing the phase discrepancy term, Φ_d (u).

Ultrasound preprocessing

Our approach is similar to the one followed by other authors [7,8] where the registration is achieved using edge information. The ultrasound signal is generated by a scattering process which causes characteristic speckle noise. Although the speckle carries useful information about the object medium, this information has a phase component that is not present in the CT image; therefore reducing the speckle component can improve the registration process.

Before performing the edge detection, the US signal is processed in the following manner:

• The RF ultrasound signal is usually compressed to accommodate the dynamic range of the display device. This compression has been suggested to be a logarithm mapping [5], f_USc = D log(f_US) + C. To recover the RF signal we compute the compression parameter D using the method proposed by Kaplan and Ma [5] based on second order moment of the log-compressed Rayleigh distribution.

• After that, we estimate the scattering power map, σ_US(x), from the uncompressed ultrasound image using the known statistic of the radio frequency (RF) envelope magnitude. Under ideal conditions and assuming that the medium contains a high number of randomly distributed scatterers, the ultrasound signal follows a Rayleigh distribution [17]. The Rayleigh distribution is specified by one parameter, the variance or power of the scatters, that can be estimated in a Maximum-Likelihood sense as

  $${\sigma }_{\text{US}}(\mathbf{x})=\sqrt{\frac{{\sum }_{x_i\in {\mathcal{N}}_{\mathbf{x}}}{f}_{\text{US}}^2({\mathbf{x}}_i)}{2N}},$$ (2)

  where is a squared neighborhood around location x and N is the number of samples in the neighborhood. Recovering this variance yields an estimation of the scattering map for that ultrasound image.

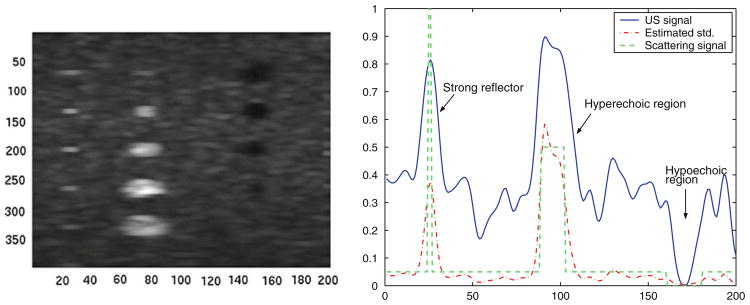
An edge detection based on the magnitude of the gradient of the estimated scattering signal, σ_US, is then applied. To illustrate this process, Fig. 5 shows the estimated σ_US for a horizontal scan-line corresponding to the cyst phantom shown in Fig. 2a. We observe that the estimated signal closely approximates the scattering map. The edge detection is performed over the estimated scattering map. The edge image is smoothed with a Gaussian kernel to remove high frequency components corresponding to spurious edges.

Fig. 5.

Estimated scattering map, σ_US(x), after decompression and variance estimation. Left Scattering map image corresponding to the ultrasound image shown in Fig. 2a. Right Horizontal line comparing the US signal, the estimated scattering map by the proposed variance estimator and the real scattering map

CT preprocessing

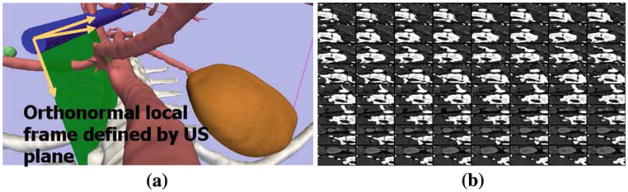
The CT is reformatted in the coordinate system of the ultrasound B-scan plane using the tracking information [2]. Figure 6a shows an schematic view of the frame attached to the US probe, as defined by the tracking information, that is used to locally reformat the CT volume. Figure 6b shows the corresponding reformatted CT as an overlay. Each image tile corresponds to one z-slice in the local CT volume. A field-of-view spanning a large enough region is usually defined based on the expected maximum displacement that can be recovered.

Fig. 6.

CT volume reformatted in the local frame defined by the US probe. a shows an illustration of the US B-scan plane and the local frame attached to the plane that is used to reformat the CT volume. b shows a tiled view of the reformatted CT images corresponding to the US plane shows in a

Since boundaries between tissues with different CT densities may show an acoustic impedance, we define acoustic interfaces as areas with a gradient magnitude in the CT. Following on with our illustrative example, Fig. 7a shows the result of applying the traditional PC method after the phase spectra has been compensated. In this case, the global maximum is close to the ideal solution. Let us denote g_CT and g_US as the resulting signals after the phase spectrum compensation (PSC) process for the CT and the US images respectively.

Fig. 7.

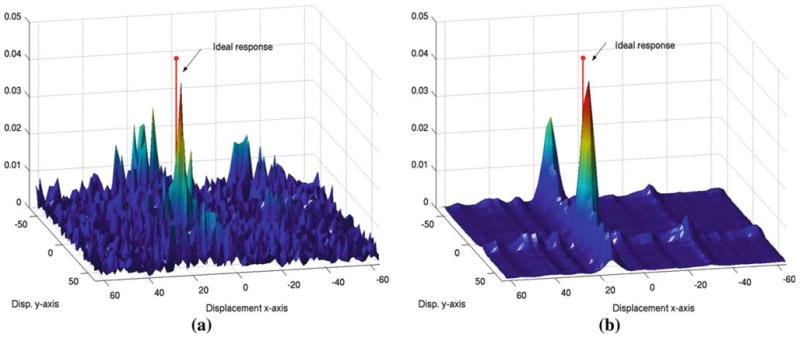
Phase correlation after phase spectrum compensation (a) and after spectral projected phase correlation (b). Note how spectral projection reduces the amount of noise in the phase correlation image; however, two local maxima still remains

LEPART: Low-pass spEctral Phase correlAtion with HaRmonic selecTion

Although the previous preprocessing introduces a normalization of the signal phase spectra, additional terms remain that preclude a robust estimation of the translation using the traditional PC method. To overcome this problem, we have developed a new method based on PC named LEPART. This method has two major components: (1) low dimensional spectral projection of the PC function into a rank-1 approximation and (2) harmonic selection.

Spectral projection

This stage follows the method proposed by Hoge [12] for accurate PC. In 2D, the PC matrix is ideally a rank-1 matrix; therefore the estimation of the displacement can be done by finding the best rank-1 matrix that approximates the estimated correlation matrix from the data. This can be achieved by means of singular value decomposition (SVD). SVD is a spectral technique that projects a matrix onto a set of r orthogonal eigenvectors that span the closest linear r-dimensional subspace to that matrix. In this case, finding the largest singular eigenvectors (one per spatial dimension) yields the best rank-1 approximation to the correlation method. This method has been also extended to deal with multiple dimensions [13] by means of the higher-order SVD [1]. Before applying the higher-order SVD, the PC is masked with a rectangular window to remove high frequency components that introduce noise into the projection and spectral distortion due to aliasing and border effects (as well as reducing the number of data points to be analyzed through the higher-order SVD). The windowed PC is defined as

$${\mathrm{\Psi }}_{g_{\text{CT}}{g}_{\text{US}}}^w(\mathbf{u})={\mathrm{\Pi }}_{B_c}(u_1)\cdots {\mathrm{\Pi }}_{B_c}(u_n){\mathrm{\Psi }}_{g_{\text{CT}}{g}_{\text{US}}},$$ (3)

where Π_Bc (u_i) is the rectangular function along dimension u_i with width 2B_c. Then, the windowed PC is decomposed using the higher-order SVD

$${\{{\mathbf{q}}_i(u_i)\}}_{i=1}^n=\text{hoSVD}({\mathrm{\Psi }}_{g_{\text{CT}}{g}_{\text{US}}}^w(\mathbf{u})),$$ (4)

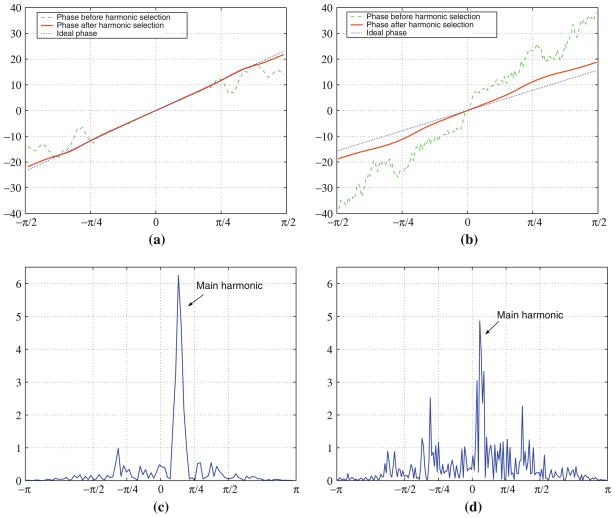
where q_i (u_i) is a complex eigenvector that spans the projection of Φ^w(u) along the dimensions i. The projected PC for our example is shown in Fig. 7b. It is interesting to note that a clear global maximum exists, although other extrema appear. The translation for each dimension can be independently worked out with sub-pixel resolution by fitting a line to the unwrapped phase of each 1D signal q_i (u_i) in a least squares sense. This is one of the main advantages of the spectral projection method. Following with our example, Fig. 8a shows the unwrapped phase of the eigenvectors corresponding to the axis x and y.

Fig. 8.

Harmonic selection for the projected phase correlation. a and b shows the phase of the filtered eigenvectors ${\mathbf{q}}_x^f(u_x)$ and ${\mathbf{q}}_y^f(u_y)$, respectively. c and d shows the Fourier transform of q_x (u_x) and q_y (u_y), respectively

Harmonic selection

As shown in Figs. 7b and 8a, the unwrapped phase of q_i (u_i) can be in some instances highly non-linear. This non-linear behavior is due to the presence of several harmonics in the projected phase that correspond to multiple potential fittings. Harmonics can appear due to remaining structured components of the phase discrepancy. To increase the robustness, we have therefore implemented a harmonic selection process.

The harmonic selection stage works as follows. The optimal harmonic, $v_i^h$, is computed by finding the principal harmonic of q_i (u_i) by means of its Fourier transform

$$v_i^h=argmax\mathit{H}(v_i)\mid \mathcal{F}\{{\mathbf{q}}_i(u_i)\}\mid ,$$ (5)

where υ_i is the frequency coordinate of q_i and H (υ_i) is a Hamming window that is designed to give more importance to low frequency harmonics, therefore smaller rather than larger displacements. Once the harmonic frequency has been found, the filtered eigenvector ${\mathbf{q}}_i^f(u_i)$ is computed by applying a band pass filtered centered at $v_i^h$.

$${\mathbf{q}}_i^f(u_i)={\mathcal{F}}^{-1}\{{\mathrm{\Pi }}_{B_{\text{hc}}}(v_i-v_i^h)\mathcal{F}\{{\mathbf{q}}_i(u_i)\}\},$$ (6)

where B_hc is the bandwidth of the bandpass filter.

The result of applying the harmonic selection to our examples is shown in Fig. 8. The Fourier magnitude spectra of q_x (u_x) and q_y (u_y) is shown in Fig. 8c, d, respectively. The filtered eigenvectors are shown in Fig. 8a, b for the displacement in x and y respectively. It is noticeable that the phase term is quite linear after the harmonic selection and comparably close to the linear phase induced by the applied translation.

Linear least squares fitting

As mentioned above, the last step in LEPART is a least squares fitting of a line to the unwrapped phase of ${\mathbf{q}}_i^f(u_i)$ for each axis. The slope of the fitting corresponds to the estimated translation term x̂₀ under consideration.

2D/3D registration

The approach outlined so far assumes that the images to be registered have the same dimensionality. In our problem this is not the case: the ultrasound image is defined in a 2D plane and the CT image is a 3D volume reformatted in the coordinates defined by the ultrasound plane.

The ultrasound B-scan plane can be rewritten as a 3-dimensional function by means of the discrete delta function as

$$g_{\text{US}}(x_1,x_2,x_3)=g_{\text{US}}(x_1,x_2)\delta (x_3),$$ (7)

where (x₁, x₂, x₃) is the 3D discrete coordinate system of the reformatted CT. Then, the 3D Discrete Fourier transform of Eq. (7) is given by

$${\widehat{g}}_{\text{US}}(u_1,u_2,u_3)={\widehat{g}}_{\text{US}}(u_1,u_2)\ast \sum _{k=0}^{L-1}\delta \left(u_3-\frac{2\pi k}{L}\right),$$ (8)

where δ is the discrete delta function [11], * is the convolution operator and L is the number of slices along the u₃ axis. In summary, the 3D Fourier representation of the 2D ultrasound plane is, no more no less, the replication the 2D spectrum along the new axis. Then, the LEPART method is applied in 3D, where the 3D Fourier representation of the US signal is constructed by replicating its 2D spectrum. The spectrum replication comes at no additional computational cost.

In summary, LEPART is a PC method for the registration of 2D ultrasound to 3D CT. After the PSC stage, the ultrasound edge image, g_US(x₁, x₂), is transformed to the Fourier domain and the spectrum is replicated according to Eq. (8). The CT edge volume, g_CT(x₁, x₂, x₃), is reformatted in the local coordinate frame given by the US and is also transformed to the Fourier domain. Then, LEPART is applied as described in “LEPART: Low-pass spEctral Phase correlAtion with HaRmonic selecTion”.

Results

Phantom study

The adequacy and accuracy of the proposed method for endoscopic and laparoscopic surgery has been validated by means of an abdominal ultrasound phantom (Fig. 9). The phantom consists of a ultrasound pad with several hypo and hyper-echoic regions. The phantom was scanned in a Siemens Sensation Somaton 64 Slice CT scanner with 0.6 mm isotropic voxel size. A sequence of ultrasound images have been acquired using a laparoscopic US probe (BK-Medical). The images were taken under controlled conditions so registration error was minimal. Additional, manually extracted features in both the CT and US were used to increase the registration accuracy between both modalities. This was considered our gold standard for validation. We selected 5 ultrasound slices where different tumors were visible. The CT was reformatted in a 0.3 mm isotropic grid and 20 mm × 5 mm × 20 mm margins were added in x, y and z direction respectively for each US image. We drew 500 realization for each location of uniformly random shifts in the range −5 to 5 mm. The parameters used in our algorithm were: B_c = π/8, B_hc = π/12, 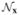= [7, 7]. The registration error results are shown in Table 2.

Fig. 9.

Model of the abdominal US phantom used for validation. The blue phantom (Blue Phantom, Kirkland, WA) is made of silicone with acoustic properties similar to human tissue. The phantom has different cystic regions with different echogenicity. The phantom was mounted on a casing simulating a human torso that can be used to explore the region using either an endoscopic or laparoscopic probe

Table 2.

Numerical analysis of LEPART as a robust multimodality registration method by Monte Carlo simulation

Method	RMS Registration Error (mm)				Execution timea (s)
	Mean	SD	Min	Max
Spectral PC [13] without PSC	12.997	0.178	12.896	13.281	3.73
Spectral PC [13] with PSC	3.376	2.599	1.135	14.241	3.85
LEPART without PSC	1.799	0.681	0.328	4.856	3.92
LEPART with PSC	1.558	0.781	0.179	4.414	4.25

^aMean execution time in an Intel Centrino 2 GHz and Matlab implementation

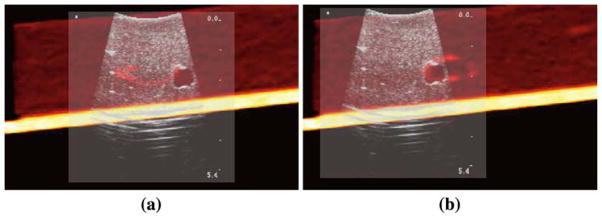
LEPART with PSC achieves a registration whose RMS error is less than 2 mm. LEPART seems to be a robust approach to multimodality image registration even when PSC is not applied, therefore accuracy can be sacrificed for the sake of performance. We have noticed that B_c plays an important role in finding a stable solution, albeit limiting the range of displacement that can be recovered. Increasing B_c above π/4 leads to unstable results. The results for one of the realizations before and after registration are shown in Fig. 10.

Fig. 10.

Example of one of the registrations for one of the tumor a before and b after applying LEPART with PSC

Retrospective study

We have tested our method under real surgical conditions using a retrospective specimen abdominal study. A laparoscopic experiment was conducted in a porcine model using the system described in Sect. 2. A preoperative CT scans was acquired with a Siemens Sensation 64 with contrast-enhancement to visualize vascular structures. The CT resolution was 0.6 mm isotropic. The US images were provided by a BK Panther Laparoscopic Ultrasound system. The laparoscopic probe was equipped with an electromagnetic tracker (Micro-BIRD, Ascension Technology Corp., Burlington, VT), and was connected to the computer through a PCI board. The sensor attached to the endoscope tip was 1.8 mm in diameter and 8.4 mm in length. Data from the US system and the tracking system were recorded using our navigation system for two targeted structures: the celiac-aorta branch with Doppler enabled and the right kidney. The acquisitions were done using the nominal system operation after an initial rigid body registration. The goal was to successfully recover the displacement using LEPART retrospectively.

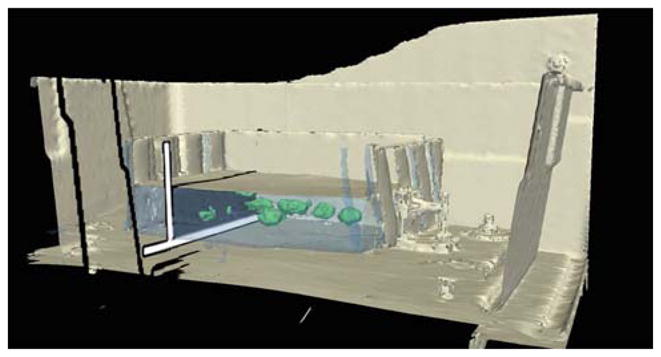
The results for the celiac-aorta branch are shown in Fig. 11. Figure 11a depicts the clear displacement in the z-direction with respect to the US probe. While the branch is imaged in the US, as it is reflected in the Doppler signal shown in Fig. 11b, the reformatted CT provided by the system, shown in Fig. 11c, does not align with the underlying US. The results after applying LEPART is shown in Fig. 11d. The displacement recovered by LEPART was (−0.6, −7.5, 2.7) mm defined with respect to the local US frame. We can see how the method is able to recover the z-displacement until the branch point is clearly visible while it was missing using standard tracked US, as depicted in Fig. 11a. Being able to recover z-displacements is critical given that in plane misregistration can be easily identified by the tracked US system operator.

Fig. 11.

Registration in an animal model: celiac-aorta branch. a 3D view of the tracked probe with respect to the anatomy extracted from CT before applying the proposed registration method. b Ultrasound image of the celiac-aorta branch corresponding to the 3D view shown in (a). Fusion of the CT and US before (c) and after (d) registration. The branch point is successfully recovered in the reformatted CT view after registration

The registration result for the kidney case is shown in Fig. 12. The displacement computed by LEPART was (−9.6, −16.8, −4.5) mm. Both an out-of-plane and in-plane displacement is recovered to yield a good alignment of the outermost surface of the kidney, as well as the internal capsule. The registration worked reasonably well given the amount of edge content present in the presented cases. The edge maps generated by the PSC step described in Sect. 5, that are used as inputs for LEPART, are shown in Fig. 13. LEPART is able to recover the discrepancy between the images even though some edges are either spurious or partially missing in the US source.

Fig. 12.

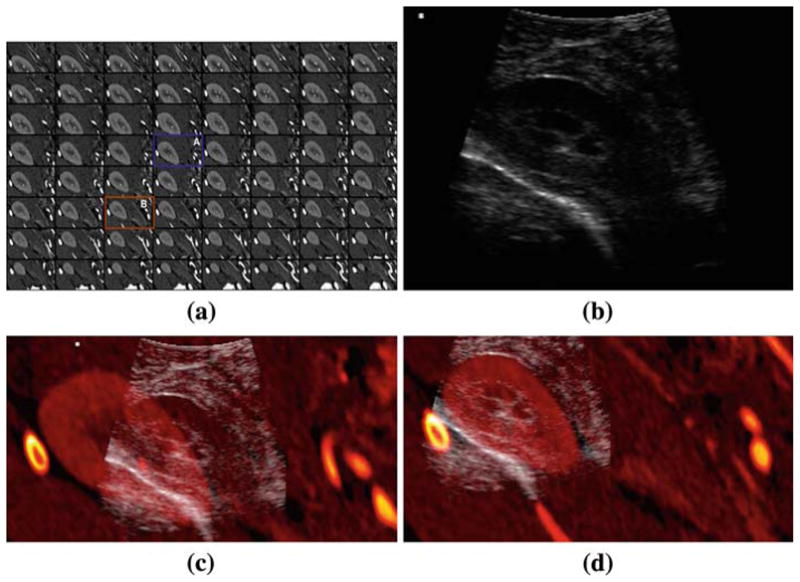
Registration in an animal model: right kidney. a Sequence of the CT volume reformatted in the local frame given by the US probe coordinate system. b The CT slice corresponding to the US plane before (A) and after (B) registration are highlighted. Fusion of the CT and US before (c) and after (d) registration. The kidney surface observable in the US is accurately aligned with the surface defined by CT

Fig. 13.

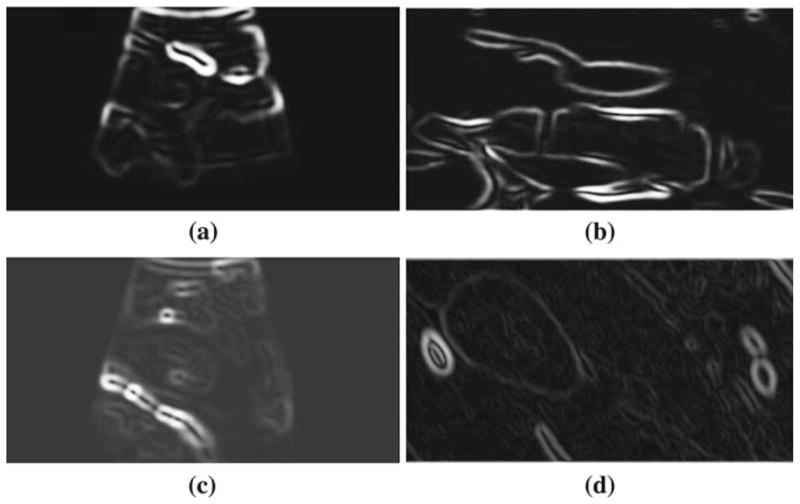
Edge images used by LEPART as input data to generate the registration results. a and b depicts the edge images from US (g_US) and CT (g_CT), respectively, for the celiac-aorta branch case. c and d shows the same edge maps for the kidney case. For the CT edge images, only one slice is shown corresponding to the optimal slice resolved by the registration algorithm

Discussion

The presented registration framework has been developed to be used with abdominal laparoscopic and endoscopic ultrasound images without relying on matching specific geometric characteristics. Instead, it uses edge information between tissues with different acoustic properties and CT densities to perform PC. In this sense, our approach is not organ specific. However, the edge features must be present in both the US and CT images. This is not always the case, due to the aberrations and distortions usually encountered in US imaging, for example shadowing. In our experience, the kidneys and the vascular structures in the abdomen present enough contrast and edge information to guide the registration process. As long as minimal conditions are met for the amount of structural content both in the US and the CT images, the algorithm is not organ-specific per se.

Edge information has been used as the main intermediate modality to achieve PSC and be able to deal with the multimodality nature of the problem. However, other approaches to PSC are possible and recent works on simulation of US images from [10,19] have shown encouraging results. In turn, the simulated US is used in conjunction with the acquired US to perform the registration. It is our interest to explore how LEPART performs when using the simulated US as its input. We expect to exploit the phase information contained in tissues with well-defined speckled characteristics that we are not currently benefiting from.

Our results show that the registration is achieved within a few seconds on a conventional laptop PC. A specialized implementation using advanced computing techniques that leverage the Graphics Processing Unit (GPU) is expected to achieve at least 10 frame per seconds registration update, which should suffice for clinical use. This target frame rate is based on the fact that the underlying core operation of the presented approach is the FFT. It has been shown that the FFT can be optimally implemented on a GPU [6]. Such implementations are currently commercially available in CUDA, the parallel computing architecture developed by NVIDIA.

Our current method poses several limitations that have to be considered. LEPART is only capable of recovering small translations of more or less rigid structures, which may limit its utility to reduced field of view imaging volumes. Larger displacements and other types of deformations might be accommodated by applying a fit of the deformation model over a temporal window. Another major limitation is related to the fact that enough structural information has to be present in the US images to achieve a successful registration. During a regular intervention, some US frames lack any information at all, mostly due to shadowing or poor acoustic coupling. Those frames ideally should not be considered in the registration process. An automatic method to perform frame selection would be desired before LEPART, or even any other registration method, is applied. We are currently exploring different alternatives based on the information content provided by the US image. Lastly, the current study only presents a phantom validation that may reveal limited information about the registration accuracy of LEPART in a clinical situation, future research lines will include an in-vivo validation of LEPART. The clinical registration examples were based on a porcine animal model. Further research is needed to assess the performance of LEPART in human studies.

The systems which may clinically use LEPART are comparatively low in cost. They consist of a personal computer workstation with parallel graphics capability, a flat panel display, and an electromagnetic tracker system. At current commercial prices, this system can be implemented in an endoscopy or laparoscopy suite for less than $15,000. In addition, the system requires very little training; as shown in prior work [15,16]; new users use it effectively with little orientation and no training.

Conclusions

In this paper, we have presented a multimodality registration method for preoperative CT images and intraoperative US endoscopic images to guide endoscopic interventions. Unlike traditional registration methods, the registration paradigm presented in this paper is unique in that:

• The registration technique can potentially work in a real-time mode producing continuous updates of the changes between the preoperative image and the US image.

• The registration technique is local to the location of the US frame. The locality of the image source allow us to use the assumption of quasi-translational misalignments.

LEPART appears to be a fast and robust technique for near real-time multimodality registration (under 5 s) of 2D to 3D data sets. For the cases studied, the LEPART approach gives significantly smaller registration error (Table 2) in comparison to traditional PC techniques.