The Effects of Concentric Ring Electrode Electrical Stimulation on Rat Skin

Abstract

Surface electrodes are commonly used electrodes clinically, in applications such as functional electrical stimulation for the restoration of motor functions, pain relief, transcutaneous electrical nerve stimulation, electrocardiographic monitoring, defibrillation, surface cardiac pacing, and advanced drug delivery systems. Common to these applications are occasional reports of pain, tissue damage, rash, or burns on the skin at the point where electrodes are placed. In this study, we quantitatively analyzed the effects of acute noninvasive electrical stimulation from concentric ring electrodes (CRE) to determine the maximum safe current limit. We developed a three-dimensional multi-layer model and calculated the temperature profile under the CRE and the corresponding energy density with electrical-thermal coupled field analysis. Infrared thermography was used to measure skin temperature during electrical stimulation to verify the computer simulations. We also performed histological analysis to study cell morphology and characterize any resulting tissue damage. The simulation results are accurate for low energy density distributions. It can also be concluded that as long as the specified energy density applied is kept below 0.92 (A²/cm⁴·s⁻¹), the maximum temperature will remain within the safe limits. Future work should focus on the effects of the electrode paste.

INTRODUCTION

Surface electrodes are the most commonly used electrodes clinically, in applications as diverse as functional electrical stimulation for the restoration of motor functions, pain relief, transcutaneous electrical nerve stimulation, defibrillation, surface cardiac pacing, and advanced drug delivery systems.²⁷ Common to these applications are occasional reports of pain, tissue damage, erythema, rash, or burns on the skin at the point where electrodes are placed.^{1,3,11,18,19,24,28,30,31,33} The origin of these electrical burns is not well understood. Heat development under the electrode during the passage of electrical current has been reported as a major cause of skin burn.^3,8,14,28,33 Temperature elevation of skin above 45 °C has been reported to result in tissue damage even from short-term exposure.^22,28 Takamiya et al.³² found that electrical energy generates joule heat. Thus, this phenomena in electrical injuries was caused by the effect of heat. In a review by Merrill et al.,²⁰ although mainly for implantable stimulation techniques, several possible mechanisms of injury are discussed which are still pertinent for noninvasive electrical stimulation. A common factor contributing to all the above mentioned mechanisms are regions of high current density.^{13,17,22,26,27} Overmyer et al.²⁴ modeled this phenomenon and found from experimental observations that the area of the highest temperature increase, or burns, was usually at the edge of the electrode. Wiley and Webster³⁴ provided an analytical solution of current density distribution on the surface of a circular metal disc electrode showing a highly non-uniform distribution with the highest current density at the periphery. As one of the possible practical implementations of this condition, they suggested a segmented circular disc electrode by dividing the solid metal disc into many annular rings with a small solid disc at the center. Kim and Schimpf,¹³ Papazov et al.,²⁶ Krasteva and Papazov¹⁷ also suggested that segmenting the electrode into concentric rings will reduce the edge effect and make a more uniform current density distribution. A study by Van Oosterom and Strackee²³ evaluated the lead field from stimulation with bipolar concentric ring electrodes (CREs) and disc electrodes. The lead field is the electric field produced by stimulation from a reciprocally charged electrode. Their research suggested that CREs have a greater sensitivity directly under the electrode than disc electrodes.

Besio et al.⁶ found that noninvasive electrical stimulation, applied 5 min after status epilepticus onset via novel CREs on the scalp, reduced or abolished electrographic and behavioral seizure activity in pilocarpine-induced status epilepticus in rats. It may be possible that there are other applications where stimulation via CREs may have beneficial therapeutic properties. Further analysis is necessary to quantify stimulation characteristics such as current intensity, pulse duration, and pulse repetition rate parameters to determine the safety of electrical stimulation via CREs.

There are various types of noninvasive electrical stimulation that are approved by the Federal Drug Administration (FDA) as safe. One such form of transcranial electrical stimulation (TES) is electroconvulsive therapy (ECT), used to treat depression, which applies stimulation pulses up to 1000 mA.²⁹ Pacelat et al. reports on using up to 300 mA TES for intraoperative neurophysiology monitoring.²⁵ Transcutaneous electrical nerve stimulation (TENS), frequently used for blocking pain, employs currents typically up to 30 mA.⁷ Transcranial direct current stimulation (tDCS), which has shown promise in epilepsy, is below 5.0 mA.¹⁰ For transthoracic defibrillation (cardioversion), the Advancement of Medical Instrumentation (AAMI) specification for cardiac defibrillator devices sets the peak currents at 80,000 mA for a 25Ω load. Kerber et al. tested the efficacy of different currents up to 40,000 mA and impedances on cardioversion.¹² In our epilepsy experiments we used 50 or 60 mA.⁶ For the tissue analysis of this paper, we kept the TcES constant at 50 mA.

In this study we quantitatively analyzed the effects of acute noninvasive electrical stimulation using CREs and determined the maximum safe current limit. We determined the relative energy density factor J²t introduced by Pearce et al.,²⁸ which is proportional to the delivered energy and is a measure of skin heating. A three-dimensional multi-layer finite element model was developed to perform an electrical-thermal coupled field analysis to calculate the temperature profile under the CRE and the corresponding energy density. In order to verify the results from the computer simulations, we performed animal experiments stimulating rats on the skin with the parameters of the simulation. The skin temperature was measured by infrared thermography. Controlled morphological studies using standard histological techniques to pathologically characterize any resulting tissue damage were also performed.

METHODS

Computer Model

To understand what stimulation parameters would be safe using CREs, we first performed computer modeling and then physical experiments. The computer models described in this research were finite element models created with FEMLAB (Comsol, Inc., Birmingham, MA). We used the FEMLAB pre-coupled ‘Joulean Heating’ template to perform an electrical-thermal coupled field analysis with temperature dependent properties.

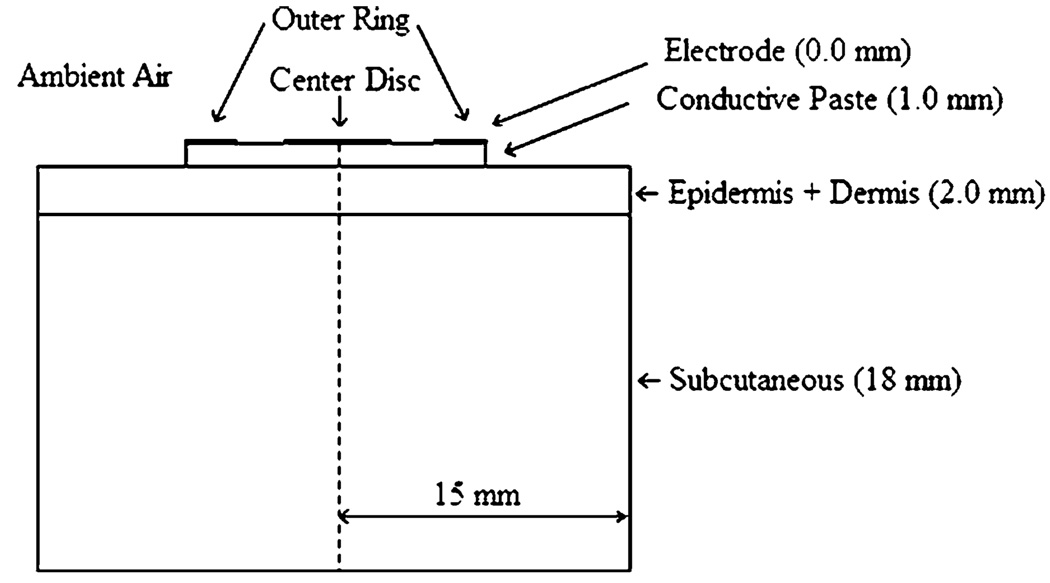
We developed a simplified three-dimensional multilayer cylindrical model. Figure 1 shows a cross section of the three-dimensional model. The top layer was modeled as electrode-plus-paste, followed by the epidermis-plus-dermis layer, and the subcutaneous region, respectively. The 1.0 cm diameter CREs used in the study had an inner/outer ring radius of 4.6/5.1 mm and the inner disc had a diameter of 1.2 mm. The CREs were modeled as a layer of 0.0 mm thickness followed by a 1.0 mm thick conductive paste layer. The epidermis and the dermis were modeled as one layer. In Fig. 1 the dimensions of each layer are specified in parenthesis. The dimensions of the overall model were 15 mm radius by 20 mm height. We performed simulations by supplying 50, 75, and 100 mA, respectively, to the outer ring. The disc was grounded in each simulation. All combinations of frequencies 100, 250, 350, 500, and 750 Hz and pulse-widths 50, 100, 150, 200, 250, and 300 µs were used for each of the stimulation currents.

FIGURE 1.

The schematic representation of the finite element computer model showing the electrode and conductive paste on top of the tissue.

Boundary Conditions

The electrical and thermal boundary conditions used for the model are listed in Table 1. We applied input current pulses with current density (J_n) at the outer ring of the CRE such that n · J = J_n; where n is the unit vector normal to the surface, J is the inward current density vector, and J_n is the normal component of the applied current density. The center disc served as an electrical ground return (V = 0). An electrical insulating boundary condition was applied to all the outer boundaries of the model such that n · J = 0; where n is the unit vector normal to the surface and J is the inward current density vector. All the internal boundaries at the interface of two layers were assigned continuity boundary condition n · (J₁ – J₂) = 0, where J₁ and J₂ are current densities in the neighboring layers such that the normal component of current was continuous across the internal boundaries.

TABLE 1.

Boundary conditions.

Type	Boundary	Expression
DC conductive media module
Inward current flow	Outer ring	n · J = Jn
Ground	Center disc	V = 0
Electrical insulation	All remaining boundaries	n · J = 0
Continuity	All internal boundaries	n · (J1 – J2) = 0
Heat transfer module
Convective heat flux	Epidermis, conductive paste	n · (k∇T) = h(T∞ − T)
Prescribed temperature	Subcutaneous	T = T0
Thermal insulation	All remaining boundaries	n · (k∇T) = 0
Continuity	All internal boundaries	n · (q1 – q2) = 0

We applied a thermal boundary condition of T = T₀ to the outermost boundary of the subcutaneous layer to simulate constant body core temperature at all times. A convective heat flux boundary condition n · (k∇T) = h(T_∞ − T) was specified at the upper epidermis and the conductive paste in contact with the environment. The epidermis convected heat into the surrounding environment at temperature T∞ with heat transfer coefficient h = 5 (W/m² °C) and the conductive gel convected heat with heat transfer coefficient h = 10 (W/m² °C). All the internal boundaries at the interface of two layers were assigned continuity boundary conditions n · (q₁ – q₂) = 0, where q₁ and q₂ are heat flux in the neighboring layers such that the normal component of heat flux was continuous across the internal boundaries. All the other surfaces of the model were assigned a thermal insulating boundary condition such that n · (k∇T) = 0. We assumed the initial potential distribution throughout the model to be constant (V = 0) and set the initial temperature of each layer to the body core temperature (T = 33 °C). We applied biphasic charge balanced current pulses to the outer ring of the CRE.

Experimental Verification

To verify the results from the computer simulations, we performed experiments stimulating rats using the parameters of the computer simulations. The skin temperature distribution was measured using a high-speed detector thermography camera (60 frames per second 320X240, NEC TS300, Micro Health Systems, FL, USA). We used Sprague–Dawley rats. They were housed in shoe-box cages on a 12 h light/dark cycle. Our protocol was approved by the Louisiana Tech University IACUC.

Electrical Stimulation

We anesthetized all the animals (n = 7) with ketamine (80 mg/kg, 50 mg/mL, i.p.) and xylazine (12 mg/kg, 100 mg/mL, i.p.) combination. Once they were anesthetized, we shaved the scalp and the back for the placement of the CREs. The rat skin was prepared using NuPrep™ (Weaver & Co., Aurora, CO) abrasive gel. The CREs were coated with high conductivity Ten20™ electrode paste (Weaver & Co., Aurora, CO) to adhere the CRE to the skin and reduce the electrode-skin impedance. We used a template to wipe the CRE-paste combination and provide a smooth 1.0 mm thick layer of Ten20™ electrode paste. Then we placed the CRE-paste combination on the skin of the rat for the experiment. The CRE paste combination was allowed to equilibrate with the skin. We found that it took approximately 5 min for the equilibrium, but we waited 15 min. Five or six experiments with different current, frequency, pulse width combinations were preformed on each animal at different locations. We applied each stimulation for a period of 60 s. After the stimulation, we removed the CREs and then prepared the stimulation site for histological analysis as described next.

The stimulation pulses were constant current symmetric biphasic charge-balanced square pulses. For verification of proper stimulation, we recorded the voltage impressed by the stimulation pulses across a one Ohm resistor. At the end of the experiments, we euthanized the animals and histologically examined the skin to determine the extent of tissue damage.

Histological Analysis

We performed tissue fixation by transcardial perfusion with 10% neutral buffered formalin of the deeply anesthetized animal. Skin samples, approximately 15 × 15 mm square, centered on each of the five or six electrode positions were removed and placed in 10% formalin to complete the fixation. We bisected each sample through the center of the stimulation site. Then we dehydrated the samples by immersing the tissue in a series of solutions of ethyl alcohol and water, with gradually increasing percentage of (75, 95, and 100%) alcohol. Next we cleared (Histoclear™) the tissue and embedded it in paraffin. We cut sections at 10 µm, stained them with hematoxylin and eosin and viewed them with bright-field microscopy or polarizing microscopy. Hematoxylin is a basic stain which has affinity for acidic substances such as DNA, RNA, etc. It therefore stains nuclei, ribosomes and cartilage matrix bluish violet, and these structures are referred to as ‘basophilic’. Eosin is an acid stain which has affinity for basic substances such as protein. It stains almost everything red except DNA and RNA. Images were made and are provided in the “Results” section.

RESULTS

As an initial verification of the computer models, we simulated the physical animal experiments of Pearce et al.²⁸ in the form of three-dimensional finite element models. These models were built according to Pearce et al.²⁸ specified experimental conditions. Separate models were made for each stimulation parameter combination experiment. A paired two-sided t-test showed no statistically significant difference between the computer models and the results reported by Pearce for the maximum temperatures at low energy (p = 0.082 left, 0.142 right) and medium energy (p = 0.068 left, 0.082 right) density stimulations, respectively, but showed a statistically significant difference (p = 0.011 left, 0.037 right) for high energy density stimulations.

Simulation Results for CRE

We compared the maximum temperatures resulting from the simulated electrical stimulation with different energy densities. The three-dimensional multilayer cylindrical models described previously were implemented to generate these results. The simulated maximum temperature at the skin surface for energy density factor J²t<.92 (A²/cm⁴·s⁻¹) beneath the 1.0 cm CRE never exceeded 45 °C which is the threshold temperature for skin damage. For energy density factor J²t = 0.92–1.5 (A²/cm⁴·s⁻¹), the maximum simulated skin temperature below the CRE was between 45 and 56 °C. For energy density factor J²t>1.5 (A²/cm⁴·s⁻¹), the skin temperature was greater than 56 °C.

Results of the Experimental Verification

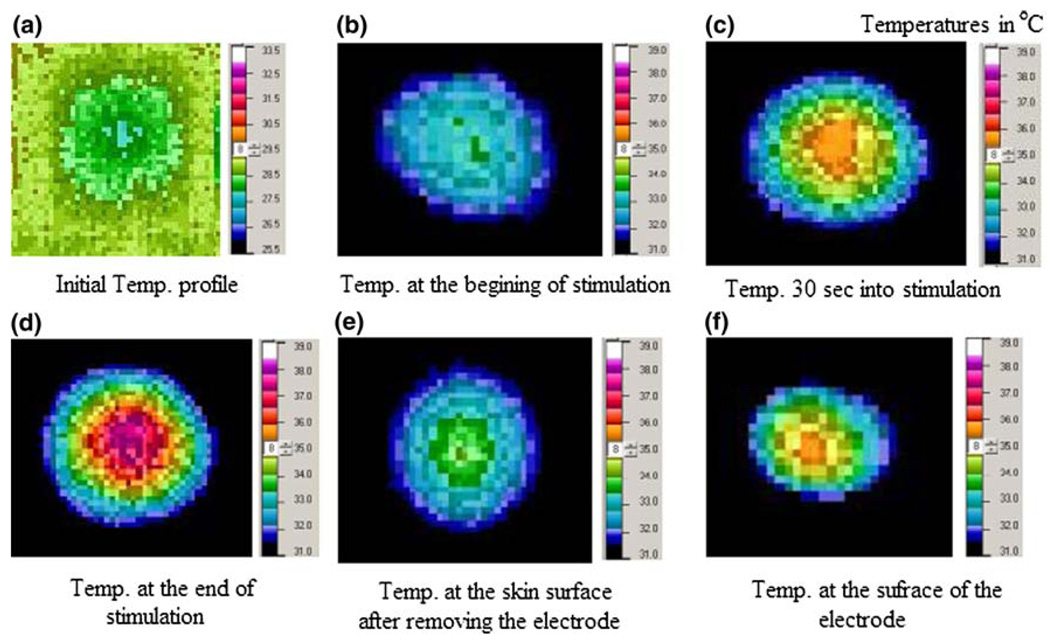
The objective of the animal experiments was to measure the maximum temperature from different stimulation parameters applied to the skin surface of rats to verify our simulation results. The stimulation parameters included those thought to be necessary for humans. This is based on estimates of the current density thresholds for stimulation of peripheral nerve²¹ and of the motor cortex¹⁶ using magnetic stimulation yielding rheobase values of approximately 2.5 A/m². According to a separate finite element model, not reported on here, we can achieve 2.5 A/m² approximately 1.0 cm deep into the cortex of the human brain with 50 mA stimulation from a 1.0 cm CRE. We used infrared thermography to measure the temperature distribution under and around the CRE while electrical stimulation was applied. We studied two different sets of stimulation parameters: a stimulus of 50 mA, 200 Hz, 300 µs—low energy density (J²t = 0.7) (A²/cm⁴·s⁻¹), and a stimulus of 50 mA, 500 Hz, 300 µs—high energy density (J²t = 2.7) (A²/cm⁴·s⁻¹). Temperature profiles for low energy density factor were recorded after the CREs were placed prior to stimulation (Fig. 2a), 1 s after the stimulation was turned ON (Fig. 2b), 30 s into the stimulation (Fig. 2c), and at the end of stimulation (60 s) (Fig. 2d), respectively. Immediately after the stimulation, we removed the CREs and recorded the temperature profile of the skin surface (Fig. 2e) and the CRE surface (Fig. 2f). As seen in Fig. 2, the temperature distribution under the CRE is non-uniform and the maximum temperature was observed under the disc. These observations were in agreement with the results from simulations of the models.

FIGURE 2.

Temperature profiles for low energy density factor stimulation (J²t = 0.7) (A²/cm⁴·s⁻¹). The panel (a) temperature scale is from 25.5 to 33.5 °C while all other panels are from 31.0 to 39.0 °C.

The maximum temperature measured from the rat experiments using low energy density stimulations was 38 °C. This result is very similar to the simulation result, which was 39 °C for low energy density stimulation. The maximum temperature measured from the experiments using high energy density stimulations was 47 °C. The maximum temperature from simulations for high energy density was nearly 78 °C.

Results of the Histological Analysis

We examined tissue from three different energy density factors for evidence of histopathology. The following pathological changes were noted (Table 2): (1) Epidermal necrosis as indicated by changes in density, compaction, and/or nuclei; (2) Damage to sebaceous glands and hair follicles as indicated by changes in density, compaction, and/or nuclei; and (3) Damage in the dermis as indicated by changes in density and orientation of collagen fiber bundles.

TABLE 2.

Summary of histopathological data.

					Damage to epidermis					Damage to dermis
Energy density	# Sites observed	Nuclear damage			Follicles & sebaceous glands			Epidermis Absent	Similar to control	Collagen bundles in bright-field			Collagen bundles in polarizing
		+	++	+++	+	++	+++		2	+	++	+++	+	++	+++
Control	8				2								2
Low	6	4			2	1			1	2			4
Low medium	10	1	5	2	4	2				1	7	2	1	8	1
High medium	6		5	1		3					4	2		4	2
High	5			5	2		5	1				5			2

+ = minimal damage; ++ = moderate damage; +++ = severe damage. Low = 0.3 A²/cm⁴·s⁻¹, 50 mA, 200 µS, 250 Hz; low medium = 1.2 A²/cm⁴·s⁻¹, 50 mA, 500 µS, 200 Hz; high medium = 1.2A²/cm^·s⁻¹,100 mA, 200 µS, 250 Hz; high = 10.81A²/cm⁴·s⁻¹, 100 mA, 500 µS, 300 Hz.

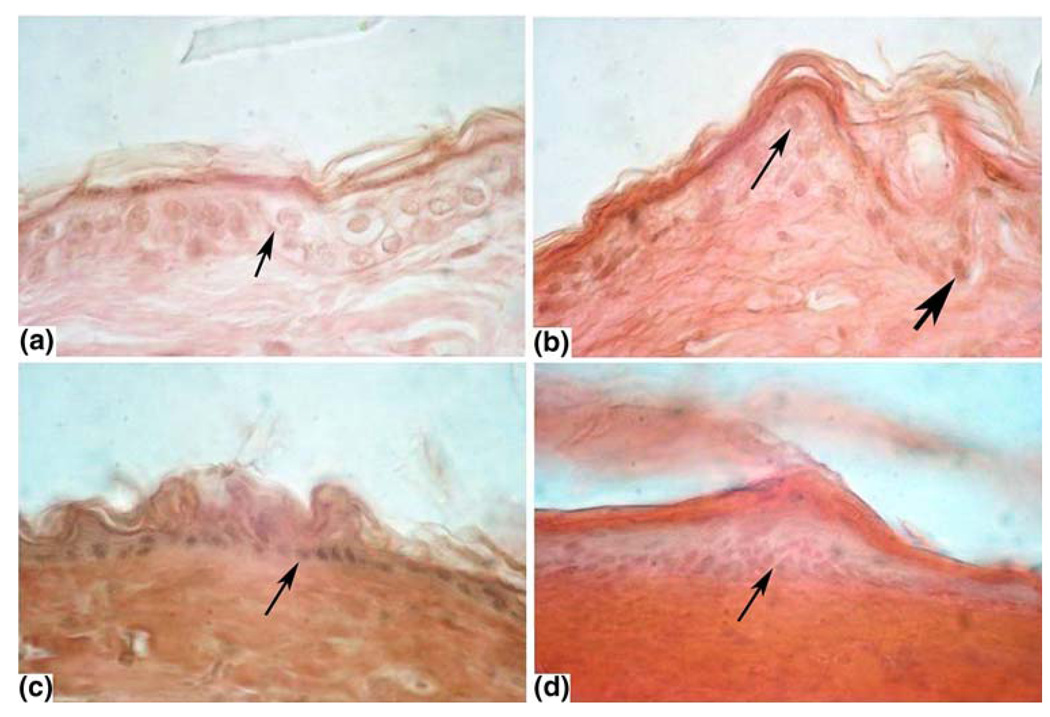
A section of un-stimulated skin is shown in Fig. 3a. The epidermis is intact, with moderately stained cytoplasm and lightly stained circular nuclei. The collagen fibers, although not shown in this section, are evenly distributed and in small bundles.

FIGURE 3.

Selected microscopic images: Initial magnification of 40×. (a) Control: cells appear distinct with nuclei visible. (b) Low energy: most nuclei appear normal (thin arrow). Some are more densely stained (bold arrow). (c) Medium energy: epidermis is more compact and most nuclei are more densely stained (arrow). (d) High energy: cytoplasm is densely stained and nuclei are shrunken, densely stained or missing above the germinal area. Nuclei in the germinal area are dense and elongated.

Stimulation at the low energy density factor J²t<0.92 (A²/cm⁴·s⁻¹) showed little or no damage (Fig. 3b). The basal nuclei of the epidermis were more darkly stained. The medium energy density factor J²t = 0.92–1.5 (A²/cm⁴·s⁻¹) showed some moderate changes (Fig. 3c). The epidermal cells were less distinct at most of the stimulation sites. The nuclei were shrunken darkly stained and sometimes indistinct. The thickness of the epidermis appeared thinner than in the controls. We also observed damage to the hair follicles and sebaceous glands. High energy density factor stimulation J²t> −1.5 (A²/cm⁴·s⁻¹) showed more pronounced damage to the epidermis (Fig. 3d). The epidermis was compact and homogenously stained and no nuclei were present. The cells in the deeper epidermis were indistinct with darkly stained elongated nuclei. Collagen fibers in the dermis were clumped and different in orientation compared with the control tissue.

DISCUSSION

The objective of this study was to quantitatively analyze the effects of acute noninvasive electrical stimulation using CREs and determine the maximum safe current limit. We made this determination by computer modeling and physical experiments.

We developed a three-dimensional multilayer model to determine the temperature profile under the CRE using FEMLAB. The FEMLAB pre-coupled ‘Joulean Heating’ template was used to perform an electricalthermal coupled field analysis with temperature dependent properties. Since heat transfer between arterial blood and the surrounding tissue should occur only in the deep dermis, unknown and uncontrolled parameters such as blood perfusion and metabolic activity were not modeled to simplify the heat transfer equation. As a further simplification, we assumed that the conductive paste was a perfect conductor and there was perfect contact between skin and the CRE. The current could not enter or leave the model except at the active and ground electrodes. All the outer boundaries were electrically and thermally insulated. We assumed the electrical and thermal properties of all the layers to be homogenous, isotropic and independent of temperature to minimize the mathematical complexity of the differential equations. It was shown that the inclusion of electrical conductivity values for both grey and white brain matter unnecessarily increased the complexity of the model.⁹ Although they did not calculate the temperatures they reported that induced electric fields in models with homogenous brain tissue varied slightly from the electric fields in models with a heterogeneous brain layer, and were therefore more efficient. All of the outer surfaces of the model were assumed to be adiabatic and the initial temperature distributions within the conductive paste and tissue layers were uniform at T = 33 °C.

Despite these extensive simplifications, the reproduction of Pearce et al.²⁸ experimental results correlating the maximum temperature and safe level of electrical stimulation suggests that the simulation results provide a good estimate of the tissue temperature comparable to that obtained from the animal experiments. The resultant maximum temperatures from the simulations match those from Pearce et al.²⁸ experiments except at the higher energy density factors. There was no statistically significant difference between the computer models and the results reported by Pearce et al. for the maximum temperatures of low and medium energy density stimulations but a statistically significant difference existed for high energy density stimulations.

The statistically significant difference in the results for high energy density stimulations may be explained by the increasing electrical conductivity of conductive paste and tissue with increasing temperature. High energy density stimulations result in very high temperatures under the CREs which may lead to unpredictably large changes in the thermal and electrical properties of both tissue and the electrode paste which cannot be accounted for in the simplified models used for this study.

In order to verify the results from the computer simulation, we performed physical experiments stimulating rats using the parameters of the simulation. The temperature distribution on the skin was measured using infrared thermography. The infrared thermographs closely corresponded to those predicted by the simulations, showing a non-uniform temperature distribution under the CRE with maximum temperature observed under the disc. The maximum temperature measured from the thermographs for Low energy density stimulations was 38 °C and was very close to the 39 °C of the simulation results for low energy density stimulation. The maximum temperature measured from the experiments for high energy density stimulations was 47 °C and the maximum temperature from simulations for high energy density was nearly 78 °C. This gap may be due to the fact that the melting point of the conductive paste was 43 °C. As the temperature increases above 43 °C, the paste starts melting and its electrical and thermal conductivity increases, resulting in a decrease in the maximum temperature. It could also relate to the actual thermal properties of vascular tissue which was not simulated.

A possible limitation of the study was that we tested the stimulation on rat skin rather than human skin. Rat scalp/skin is commonly used as a skin model instead of testing on humans.² We shaved the rat scalp and skin to apply the electrode Ten20™ paste combination. This was necessitated by the dense coat of hair that rats have. Fortunately human hair is not as dense as rat hair. We have recorded various evoked potential electroencephalography (EEG) signals from humans without having to shave their heads.^4,5,15 We simply use a mild abrasive and then apply a layer of Ten20 ™ paste, approximately 1.0 mm thick, using a template. Conceptually, when applying the stimulation to humans without shaving the scalp, any hair under the electrode may act as a thermal insulator blocking heat from transferring from the electrode through the paste to the scalp or skin.

In order to determine if damage occurred as a result of the stimulation, we examined the tissue in the areas of the stimulation events microscopically. Low energy density showed minor changes in the upper layers of the epidermis where the CRE electrode made contact. The dermis appeared normal when observed with bright-field microscopy. Polarizing microscopy of stained tissue showed a slight loss in birefringence compared to the controls, not shown. The damage to the cytoplasm and nuclei were consistent with reversible changes. The medium and high energy tissues showed more damages and are less likely to be reversible.

CONCLUSIONS

We conclude from this study that the simulation results of the three-dimensional models are accurate for low energy density distributions. It can also be concluded that as long as the specified energy density applied through the CRE is kept below 0.92 (A²/cm⁴·s⁻¹), the maximum temperature will remain within the safe limits and also within the limits of the melting point of conductive paste and provide a safe current density distribution. Further, there are no specifications on the conductivity of the Ten20™ electrode paste. Future work should focus on the effects of the conductivity and thickness of the electrode paste.