Interaural coherence for noise bands: Waveforms and envelopes

Abstract

This paper reports the results of experiments performed in an effort to find a formulaic relationship between the interaural waveform coherence of a band of noise γ_W and the interaural envelope coherence of the noise band γ_E. An interdependence described by γ_E=π∕4+(1−π∕4)(γ_W)^2.1 is found. This relationship holds true both in a computer experiment and for binaural measurements made in two rooms using a KEMAR manikin. Room measurements are used to derive a measure of reliability for the formula. Ultimately, a user who knows the waveform coherence can predict the envelope coherence with a small degree of uncertainty.

INTRODUCTION

The waveform interaural coherence is defined as the maximum of the interaural cross-correlation function for values of lag within limits, e.g., ±1 or ±2 ms. In psychoacoustical studies, it is often measured in one-third octave bands, which approximately correspond to the critical bandwidth of the human auditory system (Glasberg and Moore, 1990). Measurements of the waveform coherence are relevant in certain aspects of acoustics, and waveform coherence is often quoted in studies of rooms. It has been useful, for instance, in determining minimum microphone spacing when taking room measurements, especially in reverberant rooms (Jacobsen and Roisin, 2000; Kuster, 2008), and predicting acoustical sound quality of concert halls (Hidaka et al., 1995). It has increasingly become an important measure in studies of both human and animal hearing, with applications to a variety of binaural detection and discrimination tasks (Bernstein and Trahiotis, 2007; van de Par et al., 2001), binaural unmasking (Bernstein and Trahiotis, 1992; Culling et al., 2001; Durlach et al., 1986), auditory motion tracking (Grantham and Wightman, 1979), and is a basic component of most binaural models, especially involving interaural time difference detection (Colburn and Durlach, 1978; Jeffress et al., 1962; Shackleton et al., 2005). Waveform coherence is related to the apparent auditory source width, wherein the apparent auditory source width increases as coherence decreases (Ando, 1998; Blauert and Lindemann, 1986). Recently, it has also been linked to loudness perception (Edmonds and Culling, 2009). In summary, waveform coherence is an important factor in matters regarding modeling the human auditory system, the design of various listening spaces, applications involving virtual audio systems, and measurement of acoustical systems. In these applications, the effect of coherence on the listener is of primary importance.

At high frequencies, the ear is insensitive to interaural differences in the fine structure of signals, but differences in the envelopes of the signals become important (McFadden and Pasanen, 1978; Trahiotis et al., 2005). Coding of fine structure in the binaural system is lost at frequencies above 1.3 kHz (Zwislocki and Feldman, 1956), and so only acoustical envelopes are represented in binaural neural activity. Consequentially, the coherence of the envelopes of the signals in the left and right ears, the “envelope coherence,” is a more interesting binaural measure than the coherence of the waveforms of those signals for high-frequency bands (van de Par and Kohlrausch, 1995). Envelope coherence has been linked, for example, to binaural unmasking at high frequencies (Bernstein and Trahiotis, 1992). Across different environments, one expects that these two forms of coherence—waveform coherence and envelope coherence—will be related. In an acoustically dry environment where there are relatively few reflections off room surfaces, one expects that both coherences will be near unity. In a highly reverberant environment, both will be small.

The goal of the present work is to explore the relationship between the waveform coherence and the envelope coherence. In the literature, reported coherences are waveform coherences, but a reader may need to know the envelope coherence present in those studies. It is easier to measure the waveform coherence than to measure the envelope coherence since no manipulation of the measured signals needs to be done prior to calculating the waveform coherence. By contrast, in order to calculate envelope coherence, it is necessary to first construct the envelope of the signals, which involves either careful low-pass filtering or taking the absolute value of the analytic Hilbert transforms of the signals. The ideal result of this work would be a formula by which one could calculate the envelope coherence having measured the waveform coherence. The present work first finds such a formula for noise bands through a computer simulation. It then reports measurements of the two forms of coherence in two very different acoustical environments, as measured with a KEMAR manikin. It is shown that the most plausible relationship between coherences in actual room environments agrees with the formula that emerges from the computer simulation. Finally, the actual room measurements are used to derive a measure of reliability for the formula.

ELEMENTARY IDEAS

The waveform coherence γ_W is the maximum value of the cross-correlation function between a signal in the left ear x_L(t) and a signal in the right x_R(t). The cross-correlation function is

$$\text{cc}\left(\tau \right)=\frac{1}{T_D\sqrt{P_L{P}_R}}{\int }_0^{T_D}dt{x}_R\left(t\right)x_L\left(t+\tau \right),$$ (1)

where τ is the lag, and P refers to the average power of a signal, averaged over the same span of time, 0 to T_D. In practice, the duration of integration T_D is hundreds of times longer than the longest lag τ.

Thus the cross-correlation function is a measure of the similarity of a signal in the right ear to a signal as it occurs in the left ear at a later time—a time that is later by τ. The coherence is the maximum value of the cross-correlation function over all allowed values of τ. Therefore, the definition of coherence must include a limit on τ. In this article that limit is taken to be ±1 ms, consistent with standards in the literature, e.g., Beranek (1986), since this is approximately the largest naturally occurring interaural delay in free field.

The envelope coherence γ_E is defined in the same way as the waveform coherence except that the envelopes E_L(t) and E_R(t) replace the waveforms x in the equation for the cross-correlation:

$${\text{cc}}_E\left(\tau \right)=\frac{1}{T_D\sqrt{P_{E,L}{P}_{E,R}}}{\int }_0^{T_D}dt{E}_R\left(t\right)E_L\left(t+\tau \right).$$ (2)

The envelopes of the signals are calculated as the absolute value of the analytic signal, for example,

$$E_R\left(t\right)=\left|x_R\left(t\right)+\iota \mathcal{H}\left\{x_R\left(t\right)\right\}\right|,$$ (3)

where H represents the Hilbert transform. P is then replaced by P_E, the envelope power, for instance,

$$P_{E,L}=\frac{1}{T_D}{\int }_0^{T_D}dtE_L{}^2\left(t\right).$$ (4)

Some limits to these formulas can be easily derived. If the signals in the left and right ears are identical then the waveform coherence and envelope coherence are both equal to 1.0, the value of the cross-correlation function at τ=0. A value of 1.0 is the largest that the cross-correlation can ever be. Therefore, the largest possible coherence is 1.0 or 100%. Also, if the signals are sine tones, the waveform coherence is 1.0 because there is always some value of the lag for which the tones in the left and right ears are identical so long as the period of the sine is shorter than twice the maximum lag. In our case, twice the maximum lag is 2 ms, and the waveform coherence cannot be limited by that maximum lag so long as the sine period is shorter than 2 ms (frequency greater than 500 Hz). The envelope coherence for a sine is always 1, whatever the frequency, because the envelope is a constant.

In the present letter, the signals of interest are bands of Gaussian noise, which were chosen as representative of a generic signal. The bandwidths are given by the auditory filter widths of Glasberg and Moore (1990), approximately 1∕3-octave.

For noise bands, the waveform coherence and the envelope coherence have well defined limits. As noted above, if the noises are the same in both ears, both the waveform coherence and the envelope coherence are 1.0. In anechoic environments, where the signals arriving at the two ears are very similar, waveform coherences arbitrarily close to 1 can be observed. That limit of perfect coherence places a simple restriction on any formula designed to relate the envelope coherence to the waveform coherence—the limit of perfect correlation. If, on the other hand, the noises in the two ears are perfectly uncorrelated then the waveform coherence is 0 because epochs when the two channels have the same sign will be matched, on the average, by epochs when the two channels have opposite signs. In practice, such a case of ideally perfect incoherence can occur only if the two waveforms are deliberately made to be orthogonal. However, in highly reverberant environments the waveform coherence can become close to zero. Thus the perfectly uncorrelated limit can easily be approached in practice.

In the perfectly uncorrelated limit, the envelope coherence will not be zero because the envelope is never negative. In this limit, the integral in the cross-correlation is easy to calculate because the temporal average of the product of the envelopes is equal to the product of the temporal averages. van de Par and Kohlrausch (1998) noted that for Gaussian noise, the envelope is Rayleigh distributed. For a Rayleigh distribution, the average value is related to the rms value by a factor of $\sqrt{\pi }∕2$. Therefore, the coherence is π∕4 or 0.7854. This value sets a second restriction on the relationship between envelope and waveform coherences, namely, when the waveform coherence is 0, the expected value of the envelope coherence is π∕4. Because of the absolute value in Eq. 3, finding an analytic relationship between waveform and envelope coherences is made difficult, or perhaps impossible.

In an unpublished memorandum of 2004, Bernstein reported a computer experiment to determine the relationship between interaural waveform coherence and interaural envelope coherence. He tested the form

$${\gamma }_E=\frac{\pi }{4}+b{\left({\gamma }_W\right)}^n,$$ (5)

where parameters b and n were unrestrained (n is not an integer). He found that this form provided a reasonable fit to the results of his numerical experiments with b=0.2142 and n=2.2. Making use of the limits of perfect coherence, we may refine Bernstein’s equation somewhat to give

$${\gamma }_E=\frac{\pi }{4}+\left(1-\frac{\pi }{4}\right){\left({\gamma }_W\right)}^n.$$ (6)

This is now an equation with one free parameter, the power n. It should be noted that Bernstein’s value, b=0.2142, is very close to the exact value 1−π∕4=0.2146.

It is important to note that across the possible range of coherences (0–1), the value of n has a rather subtle effect on γ_E in Eq. 6. Consider, for example, n=2.0 versus n=2.2; the greatest difference between these two functions occurs at γ_W=0.62, where the difference is 0.0075—less than 1%. Because Eq. 6 is somewhat insensitive in this respect to the exact value of n, all reported values of n given in this paper will be rounded to the nearest tenths, and uncertainties (in the form of standard deviations) in the value of n smaller than ±0.05 will be ignored.

COMPUTER EXPERIMENT

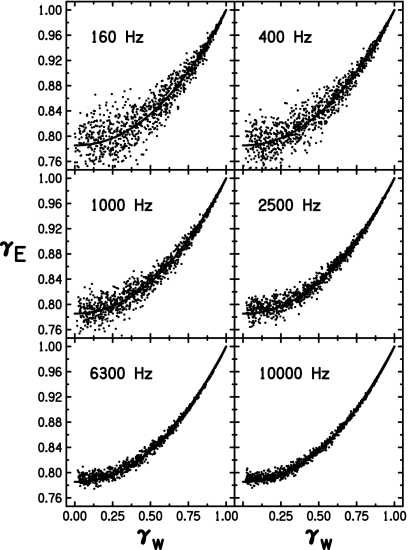
This section describes computer experiments using bands of noise. The experiments computed the waveform coherence and the envelope coherence and plotted one against the other for thousands of trials. The plots were then fitted to a function of the form of Eq. 6. In these computer experiments, two Gaussian noises were admixed in different proportions to lead to noise waveforms x_L and x_R with differing interaural coherences. The noises were 262 143 samples in length, sampled at a rate of 97.7 kHz. A total of 1001 different admixture proportions were used ranging from 0% to 100% and leading to waveform coherences ranging from 1.0 to 0.0. The 1001 different noises were time-domain filtered using gammatone filters1 centered on ISO one-third octave frequencies from 160 to 10 000 Hz. Because there are 19 such filters, our experiment consisted of 19 019 different computations. Plots of waveform and envelope coherences, measured from the maxima of waveform and envelope cross-correlations within the limits −1 ms≤τ≤1 ms, are shown in Fig. 1 for six representative frequency bands. For each of the 19 bands, a value of n=2.1 resulted in the best fit to the data. 95% confidence intervals about the average value of n within each band were all less than ±0.05.

Figure 1.

Plots of envelope interaural coherence versus waveform interaural coherence for simulated binaural signals using Gaussian noise pairs in six different 1∕3-octave bands. Each band contains 1001 coherence pairs, each of which is a single data point. A best-fitting line to Eq. 6 is shown as a thick solid line in each plot, though it may be obscured by the data points. The value of the power parameter n, to two significant figures, is 2.1 for each set of points in each panel.

The spread of the data about the best-fitting curve, measured as root-mean-square error (RMSE), is generally greater at lower frequencies than at higher frequencies. RMSEs were calculated on the scale of coherence (from 0 to 1). The calculated RMSEs are as high as 0.020 in the 160-Hz band and decrease steadily to a minimum of 0.0045 for the 10 000-Hz band. This is likely a bandwidth effect. Since bandwidth is proportional to the center frequency of the filter band, the number of degrees of freedom is proportional to the center frequency. One expects then that the RMSE will be inversely proportional to the square root of the center frequency. The best fit power law is close to that rule, RMSE=0.13f^−0.36.

ROOM EXPERIMENT

Methods

The computer experiments do not necessarily correspond to any real acoustical environment. Therefore, an experiment was performed with the goal of measuring waveform and envelope coherences through ears and comparing them as in the computer experiments. To accomplish this, maximum length signals of order 18 (2¹⁸−1=262 143) were played at a sample rate of 97.7 kHz through a loudspeaker in two different rooms. This made for signals about 2.6 s in duration, longer than the broadband reverberation times of the rooms used in this experiment. Signals were recorded in the ears of a KEMAR and filtered into 19 different bands with a gammatone filter bank. Cross-correlations of the waveforms and of the envelopes were computed within each band.

One of the rooms used was an uncluttered laboratory space with hard surfaces and no carpeting, 6.5 m×7.5 m×4.5 m high. The broadband RT₆₀ of this room was approximately 0.8 s; the RT₆₀ in octave bands between 0.25 and 8 kHz were all between 0.7 and 0.9 s. The other room was a reverberant room, with dimensions 7.67 m×6.35 m×3.58 m high. The broadband RT₆₀ of the reverberant room was approximately 2.0 s; the RT₆₀ in octave bands was between 2.0 and 2.5 s for the bands from 0.5 to 2 kHz and was about 1.2 s in the 0.25- and 8-kHz bands. These rooms are, as reported in Hartmann et al., 2005, rooms 10B and RR.

For all measurements, the KEMAR and loudspeaker were made to “face” one another. Measurements of coherence were made for four different distances between the loudspeaker and KEMAR—0.5, 1.0, 3.0, and 5.0 m. For each source distance, a measurement was made in ten different places in each room. For each measurement, both KEMAR and the loudspeaker were moved to different places in the room while keeping the distance between them the same. This yielded 19×10=190 waveform-envelope coherence pairs for each distance in each room.

Results

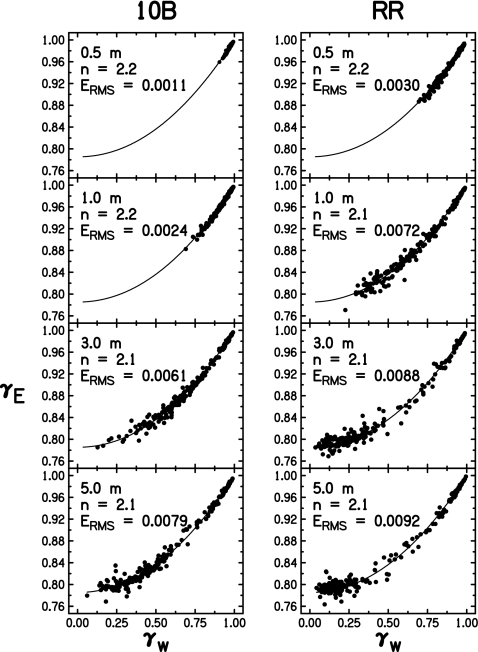
Within bands, Eq. 6 successfully describes the relationship between waveform and envelope coherences, though the value of the power parameter n within each band varies slightly. Consider, for example, room 10B at a distance of 3.0 m. The values of n found by fitting the data to Eq. 6 are as small as 1.9 in the 500-Hz band and as large as 2.2 in the 8000-Hz band. The variance in the best-fitting value of n is likely due to the narrow range of waveform coherences measured in individual bands. In some cases, where the total range of waveform coherences was small, the measured range of envelope coherences was also quite small. The regression which led to the value of n in those cases may be inaccurate. The average value of n across bands, plus and minus one standard deviation, was n=2.1±0.1.

The relative insensitivity of Eq. 6 makes determining an accurate value of n from a set of data with a small range of waveform coherences γ_W unreliable. Instead, data can be combined across all bands to get a picture of the waveform-envelope coherence relationship for any given room and source distance, as in Fig. 2. The resulting value of n given in Fig. 2 should apply reasonably well within any particular band. It can be seen that the combined data at every distance yield n=2.1 or 2.2. Standard deviations about these values were in all cases less than ±0.1. The collected coherences are lower on average as distance from the source increases and the direct-to-reverberant sound intensity ratio increases. Low-frequency bands still tend to have high coherence, and these form most of the points of high coherence in the cases where the distance was 3.0 or 5.0 m.

Figure 2.

Combined envelope versus waveform-coherence data across all 1∕3-octave bands measured in rooms 10B and the reverberant room at each source distance. Trend lines show the best fit of the data in each panel to Eq. 6. The value of the fitting parameter n is shown in the upper-left corner of each panel. Because of the relative insensitivity of the curve to the exact value of n, only standard deviations greater than ±0.05 are given. The rms error of the data to the best fit E_rms is given on the scale of coherence (0–1.0). Therefore, in room 10B at 1.0 m, where the mean γ_E is 0.96 and the rms error is 0.0024, the rms error is 0.25%.

CONCLUSIONS

The relationship between envelope and waveform interaural coherences measured in real rooms agrees quite well with computer simulations which calculate coherences from Gaussian white noises, as computed in bands simulating auditory filters. The bands were approximately 1∕3-octave in width. This close agreement suggests that the relationship between waveform and envelope coherences may be insensitive to the acoustic environment (reverberation time, source distance, etc.), though only two rooms and four distances were tested in this experiment. Within 1∕3-octave bands, Eq. 6 provides a reliable relationship between waveform and envelope coherences, which can be expected to generalize to other rooms and distances. It may also be conjectured that Eq. 6 would generalize to bands of arbitrary width. Determination of the value of n measured within any given band is subject to error. By combining data across bands for a given source distance, a reliable value of n can be found that actually applies to any particular band. Current observations suggest that there may be little difference between rooms with vastly different reverberation times.

The exact value of n (i.e., a value with greater precision than mentioned here) is very sensitive to small variations in the data. This is because the exact value of n does not have a large impact on the shape of the curves, and so curves of similar shape can have quite different values of n. This also implies that the exact value of n may not be important to describe the behavior of the relationship between envelope and waveform coherences, but a “ballpark” estimate may suffice in most cases. In this study, a ballpark estimate is arrived at by rounding the relevant values of n to the nearest tenth. In both the computer experiment and in the rooms, the average value of n was 2.1. Thus, it is suggested that a reliable equation describing the relationship between waveform coherence γ_W and envelope coherence γ_E in any room and for any source distance is

$${\gamma }_E=\frac{\pi }{4}+\left(1-\frac{\pi }{4}\right)\gamma _W{}^{2.1}.$$ (7)

The envelope coherences arrived at using Eq. 7 are not exact. Especially for situations in which the value of the waveform coherence γ_W is small, the variance in the related envelope coherence γ_E seems significant (see Figs. 12). It would be useful to quantify an expected error in envelope coherence.

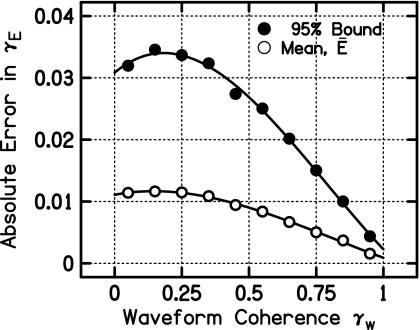
In order to quantify the expected deviation of envelope coherences from Eq. 7, waveform-coherence–envelope-coherence pairs were combined across all frequencies into one large set. Three such sets were constructed—one for each of the rooms and one for the computer simulation data. The data in each set were binned by the value of their waveform coherence into bins of width 0.1, thus creating ten bins across the range of waveform coherences. Within each bin, two methods of measuring error were employed: (1) calculation of the mean absolute difference $\overline{E}$ between the measured envelope coherences and envelope coherences as predicted by Eq. 7 and (2) calculation of the absolute difference from Eq. 7 for which 95% of the data deviate less than that, i.e., the “95% bound.”

The absolute errors for the rooms turned out to be equal to or slightly less than the errors in the simulated coherences for both methods of error estimation. Thus, a conservative estimate of the absolute error in Eq. 7 is given by the errors measured in the computer simulation of coherences. The absolute errors for both the mean and 95% bound method are shown as a function of the waveform coherence γ_W in Fig. 3. This figure shows third-order polynomial function fits to the absolute errors. The mean absolute error $\overline{E}$ can then be described as a function of the waveform coherence by

$$\overline{E}=0.011+0.0083{\gamma }_W-0.031\gamma _W{}^2+0.013\gamma _W{}^3.$$ (8)

The 95% bound is approximately three times as large as the mean absolute error and reaches an upper limit less than 0.04. It is unlikely that listeners could discriminate between envelope coherences that are different by this amount. A user of Eq. 7 may expect the difference between envelope coherences calculated from Eq. 7 and the actual envelope coherences to be approximately $\pm \overline{E}$ on average and may expect envelope coherences to deviate no more than $\pm 3\overline{E}$ from Eq. 7. It should be noted that Eq. 7 works quite well, even for cases where the waveform coherence is low. At worst, the expected error is about ±0.035.

Figure 3.

The 95% bound curve (closed circles) gives the absolute error in envelope coherence for which 95% of the simulated coherences deviate by that amount or less from the coherence predicted by Eq. 7. The mean curve (open circles) gives the mean absolute error $\overline{E}$ relative to Eq. 7 for simulated envelope coherences. Both curves are third-order polynomials fitted to the absolute errors of the binned data.

It is interesting to wonder whether different waveforms would yield different results. An obvious choice to test would be speech signals. In a short study involving a measurement procedure identical to that used in the room experiment, male speech was used as a signal in place of broadband noise. The same distances between the speaker and KEMAR were used as in the above experiments, and measurements were made in both rooms, 10B and RR. Speech signals do not yield good signal-to-noise ratios at very high frequencies, so the analysis was limited to bands no higher than 10 kHz. Though an in-depth error analysis was not performed as it was for noise bands, it was found that n=2.1 works quite well to describe the relationship between waveform coherence and envelope coherence for these speech signals.