Regulation of phenotypic variability by a threshold-based mechanism underlies bacterial persistence

Abstract

In the face of antibiotics, bacterial populations avoid extinction by harboring a subpopulation of dormant cells that are largely drug insensitive. This phenomenon, termed “persistence,” is a major obstacle for the treatment of a number of infectious diseases. The mechanism that generates both actively growing as well as dormant cells within a genetically identical population is unknown. We present a detailed study of the toxin–antitoxin module implicated in antibiotic persistence of Escherichia coli. We find that bacterial cells become dormant if the toxin level is higher than a threshold, and that the amount by which the threshold is exceeded determines the duration of dormancy. Fluctuations in toxin levels above and below the threshold result in coexistence of dormant and growing cells. We conclude that toxin–antitoxin modules in general represent a mixed network motif that can serve to produce a subpopulation of dormant cells and to supply a mechanism for regulating the frequency and duration of growth arrest. Toxin–antitoxin modules thus provide a natural molecular design for implementing a bet-hedging strategy.

Biological systems are inherently noisy (1, 2). Analysis of the way cells either combat (3) or utilize noise has led to deep insights into the design and evolution of genetic networks (4–7). In particular, it has been shown that the stochastic differentiation of a population of genetically identical cells into two distinct phenotypes can provide a strong advantage in an unpredictable and fluctuating environment (6, 8–12). Bacterial persistence, which plays a major role in the failure of various antibiotic treatments against pathogens, is a striking example of the advantage of variability (13). In contrast to resistance, which is genetically acquired, persistence is a transient phenotypic recalcitrance to antibiotics observed in only a small fraction of the bacterial population (14). When these “persister” bacteria are isolated and recultured without antibiotics, they result in a population that contains both persister and nonpersister bacteria like the original population (15). Persistence was shown to be due to an inherent bimodality of growth rates in bacterial populations, where the slow growth, or dormancy, of the persister bacteria protects them from the lethal action of antibiotics that are more potent against actively growing cells (16).

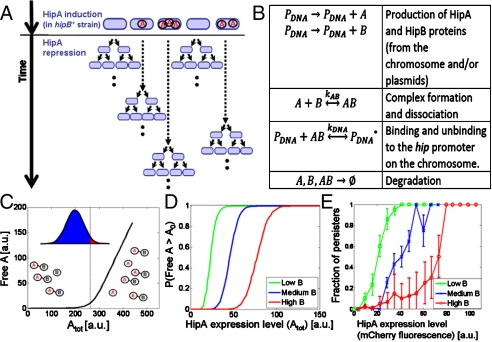
Moyed and Bertrand isolated a strain of Escherichia coli with a thousandfold increase in persistence (17) and the mutation, named hipA7, was mapped to a gene encoding the HipA toxin (18) of the hipBA toxin–antitoxin module (Fig. 1A). Toxin–antitoxin (TA) modules consist of pairs of genes, usually located in the same operon, where one gene acts as a toxin and the other cancels out its effect. TA modules were first identified on plasmids, and their function was understood to be plasmid maintenance (19). It was later found, however, that many homologues, as well as new TA modules, are present in the chromosomes of diverse bacteria, with more than 50 modules on the chromosome of Mycobacterium tuberculosis alone (20). The discovery that TA modules are chromosomal triggered a search for their other functions and this unresolved issue has prompted much debate and research (21, 22). The hipBA module controls the expression of two gene products, the HipA toxin and the HipB antitoxin, which form a tight complex and repress their own expression (Fig. 1A). Overexpression of the toxin was demonstrated to lead to a growth arrest that could be reversed by the expression of the antitoxin (23–26). These findings confirm that the hipBA TA module plays a key role in determining bacterial persistence. However, even though the structure of the HipBA complex is known (27) and growth arrest is shown to be due to HipA toxicity, any account of persistence must include an explanation of phenotypic variability: How does the coexistence of two distinct growth phenotypes within a genetically uniform population come about?

Fig. 1.

Effect of HipA expression on detectable cfus. (A) Schematic view of the wild-type hipBA module. HipB (antitoxin) and HipA (toxin) are expressed from the hip promoter, form a complex, and autorepress their own transcription. (B) Plating efficiency of different strains: Cells deleted for both hipA and hipB (hipA^-, hipB^-) have the same plating efficiency (in colony-forming units per milliliter) as cells expressing only HipB (hipA^-, hipB⁺), or cells expressing HipA together with HipB (hipA⁺, hipB⁺). Cells expressing only HipA (hipA⁺, hipB^-) do not form cfus. Plates were incubated for a week. Error bars denote standard deviations of three independent experiments.

Our goal was to characterize the mode of action of toxin–antitoxin network motifs in general, and the hipBA module in particular, and understand how they can generate phenotypic variability. Specifically, we asked how the HipA toxin affects only a small subpopulation of bacteria and why the dormant subpopulation is larger in the presence of the hipA7 mutation. For this purpose, we used genetic perturbations and detailed single-cell measurements to characterize changes in the persistence phenotype under multiple conditions. We complemented this approach with a theoretical model that incorporates the regulatory circuit shown in Fig. 1A and the inherent randomness of chemical reactions. We use the model to examine whether this simple system can reproduce the main characteristics of persistence, as well as to consider the consequences of various assumptions so that they can be validated or rejected experimentally.

Results

HipA Expression in a hipB⁺ Strain Results in an Extended Growth Arrest, with a Typical Time-Scale Set by the Level of HipA.

We first measured the phenotypic effect of the toxin in the absence of the antitoxin by expressing HipA in an E. coli strain deleted for hipBA, and bearing a plasmid encoding HipA under the control of the tet promoter (Table S1). We induced HipA expression in cells for 3 h and plated them in conditions in which the HipA expression was repressed. We found that, without HipB, even leakage levels of expression of HipA interrupts cell growth and prevents the subsequent appearance of colonies, as previously observed (23, 24). In contrast, in a hipB⁺ strain, cells are fully rescued from the toxic effect of HipA expression (Fig. 1B), in agreement with previous observations (23). But whereas the number of colonies was not affected by HipA in the presence of HipB, their growth dynamics were, and some of the colonies appeared over an extended period of time, compared to colonies that did not express HipA, as apparent also in ref. 23.

In order to get a quantitative evaluation of these growth-arrest dynamics, we developed a protocol for monitoring thousands of individual colonies simultaneously and measured the appearance time of colonies for populations expressing different mean levels of HipA, with commercial scanners and automated image analysis (28) (see Methods and Movie S1). When no HipA was expressed (Fig. 2A, blue histogram), colony appearance was rapid and the distribution of appearance times found to be narrow. When HipA is strongly expressed (magenta and purple histograms), the mean of the distribution of appearance times is shifted to longer times by 5.6 and 15.2 h, respectively. In addition to a shift in mean appearance time, HipA expression resulted in a very broad distribution of appearance times with a standard deviation of several hours. In summary, in a hipB⁺ strain, the expression level of HipA determines the typical duration of growth arrest.

Fig. 2.

Quantitative measurements of growth-arrest heterogeneity upon HipA expression in hipB⁺ cells. (A) HipA was induced in hib⁺ with atc to the indicated levels for 3 h before plating on LB plates. The appearance time of colonies was continuously monitored by the automated scanners system. The histograms show the fraction of cfus detected at each time point. Growth-arrested bacteria form colonies at later times, but those colonies grow at the same rate (see Inset). High levels of HipA (magenta and violet) result in long and widely distributed growth-arrest times. (see Inset) The colonies’ area growth rate distribution is the same for the different levels of HipA induction. (B) Same data as shown in A plotted as the fraction of growth-arrested cfus on log-scale, to better visualize the dynamics at later times. The blue, green, magenta, and violet curves exhibit a single exponential decay (with time constants that increase with HipA induction level). However, the red curve exhibits a more complex behavior, with an initial rapid decay (same rate as blue curve), that yields to a significantly slower decay (transition marked by red arrow). (C) Schematic representation of the strain used for the experiments shown in this figure. (D) Time-lapse microscopy images showing growth-arrested cells coexisting with rapidly growing cells. The first image is the overlay of phase-contrast and fluorescence images showing the initial level of HipA expression. The arrow marks the location of a bacterium that started growing more than 2 h after nearby bacteria started dividing. (Scale bar: 4 μm.) (E) Time-lapse microscopy results: Each point represents the growth-arrest duration of a bacterium, and its HipA expression level fluorescence at t = 0 (indicated by mCherry fluorescence). Higher levels of HipA expression correlate with longer growth-arrest duration but only above a threshold of expression (orange arrow). The level of HipA expression that prevents growth in the absence of HipB is marked by the blue arrow. (Inset) Monte-Carlo simulations of the level of HipA, [A_tot], and of the corresponding growth arrest in single bacteria. The growth arrest is shown in arbitrary units, as its exact computation requires more accurate determination of the relevant experimental parameters. (F) Histogram of growth-arrest times for the single-cell data of E for intermediate level of HipA induction. Cells with levels of HipA below and above the threshold (marked as orange arrow in E) are represented in black and orange, respectively. Within the same population, cells with either short or extended growth-arrest times coexist.

Intermediate Levels of HipA Expression Result in the Coexistence of Two Disparate Time Scales.

As HipA expression levels increase, the mean colony-appearance time becomes longer; but the smooth change in the mean hides a more complex change in the underlying distribution. At intermediate levels of HipA induction, with HipA controlled either by the tetracycline (P_tet) (Fig. 2A, red histogram) or the arabinose promoter (Fig. S1A), we consistently observed a peak of fast appearance, together with a broad tail at longer times, as if a subpopulation of cells was not affected by the expression of HipA. To better evaluate the time scales of colony appearance for each HipA expression level, the distributions shown in Fig. 2A were converted to one minus the cumulative density function, shown in Fig. 2B. In these plots, if the process by which cells emerge from dormant state were a perfect exponential decay, the curves would be straight lines with slopes corresponding to the decay rates. Indeed, when HipA is not expressed (blue line), the curve has a steep slope, consistent with an exponential decay with a typical time of 11 ± 2 min and reflecting the rapid appearance of colonies in this case. Increasing HipA expression slows down the process and increases the typical time scale of the growth arrest, as can be seen by the moderation of the slopes of the corresponding curves. Notably, at intermediate levels of HipA expression (red line), the curve consists of two sections, each with a different slope, where the crossover between those slopes is indicated by the red arrow. The behavior can be described as the superposition of two different time scales: Initially, the behavior follows the fast dynamics exhibited by the cells that do not express HipA, but at longer times, a slow exponential decay is observed, with a typical time scale of 220 ± 6 min. As described above, HipB rescues all the cells, eventually. But the presence of two radically different time scales found here (11 vs. 220 min) suggests that cells in the population are affected by HipA in two very different ways: For some cells, the antitoxin counteracts the effect of the toxin fully and immediately, and growth proceeds at the same rate as for cells in which HipA has never been expressed. Other cells do enter a dormant state, and the process by which HipB ultimately restores growth to these cells is characterized by an extremely broad distribution of growth-arrest times, with colonies continuing to appear for several days after plating. Note that the early and late appearing colonies grow at the same rate (Fig. 2A, Inset), showing that late appearance is due to a transient growth arrest and not to slower growth.

Single-Cell Measurements of HipA Expression and Growth Arrest Reveal That HipA Is Active Only Above a Threshold of Expression.

In order to measure the HipA expression level in each cell together with its phenotypic effect (29), we constructed a transcriptional fusion of HipA to the fluorescent protein mCherry (Fig. 2C and SI Text) and determined both fluorescence level and growth-arrest duration directly by time-lapse microscopy (Fig. 2D). As expected from the colony-appearance assay, we found a positive correlation between the level of HipA expression in single hipB⁺ bacteria and the duration of the growth arrest (Fig. 2E and Fig. S1B). However, we found that the effect of HipA was apparent only after it exceeded a threshold of expression. Note that the threshold fluorescence expression level (denoted by orange arrow in Fig. 2E) is several times higher than the level needed to completely block growth in a hipB^- strain (marked by a blue arrow). Focusing on a single population at intermediate mean level of HipA induction, we show in Fig. 2F the histogram of single-cell growth-arrest times. The measurement of HipA expression levels in single cells allows us to mark in black all cells that express HipA below the threshold, and in orange, those that have higher levels of expression. The distribution of growth times seems to have two components—a sharp peak at short times and a broader peak with longer times of appearance. What Fig. 2F reveals is that the classification of individual cells to one of these two subpopulations is based on the cell-specific level of HipA relative to a threshold.

Taken together, these observations show that (i) HipA can arrest the growth of bacteria for periods that can exceed by far the typical lag time of E. coli; (ii) this growth arrest is effective only when HipA exceeds a threshold of expression; and (iii) when the average level of expression is close to the threshold, only part of the population transiently stops growing and constitutes the so-called persister fraction (Fig. 3A). Our results suggest that it is cells of the latter subpopulation that survive extensive antibiotic treatments, such as beta-lactams, so long as they remain growth arrested (Fig. S2 and SI Text).

Fig. 3.

The dependence of the threshold on HipB. (A) A cartoon illustrating the effect of HipA induction in a hipB⁺ strain. Free HipA is marked as red A. Growth arrest is represented by a dotted arrow and arrow length indicates the duration of the growth arrest. The higher the initial number of free HipA proteins, the longer the growth arrest. (B) Summary of the processes taken into account in the stochastic simulations of the various strains used in this work. (C) Simulation results and illustration for the amount of free HipA as a function of total initial HipA in a cell, [A_tot]. The amount of free HipA is negligible until [A_tot] reaches a threshold. For a given distribution of A_tot in the population, cells with A_tot below the threshold will grow normally (blue), whereas cells with A_tot above the threshold will be persistent (red). (D) Monte-Carlo simulation results: Probability for persistence, namely, [A] > A₀ vs. the total number of HipA proteins ([A_tot] = [A] + [AB]), for different values of HipB production rates. (E) Experiments: HipA expression was induced from pBAD33A-mCherry at the same level, and the number of persisters measured by microscopy for different levels of HipB from plasmid pZS21B in MGN. Green, low HipB (61 cells); blue, medium HipB (179 cells); red, high HipB (201 cells). Simulations (C) and experimental (D) data show that the higher the level of HipB, the higher the threshold of HipA expression required to induce persistence.

Stochastic Simulations of the hipBA Toxin–Antitoxin Module Reproduce the Observed Dependence of Growth Arrest on HipA Expression Level.

With a view to understanding the mechanism behind the observed coexistence of time scales, we developed a theoretical model that takes into account the protein production of HipA and HipB, their binding, and degradation (Fig. 3B). A model of the hip module that uses deterministic rate equations formalism has recently been proposed to lead to bistability (30, 31). We developed an alternative model in which stochasticity of chemical reactions and our experimental observations of growth-arrest duration can be explicitly implemented (Fig. 1B, Methods, Table S2, and SI Text). The output of the simulations (Fig. 2E, Inset), reproduces the main features of our empirical single-cell results upon increasing level of initial level of HipA, A_tot. Specifically, the simulations show that the coexistence of two different phenotypes occurs when the production rates of HipA and HipB are close and fluctuations either in HipA or HipB production have a strong influence on the number of free HipA proteins (32) (Fig. 3C). Of note, similar phenomena have been reported in very different systems where the strong interaction between two chemical entities (33, 34) such as mRNA–sRNA (35, 36) or protein–protein (37) has been shown to result in ultrasensitivity, namely to a very sharp dependence in the level of one chemical entity on the production rate of the other. As in previous analyses of ultrasensitive processes, the key factor for the amplification of noise is the strong binding of the two entities (Fig. S3). Here the ultrasensitive core motif is through protein–protein interaction (38). We conclude that HipA–HipB binding (39), through the nonlinearity of the threshold behavior, can generate a mixed population where two phenotypes coexist. The subpopulation that is growth arrested for extremely long times will be able to persist despite various antibiotic treatments that target mainly actively growing cells.

Threshold Level of HipA Expression Above Which Persistence Is Triggered Depends on HipB.

We used the model to study the effect on persistence of increasing concentrations of HipB in the cells. Using Monte Carlo simulations, we computed the probability for a cell to become persister and found that, as A_tot increases and approaches a threshold, the probability for a significant number of free HipA proteins quickly increases, leading to persistence, and that the threshold location is set by the antitoxin level, B_tot (Fig. 3D). This point was experimentally evaluated by measuring the number of persisters under the microscope, for different HipB levels. To this end, a strain was generated deleted for hipBA but bearing one plasmid encoding HipA under the control of the arabinose promoter and another plasmid encoding HipB under the control of the tet promoter (SI Text). We found that, as the level of HipB increases, the threshold shifts and the level of HipA required for a probability of persistence above 50% moves toward higher values (Fig. 3E), as predicted by the simulations (Fig. 3D).

Decrease in the Binding of HipA7 to HipB Results in the High-Persistence Phenotype.

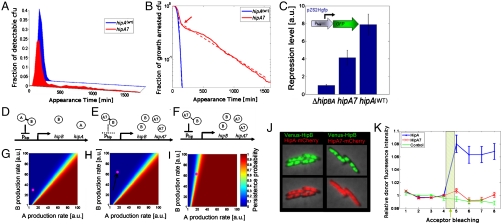
Another context in which the relation between the hipBA module and persistence can be examined is the one that originally indicated that such a relation exists—the hipA7 high-persistence mutant (Fig. S4). In these cells, a remarkable persistence phenotype—a thousandfold increase in the frequency of persistence in the population (17)—was linked to two mutations in hipA (18) and shown to result in transient growth arrest of a subpopulation of cells (Fig. 4 A and B) (40). We can use the model to investigate which aspect of the hipBA module is likely to have been affected by the mutations for an increase in persistence to arise. In Fig. 4G, we plot the “persistence phase space,” namely, the probability of a cell becoming persistent, P, as a function of the independent production rates of HipA and HipB. The chromosomal WT hipBA module is represented by a single point (pink) in that phase space, where the rate of HipB production is severalfold in excess of that of HipA (39) and located in the blue region (P ∼ 0). In order to find out which parameters are affected in hipA7 and lead to P ∼ 0.2 (Fig. 4 A and B), we further characterized the differences between the hipA7 mutant and WT E. coli. We compared the transcriptional activity from the hip promoter (P_hip) using a reporter plasmid with P_hip controlling the expression of GFP. We found that P_hip is a strong promoter, stronger than the tet promoter used to express HipA (Fig. S5). We observed that the repression level of the hip promoter was twofold lower in the mutant (Fig. 4C) (SI Text), indicating that the ability of the HipBA complex to exert strong repression (39) is impaired in hipA7 mutants. This reduced corepressor activity of HipA7 could be due to a lower affinity of the HipA7–HipB complex for promoter binding sequences, namely a lower k_DNA (Fig. 4E), or to a lower affinity between HipA7 and HipB, namely, lower k_AB, that will make HipB more available for degradation (Fig. 4F). Our simulations show that changes in k_DNA cause the position of the WT dot in the phase space to move along the straight black line shown in Fig. 4H, without getting closer to the high-persistence region. In contrast, a reduction in the value of k_AB causes the phase space itself to change and enlarges the persistence domain (Fig. 4I), in addition to increasing the production rates. This analysis suggests that the hipA7 mutation results in high persistence because of a decrease in the binding affinity between HipA7 and HipB (Fig. 4F).

Fig. 4.

Understanding high persistence. (A) The appearance time of colonies for the hipA7 strain and the corresponding WT (hipA) was continuously monitored by the automated scanners system. The histograms show the fraction of cfus detected at each time point. (B) Same data as shown in A, plotted as the fraction of growth-arrested cfus on log-scale, to better visualize the dynamics at later times. Similar to ectopic expression of HipA, the hipA7 curve exhibits an initial rapid decay (same rate as blue curve), that yields to a significantly slower decay (transition marked by red arrow). (C) Lower repression of the hip promoter (P_hip) in the hipA7 strain. A plasmid bearing a P_hip-GFP was introduced in wild-type bacteria (WT), in bacteria deleted for the hip module (ΔhipBA) and in hipA7 bacteria. As expected, P_hip-GFP was strongly expressed in ΔhipBA cells and this weak repression level was set as one. (D) Schematic illustration of the WT module. (E) Schematic illustration of one possible mechanism that could underlie the lower repression observed in the hipA7 strain, namely, a lower binding affinity of HipBA7 complexes to the hip promoter. (F) Schematic illustration of an alternative mechanism, where a lower binding affinity between HipB and HipA7 leads to less repressor complexes and therefore less repression. (G–I) Plots of the persistence phase space, namely, the probability of a cell becoming persistent (P), as a function of the independent production rates of HipA and HipB. The probabilities are color coded such that blue represents a majority of normal cells (P ∼ 0), red represents a majority of persistent cells (P ∼ 1), and other colors represent cells with intermediate probabilities of persistence, which would generate a population where actively growing cells and persisters coexist (high-persistence phenotype). (G) WT E. coli is represented by a single pink dot located in the low-persistence domain. (H) A mutation that reduces the repression strength of the WT by decreasing the parameter k_DNA (scenario E), will move the dot along the straight black line, without getting closer to the high-persistence domain. (I) In contrast, a reduction in k_AB (scenario F), is predicted to alter the phase space itself, and enlarge the persistence domain, thus moving the WT position (pink dot) toward the crossover regime where persister and normal behaviors coexist. (J) Colocalization of HipB with HipA or with HipA7, in single cells. (Left) HipA: Images (phase and fluorescence overlays) of cells deleted for the endogenous hipBA module expressing fusion proteins Venus-HipB (green) and fusion protein HipA-mCherry (red). A similar localization pattern to the nucleoid can be seen in both channels. (Right) HipA7: Same as shown in the left panel but for cells expressing mutant HipA7-mCherry (red). Note the diffuse appearance of the red fluorescence. Each experiment was repeated at least three times. (K) FRET signal between Venus and mCherry, by acceptor photobleaching: Four consecutive frames of the donor fluorescence signal (Venus) are plotted before and after acceptor photobleaching. A FRET signal is observed between fusion proteins HipA–mCherry and Venus–HipB, and is decreased by the A7 mutation (p < 0.005). No FRET signal is apparent in the control strain where HipA + free mCherry are expressed. Error bars represent the standard error of the mean between eight different measurements.

We tested the hypothesis suggested by the model by comparing in vivo the binding of HipB to HipA with its binding to HipA7, using FRET. For this purpose, we constructed the fluorescent fusions proteins Venus-HipB and HipA-mCherry, with and without the hipA7 mutation (Table S3). We tested that those fusion proteins are functional, namely that their induction leads to similar toxicity as the native proteins and that this toxicity can be reversed by the antitoxin (Fig. S4B). The weaker interaction between the mutant HipA7 toxin and its antitoxin is apparent in the reduced colocalization of the two proteins (Fig. 4J) as well as in the decreased FRET signal by acceptor bleaching (Fig. 4K) (41). We verified, by Western blot analysis, that this reduced FRET signal was not due to cleavage of the fusion protein (Fig. S4D and SI Text). This evidence is compatible with the inference from the model, and indicates that the hipA7 mutations reduce the binding affinity of HipA to HipB, and in this way leads to a higher probability for persistence (Fig. 4F). We note that reduced binding of the complex is not the sole effect of the mutations, because it cannot explain the reduced toxicity of HipA7 relative to HipA (23).

Discussion

Our systematic analysis of the hipBA module spans the different modes of action that may be implemented using such a motif. The frequency of persistent cells in the population depends on the values of its underlying parameters (Fig. 4 H and I). The case where the majority of the population is growing normally but a few cells are dormant describes a bet-hedging strategy that enables better survival in fluctuating environments, where conditions that promote rapid growth occasionally alternate with periods of stress. Although normally growing cells will thrive in good conditions, they will be more effectively killed by many different stresses such as antibiotics, acids, heat, prophage (42) induction, etc., whereas nongrowing bacteria will be protected by their dormancy from those stresses, but pay a high fitness cost under normal growth conditions. The optimal frequency of persisters in the population, as well as the optimal duration of dormancy, depend on the characteristic time scales of stressful conditions in the environment (9). That the hipBA module controls these aspects of growth arrest suggest that the module may be a substrate for adaptive evolution. In fact, the hipA7 mutant has been originally isolated using a regime where antibiotic stress alternated with normal growth conditions, and can be viewed as an instance of evolution of the hipBA module parameters in order to optimize the stochastic strategy for a new regime.

In summary, quantitative measurements in single cells have revealed that the hipBA module determines the onset as well as duration of a transient growth arrest. Depending on the levels of toxin and antitoxin, this transient dormancy takes place only above a threshold of expression. This threshold, in turn, provides a mechanism by which variability in gene expression results in coexistence of normally growing and growth-arrested cells. The dormant cells have the potential to survive antibiotic treatments, as long as those are shorter than the growth-arrest duration. Using stochastic modeling and colocalization measurements of proteins in cells, we were able to attribute the observed heightened frequency of persistence in hipA7 mutants to a decrease in the binding affinity of the toxin to its antitoxin. However, how HipA mediates growth arrest is still unknown. It was found that HipA may phosphorylate elongation factor EF-tu (27), but HipA overexpression has been shown to arrest both translation and transcription (23), suggesting other targets for HipA.

Toxin–antitoxin modules are ubiquitous in microorganisms, although their function is enigmatic and is still topic for debate. The generality of our analysis, which builds on conserved features of toxin–antitoxin modules, suggests that TA modules might control the level of persistence through redundant mechanisms. Threshold regulation of phenotypic variability may be a general property of those motifs, whose function would be to differentiate bacterial populations into distinct subpopulations to cope with stress (21). Recent evidence that implicates TA modules in Myxococcus development (43) and in biofilm formation (44, 45) support that view. Finally, through linking a genetic regulatory motif and its phenotypic effect, we now have a basic understanding of the connections between multiple elements of bacterial persistence: genotype, phenotype, and fitness. Such a comprehensive description provides an opportunity for exploring the fundamental interplay between genetic networks, ecology, and evolution.

Methods

Growth-Arrest Distribution Measurements Using Scanners.

Cells were grown in LB, at 37 °C, in 24-well plates, in a Wallac VICTOR® reader with shaking. At OD₆₃₀ ∼ 0.01, the inducer for hipA [either anhydrous tetracycline (atc) or arabinose] was added at different concentrations. Three hours later, cells were diluted 10^-6 and plated on LB agar plates with the appropriate antibiotics. The plates were placed in a 37 °C incubator upon EPSON Perfection 3490 scanners that took pictures of the plates every 10–15 min (28). We developed an automated image acquisition application using C# and Windows Image Acquisition, capable of timing the scanning in all the scanners continuously for several days, as well as an automated analysis application using Matlab (The MathWorks). The application finds the cfu in each picture and tracks the colonies that were identified at different times. Thus we can extract the area growth rate of each colony and its time of appearance. We find that the colonies appearing early and at later times grow at the same rate (Fig. 2A, Inset). The method thus allows the differentiation between transient growth arrest and slow growth of colonies.

Repression Level Measurements.

OD₆₃₀ and GFP fluorescence measurements (excitation at 485 nm; emission at 535 nm) were done in a shaking Wallac VICTOR® reader in 24-well plates with 200 μL of mineral oil to prevent evaporation. Growth rates of the different strains were between 40 and 60 min in M9 minimal medium. The background fluorescence level was determined using a strain without plasmid. We defined promoter activity (PA) as (dGFP/dt)·(1/OD). The promoter activity in the strain deleted for hipBA was taken as one, and PA of other strains normalized accordingly. The repression level is defined as 1/PA.

Computer Simulations.

The theoretical results were obtained by Monte Carlo simulations of the model using the Gillespie algorithm. In these simulations, we keep track of the copy number of various free and bound proteins in the cell as a function of time. At each step, we compute the rate for all the possible processes listed in Fig. 3A. We then randomly choose the next process to take place from all the possible processes where each process is assigned with a suitable weight proportional to its rate. The number of proteins and the elapsed time are then updated according to the process chosen. The phase space in Fig. 4 E and F is based on smoothing and fitting simulation data to a “Fermi-Dirac” distribution function.

As seen in our experiments, in the absence of HipB, HipA transient expression arrests growth indefinitely (Fig. 1B), even for very low expression levels, suggesting that a cell cannot grow if the amount of free HipA proteins ([A]) exceeds some small concentration A₀. The lag times (Fig. 2E, Inset) were calculated as follows: We started with an empty cell and ran the simulation enough time (few cell cycles) in order to reach steady state (this part represents the exponential growth phase). The total number of HipA proteins was recorded at this point. Then the production rate of A was set to zero (representing the cells transfer to a medium without inducer) and we continued the simulation until the number of free HipA molecules dropped below A₀. The exact value of A₀ had little effect on the outcome of the simulations. The time elapsed from the removal of inducer until this event happened defines the lag time. Bacteria were defined as persistent if their growth arrest was sufficiently long (for a precise definition, see SI Text). Simulations were repeated a large number of times with different values for the initial production rate of HipA (representing the external noise from the plasmid copy number fluctuations and the inducer concentration in each cell).