Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2010 May 3;107(21):9502–9506. doi: 10.1073/pnas.0912066107

Hierarchical, multilayered cell walls reinforced by recycled silk cocoons enhance the structural integrity of honeybee combs

Kai Zhang a,b, Huiling Duan a, Bhushan L Karihaloo b,1, Jianxiang Wang a
PMCID: PMC2906885  PMID: 20439765

Abstract

We reveal the sophisticated and hierarchical structure of honeybee combs and measure the elastic properties of fresh and old natural honeycombs at different scales by optical microscope, environmental scanning electron microscope, nano/microindentation, and by tension and shear tests. We demonstrate that the comb walls are continuously strengthened and stiffened without becoming fragile by the addition of thin wax layers reinforced by recycled silk cocoons reminiscent of modern fiber-reinforced composite laminates. This is done to increase its margin of safety against collapse due to a temperature increase. Artificial engineering honeycombs mimic only the macroscopic geometry of natural honeycombs, but have yet to achieve the microstructural sophistication of their natural counterparts. The natural honeycombs serve as a prototype of truly biomimetic cellular materials with hitherto unattainable improvement in stiffness, strength, toughness, and thermal stability.

Keywords: biomimetic cellular solids, hierarchical structure, natural honeycombs, survivability, recycling

Natural honeycombs are used to store honey and pollen, and to rear the brood. By contrast to most insects and birds, bees construct their nests from their own secretions. The comb cells are constructed from wax secreted by worker bees. Then fertilized eggs are deposited in these cells. The eggs develop into larvae, which surround themselves with silk cocoons before their pupation (1). After the pupae have metamorphosed into bees and left the cells, the worker bees cover this silk with wax. Thus, the comb becomes a composite material with usage (2). In addition to structural functions, the honeycomb is an important clue to recognize the nestmate (3–5) and to understand the evolution of honeybees (6). The age of honeycombs affects the honeybee growth and brood survivorship (7). Thus, whilst the honeybee comb is a most studied natural cellular structure that has long fascinated mathematicians, physicists, and biologists (8–18), it was not known until recently why the bees built the combs out of hexagonal cells (13). The mechanical properties of beeswax and the cell walls of the combs of African honeybees, Apis mellifera scutellata, have been studied using conventional tensile test methods (2, 15). The stress-strain characteristics of the silk hand-drawn from the living larvae of the bees have also been measured in air and different aqueous media (16, 17). The detailed microstructures and the in situ properties of the walls, wax, silk, and the macroscopic properties of the honeybee combs have still not been clearly revealed, nor have their implications for biomimetic designs been fully explored. The microstructures of biomaterials are increasingly providing a fertile route to the synthesis of artificial composites with superior properties (19–22). In particular, hierarchical structures common in nature can lead to breakthroughs in the design of new materials (23, 24). Natural honeybee combs have long been a paradigm for engineering cellular structures (11). However, the current engineering honeycombs only mimic the macroscopic geometry of natural honeycombs, but have yet to achieve the microstructural sophistication of their natural counterparts.

Results

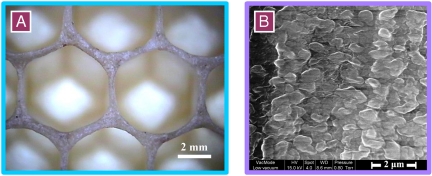
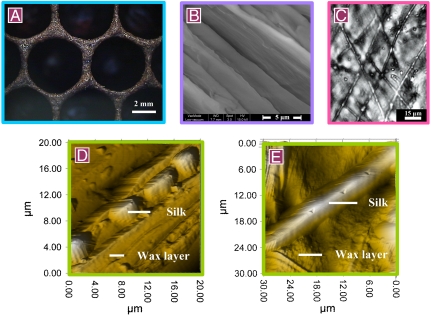
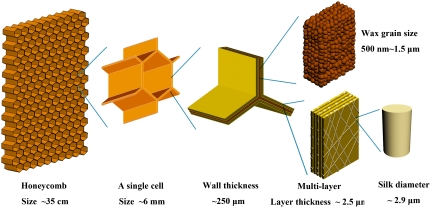
We studied two-day-old fresh (10 combs), five-month-old (6 combs), one-year-old (10 combs), and two-year-old (6 combs) honeycombs of the Italian honeybees, Apis mellifera Ligustica, which are the most popular variety for beekeeping in the world. Fig. 1 shows typical sections of the walls cut along the longitudinal axis of the cell of the fresh and old combs. All the walls are practically uniform in thickness, apart from a region typically about 1 mm at the top (outlet end) of the cells where they are thicker in the fresh, five-month-old, and one-year-old combs (Fig. 1 A–C) and tapered in the two-year-old (Fig. 1D). The thickness of the uniform part of the cell wall of the fresh comb is 88 ± 10 μm and that of the five-month-old, one-year-old, and two-year-old combs is 120 ± 11 μm, 246 ± 30 μm, and 297 ± 48 μm, respectively. The wall of the fresh honeycomb consists of small wax grains whose size varies from 500 nm to 1.5 μm (Fig. 2B). The old honeycomb cell wall can be divided into two parts: an inner part corresponding to the fresh honeycomb constructed by the worker bees, and an outer additive part generated during the use of the honeycomb. In contrast to the fresh honeycomb, the additive part of the old honeycomb wall exhibits a layered structure (Fig. 3B). We show the detailed structure of the one-year-old comb at different scales in Fig. 3, and note that the five-month-old and two-year-old combs exhibit similar features. The thickness of one layer, measured on specimens from all old combs is 2.45 ± 0.81 μm irrespective of the age. Fig. 3C is an optical image of the longitudinal surface of a layer peeled from the old honeycomb wall. Fig. 3 C–E clearly show that the additive part of the old wall is a composite material consisting of wax reinforced with silk. The diameter of the silk is about 2.92 ± 1.12 μm and they are embedded in the wax in a mostly random, with an occasional regular arrangement. The mass fraction of silk cocoons in the walls of one-year-old honeycomb is 33.4%. The silk of honeybee larvae cocoons is an alpha-helical fibroin in which the micelles form a four-stranded array of twisted coils with the major axis parallel to the silk axis (25, 26). We measured the indentation moduli of the silk in the axial and transverse directions by nanoindentation using a 50 nm indenter. The indentation modulus in the fiber axis direction measured on the cross sections is 7.05 ± 0.56 GPa, whereas the indentation modulus perpendicular to the fiber axis measured by indenting the longitudinal surface of the silk, as shown in Fig. 3E, is 3.62 ± 0.26 GPa. Fig. 3D shows the cross section of several silks. The hierarchical structure of the one-year-old honeycomb at nano-, micro-, and macroscales is shown in Fig. 4. The honeybee silk can be further studied at the molecular level, as has been done by Keten et al. (24) for silkworm and spider silks. They found that the stiffness, strength, and toughness of these β-sheet nanocrystals with weak transverse hydrogen bonds can be improved by nanoconfinement.

Fig. 1.

Fig. 1.

Open in a new tab

Honeycomb walls at different ages. (A) Fresh. (B) 5 months. (C) One year. (D) Two years.

Fig. 2.

Fig. 2.

Open in a new tab

Fresh honeycomb walls. (A) Top view of walls and cells. (B) Environmental scanning electron microscope (ESEM) image of a cross section of the cell wall showing wax grains.

Fig. 3.

Fig. 3.

Open in a new tab

One-year-old honeycomb at different scales. (A) Top view. (B) ESEM image of a cross section of the cell wall. (C) Optical image of the surface of a peeled layer. (D) 3D microstructure of the cell wall cross section. (E) Silk with indentations.

Fig. 4.

Fig. 4.

Open in a new tab

Hierarchical structure of one-year-old honeycomb at macro-, micro- and nanoscales.

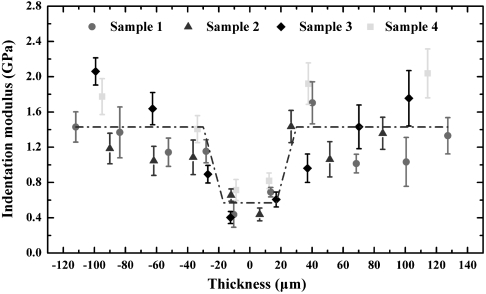
We also measured the variation in the in situ indentation modulus across the thickness of the wall of the one-year old honeycomb by indenting the cross section of the wall (Fig. 5). It exhibits a pronounced gradient between the interior and the exterior of the cell wall. It is low, 0.57 ± 0.08 GPa, around the middle region of the one-year-old wall (which is equal to that of the fresh wall), and increases rapidly to 1.43 ± 0.14 GPa toward the exterior regions of the wall. These regions are the composite layers deposited during the use of the honeycomb. Thus, the wall is progressively stiffened by recycling the silk cocoons.

Fig. 5.

Fig. 5.

Open in a new tab

Variation of indentation modulus across a one-year-old honeycomb wall (4 different samples).

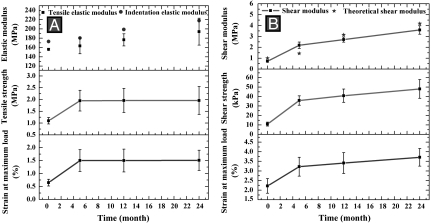
As the walls of both the fresh and old combs are made of wax grains and are thus heterogeneous at the microscale, we have measured their indentation modulus at the mesoscale (i.e., at the scale of the wall as a whole) by microindentation with a 400 μm spherical indenter (27), and their elastic modulus by direct tension (Fig. 6A). Both tests confirmed an increase in the stiffness of comb wall with age. The direct tension test also provided the tensile strength of the wall, and the strain at maximum load. They all show an increase up to the age of 5 months from the fresh state (Fig. 6A) but practically no increase thereafter.

Fig. 6.

Fig. 6.

Open in a new tab

Variation of the mechanical properties of the wall and comb with age. (A) Elastic modulus, tensile strength, and strain at maximum load of a wall. (B) Macroscopic shear modulus, nominal shear strength, and the shear strain at maximum load of a comb.

As the indentation and elastic moduli are approximately related as Er ≈ E/(1 - ν2), we estimate the Poisson ratio of the fresh wall to be 0.313. The elastic moduli of walls of the Italian honeybee fresh and old combs at the mesoscale are appreciably larger than those of the fresh and old honeycomb wall specimens of the African honeybees Apis mellifera scutellata (2) measured by tensile tests at 9.1 and 29.9 MPa, respectively. The most likely reason for this is the differing stiffness requirements of the combs; the African bees are smaller and produce and store less honey than the larger Italian bees (14). On the other hand, the substantial difference between the elastic moduli of the Italian honeybee comb wall measured at the micro- and mesoscales is due to incomplete fusion of the wax grains (27). As fusion of the wax grains needs heating, it seems the bees do not expend energy to fuse the wax grains to stiffen and strengthen the new wall when there is no need for it, but instead do it by coating as the need arises during its use.

Discussion

Bees construct honeycombs with the hexagonal cell prism axis aligned at an angle 13° to the ground, as shown in Fig. 4 and Fig. S1A (14). Each comb consists of two back-to-back sides with the cells in each side being nearly perpendicular to the surface dividing the two sides (14). As the cells are connected to form an array, and as their depth is much shorter than the height of the comb, the ensemble of the cells can be treated as a deep cantilever beam with a very short span. Under the transverse loading from the weight of honey, pollen, the brood, and of the comb itself, the deformation of such an extremely short cantilever beam is primarily governed by its macroscopic shear rigidity (28); i.e., the out-of-plane shear modulus of the honeycomb (11) as a whole. We measured the macroscopic out-of-plane shear modulus of the fresh and old combs (SI Text) to be 0.72 ± 0.09 MPa (fresh), 2.19 ± 0.30 MPa (five-month-old), 2.71 ± 0.24 MPa (one-year-old), and 3.59 ± 0.39 MPa (two-year-old), as shown in Fig. 6B. Thus, the shear stiffness of the comb has increased more than three-fold in one year and four-fold in two years. From the previously measured tensile elastic modulus of the wall at the mesoscale and the estimated Poisson’s ratio, we can estimate first the shear modulus of the wall using the formula μwall = 0.5E/(1 + ν), and then the shear modulus of the comb using the formula (11) μLe = 0.577 μwallt/L, where t denotes the thickness of the wall, and L the length of the side of the hexagonal cell. In this manner, we estimate the macroscopic shear modulus of the combs to be 1.01 (fresh), 1.43 (five-month-old), 3.15 (one-year-old), and 4.18 MPa (two-year-old), as shown in Fig. 6B. These estimates are in good agreement with the above experimental data, again confirming that the shear stiffness of the comb has increased more than three-fold in one year and four-fold in two years.

The macroscopic shear test also provided the nominal shear strength and the shear strain at maximum load of the comb as a whole, as shown in Fig 6B. The shear strength and the strain at maximum load of the comb continue to increase with age; the shear strength has increased about four-fold in one year and five-fold in two years. The shear strain at maximum load of the one-year-old comb is about 1.5 times higher than that of the fresh comb. In view of the potential stress concentration at the corners near the clamped end of the comb, we also simulated the shear tests of the fresh and one-year-old combs using the finite element method (FEM) (SI Text). The shear strains at the maximum load for the fresh and one-year-old combs as a whole are 4.3% and 7.0%, respectively, as shown in Fig S2, suggesting a strain concentration factor near the corners of around 2 at both ages.

The reason that the bees need to stiffen and strengthen the comb without becoming fragile can be explained by performing a finite element analysis of the comb. We calculated the stress and strain fields in the fresh and old combs using the linear elastic finite element model at 25 °C (SI Text). For the fresh comb, under the weight of honey and worker bees, the maximum normal stress and the corresponding strain along the axis of the cell were found to be 72 kPa and 0.05%, respectively. These are well below the tensile strength (1.1 MPa) and the corresponding strain (0.65%) of the wall that we measured at 25 °C (Fig 6A). The computed maximum nominal out-of-plane shear stress (0.11 kPa) and the corresponding shear strain (0.04%) in the fresh comb are also below the nominal shear strength (11 kPa) and the corresponding shear strain (2.2% or 4.3% if one allows for strain concentration at the clamped end) at 25 °C (Fig 6B). These results indicate that the fresh comb can safely carry the weight of honey and bees.

It is known however (2) that the temperature inside a honeybee comb can fluctuate from 25 °C to 45 °C. It is also known (2) that fresh wax wall of an African honeybee comb softens when the temperature rises from 25 to 45 °C losing its elastic modulus by a factor of 3.5 and its tensile strength by an order of magnitude, whereas those of an old comb wall that contains 34% silk cocoons by mass are considerably less sensitive to an increase in temperature. Given the fact, that the mass fraction of silk cocoons in the walls of Italian honeybee combs is practically equal to that in the African honeybee comb, it can be assumed that a similar temperature dependence prevails in the Italian honeybee combs. We have examined the effect of the viscoelastic nature of the fresh beeswax on the stress and strain fields in the wall of the fresh comb. The finite element method and an appropriate viscoelastic model were used to calculate the stress and strain fields in the fresh comb at 45 °C (SI Text). We found that as a result of creep deformation the maximum out-of-plane shear strain in a fully laden fresh comb has reached 1.9% (Fig S1D); i.e. higher than the shear strain at the maximum load of the fresh comb (1.5%) at 45 °C (SI Text). Thus, a temperature increase inside the comb from 25 °C to 45 °C would result in the collapse of a fully laden fresh comb. That this does not actually happen is because the comb walls are continuously reinforced by silk cocoons during its use.

The old comb walls that contain 34% silk cocoons by mass are practically insensitive to temperature fluctuations (2). Finite element calculations (SI Text) show that the maximum out-of-plane shear strain in the one-year-old comb under the weight of honey and bees is only 0.014% (Fig. S1E), which is well below its shear strain at the maximum load of 7.0% (Fig. S2B). Thus, even if there is some decrease in the shear modulus and strain of the one-year-old comb with increasing temperature, the comb will still have a sufficient margin of safety against collapse.

Engineering lightweight cellular materials are indispensable to modern industry. Remarkable efforts have been made to improve their performance (29). However, the properties of conventional man-made porous or cellular media including honeycombs with homogeneous walls are bounded by two inherent constraints. First, the overall stiffness of a porous medium cannot exceed that of the solid wall; second, the coefficient of thermal expansion (CTE) of a porous medium is always equal to that of the wall material, irrespective of the microstructure of the medium (30). These two intrinsic constraints impose important restrictions on the engineering application of porous materials. The low stiffness has to be compensated by a large size to maintain structural rigidity and stability; the invariability of the CTE is a disadvantage for maintaining a stable shape in an environment with a varying temperature such as in outer space, and it may result in severe stress concentrations and failure due to the mismatch of the thermal expansions of abutting materials in a structural component. A cellular solid that truly mimics the microstructure of natural honeycombs, in particular the nonhomogeneity of its walls, will overcome these restrictions and thus provide a remarkable degree of design flexibility. For cellular solids with a honeycomb cell structure with straight walls, the latter can be stiffened and strengthened by a judicious choice of the geometric and mechanical properties of a coating material in much the same manner as above in an old honeycomb (Fig. 7A). For example, the overall out-of-plane shear modulus of a cellular solid with aligned coated cylindrical pores in a hexagonal configuration is (31) μLe = μm[1 - f + (1 + f)B]/[1 + f + (1 - f)B], where μm is the shear modulus of the matrix material, and f is the porosity, as shown in Fig. 7B. The parameter B is defined as B = tcoatingμcoating/(Rμm), where tcoating and μcoating denote the thickness and shear modulus of the coating layer, and R is the radius of the pores. When B is larger than the critical value Bcr = 1, the shear modulus of the cellular material will exceed that of the matrix material from which it is made (i.e., μLe > μm) irrespective of the porosity f. However, when f is large, as in a honeybee comb, and the effectiveness of coating can be better described by the ratio μLe/μme of the shear modulus μLe of the coated cellular solid to that of the uncoated cellular solid μme = μm(1 - f)/(1 + f) (Fig. 7C). It is seen that the larger the porosity, the more effective the coating, even with B < 1. Other elastic constants of the cellular solids with aligned pores can also be tailored via pore surface coating (31). The coating technique is applicable to pores irrespective of their size; it can range from nm to mm (31). However, as the coating parameter B depends on the ratio tcoating/R, the coating layer will have to be much thinner for nanopores than for macropores to give the same stiffening effect.

Fig. 7.

Fig. 7.

Open in a new tab

(A) Cross section of a one-year-old comb near a triple junction showing the walls reinforced by additive composite layers. (B) A biomimetic cellular solid with coated cylindrical holes (blue color represents the matrix and gray color represents the surface coating). (C) Ratio μLe/μme versus porosity f and coating parameter B.

As the CTE of cellular solids are coupled with their overall stiffness (32), the coating will thus make the overall CTE of the cellular solids tunable. Stiff, strong, and lightweight porous materials with tunable CTE are vital for high-precision optical devices and sensors whose properties must not degrade as the temperature varies (33, 34). In particular, they are ideal for aerospace applications in an environment with large temperature fluctuations.

Materials and Methods

All honeycombs used in this study were collected from the Bee Research Institute of Chinese Academy of Agricultural Sciences. The macrostructure of the honeycombs was examined by an optical microscope and the microstructure by an environmental scanning electron microscope. The mass fraction of the silk cocoons was obtained after dissolving the beeswax. The indentation modulus was measured using a TriboIndenter with a standard 50 nm Berkovich diamond tip or a sapphire spherical (400 μm radius) tip.

Macroscopic tensile tests of slabs cut from the comb walls and shear tests of whole combs were conducted in a MicroTester at a displacement rate of 0.1 mm/ min. At least 10 (5) specimens each from the fresh and old honeycombs were tested in tension (shear).

The fresh and one-year-old combs fully laden with honey and bees were analyzed by the FEM using the commercial package ANSYS. Full details of the tests and the finite element analysis are provided in SI Text.

Supplementary Material

Supporting Information
supp_107_21_9502__index.html (952B, html)

Acknowledgments.

We thank Xin Yi and Fangwei Si for contributions to calculation and experiments. This work was supported by the National Natural Science Foundation of China Grants 10525209, 10872003, and 10932001; the China–United Kingdom Science Network Scheme of the Chinese Scholarship Council; and The Royal Society, London, the Foundation for the Author of National Excellent Doctoral Dissertation of China Grant 2007B2.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.0912066107/-/DCSupplemental.

References

  • 1.Jay SC. The cocoon of the honeybee Apis mellifera L. Can Entomol. 1964;96:784–792. [Google Scholar]
  • 2.Hepburn HR, Kurstjens SP. The combs of honeybees as composite materials. Apidologie. 1988;19:25–36. [Google Scholar]
  • 3.Dorset DL. The crystal structure of waxes. Acta Crystallogr B. 1995;51:1021–1028. doi: 10.1107/s0108768195005465. [DOI] [PubMed] [Google Scholar]
  • 4.Brockmann A, Groh C, Frohlich B. Wax perception in honeybees: Contact is not necessary. Naturwissenschaften. 2003;90:424–427. doi: 10.1007/s00114-003-0442-3. [DOI] [PubMed] [Google Scholar]
  • 5.D’Ettorre P, et al. Wax combs mediate nestmate recognition by guard honeybees. Anim Behav. 2006;71:773–779. [Google Scholar]
  • 6.Seeley TD, Morse RA. The nest of the honey bee Apis Mellifera L. Insect Soc. 1976;23:495–512. [Google Scholar]
  • 7.Berry JA, Delaplane KS. Effects of comb age on honey bee colony growth and brood survivorship. J Apic Res. 2001;40:3–8. [Google Scholar]
  • 8.Thompson DW. On Growth and Form. Cambridge: Cambridge University Press; 1961. pp. 88–119. [Google Scholar]
  • 9.Weyl H. Symmetry. Princeton: Princeton University Press; 1980. pp. 83–91. [Google Scholar]
  • 10.Weaire D, Phelan R. Optimal design of honeycombs. Nature. 1994:367–123. [Google Scholar]
  • 11.Gibson LJ, Ashby MF. Cellular Solids: Structures and Properties. Cambridge: Cambridge University Press; 1997. pp. 93–174. [Google Scholar]
  • 12.Ball Philip. The Self-Made Tapestry: Pattern Formation in Nature. London: Oxford University Press; 1999. pp. 16–49. [Google Scholar]
  • 13.Mackenzie D. Mathematics-Proving the perfection of the honeycomb. Science. 1999;285:1338–1339. [Google Scholar]
  • 14.Winston ML. The Biology of the Honey Bee. Massachusetts: Harvard University Press; 1987. pp. 72–88. [Google Scholar]
  • 15.Hepburn HR. Honeybees and Wax: An Experimental Natural History. Berlin: Springer; 1986. pp. 93–114. [Google Scholar]
  • 16.Hepburn HR, Chandler HD, Davidoff MR. Extensometric properties of insect fibroins: The green lacewing cross-β, honeybee α-helical and greater waxmoth parallel-β conformations. Insect Biochem. 1979;9:69–77. [Google Scholar]
  • 17.Zhang K, Si FW, Duan HL, Wang J. Microstructures and mechanical properties of silks of silkworm and honeybee. Acta Biomater. 2010 doi: 10.1016/j.actbio.2009.12.030. doi: 10.1016/j.actbio.2009.12.030. [DOI] [PubMed] [Google Scholar]
  • 18.Gould JL, Gould CG. Animal Architects: Building and the Evolution of Intelligence. New York: Basic Books; 2007. pp. 99–131. [Google Scholar]
  • 19.Kamat S, Su X, Ballarini R, Heuer AH. Structural basis for the fracture toughness of the shell of the conch Strombus giggas. Nature. 2000;405:1036–1040. doi: 10.1038/35016535. [DOI] [PubMed] [Google Scholar]
  • 20.Gao H, Ji B, Jäger IL, Arzt E, Fratzl P. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc Natl Acad Sci USA. 2003;100:5597–5600. doi: 10.1073/pnas.0631609100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Bonderer LJ, Studart AR, Gauckler LJ. Bioinspired design and assembly of platelet reinforced polymer films. Science. 2008;319:1069–1073. doi: 10.1126/science.1148726. [DOI] [PubMed] [Google Scholar]
  • 22.Miserez A, Schneberk T, Sun C, Zok FW, Waite JH. The transition from stiff to compliant materials in squid beaks. Science. 2008;319:1816–1819. doi: 10.1126/science.1154117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Buehler MJ, Ackbarow T. Fracture mechanics of protein materials. Materials Today. 2007;10:46–58. [Google Scholar]
  • 24.Keten S, Xu Z, Ihle B, Buehler MJ. Nanoconfinement controls stiffness, strength, and mechanical toughness of β-sheet crystals in silk. Nat Mater. 2010;9:359–367. doi: 10.1038/nmat2704. [DOI] [PubMed] [Google Scholar]
  • 25.Rudall KM. Silk and other cocoon proteins. In: Flokin M, Mason HS, editors. Comparative Biochemistry. New York: Academic; 1962. pp. 397–433. [Google Scholar]
  • 26.Atkins EDI. A four-strand coiled-coil model for some insect fibrous proteins. J Mol Biol. 1967;24:139–141. [Google Scholar]
  • 27.Ulm FJ, Vandamme M, Bobko C, Alberto J. Statistical indentation techniques for hydrated nanocomposites: Concrete, bone, and shale. J Am Ceram Soc. 2007;90:2677–2692. [Google Scholar]
  • 28.Timoshenko S, Gere JM. Mechanics of Materials. New York: Van Nostrand Reinhold Co; 1973. pp. 141–152. [Google Scholar]
  • 29.Evans AG, et al. The topological design of multifunctional cellular metals. Prog Mater Sci. 2001;46:309–327. [Google Scholar]
  • 30.Hashin Z. Analysis of composite materials—A survey. J Appl Mech. 1983;50:481–505. [Google Scholar]
  • 31.Duan HL, Wang J, Karihaloo BL, Huang ZP. Nanoporous materials can be made stiffer than non-porous counterparts by surface modification. Acta Mater. 2006;54:2983–2990. [Google Scholar]
  • 32.Duan HL, Karihaloo BL. Thermo-elastic, properties of heterogeneous materials with imperfect interfaces: Generalized Levin's formula and Hill’s connections. J Mech Phys Solids. 2007;55:1036–1052. [Google Scholar]
  • 33.Ernst G, Broholm C, Kowach GR, Ramirez AP. Phonon density of states and negative thermal expansion in ZrW2O8. Nature. 1998;396:147–149. [Google Scholar]
  • 34.Zhang Y, et al. Zero thermal expansion in a nanostructured inorganic-organic hybrid crystal. Phys Rev Lett. 2007;99 doi: 10.1103/PhysRevLett.99.215901. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_107_21_9502__index.html (952B, html)
0912066107_pnas.0912066107_SI.pdf (389.1KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES