Propensity score estimation: machine learning and classification methods as alternatives to logistic regression

Summary

Objective

Propensity scores for the analysis of observational data are typically estimated using logistic regression. Our objective in this Review was to assess machine learning alternatives to logistic regression which may accomplish the same goals but with fewer assumptions or greater accuracy.

Study Design and Setting

We identified alternative methods for propensity score estimation and/or classification from the public health, biostatistics, discrete mathematics, and computer science literature, and evaluated these algorithms for applicability to the problem of propensity score estimation, potential advantages over logistic regression, and ease of use.

Results

We identified four techniques as alternatives to logistic regression: neural networks, support vector machines, decision trees (CART), and meta-classifiers (in particular, boosting).

Conclusion

While the assumptions of logistic regression are well understood, those assumptions are frequently ignored. All four alternatives have advantages and disadvantages compared with logistic regression. Boosting (meta-classifiers) and to a lesser extent decision trees (particularly CART) appear to be most promising for use in the context of propensity score analysis, but extensive simulation studies are needed to establish their utility in practice.

Introduction

Propensity scores are the “conditional probability of assignment to a particular treatment given a vector of observed covariates” [1]. Originally introduced in 1983 by Rosenbaum and Rubin, use of propensity scores has increased dramatically in the past few years: a Medline search for “propensity score” reveals that the number of citations has increased exponentially during since the late 1990s, from around 8 per year from 1998–2000 to 215 in 2007.

The overall goal of a propensity score analysis is to control confounding bias in the assessment of the average effect of a treatment or exposure (assumed in this discussion to be dichotomous). A propensity score model helps achieve this goal by estimating the probability of treatment given individual covariates such that conditioning on this probability (the propensity score) ensures that the treatment is independent of covariate patterns [2], and in particular by achieving balance on confounders by propensity score [3]. The key assumption made is that, given an exposed individual and an unexposed individual with the same (or nearly the same) propensity score, treatment assignment for these two individuals is independent of all confounding factors, and so the two observations can serve as counterfactuals for the purpose of causal inference. Under the key assumption of no unobserved or unmeasured confounding, matching exposed and unexposed individuals in a cohort will allow the data analyst to obtain an unbiased estimate of the average causal effect of the treatment on the outcome [1] while maintaining good precision compared to more traditional maximum likelihood regression analysis [4]. Propensity scores can also be used as continuous predictors in regression analysis, or to construct propensity categories (typically by quintile or decile). In the latter case, averaging crude estimates by category will usually eliminate the majority (about 90%) of confounding bias, assuming that the distribution of covariates is balanced in the unexposed and exposed subjects [2]. Propensity scores can only control for observed confounders; that is, the propensity score cannot be counted upon to balance unobserved covariates [3]

Propensity scores themselves are, almost without exception in the published literature, created using maximum likelihood logistic regression models [4, 5], despite relatively early suggestions of alternative approaches (e.g. Cook et al. [6]). A 2004 review of the literature found that of 48 selected manuscripts, logistic regression was used to estimate propensity scores in 47 of those manuscripts. The last used polytomous logistic regression [5].

Logistic regression is a useful technique for estimating propensity scores for several reasons, to be discussed more fully below. However, logistic regression is only one of many methods that might be used; for instance, D’Agostino [4] and Glynn [7] both raised the possibility of calculating propensity scores using discriminant analysis, while McCaffrey et al. have published work using generalized boosted models to create propensity scores [8]. Likewise, Setoguchi et al. recently published a simulation study using neural networks and classification trees to estimate propensity scores [9].

However, none of these investigations has reviewed the possible techniques that might be used to estimate propensity scores. In the remainder of this review, therefore, we will briefly note some of the advantages and disadvantages of logistic regression for propensity score estimation, and review and discuss the relative advantages and disadvantages of several representative methods from the machine learning literature that might be considered as alternatives. These methods were identified by a domain expert (JL) with extensive experience in the application of machine learning techniques in industry and from reference to two key texts in machine learning [10, 11]. Previous use and discussion of alternatives to logistic regression in the propensity score literature were identified by a PubMed search using the terms “propensity score” and “propensity scores” and key words for the machine learning techniques identified.

This paper is a pure review of statistical and medical literature, and as such IRB approval was not necessary.

Logistic regression

The vast majority of published propensity score analyses use logistic regression to estimate the scores. Logistic regression is attractive for probability prediction because (unlike log-binomial regression, for example) it is mathematically constrained to produce probabilities in the range [0,1] [12], and generally converges on parameter estimates relatively easily. Further, logistic regression is a familiar and reasonably well-understood tool of researchers in a variety of disciplines, and is easy to implement in most statistical packages (e.g., SAS, STATA, R).

This familiarity may predispose investigators to using logistic regression even when better alternatives may be available. For instance, proper modeling technique requires the assessment of the linearity of risk with respect to the log-odds parametric transformation (implicit in logistic regression) before logistic regression is used [12], yet there is little evidence in the propensity score literature indicating that such assessments are routinely made. For example, one review found that of 45 propensity score applications including linear predictors of treatment and using logistic regression, only one reported an assessment of the assumption of linearity in the logit [4]. The same review found that use of interaction terms in propensity score models was infrequent at best [4]. These oversights may result in poor model fit, and in turn to residual confounding in the propensity score analysis and a biased effect estimate [4].

The relationship between model fit and bias is not as clear as this, in that inclusion of a strong predictor of treatment in a propensity score model might improve model fit without markedly affecting bias, if that predictor of treatment is a risk factor for the exposure but not the outcome [13]. Moreover, some of these issues can be addressed within the context of logistic regression: analysts can (and should) consider interaction terms for inclusion in their models. Other problems are more persistent: including interactions terms (or for that matter, splines or polynomials) as predictors of treatment does not guarantee that the assumption of linearity in the logit is met for that term or any other.

Nonetheless, the typical way in which propensity scores are estimated appears to be naïve, eschewing higher order terms and giving insufficient attention to key assumptions [5]. There may be benefit, therefore, in considering approaches which in their most naïve implementations are more flexible and make fewer assumptions than logistic regression: approaches entirely outside the realm of regression modeling. Perhaps the simplest such approach would be a simple, tabular analysis: for each covariate pattern we can calculate a simple proportion of individuals with and without exposure. Tabular analysis makes few assumptions, but is impeded by sparse data and (therefore) by continuous covariates. Non-parametric techniques from discrete mathematics, computer science, and information theory may be more generally applicable, and have been shown in many cases to be more efficient at classifying highly dimensional data than the parametric regression techniques more typically used to estimate propensity scores.

Algorithmic approaches to predicting propensity scores

In his 2001 paper Statistical Modeling: The Two Cultures, Leo Breiman points out that many classification algorithms from the machine learning literature (what he terms the “Algorithmic Culture”) can outperform classical statistical techniques such as regression (the “Data Culture”) [14], especially when dealing with high dimensional data – that is, data with a large number of covariates. For instance, in logistic regression if the number of covariates exceeds the number of data points we would be unable to construct a model that incorporates valuable information from each covariate [14]. In contrast, many machine learning algorithms such as neural networks perform well in precisely this situation [14]. This is of particular interest in a propensity score setting, as propensity scores themselves are recommended for control of confounding in similar circumstances; for instance, Cepeda et al. [2] report that propensity scores will outperform logistic regression in terms of coverage probabilities when there are seven or fewer events per confounder.

The number of automated classification and learning algorithms available to generate propensity scores or propensity categories is far in excess of what can be described here, but a few notable examples can capture much of what is available. We will concentrate on neural networks, linear classifiers (in particular, support vector machines), decision trees, and meta-classifiers (specifically, boosting), each of which represents a different approach to the classification problem [10]. While these techniques are often mathematically equivalent (e.g., both decision trees and linear classifiers define a separating hyperplane), they differ in learning algorithm, interpretation, and technical representation. The main drawback to all these techniques is that, in contrast to logistic regression, the output of machine learning classifiers sometimes lacks easy etiologic interpretation. However, as etiologic inference is not key to propensity score estimation [4], and classifier outputs can still be used in the ultimate etiologic model, we believe the “black box” nature of these techniques does not rule them out as potentially useful tools for propensity score analysis. A summary of some key advantages and disadvantages of these four machine learning techniques are available in Table 1.

Table 1.

Selected advantages and disadvantages of logistic regression and four machine learning algorithms for the estimation of propensity scores.

Method	Software available?1			Parametric	Functional assumptions	Outputs explicit probabilities	Required inputs3
	R	SAS	Stata
Logistic regression	Yes	Yes	Yes	Fully	Log-linear	Yes	Regression equation
Neural networks	Yes	Yes	No	Non	None	Some	Hidden layer size; training procedures
Support vector machines	Yes	Exp	No	Semi (kernel function)	Linearly separable classes	Some (import vector machines)	Kernel function, number classes
CART/decision trees	Yes	Yes	Yes	Non	None (CART) Some (by technique)	Some (CART)	None
Meta-classifiers/boosting	Yes	Yes	Yes	Non2	None	Yes	None2

¹Yes: available either in core functionality or as user-written add-on. Exp: available as experimental routine only. No: not available.

²Underlying classifiers may be parametric.

³Does not include those inputs related to the fitting/learning algorithm itself, for example training procedures for a neural network

Neural networks

Inspired by the structure of the nervous system, neural networks (sometimes, artificial neural networks) are highly opaque to the data analyst. A neural network comprises an input layer, some number of “hidden” layers, and an output layer, each containing a number of nodes connected to every node in the next layer by directed, weighted edges [10] (Figure 1). While in theory a neural-network may consists of an arbitrary number of layers, in practice only three layer (input layer, one hidden layer, output layer) and two layer (input layer and output layer) networks are practical.

Figure 1.

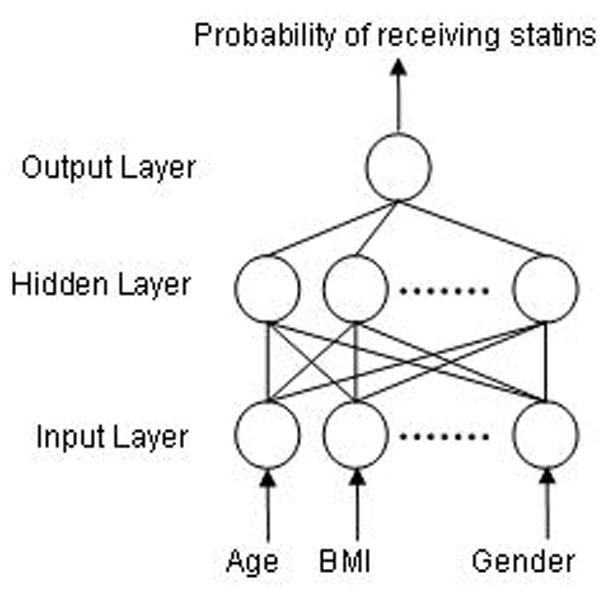
The basic form of a three layer neural network used to predict the probability of receiving statins based on possible confounders of the relationship between use of statins and all-cause mortality.

An example neural net is shown in Figure 1. Simply, a neural network takes input values and transforms them according to weights on its directed edges, and outputs a value or set of values, which may (among other possibilities) be a probability of class membership or a sequence of “yes/no” decisions on class membership. Neural networks are “trained” to classify items by examining a training data set with known outcomes, holding the output and input values fixed, and re-weighting the internal edges appropriately. Unlike a fit logistic regression model, the resulting, “trained” network edges have no causal interpretation, representing a highly complex function of the input values.

Neural networks have at least two advantages over logistic regression. First, they are designed to deal with high dimensional data, each value of which may have only a slight effect on the probability of class membership, but which as a group can classify accurately [15]. Second, a neural network of sufficient complexity (i.e., enough internal nodes, see below) can approximate any smooth polynomial function, regardless of the order of the polynomial or the number of interaction terms [16, 17]. This frees the investigator from having to a priori determine what interactions and functional forms are likely to exist, as they would with logistic regression. These factors, combined with the ability to generate predicted probabilities and the fact that neural network implementations are already available in many statistical computing packages including SAS [18] and R [19], though apparently not Stata [20], make neural nets appear a good candidate for propensity score generation.

The drawback of this approach is that the training of neural networks is still as much an art as a science. There are no hard and fast rules for selecting the number of hidden nodes in a network, avoiding local minima in the learning process, and avoiding overfitting. There is a vast literature on the design and training of neural-networks for a variety of purposes (see [21] for a review), but this literature is not accessible enough to the non-expert to make neural-networks an “out of the box” technique. Optimizing a neural network for a particular propensity score application and standardizing general procedures whereby neural networks can be routinely used to estimate propensity scores are both likely to take substantial investigation and effort.

Perhaps as a result of these unresolved issues and complexities, while neural networks have been mentioned as a possible means of generating propensity scores by several authors [7, 22], have been shown to be effective classifiers in general [14] and in comparison to logistic regression [23, 24], we have been able to find only a single example of their use in the context of propensity scores in the medical literature [9]. This example, by Setoguchi et al., found in a series of simulations that neural network approaches to propensity score estimation provided less bias than comparable logistic regression approaches especially in the presence of non-linearity [9], suggesting that neural network approaches may have good potential in this context.

Linear classifiers (support vector machines)

Linear classifiers make classification decisions based on a linear combination of the features (i.e., covariates) of the data points [10]. For example, in the two-class case, the decision rule learned by a linear classifier can be considered to be a dividing hyperplane in the feature space, separating those data points into two classes (Figure 2). Logistic regression itself, used to make classification decisions, is a kind of dichotomous linear classifier; however, the class of machine-learning linear classifiers is perhaps best exemplified by support vector machines (SVMs) [25].

Figure 2.

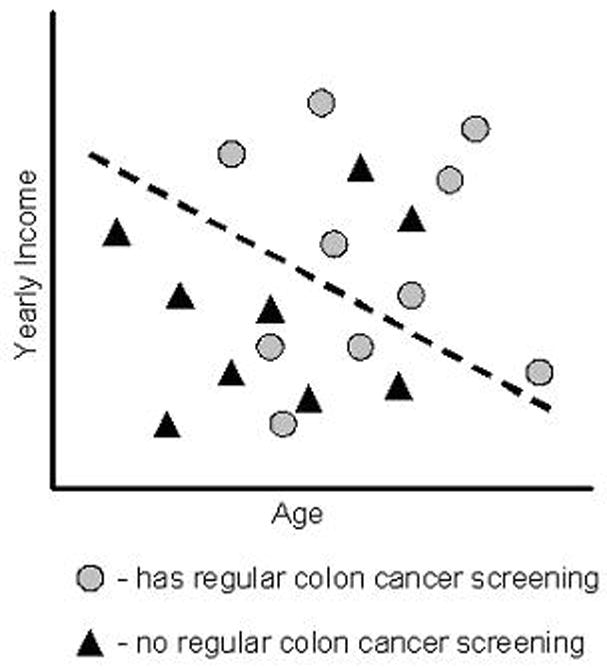
A simple linear classifier. Those points above the dotted line (the dividing hyper-plane) are classified as having regular screening, while those below the line are classified as not having regular screening.

SVMs and logistic regression are similar in that both calculate a set of coefficients (or weights) for variables based on a transformation of the feature (covariate) space [10]. The major difference between SVMs and logistic regression is that while logistic regression attempts to explicitly model the probability (via the odds) of outcomes, SVMs attempt to directly find the best dividing hyperplane (or hyperplanes, in the case of more than two classes) regardless of the actual probability of class membership [26]. Thus, an SVM could be used to directly construct propensity categories. Innovative new techniques in SVMs, such as import vector machines (IVMs), do calculate an explicit probability of class membership, and hence have great promise for the calculation of propensity scores if they are proven to have performance equivalent to that of more standard SVM methods [26].

There are several advantages of SVM compared to logistic regression. While in logistic regression the data analyst must explicitly choose to increase the dimensionality of the feature space through the addition of interaction or polynomial terms among predictors, such transformations are standard practice in SVM approaches to classification [14]. In addition, SVMs deal well with high-dimensional data, and they do not assume a parametric relationship between the model predictors and outcome. The main disadvantage of SVMs for generation of propensity scores is that in general, the actual propensity scores themselves may remain unknown, with the SVM only determining group membership. As noted above, IVMs solve this problem, but IVM (and SVM) software is not widely available: while an implementation of SVMs is available in R [27], the procedure remains experimental in SAS [18], and we have been unable to identify an implementation of the software in Stata [20] (Table 1). The use of multiple linear classifiers to subdivide strata or create actual probabilities of class membership can also overcome this problem (see Boosting, below). A last disadvantage of SVM approaches is the need to select the function used to transform the covariates, called the kernel function. Selecting the appropriate kernel function for a particular classification task is non-trivial; in general several alternatives are considered and compared via cross validation or another method [28]. Due to the need to select the kernel function, the naïve implementation of an SVM or IVM may not evidence substantial advantages over logistic regression.

SVMs have proven effective in practical classification tasks such a spam detection [29] and the classification of cancers [30, 31], but we are aware of only one instance in which an SVM has been used to estimate propensity scores [32].

Decision trees

Decision trees are classification algorithms which specify a “tree” of cut points that minimize some measure of diversity in the final nodes once the tree is complete. The final nodes then represent relatively homogenous individual classes [10] (Figure 3). To the extent that all data points classified at a given end node have a similar probability of class membership (that is, probability of treatment), then the output of decision trees can be used to directly construct propensity categories [6].

Figure 3.

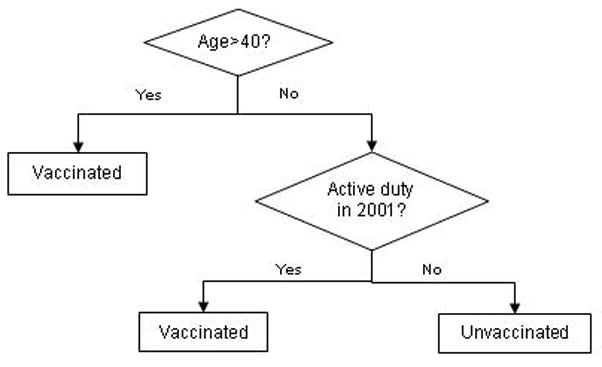
A simple decision tree predicting smallpox vaccine status among military personnel.

Decision trees are well researched, and relatively easy both to interpret and to implement; decision tree software is available for standard software packages [18, 33, 34] (Table 1). Like SVMs and neural networks, many methods for decision trees (e.g., ID3, C4.5) do not provide a probability of class membership although some variants, in particular classification and regression trees (CART), do provide such probabilities. However, performance of all decision trees is dependent on both their method of construction and the amount of pruning (removal of highly specific nodes) performed.

There are several examples of decision tree analysis in the medical literature, almost invariably in the form of a particular kind of decision tree algorithm, Classification and Regression Trees (CART) [35]. For instance, one recent study used CART along with logistic regression to implement a prediction model for individuals at high risk of incident STDs during pregnancy [36] while another used CART directly for propensity score calculation [37]; in contrast to some other kinds of decision trees, CART can provide explicit probabilities. Setoguchi also used classification trees to estimate propensity scores, generally finding that such propensity scores yielded effect estimates that were less biased than those derived using main effects logistic regression [9]. Setoguchi et al. also found that pruning their classification trees resulted in markedly higher bias in many scenarios, though they caution that alternative approaches to pruning might prove more successful [9].

Boosting (meta-classifiers)

Training a single classifier for high performance may be difficult and require extensive expertise in tuning the algorithms involved. In addition, as mentioned above, many classification algorithms do not model a probability, hence are limited in their utility for propensity score analysis. Meta-classification algorithms – and in particular, boosting algorithms – solve both of these problems. Boosting combines the results of many weak classifiers – that is, classifiers with performance only slightly better then chance – to form a single strong classifier [10].

Boosting boasts several advantages. Because the component classifiers need only perform at a level only slightly better than chance alone, less expertise with the particular classification algorithm being used may be required. The underlying classifier used in boosting may be selected at the discretion of the researcher, but in general simple and computationally efficient classifiers such as decision trees are preferable because high accuracy is not required of the underlying classifier. Boosting is also less susceptible to overfitting than single classifier techniques. Especially relevant to the generation of propensity scores is the fact that many boosting algorithms can be used to construct a classifier that produces a probability of class membership using component classifiers that do not produce such a probability (e.g., decision trees, SVMs) [38]. Last, implementations of boosting are available for R [39, 40], SAS [18], and Stata [41] (Table 1). A drawback of boosting (and, again, of many meta-classification algorithms) is that boosting does not provide interpretable coefficients, even if the underlying classification algorithm alone produces such results.

Both McCaffrey et al. and Harder et al. have used generalized boosted models (a decision tree-based boosting technique that provides probabilities) to successfully generate propensity scores [8, 42]. Breiman’s “random forests” algorithm is a decision tree based meta-classification algorithm similar to boosting that may also be a good choice for propensity score generation [39].

Discussion

Propensity scores provide a powerful tool for controlling confounding in observational studies; however, their power may be limited by the exclusive and near-automatic use of logistic regression for estimation of propensity scores. We have reviewed several techniques that have potential to perform better than logistic regression in helping to control confounding in a propensity score setting. In particular, we believe that boosting methods have the best potential for estimation of propensity scores because of the power and flexibility of their naïve implementations. CART has similar promise, but the need for pruning in decision tree algorithms makes CART less attractive. Neural networks and support vector machines also show less potential because of the expertise involved in tuning the learning algorithm.

It is worth noting that propensity scores (estimated probability of exposure given covariates) form an important component of several other recent innovations in causal modeling. For instance, inverse probability of treatment weighting [43] begins with the calculation of a propensity score, which is then transformed and stabilized to create weights. Inverse probability weighted marginal structural models [43, 44] and some doubly robust models [45, 46] similarly use propensity scores for re-weighting observations to eliminate confounding and selection bias in observational settings. Those methods presented here that do not provide an actual probability of class membership are obviously not appropriate for estimators that require re-weighting; however a number of the techniques we have presented may still prove useful in developing new ways of approaching weighted models.

Some of the problems we have identified with logistic regression (or parametric regression) can be overcome with conscientious implementation of those statistical models. For example, published examples of regression models for calculation of propensity scores typically do not report use of interaction terms [5], splines, or higher order polynomials. Failing to include these terms in a model is equivalent to assuming that they collectively contribute nothing to model fit, a strong assumption and one which is (likely) frequently inadvisable. Inclusion of these terms and closer attention to the parametric assumptions of logistic regression might lead to sufficient improvement in the usual approach to propensity score estimation that it would make the potential gains in control of confounding using less-familiar “algorithmic” approaches presented here too small to be worth pursuing.

In practice, however, the widespread use of naïve logistic regression for estimation of propensity scores suggests (to us, at least) that there is resistance against the inclusion of such higher order terms in regression models. Additionally, the consideration of these terms introduces additional questions (with splines, for example: how many knots, and where should those knots be placed?). Logistic regression always makes a parametric assumption of the log-odds transformation, whether the predictors in that model are simple or higher order. We would argue that given the evident preference for naïve applications of logistic regression [4], the optimal tool for the estimation of propensity scores is one which performs very well in its naïve implementations, rather than in its most sophisticated. Machine learning techniques make fewer assumptions than logistic regression, and often deal implicitly with interactions and non-linearities, in their naïve implementations. We believe that one of these techniques might find recommendation to replace logistic regression as the presumptive mechanism for estimation of propensity scores, although extensive simulation research is required to verify this intuition.

However, the techniques we have reviewed have the potential to eliminate confounding to a greater degree than logistic or other parametric regression in a wide variety of settings. While the work of Setoguchi et al. [9] and work in preparation by Lee et al. [47] begins this work, further simulation studies are needed to compare performance of these different techniques in different settings, and with data structures with a wide range of strengths of exposure-outcome, covariate-exposure, and covariate-outcome relationships, covariance structures among all covariates, and parametric (and non-parametric) relationships among exposure and covariates. In particular, while Setoguchi et al. emphasized that their results were meant to be representative of pharmacoepidemiologic studies, future simulations should explore a wider range of epidemiologic applications. Fortunately implementations of many of the algorithms described are available on a variety of statistical and mathematical computing platforms, so as performance of these algorithms is validated against logistic regression in simulation, they can be relatively easily adopted by practicing epidemiologists and data analysts. In addition to the initial findings that both neural networks and CART (recursive partitioning) may be useful in estimating propensity scores [9], we believe that the other techniques discussed here, and in particular boosting, should be the focus of future simulation studies. Generalized boosting models, in particular, work well out of the box, are available in three widely used statistical computing platforms (SAS, Stata, and R, see Table 1), and are resistant to overfitting. Preliminary results from Lee et al. [47] support this recommendation of boosting.

As mentioned earlier, the “black box” nature of these techniques may make some scientists and data analysts uncomfortable, even while they have proven effective in practical applications [14]. Additionally, as with any algorithm that can be used easily used “out of the box”, there is always the danger with these techniques of making fundamental assumptions that do not hold. Hence, it is important that researchers familiarize themselves with the assumptions being made by the particular approach that they choose.

Further reading

There is a wide variety of literature on machine learning for specific applications and general use. Pattern Classification by Duda, Hart, and Stork [10] and Machine Learning by Mitchell [11] both serve as excellent introductions and reference material for those interested in the technical details behind the techniques we have presented here.

Dreiseitl and Ohno-Machado also provide an accessible overview of classification techniques in their discussion of the use of logistic regression and neural networks in the medical literature [48].

WHAT IS NEW?

Propensity scores are, almost without exception, estimated using logistic regression, but there are a number of statistical and classification techniques that may do better than logistic regression. We encourage researchers to explore the use of these other techniques, in particular boosting techniques and decision trees (CART), in subsequent simulation studies and data analysis where propensity scores are appropriate.