Genome-Wide Association Studies and the Problem of Relatedness Among Advanced Intercross Lines and Other Highly Recombinant Populations

Abstract

Model organisms offer many advantages for the genetic analysis of complex traits. However, identification of specific genes is often hampered by a lack of recombination between the genomes of inbred progenitors. Recently, genome-wide association studies (GWAS) in humans have offered gene-level mapping resolution that is possible because of the large number of accumulated recombinations among unrelated human subjects. To obtain analogous improvements in mapping resolution in mice, we used a 34th generation advanced intercross line (AIL) derived from two inbred strains (SM/J and LG/J). We used simulations to show that familial relationships among subjects must be accounted for when analyzing these data; we then used a mixed model that included polygenic effects to address this problem in our own analysis. Using a combination of F₂ and AIL mice derived from the same inbred progenitors, we identified genome-wide significant, subcentimorgan loci that were associated with methamphetamine sensitivity, (e.g., chromosome 18; LOD = 10.5) and non-drug-induced locomotor activity (e.g., chromosome 8; LOD = 18.9). The 2-LOD support interval for the former locus contains no known genes while the latter contains only one gene (Csmd1). This approach is broadly applicable in terms of phenotypes and model organisms and allows GWAS to be performed in multigenerational crosses between and among inbred strains where familial relatedness is often unavoidable.

SUSCEPTIBILITY to diseases such as drug abuse is partially determined by genetic factors. The identification of the alleles that underlie disease susceptibility is an immensely important goal that promises to revolutionize both the diagnosis and the treatment of human disease. Genome-wide association studies (GWAS) in humans can locate common alleles with great precision. However, GWAS may be unable to identify the bulk of the heritable variability for common genetic diseases; some of this “missing heritability” is thought to be due to rare alleles (Manolio et al. 2009). Model organisms are complementary to human genetic studies and offer unique advantages including the ability to control the environment, perform dangerous or invasive procedures, and test hypotheses by manipulating genes via genetic engineering; a final advantage is that crosses between two inbred strains avoid many of the difficulties associated with rare alleles.

Studies in model organisms have frequently employed intercrosses (F₂'s) to identify quantitative trait loci (QTL) that underlie phenotypic variability. F₂ crosses are easy to produce and easy to analyze; however, due to a lack of recombination they can identify only larger genomic regions and are thus unsuitable for identifying the genes that cause QTL (Flint et al. 2005; Peters et al. 2007). This is a serious limitation that can be addressed by using populations with greater numbers of accumulated recombinations. Darvasi and Soller (1995) suggested the creation of advanced intercross lines (AILs) by successive generations of random mating after the F₂ generation to produce additional recombinations. An AIL offers vastly improved mapping resolution while maintaining the desirable property that all polymorphic alleles are common.

We used an AIL to study sensitivity to methamphetamine, which is a genetically complex trait that may be useful for identifying genetic factors influencing the subjectively euphoric response to stimulant drugs and susceptibility to drug abuse (Palmer et al. 2005; Phillips et al. 2008; Bryant et al. 2009). For example, a prior study suggested that the gene Casein Kinase 1 Epsilon (Csnk1e) might influence sensitivity to the acute locomotor response to methamphetamine in mice (Palmer et al. 2005). This conclusion has been bolstered by additional pharmacological (Bryant et al. 2009) and genetic studies. In addition, we have shown that polymorphisms in this gene are associated with sensitivity to the euphoric effects of amphetamine in humans (Veenstra-Vanderweele et al. 2006). Another group has subsequently reported that this same gene is associated with heroine addiction (Levran et al. 2008). Thus, genes that modulate the acute locomotor response to a drug in mice may also be important for sensitivity to similar drugs in humans as well as the risk for developing drug abuse.

The purpose of this study was to develop a framework for rapid identification of high precision QTL and ideally specific genes that influence sensitivity to methamphetamine in mice by employing an AIL. We produced an F₂ cross (n = 490) and a corresponding 34th generation AIL (n = 688) derived from the inbred strains SM/J and LG/J. This allowed us to compare and integrate the results from F₂ and AIL mice. We examined the locomotor stimulant response to a 2-mg/kg dose of methamphetamine, which is extremely disparate in the two progenitor strains. We performed a GWAS using either simple regression, which ignored relatedness, or a mixed model that accounted for relatedness by using identity coefficients that were calculated from the pedigree. We also explored two methods to estimate significance: simple permutation and gene dropping. We discuss the performance of a mixed model that includes polygenic effects vs. simple regression and the performance of permutation vs. gene dropping. The methods used in this study are applicable to a variety of other phenotypes and populations.

MATERIALS AND METHODS

Subjects:

Mice were housed in standard laboratory conditions with a 12:12-hr light cycle and ad libitum access to food and water. We obtained inbred SM/J and LG/J mice from Jackson Labs (Bar Harbor, ME). Some of these mice were used to breed additional inbred mice that were phenotyped while others were used to produce SM × LG F₁ mice. Similarly, some F₁ mice were phenotyped while others were used to produce the F₂ generation (n = 490).

In addition, we obtained 140 F₃₃ breeders from the laboratory of James Cheverud (Washington University, St. Louis). The F₃₃ mice were outbred, with >50 families having been maintained per generation since their inception. Breeding was random except that siblings were not mated with one another. Records from Dr. Cheverud's lab allowed us to construct a pedigree for each F₃₃ mouse that traced back to the original inbred founders. From these 140 F₃₃ mice, 119 were successfully bred to create an F₃₄ generation (n = 688), in which phenotypes were measured. We produced only one F₃₄ litter per breeding pair; breeding pairs were rotated after each litter to avoid producing large numbers of full sibs; however, the phenotyped (F₃₄) generation inevitably contained many sibs, half-sibs, and cousins as well as more distant and complex relationships.

We chose to study the SM/J and LG/J strains mainly because of the availability of an F₃₃ AIL, which represents almost 10 years of breeding. Another advantage was the availability of a known pedigree. In addition, these strains also showed marked differences in the traits we chose to study, as discussed below. All procedures were approved by the University of Chicago institutional animal care and use committee (IACUC).

Behavioral testing:

We used a standard procedure to evaluate the locomotor response to methamphetamine (Bryant et al. 2009). The procedure involved testing mice over a 3-day period; on days 1 and 2 mice were weighed and then received vehicle (saline) injections while on day 3 mice were weighed and then injected intraperitoneally with 2.0 mg/kg methamphetamine. On each test day mice were placed into an automated test chamber (Accuscan Instruments, Columbus, OH) outfitted with a two-dimensional array of infrared photobeams that recorded the position of each mouse 50 times per second. These data were subsequently analyzed by a computer to determine the total distance traveled, which was the dependent measure for all analyses. Each test session was 30 min long. Mice were placed in the chambers immediately after injection and were returned to their home cages at the end of each session. Additional phenotypes were measured in these mice after methamphetamine testing; results from the QTL analyses of some of those phenotypes may be reported in future publications.

Genotyping of F₂ mice:

DNA from F₂ mice were extracted and genotyped at 123 SNP markers that were genotyped in the AIL mice as well as 39 unique SNP markers; genotyping was performed by KBiosciences (Hoddesdon, UK).

Genotyping of AIL mice:

We designed a custom SNP genotyping array that assayed SNPs using the Illumina Infinium platform. This array was used for several projects and thus contained many SNPs that were not polymorphic between SM/J and LG/J mice. SNPs were selected from databases maintained by The Broad Institute (http://www.broad.mit.edu/personal/claire/MouseHapMap/), the Wellcome Trust (http://gscan.well.ox.ac.uk), and a prerelease of imputed genotypes from the Center for Genome Dynamics (Szatkiewicz et al. 2008). These SNPs were chosen to provide uniform coverage of the mouse genome using either a genetic map constructed by Shifman et al. (2006) or linear interpolations based on that map and the physical position of the SNPs as reported in build 36 of the mouse genome (http://www.ncbi.nlm.nih.gov/genome/guide/mouse/). We preferentially chose SNPs that were polymorphic between SM/J and LG/J, had high Illumina quality scores, and had genotypes that were experimentally observed rather than imputed. Despite these efforts, several chromosomal regions contained no known polymorphic SNPs for SM/J and LG/J (Figure 1B). In other cases, low allele frequencies made genotypes difficult to call, leading to gaps in our map in regions known to be polymorphic between SM/J and LG/J. This array was designed for multiple applications and contained ∼4000 markers that were predicted to be polymorphic between SM/J and LG/J as well as ∼4500 that were not expected to be polymorphic between these two strains. A full list of these SNPs is available at http://phenome.jax.org/SNP/ under the name “Chicago1”.

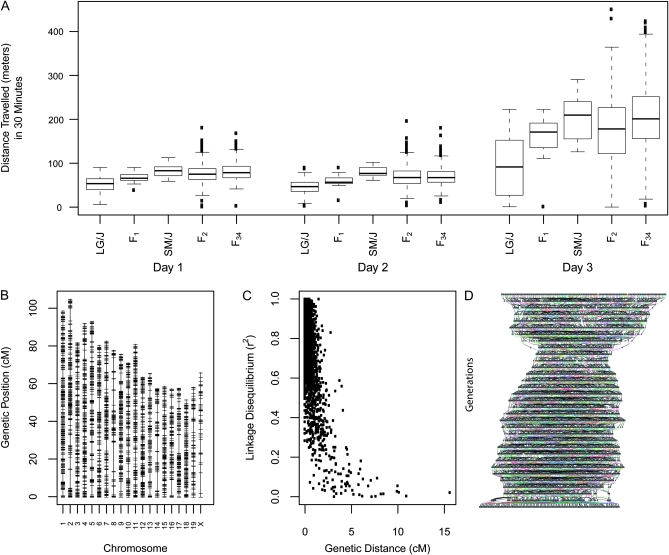
Figure 1.—

Key parameters for SM/J, LG/J, and recombinant mice. (A) Box and whisker plots of locomotor behavior on days 1 and 2 when vehicle was administered and on day 3 when methamphetamine was administered. (B) The genetic map estimated from recombinations between generation 33 and generation 34 of the AIL. (C) Linkage disequilibrium (LD) between makers (r²) on the same chromosome vs. genetic distance (cM). (D) The pedigree of the AIL population from the F₂ to the F₃₄ generation. Generations are arranged vertically, each very small box is an individual, and colored lines indicate relationships across generations.

DNA samples were extracted from 839 mice (134 F₃₃, 695 F₃₄, and 10 controls: LG/J, SM/J, and LG × SM F₁). DNA was hybridized to the Illumina array in accordance with the manufacturer's instructions at the Keck Microarray Resource (New Haven, CT). Raw intensity data were analyzed using BeadStudio V3.2. We used the following metrics to perform SNP and subject quality control: cluster separation, call frequency, AB R mean, AB θ mean, reproducibility errors, heterozygosity excess, minor allele frequency, and X-linked SNPs (for male heterozygotes). Four mice were excluded due to low call rates, as were several hundred SNPs. In some cases multiple adjacent SNPs were excluded because calling was more difficult when the minor allele frequencies (MAF) were low.

The remaining mice (n = 835) and SNPs were subjected to further error checking. During this process an additional five unintended duplicate samples were identified and excluded. One SNP that was expected to be located on chromosome 6 showed strong linkage to markers on chromosome 9; we excluded this single SNP from further analysis. Five SNPs from four different regions showed unusual clustering patters that suggested the presence of copy number variations, and these SNPs were recoded as unknown. Checks for Mendelian inheritance and the genotypes of SNPs on the X chromosome identified several errors in sample identification that we were able to correct by making use of the pedigree and available breeding records. Mendelian inheritance was also used to impute a small number of missing genotypes. We identified 21 SNPs that Szatkiewicz et al. (2008) had predicted would be monomorphic between SM/J and LG/J but were actually polymorphic in both the control and the AIL samples.

There were a total of 3345 missing genotype values for 820 mice (excluding the 10 controls). Three hundred sixty-two of the 820 mice had at least one missing genotype value and 43 mice had at least 10 missing values and accounted for 81.6% of all missing values. Since missing genotype data accounted for only a small portion of all genotype data and the SNPs were densely distributed, some of the missing genotypes could be imputed with a high reliability using available genotype information. However, 1966 genotypes could not be imputed with high confidence. Some pairs of adjacent SNPs were identical (r² = 1; both SM/J or both LG/J) for all mice with complete genotype data, indicating that they had never been separated by recombination. For such pairs, we excluded whichever SNP had the most missing genotypes from further analysis. At the conclusion of our quality control steps we had 830 AIL mice that were genotyped at 3105 SNPs.

We produced a genetic map using CRI-MAP v2.4 in conjunction with the F₃₃ and F₃₄ generations. This map contained all 3105 of the SNPs that were genotyped in the AIL as well as 39 SNPs that were genotyped in the F₂ but not the AIL; thus the map contained a total of 3144 SNPs. SNP markers were densely distributed along the genome. The mean distance between two adjacent SNPs was 0.4727 cM; however, there were several gaps on the map, the largest of which was 15.61 cM. Comparison of our genetic map to a map produced using our F₂ data or to the map from Shifman et al. (2006) yielded broadly similar results.

Calculation of relationship matrices:

Kinship coefficients and identity coefficients were calculated using the pedigree for the AIL, which began in the F₁ and continued to the F₃₄ generation, using the method of Karigl (1981). We developed an algorithm that combined top-down and bottom-up methods of estimation to obtain the generalized kinship coefficients. While other methods exist for calculating kinship coefficients and identity coefficients (Abney 2009), the size of this pedigree required us to develop an alternate strategy that was less memory intensive (see supporting information, File S1 for more details).

Association in F₂:

We analyzed data from the F₂ by using a standard regression model; the model can be written as

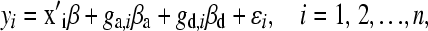(1)

where x′_i is a vector of covariates (e.g., sex) and β is a vector of the corresponding effect parameters. The additive genotype g_a,i is coded as (−1, 0, 1) corresponding to genotypes (AA, AB, or BB). β_a is the additive effect of the QTL, given as one-half of the difference between the mean of the AA and BB groups. The dominance genotype g_d,i is coded as 1 if mouse i's genotype is heterozygous; otherwise it is 0. β_d is the dominance effect, given as the deviation between the mean of the heterozygous group and the expected trait value assuming an additive QTL. The ɛ_i accounts for all unmodeled variation and is assumed to be distributed independently, N(0, σ²), i = 1, 2, … , n. A likelihood-ratio test is performed to determine if each marker is a QTL (H₀: β_a = β_d = 0 vs. H₁: β_a ≠ 0 or β_d ≠ 0).

Association in the AIL:

We considered two regression models for the analysis of the AIL. The first model was identical to the one just described for the analysis of the F₂. That model is appropriate only when subjects are independent, which is not the case in an AIL. The second model addressed the nonindependence of subjects (due to relatedness) by using a mixed model,

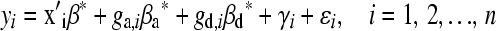(2)

(Harris 1964), where γ_i is a random effect representing the polygenic influence of subject i and asterisks are added, β*, β*_a, and β*_d, to distinguish them from β, β_a, and β_d in Equation 1; however, their meanings are the same. We assume the polygenic effects γ = (γ₁, γ₂, … , γ_n) ∼ N_n(0, Σ) with Σ = (σ_ij) and independent of ɛ = (ɛ₁, ɛ₂, … , ɛ_n). Abney et al. (2000) demonstrated that 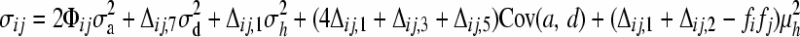, where Φ_ij is the kinship coefficient between mice i and j and Δ_ij's are Jacquard's condensed identity coefficients (Jacquard 1974) that give the probability that a pair of mice have certain alleles identical by descent. Jacquard's condensed identity coefficients were calculated from the pedigree structure as described above (see File S1 for further details). In matrix form, Equation 2 can be denoted as

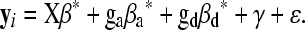The likelihood of Equation 2 under the alterative hypothesis is

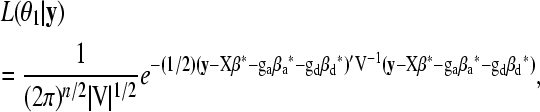(3)

where θ₁ denotes the regression parameters and variance components in Equation 2 and V = Σ + I_nσ² with I_n being an n × n identity matrix. Under the null hypothesis of no QTL, Equation 3 reduces to

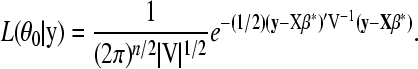(4)

We use a likelihood-ratio test statistic to test H₀: β*_a = β*_d = 0 vs. β*_a ≠ 0 or β*_d ≠ 0 at each marker. Our test statistic for marker i has the form

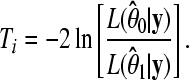(5)

The maximum-likelihood estimates (MLEs) of the variance components and fixed effects were obtained using the Nelder–Mead nonlinear optimization algorithm (Press et al. 1992). Before performing tests to identify QTL, we first determined the appropriate model for the polygenic effect and fixed effects. This was done by calculating the log-likelihood of the data for each permissible model using MLEs of the parameters for that model, but not fitting the QTL (refer to “Maximum-Likelihood Estimation” in File S1 for more information). We used Bayes' Information Criteria (BIC) to determine which model was the most parsimonious with the data while accounting for the improved fit from including a new parameter (Lehmann 1997). For days 1 and 2 only the additive variance component was included, whereas for day 3 both the additive and the dominant variance components were included. The fixed effects sex and body weight were always included. Using these models and MLEs, each marker was tested for association.

Analysis of integrated F₂ and AIL data:

F₂ data can provide more statistical power for QTL detection whereas an AIL can provide better resolution for fine mapping of QTL. Furthermore, increasing the total number of subjects can also increase power to detect QTL. In an effort to improve both power and accuracy, we performed a single analysis that incorporated data from both the F₂ and the AIL populations. Because only a subset of the markers that were genotyped in the F₂ were also genotyped in the F₃₄, and because 39 markers genotyped in the F₂ were not typed in the F₃₄, it was necessary to impute a significant number of genotypes. Furthermore, the five largest gaps in the genetic map were between 9.9 and 15.6 cM. To address these issues we used an interval mapping approach. We used the model defined in Equation 2, but considered both markers and an additional ∼2000 scanning loci. We chose scanning loci such that the largest cumulative recombination rate between any two markers was not >0.05. The scanning loci were imputed using the Haley–Knott methods (Haley and Knott 1992). The F₂ samples were treated as equally related to one another and unrelated to the F₃₄ mice. All phenotypic data were scaled to have mean 0 and standard deviation of 1 separately for the F₂ and AIL. After scaling the phenotypes the F₂ and F₃₄ data sets were combined. All genotype, phenotype, and pedigree data are available online (see File S2).

Estimating thresholds for genome-wide significance:

Determining the correct genome-wide significance threshold is complicated by two factors. First, when we analyze the AIL using the regression model that ignores relatedness, the independence assumption is unlikely to be met, and therefore the test statistics' distribution, even under the null hypothesis, is not known. Second, regardless of the model or population used, the genotypes at the marker being tested are correlated as a result of linkage disequilibrium (LD), and a simple correction like Bonferroni will be overly conservative. Given these challenges, we considered simple permutation (O'Gorman 2005) and gene dropping (MacCluer et al. 1986) for estimating genome-wide significance thresholds in conjunction with Equations 1 and 2. While using permutation to empirically determine the distribution of the test statistic is a common approach in QTL mapping (Churchill and Doerge 1994), it is not a valid strategy when the subjects are not equally related because both the genotypes and the phenotypes are intercorrelated and thus are not exchangeable units (Lehmann 1997). As described in the next paragraph, gene dropping maintains these relationships by creating alternative genotypes that are consistent with the genetic map and pedigree; gene dropping does not make assumptions about independence among subjects.

To perform gene dropping, we simulated genotypes given the pedigree from our AIL and the genetic map that we estimated from the F₃₃ and F₃₄ generations. We simulated meioses that were consistent with the genetic map, using the Kosambi map function, for each generation until the F₃₄ generation had been reached. This procedure provides simulated genotypes that preserve the familial relationship among marker genotypes. Because the genotypes are simulated, the null hypothesis is true for all genotypes obtained by using gene dropping.

We explored different approaches to determining significance thresholds by using simulations in which the null hypothesis was correct by performing 500 iterations of the following procedure:

1. We calculated relationship matrices for the real AIL pedigree.

2. We produced simulated phenotype data using Equation 2 with no QTL effects, incorporating additive (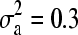), dominant (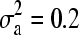), and error variances (σ² = 0.36) as estimated from our observed data (data from day 3 were used). Because we did not simulate any QTL effects, phenotypes were determined only by relatedness and error.

3. We performed a genome scan using the real genotype data and the simulated phenotype data generated in step 2.

4. We then performed 5000 permutations to assess the significance of the test statistic from step 3 using both Equation 1 (regression) and Equation 2 (mixed model).

5. In addition, we also performed 5000 iterations of the gene dropping procedure to assess the significance of the test statistic from step 3, using both Equations 1 and 2.

6. Steps 2–5 were repeated 500 times; after each iteration, we recorded whether any marker would have been deemed significant for either gene dropping (Equation 1 or Equation 2) or permutation (Equation 1 and Equation 2). In Table 3 we refer to Equation 1 as “regression” and Equation 2 as “mixed model.” Table 3 contains the proportion of these 500 iterations in which the simulated data would have been judged to contain a significant result. Because the null hypothesis was true in all simulations, the test statistic should return the expected type I error rate; deviations indicate under- or overconservative test statistics.

TABLE 3.

Type I error rates for simulations of different models and tests for significance

		Significance level
Model	Significance test	α = 0.10	α = 0.05	α = 0.01
Mixed model	Gene dropping	0.110 ± 0.0140	0.066 ± 0.0111	0.010 ± 0.0044
	Permutation	0.104 ± 0.0137	0.064 ± 0.0109	0.012 ± 0.0049
Regression	Gene dropping	0.136 ± 0.0153a	0.072 ± 0.0116	0.018 ± 0.0059
	Permutation	0.914 ± 0.0125b	0.812 ± 0.0175b	0.518 ± 0.0223b

The type I error rates (mean ± standard error) were estimated from 500 simulations with thresholds being estimated from 5000 simulations separately for each model.

^aThe desired type I error rate falls outside of the 95% confidence interval.

^bThe desired type I error rate falls outside of the 99% confidence interval.

Software to perform all analyses described in this article is publicly available at http://www.palmerlab.org.

RESULTS

For QTL mapping to be successful, polymorphic alleles that influence the phenotype of interest must segregate between the two inbred strains. To assess whether this was likely to be the case, we examined the phenotype of the inbred progenitor strains (SM/J and LG/J); we also examined the phenotype of F₁ mice, which provides insight into whether dominant/recessive alleles might be present. We found that locomotor behavior in both the absence (days 1 and 2) and presence (day 3) of methamphetamine (2.0 mg/kg) was much greater in the SM/J relative to the LG/J inbred mice. F_1, F₂, and AIL mice showed intermediate levels of behavior (Figure 1A). As expected, the segregating (F₂ and AIL) mice showed much greater phenotypic variability than the inbred mice, reflecting random assortment of QTL alleles in these populations (Figure 1A). For all subsequent analyses, traits were scaled to have a mean of 0 and a standard deviation of 1 (this was done separately for the F₂ and the AIL).

We used genotype data from the 33rd and 34th AIL generations to construct a genetic map for our markers (Figure 1B) and found that it was generally in agreement with other published maps and with the map generated using our F₂ population.

A key advantage of an AIL is that LD between markers should be reduced relative to an F₂ cross. As expected, LD between markers (r²) in the AIL rapidly degraded as a function of either genetic distance (Figure 1C) or physical distance (data not shown).

We used breeding records to construct the complete pedigree from the inbred SM/J and LG/J strains to the F₃₄ mice that were the focus on this study; this pedigree, which contains 5647 individuals, is shown in Figure 1D. This pedigree information was essential both for the calculation of identity coefficients and for gene dropping.

The first stage of our analysis used the 490 F₂ mice to identify QTL for behavior on days 1, 2, and 3. We used single-marker regression to examine the relationship between behavior and each SNP marker. These analyses yielded multiple genome-wide significant QTL (Figure 2). Because all F₂ mice are full-sibs with respect to one another, there was no need to incorporate information about the relationship among these mice into our analysis. We used both permutation and gene dropping to calculate genome-wide significance thresholds; as expected, these two approaches to calculating a significance threshold yielded very similar results.

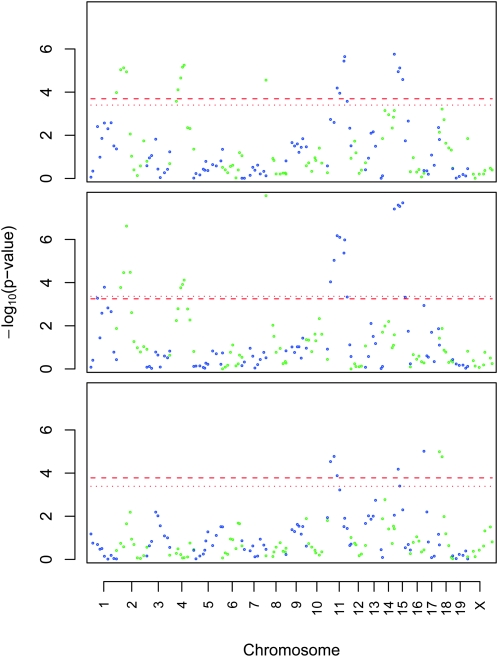
Figure 2.—

QTL identified using the F₂ mice: QTL for locomotor activity following saline administration on days 1 (top) and 2 (middle) or following methamphetamine administration on day 3 (bottom). Alternating colors denote odd- or even-numbered chromosomes. The horizontal lines indicate genome-wide significance of P < 0.05 based on either permutation (dotted lines) or gene dropping (dashed lines).

We identified a similar set of QTL for both days 1 and 2, when saline was administered; however, we identified a very different set of QTL for day 3, when methamphetamine was administered (Figure 2). A major QTL for activity in the absence of methamphetamine was observed on chromosome 8 (LOD = 8.16); this QTL accounted for 10.12% of the variance on day 2. We used a 2-LOD support interval in an effort to be conservative in judging the outer boundaries of the identified QTL. As expected, the 2-LOD support interval for this QTL was broad (0.16–18.92 cM) and encompassed a 38.80-Mb region. Several significant QTL were observed for response to methamphetamine on day 3, including one on chromosome 18 (LOD = 5.38) that accounted for 5.51% of trait variance. This QTL had a broad confidence interval (1.03–17.14 cM) and encompassed a 25.49-Mb region. These results are summarized in Tables 1 and 2.

TABLE 1.

QTL on chromosome 8 for activity on day 2 (saline) using F2, AIL, and integrated analysis

Population	LOD	% variance	2-LOD support (cM)	2-LOD support (Mb)
F2	8.16	10.12	18.76	38.80
AIL	12.59	5.37	0.33	0.50
Integrated	18.90	7.29	0.65	0.50

A significant QTL was identified on chromosome 8 using F₂, AIL, and the integrated analysis of both populations. The SM/J allele was associated with greater locomotor activity; heterozygotes were intermediate but somewhat more similar to LG/J homozygotes. The 2-LOD support intervals are based on interval mapping. The support interval was smaller in the AIL than in the integrated analysis when expressed in centimorgans but not when expressed in megabases because we did not attempt to interpolate the physical positions of untyped (scanning) loci.

TABLE 2.

QTL on chromosome 18 for activity on day 3 (2 mg/kg methamphetamine), using F2, AIL, and integrated analysis

Population	LOD	% variance	2-LOD support (cM)	2-LOD support (Mb)
F2	5.38	5.51	16.11	25.49
AIL	5.06	2.18	0.87	1.56
Integrated	10.50	3.74	0.87	1.56

A significant QTL was identified on chromosome 18 using F₂, AIL, and the integrated analysis of both populations. The LG/J homozygotes showed a greater response to methamphetamine; the heterozygotes and SM/J homozygotes showed approximately similar responses, consistent with a recessive LG/J allele effect.

In preparation for the analysis of the AIL we investigated methods for addressing the complex genetic relationships among members of an AIL. To this end, we performed simulations to explore the effectiveness of accounting for relatedness using a mixed model that included identity coefficients for controlling type I errors. We simulated phenotypes such that the null hypothesis of no QTL present was correct. This produced simulated phenotypes that were correlated due to the familial relationships among individuals. Both gene dropping and permutation of the simulated data were employed to estimate genome-wide significance thresholds. For the gene dropping simulations, we used the pedigree from our AIL to produce simulated genotypes. When the mixed model was used, both gene dropping and permutation effectively controlled the type I error rate (Table 3). When we used simple regression, which ignores relatedness, gene dropping showed a modest inflation of type I errors, while permutation completely failed to control the type I error rate. On the basis of these results we concluded that it was necessary to use a mixed model to account for relatedness to control type I errors (Table 3).

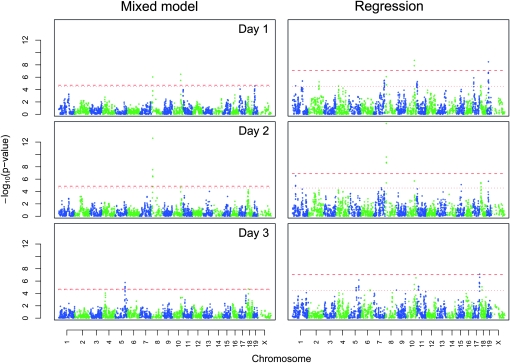
In the next stage of our analysis we used the 688 AIL mice to identify QTL for behavior on days 1, 2, and 3. Similar to the approaches used in our simulations, we analyzed the AIL data using both the mixed model and simple regression (Figure 3). Setting aside the question of a significance threshold, the two models produced somewhat different results, as can be seen by comparing the plots in Figure 3 or by examining the difference between the LOD scores for each marker (Figure S1). This observation is consistent with our expectation that the mixed model would produce more accurate results because it better accounts for the true sources of trait variance. Similar to the simulations, we used both simple permutation and gene dropping to assess the significance of these results. For the mixed model there was little difference in the estimated significance thresholds between these two approaches. In contrast, when we used simple regression, permutation suggested a much lower threshold for significance (Figure 3). The results from our simulations (Table 3) suggest that the lower significance threshold set by permutation is anticonservative.

Figure 3.—

QTL identified using AIL mice. QTL are for locomotor activity following saline administration on days 1 (top) and 2 (middle) or following methamphetamine administration on day 3 (bottom). The left three panels show the results for a mixed model in which relatedness was accounted for while the right panels show the results for a regression model that did not account for relatedness. Alternating colors denote odd- or even-numbered chromosomes. The horizontal lines indicate genome-wide significance of P < 0.05 based on either permutation (dotted lines) or gene dropping (dashed lines).

The results of the analysis of the AIL mice using the mixed model (Equation 2) identified a highly significant QTL for activity on days 1 and 2 on chromosome 8 (Table 1). For behavior on day 2 this QTL was significant (LOD = 12.59) and accounted for 5.37% of trait variance. The 2-LOD support interval was 0.33 cM (8.38–8.70 cM), which corresponded to a 0.50-Mb region (16.61–17.11 Mb). That region contains only 1 known gene: CUB and Sushi multiple domains 1 (Csmd1). In addition, we identified significant QTL on chromosomes 5 (LOD = 5.98) and 18 (LOD = 5.06; Table 2) for methamphetamine-induced locomotor activity on day 3. These QTL accounted for 2.35 and 2.18% of trait variance, respectively. The 2-LOD support interval for the chromosome 5 QTL was 2.59 cM (62.87–65.46 cM), corresponding to a 2.07-Mb region (117.46–120.11 Mb). This interval contains >12 genes. For the chromosome 18 QTL the 2-LOD support interval was 0.87 cM (11.13–12.01 cM), corresponding to a 1.56-Mb region (26.83–28.40 Mb). This interval contains no known genes.

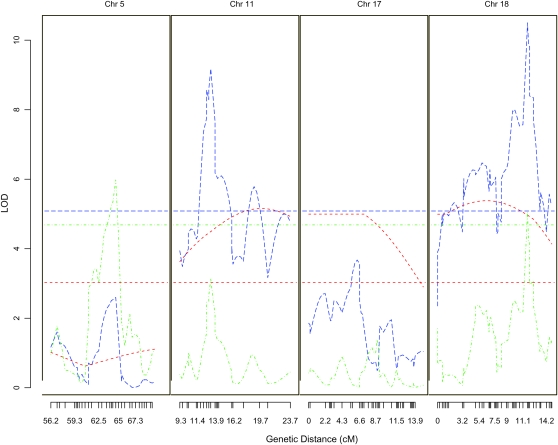
Finally, we sought to combine the power of our F₂ with the greater precision of our AIL by using an integrated analysis of both data sets (Figure 4 and Figure S2, Figure S3, and Figure S4). This approach used >5000 loci that were a combination of all available physical markers and “scanning loci” that were chosen to fill gaps in the genetic map. We used a mixed model to account for relatedness and gene dropping to determine genome-wide significance. Our combined analysis identified multiple genome-wide significant QTL.

Figure 4.—

Plots showing detailed views of Haley–Knott's interval mapping for methamphetamine response on day 3 using F₂ (red), AIL (green), and integrated analysis (blue) in specific regions of the indicated chromosomes. Tick marks along the x-axis indicate the location of physical markers that were successfully genotyped. These data are identical to those shown in more detail in Figure S2, Figure S3, and Figure S4.

We observed a QTL on chromosome 8 for activity following saline administration in both the F₂ and the AIL studies. The integrated analysis also detected this QTL (LOD = 18.90), which was estimated to account for 7.29% of trait variance on day 2. The integrated analysis identified a 2-LOD support interval of 0.65 cM (8.38–9.03 cM; Table 1). The integrated analysis also supported several QTL for methamphetamine-induced locomotor activity, for example, on chromosome 11 (LOD = 9.18), which was significant in the F₂ but not in the AIL. This QTL accounted for 3.37% of trait variance. The integrated analysis reduced the 2-LOD support interval of this QTL to a 3.35-cM region (27.49–30.84 cM) that corresponded to 6.39 Mb (46.30–52.70 Mb). Another QTL on chromosome 18 (LOD = 10.50) was significant in both the F₂ and the AIL samples. This QTL was estimated to account for 3.74% of trait variance when using the integrated analysis. The integrated analysis identified a 2-LOD support interval of 0.87 cM (11.13–12.01 cM) that corresponded to 1.56 Mb (26.83–28.40 Mb; Table 2); the 2-LOD support interval for this QTL is similar to the results from the AIL alone. Thus, the integrated analysis is most useful for QTL like the one on chromosome 11, where the F₂ provided the power to detect the QTL and the AIL, while unable to detect the QTL with genome-wide significance, contributes the ability to significantly narrow the interval of this QTL.

DISCUSSION

We developed a method that accounts for relatedness among subjects when analyzing an AIL and demonstrated its ability to identify genome-wide significant, subcentimorgan QTL. We used simulations to show that failure to account for relatedness led to a dramatic increase in type I errors. Our combined analysis allowed us to identify small chromosomal regions by taking advantage of the greater power of an F₂ and the greater precision of an AIL. This approach can be applied to any quantitative trait in any model organism and should enhance the ability to identify quantitative trait genes (QTGs).

AILs have been used for fine mapping of QTL in a number of species including mice (Iraqi 2000; Iraqi et al. 2000; Wang et al. 2003a,b; Swanberg et al. 2005; Zhang et al. 2005; Behnke et al. 2006; Yu et al. 2006, 2009; Norgard et al. 2009), rats (Jagodic et al. 2004; Swanberg et al. 2005, 2009; Becanovic et al. 2006; Bäckdahl et al. 2009), chickens (Tercic et al. 2009), mosquitoes (Gomez-Machorro et al. 2004; Bennett et al. 2005), and corn (Balint-Kurti et al. 2007). Whereas F₂ subjects are equally related and thus independent, subjects in an AIL share complex and varied levels of relationship with one another. This genetic relatedness creates correlations in both the genotypes and the phenotypes that should be accounted for in the statistical model and when estimating the significance of the resulting test statistic. Simple permutation tests (Churchill and Doerge 1994), which have been used in the vast majority of prior AIL studies to assess significance, assume that all subjects are independent; however, this assumption is violated in an AIL. Failing to account for relatedness may increase type I (false positive) errors (Peirce et al. 2008; Valdar et al. 2009); our simulations showed that for our data set this increase in type I errors was nontrivial (Table 3). This problem is not unique to AILs; it applies to human population isolates such as Hutterites (Newman et al. 2001) and Amish (McArdle et al. 2007), as well as to model organisms like heterogeneous stocks, outbred stocks, and wild accessions. Despite its broad significance, this problem is not widely appreciated nor has it been adequately addressed in the model organism community.

The results from our study illustrate several important concepts about fine mapping. As expected, some QTL were detected by both the F₂ and the AIL populations. One such example is a region on chromosome 18 that showed significant associations in the F₂, AIL, and combined analyses (Figure 4). The region implicated by the F₂ analysis was large and contained many potential candidate genes. In contrast, the region implicated by the AIL and the integrated analysis was more than an order of magnitude smaller (Table 2). This region contains no known genes; we infer that it may contain either a polymorphism that alters gene expression or an uncharacterized transcript. Independent studies that assess the phenotypic consequences of targeted genetic manipulations would be necessary to prove that this association is correct. This example illustrates the potential to generate extremely small and specific candidate regions by using an AIL.

Not all QTL were significant in both populations. In the case of chromosome 11, there was a significant QTL detected in the F₂, but not in the AIL (Figure 4); however, the combined analysis identified a small, genome-wide significant QTL that was much more precisely resolved than in the F₂ (Table 3). In this case, the greater power of the F₂ and greater precision of the AIL synergized to identify a genome-wide significant and narrow QTL.

The QTL on chromosome 17 was significant in the F₂ but not in the AIL while the QTL on chromosome 5 was significant in the AIL but not in the F₂ (Figure 4). These apparent inconsistencies are expected and illustrate important concepts. Obviously, one explanation is that the significant results mentioned above were due to false positive (type I) errors. Alternatively, a false negative (type II) error could have prevented detection of a true QTL. While an AIL provides far superior mapping precision, this precision comes at the cost of power. This reduction in power is due in part to the greater number of markers that must be tested to account for the reduction in LD between markers. Power in an AIL can also be reduced in specific chromosomal regions either by genetic drift, which can produce low QTL minor allele frequencies, or by poor marker coverage of a specific region. The former problem can be mitigated by maintaining large population sizes when creating an AIL. The latter concern will be of diminishing importance as improvements in genotyping technology and related genomic resources become available.

Alternatively, the disparate results observed on chromosomes 5 and 17 may illustrate limitations of F₂ populations. If multiple small QTL are close to one another on a single chromosome, an F₂ population may either detect what appears to be a single QTL or fail to detect any QTL, depending on the directions of the QTL effects. In the first case, further efforts at fine mapping (for example, with an AIL) will separate these multiple QTL from one another; however, their individually small effect sizes will frustrate attempts to identify the underlying genes. In the second case, potentially major QTL may not be discovered in an F₂. Both of these scenarios underscore the limitations of an F₂ and the advantages of an AIL.

In addition to identifying multiple QTL for the response to methamphetamine, we also identified an especially compelling QTL for locomotor behavior in the absence of methamphetamine administration on chromosome 8 (Figure S5). This QTL attained genome-wide significance in both the F₂ and the AIL on both days 1 and 2, when no drug was administered. The F₂ identified a broad QTL on chromosome 8; this interval was reduced >50-fold by the AIL (Table 1) to a 500-kb region that contains a single gene: CUB and sushi multiple domains 1 (Csmd1). This gene is highly expressed in the developing and adult brain, especially in the hippocampus, and is thought to be involved in neuronal development (Kraus et al. 2006). Future studies are underway that will directly manipulate Csmd1 and thus provide independent evidence as to whether Csmd1 is a QTG. The ability to efficiently obtain a genome-wide significant association between a single gene and a complex behavioral trait vividly demonstrates the potential of this approach.

The success of our approach highlights the utility of AILs, which was first proposed by Darvasi and Soller (1995). In addition to revealing the potential of an AIL, our results also emphasize the importance of a statistical model that correctly accounts for relatedness. Our simulations showed that a simple regression model that did not account for relatedness in conjunction with a simple permutation test to estimate significance resulted in extremely poor control of the type I error rate (Table 3). When we applied such an approach to our data, many loci appeared to show significant associations (Figure 3 and Figure S1); however, we presume that these results contain an excess of type I errors. It is our intuition that accounting for relatedness in the model should also increase power because it more correctly accounts for the relevant sources of variance; however, this was not directly tested by our simulations. Because these simulations used the pedigree from our AIL, they do not address the more general question of whether permutation in conjunction with mixed models would perform well in other situations (but see Aulchenko et al. 2007). On the basis of our data we conclude that, for pedigrees similar to ours, regression followed by simple permutation, which has been widely used by other investigators to analyze AILs, is an inappropriate strategy for the analysis of AILs.

This problem has been understood by human geneticists for some time (McPeek 2000) and has recently been noted by model organism geneticists (Peirce et al. 2008; Valdar et al. 2009). We emulated the approach of Abney et al. (2000) that was developed for QTL mapping in Hutterites, a human population isolate that is conceptually somewhat similar to an AIL. This approach accounts for relatedness using a polygenic model that includes additive, dominance, and inbreeding coefficients. While our AIL was bred with the goal of minimizing inbreeding, all individuals share multiple common ancestors. Therefore, dominance and inbreeding should be considered when modeling the polygenic effects. We used standard model selection criteria to determine which of these variance components to include in our model. To our knowledge this is the first time that this approach has been applied to model organisms.

Other models have been previously employed to address similar issues. For example, a chicken AIL was analyzed using a model in which the family mean is included in the model to account for relatedness (Jennen et al. 2005). A polygenic model that includes only the additive genetic variance was used to account for relatedness in complex pedigrees (Aulchenko et al. 2007; Valdar et al. 2009). A philosophically different approach is to use model selection and model averaging of multiple QTL models with the expectation that this will account for relatedness (Valdar et al. 2009). Several of these approaches have the advantage of not requiring knowledge of the pedigree. We focused on this AIL partially because the pedigree was known. This provided a means of testing the importance of incorporating pedigree information. Our methods can be extended to use genotype data, rather than pedigree data, to estimate identity coefficients. This would allow our approach to be applied to other populations such as heterogeneous stocks (Valdar et al. 2006), outbred stocks (Yalcin et al. 2004; Macdonald and Long 2007; Ghazalpour et al. 2008), or wild populations (Laurie et al. 2007), in which full pedigree information is unavailable.

Our results suggest that if relatedness is accounted for in the model, then simple permutation would provide an acceptable (though not optimal) means to control false positive rates (Table 3). The present results do not address whether this will be true in all cases; however, Aulchenko et al. (2007) suggested that permutation is broadly applicable in such situations. Peirce et al. (2008) proposed a method called genome reshuffling for advanced intercross permutation (GRAIP) for analyzing an AIL in the absence of pedigree information. In GRAIP, a regression model that does not account for relatedness is used in conjunction with a nested permutation approach. We also considered a simple regression model in conjunction with gene dropping (Figure 3, right), which is similar to GRAIP, but concluded that this approach suffered from at least two weaknesses. First, the results obtained from regression and our mixed model were somewhat different (Figure 3 and Figure S1), and it is our intuition that the mixed model should provide better power because it more accurately accounts for the true sources of variance. Second, regression paired with gene dropping was not completely satisfactory in controlling type I error rates (Table 3). On the basis of these results we conclude that relatedness should be addressed in the model rather than being viewed as purely a concern for estimation of significance thresholds.

Most prior QTL studies in model organisms used a multistage approach in which an initial course-mapping step is followed up by one or more fine-mapping steps (Darvasi 1998). We developed a procedure to integrate data from F₂ and AIL studies to facilitate such an approach. In cases where phenotyping is expensive relative to genotyping, it may be preferable to skip the course-mapping step and to instead study only highly recombinant subjects. As discussed above, course mapping sometimes identifies regions that contain multiple small QTL (e.g., Figure 4, chromosome 17) and fine-mapping studies may sometimes identify QTL that are not observed in course mapping (e.g., Figure 4, chromosome 5). Both situations suggest that it may be preferable to forgo course mapping in favor of fine mapping, which would represent a significant paradigm shift.

When breeding an AIL, the goal is to minimize relatedness and maximize the effective population size. In practice relatively simple breeding programs are well suited to this task (Rockman and Kruglyak 2008). Certain model organisms (e.g., Drosophila) can easily be maintained in very large numbers (Macdonald and Long 2007). If individuals are drawn from a sufficiently large population, relatedness can probably be ignored (Voight and Pritchard 2005). When working with mammalian model organisms, it is expensive and thus impractical to maintain very large breeding populations. As a result, laboratory breeding colonies are typically small, and experimental subjects share close familial relationships. In these cases, accounting for relatedness in the model will be essential to obtain statistically robust results.

Whereas F₂ crosses of inbred model organisms have been extremely effective for identifying QTL, they are inherently ill suited for identifying the underlying QTGs. GWAS in humans have made it clear that populations with large numbers of accumulated recombinations are better suited for this purpose. GWAS in humans are hindered by a multitude of rare variants (Manolio et al. 2009). Some of the alleles that segregate between the two inbred strains used to create our AIL may be rare in ancestral wild populations; however, for purposes of mapping QTL, AILs present a much simpler situation in which all alleles that are polymorphic between the two inbred strains should have relatively high allele frequencies in the AIL, provided that drift or inadvertent selection has not had a major effect (discussed further in File S1). Furthermore, human GWAS are confounded by numerous environmental factors that might interact with alleles and thereby reduce power (Manolio et al. 2009). In contrast, model organisms provide superior control of environmental factors. The extent to which these two advantages might improve the results of QTL mapping studies in model organisms remains to be determined.

In summary, we introduce a method of analyzing an AIL that properly controls type I errors while retaining enough power to identify single-gene intervals with genome-wide significance. We identified small regions that may underlie differences in behavior following administration of saline or methamphetamine. Results such as these would not be expected in similarly sized human GWAS. This method should work across different phenotypes and model organisms. Our approach combines the superior resolution typical of human GWAS and the experimental advantages of model organisms.