Abstract
Inactivation of L-type Ca channels (LTCC) is regulated by both Ca and voltage-dependent processes (CDI and VDI). To differentiate VDI and CDI, several experimental and theoretical studies have considered the inactivation of Ba current through LTCC (IBa) as a measure of VDI. However, there is evidence that Ba can weakly mimic Ca, such that IBa inactivation is still a mixture of CDI and VDI. To avoid this complication, some have used the monovalent cation current through LTCC (INS), which can be measured when divalent cation concentrations are very low. Notably, INS inactivation rate does not depend on current amplitude, and hence may reflect purely VDI. However, based on analysis of existent and new data, and modeling, we find that INS can inactivate more rapidly and completely than IBa, especially at physiological temperature. Thus VDI that occurs during IBa (or ICa) must differ intrinsically from VDI during INS. To account for this, we have extended a previously published LTCC mathematical model of VDI and CDI into an excitation-contraction coupling model, and assessed whether and how experimental IBa inactivation results (traditionally used in VDI experiments and models) could be recapitulated by modifying CDI to account for Ba-dependent inactivation. Thus, the view of a slow and incomplete INS inactivation should be revised, and INS inactivation is a poor measure of VDI during ICa or IBa. This complicates VDI analysis experimentally, but raises intriguing new questions about how the molecular mechanisms of VDI differ for divalent and monovalent currents through LTCCs.
Keywords: L-type calcium current, Voltage-dependent inactivation, Calcium-dependent inactivation Barium, Non specific current
1. INTRODUCTION
The L-type Ca current (ICa) contributes to the action potential plateau and initiates excitation-contraction coupling (ECC) in cardiac myocytes (Bers, 2001). It is conducted by CaV1.2 channels consisting of a pore-forming α1C subunit, with four homologous domains of six transmembrane segments, in association with β and α2-δ subunits (Catterall, 2000). The C terminal domain of the α1C subunit contains several regulatory sites, such as a PKA phosphorylation site, an EF-hand region and an IQ motif at which calmodulin (CaM) can bind.
Cardiac ICa is rapidly activated by membrane depolarization, whereas inactivation of L-type Ca channels (LTCC) is regulated by both Ca- and voltage-dependent inactivation (CDI and VDI) (Lee et al., 1985). CDI is due to binding of Ca to CaM (Peterson et al., 1999; Zuhlke et al., 1999), which causes a channel conformational change that prevents the EF-hand in the C-terminus from interacting with the cytosolic I-II linker, which then occludes the channel pore, thus accelerating inactivation (Cens et al., 2006). CDI is an important feedback mechanism that limits the amount of Ca entry during each Ca transient, regulates sarcoplasmic reticulum (SR) Ca load and modulates action potential duration (Bers, 2001). Indeed, prevention of CDI by expression of a mutant Ca-insensitive CaM in adult cardio-myocytes induces a dramatic (4- to 5-fold) prolongation of the cardiac action potential (Alseikhan et al., 2002). Computational analysis also identified CDI as the key player in shortening the action potential when external [Ca] is increased (Grandi et al., 2009). The physiological significance of VDI is illustrated by the dramatic consequences of Timothy syndrome (Brunet et al., 2009; Splawski et al., 2005; Splawski et al., 2004), which impairs VDI and causes severe ventricular arrhythmias (and dysfunction in other tissues, e.g. brain).
ICa inactivates with a biexponential time course when Ca is the charge carrier, and it has been widely assumed that the initial fast decay represents CDI, and the slower phase reflects VDI. During ECC, with normal SR Ca release and Ca transients, local [Ca]i near the L-type Ca channel is elevated and inactivation is rapid (Fig. 1A top ICa trace, t1/2 = 17 ms). When Ca transients are abolished (e.g. by ryanodine or very strong [Ca]i buffering), ICa inactivation is slower (Fig. 1A, t1/2 = 37 ms) and reflects a small rise in local [Ca]i near the mouths of Ca channels due to Ca entering via the channels themselves. In addition to Ca LTCC allow permeation by other ions including Na, K, Sr, Cs, Ba, depending on ionic conditions, but inactivation is slower than with Ca and monoexponential when Ba, Sr, or Na are the charge carrier.
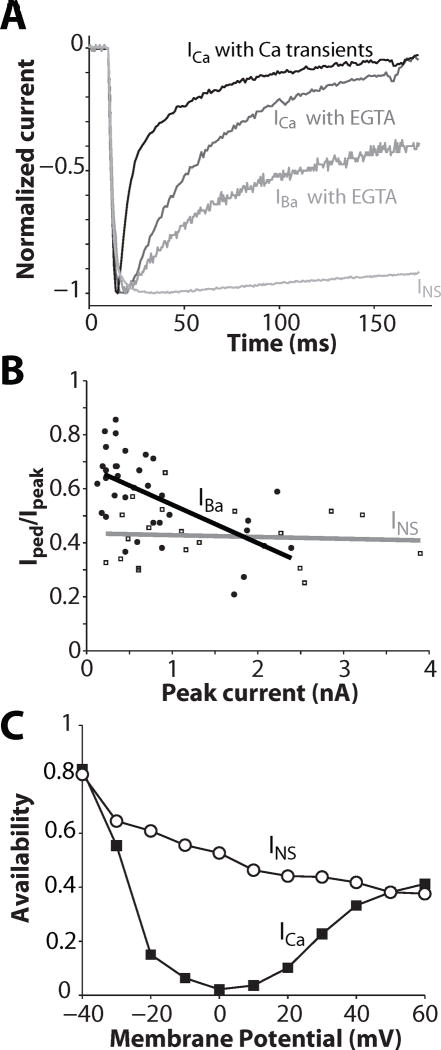
Figure 1.
ICa inactivation: role of Ca released from the SR and of Ca permeating LTCC; IBa and INS inactivation. A. Normalized Ca, Ba and Na currents (ICa, IBa & INS) measured at 0 mV (except INS at −30 mV to obtain comparable activation state). ICa was recorded under conditions where normal SR Ca release and Ca transients were allowed to occur (perforated patch) or prevented (ruptured patch with cells dialyzed with 10 mM EGTA). IBa was also recorded in absence of Ca release and transient. INS was measured in divalent-free conditions (10 mM EDTA inside and out). B: Ratio between pedestal and peak current, in response to a 1000 ms- depolarizing step to 0 mV, is plotted against current amplitude of IBa and INS. The lines represent linear regressions. Data are from Brunet et al. (Brunet et al., 2009). C. INS and ICa availability through Ca channels (at −10 mV) after 500 ms pulses to the indicated Em in guinea-pig ventricular myocytes (redrawn from (Hadley and Hume, 1987)).
To differentiate VDI from CDI, several experimental and theoretical studies have used inactivation of Ba current via LTCC (IBa) as a measure of VDI (Cens et al., 2006; Lee et al., 1985; Mahajan et al., 2008; Peterson et al., 2000; Thiel et al., 2008). However, there is evidence that Ba can weakly mimic Ca (Ferreira et al., 1997), such that IBa inactivation is still a mixture of CDI and VDI, and IBa inactivation depends on current amplitude (Fig. 1A, t1/2 = 161 ms and Fig. 1B). To avoid this complication, some have used the monovalent cation current through LTCC (INS), which can be measured only when divalent cation concentrations are very low (Brunet et al., 2009; Hadley and Hume, 1987; Hryshko and Bers, 1992; Sun et al., 2000; Yuan et al., 1996). That is, extracellular Ca and Mg block INS (ki ~1 and 50 μM respectively). Notably, INS inactivation rate does not depend on current amplitude (Fig. 1B, grey line) and hence could reflect purely VDI (Brunet et al., 2009). Inward INS has been reported to inactivate very slowly (Fig. 1A, t1/2 >500 ms at Em = −30 mV). Even at more positive Em where inactivation is faster it is still incomplete (Fig. 1C). Note that extracellular divalent cations screen external membrane surface charge, shifting the membrane field and channel gating to more positive Em. Thus, the activation state of INS at −30 mV is comparable to that of ICa or IBa at ~0 mV in Fig. 1A (Bers, 2001; Hadley and Hume, 1987; Linz and Meyer, 1998).
In the present study, we sought to determine whether INS or IBa is appropriate for the study of the VDI component of ICa. New and existing data, and modeling, suggest that VDI of INS is faster and more complete than IBa inactivation, and that IBa exhibits Ba-dependent inactivation. Thus, neither IBa nor INS are accurate measures of VDI for ICa, although IBa VDI is largely like ICa VDI. This complicates VDI analysis experimentally, but raises intriguing new questions about how the molecular mechanisms of VDI differ for divalent and monovalent currents through LTCCs.
2. METHODS
2.1 INS measurements
Ventricular myocytes were dissociated enzymatically from hearts of adult male New Zealand White rabbits using a standard Langendorff perfusion procedure, as has been described previously (Bassani et al., 1994). Isolated cells were allowed to adhere to laminin-treated coverslips and were used acutely.
Monovalent current via LTCCs was recorded in whole cell ruptured-patch mode as described previously (Yuan et al., 1996). Cells were held at -65 mV and stimulated with infrequent (<0.1 Hz) depolarizing steps. The bathing solution contained (mM): 10 NaCl, 6 CsCl, 5 EDTA, 120 TEA-Cl, 10 glucose and 10 H-Hepes, adjusted to pH 7.4 with TEA-OH. The pipette solution contained (mM): 3 NaCl, 120 CsCl, 10 EGTA, 5 MgATP, 0.3 GTP, buffered to pH 7.2 with 20 mM H-Hepes and CsOH. Importantly, in recording INS EDTA was used to ensure chelation of both Ca and Mg, to prevent Mg from blocking the current (ki ~ 50 μM (Hryshko and Bers, 1992; Matsuda, 1986)). A measured liquid junction potential of 5 mV was corrected during analysis. Experiments were conducted at room temperature (22°C); a few recordings were obtained at 25°C and 35°C as specified in the results. Current decay was fitted with a monoexponential time constant (τ), with a steady-state plateau at the end of the voltage step. Use of biexponential functions did not improve the fitting.
2.2 Model development
We used a minimal Markovian model for ICa (Figure 2) that was developed previously by the Weiss group (Mahajan et al., 2008) based on ICa and IBa measurements in rabbit ventricular myocytes at physiological temperature. Inactivation of ICa is described as occurring via a voltage-dependent pathway (VDI) and an ion-dependent pathway (IDI). In the Mahajan formulation IBa inactivation was considered to define the VDI pathway. Here, we used both their 5-state model of IBa and an alternative 7-state IBa model, which uses the IDI pathway with parameters tuned to mimic a reduced affinity of Ba vs. Ca for CaM (i.e. [Ba] was reduced by a factor 1, 3, 10, 20, 30, 50 100 in the expression of the ion-dependent transition rates, Fig.2). We scaled the permeability (and single channel conductance) of LTCCs for Ba as reported in (Bers, 2001). Models of IBa were inserted in a model of ECC (Mahajan et al., 2008).
Figure 2.
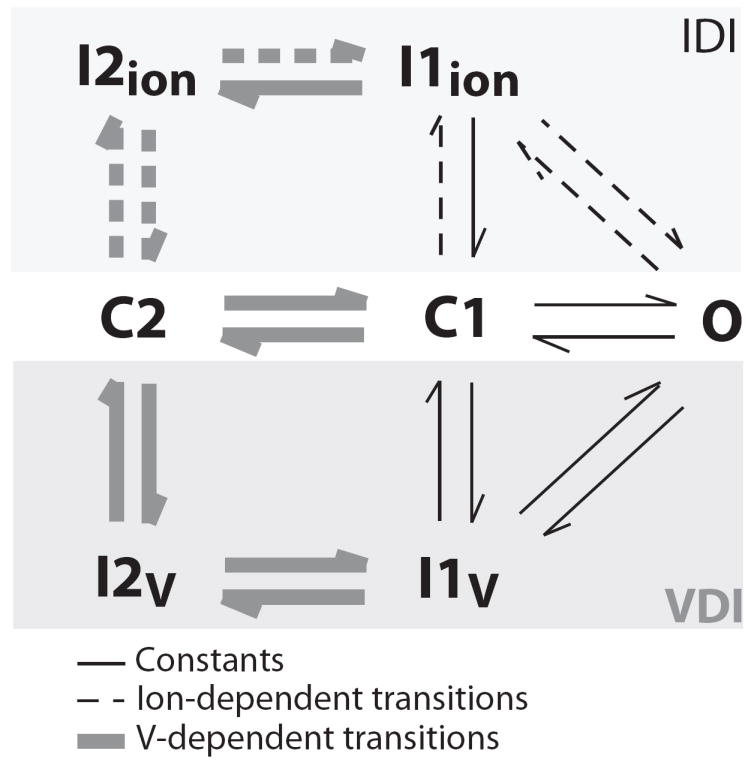
Seven-state Markov model of ICa. Grey lines correspond to voltage-dependent transitions and dashed lines correspond to ion-dependent transitions. A 5-state model (5 lower states) without ion-dependent transitions was used for comparison in some simulations.
Model differential equations were implemented in Matlab (Mathworks Inc., Natick, MA, U.S.A.) and solved numerically using a variable order solver (ode15s) (Shampine and Reichelt, 1997). The digital cell was stimulated with voltage steps replicating the experimental protocols.
3. RESULTS
3.1 Inactivation kinetics
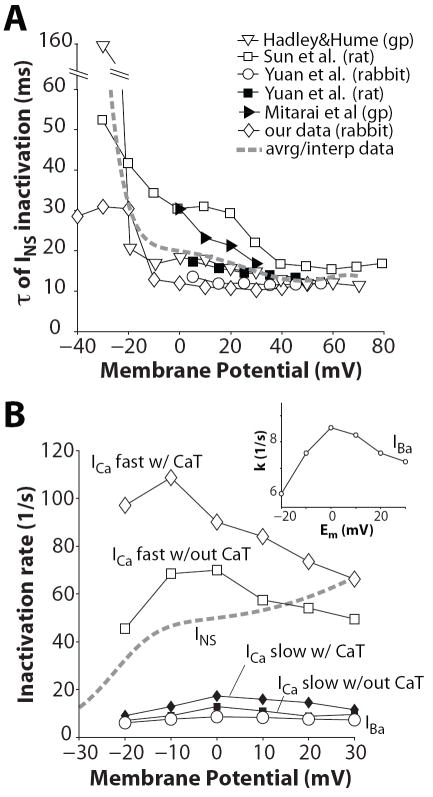
Typical recordings of INS (with Na and Cs as charge carriers) are shown in Fig. 3A, elicited by depolarizing pulses described in inset. With increasing depolarization, the net current changes from inward to outward, due to reduction in the driving force for Na and an increased driving force for Cs (INS reversal potential is about -4.5 mV). We characterized INS kinetics by considering the time course of current decay throughout the duration of depolarization. Inactivation τs are reported in Fig. 3B for each depolarization Em. Current decay is slower at Em < −10 mV, and is hastened as the voltage steps are more depolarized (and the current becomes outward). Nevertheless, INS inactivation τs measured in rabbit ventricular myocytes at room temperature are relatively fast (especially compared to the INS trace in Fig. 1A). INS inactivation was assessed in the same cell at two different temperatures (25 and 35°C, Figure 3 C vs. D). Availability curves were recorded using various durations of the inactivating pre-pulses, and τ of inactivation was estimated as described in (Findlay, 2002b). At physiological temperature INS inactivated more completely and rapidly than at room temperature. From these measurements, we calculated an average Q10 of ~1.85 for INS inactivation kinetics over the full range of Em (although Q10 was larger at more negative Em; ~2.3 at -20 mV). We compared our data (corrected at 37°C, Figure 4A, ◇) with previously published inactivation τ and found concordance with several previous studies of INS inactivation.
Figure 3.
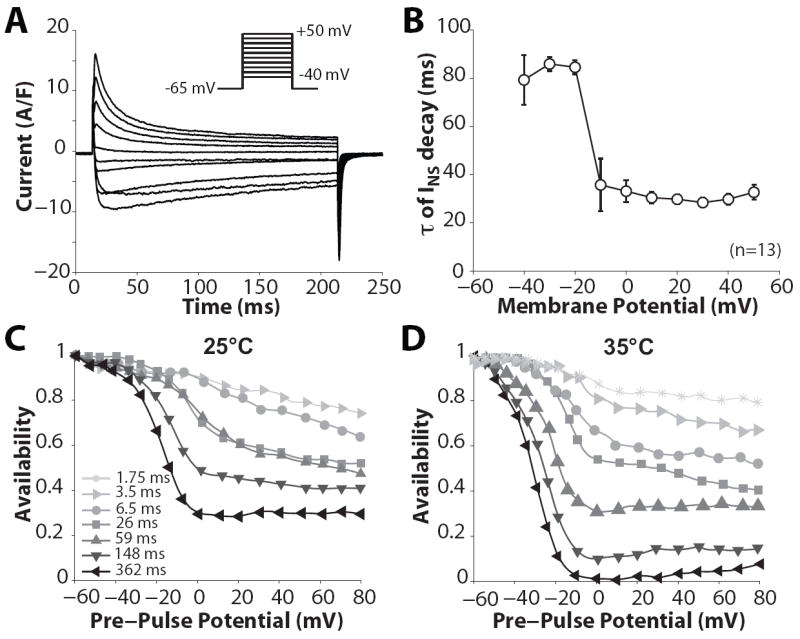
INS inactivation. A: representative recordings of membrane currents in rabbit ventricular myocytes elicited by 200-ms steps (inset) from -65 mV to the indicated Em. B: τ of INS decay. C, D: INS availability was recorded at 25 °C and 35 °C following pre-pulse steps of 362, 148, 59, 26, 6.5, 3.5, 1.75 ms duration. Data from C and D have been transposed onto a time scale (availability against prepulse interval) and τs were calculated as in (Findlay, 2002b).
Figure 4.
A: Voltage dependence of the decay time of INS. Data from Mitarai et al. (▸) were collected at physiological temperature. All the other experimental data were obtained at room temperature and here rescaled at 37 °C (Q10=1.85). The dashed line is obtained by interpolation of the averaged τs. B: Rates of the fast (◇,□) and slow (◆,■) components of a double exponential fit of ICa decay vs. Em recorded by Mahajan et al. (Mahajan et al., 2008) with and without Ca transient (CaT). Rates of IBa (○ and inset) and INS (dashed lines) inactivation are obtained from monoexponential fits of current decay.
INS τ values were averaged (broken curve in Fig. 4A) and plotted vs. Em as inactivation rate constants (k= 1/τ) in Figure 4B, along with rate constants of inactivation of IBa and ICa (bi-exponential for ICa from (Mahajan et al., 2008)). ICa inactivation is faster when SR Ca release is present (top curve). Notably, INS inactivation was much faster than IBa inactivation, which was comparable to the slow component of ICa inactivation. INS inactivation becomes faster with increasing depolarization consistent with VDI, and gets faster when the current is outward. Thus, INS inactivates more rapidly and completely than IBa at 35-37°C (even if one accounts for surface charge effects). Thus, these cannot both reflect the same VDI process. Moreover if INS exhibits pure VDI, then the rate of IBa inactivation (which may include some weak CDI) would have to be faster than INS inactivation (i.e. kVDI + f(kCDI)). So INS inactivation is too fast to reflect the VDI that occurs during IBa. On the other hand, IBa is not purely VDI either, because the rate of inactivation has a bell-shaped Em-dependence (Fig. 4B inset and Fig. 6, circles, (Mahajan et al., 2008)) and increases with larger peak Ba current amplitude, as shown in Fig. 1B (Brunet et al., 2009).
Figure 6.
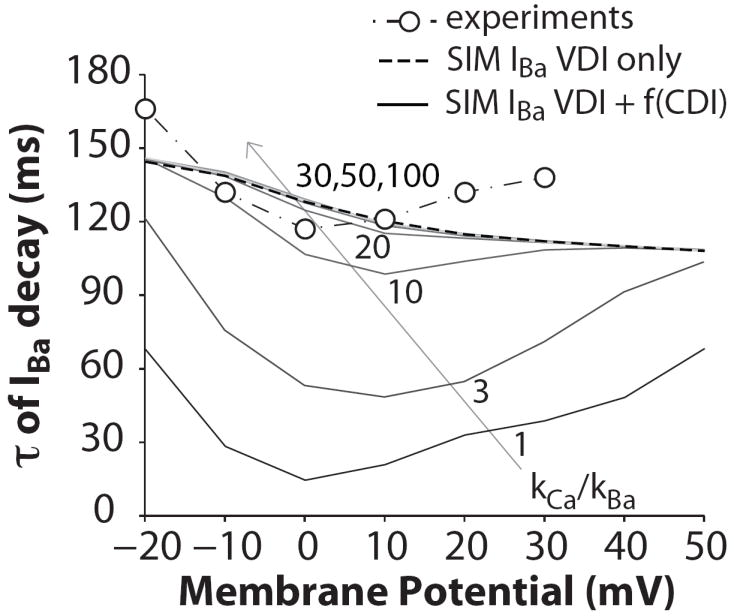
τs of IBa decay at the indicated Em when IBa inactivation is simulated as independent of Ba ion flux (VDI only, dashed line) and when Ba affinity for CaM is varied ((VDI+f(CDI)), kCa/kBa equal to 100, 50, 30, 20, 10, 3, 1). Experimental data are from (Mahajan et al., 2008).
We suggest that INS inactivation is VDI, but that it is fundamentally (mechanistically) different from VDI that occurs during IBa or ICa, and may therefore not be useful to characterize the VDI component of ICa. Further, IBa inactivation includes a moderate component of CDI (where Ba substitutes for Ca) and also VDI that is the same as the VDI component of ICa. Indeed, with strong fast intracellular Ca buffering, ICa inactivation is reduced (Katzka and Morad, 1989; Linz and Meyer, 1998) and approaches that seen for IBa.
3.2 Model analysis
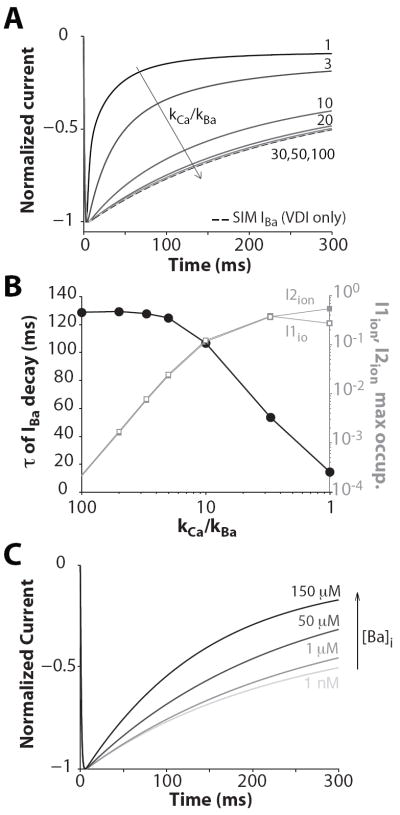
We sought to determine whether and how experimental IBa inactivation (traditionally used in VDI experiments and models) could be recapitulated by extending a previously published model of CDI (Mahajan et al., 2008) to account for Ba-dependent inactivation. To mimic a reduced affinity of Ba (vs. Ca) in CDI, the parameters describing the Ca-dependent transitions (Fig. 2, dashed arrows) were modified to make it 3-100 times less sensitive to [Ba] (vs. [Ca]). In Figure 5A normalized IBa simulated in response to a voltage step to 0 mV are shown. As the apparent affinity of Ba for CaM increases (approaching that of Ca), IBa exhibits faster inactivation (Fig. 5B). The τ of IBa decay (at 0 mV) is ~125 ms when the current inactivation is modeled as Ba-independent (e.g. only including VDI). When Ba affinity is much smaller than that of Ca (20-100 times), the predicted Ba-dependent inactivation is negligible, still indistinguishable from only the 5-state VDI model. Only when the relative kCa/kBa affinity falls to 10 or below does Ba-dependent inactivation become appreciable.
Figure 5.
IBa inactivation. A: Normalized IBa traces obtained when applying a voltage step to 0 mV (from a holding potential of -80 mV) and kCa/kBa is equal to 100, 50, 30, 20, 10, 3, 1 (VDI+f(CDI)). IBa was also simulated as independent of Ba ion flux (VDI only, dashed line). B: Left ordinate: τ of IBa decay decreases as the simulated Ba affinity for CaM is increased (i.e. kCa/kBa decreased). Right ordinate: Ion(Ba)-dependent state occupancy during IBa decay (in response to a voltage step to 0 mV) is enhanced with increasing affinity of Ba for CaM (i.e., decreasing kCa/kBa). C: Effect of intracellular Ba accumulation on current inactivation. Normalized IBa traces obtained in response to a voltage step to 0 mV are shown in correspondence of various levels of [Ba]i (from 1 nM to 150 μM).
Figure 5B also shows the maximal probability of occupancy of the two Ba-dependent inactivation states (filled and open squares). The channel never visits these states by design when only VDI is implemented, and state occupancies are infrequent when Ba affinity for CaM is low. Ion-dependent inactivated states are more likely to be occupied when Ba affinity increases (e.g. when kCa/kBa is equal to 10, τ is reduced by about one fifth). When Ba affinity equals that of Ca, τ of IBa inactivation is the same as ICa (without SR Ca release), and the probabilities of occupancy of I1ion and I2ion are maximal.
When Ba is used instead of Ca in experiments, the normal myocyte Ca extrusion pathways do not remove Ba well, so that intracellular Ba would accumulate over several beats. Simulations show that the τ of IBa decay decreases as intracellular [Ba] increases (Fig. 5C), whereas it is unchanged when using the 5-state VDI only IBa model (not shown).
In Figure 6 the effect of Ba-dependent inactivation is shown over a wide range of voltages. Note that the τ for ICa (or IBa at kCa/kBa =1) reflects the strong CDI seen for ICa, whereas the curve for kCa/kBa =10 approaches the shape seen for IBa measurements. While the model is an imperfect match to the data, this simple version provides a useful framework for separating VDI and CDI for ICa and IBa.
4. DISCUSSION
ICa plays an essential role in cardiac electrophysiology, affecting action potential and arrhythmogenesis, and also is central to ECC, by controlling SR Ca release and contributing to the SR replenishment (Bers, 2001). Inactivation of ICa is both Ca- and Em- dependent, and there is evidence that (1) the degree and the rate of inactivation depends on the amount of Ca current (Brehm and Eckert, 1978; Peterson et al., 2000); (2) SR Ca release increases the rate of ICa inactivation (Adachi-Akahane et al., 1996; Puglisi et al., 1999); (3) inactivation is reduced when Ba is the current carrier (Ferreira et al., 1997; Mahajan et al., 2008; Sun et al., 1997). In cardiac myocytes, whether there is true CDI when SR Ca release is prevented is debated. Em-dependent inactivation is indicated by the current decay when monovalent cations are the charge carrier. In these conditions, the rate and the extent of current inactivation do not depend on current amplitude (Brunet et al., 2009).
Based on these observations, INS and IBa are commonly used in experiments and models as a surrogate of VDI. The aim of this study was to determine whether INS or IBa inactivation are a true measure of VDI for ICa, and if not to develop a practical model incorporating CDI and VDI.
4.1 Monovalent current
INS inactivates incompletely at room temperature (Hadley and Hume, 1987; Sun et al., 1997; Sun et al., 2000), but when the temperature was raised to 30°C the extent of inactivation was greater (Hryshko and Bers, 1992). Inactivation was even more complete at physiological temperature (compare Figure 3C to 3D). Mitarai et al. (Mitarai et al., 2000) also showed strong VDI of INS at physiological temperature (Figure 4, ▸), and rescaling available experimental data to 37°C gave comparable results. Mitarai et al. (Mitarai et al., 2000) explained some previous work reporting slower INS decay by suggesting that β-adrenergic stimulation could slow LTCC inactivation (as shown previously (Yuan and Bers, 1995)). Indeed, when measuring INS in the presence of extracellular divalent cations (which partially block INS), isoproterenol was added to compensate for INS reduction (e.g. (Linz and Meyer, 1998; Matsuda, 1986)). However, since divalent cations can strongly block INS, it is debatable whether intrinsic INS gating can be measured in the presence of divalent cations in the bathing solution.
There are two tacit assumptions usually made when using INS as an experimental model to study ICa VDI: 1) the absence of ion-dependent inactivation, which seems appropriate, and was recently confirmed by (Brunet et al., 2009); 2) VDI of INS, IBa and ICa are the same process, which we now think may not be the case (see 4.3 and 4.4 for discussion).
4.2 Ba current
The substitution of Ba ions for Ca has been widely used to separate VDI from CDI of the macroscopic LTCC currents, and this is pragmatic because Ba produces only modest ion-dependent inactivation (Brunet et al., 2009; Ferreira et al., 1997) and probably has similar (but not identical) binding properties to Ca in the pore. However, IBa inactivation depends on Ba flux, and it seems clear now that Ba can recapitulate a weak version of CDI. Ba is known to complex with CaM and activate interaction with CaM targets (Ozawa et al., 1999; Yamazaki et al., 1996), but its apparent affinity in other systems has typically been ≥100-fold lower than for Ca. While our change in rate constants that produces appropriate IBa CDI could be construed to represent only a ~10-fold reduction in affinity, this lower value should not be taken to imply an actual affinity difference in the classical biochemical sense.
To account for the moderate Ba-dependent inactivation, we have extended a previously published LTCC mathematical model of VDI and CDI into an ECC model, and assessed whether and how experimental IBa inactivation results could be recapitulated by modifying CDI to account for Ba-dependent inactivation. We found that making 10-fold reductions in the Ca-dependent transition rates (in Fig 2) resulted in appropriate Ba-dependent IBa inactivation. Sun et al. (Sun et al., 2000) similarly fit their data of IBa by decreasing the Ba association constant to 10% of that of Ca. Thus their model suggested a smaller reduction of Ba affinity vs. Ca compared to Ferreira et al. (Ferreira et al., 1997), where the affinity for the inactivation site was reckoned to be ~ 100 times lower for Ba than Ca for Cav1.2 using a heterologous expression system. Reasons that the relatively modest 10-fold reduction in Ba- vs. Ca-dependent inactivation (vs. ≥100-fold expected for CaM binding) could have to do with a) the way CaM is prebound to the LTCC, b) potentially weaker local Ba vs. Ca buffering, c) higher single channel conductance for Ba, d) dynamic considerations during current flow (Ba may equilibrate faster than Ca). In any event, given the Ba-dependent inactivation implemented here, one could derive a slower VDI model, which should be a more faithful representation of purely VDI during ICa. This may be an important distinction when one seeks to dissect the relative roles of Ca and Em in mediating normal function and pathophysiology (e.g. arrhythmogenesis).
4.3 Ba vs. Na current via LTCCs
Some studies in guinea pig ventricular myocytes showed similar inactivation of Ba, Sr, and Na currents (Findlay, 2002a), at least at room temperature. Analogously, Sun et al. (Sun et al., 2000) also reported similar inactivation τ for INS and IBa in rat cardiomyocytes (at room temperature), whereas INS (and ISr) inactivated more slowly than IBa in human atrial cells at 23°C (Sun et al., 1997). Mahajan et al. measured IBa (and ICa) in rabbit cardiomyocytes at physiological temperature and reported that IBa inactivates incompletely with a monoexpo-nential decay with τ ~150 ms (with little voltage-dependence) in the absence of β-adrenergic stimulation. Here, we found that INS inactivation is accelerated as temperature increases (especially at negative Em, where INS inactivation is slowest). Thus, we find that INS can inactivate more rapidly and completely than IBa, especially at physiological temperature (Figure 3), suggesting that VDI that occurs during IBa (or ICa) must differ intrinsically from VDI during INS. During ICa and IBa flow, it is thought that the channel is essentially always occupied by at least one divalent cation occupying the pore (Yang et al., 1993), and this binding prevents monovalent permeation. We suggest that in the absence of divalent cation occupancy (during INS), VDI of the LTCC is fundamentally different, exhibiting steeper Em-dependence, which is faster than when divalent cations occupy the channel pore.
4.4 Ca vs. V-dependent inactivation
Some studies have suggested that VDI predominates over CDI in cardiac myocytes (Findlay, 2002a; Findlay, 2002b; Findlay et al., 2008), but most studies suggest that CDI predominates under physiological conditions, especially where local SR Ca release amplifies Ca influx (Adachi-Akahane et al., 1996; Linz and Meyer, 1998; Pelzer et al., 1990; Puglisi et al., 1999; Shannon et al., 2000; Sun et al., 1997; Yuan and Bers, 1995). As indicated in Figs. 1A and 4B, it is clear that ICa inactivates much faster than IBa, even when there is no SR Ca release. Indeed, the integrated Ca entry for ICa without SR Ca release in Fig. 1A (normalizing to peak current) is 61% of that for IBa, and with SR Ca release it drops to 32% of that for IBa. Similarly, during the cardiac action potential SR Ca release diminished integrated Ca influx via ICa by approximately 50% at both 25°C and 35°C (Puglisi et al., 1999) whereas peak ICa hardly changed. These results indicate that CDI is dominant in ICa inactivation in a physiological setting, but this also suggests that VDI is not negligible.
In most studies, including the present model of ICa inactivation, it is assumed that CDI and VDI are independent processes. However, based on single channel recordings, Josephson et al. concluded that Ca- and voltage- dependent mechanisms involved in the decay of the ensemble LTCC current were highly interdependent, so that both the slow and fast phase of ICa decay are related to CDI (Josephson et al., 2009). Thus, it is possible that the two processes interact, and VDI when monovalent ions serve as charge carrier is intrinsically different from IBa and ICa VDI.
4.5 Conclusions
Our work indicates that neither IBa nor INS reflect pure VDI for ICa. This raises new questions of whether fast inactivation of INS is due to the absence of divalent cations that bind in the channel pore, or whether inactivation of inward INS differs from outward INS (e.g. due to the intracellular milieu). The main limitation to the use of IBa as a measure of VDI is its ability to modestly mimic Ca-dependent inactivation. Modeling results predicted a detectable Ba-dependent inactivation (i.e., bell-shaped dependence on Em) when apparent Ba affinity for CaM is one tenth than that of Ca. Nevertheless, if intracellular Ba accumulation is avoided (and if IBa amplitude is kept small), IBa is probably a better VDI model for ICa than is INS.
Acknowledgments
Sources of support: This work was supported by NIH grants HL30077 and HL80101 to DMB and the Italian Ministry of University and Research (Italian National Project, PRIN2007) to SS.
- ICa
L-type Ca current
- IBa
Ba current through LTCC
- INS
Non specific (monovalent) current through LTCC
- LTCC
L-type Ca channel
- CDI
Ca-dependent inactivation
- IDI
Ion-dependent inactivation
- VDI
Voltage-dependent inactivation
- ECC
Excitation-contraction coupling
- SR
Sarcoplasmic reticulum
- τ
time constant
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Eleonora Grandi, Email: egrandi@ucdavis.edu.
Stefano Morotti, Email: smorotti@gmail.com.
Kenneth S. Ginsburg, Email: ksginsburg@ucdavis.edu.
Stefano Severi, Email: stefano.severi@unibo.it.
Donald M. Bers, Email: dmbers@ucdavis.edu.
References
- Adachi-Akahane S, Cleemann L, Morad M. Cross-signaling between L-type Ca2+ channels and ryanodine receptors in rat ventricular myocytes. J Gen Physiol. 1996;108:435–54. doi: 10.1085/jgp.108.5.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alseikhan BA, DeMaria CD, Colecraft HM, Yue DT. Engineered calmodulins reveal the unexpected eminence of Ca2+ channel inactivation in controlling heart excitation. Proc Natl Acad Sci U S A. 2002;99:17185–90. doi: 10.1073/pnas.262372999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassani JW, Bassani RA, Bers DM. Relaxation in rabbit and rat cardiac cells: species-dependent differences in cellular mechanisms. J Physiol. 1994;476:279–93. doi: 10.1113/jphysiol.1994.sp020130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bers DM. Excitation-Contraction Coupling and Cardiac Contractile Force. Kluwer Academic Press; Dordrecht, The Netherlands: 2001. p. 427. [Google Scholar]
- Brehm P, Eckert R. Calcium entry leads to inactivation of calcium channel in Paramecium. Science. 1978;202:1203–6. doi: 10.1126/science.103199. [DOI] [PubMed] [Google Scholar]
- Brunet S, Scheuer T, Catterall WA. Cooperative regulation of Cav1.2 channels by intracellular Mg2+, the proximal C-terminal EF-hand, and the distal C-terminal domain. J Gen Physiol. 2009;134:81–94. doi: 10.1085/jgp.200910209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catterall WA. Structure and regulation of voltage-gated Ca2+ channels. Annu Rev Cell Dev Biol. 2000;16:521–555. doi: 10.1146/annurev.cellbio.16.1.521. [DOI] [PubMed] [Google Scholar]
- Cens T, Rousset M, Leyris JP, Fesquet P, Charnet P. Voltage- and calcium-dependent inactivation in high voltage-gated Ca2+ channels. Prog Biophys Mol Biol. 2006;90:104–117. doi: 10.1016/j.pbiomolbio.2005.05.013. [DOI] [PubMed] [Google Scholar]
- Ferreira G, Yi J, Rios E, Shirokov R. Ion-dependent Inactivation of Barium Current through L-type Calcium Channels. J Gen Physiol. 1997;109:449–461. doi: 10.1085/jgp.109.4.449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Findlay I. Voltage- and cation-dependent inactivation of L-type Ca2+ channel currents in guinea-pig ventricular myocytes. J Physiol. 2002a;541:731–740. doi: 10.1113/jphysiol.2002.019729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Findlay I. Voltage-dependent inactivation of L-type Ca2+ currents in guinea-pig ventricular myocytes. J Physiol. 2002b;545:389–97. doi: 10.1113/jphysiol.2002.029637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Findlay I, Suzuki S, Murakami S, Kurachi Y. Physiological modulation of voltage-dependent inactivation in the cardiac muscle L-type calcium channel: a modelling study. Prog Biophys Mol Biol. 2008;96:482–98. doi: 10.1016/j.pbiomolbio.2007.07.002. [DOI] [PubMed] [Google Scholar]
- Grandi E, Pasqualini FS, Pes C, Corsi C, Zaza A, Severi S. Theoretical investigation of action potential duration dependence on extracellular Ca2+ in human cardiomyocytes. J Mol Cell Cardiol. 2009;46:332–42. doi: 10.1016/j.yjmcc.2008.12.002. [DOI] [PubMed] [Google Scholar]
- Hadley RW, Hume JR. An intrinsic potential-dependent inactivation mechanism associated with calcium channels in guinea-pig myocytes. J Physiol. 1987;389:205–222. doi: 10.1113/jphysiol.1987.sp016654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hryshko LV, Bers DM. Citrate alters Ca channel gating and selectivity in rabbit ventricular myocytes. Am J Physiol. 1992;262:C191–8. doi: 10.1152/ajpcell.1992.262.1.C191. [DOI] [PubMed] [Google Scholar]
- Josephson IR, Guia A, Lakatta EG, Lederer WJ, Stern MD. Ca2+-dependent components of inactivation of unitary cardiac L-type Ca2+ channels. J Physiol. 2009;588:213–23. doi: 10.1113/jphysiol.2009.178343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzka DA, Morad M. Properties of calcium channels in guinea-pig gastric myocytes. J Physiol. 1989;413:175–97. doi: 10.1113/jphysiol.1989.sp017648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KS, Marban E, Tsien RW. Inactivation of calcium channels in mammalian heart cells: joint dependence on membrane potential and intracellular calcium. J Physiol. 1985;364:395–411. doi: 10.1113/jphysiol.1985.sp015752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linz KW, Meyer R. Control of L-type calcium current during the action potential of guinea-pig ventricular myocytes. J Physiol. 1998;513(Pt 2):425–42. doi: 10.1111/j.1469-7793.1998.425bb.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahajan A, Shiferaw Y, Sato D, Baher A, Olcese R, Xie L-H, Yang M-J, Chen P-S, Restrepo JG, Karma A, Garfinkel A, Qu Z, Weiss JN. A Rabbit Ventricular Action Potential Model Replicating Cardiac Dynamics at Rapid Heart Rates. Biophys J. 2008;94:392. doi: 10.1529/biophysj.106.98160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuda H. Sodium conductance in calcium channels of guinea-pig ventricular cells induced by removal of external calcium ions. Pflugers Arch. 1986;407:465–75. doi: 10.1007/BF00657502. [DOI] [PubMed] [Google Scholar]
- Mitarai S, Kaibara M, Yano K, Taniyama K. Two distinct inactivation processes related to phosphorylation in cardiac L-type Ca2+ channel currents. Am J Physiol Cell Physiol. 2000;279:C603–10. doi: 10.1152/ajpcell.2000.279.3.C603. [DOI] [PubMed] [Google Scholar]
- Ozawa T, Sasaki K, Umezawa Y. Metal ion selectivity for formation of the calmodulin-metal-target peptide ternary complex studied by surface plasmon resonance spectroscopy. Biochim Biophys Acta. 1999;1434:211–20. doi: 10.1016/s0167-4838(99)00185-5. [DOI] [PubMed] [Google Scholar]
- Pelzer D, Pelzer S, McDonald TF. Properties and regulation of calcium channels in muscle cells. Rev Physiol Biochem Pharmacol. 1990;114:107–207. doi: 10.1007/BFb0031019. [DOI] [PubMed] [Google Scholar]
- Peterson BZ, DeMaria CD, Adelman JP, Yue DT. Calmodulin is the Ca2+ sensor for Ca2+ -dependent inactivation of L-type calcium channels. Neuron. 1999;22:549–58. doi: 10.1016/s0896-6273(00)80709-6. [DOI] [PubMed] [Google Scholar]
- Peterson BZ, Lee JS, Mulle JG, Wang Y, de Leon M, Yue DT. Critical determinants of Ca2+-dependent inactivation within an EF-hand motif of L-type Ca2+ channels. Biophys J. 2000;78:1906–20. doi: 10.1016/S0006-3495(00)76739-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puglisi JL, Yuan W, Bassani JW, Bers DM. Ca2+ influx through Ca2+ channels in rabbit ventricular myocytes during action potential clamp: influence of temperature. Circ Res. 1999;85:e7–e16. doi: 10.1161/01.res.85.6.e7. [DOI] [PubMed] [Google Scholar]
- Shampine LF, Reichelt MW. The MATLAB ODE Suite. SIAM J Sci Comp. 1997;18:1–22. [Google Scholar]
- Shannon TR, Ginsburg KS, Bers DM. Potentiation of fractional sarcoplasmic reticulum calcium release by total and free intra-sarcoplasmic reticulum calcium concentration. Biophys J. 2000;78:334–43. doi: 10.1016/S0006-3495(00)76596-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Splawski I, Timothy KW, Decher N, Kumar P, Sachse FB, Beggs AH, Sanguinetti MC, Keating MT. Severe arrhythmia disorder caused by cardiac L-type calcium channel mutations. Proc Natl Acad Sci U S A. 2005;102:8089–8096. doi: 10.1073/pnas.0502506102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Splawski I, Timothy KW, Sharpe LM, Decher N, Kumar P, Bloise R, Napolitano C, Schwartz PJ, Joseph RM, Condouris K, Tager-Flusberg H, Priori SG, Sanguinetti MC, Keating MT. CaV1.2 Calcium Channel Dysfunction Causes a Multisystem Disorder Including Arrhythmia and Autism. Cell. 2004;119:19. doi: 10.1016/j.cell.2004.09.011. [DOI] [PubMed] [Google Scholar]
- Sun H, Leblanc N, Nattel S. Mechanisms of inactivation of L-type calcium channels in human atrial myocytes. Am J Physiol. 1997;272:H1625–35. doi: 10.1152/ajpheart.1997.272.4.H1625. [DOI] [PubMed] [Google Scholar]
- Sun L, Fan J, Clark J, Palade P. A model of the L-type Ca2+ channel in rat ventricular myocytes: ion selectivity and inactivation mechanisms. J Physiol. 2000;529:139–58. doi: 10.1111/j.1469-7793.2000.00139.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiel WH, Chen B, Hund TJ, Koval OM, Purohit A, Song L-S, Mohler PJ, Anderson ME. Proarrhythmic Defects in Timothy Syndrome Require Calmodulin Kinase II. Circulation. 2008;118:2225–2234. doi: 10.1161/CIRCULATIONAHA.108.788067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamazaki J, Urushidani T, Nagao T. Barium activates rat cerebellar nitric oxide synthase. Jpn J Pharmacol. 1996;70:351–4. doi: 10.1254/jjp.70.351. [DOI] [PubMed] [Google Scholar]
- Yang J, Ellinor PT, Sather WA, Zhang JF, Tsien RW. Molecular determinants of Ca2+ selectivity and ion permeation in L-type Ca2+ channels. Nature. 1993;366:158–61. doi: 10.1038/366158a0. [DOI] [PubMed] [Google Scholar]
- Yuan W, Bers DM. Protein kinase inhibitor H-89 reverses forskolin stimulation of cardiac L-type calcium current. Am J Physiol. 1995;268:C651–9. doi: 10.1152/ajpcell.1995.268.3.C651. [DOI] [PubMed] [Google Scholar]
- Yuan W, Ginsburg KS, Bers DM. Comparison of sarcolemmal calcium channel current in rabbit and rat ventricular myocytes. J Physiol. 1996;493:733–746. doi: 10.1113/jphysiol.1996.sp021418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuhlke RD, Pitt GS, Deisseroth K, Tsien RW, Reuter H. Calmodulin supports both inactivation and facilitation of L-type calcium channels. Nature. 1999;399:159–62. doi: 10.1038/20200. [DOI] [PubMed] [Google Scholar]