The viscoelastic properties of microvilli are dependent upon the cell surface molecule

Abstract

We studied at nanometer resolution the viscoelastic properties of microvilli and tethers pulled from myelogenous cells via P-selectin glycoprotein ligand 1 (PSGL-1) and found that in contrast to pure membrane tethers, the viscoelastic properties of microvillus deformations are dependent upon the cell-surface molecule through which load is applied. A laser trap and polymer bead coated with anti-PSGL-1 (KPL-1) were used to apply step loads to microvilli. The lengthening of the microvillus in response to the induced step loads was fitted with a viscoelastic model. The quasi-steady state force on the microvillus at any given length was approximately four-fold lower in cells treated with cytochalasin D or when pulled with concanavalin A-coated rather than KPL-1-coated beads. These data suggest that associations between PSGL-1 and the underlying actin cytoskeleton significantly affect the early stages of leukocyte deformation under flow.

Introduction

Leukocyte microvilli display the adhesion protein L-selectin and one of its ligands, P-selectin glycoprotein ligand 1 (PSGL-1). Bonds between these molecules and selectins and selectin ligands on vascular endothelium mediate leukocyte capture and rolling in response to inflammatory signals. Once an intermolecular bond with the endothelium is formed, sustained stress from blood flow acting on the leukocyte will deform microvilli. At first, it is thought, both the membrane and the cortical cytoskeleton deform, but eventually “delaminate” leading to the formation of membrane tethers [23;27]. The word “tether” has come to have a very specific meaning in the field of leukocyte adhesion - a long, thin cylinder of cell membrane devoid of cytoskeletal elements that is pulled from the body of the cell (or by implication, from microvilli tips) by an applied load.

The mechanics of microvilli and tethers may be critical in determining selectin-ligand bond lifetimes during rolling and adhesion under flow. This is because the lifetime of selectin-ligand bonds is both load- and load-history dependent [6;7;12;20;21;26;35], and microvilli with higher spring constants or effective viscosities may lead to higher forces or altered loading rates at the adherent tip. Thus the detailed mechanical properties of leukocyte microvilli and tethers are of great interest for predicting the roles of transient adhesive bonds in cell rolling. While we and others have measured the mechanics of leukocyte tethers [6;14;16–19;24;30] (amongst others), the estimates of microvillus and tether stiffness vary widely.

It has been reported that tethers pulled via PSGL-1 are mechanically indistinguishable from those pulled via Fcγ recptors [19], suggesting that the force required to initiate tether formation is independent of the protein through which force is applied. A similar observation has been made in human umbilical vein endothelial cells [9]. These findings are surprising given the variable linkages of transmembrane proteins to the cytoskeleton. For example, PSGL-1 is associated in some cells with moesin [2], an ERM protein that bridges the receptor to the actin cytoskeleton and may serve a signaling role, while some proteins bound by concanavalin A are free to diffuse in the membrane. Thus while it is feasible that while the properties of pure membrane tethers may be the same regardless of cell surface molecule, it is counterintuitive that the same should be said of microvilli before the cytoskeleton delaminates from the membrane.

Thus, to further investigate the role of the cytoskeleton and receptor protein linkages in microvillus deformation, we used a unique laser trap approach to measure the viscoelastic properties of membrane deformations pulled via PSGL-1 in the presence and absence of cytochalasin D to partially disrupt the actin cytoskeleton. We compared these data to tethers pulled via cell surface glycoproteins using concanavalin A. We found that the mechanics of microvilli are dependent not only upon the presence of an intact cytoskeleton, but also upon the cell surface protein by which force was applied; these differences appear to vanish once the cytoskeletal linkage is ruptured and a tether forms.

Methods

Microspheres

1.2 μm polystyrene microspheres were covalently cross-linked to anti-PSGL-1 (KPL-1) or concanavalin A. Ideally a single bond would be formed between KPL-1 on the microsphere and PSGL-1 on the surface of the cell. To achieve a single initial bond, we varied the concentration of antibody on the microsphere surface. We assumed a single bond has been formed when the ratio of successful bond formations to the total number of attempts was 1/10 or less. We met this criterion when 125 ng of KPL-1 was cross-linked to 2x10⁹ carboxylated microspheres using 1-ethyl-3-3-dimethylaminopropyl carbodiimide (EDAC, Sigma-Aldrich) as per the manufacturer’s instructions. Concanavalin A was chosen for it’s broad reactivity with cell surface glycoproteins [22]; it was cross-linked to beads as described for KPL-1.

Flow cell preparation

30 μl flow cells were constructed from glass coverslips separated by Mylar shims (Practishim) assembled using optical adhesive (Norland) which was cured under ultraviolet light. Flow cells were coated with poly-L-lysine at a concentration of 1mg/ml for 20 minutes to promote cell adhesion.

HL-60 cells were grown in suspension for 2–3 days to an approximate density of 700,000 cells/cm³. HL-60 cells in culture medium were added to the flow cell and allowed to adhere for 40 minutes at room temperature. Non-adherent cells were flushed away. Finally, microspheres were added at a 1:250 dilution from the original stock solution in 1 mg/ml BSA in PBS. When appropriate, 0.1 μM cytochalasin D was added to the diluted bead solution before it was introduced to the flow cell. The duration of cytochalasin treatment was recorded at the time each datum was collected.

Data collection

The laser trap transducer used in these experiments has been described in detail [10], except that a 1W NdYAG laser was used (Intellite). The position of the flow cell was controlled by a piezoelectric stage (Nanonics). The position of the laser trap relative to the specimen was controlled by an acousto-optic deflector (AOD; NEOS Technology) which allowed us to reposition the laser trap in the specimen plane in approximately 10 μs [10;11].

During experiments, a microsphere was captured with a laser trap and brought into contact with the cell surface (Figure 1A). The laser beam was displaced in 270 nm steps (B) every three seconds, producing a load on the microsphere and cell membrane. The microvillus was thus deformed into a long extension of the membrane typical of a “tether” (C).

Figure 1.

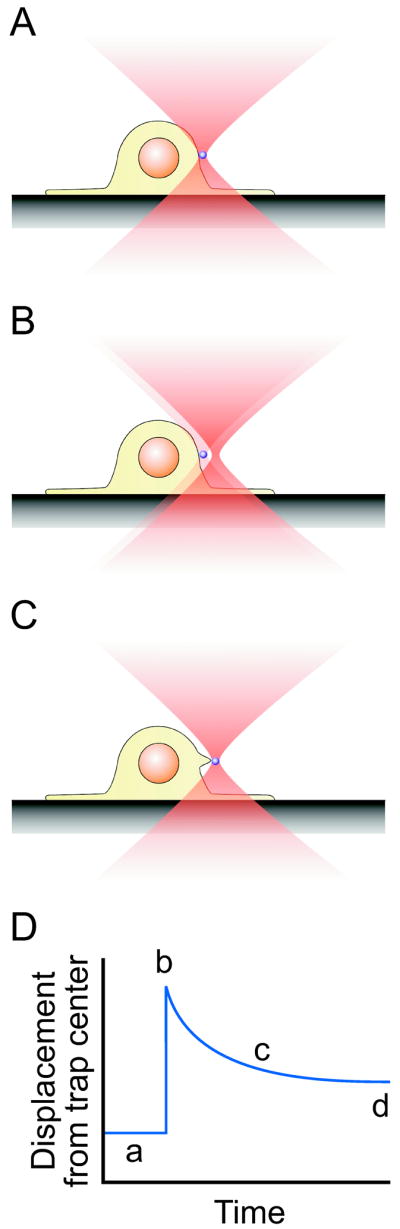
Experimental protocol. A: A microsphere coated with either concanavalin A or KPL-1 (anti-PSGL-1) is trapped and brought into contact with an adherent cell. B: The laser trap is displaced away from the cell ~ ¼ μm. C: The microvillus deforms under the new imposed load and the microsphere creeps back toward cell center. D: Output from the quadrant detector reporting the position of the microsphere relative to trap center. Phases a–c are as above, while d indicates where we measure quasi-steady state force on the microvillus.

Back focal plane interferometry [1] was used to measure the position of the trapped bead relative to the center of the trap, thus providing measurements of displacement and force. The interferometer sensitivity and the trap stiffness (α) were calibrated by the step response method [5;10;32] and by fits to the power spectral density [1;10;32]. Load on the membrane was calculated as the product of α and the instantaneous displacement of the microsphere from trap center. Data was collected using a Tektronix TDS3012 digital oscilloscope and analyzed using Microsoft Excel and SPSS SigmaPlot software.

The raw data were expected to follow the pattern in Figure 1D. From an initial baseline displacement of the bead from trap center (a), when the trap is displaced we see an instantaneous rise in bead displacement relative to the center of the trap (b). The added displacement of the bead from trap center imposes a load on the microsphere and membrane. As the membrane deforms, the bead creeps back toward trap center (c) under constantly varying load, which is always proportional to displacement. The displacement to which the bead has crept 3 seconds after the step was imposed is taken as an approximation of steady-state force (quasi-steady state force) on the tether.

Results

Force-length relationship

Raw data appeared as a series of steps, representing laser trap displacement, followed by decay back toward base representing lengthening of the membrane deformation and motion of the bead back toward trap center. The length (l) of the membrane deformation was determined by

$$l=nD-d$$ Equation 1

where D is the step size (270 nm), n is the number of steps taken away from the cell surface, and d is the displacement of the microsphere relative to the center of the trap. 1.2 μm beads give essentially constant trap stiffness and sensitivity (to within ~20%) for displacements up to 500 nm, since they are somewhat larger than the beam waist itself. Displacements from the trap (as opposed to microvillus elongations) of greater than 500 nm were therefore excluded from detailed statistical analysis.

Tether force remaining at the end of each step when pulled via PSGL-1 was taken as a rough measure of the force necessary to maintain displacement. The residual displacement of the bead from trap center at the end of each step was multiplied by the trap stiffness α to find a quasi-steady state load on the membrane. Linear fits to the initial 1 μm of deformation provided an estimate of microvillus stiffness − 33 ± 2 pN/μm (Figure 2). We also observe a pattern qualitatively similar to that first reported by Raucher and Sheetz [25] in that the force required to deform the membrane increases with tether length up to 1.1 μm, but force remains constant beyond this length (Figure 2, open circles) at ~32 pN.

Figure 2.

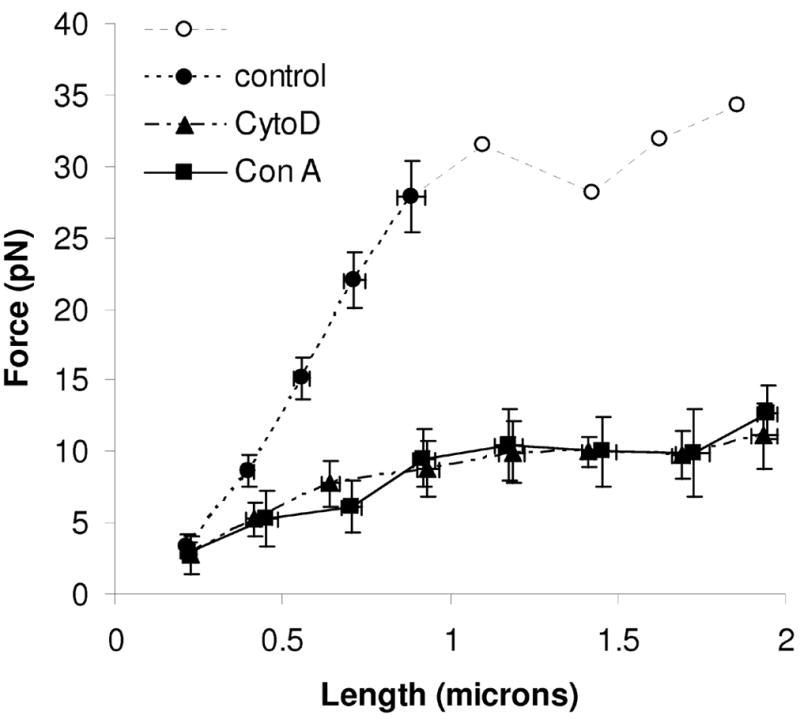
Quasi-steady state force versus microvillus length for control (KPL-1/PSGL-1, ●○), cytochalasin D treated (▲) and microvilli pulled via conanavalin A (■). Each data marker represents the mean of all similarly sized steps for that condition. Error bars represent s.e.m. Microvillus elongations that yield forces above 30 pN are shown as open symbols (○) and without error bars because trap properties become non-linear (see text); those values should be treated as approximate.

At lengths greater than ~1 μm, we commonly observed events where the tether lengthened suddenly rather than undergoing smooth relaxation. In each instance, the quasi-steady state force was reduced by approximately half. This was observed in every experimental condition, but was much more frequently observed in untreated cells with tethers pulled via PSGL-1. These data presumably represent the existence of multiple “tethers” [8;31]. Indeed the sudden ~50% reductions in force we observed were reminiscent of those observed by Sun et al. [31, figure 3]. These data were excluded from the analysis.

Figure 3.

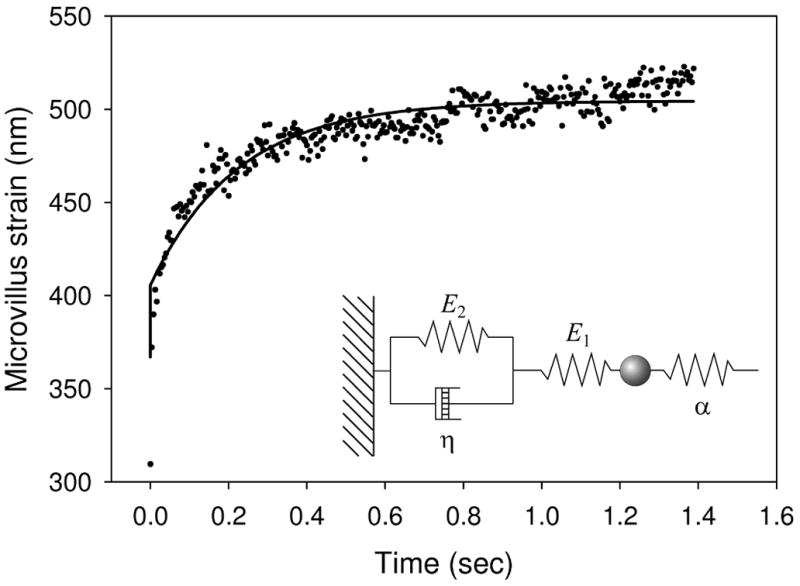
Ensemble averaged data from a single step, fitted by equation 4 (solid line). Inset: schematic showing a standard linear solid in the form used here.

Treatment of cells with 0.1 μM cytochalasin D resulted in a progressive reduction in plateau force, settling after 25 minutes of exposure. Thus, only cells pulled between 25 and 33 minutes of cytochalasin D treatment were included in the final analysis. This concentration of cytochalasin D was chosen because it has been shown to be the minimum concentration necessary to prevent polymerization of actin filaments [3]. The stiffness of the initial 1μm deformation was 8 ± 2 pN/μm – much lower than in the presence of an intact cytoskeleton. Interestingly, the data when pulled by concanavalin A-coated beads was indistinguishable from those pulled via PSGL-1 in the presence of cytochalasin D, with an initial stiffness of 8 ± 2 pN/μm and a plateau force of ~10 pN. Unlike those pulled via PSGL-1 in untreated cells, tethers pulled via concanavalin A or in cytochalasin D-treated cells could easily be extended to several microns.

Viscoelastic properties

In an approach similar to that recently reported by Schmitz et al. [28], step responses were modeled as a standard linear solid (Kelvin body) coupled to an external elastic element – the trap (Figure 3 inset). Upon each step the laser trap is displaced by a distance D at time t=0, applying a force =σ Dα to the membrane. In response, the membrane deforms with strain ε, relieving the force on the membrane:

$$\sigma =\alpha (D-\epsilon )$$ Equation 2

The equation for a standard linear solid,

$$\eta E_1\stackrel{.}{\epsilon }+E_1{E}_2\epsilon =\eta \stackrel{.}{\sigma }+(E_1+E_2)\sigma$$ Equation 3

where E₁ and E₂ are the spring constants for the respective elastic elements and η is the apparent viscosity of the viscous element, was solved for the special condition of Eq. 1:

$$\epsilon (t)=\left[\frac{\alpha D(E_1+E_2)}{E_1{E}_2+\alpha (E_1+E_2)}\right]u(t)-\left[\frac{\alpha D{E}_1^2}{[E_1{E}_2+\alpha (E_1+E_2)](E_1+\alpha )}\right]exp\left(-\frac{E_1{E}_2+\alpha (E_1+E_2)}{\eta (E_1+\alpha )}t\right)u(t)+{\epsilon }_0.$$ Equation 4

Where ε₀ is the pre-strain existing on the solid. Fits of this equation to step responses in individual experiments were highly variable and prone to error. Therefore step responses from different cells but at matched tether lengths were aligned and time-averaged to yield an ensemble averaged strain (Figure 3) that was subsequently fitted with equation 4.

The viscoelastic parameters were similar for tethers pulled from cells using concanavalin A-coated beads, and those treated with cytochalasin D and pulled using KPL1-coated beads (Figure 4). E₁ was 0.062±0.008 pN/nm in cytochalasin D-treated tethers, and 0.1±0.02 in concanavalin A tethers (p=0.01 by ANOVA). Both had a slight but significant positive trend with increasing tether length, with slopes of 2.6×10⁻⁵ and 8.1×10⁻⁵ pN/nm² for cytochalasin D and concanavalin A conditions, respectively. In contrast, neither E₂ nor η for either condition was significantly correlated with tether length, nor did they differ significantly between the two conditions. In aggregate their values were 0.016±0.003 pN/nm for E₂ and 0.023±0.002 pN·s/nm for η.

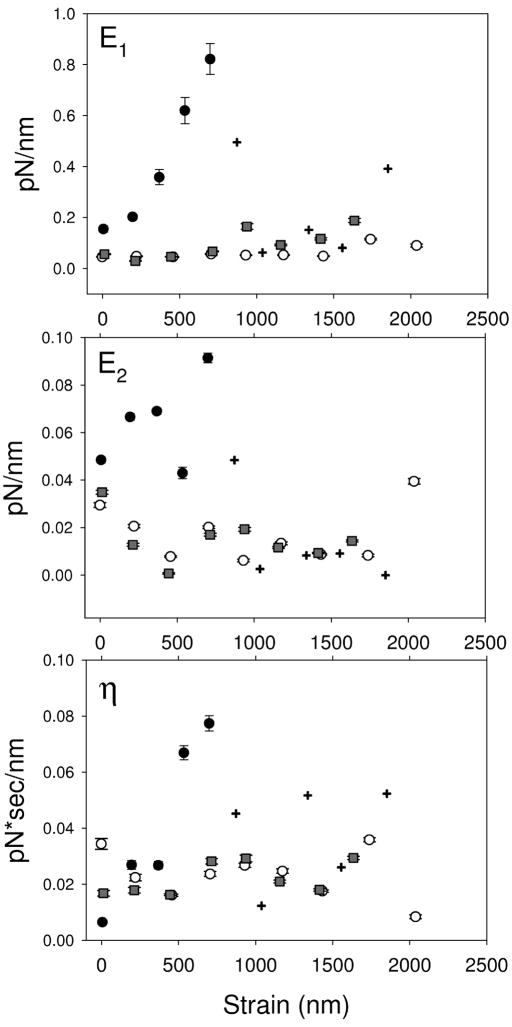
Figure 4.

Viscoelastic parameters as a function of microvillus length for control cells pulled via KPL-1/PSGL-1 (●,+), cytochalasin-D treated cells pulled via KPL-1/PSGL-1 (○) and cells pulled via concanavalin-A (■). Crosshairs (+) specifically indicate values for KPL-1/PSGL-1 that are above the limit for linear trap behavior; the exact values have low confidence.

At short lengths, the elastic modulus of microvilli in control cells pulled via PSGL-1 are distinct from the other two conditions. As the tether lengthens, E₁ increases steeply to 0.9±0.2 pN/nm at a microvillus elongation of 650±40 nm (values and errors derived by fitting of a Lorenzian to the data in Figure 4) then rapidly falls to ~ 0.10 pN/nm.

E₂ is significantly lower in magnitude than E₁ as determined by ANOVA. At tether lengths less than 1 μm, E₂ was 0.06 ± 0.02 pN/nm, while at greater lengths it fell rapidly to ~ 0.005 pN/nm. These values for the elastic elements of the standard linear solid are of similar magnitude to those reported in Jurkat cells studied using an atomic force microscope [28].

Apparent viscosity of the tether is statistically independent of length in all conditions. However, viscosity was significantly higher in control cells (0.039±0.007 pN·s/nm) than in the other two conditions (p=0.043).

Discussion

Step-wise extension of microvilli using the laser trap enabled us to study with very high spatial resolution the length-dependent viscoelastic properties of the microvillus and its transition to a tether. Microvilli in HL60 cells respond differently when loaded via PSGL-1 versus concanavalin A-binding cell surface glycoproteins. Under a rate of deformation equivalent to ~ 90 nm/sec, microvilli deformed via PSGL-1initially respond elastically (33 pN/μm) up to a length of ~ 1 μm. These values are similar to those reported by Shao et al. for microvillus extension in neutrophils [30]. In contrast, microvilli deformed via concanavalin A reached only 1/3 that plateau force with an apparent spring constant of 8 pN/μm. Interestingly, when the cortical cytoskeleton is partially disrupted using a low concentration of cytochalasin D, microvilli deformed via PSGL-1 quantitatively resemble those pulled via concanavalin A, and tethers pulled by others. Unlike others [18;19;29] we therefore found that the properties of the microvillus, including the force necessary to rupture cytoskeletal connections, are strictly dependent upon the point of membrane attachment.

Apparent viscosity has been measured previously in red blood cells, neutrophils, Chinese hamster ovary cells and HB cells as membrane and cytoplasm flow from the cell body into the evolving tether, and the estimates fall in the range of 0.002–0.007 pN·s/nm [16–18;28]. This is considerably lower than the viscous parameter measured here using concanavalin A-coupled beads to deform the membrane (0.02 pN·s/nm) (Figure 4C). The reason for this difference is not clear, but may be related to our high temporal and spatial resolutions that allow us to separate purely elastic from viscoelastic responses. In fact, our higher value appears to be compatible with the data of Park et al. [24] who found significantly higher tether stiffnesses that depend upon shear stress.

The minimum force necessary to initiate a tether is usually interpreted as an “adhesion energy” between the cell membrane and the underlying cytoskeleton [14]; that is, the membrane and/or its associated proteins are adhered to the underlying actin cytoskeleton, and these adhesions must be ruptured in order to initiate formation of a cytoskeleton-free tether. When interpreted in this manner, we estimate an adhesion energy of ~64 pN/μm for tethers pulled via PSGL-1 under control conditions, assuming that 32 pN (Figure 2) is the force required to initiate tether growth. This is in an intermediate range of the adhesion energies that have been reported [18]. Similar to Marcus and Hochmuth, we observed a significant drop in the force necessary to form a tether when the cell was treated with an agent that disrupts the actin cytoskeleton [18].

The “adhesion energy” model says nothing about microvillus deformation prior to rupture of the cytoskeleton-membrane adhesions. While somewhat phenomenological, the standard linear solid not only allowed us to separate viscous and elastic effects in the pre-tether state, but should offer predictive power for modeling of leukocyte rolling and tether formation. Nonetheless, it would be helpful to assign the E₁, E₂ and η parameters to specific cellular structures or processes.

η is presumably representative of the flow of membrane, cytoplasm and associated material into the evolving tether. In support of this presumption, we measured the initial velocities of recoil of the microvillus/tether back into the cell body when the trap was turned off as 3.4±1.1 and 4.4±0.5 μm/s for concanavalin A and KPL-1 tethers, respectively. Were this velocity limited by simple viscoelastic dissipation, one would expect an initial recoil velocity of ~1.6 μm/s based on our measured η. The remaining discrepancy is probably due to the limited temporal resolution of the recoil measurement (Δt = 0.1 s), during which time the load on the microvillus and therefore the recoil velocity both decrease. The discrepancy is not the result of hydrodynamic drag on the microsphere at the tip of the microvillus, which would contribute a drag coefficient of only 0.01 fN·s/nm.

E₂ probably represents out-of-plane bending of the composite membrane-cytoskeleton complex. From Helfer et al [13], a composite membrane has a 2D elastic modulus κ of κ = Eh³/[12(1−σ²)] where E is the Young’s modulus, h is the thickness of the composite membrane and σ is the Poisson’s ratio. The composite membrane then acts effectively as a linear spring with stiffness k_m =κ/A₀Rh, where A₀ = [6(1−σ)+ 1]⁻¹ in pure shear. Assuming a cell of radius 5 μm with a composite membrane thickness (membrane + cortex) of 1 μm, an elastic modulus of 1000 Pa, and σ= 0.5 we find that k_m ≈ 0.09 pN/nm. This is orders of magnitude higher than one would expect for a pure membrane, yet very similar to the peak value for E₂ measured by us in control cells. An alternative model that could explain the higher E₂ is a local doubling in the effective lipid membrane tension [4;15]. This, however, is more difficult to imagine physically, and is arguably inconsistent with our observation that E₂ is lower and length-independent in tethers pulled using concanavalin A.

Our high values for E₁ cannot easily be reconciled with normal deformation of a composite membrane. In fact, the peak value observed (~0.8 pN/nm) is similar to estimates of stiffness for single cytoskeletal protein molecules [33;34]. We therefore interpret E₁ as representing stretch (in aggregate) of the cross-linked cytoskeletal filaments, linking proteins (e.g. moesin) and PSGL-1 itself. In fact, the shape of the ascending limb of the E₁(l) curve is consistent with extension of a freely-jointed chain.