SUMMARY
In cluster randomized trials (CRT), individuals belonging to the same cluster are very likely to resemble one another, not only in terms of outcomes, but also in terms of treatment compliance behavior. Whereas the impact of resemblance in outcomes is well acknowledged, little attention has been given to the possible impact of resemblance in compliance behavior. This study defines compliance intraclass correlation as the level of resemblance in compliance behavior among individuals within clusters. On the basis of Monte Carlo simulations, it is demonstrated how compliance intraclass correlation affects power to detect intention-to-treat (ITT) effect in CRT. As a way of improving power to detect ITT effect in CRT accompanied by noncompliance, this study employs an estimation method, where ITT effect estimates are obtained based on compliance-type-specific treatment effect estimates. A multilevel mixture analysis using an ML-EM estimation method is used for this estimation.
Keywords: cluster randomized trials, noncompliance, intention-to-treat effect, outcome intraclass correlation, compliance intraclass correlation, multilevel mixture analysis
1 Introduction
In conducting randomized field experiments, individual-level randomization is not always possible for practical and ethical reasons. Two examples are situations in which a number of patients belong to each doctor in primary care settings (e.g., [1]), and in school settings, a number of students belong to each teacher (e.g., [2]). In these situations, it is problematic (e.g., administrative burden, teacher/parent complaints, ethical reasons) to assign individuals to different treatment conditions ignoring their cluster membership (i.e., physician, teacher). Therefore, cluster randomized trials (CRT) have been widely used in practice, treating a cluster of individuals as the unit of randomization. Although practical/ethical reasons are the main motivation, there is also a statistical advantage to employing CRT. That is, by assigning individuals that are very likely to interact to the same condition, each treatment condition is less likely to be contaminated by other conditions, therefore making the comparison between different treatment conditions more valid [3]. As a result of cluster-level randomization, individuals in the same cluster are very likely to resemble one another, not only in terms of pretreatment characteristics, but also in terms of treatment receipt behavior and posttreatment outcomes.
If resemblance among individuals is ignored (i.e., data are treated as if they were from individual-level randomized trials), small variations within the same cluster may result in underestimated standard errors, exaggerating the statistical significance (i.e., results in incorrect confidence intervals and significance levels) of the effect of treatment assignment, which is a cluster-level variable. An honest (valid) way of analysis in this situation is to take into account increased variance across clusters (due to reduced variance within clusters). For proper analyses accounting for clustered data structures, multilevel analysis techniques developed in various statistical frameworks can be employed (e.g., [4–9]). In designing CRT, it is critical to adjust expected power and required sample sizes assuming that the data will be properly analyzed taking into account within-cluster resemblance among individuals (e.g., [10–11]).
Whereas a good amount of attention has been paid to handling resemblance among individuals in terms of posttreatment outcomes in CRT, little attention has been given to handling resemblance among individuals in terms of treatment compliance behavior. Individuals with the same cluster membership share the environment of the cluster they belong to, resulting in resemblance among individuals in terms of compliance behavior. For example, some doctors or teachers, which represent cluster units, may more eagerly encourage their patients or students to comply with the given treatment. A recent study [12] called attention to this problem, demonstrating the necessity and possibility of estimating compliance-specific treatment assignment effects considering both CRT and noncompliance. Whereas their study focused on compliance-specific treatment assignment effects (e.g., [13]), the main interest of the current study is in investigating how resemblance among individuals in compliance behavior influences the intention-to-treat (ITT) effect and whether the situation can be improved by considering both CRT and treatment noncompliance in the analysis.
Standard ITT analysis is commonly used in analyzing data from randomized trials to estimate an overall effect of treatment assignment (i.e., effectiveness) by comparing groups as randomized. In analyzing data from CRT, the same analysis may be used with an adjustment for the design effect, or multilevel analysis techniques can be employed accounting for resemblance among individuals with the same cluster membership. Given that we are not interested in compliance-type-specific treatment effects (such as for compliers) and that the effect of cluster-level randomization can be taken into account in the analysis, it is unclear whether we need to worry about the effect of treatment noncompliance in estimating ITT effect in CRT. This study shows how resemblance in compliance behavior within clusters can affect the evaluation of ITT effect in CRT and suggests the use of analyses that consider both clustering and noncompliance.
2 Motivating Example: JHU PIRC Family-School Partnership (FSP) Intervention Study
The Johns Hopkins University Preventive Intervention Research Center’s (JHU PIRC) Family-School Partnership (FSP) intervention trial [2], which was used as a prototype for the Monte Carlo simulations reported in this study, was designed to improve academic achievement and to reduce early behavioral problems of school children. First-grade children were randomly assigned to the intervention or to the control condition, and the unit of randomization was a classroom (9 classrooms were assigned to the intervention condition, and another 9 classrooms were assigned to the control condition). Focusing on the shy behavior outcome, the intraclass correlation was about 0.125 at the 6-month follow-up assessment. It is well known that, unless properly handled in the analysis, intraclass correlation in posttreatment outcomes may lead to misestimation of variances, exaggerating statistical significance of treatment effects in CRT.
In addition to the fact that the unit of randomization was a classroom, another main complication in the JHU PIRC trial was poor compliance of parents. In the FSP intervention condition, parents were asked to implement 66 take-home activities related to literacy and mathematics. It was expected that the intervention would not show any desirable effects unless parents report a quite high level of completion (over-reporting of completion level was very likely given that parents self-reported). Compliance behavior was observed in the FSP intervention condition, but not in the control condition, since parents assigned to the control condition were not invited to implement intervention activities. When the receipt of intervention is defined as completing at least two thirds of activities, about 46% of children in the intervention condition properly received the intervention. Further, parents’ compliance with the intervention activities substantially varied depending on the classroom their children belonged to. Table 1 shows proportions of students whose parents completed at least two thirds of intervention activities.
Table 1.
JHU PIRC FSP Intervention Condition: Proportion of students whose parents completed at least two thirds of intervention activities.
| Classroom | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Number of students | 21 | 22 | 24 | 21 | 23 | 25 | 29 | 30 | 23 |
| Compliance Rate | 1.00 | 0.68 | 0.83 | 0.05 | 0.35 | 0.16 | 0.41 | 0.20 | 0.57 |
Varying compliance rates across clusters indicate that parents belonging to the same classroom tend to be similar in terms of compliance behavior (intraclass correlation of compliance is about 0.377). One possible explanation for this variation would be that, in some classrooms, teachers (or parents) are more motivated than in other classrooms (e.g., in Table 1, 100% of parents in one classroom properly implemented the intervention treatments, whereas in another classroom, only 5% did). The question here is how resemblance in compliance will affect the estimation of ITT effect.
3 Common Setting: CRT with Noncompliance
Assume a CRT setting in line with the JHU PIRC trial, where some study participants do not comply with the given treatment. Individual i (i = 1, 2, 3,…, mj) belongs to cluster j (j = 1, 2, 3,…, G). The assignment status Zj denotes the cluster-level randomization status, and Zj = 1 if cluster j is randomly assigned to the treatment condition, and Zj = 0 if assigned to the control condition. The observed treatment receipt status Dij = 1 if individual i in cluster j receives the treatment, and Dij = 0 otherwise. Let Dij(1) denote the potential treatment receipt status for i when Zj = 1, and Dij(0) when Zj = 0. In this paper, we assume that treatment receipt in the treatment condition is measured without error. However, this assumption can be questionable in some trials, especially when study participants self-report their level of treatment receipt.
In line with the JHU PIRC trial, it is assumed that study participants were prohibited from receiving a different treatment than the one that they were assigned to. Therefore, only two compliance types are possible based on Z and D. The latent compliance type Cij = 1 if individual i would receive the treatment when the treatment is offered, and Cij = 0 if individual i would not receive the treatment regardless of the intervention assignment. According to Angrist et al. [13], these two types of individuals are compliers and never-takers. Since there is only one type of noncomplier (i.e., never-takers), noncomplier will be used to refer to never-taker. That is,
Assuming these two compliance types, a continuous outcome Y for individual i in cluster j can be expressed as
| (1) |
where αn is the mean potential outcome for noncompliers when Z = 0, αc is the mean potential outcome for compliers when Z = 0, and αc − αn represents the mean shift due to compliance. The macro-unit residual εbj represents cluster-specific effects given Z, which are assumed to be normally distributed with zero mean and between-cluster variance . The micro-unit residual εwij is assumed to be normally distributed with zero mean and within-cluster variance , which is equal across clusters. The average effect of treatment assignment for compliers is γc (i.e., CACE: complier average causal effect). It is assumed that there is no effect of treatment assignment for noncompliers, given that noncompliers do not receive the treatment in either condition. This assumption is often referred to as the exclusion restriction (e.g., [13]), which is likely to hold when treatment is truly all-or-none, in particular in blinded trials. However, the assumption may be violated in trials where treatment is not truly all-or-none. For example, in the JHU PIRC trial, there was a large variation in completed intervention treatment activities (range 0 to 66). Therefore, if the amount of treatment received is dichotomized (e.g., at the median, which is about 45 activities), individuals categorized as noncompliers would partially receive the treatment if they were assigned to the treatment condition, while they would not receive the treatment at all if assigned to the control condition.
In the absence of covariates that predict compliance, the proportions of compliers and noncompliers can be expressed in the empty logistic regression as
| (2) |
where πij is the probability of being a complier for individual i in cluster j, and β0 is the logit intercept. The between-cluster residual ξj has zero mean and a variance of . The logit value varies across clusters (β0+ ξj), meaning that the proportion of compliers differs across clusters. Let πc denote the average compliance rate across all individuals. In this paper, we assume that the correlation between compliance and outcome at the cluster level (i.e., between ξj and εbj) is zero. However, this assumption can be relaxed in the proposed estimation framework that considers both noncompliance and data clustering. This correlation may increase in some trials, for example, where clusters with higher proportions of compliers tend to have better outcomes given treatment assignment.
3.1 Intraclass Correlations in CRT with Noncompliance
Intraclass correlation (ICC) has been widely used to represent the level of resemblance among individuals belonging to the same cluster in terms of outcomes. As ICC increases, variance within clusters will decrease, resulting in inflation of variance across clusters. The direct consequence of this variance inflation is reduced power (compared to power in individual-level randomized trials) to detect the effect of treatment assignment, which is a cluster-level variable in CRT. However, if this variance inflation is ignored in the analysis, the resulting type I error rate will be incorrectly inflated.
From equation (1), the ICC coefficient in outcome Y given Z is defined as
| (3) |
where denotes the between-cluster variance of outcome Y given Z. The total variance is the sum of the between-and within-cluster variances ( ).
In addition to the conventional outcome ICC, another ICC is defined in this study to represent resemblance among individuals belonging to the same cluster in terms of compliance behavior. In CRT, individuals belonging to the same cluster are likely to show resemblance not only in terms of outcomes, but also in terms of compliance behavior. The compliance ICC represents a unique complication in CRT accompanied by treatment noncompliance.
There are several ways to present heterogeneity across clusters in proportions [14–18]. In line with McKelvey and Zavoina [19], the intraclass correlation coefficient in compliance can be defined from equation (2) as
| (4) |
where is the between-cluster variance (i.e., variance of ξj) and π2/3 is the variance for the within-cluster residual in the logistic distribution. ICCC represents the degree of resemblance in compliance among individuals belonging to the same cluster. For example, in the FSP intervention condition in the JHU PIRC trial, the ICCC estimate is 0.37, which reflects a substantial variation in the compliance rate across classrooms.
4 ITT Analysis Considering Clustering
Under the assumption of Stable Unit Treatment Value (SUTVA; [20–22]), each individual’s potential outcomes are uncorrelated with other individuals’ treatment assignment status. SUTVA is a critical assumption that makes identification of causal treatment effects possible. When dealing with individuals nested within clusters in randomized trials, plausibility of SUTVA is highly suspect. Cluster-level randomization plays a critical role in making this obvious violation of SUTVA a more manageable problem by concentrating individuals who are most likely to interact with one another in the same treatment condition. For example, in the FSP intervention trial, the unit of randomization was a classroom. By employing cluster randomization, the interaction rate among individuals across different treatment conditions remains about the same as that observed without systematic nesting structures (i.e., classrooms). However, interaction in the same cluster is highly likely, which can be handled statistically by considering resemblance among individuals with the same cluster membership in the analysis.
4.1 Two-level ML analysis
Standard ITT analysis is commonly used in analyzing data from randomized trials to estimate an overall effect of treatment assignment. In analyzing data from CRT, the same analysis may be used in conjunction with multilevel analysis techniques. Since noncompliance is not considered in this method, individual-level and cluster-level variations in compliance behavior is not taken into account. Given that, the situation described in equation (1) is simplified as follows. That is,
| (5) |
where α is the overall mean potential outcome when Z = 0, and the average effect of treatment assignment (i.e., ITT effect) is γ. The macro-unit residual εbj is assumed to be normally distributed with zero mean and between-cluster variance . The micro-unit residual εwij is assumed to be normally distributed with zero mean and within-cluster variance .
The analysis model described in equation (5) is a standard hierarchical linear model and can be estimated with the ML estimator. A number of different algorithms are available for obtaining the ML estimates [9]. In this paper, we used the EM algorithm [23–25] implemented in Mplus version 5 [26].
We define a two-level ML estimate of ITT effect as
| (6) |
where μ̂12ML and μ̂02ML are the estimates of μ1 and μ0 based on two-level ML analysis.
4.2 Two-level ML mixture analysis
Another way to look at the ITT effect is as a combination of the treatment assignment effect for compliers and the treatment assignment effect for noncompliers. In this approach, the existence of noncompliance can be taken into account. Considering non-compliance may have some impact on ITT effect estimation when information on the mixture distribution of compliers and noncompliers is utilized in CACE estimation. The ML mixture approach is known to be often more efficient than the IV approach in the estimation of CACE [27–28 ]. Estimation of ITT effect may also benefit from this improved efficiency if the additional assumptions necessary to identify CACE, such as the exclusion restriction and monotonicity [13], hold.
In the current setting we consider (i.e., individuals assigned to the control condition have no access to the actual treatment as in the JHU PIRC trial), monotonicity is a plausible assumption (i.e., no individuals do the opposite of what they are assigned to do). The exclusion restriction may not hold if the treatment is not truly all-or-none, especially in non-blinded studies. When this assumption is violated, CACE estimation is likely to benefit from the ML mixture analysis, which mitigates the impact of violation by utilizing auxiliary information such as from distributional heterogeneity, parametric assumptions, and covariates [29]. However, ITT effect estimation based on these adjusted CACE estimates in conjunction with the exclusion restriction may result in biased results. In principle, it is possible to relax the exclusion restriction relying on auxiliary information such as from proper priors and covariates [30–32], although it is not well known how these methods work in the context of CRT. In the current paper, we focus on situations where the exclusion restriction is a plausible assumption.
To simultaneously handle data clustering, noncompliance, and interaction between these two, the two-level ML mixture approach considers the same model described in equations (1) and (2) in estimating the ITT effect. On the basis of the model described in equations (1) and (2), a formal multilevel mixture analysis [33–34] using the ML estimator can be conducted. The observed data likelihood for the treatment and the control group is different because the compliance variable Cij is observed when Zj = 1 but it is unobserved when Zj = 0.
In the treatment group, the observed data likelihood for cluster j is described as
| (7) |
where f1(Yij | Cij, εbj) is the normal density function
| (8) |
φbj(εbj) is the normal density function for εbj
| (9) |
φj(ξj) is the normal density function for ξj
| (10) |
and the probability of compliance
| (11) |
In the control group, Cij is unobserved and thus the observed data likelihood is
| (12) |
where f0(Yij | Cij, εbj) is the normal density function
| (13) |
The total likelihood function
| (14) |
does not have a closed form expression and to compute it we use 2-dimensional numerical integration. By maximizing L with respect to the parameters in the model we obtain the ML estimates. The likelihood can be maximized directly by using a general maximization algorithm. Numerical methods can be used to compute the derivatives of L with respect to the parameters. A more efficient method for maximizing the likelihood, however, is the EM algorithm, which is implemented in Mplus version 5 [29]. This algorithm treats the unknown compliance status in the control group as well as the between level random effects as missing data. Details on the implementation of this algorithm are available in Muthén and Asparouhov [35]. Parametric standard errors are computed from the information matrix using the second-order derivatives of L.
We assume random assignment of treatment conditions, SUTVA, and the exclusion restriction in this analysis. In CRT, interaction among individuals in the same cluster is highly likely. As in two-level ML analysis, we statistically deal with resemblance among individuals with the same cluster membership in two-level ML mixture analysis. In that sense, SUTVA is not a necessary assumption. However, in CRT, the interaction rate among individuals across different treatment conditions remains about the same as that observed without systematic nesting structures. Therefore, although it may not be serious, some deviation from SUTVA is possible as in any randomized trial.
A two-level ML mixture estimate of CACE is described as
| (15) |
where and are the two-level ML mixture estimates of μ1c and μ0c.
Then, a two-level ML mixture estimate of ITT effect is
| (16) |
where is the t wo-level ML mixture estimate of πc.
Standard errors of the ITT estimates are obtained using the delta method as
| (17) |
5 Comparison of Analysis Options: Monte Carlo Simulations
To examine the impact of ICCC and ICCY on the estimation of ITT effect in the analysis options described above, Monte Carlo simulations are employed, since it is not straightforward to analytically derive possible bias in variance estimation given missing compliance information and mixture distributions of different compliance types. In this paper, we focus on how compliance intraclass correlation affects power to detect ITT effect. Compliance intraclass correlation has different consequences in CACE estimation, which is dealt with in a separate paper [32].
5.1 Data Generation
The Monte Carlo simulation results presented in this study are based on 500 replications. The size of each cluster (m) is 20, and the total number of clusters (G) is 100 (50 in the control and 50 in the treatment condition). A large number of clusters (100 in this study compared to 18 in the JHU Study) is employed to avoid another source of variance misestimation and to focus on variance misestimation only due to intraclass correlations. The true ratio of the treatment and control groups is 50%:50%. The size of ITT effect increases or decreases proportionally as a function of the compliance rate, and therefore noncompliance has a direct impact on power to detect ITT effect [36]. In this paper, beyond this direct impact through compliance rates, we are more interested in studying the impact of noncompliance on power through within-cluster resemblance in compliance. Therefore, we used the same true compliance rate (50%) across all simulation settings.
The true ICCC value ranges from 0.0 to 0.8. A zero ICCC indicates that compliance behavior is independent of the clusters individuals belong to. A high ICCC (e.g., 0.8) indicates a situation, where individuals in the same cluster show a very similar compliance behavior. Although how ICCY affects ITT effect estimation is well known, two non-zero ICCY values (0.05 and 0.10) were considered in simulations to provide reference information (i.e., we can tell how much difference ICCC makes in the presence of ICCY ).
Data were generated according to equations (1) and (2). Complier and noncomplier outcome means (i.e., αn and αc) may differ in the control condition. If it is not parameterized properly in the analysis model, the distance between the two means takes the form of additional variance in conjunction with variation in compliance (i.e., together with compliance indicator Cij, having a non-zero distance is like having a missing co-variate that predicts Y). The effect of having this additional variance can be substantial in CRT because the additional variance may include between-cluster variance (i.e., due to non-zero ICCC). Therefore, we focus on the distance between the two distributions as a key source of variance misestimation in analyses that do not consider within-cluster resemblance in compliance. The true control condition noncomplier mean αn is 1.0, and the true control condition complier mean αc takes values of 1.0, 1.5, and 2.0 to reflect the distance between noncompliers and compliers (0.0, 0.5, and 1.0 SD apart).
The true within-cluster variance takes values of 1.00, 0.95, and 0.90. The true between-cluster variance takes values of 0.00, 0.05, and 0.10 to reflect ICCY of 0.00, 0.05, and 0.10 given the total variance of 1.0. The true treatment assignment effect for compliers γc (i.e., CACE) is 0.40, and the true overall ITT effect γ is 0.20. The true logit intercept β0 is zero (i.e., 50% compliance) and the true between-cluster compliance variance takes values of 0.00, 0.82, 2.19, and 13.15 on the logit scale to reflect ICCC of 0.0, 0.2, 0.4, and 0.8 according to equation (4).
In summarizing analysis results with the simulated data, coverage is defined as the proportion of replications out of 500 replications where the true parameter values are covered by the nominal 95% confidence interval of the parameter estimates. Power is defined as the proportion of replications out of 500 replications where the ITT effect estimates are significantly different from zero (α = .05).
5.2 ITT Analysis Considering Clustering
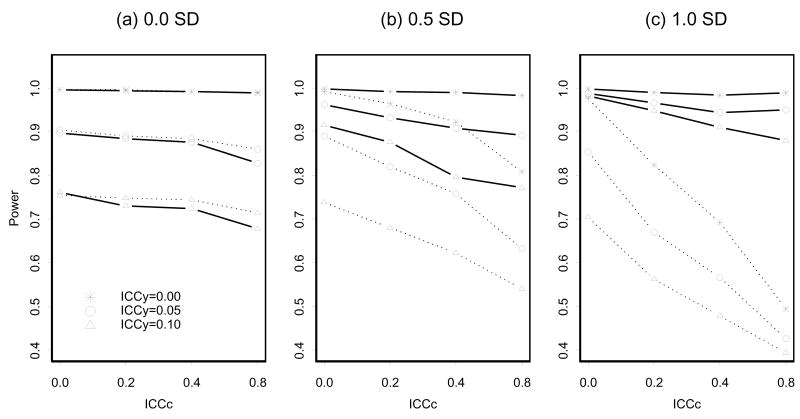
Figure 1 shows simulation results based on two-level ML analysis and two-level ML mixture analysis. Since both approaches consider data clustering in the analyses, coverage rates in these analyses stay close to the nominal level regardless of ICCY and ICCC (coverage rates are not reported in Figure 1 because they are always very close to the nominal level). Given that standard errors are correctly estimated in these analyses, estimated statistical power can be considered valid.
Figure 1.
Two-level ML analysis and two-level ML mixture analysis: Statistical power in detecting ITT effect as a function of ICCC and ICCY (100 clusters, 20 individuals per cluster). The dotted lines represent power when two-level ML analysis is employed. The solid lines represent power when two-level ML mixture analysis is employed. Complier and noncomplier means (i.e., αc − αn) are (a) 0.0, (b) 0.5, and (c) 1.0 standard deviation apart given treatment assignment.
Figure 1 shows power to detect ITT effect when two-level ML analysis and two-level ML mixture analysis are employed. In two-level ML analysis (see the dotted lines), possible sources of variance misestimation can be seen by comparing the simplified model in equation (5) and the full model in equation (1). The cluster-level outcome residual εbj in equation (1) is properly modeled in two-level ML analysis, and therefore is not a source of variance misestimation. However, the variance associated with (αc − αn) Cij in equation (1) is not accounted for, and instead is absorbed by residual variances and . Depending on the level of ICCC, the variance associated with (αc − αn) Cij is differently partitioned into and . For example, the whole variance associated with (αc − αn) Cij will be added to if ICCC = 0, and to if ICCC = 1. Since any variance associated with Cij is properly added to separate residual variances (i.e., within-cluster and between-cluster), inflated and should not be considered the result of variance misestimation. Rather, it is the result of correcting for variance that is not accounted for in the model. Figure 1 shows that, when two-level ML analysis is employed, as a result of this additional cluster-level variance associated with compliance, power to detect ITT effect decreases more rapidly in response to ICCC as the distance between αn and αc increases. The pure impact of ICCC, which can be observed when ICCY = 0, depicts reduction in power when individuals in the same cluster are similar in terms of compliance, but not in terms of outcomes. The impact of ICCC alone is quite remarkable, and this phenomenon has not received enough attention in analyzing data from CRT.
In two-level ML mixture analysis (see the solid lines), data generated on the basis of the model described in equations (1) and (2) are analyzed using the same model considering the fact that randomization was done at the cluster level and that some individuals did not comply with the given treatment. Since within- and between-cluster variances ( and ) are correctly estimated by simultaneously considering ICCY, ICCC, variances associated with Cij, and the distance between αc and αn, the resulting ITT estimates have smaller average standard errors and mean squared errors when using two-level ML mixture analysis than when using two-level ML analysis. The resulting difference between the two methods in terms of statistical power is quite remarkable when the distance between αc and αn is large (e.g., see Panal (c) in Figure 1). When using the two-level ML approach, as this distance increases, power to detect ITT effect decreases rapidly in response to ICCC due to the additional cluster-level variance associated with compliance. When using the two-level ML mixture approach, this distance instead increases precision in the estimation of unknown compliance status, and therefore improves power. As a result, the difference in power between the two analysis approaches becomes substantially larger as the distance between αc and αn increases.
6 Conclusions
Frangakis and Rubin [37] previously pointed out that estimation of intention-to-treat effect can be biased in the analysis that ignores treatment noncompliance due to interaction between noncompliance and nonresponse (i.e., availability of outcome data at posttreatment assessments). The current study calls attention to a similar phenomenon (i.e., how we deal with compliance information in the analysis affects the evaluation of treatment effects even if we are not interested in estimating compliance-type-specific treatment assignment effects) in a different context, where noncompliance may interact with clustering of individuals. It was demonstrated in this study that ignoring compliance information in analyzing data from CRT may result in substantially decreased power to detect ITT effect.
To simultaneously handle data clustering and noncompliance, this study employed a formal multilevel analysis combined with the mixture analysis. The joint analysis of both complications is computationally demanding, but it provides a general framework that can accommodate various forms of clustered data structures considering mixture distributions of compliers and noncompliers. The ML-EM estimation of the multilevel mixture models has been implemented in the Mplus program [26], providing an accessible tool for complex statistical modeling. Although not covered in this study, other complications in randomized trials such as missing outcomes can also be incorporated in this estimation framework in addition to noncompliance and data clustering. Further study is needed for better understanding of how ITT effect estimation may benefit from the joint modeling of multiple complications in various contexts of randomized trials.
As a way of improving power to detect ITT effect in CRT accompanied by non-compliance, this study employed an estimation method, where ITT effect estimates are obtained on the basis of compliance-type-specific treatment effect estimates. The same approach was used by Frangakis and Rubin [37] to avoid bias in the estimation of ITT effect. The limitation of this approach is that ITT effect estimates can be biased if underlying assumptions employed to identify compliance-type-specific treatment effects are violated. Given that, although they may seem irrelevant, methods to better handle identification problems in estimating compliance-type-specific treatment effects are likely to improve estimation of ITT effect when faced with various complications in randomized trials. Extensive treatment of this topic is left for future study.
Along with possible violation of assumptions employed to identify compliance-type-specific treatment effects, another complication that poses a major problem in applying the multilevel mixture analysis method is having small numbers of clusters. In simulation results reported in this paper, a large number of clusters has been employed (i.e., 100) to focus on variance misestimation only due to intraclass correlations. In practice, however, much smaller numbers of clusters are often employed in CRT as in the JHU PIRC trial (i.e., 18). When applying multilevel mixture analysis, having small numbers of clusters poses serious consequences. That is, with small numbers of clusters, not only standard errors, but also compliance-specific treatment effects are likely to be poorly estimated at the cluster level (e.g., CACE will be basically estimated based on 9 classroom observations in the JHU trial).
In situations where multilevel ML mixture analysis is not recommended, such as in the JHU PIRC trial, multilevel ML analysis considering only clustering seems to be a reasonable solution. A few strategies such as the use of the bootstrap method, the use of the Bayesian method with strong priors, and the use of an approximate F-test have been used to improve estimation in one-class multilevel analyses with small numbers of clusters. When we apply one-class multilevel ML analysis (adjusted for small numbers of clusters), a combination of simpler analyses and the simulation results reported in this paper can be used together to guide interpretation of the results. For example, on the basis of a two-level logistic regression analysis using only the intervention group data, ICCC can be estimated. Complier and noncomplier means (αc and αn) can be estimated using one-level mixture analysis. If the distance between these means is small and ICCC is small, there is less need to employ the two-level mixture approach. As shown in Figure 1, if this distance is substantial, one should interpret the results of two-level ML analyses as more conservative than necessary, especially if ICCC is also substantial. Ultimately, for better estimation and interpretation, we need one-step analysis methods that can accommodate both data clustering and noncompliance when faced with small numbers of clusters. In principle, the methods of improving estimation in multilevel analysis, such as the bootstrap method, can be incorporated in multilevel mixture analysis. However, little is known how these methods perform with mixture distributions in the CRT context. Further investigation is necessary to provide practical guidelines in conducting multilevel mixture analysis given small numbers of clusters.
Contributor Information
Booil Jo, Email: booil@stanford.edu, Department of Psychiatry & Behavioral Sciences, Stanford University, Stanford, CA 94305-5795.
Tihomir Asparouhov, Muthén & Muthén.
Bengt O. Muthén, Graduate School of Education & Information Studies, University of California, Los Angeles
References
- 1.Dexter P, Wolinsky F, Gramelspacher G, Zhou XH, Eckert G, Waisburd M, Tierney W. Effectiveness of computer-generated reminders for increasing discussions about Advance Directives and completion of Advance Directives. Annals of Internal Medicine. 1998;128:102–110. doi: 10.7326/0003-4819-128-2-199801150-00005. [DOI] [PubMed] [Google Scholar]
- 2.Ialongo NS, Werthamer L, Kellam SG, Brown CH, Wang S, Lin Y. Proximal impact of two first-grade preventive interventions on the early risk behaviors for later substance abuse, depression and antisocial behavior. American Journal of Community Psychology. 1999;27:599–642. doi: 10.1023/A:1022137920532. [DOI] [PubMed] [Google Scholar]
- 3.Sobel ME. What do randomized studies of housing mobility demonstrate: Causal inference in the face of interference. Journal of the American Statistical Association. 2006;101:1398–1407. [Google Scholar]
- 4.Aitkin M, Longford N. Statistical modeling issues in school effectiveness studies (with discussion) Journal of Royal Statistical Society, Ser A. 1986;149:1–43. [Google Scholar]
- 5.Goldstein H. Multilevel mixed linear model analysis using iterative generalized least squares. Biometrika. 1986;73:43–56. [Google Scholar]
- 6.Liang KH, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 7.McCulloch CE. Maximum likelihood algorithms for generalized linear mixed models. Journal of the American Statistical Association. 1997;92:162–170. [Google Scholar]
- 8.Muthén BO, Satorra A. Complex sample data in structural equation modeling. In: Marsden PV, editor. Sociological Methodology. Blackwell; Cambridge, MA: 1995. pp. 267–316. [Google Scholar]
- 9.Raudenbush SW, Bryk AS. Hierarchical Linear Models: Applications and Data Analysis Methods. Sage; Thousand Oaks, CA: 2002. [Google Scholar]
- 10.Donner A, Klar N. Statistical considerations in the design and analysis of community intervention trials. Journal of Clinical Epidemiology. 1996;49:435–439. doi: 10.1016/0895-4356(95)00511-0. [DOI] [PubMed] [Google Scholar]
- 11.Murray DM. Design and Analysis of Group-Randomized Trials. Oxford University Press; New York: 1998. [Google Scholar]
- 12.Frangakis CE, Rubin DB, Zhou XH. Clustered encouragement design with individual noncompliance: Bayesian inference and application to advance directive forms. Biostatistics. 2002;3:147–164. doi: 10.1093/biostatistics/3.2.147. [DOI] [PubMed] [Google Scholar]
- 13.Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91:444–455. [Google Scholar]
- 14.Agresti A. Categorical Data Analysis. Wiley; New York: 1990. [Google Scholar]
- 15.Commenges D, Jacqmin H. The intraclass correlation coefficient: distribution-free definition and test. Biometrics. 1994;50:517–526. [PubMed] [Google Scholar]
- 16.Haldane JBS. The mean and variance of χ2, when used as a test of homogeneity, when expectations are small. Biometrika. 1940;31:346–355. [Google Scholar]
- 17.McCullagh P, Nelder JA. Generalized Linear Models. Chapman & Hall; London: 1989. [Google Scholar]
- 18.Snijders TAB, Bosker RJ. Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling. Sage; Thousand Oaks, CA: 1999. [Google Scholar]
- 19.McKelvey RD, Zavoina W. A statistical model for the analysis of ordinal level dependent variables. Journal of Mathematical Sociology. 1975;4:103–120. [Google Scholar]
- 20.Rubin DB. Bayesian inference for causal effects: The role of randomization. Annals of Statistics. 1978;6:34–58. [Google Scholar]
- 21.Rubin DB. Discussion of “Randomization analysis of experimental data in the Fisher randomization test” by D. Basu. Journal of the American Statistical Association. 1980;75:591–593. [Google Scholar]
- 22.Rubin DB. Comment on “Neyman (1923) and causal inference in experiments and observational studies. Statistical Science. 1990;5:472–480. [Google Scholar]
- 23.Dempster A, Laird N, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B. 1977;39:1–38. [Google Scholar]
- 24.Little RJA, Rubin DB. Statistical Analysis with Missing Data. Wiley; New York: 2002. [Google Scholar]
- 25.McLachlan GJ, Krishnan T. The EM Algorithm and Extensions. Wiley; New York: 1997. [Google Scholar]
- 26.Muthén LK, Muthén BO. Mplus User’s Guide. Muthén & Muthén; Los Angeles: 1998–2008. [Google Scholar]
- 27.Imbens GW, Rubin DB. Bayesian inference for causal effects in randomized experiments with non-compliance. The Annals of Statistics. 1997;25:305–327. [Google Scholar]
- 28.Little RJA, Yau LHY. Statistical techniques for analyzing data from prevention trials: Treatment of no-shows using Rubin’s causal model. Psychological Methods. 1998;3:147–159. [Google Scholar]
- 29.Jo B. Model misspecification sensitivity analysis in estimating causal effects of interventions with noncompliance. Statistics in Medicine. 2002;21:3161–3181. doi: 10.1002/sim.1267. [DOI] [PubMed] [Google Scholar]
- 30.Hirano K, Imbens GW, Rubin DB, Zhou XH. Assessing the effect of an influenza vaccine in an encouragement design. Biostatistics. 2000;1:69–88. doi: 10.1093/biostatistics/1.1.69. [DOI] [PubMed] [Google Scholar]
- 31.Jo B. Estimation of intervention effects with noncompliance: Alternative model specifications. Journal of Educational and Behavioral Statistics. 2002;27:385–409. [Google Scholar]
- 32.Jo B, Asparouhov T, Muthén BO, Ialongo NS, Brown CH. Cluster randomized trials with treatment noncompliance. Psychological Methods. 2008;13:1–18. doi: 10.1037/1082-989X.13.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Asparouhov T, Muthén BO. Multilevel mixture models. In: Hancock GR, Samuelsen KM, editors. Advances in latent variable mixture models. Information Age Publishing; Greenwich, CT: 2007. [Google Scholar]
- 34.Muthén BO. Latent variable analysis: Growth mixture modeling and related techniques for longitudinal data. In: Kaplan D, editor. Handbook of quantitative methodology for the social sciences. Sage; Newbury Park, CA: 2004. pp. 345–368. [Google Scholar]
- 35.Muthén BO, Asparouhov T. Growth mixture analysis: Models with non-Gaussian random effects. In: Fitzmaurice G, Davidian M, Verbeke G, Molenberghs G, editors. Advances in Longitudinal Data Analysis. Chapman & Hall; London: 2007. [Google Scholar]
- 36.Jo B. Statistical power in randomized intervention studies with noncompliance. Psychological Methods. 2002;7:178–193. doi: 10.1037/1082-989x.7.2.178. [DOI] [PubMed] [Google Scholar]
- 37.Frangakis CE, Rubin DB. Addressing complications of intent-to-treat analysis in the combined presence of all-or-none treatment-noncompliance and subsequent missing outcomes. Biometrika. 1999;86:365–379. [Google Scholar]