Local Rank Inference for Varying Coefficient Models

Abstract

By allowing the regression coefficients to change with certain covariates, the class of varying coefficient models offers a flexible approach to modeling nonlinearity and interactions between covariates. This paper proposes a novel estimation procedure for the varying coefficient models based on local ranks. The new procedure provides a highly efficient and robust alternative to the local linear least squares method, and can be conveniently implemented using existing R software package. Theoretical analysis and numerical simulations both reveal that the gain of the local rank estimator over the local linear least squares estimator, measured by the asymptotic mean squared error or the asymptotic mean integrated squared error, can be substantial. In the normal error case, the asymptotic relative efficiency for estimating both the coefficient functions and the derivative of the coefficient functions is above 96%; even in the worst case scenarios, the asymptotic relative efficiency has a lower bound 88.96% for estimating the coefficient functions, and a lower bound 89.91% for estimating their derivatives. The new estimator may achieve the nonparametric convergence rate even when the local linear least squares method fails due to infinite random error variance. We establish the large sample theory of the proposed procedure by utilizing results from generalized U-statistics, whose kernel function may depend on the sample size. We also extend a resampling approach, which perturbs the objective function repeatedly, to the generalized U-statistics setting; and demonstrate that it can accurately estimate the asymptotic covariance matrix.

1 Introduction

As introduced in Cleveland, Crosse and Shyu (1992) and Hastie and Tibshirani (1993), the varying coefficient model provides a natural and useful extension of the classical linear regression model by allowing the regression coefficients to depend on certain covariates. Due to its flexibility to explore the dynamic features which may exist in the data and its easy interpretation, the varying coefficient model has been widely applied in many scientific areas. It has also experienced rapid developments in both theory and methodology, see Fan and Zhang (2008) for a comprehensive survey. Fan and Zhang (1999) proposed a two-step estimation procedure for the varying coefficient model when the coefficient functions have possibly different degrees of smoothness. Kauermann and Tutz (1999) investigated the use of varying coefficient models for diagnosing the lack-of-fit of regression, regarding the varying coefficient model as an alternative to a parametric null model. Cai, Fan and Li (2000) developed a more efficient estimation procedure for varying coefficient models in the framework of generalized linear models. As special cases of varying coefficient models, time-varying coefficient models are particularly appealing in longitudinal studies, survival analysis and time series data since they allow one to explore the time-varying effect of covariates over the response. Pioneering works on novel applications of time-varying coefficient models to longitudinal data include Brumback and Rice (1998), Hoover, et al. (1998), Wu, et al. (1998) and Fan and Zhang (2000), among others. For more details, readers are referred to Fan and Li (2006) and the references therein. Time-varying coefficient models are also popular in modeling and predicting nonlinear time series data and survival data, see Fan and Zhang (2008) for related literature.

Estimation procedures in the aforementioned papers are built on either local least squares type or local likelihood type methods. Although these estimators remain asymptotically normal for a large class of random error distributions, their efficiency can deteriorate dramatically when the true error distribution deviates from normality. Furthermore, these estimators are very sensitive to outliers. Even a few outlying data points may introduce undesirable artificial features in the estimated functions. These considerations motivate us to develop a novel local rank estimation procedure that is highly efficient, robust and computationally simple. In particular, the proposed local rank regression estimator may achieve the nonparametric convergence rate even when the local linear least squares method fails to consistently estimate the regression coefficient functions due to infinite random error variance, which occurs for instance when the random error has a Cauchy distribution.

The new approach can substantially improve upon the commonly used local linear least squares procedure for a wide class of error distributions. Theoretical analysis reveals that the asymptotic relative efficiency (ARE), measured by the asymptotic mean squared error (or the asymptotic mean integrated squared error), of the local rank regression estimator in comparison with the local linear least squares estimator has an expression that is closely related to that of the Wilcoxon-Mann-Whitney rank test in comparison with the two-sample t-test. However, different from the two-sample test scenario where the efficiency is completely determined by the asymptotic variance, in the current setting of estimating an infinite-dimensional parameter both bias and variance contribute to the asymptotic efficiency. The value of ARE is often significantly greater than one. For example, the ARE is 167% for estimating the regression coefficient functions when the random error has a t₃ distribution, is 240% for exponential random error distribution, and is 493% for lognormal random error distribution.

A striking feature of the local rank procedure is that its pronounced efficiency gain comes with only a little loss when the random error actually has a normal distribution, for which the ARE of the local rank regression estimator relative to the local linear least squares estimator is above 96% for estimating both the coefficient functions and their derivatives. For estimating the regression coefficient functions, the ARE has a sharp lower bound 88.96%, which implies that the efficiency loss is at most 11.04% in the worst case scenario. For estimating the first derivative of the regression coefficient functions, the ARE possesses a lower bound 89.91%. Kim (2008) developed a quantile regression procedure for varying coefficient models when the random errors are assumed to have a certain quantile equal to zero. She used the regression splines method and derived the convergence rate, but the lack of asymptotic normality result does not allow the comparison of the relative efficiency. On the other hand, one may extend the local quantile regression approach (Yu and Jones, 1998) to the varying coefficient models. However, this is expected to yield an estimator which still suffers from loss of efficiency and may have near zero ARE relative to the local linear least squares estimator in the worst case scenario.

The new estimator proposed in this paper minimizes a convex objective function based on local ranks. The implementation of the minimization can be conveniently carried out using existing functions in the R statistical software package via a simple algorithm (§4.1). The objective function has the form of a generalized U-statistic whose kernel varies with the sample size. Under some mild conditions, we establish the asymptotic representation of the proposed estimator and further prove its asymptotic normality. We derive the formula of the asymptotic relative efficiency of the local rank estimator relative to the local linear least squares estimator, which confirms the efficiency advantage of the local rank approach. We also extend a resampling approach, which perturbs the objective function repeatedly, to the generalized U-statistics setting; and demonstrate that it can accurately estimate the asymptotic covariance matrix.

This paper is organized as follows. Section 2 presents the local rank procedure for estimating the varying coefficient models. Section 3 discusses its large sample properties and proposes a resampling method for estimating the asymptotic covariance matrix. In Section 4, we address issues related to practical implementation and present Monte Carlo simulation results. We further illustrate the proposed procedure via analyzing an environment data set. Regularity conditions and technical proofs are presented in the Appendix.

2 Local rank estimation procedure

Let Y be a response variable, and U and X be the covariates. The varying coefficient model is defined by

$$Y=a_0(U)+{\mathbf{X}}^T\mathbf{a}(U)+\epsilon ,$$ (1)

where a₀(·) and a(·) are both unknown smooth functions. The random error ε has probability density function g(·) which has finite Fisher information, i.e., ∫ {g(x)}⁻¹ g′(x)²dx < ∞. In this paper, it is assumed that U is a scalar and X is a p-dimensional vector. The proposed procedures can be extended to the case of multivariate U with more complicated notations by following the same idea in this paper.

Suppose that {U_i, X_i, Y_i}, i = 1, …, n, is a random sample from model (1). Write X_i = (X_i1, …, X_ip)^T and a(·) = (a₁(·), …, a_p(·))^T. For u in a neighborhood of any given u₀, we locally approximate the coefficient function by a Taylor expansion

$$a_m(u)\approx a_m(u_0)+a_m^{\prime }(u_0)(u-u_0),m=0,1,\dots ,p.$$ (2)

Denote α₁ = a₀(u₀), ${\alpha }_2=a_0^{\prime }(u_0)$, β_m = a_m(u₀) and ${\beta }_{p+m}=a_m^{\prime }(u_0)$, for m = 1, …, p. Based on the above approximation, we obtain the residual for estimating Y_i at U_i = u₀

$$e_i=Y_i-{\alpha }_1-{\alpha }_2(U_i-u_0)-\sum _{m=1}^p[{\beta }_m+{\beta }_{p+m}(U_i-u_0)]X_{im}.$$ (3)

We define the local rank objective function to be

$$Q_n(\mathit{\beta },{\alpha }_2)=\frac{1}{n(n-1)}\sum _{1\le i,j\le n}\mid e_i-e_j\mid K_h(U_i-u_0)K_h(U_j-u_0),$$ (4)

where β = (β₁, …, β_p, β_p+1, …, β_2p)^T, and for a given kernel function K(·) and a bandwidth h, K_h(t) = h⁻¹K(t/h). Note that Q_n(β, α₂) does not depend on α₁ because α₁ is canceled out in e_i − e_j. The objective function Q_n(β, α₂) is a local version of Gini’s mean difference, which is a classical measure of concentration or dispersion (David, 1998). Without the kernel functions, [n(n − 1)]⁻¹ Σ_{1 ≤ i, j ≤ n}|e_j − e_j| is the global rank objective function that leads to the classical rank estimator in linear models based on Wilcoxon scores. Rank-based statistical procedures have played a fundamental role in nonparametric analysis of linear models due to its high efficiency and robustness. We refer to the review paper of McKean (2004) for many useful references.

For any given u₀, minimizing Q_n(β, α₂) yields the local Wilcoxon rank estimator for ${({\mathit{\beta }}_0^T,{\alpha }_2)}^T$, where ${\mathit{\beta }}_0=\mathit{\beta }(u_0)={(a_1(u_0),\dots ,a_p(u_0),a_1^{\prime }(u_0),\dots ,a_p^{\prime }(u_0))}^T$. Denote the minimizer of Q_n(β, α₂) by (β̂^T, α̂₂)^T. Then for m = 1, …, p,

$${\widehat{a}}_m(u_0)={\widehat{\beta }}_m,{\widehat{a}}_m^{\prime }(u_0)={\widehat{\beta }}_{p+m}\text{and}{\widehat{a}}_0^{\prime }(u_0)={\widehat{\alpha }}_2,$$

In the sequel, we also use the vector notation α̂(u₀) = (â₁(u₀), …, â_p(u₀))^T and ${\widehat{\mathbf{a}}}^{\prime }(u_0)={({\widehat{a}}_1^{\prime }(u_0),\cdots ,{\widehat{a}}_p^{\prime }(u_0))}^T$ when convenient.

The location parameter a₀(u₀) needs to be estimated separately. This is analogous to the scenario of global rank estimation of intercept in the linear regression model. In order to make the intercept identifiable, it is essential to have additional location constraint on the random errors. We adopt the commonly used constraint that ε_i has median zero. Given (β̂^T, α̂₂)^T, we estimate a₀(u₀) by α̂₁, the value of α₁ that minimizes

$$n^{-1}\sum _{i=1}^n\left|Y_i-{\alpha }_1-{\widehat{\alpha }}_2(U_i-u_0)-\sum _{m=1}^p[{\widehat{\beta }}_m+{\widehat{\beta }}_{p+m}(U_i-u_0)]X_{im}\right|K_h(U_i-u_0),$$ (5)

which is a local version of a weighted L₁-norm objective function.

3 Theoretical Properties

3.1 Large sample distributions

In this subsection, we investigate the asymptotic properties of β̂ and α̂₂. The main challenge comes from the non-smoothness of the objective function Q_n(β, α₂). To overcome this difficulty, we first derive an asymptotic representation of β̂ and α̂₂ via a quadratic approximation of Q_n(β, α₂), which holds uniformly in a local neighborhood of the true parameter values. Aided with this asymptotic representation, we further establish the asymptotic normality of the local rank estimator.

Let us begin with some new notation. Let γ_n = (nh)^−1/2, and define

$$\begin{array}{l}{\mathit{\beta }}^{\ast }={\gamma }_n^{-1}{({\beta }_1-a_1(u_0),\dots ,{\beta }_p-a_p(u_0),h({\beta }_{p+1}-a_1^{\prime }(u_0)),\dots ,h({\beta }_{2p}-a_p^{\prime }(u_0)))}^T,\\ {\mathit{\alpha }}^{\ast }={({\alpha }_1^{\ast },{\alpha }_2^{\ast })}^T={\gamma }_n^{-1}{({\alpha }_1-a_0(u_0),h({\alpha }_2-a_0^{\prime }(u_0)))}^T\\ {\mathrm{\Delta }}_i(u_0)=\sum _{m=1}^p[a_m(U_i)-a_m(u_0)-a_m^{\prime }(u_0)(U_i-u_0)]X_{im}\\ +[a_0(U_i)-a_0(u_0)-a_0^{\prime }(u_0)(U_i-u_0)].\end{array}$$

Let ${({\widehat{\mathit{\beta }}}_n^{\ast T},{\widehat{\alpha }}_{2n}^{\ast })}^T$ be the value of ${({\mathit{\beta }}^{\ast T},{\alpha }_2^{\ast })}^T$ that minimizes the following reparametrized objective function

$$\begin{array}{l}{Q}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })=\frac{1}{n(n-1)}\sum _{1\le i,j\le n}|({\epsilon }_i-{\gamma }_n{\alpha }_2^{\ast }(U_i-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_i+{\mathrm{\Delta }}_i(u_0))\\ -({\epsilon }_j-{\gamma }_n{\alpha }_2^{\ast }(U_j-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_j+{\mathrm{\Delta }}_j(u_0))|K_h(U_i-u_0)K_h(U_j-u_0),\end{array}$$ (6)

Where ${\mathbf{Z}}_i={({\mathbf{X}}_i^T,((U_i-u_0)/h){\mathbf{X}}_i^T)}^T$. Let H = diag(1, h)⊗I_p, where ⊗ denotes the operation of Kronecker product and I_p denotes a p × p identity matrix. Then it can be easily seen that

$${\widehat{\mathit{\beta }}}_n^{\ast }=\sqrt{nh}\mathbf{H}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\text{and}{\widehat{\alpha }}_{2n}^{\ast }=\sqrt{n{h}^3}[{\widehat{\alpha }}_2-a_0^{\prime }(u_0)].$$

We next show that the non-smooth function $Q_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$ can be locally approximated by a quadratic function of ${({\mathit{\beta }}^{\ast T},{\alpha }_2^{\ast })}^T$. Let μ_i = ∫ tⁱK(t)dt, i = 1, 2, and ν_i = ∫ tⁱK²(t)dt, i = 0, 1, 2. In this paper, we assume that the kernel function K(·) is symmetric. This is not restrictive considering that most of the commonly used kernel functions, such as the Epanechnikov kernel K(t) = 0.75(1 − t²)I(|t| < 1), are symmetric. We use $S_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })={(S_{n1}^T({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast }),S_{n2}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast }))}^T$ to denote the gradient function of $Q_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$, i.e., $S_{n1}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })={\nabla }_{{\mathit{\beta }}^{\ast }}{Q}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$ and $S_{n2}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })={\nabla }_{{\alpha }_2^{\ast }}{Q}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$. More specifically,

$$\begin{array}{l}{S}_{n1}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })=2{\gamma }_n{[n(n-1)]}^{-1}\sum _{i\ne j}[I({\epsilon }_i-{\gamma }_n{\alpha }_2^{\ast }(U_i-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j\\ -{\gamma }_n{\alpha }_2^{\ast }(U_j-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_j+{\mathrm{\Delta }}_j(u_0))-1/2]({\mathbf{Z}}_i-{\mathbf{Z}}_j)K_h(U_i-u_0)K_h(U_j-u_0),\end{array}$$

and

$$\begin{array}{l}{S}_{n2}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })=2{\gamma }_n{[n(n-1)]}^{-1}\sum _{i\ne j}[I({\epsilon }_i-{\gamma }_n{\alpha }_2^{\ast }(U_i-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j\\ -{\gamma }_n{\alpha }_2^{\ast }(U_j-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_j+{\mathrm{\Delta }}_j(u_0))-1/2]((U_i-U_j)/h)K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$

Furthermore, we consider the following quadratic function of ${({\mathit{\beta }}^{\ast T},{\alpha }_2^{\ast })}^T$:

$$B_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })={\gamma }_n^{-1}({\mathit{\beta }}^{\ast T},{\alpha }_2^{\ast })\left(\begin{array}{c}{S}_{n1}(\mathbf{0},0)\\ S_{n2}(\mathbf{0},0)\end{array}\right)+\frac{1}{2}{\gamma }_n({\mathit{\beta }}^{\ast T},{\alpha }_2^{\ast })\mathbf{A}\left(\begin{array}{c}{\mathit{\beta }}^{\ast }\\ {\alpha }_2^{\ast }\end{array}\right)+{\gamma }_n^{-1}{Q}_n^{\ast }(\mathbf{0},0),$$ (7)

where

$$\mathbf{A}=4\tau f^2(u_0)\left(\begin{array}{ccc}\mathrm{\sum }(u_0)& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mu }_2\mathrm{\sum }(u_0)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mu }_2\end{array}\right),$$ (8)

$\mathrm{\sum }(u_0)=E[{\mathbf{X}}_i{\mathbf{X}}_i^T\mid U_i=u_0]$, 0 denotes a matrix (or vector) of zeroes whose dimension is determined by the context, τ = ∫ g²(t)dt is the Wilcoxon constant, and g(·) is the density function of the random error ε.

Lemma 3.1

Suppose that Conditions (C1) — (C4) in the Appendix hold. Then ∀ ε > 0, ∀ c > 0,

$$P\left[\underset{\mid \mid ({\mathit{\beta }}^{\ast T},{\alpha }_2^{\ast })\mid \mid \le c}{sup}\left|{\gamma }_n^{-1}{Q}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })-B_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })\right|\ge \epsilon \right]\to 0,$$

where || · || denotes the Euclidean norm.

Lemma 3.1 implies that the non-smooth objective function $Q_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$ can be uniformly approximated by a quadratic function $B_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$ in a neighborhood around 0. In the appendix, it is also shown that the minimizer of $B_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$ is asymptotically within a o(1) neighborhood of ${({\widehat{\mathit{\beta }}}_n^{\ast T},{\widehat{\alpha }}_{n2}^{\ast })}^T$. This further allows us to derive the asymptotic distribution.

The local linear Wilcoxon estimator of a(u₀) = (a₁(u₀), …, a_p(u₀))^T is â(u₀). The theorem below provides an asymptotic representation of â(u₀) and the asymptotic normal distribution. Let $S_{n1}(\mathbf{0},0)={(S_{n11}^T(\mathbf{0},0),S_{n12}^T(\mathbf{0},0))}^T$, where S_n11(0, 0) and S_n12(0, 0) are both p × 1 vectors.

Theorem 3.2

Suppose that Conditions (C1) — (C4) in the Appendix hold. Then we have the following asymptotic representation

$$\sqrt{nh}[\widehat{\mathbf{a}}(u_0)-\mathbf{a}(u_0)]=-{\gamma }_n^{-2}{[4\tau f^2(u_0)\mathrm{\sum }(u_0)]}^{-1}{S}_{n11}(\mathbf{0},0)+o_P(1),$$ (9)

where f(u) is the density function of U. Furthermore,

$$\sqrt{nh}\left[\widehat{\mathbf{a}}(u_0)-\mathbf{a}(u_0)-\frac{{\mu }_2}{2}{\mathbf{a}}^{″}(u_0)h^2+o(h^2)\right]\to \mathbf{N}\left(0,\frac{{\nu }_0}{12{\tau }^{2}f(u_0)}{\mathrm{\sum }}^{-1}(u_0)\right)$$ (10)

in distribution, where ${\mathbf{a}}^{″}(u_0)={(a_1^{″}(u_0),\dots ,a_p^{″}(u_0))}^T$.

Remark

For the estimators of the derivatives of the coefficient functions, we have the following asymptotic representations:

$$\sqrt{n{h}^3}[{\widehat{\alpha }}_2-a_0^{\prime }(u_0)]=-{\gamma }_n^{-2}{[4\tau f^2(u_0){\mu }_2]}^{-1}{S}_{n2}(\mathbf{0},0)+o_P(1),$$ (11)

$$\sqrt{n{h}^3}[{\widehat{\mathbf{a}}}^{\prime }(u_0)-{\mathbf{a}}^{\prime }(u_0)]=-{\gamma }_n^{-2}{[4\tau f^2(u_0){\mu }_2\mathrm{\sum }(u_0)]}^{-1}{S}_{n12}(\mathbf{0},0)+o_P(1).$$ (12)

Following similar proof as that for Theorem 3.2 in the appendix, it can be shown that $\sqrt{n{h}^3}[{\widehat{\alpha }}_{n2}-a_0^{\prime }(u_0)]$ and $\sqrt{n{h}^3}[{\widehat{\mathbf{a}}}^{\prime }(u_0)-{\mathbf{a}}^{\prime }(u_0)]$ are both asymptotically normal. The proof of the asymptotic normality of α̂₂ and â′(u₀) is given in the technical report version of this paper ((Wang, Kai and Li, 2009).

3.2 Asymptotic relative efficiency

We now compare the estimation efficiency of the local rank estimator (denoted by b â_R(u₀)) with that of the local linear least squares estimator (denoted by â_LS(u₀)) for estimating a(u₀) in the varying coefficient model. To measure efficiency, we consider both the asymptotic mean squared error (MSE) at a given u₀ and the asymptotic mean integrated squared error (MISE). When evaluating both criteria, we plug in the theoretical optimal bandwidth.

Zhang and Lee (2000) gives the asymptotic MSE of â_LS(u₀) for estimating a(u₀):

$${\text{MSE}}_{LS}(h;u_0)=E\mid \mid {\widehat{\mathbf{a}}}_{LS}(u_0)-\mathbf{a}(u_0)\mid {\mid }^2=\frac{{\mu }_2^2\mid \mid {\mathbf{a}}^{″}(u_0)\mid {\mid }^2}{4}{h}^4+\frac{{\nu }_0{\sigma }^2}{f(u_0)}\text{tr}\{{\mathrm{\sum }}^{-1}(u_0)\}\frac{1}{nh},$$

where σ² = var(ε) is assumed to be finite and positive. Thus, the theoretical optimal bandwidth, which minimizes the asymptotic MSE of â_LS(u₀), is

$$h_{LS}^{\mathit{opt}}(u_0)={\left[\frac{{\nu }_0{\sigma }^2\text{tr}\{{\mathrm{\sum }}^{-1}(u_0)\}}{{\mu }_2^2\mid \mid {\mathbf{a}}^{″}(u_0)\mid {\mid }^{2}f(u_0)}\right]}^{1/5}{n}^{-1/5}.$$ (13)

From (10), the asymptotic MSE of the local rank estimator â_R(u₀) is

$${\text{MSE}}_R(h;u_0)=E\mid \mid {\widehat{\mathbf{a}}}_R(u_0)-\mathbf{a}(u_0)\mid {\mid }^2=\frac{{\mu }_2^2\mid \mid {\mathbf{a}}^{″}(u_0)\mid {\mid }^2}{4}{h}^4+\frac{{\nu }_0}{12{\tau }^{2}f(u_0)}\text{tr}\{{\mathrm{\sum }}^{-1}(u_0)\}\frac{1}{nh}.$$

The theoretical optimal bandwidth for the local rank estimator thus is

$$h_R^{\mathit{opt}}(u_0)={\left[\frac{{\nu }_0\text{tr}\{{\mathrm{\sum }}^{-1}(u_0)\}}{12{\tau }^2{\mu }_2^2\mid \mid {\mathbf{a}}^{″}(u_0)\mid {\mid }^{2}f(u_0)}\right]}^{1/5}{n}^{-1/5}.$$ (14)

This allows us to calculate the local asymptotic relative efficiency.

Theorem 3.3

The asymptotic relative efficiency of the local rank estimator to the local linear least squares estimator for a(u₀) is

$$\mathit{ARE}(u_0)=\frac{{\mathit{MSE}}_{LS}\{h_{LS}^{\mathit{opt}}(u_0),u_0\}}{{\mathit{MSE}}_R\{h_R^{\mathit{opt}}(u_0),u_0\}}={(12{\sigma }^2{\tau }^2)}^{4/5}.$$

This asymptotic relative efficiency has a lower bound 0.8896, which is attained at the random error density $f(t)=\frac{3}{20\sqrt{5}}(5-x^2)I(\mid x\mid \le 5)$.

Remark 1

Alternatively, we may consider the asymptotic relative efficiency obtained by comparing the MISE, which is defined as MISE(h) = ∫ E||â(u) − a(u)||²w(u) du with a weight function w(·). This provides a global measurement. Interestingly, it leads to the same relative efficiency. This follows by observing that the theoretical optimal global bandwidths for the local linear least squares estimator and the local rank estimator are

$$h_{LS}^{\mathit{opt}}={\left[\frac{{\nu }_0{\sigma }^2\int w(u)\text{tr}\{{\mathrm{\sum }}^{-1}(u)\}/f(u)du}{{\mu }_2^2\int \mid \mid {\mathbf{a}}^{″}(u)\mid {\mid }^{2}w(u)du}\right]}^{1/5}{n}^{-1/5},$$ (15)

and

$$h_R^{\mathit{opt}}={\left[\frac{{\nu }_0\int w(u)\text{tr}\{{\mathrm{\sum }}^{-1}(u)\}/f(u)du}{12{\tau }^2{\mu }_2^2\int \mid \mid {\mathbf{a}}^{″}(u)\mid {\mid }^{2}w(u)du}\right]}^{1/5}{n}^{-1/5},$$ (16)

respectively. Thus, with the theoretical optimal bandwidths,

$$\text{ARE}=\frac{{\text{MISE}}_{LS}(h_{LS}^{\mathit{opt}})}{{\text{MISE}}_R(h_R^{\mathit{opt}})}={(12{\sigma }^2{\tau }^2)}^{4/5}.$$

Define φ = (12σ²τ²)^4/5. Then ARE(u₀) = ARE = φ.

Note that the above ARE is closely related to the asymptotic relative efficiency of the Wilcoxon-Mann-Whitney rank test in comparison with the two-sample t-test. Table 1 depicts the value of φ for some commonly used error distributions. It can be seen that the desirable high efficiency of traditional rank methods for estimating a finite-dimensional parameter completely carries over to the local rank method for estimating an infinite dimensional parameter.

Table 1.

Asymptotic Relative Efficiency

Error	Normal	Laplace	t3	Exponential	Log N	Cauchy
φ	0.9638	1.3832	1.6711	2.4082	4.9321	∞
ψ	0.9671	1.3430	1.5949	2.2233	4.2661	∞

By a similar calculation, we can show that the asymptotic relative efficiencies of the local rank estimator to the local linear estimator for a′(u₀) and a′(·) both equal ψ = (12σ²τ²)^8/11, which has a lower bound 0.8991. This value is also reported in Table 1 for some common error distributions.

Remark 2

We may also apply the local median approach (Yu and Jones, 1998) to estimate the coefficient functions and their first derivatives. Similarly, we can prove that such estimators are asymptotically normal. The ARE of the local median estimator versus the local linear least squares estimator is closely related to that of the sign test versus the t-test. It is known that the ARE of the sign test versus the t-test for the normal distribution is 0.63. Thus we expect the efficiency loss of the local median procedure to be substantial for normal random error.

3.3 Asymptotic normality of α̂₁

Following (5), ${\widehat{\alpha }}_1^{\ast }=\sqrt{nh}\{{\widehat{\alpha }}_1-a_0(u_0)\}$ is the value of ${\alpha }_1^{\ast }$ that minimizes

$$\begin{array}{l}{Q}_{n0}^{\ast }({\alpha }_1^{\ast },{\widehat{\alpha }}_2,\widehat{\mathit{\beta }})=n^{-1}\sum _{i=1}^n|{\epsilon }_i-{\gamma }_n{\alpha }_1^{\ast }-({\widehat{\alpha }}_2-a_0^{\prime }(u_0))(U_i-u_0)\\ -\sum _{m=1}^p[({\widehat{\beta }}_m-a_m(u_0))+({\widehat{\beta }}_{p+m}-a_m^{\prime }(u_0))(U_i-u_0)]X_{im}+{\mathrm{\Delta }}_i(u_0)|K_h(U_i-u_0).\end{array}$$

Similarly as Lemma 3.1, we can establish the following local quadratic approximation which holds uniformly in a neighborhood around 0:

$${\gamma }_n^{-1}{Q}_{n0}^{\ast }({\alpha }_1^{\ast },{\widehat{\alpha }}_2,\widehat{\mathit{\beta }})={\gamma }_n^{-1}{\alpha }_1^{\ast }{S}_{n0}+{\gamma }_{n}g(0)f(u_0){\alpha }_1^{\ast 2}+{\gamma }_n^{-1}{Q}_{n0}^{\ast }(0,a_0^{\prime }(u_0),{\mathit{\beta }}_0)+o_p(1),$$ (17)

where

$$S_{n0}=2{\gamma }_n{n}^{-1}\sum _{i=1}^n[I({\epsilon }_i\le -{\mathrm{\Delta }}_i(u_0))-1/2]K_h(U_i-u_0).$$ (18)

This further leads to an asymptotic representation of α̂₁:

$$\sqrt{nh}({\widehat{\alpha }}_1-a_0(u_0))=-{\gamma }_n^{-2}{[2g(0)f(u_0)]}^{-1}{S}_{n0}+o_p(1).$$ (19)

The theorem below gives the asymptotic distribution of α̂₁.

Theorem 3.4

Under the conditions of Theorem 3.2, we have

$$\sqrt{nh}\left[{\widehat{\alpha }}_1-a_0(u_0)-\frac{{\mu }_2{a}_0^{″}(u_0)}{2}{h}^2+o(h^2)\right]\to \mathbf{N}\left(0,{[12g^2(0)f(u_0)]}^{-1}{\nu }_0\right).$$

3.4 Estimation of the standard errors

To make statistical inference based on the local rank methodology, one needs to estimate the standard error of the resulting estimator. As indicated by Theorem 3.2, the asymptotic covariance matrix of the local rank estimator is rather complex and involves unknown functions. Here we propose a standard error estimator using a simple resampling method proposed by Jin, Ying and Wei (2001).

Let V₁, …, V_n be independent and identically distributed nonnegative random variables with mean 1/2 and variance 1. We consider a stochastic perturbation of (4):

$${\overline{Q}}_n(\mathit{\beta },{\alpha }_2)=\frac{1}{n(n-1)}\sum _{1\le i,j\le n}(V_i+V_j)\mid e_i-e_j\mid K_h(U_i-u_0)K_h(U_j-u_0),$$ (20)

where e_i is defined in (3). In Q̄_n(β, α₂), the data {Y_i, U_i, X_i} are considered to be fixed, and the randomness comes from the V_i’s. Let (β̄^T, ᾱ₂)^T be the value of (β^T, α₂)^T that minimizes Q̄_n(β, α₂). It is easy to obtain (β̄^T, ᾱ₂)^T by applying a simple algorithm described in Section 3.1.

Jin, Ying and Wei (2001) established the validity of the resampling method when the objective function has a U-statistics structure. Although their theory covers many important applications, they require that the U-statistic has a fixed kernel. We extend their result to our setting, where the U-statistic involves variable kernel due to nonparametric smoothing. Let ā(u₀) be the local rank estimator of a(u₀) based on the perturbed objective function (20), i.e., it is the subvector that consists of the first p components of β̄. Its asymptotic normality is given in the theorem below.

Theorem 3.5

Under the conditions of Lemma 3.1, conditional on almost surely every sequence of data {Y_i; U_i; X_i},

$$\sqrt{nh}[\overline{\mathbf{a}}(u_0)-\widehat{\mathbf{a}}(u_0)]\to \mathbf{N}\left(0,\frac{{\nu }_0}{12{\tau }^{2}f(u_0)}{\mathrm{\sum }}^{-1}(u_0)\right)$$

in distribution.

This theorem suggests that to estimate the asymptotic covariance matrix of b â(u₀), one can repeatedly perturb (4) by generating a large number of independent random samples ${\left\{V_i\right\}}_{i=1}^n$. For each perturbed objective function, one solves for ā(u₀). The sample covariance matrix of ā(u₀) based on a large number of independent perturbations provides a good approximation. The accuracy of the resulting standard error estimate will be tested in the next section.

The perturbed estimator has conditional bias equal to zero. It has been found that standard bootstrap method, which resamples from the empirical distribution of the data, also estimates bias as zero when estimating nonparametric curves (Hall and Kang, 2001). It is possible to use more delicate bootstrap technique to estimate the bias of a nonparametric curve estimator. Although some of the ideas may be adapted to the method of disturbing the objective function, this is beyond the scope of our paper and is not pursued further here.

4 Numerical Studies

4.1 A pseudo-observation algorithm

The local rank estimator can be obtained by applying an efficient and reliable algorithm. Note that the local rank estimator of ${({\mathit{\beta }}_0^T,a_0^{\prime }(u_0))}^T$ can be solved by fitting a weighted L₁ regression on $\frac{n(n-1)}{2}$ pseudo observations ( ${\mathbf{x}}_i^{\ast }-{\mathbf{x}}_j^{\ast }$, Y_i-Y_j) with weights w_ij = K((U_i − u₀)/h)K((U_j − u₀)/h), where ${\mathbf{x}}_i^{\ast }={(U_i-u_0,X_i^T,(U_i-u_0)X_i^T)}^T$, 1 ≤ i < j ≤ n. Given (β̂^T, α̂₂)^T, the estimator of a₀(u₀) can be obtained by another weighted L₁ regression on (1, $Y_i-{\widehat{\alpha }}_2(U_i-u_0)-{\sum }_{m=1}^p[{\widehat{\beta }}_m+{\widehat{\beta }}_{p+m}(U_i-u_0)]X_{im}$) With weights w_i = K((U_i − u₀)/h), 1 ≤ i ≤ n. Many statistical software packages can implement weighted L₁ regression. In our numerical studies, we use the function “rq” in the R package quantreg.

4.2 Bandwidth selection

Bandwidth selection is an important issue for all statistical models that involve nonparametric smoothing. Although we have derived the theoretical optimal bandwidth for the local rank estimator in (14) and (16), it is difficult to use the “plug-in“ method to estimate it due to many unknown quantities.

We propose below an alternative bandwidth selection method that is practically feasible. This approach is based on the relationship between $h_R^{\mathit{opt}}$ and $h_{LS}^{\mathit{opt}}$. From Section 2.3, we see that

$$h_R^{\mathit{opt}}(u_0)={\left(\frac{1}{12{\tau }^2{\sigma }^2}\right)}^{1/5}{h}_{LS}^{\mathit{opt}}(u_0)\text{and}{h}_R^{\mathit{opt}}={\left(\frac{1}{12{\tau }^2{\sigma }^2}\right)}^{1/5}{h}_{LS}^{\mathit{opt}}.$$ (21)

Thus, we can first use existing bandwidth selectors (e.g. Zhang and Lee 2000) to estimate $h_{LS}^{\mathit{opt}}(u_0)$ or $h_{LS}^{\mathit{opt}}$. The error variance σ² can be estimated based on the residuals; in particular when robustness is of concern it can be estimated using the MAD of the residuals. Hettmansperger and Mckean (1998, p.181) discussed in details how to estimate τ, which can be obtained by the function “wilcoxontau” in the R software developed by Terpstra and McKean (2005). In the end, we plug in these estimators into (21) to get the bandwidth for local rank estimator.

Alternatively, instead of the above two-step procedure, we may directly use the computationally intensive cross-validation to estimate the bandwidth for the local rank procedure. Note that under outlier contamination, standard cross-validation can lead to extremely biased bandwidth estimates because it can be adversely influenced by extreme prediction errors. Robust cross-validation method, such as that developed by Leung (2005), is therefore preferred.

4.3 Examples

We conduct Monte Carlo simulations to access the finite sample performance, and illustrate the proposed methodology on a real environmental data set. In the analysis, we use the Epanechnikov kernel K(u) =.75(1 − u²)I(|u| < 1).

Example 1

We generate random data from

$$Y=a_0(U)+a_1(U)X_1+a_2(U)X_2+\epsilon ,$$

where a₀(u) = exp(2u − 1), a₁(u) = 8u(1 − u) and a₂(u) = 2 sin²(2πu). The covariate U follows a uniform distribution on [0, 1], and is independent from (X₁, X₂), where the covariates X₁ and X₂ are standard normal random variables with correlation coefficient 2^−1/2. The coefficient functions and the mechanism to generate U and (X₁, X₂) are the same as those in Cai, Fan and Li (2000). We consider six different error distributions: N(0, 1), Laplace, standard Cauchy, t-distribution with 3 degrees of freedom, mixture of normals 0.9N(0, 1) + 0.1N(0, 10²) and lognormal distribution. Except for Cauchy error, all the other generated random errors are standardized to have median 0 and variance 1. We consider sample sizes n =400 and 800, and conduct 400 simulations for each case.

We compare the performance of the local rank estimate with the local least squares estimate using the square root of average squared errors (RASE), defined by

$$\text{RASE}={\left\{\frac{1}{n_{\text{grid}}}\sum _{m=1}^p\sum _{k=1}^{n_{\text{grid}}}{\{{\widehat{a}}_m(u_k)-a_m(u_k)\}}^2\right\}}^{1/2},$$

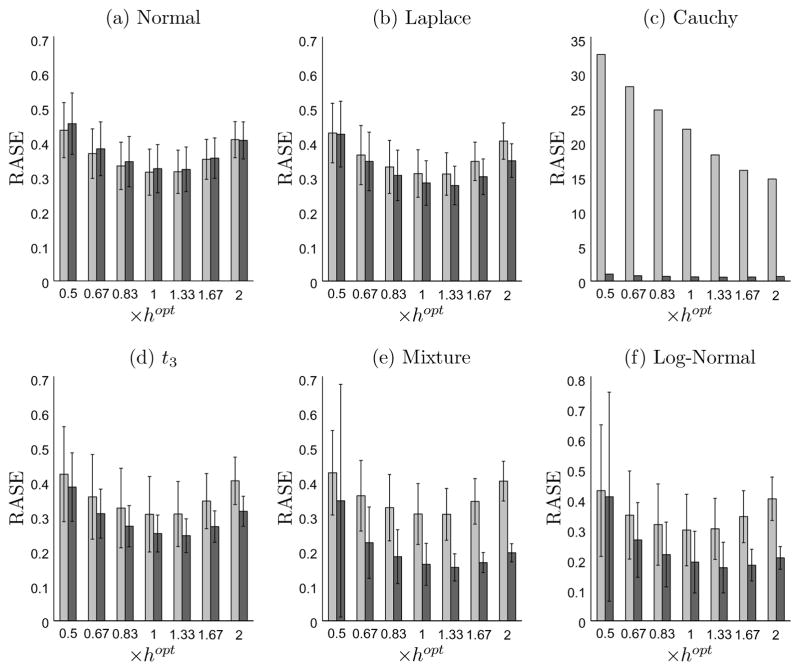
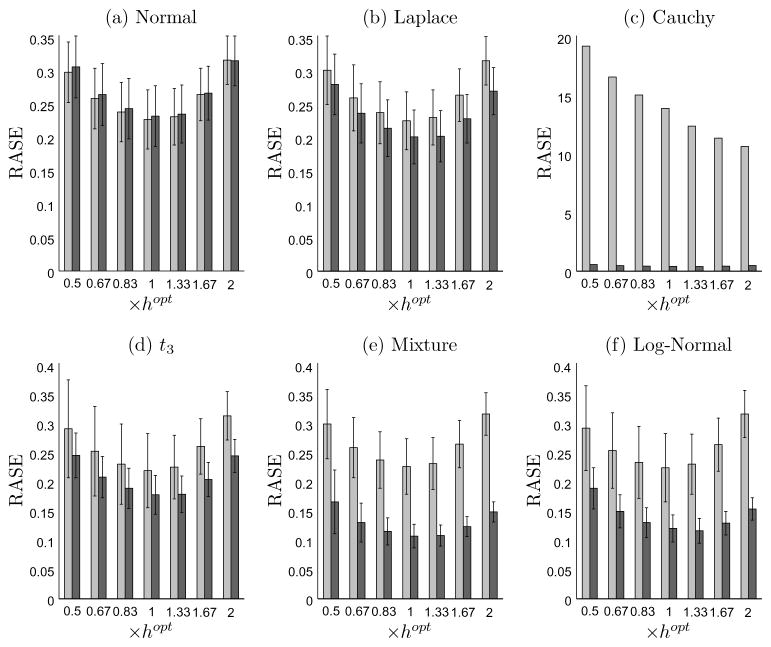
where {u_k: k = 1, ···, n_grid} is a set of grid points uniformly placed on [0, 1] with n_grid = 200. The sample mean and standard deviation of the RASEs over 400 simulations are presented in Figure 1 and Figure 2, for sample size n = 400 and 800, respectively. The two figures clearly demonstrate that the local rank estimator performs almost as well as the local least squares estimator for normal random error; and has smaller RASE for other heavier-tailed error distributions. The efficiency gain can be substantial, see for example the mixture normal case where the observed relative efficiency for the local rank estimator versus the local least squares estimator is above 2 for most choices of bandwidth. For Cauchy random error, the local rank estimator yields a $\sqrt{n}$-consistent estimator but the local least squares estimator is inconsistent, which is reflected by the extremely large value of RASE for the local least squares estimator.

Figure 1.

Bar graphs of the RASE with standard error for sample size n = 400 over 400 simulations. The light gray bar denotes the local least squares method and the dark gray bar denotes the local rank method. The horizontal axis is in the unit of h^opt, which is calculated separately for each method and error specification using either (13) or (14).

Figure 2.

Bar graphs of the RASE with standard error for sample size n = 800 over 400 simulations. The light gray bar denotes the local least squares method and the dark gray bar denotes the local rank method. The horizontal axis is in the unit of h^opt, which is calculated separately for each method and error specification using either (13) or (14).

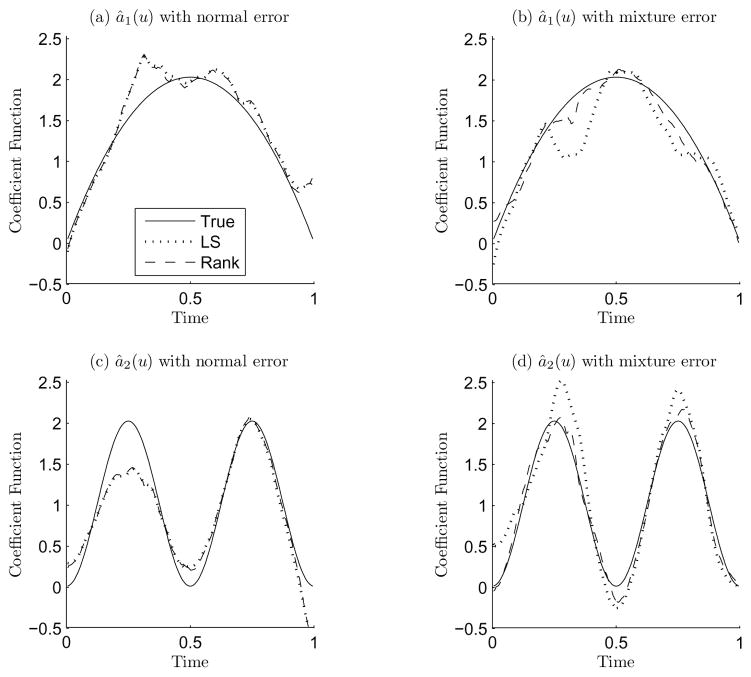
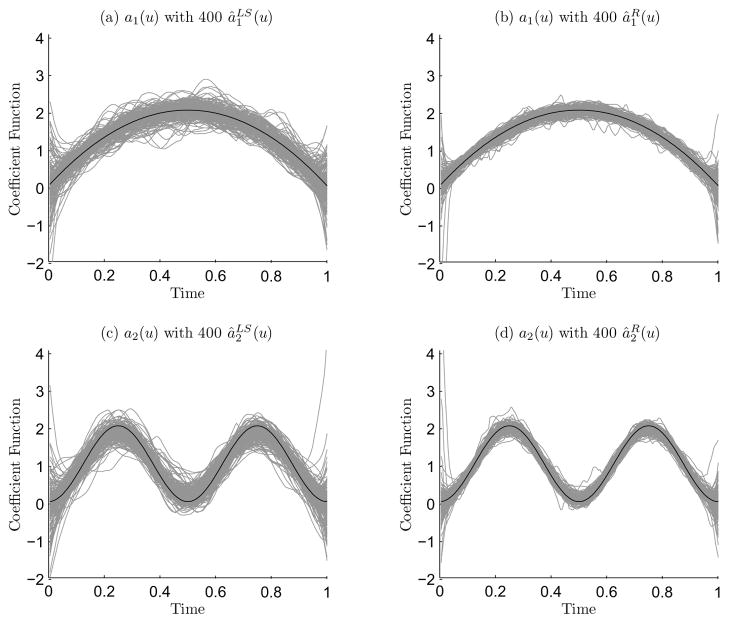
Figure 3 depicts the estimated coefficient functions for the normal random error and the mixture normal random error for a typical sample, which is selected in such a way that its RASE value is the median of the 400 RASE values. For this typical sample, we observe that the local rank estimator is almost identical to the local least squares estimator for normal random error; but falls much closer to the truth than the local least squares estimator does for mixture normal random error. Figure 4 plots the estimated coefficient functions for all 400 simulations when the random error has a mixture of normal distribution. It is clear that the local rank estimator has smaller variance. In these two figures, we set the bandwidth to be the theoretic optimal one h^opt, calculated using (15) and (16), for both the local rank estimator and the local least squares estimator.

Figure 3.

Plot of estimated coefficient functions for a typical data set

Figure 4.

(a) and (c) are plots of 400 local least squares estimators of a₁(·) and a₂(·) over 400 simulation, respectively. (b) and (d) are plots of 400 local rank estimators of a₁(·) and a₂(·), respectively.

At the end, we evaluate the resampling method (Section 3.4) for estimating the standard errors. We randomly perturb the objective function 1000 times; each time the random variables V_i in (20) are generated from the Gamma(0.25, 2) distribution. Table 2 summarizes the simulation results at three points u₀ = 0.25, 0.50 and 0.75. In the table, ‘SD’denotes the standard deviation of 400 estimated â_m(u₀) and can be regarded as the true standard error; ‘SE(std(SE))’ denotes the mean (standard deviation) of 400 estimated standard errors from the resampling method. Bandwidths are set to be the optimal ones. We observe that the resampling method estimates the standard error very accurately.

Table 2.

Standard deviations of the local rank estimators with n = 400

		â1(u)		â2(u)
Error	u0	SD	SE(Std(SE))	SD	SE(Std(SE))
Normal	0.25	0.189	0.159(0.032)	0.197	0.160(0.032)
	0.5	0.183	0.159(0.030)	0.180	0.162(0.031)
	0.75	0.191	0.162(0.033)	0.195	0.163(0.032)
Laplace	0.25	0.175	0.151(0.037)	0.174	0.151(0.037)
	0.5	0.168	0.153(0.039)	0.173	0.154(0.039)
	0.75	0.168	0.150(0.037)	0.177	0.150(0.037)
Mixture	0.25	0.095	0.107(0.051)	0.092	0.107(0.049)
	0.5	0.095	0.109(0.057)	0.091	0.109(0.055)
	0.75	0.095	0.108(0.061)	0.093	0.109(0.055)
t3	0.25	0.144	0.137(0.039)	0.145	0.138(0.036)
	0.5	0.148	0.133(0.035)	0.152	0.136(0.037)
	0.75	0.158	0.137(0.039)	0.155	0.139(0.042)
Log N	0.25	0.111	0.112(0.047)	0.112	0.114(0.049)
	0.5	0.106	0.114(0.047)	0.107	0.119(0.050)
	0.75	0.118	0.117(0.058)	0.118	0.120(0.060)

Example 2

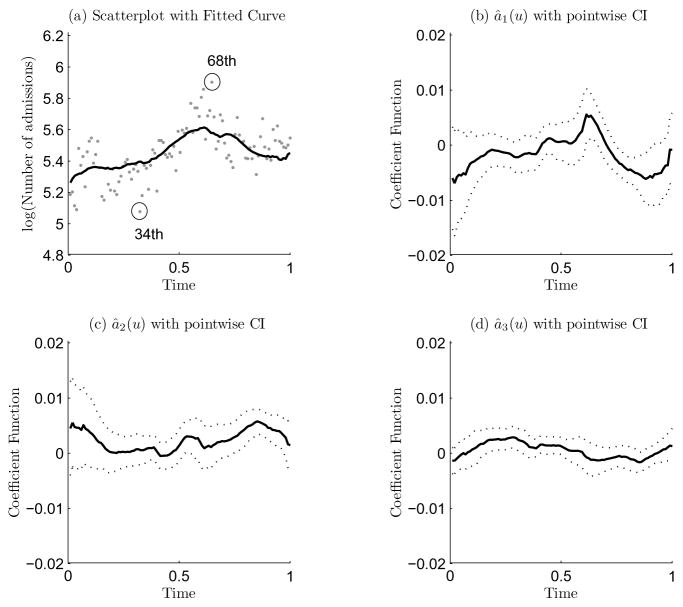
As an illustration, we now apply the local rank procedure to the environmental data set in Fan and Zhang (1999). Of interest is to study the relationship between levels of pollutants and the number of total hospital admissions for circulatory and respiratory problems on every Friday from January 1, 1994 to December 31, 1995. The response variable is the logarithm of the number of total hospital admissions, and the covariates include the level of sulfur dioxide (X₁), the level of nitrogen dioxide (X₂) and the level of dust (X₃). A scatter plot of the response variable over time is given in Figure 5(a). We analyze this data set using the following varying coefficient model

Figure 5.

(a) Scatterplot of the log of number of total hospital admissions over time, and the solid curve is an estimator of the expected log of number of hospital admissions over time at the average pollutant levels, i.e., â₀(u) + â₁(u)X̄₁ + â₂(u)X̄₂ + â₃(u)X̄₃, (b), (c) and (d) are the estimated coefficient functions via the local rank estimator for a_k(·), k = 1, 2, and 3, respectively.

$$Y=a_0(u)+a_1(u)X_1+a_2(u)X_2+a_3(u)X_3+\epsilon ,$$

where u denotes time and is scaled to the interval [0,1].

We select the bandwidth via the relation (21). More specifically, we first use 20-fold cross-validation to select a bandwidth ĥ_LS for the local least squares estimator. We then use the function ‘wilcoxontau’ in the R package for rank regression by Terpstra and McKean to estimate (12τ²)^−1/2 and use the MAD of the residuals to robustly estimate σ. All these lead to the selected bandwidth for the local rank estimator: ĥ_R = 0.26.

The estimated coefficient functions are depicted in Figures 5(b), (c) and (d), where the two dashed curves around the solid line are the estimated function plus/minus twice the standard errors estimated by the resampling method. These two dashed lines can be regarded as a pointwise confidence interval with bias ignored. The figures suggest clearly that the coefficient functions vary with time. The fitted curve is shown in Figure 5(a).

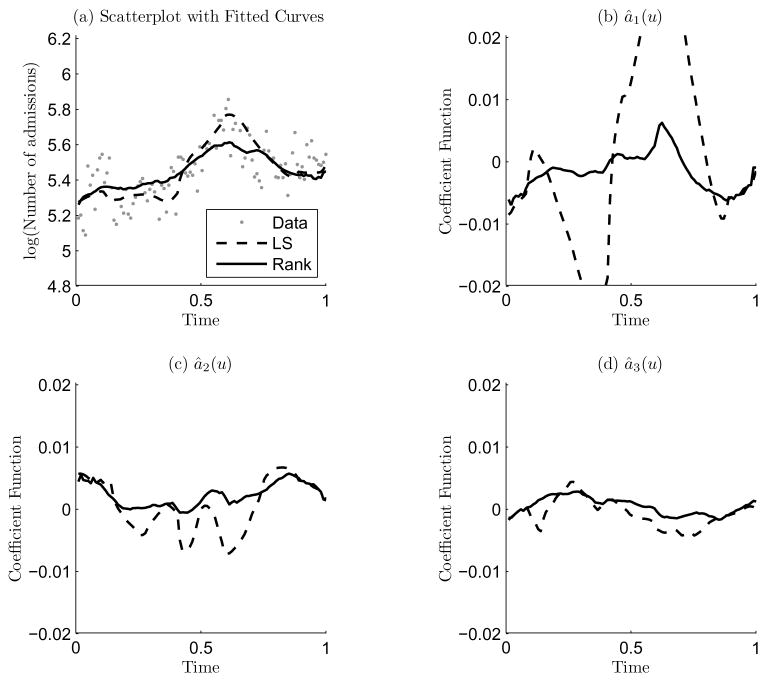
Now we demonstrate the robustness of the local rank procedure. To this end, we artificially perturb the dataset by moving the response value of the 68^th observation from 5.89 to 6.89, and the response value of the 34^th observation from 5.07 to 3.07. We refit the data with both the local least squares procedure and the local rank procedure, see Figure 6. We observe that the local least squares estimator changes dramatically due to the presence of these two artificial outliers. In contrast, the local rank estimator is nearly unaffected.

Figure 6.

(a) Scatterplot of the perturbed data (without the two outliers shown as they are outside of the range), and the local LS and the local rank estimators of the expected log of number of hospital admissions. (b), (c) and (d) are the local LS and the rank estimators of the coefficient functions for a_k(·), k = 1, 2, and 3, respectively.

Appendix: Proofs

Regularity conditions

• (C1). Assume that {U_i, X_i, Y_i} are independent and identically distributed, and that the random error ε and the covariate {U, X} are independent. Furthermore, assume that ε has probability density function g(·) which has finite Fisher information, i.e., ∫{g(x)}⁻¹g′(x)²dx < ∞; and that U has probability density function f(·).

• (C2). The function a_m(·), m = 0, 1,…, p, has continuous second-order derivative in a neighborhood of u₀.

• (C3). Assume that E(X_i|U_i = u₀) = 0 and that $\mathrm{\sum }(u)=E(X_i{X}_i^T\mid U_i=u)$ is continuous at u = u₀. The matrix Σ(u₀) is positive definite.

  (C4). The kernel function K(·) is symmetric about the origin, and has a bounded support. Assume that h → 0 and nh² → ∞, as n → ∞

These conditions are used to facilitate the proofs, but may not be the weakest ones. The assumptions on the random errors in (C1) are the same as those for multiple linear rank regression (Hettmansperger and McKean, 1998). (C2) imposes smoothness requirement on the coefficient functions. In (C3), the assumption E(X_i|U_i = u₀) = 0 (also adopted by Kim, 2007) makes the presentation simpler but can be relaxed. It can be shown that the asymptotic normality still holds without this assumption. The conditions on the kernel function and bandwidth in (C4) are common for nonparametric kernel smoothing.

In our proofs, we will use some results on generalized U-statistic, where the kernel function is allowed to depend on the sample size n. The generalized U-statistic has the form U_n = [n(n − 1)]⁻¹ΣΣ_i≠j H_n(D_i, D_j), where ${\left\{D_i\right\}}_{i=1}^n$ is a random sample and H_n is symmetric in its arguments, i.e., H_n(D_i, D_j) = H_n(D_j, D_i). In this paper, $D_i={({\mathbf{X}}_i^T,U_i,{\epsilon }_i)}^T$. Define r_n(D_i) = E[H_n(D_i, D_j)|D_i], r̄_n = E[r_n(D_i)] and ${\widehat{U}}_n={\overline{r}}_n+2n^{-1}{\sum }_{i=1}^n[r_n(D_i)-{\overline{r}}_n]$. We will repeatedly use the following lemma taken from Powell, Stock and Stoker (1989).

Lemma A.1

If E[||H_n(D_i, D_j)||²] = o(n), then $\sqrt{n}(U_n-{\widehat{U}}_n)=o_p(1)$ and U_n = r̄_n + o_p(1).

We need the following two lemmas to prove Lemma 3.1. Denote

$$\begin{array}{l}{\mathbf{A}}_{n11}=2h^{-2}E\left\{({\mathbf{Z}}_i-{\mathbf{Z}}_j){({\mathbf{Z}}_i-{\mathbf{Z}}_j)}^{T}K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\right\},\\ {\mathbf{A}}_{n12}=2h^{-2}E\left\{({\mathbf{Z}}_i-{\mathbf{Z}}_j)[(U_i-U_j)/h]K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\right\},\\ {\mathbf{A}}_{n21}={\mathbf{A}}_{n12}^T,\\ A_{n22}=2h^{-2}E\left\{[{(U_i-U_j)}^2/h^2]K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\right\},\end{array}$$

and define

$${\mathbf{A}}_n=\tau \left(\begin{array}{cc}{\mathbf{A}}_{n11}& {\mathbf{A}}_{n12}\\ {\mathbf{A}}_{n21}& A_{n22}\end{array}\right).$$

Lemma A.2

Suppose that Conditions (C1) — (C4) hold, then A_n → A, where A is defined in (8).

Proof

We can write ${\mathbf{A}}_{n11}=\left(\begin{array}{cc}{\mathbf{A}}_{n11}^1& {\mathbf{A}}_{n11}^2\\ {\mathbf{A}}_{n11}^3& A_{n11}^4\end{array}\right)$. Let

$${\mathbf{A}}_{n11}^1=2h^{-2}E\left[({\mathbf{X}}_i-{\mathbf{X}}_j){({\mathbf{X}}_i-{\mathbf{X}}_j)}^{T}K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\right].$$

Calculating the expectation by conditional on U_i and U_j first, A_n11 becomes

$$2h^{-2}\int E[({\mathbf{X}}_i-{\mathbf{X}}_j){({\mathbf{X}}_i-{\mathbf{X}}_j)}^T\mid U_i=u,U_j=v]K\left(\frac{u-u_0}{h}\right)K\left(\frac{v-u_0}{h}\right)f(u)f(v)\mathit{dudv}.$$

Using Condition (C3), straightforward calculation gives ${\mathbf{A}}_{n11}^1\to 4f^2(u_0)\mathrm{\sum }(u_0)$. Let

$${\mathbf{A}}_{n11}^2=2h^{-2}E\left\{({\mathbf{X}}_i-{\mathbf{X}}_j){[{\mathbf{X}}_i(U_i-u_0)/h-{\mathbf{X}}_j(U_j-u_0)/h]}^{T}K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\right\}.$$

Using Condition (C3) and notice that K(·) is symmetric, it can be shown that ${\mathbf{A}}_{n11}^2\to \mathbf{0}$. By symmetry, ${\mathbf{A}}_{n11}^3\to \mathbf{0}$. Similarly, we have

$$\begin{array}{l}{\mathbf{A}}_{n11}^4=2h^{-2}E\{[{\mathbf{X}}_i(U_i-u_0)/h-{\mathbf{X}}_j(U_j-u_0)/h]{[{\mathbf{X}}_i(U_i-u_0)/h-{\mathbf{X}}_j(U_j-u_0)/h]}^T\\ K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\}\to 4f^2(u_0)\mathrm{\sum }(u_0){\mu }_2.\end{array}$$

Thus ${\mathbf{A}}_{n11}\to 4f^2(u_0)\mathrm{\sum }(u_0)\left(\begin{array}{cc}{\mathbf{I}}_p& \mathbf{0}\\ \mathbf{0}& {\mu }_2{\mathbf{I}}_p\end{array}\right)$. Similarly, we can show that ${\mathbf{A}}_{n12}={\mathbf{A}}_{n21}^T\to \mathbf{0}$, and

$$A_{n22}=2\int {(t_1-t_2)}^{2}K(t_1)K(t_2)f(u_0+t_{1}h)f(u_0+t_{2}h){dt}_1{dt}_2\to 4f^2(u_0){\mu }_2.$$

Lemma A.3

Under Conditions (C1) — (C4), we have

$${\gamma }_n^{-1}[S_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })-S_n(\mathbf{0},0)]={\gamma }_n\mathbf{A}\left(\begin{array}{c}{\mathit{\beta }}^{\ast }\\ {\alpha }_2^{\ast }\end{array}\right)+o_p(1).$$

Proof

Let $U_n={\gamma }_n^{-1}[S_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })-S_n(\mathbf{0},0)]={[n(n-1)]}^{-1}\sum {\sum }_{i\ne j}{W}_n(D_i,D_j)$, where

$$\begin{array}{l}{W}_n(D_i,D_j)=2[I({\epsilon }_i-{\gamma }_n{\alpha }_2^{\ast }(U_i-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j-{\gamma }_n{\alpha }_2^{\ast }(U_j-u_0)/h\\ -{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_j+{\mathrm{\Delta }}_j(u_0))-1/2]\left(\begin{array}{c}{\mathbf{Z}}_i-{\mathbf{Z}}_j\\ (U_i-U_j)/h\end{array}\right)K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$

Let H_n(D_i, D_j) = [W_n(D_i, D_j)+W_n(D_j, D_i)]/2, then U_n = [n(n − 1)]⁻¹ ΣΣ_i≠j H_n(D_i, D_j) has the form of a generalized U-statistic. Note that $E[\mid \mid H_n(D_i,D_j)\mid {\mid }^2]\le \frac{1}{2}E[\mid \mid W_n(D_i,D_j)\mid {\mid }^2]+\frac{1}{2}E[\mid \mid W_n(D_i,D_j)\mid {\mid }^2]=E[\mid \mid W_n(D_i,D_j)\mid {\mid }^2]$. Furthermore,

$$\begin{array}{l}E[\mid \mid W_n(D_i,D_j)\mid {\mid }^2]\\ \le 4h^{-4}E\left\{[{({\mathbf{Z}}_i-{\mathbf{Z}}_j)}^T({\mathbf{Z}}_i-{\mathbf{Z}}_j)+{[(U_i-U_j)/h]}^2]K^2\left(\frac{U_i-u_0}{h}\right)K^2\left(\frac{U_j-u_0}{h}\right)\right\}\\ =O(h^{-2})=o(n)\text{since}n{h}^2\to \infty \text{by}\text{assumption.}\end{array}$$

Thus U_n = E[H_n(D_i, D_j)] + o_p(1) by Lemma A.1. Furthermore,

$$\begin{array}{l}E[H_n(D_i,D_j)]\\ =2h^{-2}E\{\int [G(\epsilon +{\mathrm{\Delta }}_j(u_0)-{\mathrm{\Delta }}_i(u_0)-{\gamma }_n{\alpha }_2^{\ast }(U_j-U_i)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}({\mathbf{Z}}_j-{\mathbf{Z}}_i))-G(\epsilon )]g(\epsilon )d\epsilon \\ \left(\begin{array}{c}{\mathbf{Z}}_i-{\mathbf{Z}}_j\\ (U_i-U_j)/h\end{array}\right)K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\}\\ =2h^{-2}{\gamma }_{n}E\{\int g[\epsilon +{\mathrm{\Delta }}_j(u_0)-{\mathrm{\Delta }}_i(u_0)]g(\epsilon )d\epsilon \left(\begin{array}{c}{\mathbf{Z}}_i-{\mathbf{Z}}_j\\ (U_i-U_j)/h\end{array}\right)({\mathbf{Z}}_i^T-{\mathbf{Z}}_j^T,(U_i-U_j)/h)\\ K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\}\left(\begin{array}{c}{\mathit{\beta }}^{\ast }\\ {\alpha }_2^{\ast }\end{array}\right)(1+o(1))={\gamma }_n{\mathbf{A}}_n\left(\begin{array}{c}{\mathit{\beta }}^{\ast }\\ {\alpha }_2^{\ast }\end{array}\right)\{1+o(1)\}.\end{array}$$

The proof is completed by using Lemma A.2.

Proof of Lemma 3.1

In view of Lemma A.3, it follows that

$$\nabla [{\gamma }_n^{-1}{Q}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })-B_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })]={\gamma }_n^{-1}[S_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })-S_n(\mathbf{0},0)]-{\gamma }_n\mathbf{A}\left(\begin{array}{c}{\mathit{\beta }}^{\ast }\\ {\alpha }_2^{\ast }\end{array}\right)=o_p(1).$$

The proof follows along the same lines of the proof of Theorem A.3.7. of Hettmansperger and McKean (1998), using a “diagonal subsequencing” argument and convexity.

Proof of Theorem 3.2

By Lemma 3.1, ${\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)=B_n({\mathbf{s}}_1,s_2)+r_n({\mathbf{s}}_1,s_2)$, where $r_n({\mathbf{s}}_1,s_2)\stackrel{p}{\to }0$ uniformly over any bounded set. Note that ${\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)$ is minimized by ${({\widehat{\mathit{\beta }}}_n^{\ast T},{\widehat{\alpha }}_{2n}^{\ast })}^T$, and B_n(s₁, s₂) is minimized by ${({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })}^T=-{\gamma }_n^{-2}{\mathbf{A}}^{-1}{(S_{n1}^T(\mathbf{0},0),S_{n2}(\mathbf{0},0))}^T$. We first establish the asymptotic representation by following similar argument as in Hjort and Pollard (1993). For any constant c > 0, define

$$\begin{array}{l}{T}_n=\underset{\mid \mid ({\mathbf{s}}_1^T,s_2)-({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\mid \mid =c}{inf}{B}_n({\mathbf{s}}_1,s_2)-B_n({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\\ R_n=\underset{\mid \mid ({\mathbf{s}}_1^T,s_2)-({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\mid \mid \le c}{sup}\mid {\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)-B_n({\mathbf{s}}_1,s_1)\mid ,\end{array}$$

then $R_n\stackrel{p}{\to }0$ as n → ∞. Let ${({\mathbf{s}}_1^T,s_2)}^T$ be an arbitrary point outside the ball { ${({\mathbf{s}}_1^T,s_2)}^T:\mid \mid ({\mathbf{s}}_1^T,s_2)-({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\mid \mid \le c$}, then we can write ${({\mathbf{s}}_1^T,s_2)}^T={({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })}^T+l{\mathbf{1}}_{2p+1}$, where l > c is a positive constant and 1_d denotes a unit vector of length d. Write

$$\frac{c}{l}[{\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)-{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })]=\frac{c}{l}{\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)+\left(1-\frac{c}{l}\right){\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })-{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast }).$$

By the convexity of ${\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)$, we have

$$\frac{c}{l}[{\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)-{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })]\ge {\gamma }_n^{-1}{Q}_n^{\ast }\left(\frac{c}{l}({\mathbf{s}}_1,s_2)+\left(1-\frac{c}{l}\right)({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\right)-{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast }).$$

Thus,

$$\begin{array}{l}\frac{c}{l}[{\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)-{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })]\ge {\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast }+c{\mathbf{1}}_{2p},{\stackrel{\sim }{\alpha }}_{2n}^{\ast }+c)-{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\\ =B_n({\stackrel{\sim }{\beta }}_n^{\ast }+c{\mathbf{1}}_{2p},{\stackrel{\sim }{\alpha }}_{2n}^{\ast }+c)+r_n({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast }+c{\mathbf{1}}_{2p},{\stackrel{\sim }{\alpha }}_{2n}^{\ast }+c)-B_n({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })-r_n({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })\\ \ge T_n-2R_n.\end{array}$$

If $R_n\le \frac{1}{2}{T}_n$, then ${\gamma }_n^{-1}{Q}_n^{\ast }({\mathbf{s}}_1,s_2)>{\gamma }_n^{-1}{Q}_n^{\ast }({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast },{\stackrel{\sim }{\alpha }}_{2n}^{\ast })$ for all ${({\mathbf{s}}_1^T,s_2)}^T$ outside the ball. This implies if $R_n\le \frac{1}{2}{T}_n$ then the minimizer of ${\gamma }_n^{-1}{Q}_n^{\ast }$ must be inside the ball. Thus

$$P\left(\mid \mid {({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })}^T-{({\widehat{\mathit{\beta }}}_n^{\ast T},{\widehat{\alpha }}_{2n}^{\ast })}^T\mid \mid \ge c\right)\le P\left(R_n\ge \frac{1}{2}{T}_n\right)=P\left(R_n\ge \frac{1}{2}\lambda c^2\right)\to 0,$$

where λ is the smallest eigenvalue of A. Therefore, ${({\widehat{\mathit{\beta }}}_n^{\ast T},{\widehat{\alpha }}_{2n}^{\ast })}^T={({\stackrel{\sim }{\mathit{\beta }}}_n^{\ast T},{\stackrel{\sim }{\alpha }}_{2n}^{\ast })}^T+o_p(1)$. This in particular implies the asymptotic representations (9), (11) and (12).

We next show the asymptotic normality of â(u₀). From (9), we have

$$\sqrt{nh}(\widehat{\mathbf{a}}(u_0)-\mathbf{a}(u_0))=-{\gamma }_n^{-2}{(4\tau f^2(u_0)\mathrm{\sum }({\mu }_0))}^{-1}{S}_{n11}(\mathbf{0},0)+o_p(1),$$ (A.1)

where

$$\begin{array}{l}{S}_{n11}(\mathbf{0},0)=2{\gamma }_n{[n(n-1)]}^{-1}\sum _{i\ne j}[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-1/2]({\mathbf{X}}_i-{\mathbf{X}}_j)\\ K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$ (A.2)

By (A.2), let us rewrite $-{\gamma }_n^2{S}_{n11}(\mathbf{0},0)=S_{n\mathbf{a}1}(\mathbf{0},0)+S_{n\mathbf{a}2}(\mathbf{0},0)$, where

$$\begin{array}{l}{S}_{n\mathbf{a}}(\mathbf{0},0)=2{\gamma }_n^{-1}{[n(n-1)]}^{-1}\sum _{i\ne j}[I({\epsilon }_i\le {\epsilon }_j)-1/2]({\mathbf{X}}_j-{\mathbf{X}}_i)K_h(U_i-u_0)K_h(U_j-u_0),\\ S_{n\mathbf{b}}(\mathbf{0},0)=2{\gamma }_n^{-1}{[n(n-1)]}^{-1}\sum _{i\ne j}[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-I({\epsilon }_i\le {\epsilon }_j)]({\mathbf{X}}_j-{\mathbf{X}}_i)\\ K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$

We next prove that

$$S_{n\mathbf{a}}(\mathbf{0},0)\to N\left(0,\frac{4}{3}{f}^3(u_0){\nu }_0\mathrm{\sum }(u_0)\right)\text{in}\text{distribution}.$$ (A.3)

Note that we can write $S_{n\mathbf{a}}(\mathbf{0},0)=\sqrt{n}{[n(n-1)]}^{-1}{\sum }_{i\ne j}{H}_n(D_i,D_j)$, where H_n(D_i, D_j) =W_n(D_i, D_j) + W_n(D_j, D_i) with

$$W_n(D_i,D_j)=h^{-3/2}[I({\epsilon }_i\le {\epsilon }_j)-1/2]({\mathbf{X}}_j-{\mathbf{X}}_i)K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right).$$

Similarly to the arguments in the proof of Lemma A.3, it can be shown that E[||H_n(D_i, D_j)||²] = o(n). By Lemma A.1, this implies that $S_{n\mathbf{a}}(\mathbf{0},0)=2n^{-1}{\sum }_{i=1}^n{r}_n(D_i)+o_p(1)$ since it is easy to check that r̄_n = 0. We have

$$\begin{array}{l}{r}_n(D_i)=E[H_n(D_i,D_j)\mid D_i]\\ =2h^{-3/2}[G({\epsilon }_i)-1/2]K\left(\frac{U_i-u_0}{h}\right)E\left\{({\mathbf{X}}_i-{\mathbf{X}}_j)K\left(\frac{U_j-u_0}{h}\right)\mid {\mathbf{X}}_i,U_i,{\epsilon }_i\right\}\\ =2h^{-1/2}[G({\epsilon }_i)-1/2]K\left(\frac{U_i-u_0}{h}\right)[\left(\int K(t)f(u_0+th)dt\right){\mathbf{X}}_i\\ -\int E(X_j\mid U_j=u_0+th)K(t)f(u_0+th)dt].\end{array}$$

Furthermore,

$$\begin{array}{l}E[r_n(D_i)r_n{(D_i)}^T]\\ =\frac{1}{3}{h}^{-1}E\{K^2\left(\frac{U_i-u_0}{h}\right)[\left(\int K(t)f(u_0+th)dt\right){\mathbf{X}}_i\\ -\int E(X_j\mid U_j=u_0+th)K(t)f(u_0+th)dt]\\ \left[\left(\int K(t)f(u_0+th)dt\right){\mathbf{X}}_i^T-\int E(X_j^T\mid U_j=u_0+th)K(t)f(u_0+th)dt\right]\}\\ \to \frac{1}{3}{f}^3(u_0){\nu }_0\mathrm{\sum }(u_0).\end{array}$$

To prove the asymptotic normality of S_na(0, 0), it is sufficient to check the Lindeberg-Feller condition: ∀ ε > 0, $n^{-1}{\sum }_{i=1}^{n}E\{r_n(D_i)r_n{(D_i)}^{T}I(\mid \mid r_n(D_i)\mid \mid >\epsilon \sqrt{n})\}\to 0$. This can be easily verified by applying the dominated convergence theorem. Next we show that

$$S_{n\mathbf{b}}(\mathbf{0},0)=\frac{2h^2}{{\gamma }_n}[\tau f^2(u_0){\mu }_2\mathrm{\sum }(u_0){\mathbf{a}}^{″}(u_0)+o(1)]+o_p(1).$$ (A.4)

We may write $S_{n\mathbf{b}}(\mathbf{0},0)={[n(n-1)]}^{-1}{\sum }_{i\ne j}{H}_n^{\ast }(D_i,D_j)$, where $H_n^{\ast }(D_i,D_j)=W_n^{\ast }(D_i,D_j)+W_n^{\ast }(D_j,D_i)$ with

$$\begin{array}{l}{W}_n^{\ast }(D_i,D_j)=n{h}^{-1}{\gamma }_n[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-I({\epsilon }_i\le {\epsilon }_j)]({\mathbf{X}}_j-{\mathbf{X}}_i)\\ K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right).\end{array}$$

Note that

$$\begin{array}{l}{\mathrm{\Delta }}_j(u_0)-{\mathrm{\Delta }}_i(u_0)\\ =\frac{1}{2}[{(U_j-u_0)}^2{\mathbf{X}}_j^T-{(U_i-u_0)}^2{\mathbf{X}}_i^T]{\mathbf{a}}^{″}(u_0)+\frac{1}{2}[{(U_j-u_0)}^2-{(U_i-u_0)}^2]a_0^{″}(u_0)\\ +o({(U_i-u_0)}^2)+o({(U_j-u_0)}^2).\end{array}$$

By applying Lemma A.1, it can be shown that $S_{n\mathbf{b}}(\mathbf{0},0)=E[H_n^{\ast }(D_i,D_j)]+o_p(1)$. It follows by using the same arguments as those in the proof of Lemma A.2 that

$$\begin{array}{l}E[H_n^{\ast }(D_i,D_j)]\\ =2n{h}^{-1}{\gamma }_{n}E\{\int [G(\epsilon +{\mathrm{\Delta }}_j(u_0)-{\mathrm{\Delta }}_i(u_0))-G(\epsilon )]g(\epsilon )d\epsilon \\ ({\mathbf{X}}_j-{\mathbf{X}}_i)K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\}\\ =2n{h}^{-1}{\gamma }_n[\tau +O(h)]E\left[({\mathrm{\Delta }}_j(u_0)-{\mathrm{\Delta }}_i(u_0))({\mathbf{X}}_j-{\mathbf{X}}_i)K\left(\frac{U_i-u_0}{h}\right)K\left(\frac{U_j-u_0}{h}\right)\right](1+o(1))\\ =\frac{2h^2}{{\gamma }_n}[\tau f^2(u_0){\mu }_2\mathrm{\sum }(u_0){\mathbf{a}}^{″}(u_0)+o(1)].\end{array}$$

This proves (A.4). By combining (A.3) and (A.4) and using the approximation given in (A.1), we obtain (10).

Proof of Theorem 3.3

A result of Hodges and Lehmann (1956) indicates that the ARE has a lower bound 0.864^4/5 = 0.8896, with this lower bound being attained at the density $f(t)=\frac{3}{20\sqrt{5}}(5-x^2)I(\mid x\mid \le 5)$.

Proof of Theorem 3.4

Let

$$\begin{array}{l}{V}_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)\\ ={(nh)}^{-1}\sum _{i=1}^n|{\epsilon }_i-{\gamma }_n{\alpha }_1^{\ast }-{\xi }_1(U_i-u_0)-{\mathit{\xi }}_2^T{\mathbf{X}}_i-{\mathit{\xi }}_3^T(U_i-u_0){\mathbf{X}}_i+{\mathrm{\Delta }}_i(u_0)|K\left(\frac{U_i-u_0}{h}\right),\end{array}$$

where ${\alpha }_1^{\ast }={\gamma }_n^{-1}({\alpha }_1-a_0(u_0))$, ξ₁ ∈ ℝ, ξ₂ ∈ ℝ^p and ξ₃ ∈ ℝ^p. The subgradient of $V_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)$ with respect to ${\alpha }_1^{\ast }$ is

$$\begin{array}{l}{S}_n^{\ast }({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)\\ =\frac{2{\gamma }_n}{nh}\sum _{i=1}^n\left[I({\epsilon }_i\le {\gamma }_n{\alpha }_1^{\ast }+{\xi }_1(U_i-u_0)+{\mathit{\xi }}_2^T{\mathbf{X}}_i+{\mathit{\xi }}_3^T(U_i-u_0){\mathbf{X}}_i-{\mathrm{\Delta }}_i(u_0))-1/2\right]K\left(\frac{U_i-u_0}{h}\right).\end{array}$$

We have $S_n^{\ast }(0,0,\mathbf{0},\mathbf{0})=2{\gamma }_n{(nh)}^{-1}{\sum }_{i=1}^n[I({\epsilon }_i\le {\mathrm{\Delta }}_i(u_0))-1/2]K\left(\frac{U_i-u_0}{h}\right)$, which is the same as the S_n0 defined in (18). Let $U_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)={\gamma }_n^{-1}[S_n^{\ast }({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)-S_n^{\ast }(0,0,\mathbf{0},\mathbf{0})]$, then

$$\begin{array}{l}{U}_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)\\ =2{(nh)}^{-1}\sum _{i=1}^n[I({\epsilon }_i\le {\gamma }_n{\alpha }_1^{\ast }+{\xi }_1(U_i-u_0)+{\mathit{\xi }}_2^T{\mathbf{X}}_i+{\mathit{\xi }}_3^T(U_i-u_0){\mathbf{X}}_i-{\mathrm{\Delta }}_i(u_0))\\ -I({\epsilon }_i\le {\mathrm{\Delta }}_i(u_0))]K\left(\frac{U_i-u_0}{h}\right).\end{array}$$

For any positive constants c_i, i = 1, 2, 3 and ∀ ξ₁, ξ₂, ξ₃ such that ||ξ₁|| ≤ c₁h⁻¹γ_n, ||ξ₂|| ≤ c₂γ_n and ||ξ₃|| ≤ c₃h⁻¹γ_n, we have

$$U_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)=2{\gamma }_{n}g(0)f(u_0){\alpha }_1^{\ast }+o_p(1).$$ (A.5)

This can be proved by directly checking the mean and variance. More specifically,

$$\begin{array}{l}E[U_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)]\\ =2h^{-1}E\{[G({\gamma }_n{\alpha }_1^{\ast }+{\xi }_1(U_i-u_0)+{\mathit{\xi }}_2^T{\mathbf{X}}_i+{\mathit{\xi }}_3^T(U_i-u_0){\mathbf{X}}_i-{\mathrm{\Delta }}_i(u_0))\\ -G(-{\mathrm{\Delta }}_i(u_0))]K\left(\frac{U_i-u_0}{h}\right)\}\\ =2h^{-1}g(0)E\left\{\left[{\gamma }_n{\alpha }_1^{\ast }+{\xi }_1(U_i-u_0)+{\mathit{\xi }}_2^T{\mathbf{X}}_i+{\mathit{\xi }}_3^T(U_i-u_0){\mathbf{X}}_i\right]K\left(\frac{U_i-u_0}{h}\right)\right\}(1+O(h))\\ =2{\gamma }_{n}g(0)f(u_0){\alpha }_1^{\ast }(1+O(h)).\end{array}$$

And

$$\begin{array}{l}\mathit{Var}[U_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)]\\ \le 4n^{-1}{h}^{-2}E\{[I({\epsilon }_i\le {\gamma }_n{\alpha }_1^{\ast }+{\xi }_1(U_i-u_0)+{\mathit{\xi }}_2^T{\mathbf{X}}_i+{\mathit{\xi }}_3^T(U_i-u_0){\mathbf{X}}_i-{\mathrm{\Delta }}_i(u_0))\\ {-I({\epsilon }_i\le {\mathrm{\Delta }}_i(u_0))]}^2{K}^2\left(\frac{U_i-u_0}{h}\right)\}\\ \le 4n^{-1}{h}^{-2}E\left\{K^2\left(\frac{U_i-u_0}{h}\right)\right\}=O(n^{-1}{h}^{-1})=o(1).\end{array}$$

By (A.5) and similar proof as that for Lemma 3.1, we have

$${\gamma }_n^{-1}{V}_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)=V_n^{\ast }({\alpha }_1^{\ast })+o_p(1),$$ (A.6)

where $V_n^{\ast }({\alpha }_1^{\ast })={\gamma }_n^{-1}{S}_n^{\ast }(0,0,\mathbf{0},\mathbf{0}){\alpha }_1^{\ast }+{\gamma }_{n}g(0)f(u_0){\alpha }_1^{\ast 2}+{\gamma }_n^{-1}{V}_n(0,0,\mathbf{0},\mathbf{0})$. Because the function $V_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)$ is convex in its arguments, (A.6) can be strengthened to uniform convergence (convexity lemma, see Pollard 1991), i.e.,

$$\underset{\begin{array}{l}{\alpha }_1^{\ast }\in \mathbb{C},\mid \mid {\xi }_1\mid \mid \le c_1{h}^{-1}{\gamma }_n\\ \mid \mid {\mathit{\xi }}_2\mid \mid \le c_2{\gamma }_n,\mid \mid {\mathit{\xi }}_3\mid \mid \le c_3{h}^{-1}{\gamma }_n\end{array}}{sup}\mid {\gamma }_n^{-1}{V}_n({\alpha }_1^{\ast },{\xi }_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3)-V_n^{\ast }({\alpha }_1^{\ast })\mid =o_p(1),$$

where ℂ is a compact set in ℝ. By Theorem 3.2, ${\widehat{\alpha }}_2-{\alpha }_0^{\prime }(u_0)=O_p(h^{-1}{\gamma }_n)$, â(u₀) − a(u₀) = O_p(γ_n) and â′ (u₀) − a′(u₀) = O_p(h⁻¹γ_n), we thus have

$$\underset{{\alpha }_1^{\ast }\in \mathbb{C}}{sup}\left|{\gamma }_n^{-1}{V}_n({\alpha }_1^{\ast },{\widehat{\alpha }}_2-a_0^{\prime }(u_0),\widehat{\mathbf{a}}(u_0)-\mathbf{a}(u_0),{\widehat{\mathbf{a}}}^{\prime }(u_0)-{\mathbf{a}}^{\prime }(u_0))-V_n^{\ast }({\alpha }_1^{\ast })\right|=o_p(1).$$

Note that $V_n({\alpha }_1^{\ast },{\widehat{\alpha }}_2-a_0^{\prime }(u_0),\widehat{\mathbf{a}}(u_0)-\mathbf{a}(u_0),{\widehat{\mathbf{a}}}^{\prime }(u_0)-{\mathbf{a}}^{\prime }(u_0))=Q_{n0}^{\ast }({\alpha }_1^{\ast },{\widehat{\alpha }}_2,\widehat{\mathit{\beta }}),S_n^{\ast }(0,0,\mathbf{0},\mathbf{0})=S_{n0}$, where $Q_{n0}^{\ast }$ and S_n0 are defined in Section 2.4. The quadratic function $V_n^{\ast }({\alpha }_1^{\ast })$ is minimized by ${\stackrel{\sim }{\alpha }}_{1n}^{\ast }=\frac{1}{2}{\gamma }_n^{-2}{[g(0)f(u_0)]}^{-1}{S}_{n0}$. Similar argument as that for Theorem 3.2 shows that ${\widehat{\alpha }}_{1n}^{\ast }={\stackrel{\sim }{\alpha }}_{1n}^{\ast }+o_p(1)$. Thus we have (19). We can write ${\gamma }_n^{-2}{S}_{n0}=T_{1n}+T_{2n}$, where

$$\begin{array}{l}{T}_{1n}=\frac{2{\gamma }_n^{-1}}{nh}\sum _{i=1}^n[I({\epsilon }_i\le 0)-1/2]K\left(\frac{U_i-u_0}{h}\right),\\ T_{2n}=\frac{2{\gamma }_n^{-1}}{nh}\sum _{i=1}^n[I({\epsilon }_i\le -{\mathrm{\Delta }}_i(u_0))-I({\epsilon }_i\le 0)]K\left(\frac{U_i-u_0}{h}\right).\end{array}$$

By the Lindeberg-Feller central limit theorem, T_1n → N (0, f (u₀)ν₀/3) in distribution. By checking mean and variance, we have

$$T_{2n}=-\frac{h^2}{{\gamma }_n}g(0)f(u_0)a_0^{″}(u_0){\mu }_2(1+o(1))+o_p(1).$$

Combining the above results and using (19), the proof is completed.

To prove Theorem 3.5, we first extend Lemma A.1 to almost sure convergence.

Lemma A.4

If E[||H_n(D_i, D_j)||²] = O(h⁻²), then U_n − Û_n = o(1) almost surely and U_n = r̄_n + o(1) a.s.

Proof

The proof of Powell, Stock and Stoker (1989) for Lemma A.1 suggests that E[||U_n − Û_n||²] = O(n⁻²h⁻²). By Theorem 1.3.5 of Serfling (1980), ${\sum }_{i=1}^{n}E[\mid \mid U_n-{\widehat{U}}_n\mid {\mid }^2]=O(n^{-1}{h}^{-2})<\infty$. This implies that U_n − Û_n = o(1) almost surely. The second result follows by an application of the strong law of large numbers to Û_n.

Proof of Theorem 3.5

Let β* and ${\alpha }_2^{\ast }$ be defined the same as before. We introduce the reparametrized objective function ${\overline{Q}}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$. Let ${\overline{S}}_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })={({\overline{S}}_{n1}^T({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast }),{\overline{S}}_{n2}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast }))}^T$ denote the gradient function of ${\overline{Q}}_n^{\ast }({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$, which is defined similarly as in Section 2.2. We first show that ${\overline{S}}_n({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$ has a similar local linear approximation as stated in Lemma A.3. To make the proof concise, we prove this for ${\overline{S}}_{n1}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$, where

$$\begin{array}{l}{\overline{S}}_{n1}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })\\ =2{\gamma }_n{[n(n-1)]}^{-1}\sum _{i\ne j}(V_i+V_j)[I({\epsilon }_i-{\gamma }_n{\alpha }_2^{\ast }(U_i-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j\\ -{\gamma }_n{\alpha }_2^{\ast }(U_j-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_j+{\mathrm{\Delta }}_j(u_0))-1/2]({\mathbf{Z}}_i-{\mathbf{Z}}_j)K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$

Let $U_n={\gamma }_n^{-1}[{\overline{S}}_{n1}({\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })-{\overline{S}}_{n1}(\mathbf{0},0)]={[n(n-1)]}^{-1}{\sum }_{i\ne j}(V_i+V_j)M_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })$, where $M_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })=\frac{1}{2}[m_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })+m_n(D_j,D_i,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })]$ and

$$\begin{array}{l}{m}_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })\\ =2[I({\epsilon }_i-{\gamma }_n{\alpha }_2^{\ast }(U_i-u_0)/h-{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j-{\gamma }_n{\alpha }_2^{\ast }(U_j-u_0)/h\\ -{\gamma }_n{\mathit{\beta }}^{\ast T}{\mathbf{Z}}_j+{\mathrm{\Delta }}_j(u_0))-1/2]({\mathbf{Z}}_i-{\mathbf{Z}}_j)K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$

Note that $U_n=2n^{-1}{\sum }_{i=1}^n{V}_i[{(n-1)}^{-1}{\sum }_{j=1,j\ne i}^n{M}_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })]$. Conditional on ${\left\{D_i\right\}}_{i=1}^n$, this is a weighted average of V_i. Note that

$$\begin{array}{l}E(U_n\mid {\left\{D_i\right\}}_{i=1}^n)={[n(n-1)]}^{-1}\sum _{i\ne j}{M}_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast }).\\ \mathit{Var}(U_n\mid {\left\{D_i\right\}}_{i=1}^n)=n^{-2}\sum _{i=1}^n{\left[{(n-1)}^{-1}\sum _{j=1,j\ne i}^n{M}_n(d_i,d_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })\right]}^2.\end{array}$$

By Lemma A.4, it can be shown that ${[n(n-1)]}^{-1}{\sum }_{i\ne j}{M}_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })={\gamma }_n{A}^{\ast }{\mathit{\beta }}^{\ast }+o(1)$ almost surely, where A* = 4τf²(u₀)diag(I_p,μ₂I_p) ⊗ Σ(μ₀). It is also easy to check that $n^{-2}{{\sum }_{i=1}^n[{(n-1)}^{-1}{\sum }_{j=1,j\ne i}^n{M}_n(D_i,D_j,{\mathit{\beta }}^{\ast },{\alpha }_2^{\ast })]}^2=o(1)$ almost surely. Thus for almost surely every sequence ${\left\{D_i\right\}}_{i=1}^n$, U_n=γ_nA*β*+o_p(1), where o_p(1) is in the probability space generated by ${\left\{V_i\right\}}_{i=1}^n$. The proofs of Lemma 3.1 and the asymptotic representation in Theorem 3.2 can be similarly carried out to show that for almost surely every sequence ${\left\{D_i\right\}}_{i=1}^n$,

$$\sqrt{nh}[{\overline{\mathbf{a}}}_n(u_0)-\mathbf{a}(u_0)]=-{\gamma }_n^{-2}{(4\tau f^2(u_0)\mathrm{\sum }({\mu }_0))}^{-1}{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)+o_p(1),$$ (A.7)

where o_p(1) is in the probability space generated by ${\left\{V_i\right\}}_{i=1}^n$, and

$$\begin{array}{l}{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)=2{\gamma }_n{[n(n-1)]}^{-1}\sum _{i\ne j}(V_i+V_j)[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-1/2]\\ ({\mathbf{X}}_i-{\mathbf{X}}_j)K_h(U_i-u_0)K_h(U_j-u_0).\end{array}$$

The approximation (A.1) can be strengthened to almost surely convergence, i.e.,

$$\sqrt{nh}[{\widehat{\mathbf{a}}}_n(u_0)-\mathbf{a}(u_0)]=-{\gamma }_n^{-2}{(4\tau f^2(u_0)\mathrm{\sum }({\mu }_0))}^{-1}{S}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)+o(1)\text{a}.\text{s}\mathrm{..}$$ (A.8)

Combining (17) and (A.7), we have that for almost surely every sequence ${\left\{D_i\right\}}_{i=1}^n$,

$$\sqrt{nh}[{\overline{\mathbf{a}}}_n(u_0)-{\widehat{\mathbf{a}}}_n(u_0)]=-{\gamma }_n^{-2}{(4\tau f^2(u_0)\mathrm{\sum }({\mu }_0))}^{-1}[{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)-S_{n\mathbf{a}}^{\ast }(\mathbf{0},0)]+o_p(1).$$

Note that

$$\begin{array}{l}{\gamma }_n^{-2}[{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)-S_{n\mathbf{a}}^{\ast }(\mathbf{0},0)]\\ =2{\gamma }_n^{-1}{[n(n-1)]}^{-1}\sum _{i\ne j}[(V_i-1/2)+(V_j-1/2)][I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-1/2]\\ ({\mathbf{X}}_i-{\mathbf{X}}_j)K_h(U_i-u_0)K_h(U_j-u_0)\\ =4{\gamma }_n^{-1}{n}^{-1}\sum _{i=1}^n(V_i-1/2)\{{(n-1)}^{-1}\sum _{j=1,j\ne i}^n[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-1/2]\\ ({\mathbf{X}}_i-{\mathbf{X}}_j)K_h(U_i-u_0)K_h(U_j-u_0)\}.\end{array}$$

And $E\left\{{\gamma }_n^{-2}[{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)-S_{n\mathbf{a}}^{\ast }(\mathbf{0},0)]\mid {\left\{D_i\right\}}_{i=1}^n\right\}=\mathbf{0}$. We have

$$\begin{array}{l}\mathit{Var}\left\{{\gamma }_n^{-2}[{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)-S_{n\mathbf{a}}^{\ast }(\mathbf{0},0)]\mid {\left\{D_i\right\}}_{i=1}^n\right\}\\ =16{\gamma }_n^{-2}{n}^{-2}{(n-1)}^2\sum _{i=1}^n\{\sum _{j=1,j\ne i}^n[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-1/2)]\\ {({\mathbf{X}}_i-{\mathbf{X}}_j)K_h(U_i-u_0)K_h(U_j-u_0)\}}^2\\ =W_1+W_2,\end{array}$$

where

$$\begin{array}{l}{W}_1=16{\gamma }_n^{-2}{n}^{-2}{(n-1)}^2{h}^{-4}\sum _{i=1}^n\sum _{j=1,j\ne i}^n{[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_j+{\mathrm{\Delta }}_j(u_0))-1/2]}^2\\ ({\mathbf{X}}_i-{\mathbf{X}}_j){({\mathbf{X}}_i-{\mathbf{X}}_j)}^T{K}^2((U_i-u_0)/h)K^2((U_j-u_0)/h),\\ W_2=16{\gamma }_n^{-2}{n}^{-2}{(n-1)}^2{h}^{-4}\sum _{i=1}^n\sum _{j_1\ne i}^n\sum _{j_2\ne i,j_1}^n[I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_{j_1}+{\mathrm{\Delta }}_{j_1}(u_0))-1/2]\\ [I({\epsilon }_i+{\mathrm{\Delta }}_i(u_0)\le {\epsilon }_{j_2}+{\mathrm{\Delta }}_{j_2}(u_0))-1/2]({\mathbf{X}}_i-{\mathbf{X}}_{j_1}){({\mathbf{X}}_i-{\mathbf{X}}_{j_2})}^T\\ K^2((U_i-u_0)/h)K((U_{j_1}-u_0)/h)K((U_{j_2}-u_0)/h).\end{array}$$

Lemma A.4 can be used to show that W₁ = o(1) almost surely; and a minor extension of Lemma A.4 to third-order U-statistic can be used to show that $W_2=\frac{4}{3}{f}^3(u_0){\nu }_0\mathrm{\sum }(u_0)+o(1)$ almost surely. The asymptotic normality of ${\gamma }_n^{-2}[{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)-S_{n\mathbf{a}}^{\ast }(\mathbf{0},0)]$ follows by showing that the condition of Lindeberg-Feller central limit theorem for triangular arrays holds almost surely. We have, for almost surely every sequence ${\left\{D_i\right\}}_{i=1}^n$,

$${\gamma }_n^{-2}[{\overline{S}}_{n\mathbf{a}}^{\ast }(\mathbf{0},0)-S_{n\mathbf{a}}^{\ast }(\mathbf{0},0)]\to N\left(\mathbf{0},\frac{4}{3}{f}^3(u_0){\nu }_0\mathrm{\sum }(u_0)\right)$$

in distribution. This completes the proof.